Abstract
We demonstrate mid-infrared dual-comb spectroscopy with an optical parametric oscillator (OPO) toward real-time field measurement. A singly resonant OPO based on a MgO-doped periodically poled lithium niobate (PPLN) crystal is demonstrated. Chirped mirrors are used to compensate the dispersion caused by the optical cavity and the crystal. A low threshold of 17 mW has been achieved. The OPO source generates a tunable idler frequency comb between 2.7 and 4.7 μm. Dual-comb spectroscopy is achieved by coupling two identical Yb-fiber mode-locked lasers to this OPO with slightly different repetition frequencies. A measured absorption spectrum of methane is presented with a spectral bandwidth of \(300\,\hbox {cm}^{-1}\), giving an instrumental resolution of \(0.4\,\hbox {cm}^{-1}\). In addition, a second OPO containing two MgO-doped PPLN crystals in a singly resonant ring cavity is demonstrated. As such, this OPO generates two idler combs (average power up to 220 mW), covering a wavelength range between 2.7 and 4.2 μm, from which a mid-infrared dual-comb Fourier transform spectrometer is constructed. By detecting the heterodyned signal between the two idler combs, broadband spectra of molecular gases can be observed over a spectral bandwidth of more than \(350\,\hbox {cm}^{-1}\). This special cavity design allows the spectral resolution to be improved to \(0.2\,\hbox {cm}^{-1}\) without locking the OPO cavity, indicating that this OPO represents an ideal high-power broadband mid-infrared source for real-time gas sensing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Laser absorption spectroscopy plays an important role in a variety of applications including industrial processing control, biomedical research, frequency metrology, and environmental monitoring. Due to the development of new laser sources and novel technologies, measurement performances continue to improve dramatically in terms of sensitivity, signal-to-noise ratio (SNR), spectrum bandwidth, frequency accuracy, and acquisition speed. Although the research on laser spectroscopy flourishes, it is still a challenge to achieve high-performance broadband measurements in a single experiment over a second timescale. Conventionally, Fourier transform spectroscopy (FTS) is the solution for such broadband measurements, from visible to far-infrared [1]. However, due to the moving mechanical part in the spectrometer and the low brightness of the light source, minutes to hours acquisition time is needed to reach a high spectral resolution and high SNR. On the other hand, wavelength modulation and frequency modulation spectroscopy based on continuous-wave (CW) lasers are typical techniques for sensitive trace gas detection with possible measurement time of 1 s. However, within these approaches, only a small portion of the wavelength region can be covered, limiting these methods for real-time applications of multi-gas detection [2]. Since its invention in the late 1990s, frequency combs have revolutionized optical frequency metrology [3], but also provide new opportunities for other applications, especially for gas detection based on laser absorption spectroscopy [4]. A single optical frequency comb source can be treated as a coherent superposition of hundreds of thousands of CW lasers, and it is noted to be an ideal source for laser spectroscopy in terms of high spectral power, broad spectral bandwidth, high coherence, and frequency accuracy [5]. Several demonstrations of direct frequency comb spectroscopy (DFCS) have been reported, employing a single frequency comb laser source combined with various detection methods [6–15]. Among them, a quantum-noise-limited absorption sensitivity of \(1.7 \, \times 10^{-12}\,\hbox {cm}^{-1}\) per spectral element at 400 s of acquisition time is achieved, based on a cavity-enhanced DFCS combined with a fast-scanning Fourier transform spectrometer [8]. The development of dual-comb FTS overcomes the disadvantages caused by the moving mechanical part in a conventional FTS and gives an opportunity for simultaneous measurement of dispersion and absorption spectra of gas samples [16–22]. Due to the requirement of optical frequency stability, most experimental work on frequency comb sources has been performed in metrology laboratories. Although the operation of an optically coherent frequency comb outside the metrology laboratory has been demonstrated [23], it is still a long way before dual-comb spectroscopy could be used in realistic field measurements. One proposed solution is adaptive real-time dual-comb spectroscopy, which opens a door for real-time field measurement [24]. In this case, tight locking of both dual-comb sources is not needed due to the applied phase correction of the recorded interferogram and compensation for the jittering of the repetition frequencies. The advantage is that an alignment-free averaging process of the retrieved spectra is allowed and that the complexity of the signal processing is simplified, increasing the SNR dramatically. As such, most demonstrations of this technique have been done in near-infrared region.
Extension of the wavelength region of the optical frequency comb source is an ongoing research field for different applications both in industrial and in academic fields, as most commercial frequency comb sources cannot go beyond 2 μm. To date, frequency comb sources can be extended to the extreme ultraviolet [6], mid-infrared [25–31], and terahertz regions [32, 33]. Specifically, for trace gas sensing applications, the wavelength region between 2 and 20 μm is of great interest, as gases, liquids, and solids have unique absorption and dispersion features in this region, associated with their molecular rotational–vibrational transitions. For mid-infrared dual-comb spectroscopy, the light sources are mainly based on different frequency generation (DFG) and optical parametric oscillation [34–36]. The advantage of DFG sources is that the offset frequency of the comb is passively locked to zero and that only the stabilization of the repetition frequency needs to be considered for mid-infrared frequency comb generation. DFG-based dual-comb systems have provided accurate spectral measurements around 3.4 μm [34]. However, microwatt power levels and the relatively narrow spectral bandwidth of the DFG source can limit its spread in applications such as real-time multi-compound detection in complex gas mixtures. In addition, it is not possible to lock the DFG comb source to a cavity to increase the sensitivity.
In this paper, we demonstrate two different OPO-based dual-comb systems, both offering hundreds of milli-Watts of mid-infrared output power. Both systems have high potential to be integrated to a cavity-enhanced method, to increase the detection sensitivity [15, 37]. The two-crystal OPO cavity has shown to be a reliable source for rapid broadband, and mid-infrared absorption and dispersion measurements.
2 Theories
2.1 Dual-comb Fourier transform spectroscopy
The method of dual-comb spectroscopy has been proposed by Schiller [16] in 2002. Similar to the conventional Fourier transform spectrometer, the approach is based on the principle of down-converting optical frequencies, but without any moving mechanical components. The principle of the spectrometer, depicted in Fig. 1, involves two comb sources with slightly different repetition frequencies (\(f_{\rm rep,1}\) and \(f_{\rm rep,2}\)). For simplicity, assume that \(f_{\rm rep,1} > f_{\rm rep,2}\) and \(f_{\rm rep,1} = f_{\rm rep,2} + \delta\). One source (comb 1) is used to probe a gas sample. Afterward, it is combined with the second comb source on a beam splitter. The heterodyned signal is therefore a comb in the radio frequency domain, which can be detected with a fast infrared detector. The acquired signal in the time domain is called an interferogram. The complex spectra containing the absorption and dispersion information of the gas sample are obtained by performing fast Fourier transform (FFT) algorithm. The frequency representations of the two frequency combs are given by:
in which \(n\) stands for the mode number of the comb line; \(f_{\rm rep,k}\) and \(f_{0,k}\) are the repetition frequency and offset frequency of comb \(k\) (\(k = 1,2\)), respectively. The electric field for each comb can be expressed as:
\(A_{n,k}\) is the amplitude of the \(n\)th mode of the comb source \(k\) and \(c.c\) is the conjugate complex. Referring to Fig. 1, Comb 1 experiences both attenuation and phase shift due to absorption and dispersion in the gas sample. These interaction effects induce a factor which can be written as \(e^{-\alpha (f)-i\phi (f)}\), where \(\alpha (f)\) is the amplitude attenuation at frequency \(f\) and \(\phi (f)\) is the phase shift of the electric field. After transmission through the gas cell, the electric field of comb 1 can therefore be expressed as:
where \(\alpha _{n,1}\) and \(\phi _{n,1}\) are, respectively, the attenuation and phase shift that comb 1 experiences at the frequency \(f_n\). The electric field of two sources can be summed up as:
The intensity on the detector will then be as follows:
where \(I_n(t)\) is the intensity measured by the detector if only the beating between one tooth \(n\) of comb 1 with one tooth \(n\) of comb 2 is considered. \(I_n(t)\) can be further expressed as:
From this expression, only the last part is of interest as it contains the full complex spectral information of the targeted sample at different frequencies, while the first sum is projected onto zero frequency. It is also noted that the cosine transformation of the intensity function \(I_n(t)\) can resolve the information of both amplitude attenuation and phase shift. After recording the background signal when the gas cell is empty, the absorption and dispersion spectra of the gas sample can be retrieved.
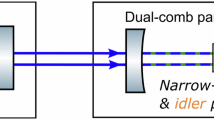
Principle of dual-comb FTS. One frequency comb (comb 1) is passing through a gas cell filled with gas sample and, afterward, interferes with a second frequency comb (comb 2) with a different repetition frequency. The heterodyned signal is detected by a fast infrared detector. This interference down-converts the spectrum from the optical frequency domain to the radio frequency (RF) domain, which is the Fourier transform of the time-domain interferogram. The scaling factor of the down-conversion is dependent on the detuning of the repetition frequencies between the two combs. The absorption and dispersion spectra are revealed by calculating the fast Fourier transform (FFT) of the acquired data
2.2 Femtosecond optical parametric oscillator
Optical parametric oscillators are attractive sources to generate high-power mid-infrared light [38], which is essential for a variety of research areas, such as spectroscopy, semiconductor analysis, photochemistry, and remote sensing. An optical parametric oscillator is a coherent light source based on optical parametric amplification in a specific nonlinear crystal. Figure 2 shows the schematic of a typical femtosecond OPO. A pump photon (pump) is split into two lower-frequency photons (signal and idler) due to the second-order nonlinear susceptibility of the crystal, defined as optical parametric generation (OPG). Combined with an appropriate resonator around the crystal to establish an optical feedback, oscillation can occur for only signal or both signal and idler, resulting in singly or multiply resonant OPOs. Differing from continuous-wave-laser-pumped OPOs, the design of a femtosecond OPO has several special requirements [39, 40]. Firstly, the cavity length of the OPO should match the repetition rate of the pump pulses; in other words, the resonating pulses are passively synchronized to the pump pulses (the cavity length can also be chosen to match a multiple of the repetition rate to generate high-repetition-rate mid-infrared pulses). Secondly, the length of the nonlinear crystal is crucial as there is temporal walk-off between the pump and the signal waves in the crystal; the intra-cavity dispersion caused by the crystal and the mirrors needs to be compensated, since the pulse broadening effect caused by the dispersion reduces the efficiency of the optical parametric oscillation.
Figure 3 gives a simplified representation on how the signal frequencies are generated and synchronized by the pump comb. For simplicity, only three successive comb lines (colored in black, red, and blue) from the pump are drawn. The signal frequencies for perfect phase-matching are presented as the dotted three comb lines, together with their parametric gain bandwidths. In practice, there are hundreds of thousands of signal comb lines and their parametric gain bandwidths which are overlapping. For femtosecond pump lasers, the duration of the pulse for which all combs lines are in phase is tens of femtoseconds, causing MW peak power of the pulse, which is needed for efficient nonlinear generation. In the frequency domain, all the depleted pump comb lines contribute to each individual signal comb line because all of the signal parametric gain bandwidths are overlapped. The free spectral range (FSR) of the OPO is equal to the FSR of the pump, as is the case for a synchronized OPO. The synchronization is inherently determined by the group velocity of the signal pulses, indicating that the signal frequencies can be tuned by changing the cavity length due to the fact that the group velocity is determined by the central wavelength of the signal light. One consequence of this is that a single OPO can be pumped by two mode-locked lasers with slightly different repetition frequencies, as long as the two signals have slightly different group velocities. This difference in group velocities is determined by the difference in central wavelengths between the two pump depletions; hence, it is possible to employ a single OPO for mid-infrared dual-comb spectroscopy. In the following two sections, we introduce two experimental setups with a single OPO for mid-infrared dual-comb spectroscopy.
3 Dual-comb FTS with a single-crystal OPO
3.1 Configuration of the single-crystal OPO
Experimental setup of the singly resonant OPO, \(p,s,i\): pump, signal, and idler beams; \(M1, M2\): curved mirrors (\(R\) = 100 mm); \(f1\): focusing lens (\(f\) = 75 mm); \(f2\): collimating lens (\(f\) = 75 mm); CM1, CM3: chirped mirrors, \(-100\,\hbox {fs}^2\) per bounce at 1,500 nm; CM2, CM4: chirped mirrors, \(20\,\hbox {fs}^2\) per bounce at 1,500 nm
The experimental setup of the OPO is depicted in Fig. 4. The pump laser (Menlo System, Germany) is a femtosecond Yb-fiber laser composed of a seed oscillator, an amplifier, and a compressor, emitting at a central wavelength of 1,040 nm \((9,615\,\hbox {cm}^{-1})\), delivering up to 2 W of average power with 80 fs optical pulse duration \((30\,\hbox {nm}\, \hbox {or}\,275\,\hbox {cm}^{-1}\) spectral width at 1/e value). The repetition frequency of the pump laser (90 MHz) is stabilized by synchronizing its 10th harmonic to a frequency generator (SMB100A), offering a single sideband phase noise of \(-\)128 dBc at 1 GHz. The pump beam is focused onto the PPLN crystal inside the cavity with a focusing lens (\(f\) = 100 mm). The 5-mm-long MgO:PPLN crystal (Covesion, UK) is temperature-stabilized and has nine poling periods, ranging from 27 to 31 μm. Both end facets of the PPLN crystal are anti-reflective (AR) coated (\(R\,<\, 1.5\%\) at 1,064 nm, \(R < 1\%\) at 1,400–1,800 nm, and \(R\, < 6\%\) at 2,600–4,800 nm). The cavity is designed to be synchronously pumped; therefore, the cavity length is about 1.7 m long. The folded X-shape cavity consists of two curved mirrors (radius of curvature 100 mm, AR coated at 1,064 nm and 3,650–4,850 nm, and high-reflective [HR] coated at 1,350–1,500 nm) and four flat, chirped mirrors (HR coated at 1,370–1,750 nm, Layertec GmbH, Germany). To compensate for the group velocity dispersion (GVD) of the signal pulses traveling inside the cavity, introduced by the crystal and the curved mirrors, the chirped mirrors have a second-order dispersion of approximately \(-100\,\hbox {fs}^2\) (CM1 and CM3) and \(20\,\hbox {fs}^2\) (CM2 and CM4) per bounce at 1,500 nm. For each round-trip, they introduce \(-240\,\hbox {fs}^2\) at 1,500 nm. The OPO idler light is emitted collinearly to the residual pump beam, and a dichroic mirror (LaserOptik GmbH, \(R\, >\, 99.9\%\) at 1,064 nm and \(R\,< 1\%\) at 3,200–3,900 nm, not shown in the figure) is used to separate both.
a Spectral intensity distribution of the idler light using seven poling periods, ranging from 27 to 31 μm, resulting in a wavelength coverage between 2750 and 4750 nm. For the various periods, the measured threshold of the OPO is indicated (stars and right axis). b Instant idler wavelength coverage (at a single period of the crystal) for five different cavity lengths changed within a distance of 3 μm
The spectral properties of the OPO are analyzed by a rapid-scanning Fourier transform spectrometer (Bruker Vertex 70), which offers a spectral resolution of \(0.16\,\hbox {cm}^{-1}\) (4.8 GHz). Idler spectra, recorded at a resolution of \(2\,\hbox {cm}^{-1}\), are illustrated in Fig. 5a, for the available seven poling periods of the PPLN crystal. The maximum spectral width of the idler is 300 nm (\(272\,\hbox {cm}^{-1}, \, 1/\hbox {e}\) value), centered at 3.3 μm. In the same panel, the OPO threshold for the different periods is shown. To achieve low threshold with narrow pulse duration, the crystal length and the intra-cavity dispersion management are crucial. The PPLN crystal has very large positive GVD in the signal wavelength region that causes prominent pulse-broadening effects. The GVD mismatch in the crystal between pump and signal pulses also causes a less efficient parametric process for this crystal length. With the 5-mm-long crystal, a very low threshold of 17 mW is obtained around 3.5 μm. With this crystal period and a maximum pump power of 1.6 W, the idler power reaches 250 mW, representing a pump-to-idler conversion efficiency of 16%. At longer wavelengths, the threshold increases, due to the reduced reflectivity of the cavity mirrors for the signal light and the increased absorption in the PPLN crystal [41, 42].
The fastest way to tune the wavelength of the OPO is to change the cavity length. The effect of the cavity length tuning on the optical spectrum is depicted in Fig. 5b. Each spectrum is the instantaneous laser emission for a given crystal period and given cavity length. As the OPO is synchronously pumped by a broadband source, while changing the cavity length over a few microns, the signal (and therefore also the idler) will shift in frequency to maintain the same round-trip time for the pulses in the cavity, corresponding to the repetition rate of the pump source. The variation in the shape of the spectrum has two origins: the variations in the mirror GVD across the tuning range and the lasing effect among various transverse modes within the OPO. Meanwhile, a variety of non-phase-matched, higher-order mixed waves between pump, signal, and idler are emitted along with the signal \((s)\) and idler \((i)\).
3.2 Experimental setup of the FTS
Combining a femtosecond OPO with a Fourier spectrometer shows great ability to record broadband mid-infrared spectra with high SNR. However, recording time and spectral resolution are limited by the features of the spectrometer and such a system may appear bulky or inconvenient for practical applications. The use of mode-locked lasers allows spectra to be recorded using real-time dual-comb spectroscopy. Interferences between two independent laser sources, with slightly different repetition frequencies, provide beat notes in the radio frequency domain, which is a down-converted image of the optical spectrum. The setup of the spectrometer, which has been developed parallel with the work described in [35], is presented in Fig. 6. It consists of two independent femtosecond Yb-fiber lasers pumping a single OPO cavity. The repetition rates of both pump lasers are synchronized to the same frequency generator (\(\hbox {R} \& \hbox {S}\), SMB100A). The repetition rate difference is set to be 185 Hz. As the singly resonant OPO is a passive light converter, the output of the OPO consists of two collinearly overlapped idler beams. Both beams are probing the gas sample before interfering on a single detector (Vigo, PVI-4TE). The interferogram is low-pass filtered (up to 50 MHz) and sample at a frequency of 150 MHz using a fast data acquisition card. A FFT of the recorded signal gives a down-converted image of the optical spectrum.
Experimental setup of the dual-comb spectrometer based on a single OPO. Two Yb-fiber lasers are coupled to a singly resonant OPO. The repetition frequencies of the two lasers have been synchronized with a difference of \(\Delta f_{\rm rep}\, = \, 185\,\hbox {Hz}\). The OPO generates two idler beams probing the sample gas. The heterodyned signal between two idlers can be detected by a single, Peltier-cooled, fast IR detector. The FFT of the interferogram in the RF domain is an image of the recorded optical spectra of both idlers
3.3 Results
Figure 7 is an illustration of the recorded interferogram, and the retrieved spectra are depicted in Fig. 8, obtained when the absorption cell is filled with methane \((\hbox {CH}_4)\) at a concentration of 0.1% in nitrogen (pressure 100 mbar, 30 cm path length). Within 16 μs, a \(300\,\hbox {cm}^{-1}\) wide spectrum was recorded with a spectral resolution of \(0.4\,\hbox {cm}^{-1}\). Taking into account the spectral resolution and recording time, the SNR of a single spectrum (SNR = 8), and the repetition rate difference between the lasers, the noise equivalent absorption sensitivity (1 s averaging per spectral element) is calculated to be \(1.1\times 10^{-5}\,\hbox {cm}^{-1}\,\hbox {Hz}^{-1/2}\) (\(6.1\times 10^{-7}\,\hbox {cm}^{-1}\,\hbox {Hz}^{-1/2}\) considering only the recording time). The spectrum shown in Fig. 8 (blue curve) is obtained by averaging over 26 single-shot spectra, improving the SNR by a factor of 5 (square root of the averaged times) [43]. Although the system gives a potential for application of accurate absorption spectroscopy in the future, the dispersion information of the sample is not accessible. Besides, the visible nonlinear effect when pulses from two mode-locked lasers overlap cannot be avoided. The nonlinear effect can be directly observed from the interferogram in Fig. 7: A slow varying envelope is superimposed on the big burst of the interferogram. To our knowledge, the mechanism of this effect is not fully understood; the distorted interferogram may cause problems for further signal processing. In the following section, a new concept in OPO cavity design is introduced avoiding these issues.
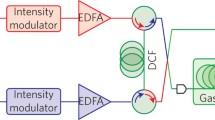
Experimental setup of the dual-comb FTS. Two Yb-fiber mode-locked lasers are coupled to a singly resonant ring cavity OPO. Repetition frequencies are synchronized to a reference frequency synthesizer. The OPO generates two spatially separated idler beams. One idler beam (i1) probes the gas sample in a 10-cm-long single-pass cell (Gas cell) and is recombined with the second idler beam (i2) at the beam splitter. Both overlapped beams are focused, and the heterodyned signal is detected by a Peltier-cooled fast infrared detector. The FFT of the detected signal is calculated by a field-programmable gate array (FPGA) board, giving a spectral image of the gas sample
4 Dual-comb FTS with a two-crystal OPO
4.1 Experimental setup
To solve the issues mentioned in the previous section, a two-crystal OPO within a ring cavity is introduced; more details of this OPO can be found in [36]. Within the OPO, two 5-mm-long PPLN crystals are used for optical frequency conversion to generate two idlers that are spatially separated. To establish the resonance of the signal pulses, a 3.4-m-long cavity composed of six chirped mirrors is designed to be synchronously pumped at 1,040 nm. The spectral range of the idler in this configuration extends from 2,300 to \(3,600 \,\hbox {cm}^{-1}\) by tuning the poling periods of the crystal. The spectral bandwidth for a single period is \(400 \,\hbox {cm}^{-1}\), centered at \(3,080\,\hbox {cm}^{-1}\); at this point, the full range of vibrational transitions of methane can be found.
The experimental setup of the dual-comb spectrometer is shown in Fig. 9. The implementation of the repetition frequency locking is for the sake of long-term frequency stability while the offset frequencies of the two combs are free-running. The repetition frequencies of the two pump lasers are both locked by synchronizing to a frequency synthesizer with a difference of 201.25 Hz between them. This locking scheme simplifies the signal processing as every two successive interferograms have a constant time delay. One idler beam (i1) transmits through a 15-cm-long cell and is recombined with the second idler beam (i2) at a beam splitter. The focused light can be detected by a Peltier-cooled fast infrared detector, giving the heterodyned signal for further Fourier analysis. A field-programmable gate array (FPGA) board is used for real-time digital signal processing and establishing a high throughput data streaming from the FPGA board to the computer storage for post-processing.
4.2 Results
Figure 10 illustrates a spectrum of the light from the output of the two-crystal OPO recorded with a visible light optical spectrum analyzer (OSA). The most dominated mixing signals are the sum frequencies of pump and signal \((p\,+\,s)\), pump and idler \((p\,+\,i)\), and doubling frequency of pump \((2p)\). These by-products, which exhibit powers of several milliwatts, can be used for stabilization of the mid-infrared frequency comb, while a photonic crystal fiber (PCF) is used to extend the pump wavelength to cover the sum frequency between pump and idler [26]. By detecting the offset frequency of idler directly, a electronic feedback can be established, applying a high feedback voltage on the PZT attached to one mirror of the OPO cavity.
Snapshot of all emitted visible light measured from the output of the ring cavity OPO along with residual pump \((p)\), leaked signal \((s)\) , and generated idler \((i)\). The vertical axis is a logarithmic scale. Blue curve Measured spectrum when OPO is off-resonance; Red curve Measured spectrum when OPO is on-resonance
To demonstrate mid-infrared dual-comb spectroscopy, a single-pass cell is filled with methane (\(\hbox {CH}_4\), 1% in nitrogen, 1 bar pressure, 15 cm path length). To impede higher-order transversal modes in the OPO cavity, two apertures are placed inside the OPO cavity. These apertures cause significant diffraction losses for the higher-order modes. This is beneficial for heterodyned detection since the two output idler beams should have an optimal spatial overlap, which can be achieved when both beams are in the \(\hbox {TEM}_{00}\) mode [36]. From the fast infrared detector, the heterodyned signal is low-pass filtered (up to 50 MHz) and sampled at 250 MHz. The experiment is performed when the two pump lasers are lasing at 2 W average power each, corresponding to a generated 200 mW mid-infrared light measured at each output port of the OPO. Figure 11a shows an apodized interferogram recorded within 36 μs, and we can see that the nonlinear effect observed in the previous experiment does not exist anymore. The interferogram has an asymmetrical structure because only one idler is probing the sample, and dispersion information can be retrieved from this asymmetrical structure.
Blue curve Normalized and averaged absorption spectrum of methane measured by the dual-comb spectrometer based on 20 successive interferograms within 0.1 s. The \(P\), \(Q\) , and \(R\) branches of the \(v_3\) vibrational transitions of methane can be clearly observed. Red curve Simulated absorption spectrum of methane (HITRAN database) used to compare with the measured spectrum. Green curve Dispersion information retrieved from the measurement
Figure 11b presents the corresponding Fourier transform power spectrum of the interferogram with a RF resolution of 15 kHz. The FPGA board streams the digitized real-time signal to the computer during 0.1 s (25M samples at 16-bit amplitude resolution) for post-averaging. Concerning the spectral stability of the system, in the case of femtosecond fiber lasers, the line width of the free-running offset frequency is normally hundreds of kilohertz. For an OPO-based mid-infrared frequency comb, the stability of the free-running offset frequency is worse due to the optical resonator open to air fluctuations. This frequency instability causes troubles when the RF spectra need to be averaged to increase the SNR, as every RF component retrieved from the FFT calculation does not always represent the same optical frequencies due to the instability of the offset frequency. The consequences are the broadening effect of the absorption lines and a frequency shift of the retrieved RF spectrum. In our case, to process the data, the 20 spectra calculated by the interferograms within 0.1 s are averaged after the alignment of the absorption peaks. In Fig. 12, the upper panel shows the measured absorption spectrum (blue curve) with 0.1 s averaging after background removal, which is normalized to compare with the HITRAN database (red curve). The \(P\), \(Q\) , and \(R\) branches of the \(v_3\) vibrational transitions of methane can clearly be observed between 2,850 and \(3,200\,\hbox {cm}^{-1}\), giving a bandwidth of more than \(350\,\hbox {cm}^{-1}\) and a resolution of \(0.2\,\hbox {cm}^{-1}\). The noise equivalent absorption sensitivity (1 s averaging per spectral element) calculated from the absorption signal is \(6.2\times 10^{-6}\,\hbox {cm}^{-1}\,\hbox {Hz}^{-1/2}\) (\(5.3\times 10^{-7}\,\hbox {cm}^{-1}\,\hbox {Hz}^{-1/2}\) considering only the recording time). The achieved sensitivity is limited due to the usage of the short single-pass cell and the single infrared detector. The implementation of a cavity-enhanced technique and auto-balanced detector can dramatically increase the efficient optical pass length and the SNR. Quantum-noise-limited results were achieved in the case of direct frequency comb Fourier transform spectroscopy [8]. The difference in repetition frequencies, acquisition rate, and the amount of data points for FFT calculation determines the resolution of the retrieved spectra and the recording time. The lower panel of Fig. 12 shows the dispersion information retrieved from the same measurement, which is immune to the intensity fluctuations of the idler, as the intensity fluctuations do not affect the phase information within the two idlers combs. The spectral resolution can be improved by either increasing the difference between two repetition frequencies, or calculating more data points for each interferogram, but the trade-off is a lower SNR. To increase SNR, an auto-balanced detector is an option; otherwise, the spectra need to be averaged over time to improve the SNR.
4.3 Discussion
The proposed two-crystal OPO cavity has several advantages for dual-comb spectroscopy. Both generated idlers originate from the same OPO cavity experiencing identical disturbances, such as mirror vibrations and air or oven temperature fluctuations. As a consequence, the common OPO cavity cancels out much of the instability compared to using two separate OPOs as dual-comb sources. The frequency of idlers can be expressed by \(f^1_{\rm i} = f^1_{\rm p} - f^1_{\rm s}\) and \(f^2_{\rm i} = f^2_{\rm p} - f^2_{\rm s}\) for comb 1 and comb 2, respectively. The frequency of one beating note between two idlers can then be calculated as \(f^1_{\rm i} - f^2_{\rm i} = (f^1_{\rm p} - f^2_{\rm p})- (f^1_{\rm s} - f^2_{\rm s})\), which simplifies to \(\Delta f_{\rm i} = \Delta f_{\rm p} - \Delta f_{\rm s}\). As commercial pump lasers have good short-term stability, the instability of the radio frequency spectra is mainly due to the term of \(\Delta f_{\rm s}\). The cavity fluctuation affects the central wavelengths of two signal combs in a similar manner, offering a better frequency stability of \(\Delta f_{\rm s}\) than using two separate OPOs when the two offset frequencies are free-running. Moreover, the two signal beams resonating in the optical cavity are counter-propagating and do not affect the generation of the two idler beams. Besides, in comparison with an OPO cavity using a single PPLN crystal for dual-comb spectroscopy, the two-crystal OPO generates two idler beams which are spatially separated, offering an opportunity to measure both absorption and dispersion spectra of gas samples simultaneously. To improve the performance of the spectrometer and to allow a longer averaging time, the offset frequencies of both two combs need to be stabilized, which is a challenging work. A fully stabilized dual-comb system will make possible the realization of real-time, sensitive multi-gas detection. It is worth mentioning that the fast recording time of such mid-infrared spectrometer will be beneficial for observation of molecular interaction kinetics [44].
5 Conclusion
We have demonstrated for the first time broadband, mid-infrared dual-comb spectroscopy measuring absorption and dispersion spectra in gas phase simultaneously with a bandwidth of more than \(350\,\hbox {cm}^{-1}\) (2,850– \(3,200\,\hbox {cm}^{-1}\)) and a spectral resolution of \(0.2\,\hbox {cm}^{-1}\). Two different configurations of OPO are tested for dual-comb spectroscopy. The proposed two-crystal, ring cavity OPO exhibits a variety of advantages including access to the dispersion information of samples when compared with a single-crystal OPO. The 0.1-s-averaged results give a dramatic improvement in SNR over a single-shot experiment. The measurement of the optical phase shift due to the target gas sample can offer a variety of advantages over measurements based on absorption sensing. For instance, the linear relationship between the dispersion spectrum and the sample concentration is beneficial; on the contrary, the absorption saturates with increasing concentration [45, 46]. For dual-comb-based spectrometers, as well as for Michelson-based Fourier spectrometers, the dispersion signal is, to some extent, immune to the intensity fluctuations of the light sources and can provide more reliable and accurate background free data than measuring the absorption signal [43, 47]. This advantage is due to the fact that the intensity noise is related to the square of the amplitude of the laser light, while the phase noise is mainly dominated by the frequency stability of the lasers. For a fully stabilized system, the intensity noise dominates compared to the phase noise, indicating the advantages of dispersion measurement. These initial results presented in this paper give a promise for field measurement such as breath analysis and environmental monitoring with advantages of broad bandwidth, fast acquisition time, and high sensitivity.
References
J. Bates, Fourier transform infrared spectroscopy. Science 191, 31–37 (1976)
J.M. Supplee, E.A. Whittaker, W. Lenth, Theoretical description of frequency modulation and wavelength modulation spectroscopy. Appl. Opt. 33, 6294–6302 (1994)
T. Udem, R. Holzwarth, T.W. Hänsch, Optical frequency metrology. Nature 416, 233–237 (2002)
A. Schliesser, M. Brehm, F. Keilmann, D. van der Weide, Frequency-comb infrared spectrometer for rapid, remote chemical sensing. Opt. Expr. 13, 9029–9038 (2005)
J. Mandon, G. Guelachvili, N. Picqué, Fourier transform spectroscopy with a laser frequency comb. Nat. Photon. 3, 99–102 (2009)
A. Cingoz, D.C. Yost, T.K. Allison, A. Ruehl, M.E. Fermann, I. Hartl, J. Ye, Direct frequency comb spectroscopy in the extreme ultraviolet. Nature 482, 68–71 (2012)
S.A. Diddams, L. Hollberg, V. Mbele, Molecular fingerprinting with the resolved modes of a femtosecond laser frequency comb. Nature 445, 627–630 (2007)
A. Foltynowicz, T. Ban, P. Masłowski, F. Adler, J. Ye, Quantum-noise-limited optical frequency comb spectroscopy. Phys. Rev. Lett. 107, 233002 (2011)
C. Gohle, B. Stein, A. Schliesser, T. Udem, T.W. Hänsch, Frequency comb vernier spectroscopy for broadband, high-resolution, high-sensitivity absorption and dispersion spectra. Phys. Rev. Lett. 99, 263902 (2007)
M.W. Haakestad, T.P. Lamour, N. Leindecker, A. Marandi, K.L. Vodopyanov, Intracavity trace molecular detection with a broadband Mid-IR frequency comb source. J. Opt. Soc. Am. B 30, 631–640 (2013)
L. Nugent-Glandorf, T. Neely, F. Adler, A.J. Fleisher, K.C. Cossel, B. Bjork, T. Dinneen, J. Ye, S.A. Diddams, Mid-infrared virtually imaged phased array spectrometer for rapid and broadband trace gas detection. Opt. Lett. 37, 3285–3287 (2012)
M.J. Thorpe, D. Balslev-Clausen, M.S. Kirchner, J. Ye, Cavity-enhanced optical frequency comb spectroscopy: application to human breath analysis. Opt. Expr. 16, 2387–2397 (2008)
M.J. Thorpe, J. Ye, Cavity-enhanced direct frequency comb spectroscopy. Appl. Phys. B 91, 397–414 (2008)
A.M. Zolot, F.R. Giorgetta, E. Baumann, J.W. Nicholson, W.C. Swann, I. Coddington, N.R. Newbury, Direct-comb molecular spectroscopy with accurate, resolved comb teeth over 43 THz. Opt. Lett. 37, 638–640 (2012)
A. Foltynowicz, P. Masłowski, A. Fleisher, B. Bjork, J. Ye, Cavity-enhanced optical frequency comb spectroscopy in the mid-infrared application to trace detection of hydrogen peroxide. Appl. Phys. B 110, 163–175 (2013)
S. Schiller, Spectrometry with frequency combs. Opt. Lett. 27, 766–768 (2002)
I. Coddington, W.C. Swann, N.R. Newbury, Coherent multiheterodyne spectroscopy using stabilized optical frequency combs. Phys. Rev. Lett. 100, 013902 (2008)
J. Roy, J.-D. Deschênes, S. Potvin, J. Genest, Continuous real-time correction and averaging for frequency comb interferometry. Opt. Expr. 20, 21932–21939 (2012)
F. Zhu, T. Mohamed, J. Strohaber, A.A. Kolomenskii, T. Udem, H.A. Schuessler, Real-time dual frequency comb spectroscopy in the near infrared. Appl. Phys. Lett. 102, 121116–4 (2013)
M. Cassinerio, A. Gambetta, N. Coluccelli, P. Laporta, G. Galzerano, Absolute dual-comb spectroscopy at 1.55 μm by free-running Er: fiber lasers. Appl. Phys. Lett. 104, 231102 (2014)
I. Coddington, W.C. Swann, N.R. Newbury, Coherent dual-comb spectroscopy at high signal-to-noise ratio. Phys. Rev. A 82, 043817 (2010)
F. Keilmann, C. Gohle, R. Holzwarth, Time-domain mid-infrared frequency-comb spectrometer. Opt. Lett. 29, 1542–1544 (2004)
L.C. Sinclair, I. Coddington, W.C. Swann, G.B. Rieker, A. Hati, K. Iwakuni, N.R. Newbury, Operation of an optically coherent frequency comb outside the metrology lab. Opt. Expr. 22, 6996–7006 (2014)
T. Ideguchi, A. Poisson, G. Guelachvili, N. Picqué, T.W. Hänsch, Adaptive real-time dual-comb spectroscopy. Nat. Commun. 5, 3375 (2014)
F. Adler, K.C. Cossel, M.J. Thorpe, I. Hartl, M.E. Fermann, J. Ye, Phase-stabilized, 1.5 W frequency comb at 2.8–4.8 μm. Opt. Lett. 34, 1330–1332 (2009)
Z. Zhang, X. Fang, T. Gardiner, D.T. Reid, High-power asynchronous midinfrared optical parametric oscillator frequency combs. Opt. Lett. 38, 2077–2079 (2013)
K.A. Ingold, A. Marandi, C.W. Rudy, K.L. Vodopyanov, R.L. Byer, Fractional-length sync-pumped degenerate optical parametric oscillator for 500-MHz 3-μm mid-infrared frequency comb generation. Opt. Lett. 39, 900–903 (2014)
F. Zhu, H. Hundertmark, A.A. Kolomenskii, J. Strohaber, R. Holzwarth, H.A. Schuessler, High-power mid-infrared frequency comb source based on a femtosecond Er: fiber oscillator. Opt. Lett. 38, 2360–2362 (2013)
A. Ruehl, A. Gambetta, I. Hartl, M.E. Fermann, K.S.E. Eikema, M. Marangoni, Widely-tunable mid-infrared frequency comb source based on difference frequency generation. Opt. Lett. 37, 2232–2234 (2012)
N. Leindecker, A. Marandi, R.L. Byer, K.L. Vodopyanov, Broadband degenerate OPO for mid-infrared frequency comb generation. Opt. Expr. 19, 6296–6302 (2011)
A. Marandi, N.C. Leindecker, V. Pervak, R.L. Byer, K.L. Vodopyanov, Coherence properties of a broadband femtosecond mid-ir optical parametric oscillator operating at degeneracy. Opt. Expr. 20, 7255–7262 (2012)
D. Burghoff, T.-Y. Kao, N. Han, C.W.I. Chan, X. Cai, Y. Yang, D.J. Hayton, J.-R. Gao, J.L. Reno, Q. Hu, Terahertz laser frequency combs. Nat. Photon. 8, 462–467 (2014)
T. Yasui, Y. Kabetani, E. Saneyoshi, S. Yokoyama, T. Araki, Terahertz frequency comb by multifrequency-heterodyning photoconductive detection for high-accuracy, high-resolution terahertz spectroscopy. Appl. Phys. Lett. 88, 241104–3 (2006)
E. Baumann, F.R. Giorgetta, W.C. Swann, A.M. Zolot, I. Coddington, N.R. Newbury, Spectroscopy of the methane \(v_{3}\) band with an accurate midinfrared coherent dual-comb spectrometer. Phys. Rev. A 84, 062513 (2011)
Z. Zhang, T. Gardiner, D.T. Reid, Mid-infrared dual-comb spectroscopy with an optical parametric oscillator. Opti. Lett. 38, 3148–3150 (2013)
Y. Jin, S.M. Cristescu, F.J.M. Harren, J. Mandon, Two-crystal mid-infrared optical parametric oscillator for absorption and dispersion dual-comb spectroscopy. Opt. Lett. 39, 3270–3273 (2014)
B. Bernhardt, A. Ozawa, P. Jacquet, M. Jacquey, Y. Kobayashi, T. Udem, R. Holzwarth, G. Guelachvili, T.W. Hänsch, N. Picqué, Cavity-enhanced dual-comb spectroscopy. Nat. Photon. 4, 55–57 (2010)
J.A. Armstrong, N. Bloembergen, J. Ducuing, P.S. Pershan, Interactions between light waves in a nonlinear dielectric. Phys. Rev. 127, 1918–1939 (1962)
L.E. Myers, R.C. Eckardt, M.M. Fejer, R.L. Byer, W.R. Bosenberg, J.W. Pierce, Quasi-phase-matched optical parametric oscillators in bulk periodically poled LiNbO3. J. Opt. Soc. Am. B 12, 2102–2116 (1995)
L.E. Myers, W.R. Bosenberg, Periodically poled lithium niobate and quasi-phase-matched optical parametric oscillators. Quantum Electron. IEEE J. 33, 1663–1672 (1997)
M.M.J.W. van Herpen, S. Li, S.E. Bisson, F.J.M. Harren, Photoacoustic trace gas detection of ethane using a continuously tunable, continuous-wave optical parametric oscillator based on periodically poled lithium niobate. Appl. Phys. Lett. 81, 1157–1159 (2002)
M.M.J.W. van Herpen, A.K.Y. Ngai, S.E. Bisson, J.H.P. Hackstein, E.J. Woltering, F.J.M. Harren, Optical parametric oscillator-based photoacoustic detection of \(\hbox {CO}_2\) at 4.23 μm allows real-time monitoring of the respiration of small insects. Appl. Phys. B 82, 665–669 (2006)
J.A. de Haseth, P. Griffiths, Fourier Transform Infrared Spectrometry (Wiley, London, 2007)
A. Fleisher, B. Bjork, T. Bui, K. Cossel, M. Okumura, J. Ye, Mid-infrared time-resolved frequency comb spectroscopy of transient free radicals. J. Phys. Chem. Lett. 5, 2241 (2014)
G. Wysocki, D. Weidmann, Molecular dispersion spectroscopy for chemical sensing using chirped mid-infrared quantum cascade laser. Opt. Expr. 18, 26123–26140 (2010)
M. Nikodem, G. Wysocki, Molecular dispersion spectroscopy new capabilities in laser chemical sensing. Ann. N. Y. Acad. Sci. 1260, 101–111 (2012)
J. Kauppinen, J. Partanen, Fourier Transforms in Spectroscopy (Wiley, London, 2001)
Acknowledgments
This work is supported by the Technologiestichting STW Foundation (Project No. 11830) and the GO-EFRO “Ultragas-gas analysis system for quality control of agricultural products and medical diagnostics” (Project No. 2009-010034).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Jin, Y., Cristescu, S.M., Harren, F.J.M. et al. Femtosecond optical parametric oscillators toward real-time dual-comb spectroscopy. Appl. Phys. B 119, 65–74 (2015). https://doi.org/10.1007/s00340-015-6035-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00340-015-6035-y