Abstract
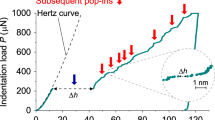
Our previous work has established that the dislocation nucleation during the onset of plasticity, the so-called pop-in, in face-centered cubic single-phased high-entropy alloy FeCoCrMnNi is controlled by vacancy defects. This implies that the tip radius would affect the pop in behavior as the number of vacancy, the available sites for dislocation nucleation, within the stressed volume is proportional to radius. To verify this in current work, a wide range of nanoindenter tips with radius across from 200 to 2013 nm were used. It was found that when tip radius is smaller than 638 nm, the pop-in or displacement burst size increases linearly with it, and that when tip radius is larger than 638 nm, the pop—in size became essentially constant. These experimental findings confirm the effect of tip radius on pop-in behavior. A theoretical model based on image force has been developed to rationalize the above observations.







Similar content being viewed by others
References
H. Bei, Y.F. Gao, S. Shim, E.P. George, G.M. Pharr, Strength differences arising from homogeneous versus heterogeneous dislocation nucleation. Phys. Rev. B 77(6), 060103 (2008)
M.M. Biener, J. Biener, A.M. Hodge, A.V. Hamza, Dislocation nucleation in bcc Ta single crystals studied by nanoindentation. Phys. Rev. B 76(16), 165422 (2007)
J.K. Mason, A.C. Lund, C.A. Schuh, Determining the activation energy and volume for the onset of plasticity during nanoindentation. Phys. Rev. B 73(5), 054102 (2006)
A.M. Minor, Direct observations of incipient plasticity during nanoindentation of Al. J. Mater. Res. 19(01), 176–182 (2004)
S. Shim, H. Bei, E.P. George, G.M. Pharr, A different type of indentation size effect. Scr. Mater. 59(10), 1095–1098 (2008)
D. Lorenz, A. Zeckzer, U. Hilpert, P. Grau, H. Johansen, H.S. Leipner, Pop-in effect as homogeneous nucleation of dislocations during nanoindentation. Phys. Rev. B 67(17), 172101 (2003)
E.T. Lilleodden, J.A. Zimmerman, S.M. Foiles, W.D. Nix, Atomistic simulations of elastic deformation and dislocation nucleation during nanoindentation. J. Mech. Phys. Solids 51(5), 901–920 (2003)
C.A. Schuh, Nanoindentation studies of materials. Mater Today 9, 32–40 (2006)
C. Zhu, Z.P. Lu, T.G. Nieh, Incipient plasticity and dislocation nucleation of FeCoCrNiMn high-entropy alloy. Acta Mater 61(8), 2993–3001 (2013)
Q.F. He, J.F. Zeng, S. Wang, Y.F. Ye, C. Zhu, T.G. Nieh, Z.P. Lu, Y. Yang, Delayed plasticity during nanoindentation of single-phase CoCrFeMnNi highentropy alloy. Mater. Res. Lett. 5, 300–305 (2017)
S. Suresh, T.G.; Nieh, B.W. Choi, Nano-indentation of copper thin films on silicon substrates. Scr. Mater. 41(9), 951–957 (1999)
C.A. Schuh, A.C. Lund, Application of nucleation theory to the rate dependence of incipient plasticity during nanoindentation. J. Mater. Res. 19(07), 2152–2158 (2004)
L. Chang, L. Zhang, Mechanical behaviour characterisation of silicon and effect of loading rate on pop-in: A nanoindentation study under ultra-low loads. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 506(1), 125–129 (2009)
Y. Shibutani, T. Tsuru, A. Koyama, Nanoplastic deformation of nanoindentation: crystallographic dependence of displacement bursts. Acta Mater. 55(5), 1813–1822 (2007)
T. Tsuru, Y. Shibutani, Anisotropic effects in elastic and incipient plastic deformation under (001),(110), and (111) nanoindentation of Al and Cu. Phys. Rev. B 75(3), 035415 (2007)
C.A. Schuh, J.K. Mason, A.C. Lund, Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 4(8), 617–621 (2005)
T. Zhu, J. Li, A. Samanta, A. Leach, K. Gall, Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 100(2), 025502 (2008)
H.G. Vineyard, Frequency factors and isotope effects in solid state rate processes. J. Phys. Chem. Solids 3(1), 121–127 (1957)
H. Hertz, Miscellaneous papers, Macmillan, London(1896)
A. Barnoush, Correlation between dislocation density and nanomechanical response during nanoindentation. Acta Mater. 60(3), 1268–1277 (2012)
G.E. Dieter, D. Bacon, Mechanical metallurgy (McGraw-Hill, New York, 1986)
G.E. Beltz, L.B. Freund, On the nucleation of dislocations at a crystal surface. Phys. Status Solidi B-Basic Solid State Phys. 180(2), 303–313 (1993)
V.B. Shenoy, R. Phillips, E.B. Tadmor, Nucleation of dislocations beneath a plane strain indenter. J. Mech. Phys. Solids 48(4), 649–673 (2000)
C.R. Weinberger, W. Cai, Surface-controlled dislocation multiplication in metal micropillars. Proc. Natl. Acad. Sci. U. S. A. 105(38), 14304–14307 (2008)
A.C. Fischer-Cripps, I. Mustafaev, Introduction to contact mechanics, Springer, Berlin (2000)
D. Hull, D.J. Bacon, Introduction to dislocations (Pergamon Press, Oxford, 1984)
T.H. Courtney, Mechanical behavior of materials, Waveland Press, Long Grove (2005)
J. Moon, M.J. Jang, J.W. Bae, D. Yim, J.M. Park, J. Lee, H.S. Kim, Mechanical behavior and solid solution strengthening model for face-centered cubic single crystalline and polycrystalline high-entropy alloys. Intermetallics 98, 89–94 (2018)
M. Haglund, D. Koehler, E.P. Catoor, V. George, Keppens, Polycrystalline elastic moduli of a high-entropy alloy at cryogenic temperatures. Intermetallics 58, 62–64 (2015)
G. Laplanche, P. Gadaud, O. Horst, F. Otto, G. Eggeler, E.P. George, Temperature dependencies of the elastic moduli and thermal expansion coefficient of an equiatomic, single-phase CoCrFeMnNi high-entropy alloy. J. Alloy. Compd. 623, 348–353 (2015)
Acknowledgements
This work was mainly conducted during Zhu’s PhD at the University of Tennessee Knoxville. Zhu would like to thank Dr. Nieh from the University of Tennessee Knoxville for his guidance. Startup funds from Wuhan University of Technology under the grant numbers 444-20411183 and 471-40120378 are also deeply acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, Y., Xiong, X. & Zhu, C. Dependence of pop-in behavior of a high-entropy alloy FeCoCrMnNi on tip radius. Appl. Phys. A 125, 115 (2019). https://doi.org/10.1007/s00339-019-2409-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-019-2409-z