Skip to main content
SpringerLink
Log in

Variational Integrators for Interconnected Lagrange–Dirac Systems

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

Abstract

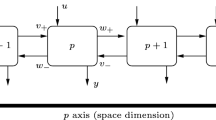
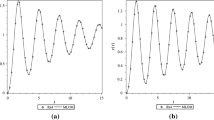
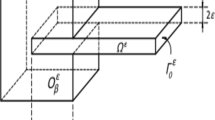
Interconnected systems are an important class of mathematical models, as they allow for the construction of complex, hierarchical, multiphysics, and multiscale models by the interconnection of simpler subsystems. Lagrange–Dirac mechanical systems provide a broad category of mathematical models that are closed under interconnection, and in this paper, we develop a framework for the interconnection of discrete Lagrange–Dirac mechanical systems, with a view toward constructing geometric structure-preserving discretizations of interconnected systems. This work builds on previous work on the interconnection of continuous Lagrange–Dirac systems (Jacobs and Yoshimura in J Geom Mech 6(1):67–98, 2014) and discrete Dirac variational integrators (Leok and Ohsawa in Found Comput Math 11(5), 529–562, 2011). We test our results by simulating some of the continuous examples given in Jacobs and Yoshimura (2014).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Absil, P.-A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press, Princeton (2008)

    Book  MATH  Google Scholar 

  • Bloch, A.M.: Nonholonomic Mechanics and Control. Springer, Berlin (2003)

    Book  Google Scholar 

  • Bou-Rabee, N., Marsden, J.E.: Hamilton–Pontryagin integrators on Lie groups. I. Introduction and structure-preserving properties. Found. Comput. Math. 9(2), 197–219 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  • Bou-Rabee, N., Owhadi, H.: Stochastic variational integrators. IMA J. Numer. Anal. 29(2), 421–443 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  • Bou-Rabee, N., Owhadi, H.: Long-run accuracy of variational integrators in the stochastic context. SIAM J. Numer. Anal. 48(1), 278–297 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  • Chang, D.-E.: On the method of interconnection and damping assignment passivity-based control for the stabilization of mechanical systems. Regul. Chaotic Dyn. 19(5), 556–575 (2014). doi:10.1134/S1560354714050049

    Article  MathSciNet  MATH  Google Scholar 

  • Cortés, J., Martínez, S.: Non-holonomic integrators. Nonlinearity 14(5), 1365–1392 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Duindam, V., Macchelli, A., Stramigioli, S., Bruyninckx, H.: Modeling and Control of Complex Physical Systems: The Port-Hamiltonian Approach. Springer, Berlin (2009)

    Book  MATH  Google Scholar 

  • Fedorov, Y.N., Zenkov, D.V.: Discrete nonholonomic LL systems on Lie groups. Nonlinearity 18(5), 2211–2241 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  • Fetecau, R., Marsden, J.E., Ortiz, M., West, M.: Nonsmooth Lagrangian mechanics and variational collision integrators. SIAM J. Appl. Dyn. Syst. 2(3), 381–416 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  • Gualtieri, M.: Generalized complex geometry. Ann. Math. 174, 75–123 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Jacobs, H.O., Yoshimura, H.: Tensor products of Dirac structures and interconnection in Lagrangian mechanics. J. Geom. Mech. 6(1), 67–98 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  • Lall, S., West, M.: Discrete variational Hamiltonian mechanics. J. Phys. A 39(19), 5509–5519 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  • Lee, T., Leok, M., McClamroch, N.H.: Lie group variational integrators for the full body problem. Comput. Methods Appl. Mech. Eng. 196(29–30), 2907–2924 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  • Lee, T., Leok, M., McClamroch, N.H.: Lagrangian mechanics and variational integrators on two-spheres. Int. J. Numer. Methods Eng. 79(9), 1147–1174 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  • Leok, M., Ohsawa, T.: Variational and geometric structures of discrete Dirac mechanics. Found. Comput. Math. 11(5), 529–562 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Leok, M., Zhang, J.: Discrete Hamiltonian variational integrators. IMA J. Numer. Anal. 31(4), 1497–1532 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Lew, A., Marsden, J.E., Ortiz, M., West, M.: Asynchronous variational integrators. Arch. Ration. Mech. Anal. 167(2), 85–146 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  • Marsden, J.E., Patrick, G.W., Shkoller, S.: Multisymplectic geometry, variational integrators, and nonlinear PDEs. Commun. Math. Phys. 199(2), 351–395 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  • Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry, 2nd edn. Springer, Berlin (1999)

    Book  MATH  Google Scholar 

  • Marsden, J.E., West, M.: Discrete mechanics and variational integrators. Acta Numer. 10, 357–514 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • McLachlan, R., Perlmutter, M.: Integrators for nonholonomics mechanical systems. J. Nonlinear Sci. 16(4), 283–328 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  • Parks, Helen: Structured approaches to large-scale systems: variational integrators for interconnected Lagrange–Dirac systems and structured model reduction on Lie groups. PhD thesis, University of California San Diego (2015)

  • Tulczyjew, W.M.: The Legendre transformation. Annales de l’Institute Henri Poincaré 27, 101–114 (1977)

    MathSciNet  MATH  Google Scholar 

  • van der Schaft, A.: Port-Hamiltonian systems: an introductory survey. In: Proceedings of the International Congress on Mathematicians, Madrid, Spain (2006)

  • Yoshimura, H., Marsden, J.E.: Dirac structures in Lagrangian mechanics part I: implicit Lagrangian systems. J. Geom. Phys. 57(1), 133–156 (2006a)

    Article  MathSciNet  MATH  Google Scholar 

  • Yoshimura, H., Marsden, J.E.: Dirac structures in Lagrangian mechanics part II: variational structures. J. Geom. Phys. 57(1), 209–250 (2006b)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge helpful comments and suggestions of the referee. HP has been supported by the NSF Graduate Research Fellowship Grant Number DGE-1144086. ML has been supported in part by NSF under Grants DMS-1010687, CMMI-1029445, DMS-1065972, CMMI-1334759, DMS-1411792, DMS-1345013.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA, USA

    Helen Parks & Melvin Leok

Authors
  1. Helen Parks
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Melvin Leok
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Melvin Leok.

Additional information

Communicated by Anthony Bloch.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Parks, H., Leok, M. Variational Integrators for Interconnected Lagrange–Dirac Systems. J Nonlinear Sci 27, 1399–1434 (2017). https://doi.org/10.1007/s00332-017-9364-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-017-9364-7

Keywords

Mathematics Subject Classification

Search

Navigation