Multiscale model within-host and between-host for viral infectious diseases

Abstract

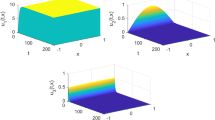
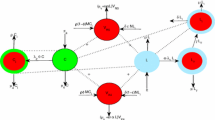
Multiscale models possess the potential to uncover new insights into infectious diseases. Here, a rigorous stability analysis of a multiscale model within-host and between-host is presented. The within-host model describes viral replication and the respective immune response while disease transmission is represented by a susceptible-infected model. The bridging of scales from within- to between-host considered transmission as a function of the viral load. Consequently, stability and bifurcation analyses were developed coupling the two basic reproduction numbers $R_0^{W}$ and $R_0^{B}$ for the within- and the between-host subsystems, respectively. Local stability results for each subsystem, including a unique stable equilibrium point, recapitulate classical approaches to infection and epidemic control. Using a Lyapunov function, global stability of the between-host system was obtained. Our main result was the derivation of the $R_0^{B}$ as an increasing function of $R_0^{W}$. Numerical analyses reveal that a Michaelis–Menten form based on the virus is more likely to recapitulate the behavior between the scales than a form directly proportional to the virus. Our work contributes basic understandings of the two models and casts light on the potential effects of the coupling function on linking the two scales.