Periodic matrix models for seasonal dynamics of structured populations with application to a seabird population

Abstract

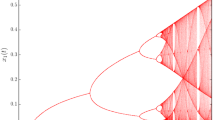
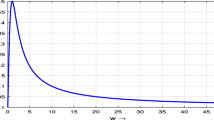
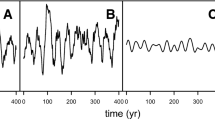
For structured populations with an annual breeding season, life-stage interactions and behavioral tactics may occur on a faster time scale than that of population dynamics. Motivated by recent field studies of the effect of rising sea surface temperature (SST) on within-breeding-season behaviors in colonial seabirds, we formulate and analyze a general class of discrete-time matrix models designed to account for changes in behavioral tactics within the breeding season and their dynamic consequences at the population level across breeding seasons. As a specific example, we focus on egg cannibalism and the daily reproductive synchrony observed in seabirds. Using the model, we investigate circumstances under which these life history tactics can be beneficial or non-beneficial at the population level in light of the expected continued rise in SST. Using bifurcation theoretic techniques, we study the nature of non-extinction, seasonal cycles as a function of environmental resource availability as they are created upon destabilization of the extinction state. Of particular interest are backward bifurcations in that they typically create strong Allee effects in population models which, in turn, lead to the benefit of possible (initial condition dependent) survival in adverse environments. We find that positive density effects (component Allee effects) due to increased adult survival from cannibalism and the propensity of females to synchronize daily egg laying can produce a strong Allee effect due to a backward bifurcation.

Appendix

The following Lemma is an extension of results in Cushing (2016).

Lemma 1

Assume A1 and A2.

(a) Suppose $\partial _{p}^{0}r>0$. Then the equilibrium $\alpha =0$ of the difference equation (12) is locally asymptotically stable if $p<p_{0}$ and is unstable if $p>p_{0}$. Suppose, on the other hand, that $\partial _{p}^{0}r<0$. Then $\alpha =0$ is locally asymptotically stable for $p>p_{0}$ and is unstable for $p<p_{0}$.

(b) On an open interval I of $p_{0}$ there exists a (twice continuously differentiable) continuum of equilibria $\alpha =\alpha \left( p\right)$ of the difference equation (12) satisfying $\alpha \left( p_{0}\right) =0$ and $\alpha \left( p\right) \ne 0$ for $p\ne p_{0}$.

(c) Suppose $\partial _{p}^{0}r>0.$ If $\partial _{\alpha }^{0}r<0$ then for $p\in I$ the equilibrium $\alpha \left( p\right)$ is positive and locally asymptotically stable if $p>p_{0}$ (and are negative for $p<p_{0}$). On the other hand, if $\partial _{\alpha }^{0}r>0$ then for $p\in I$ the equilibrium $\alpha \left( p\right)$ is positive and unstable for $p<p_{0}$ (and are negative for $p>p_{0}$).

(d) Suppose $\partial _{p}^{0}r<0.$ If $\partial _{\alpha }^{0}r>0$ then for $p\in I$ the equilibrium $\alpha \left( p\right)$ is positive and locally asymptotically stable for $p>p_{0}$ (and are negative for $p<p_{0}$). On the other hand, if $\partial _{\alpha }^{0}r<0$ then for $p\in I$ the equilibrium $\alpha \left( p\right)$ is positive and unstable for $p>p_{0}$ (and are negative for $p>p_{0}$).

Proof

(a) The linearization principle guarantees local asymptotic stability of $\alpha =0$ if $r\left( 0,p\right) <1$ and instability if $r\left( 0,p\right) >1$.

(b) Under assumption A2 we can apply the implicit function theorem to the equation $r\left( p,\alpha \right) =1$ for nontrivial equilibria of the difference equation (12) and obtain, on an open interval of $p_{0}$, a twice continuously differentiable function $\alpha =\alpha \left( 0\right) ,$ $\alpha \left( p_{0}\right) =0$ satisfying $r\left( p,\alpha \left( p\right) \right) =1.$ An implicit differentiation with respect to p yields $\alpha ^{\prime }\left( 0\right) =-\partial _{p}^{0}r/\partial _{\alpha }^{0}r\ne 0$ from which it follows that $\alpha \left( p\right) \ne 0$ for $p\ne p_{0}$.

(c) If $\alpha ^{\prime }\left( 0\right) >0$ then $\alpha \left( p\right) >0$ (respectively $\alpha \left( p\right) <0$) for $p\gtrapprox p_{0}$ (respectively $p\lessapprox p_{0}$). On the other hand, if $\alpha ^{\prime }\left( 0\right) <0$ then $\alpha \left( p\right) >0$ (respectively $\alpha \left( p\right) <0$) for $p\lessapprox p_{0}$ (respectively $p\gtrapprox p_{0}$) as asserted. With regard to the stability of the equilibrium $\alpha \left( p\right)$ for p near $p_{0},$ we apply the linearization principle by calculating

$$\begin{aligned}&\left. \frac{\partial \left( r\left( p,\alpha \right) \alpha \right) }{\partial \alpha }\right| _{\alpha =\alpha \left( p\right) }=1+\alpha \left( p\right) \left. \frac{\partial \left( r\left( p,\alpha \right) \right) }{\partial \alpha }\right| _{\alpha =\alpha \left( p\right) } \nonumber \\&\quad =1+\left( \alpha ^{\prime }\left( 0\right) \partial _{\alpha } ^{0}r\right) \left( p-p_{0}\right) +O\left( \left( p-p_{0}\right) ^{2}\right) \nonumber \\&\quad =1+\left( -\partial _{p}^{0}r\right) \left( p-p_{0}\right) +O\left( \left( p-p_{0}\right) ^{2}\right) . \end{aligned}$$

(24)

Assume $\partial _{p}^{0}r>0$. If $\partial _{\alpha }^{0}r<0$ then $\alpha ^{\prime }\left( 0\right) =-\partial _{p}^{0}r/\partial _{\alpha } ^{0}r>0$ and $\alpha \left( p\right)$ is positive and $\left| \lambda \right| <1$ for $p\gtrapprox p_{0}$. If $\partial _{\alpha }^{0}r>0$ then $\alpha ^{\prime }\left( 0\right) =-\partial _{p}^{0}r/\partial _{\alpha }^{0}r<0$ and $\alpha \left( p\right)$ is positive and $\left| \lambda \right| <1$ for $p\lessapprox p_{0}$.

(d) These conclusions are derived in closely similar manner to those in (c) by also making use of (24). $\square$

Proof of Corollary 1

It is obvious from the definition of $\hat{x}\left( t,\alpha \right)$ that $\hat{x}\left( t,0\right) =\hat{0}$ for all t. From (10) we have

$$\begin{aligned} \partial _{\alpha }^{0}r=\hat{\nu }\partial _{\alpha }^{0}Q\hat{a} \end{aligned}$$

where

$$\begin{aligned} Q\left( \alpha \right)= & {} \prod \limits _{k-2}^{t=0}W\left( \hat{x}\left( t\right) \right) =W\left( \hat{x}\left( k-2\right) \right) \cdots W\left( \hat{x}\left( 1\right) \right) W\left( \hat{x}\left( 0\right) \right) \\ \partial _{\alpha }^{0}Q= & {} \left. \frac{\partial }{\partial \alpha }\prod \limits _{k-2}^{t=0}W\left( \hat{x}\left( t\right) \right) \right| _{\alpha =0}=\sum \limits _{t=0}^{k-2}W^{k-2-t}(\hat{0})\left. \frac{\partial }{\partial \alpha }W\left( \hat{x}\left( t\right) \right) \right| _{\alpha =0}W^{t}(\hat{0}) \end{aligned}$$

By the chain rule

$$\begin{aligned} \left. \frac{\partial }{\partial \alpha }W\left( \hat{x}\left( t\right) \right) \right| _{\alpha =0}=\left[ \nabla _{\hat{x}}^{0}w_{ij}\left. \frac{\partial }{\partial \alpha }\hat{x}\left( t\right) \right| _{\alpha =0}\right] \end{aligned}$$

where

$$\begin{aligned} \nabla _{\hat{x}}^{0}w_{ij}=\left( \begin{array}{llll} \partial _{x_{1}}^{0}w_{ij}&\partial _{x_{2}}^{0}w_{ij}&\cdots&\partial _{x_{m}}^{0}w_{ij} \end{array} \right) . \end{aligned}$$

From

$$\begin{aligned} \hat{x}\left( t\right) =\left( \prod \limits _{t-1}^{i=0}W\left( \hat{x}\left( i\right) \right) \right) \alpha \hat{a} \end{aligned}$$

we obtain

$$\begin{aligned} \left. \frac{\partial }{\partial \alpha }\hat{x}\left( t\right) \right| _{\alpha =0}=W^{t}\left( 0\right) \hat{a} \end{aligned}$$

for $t=0,1,\ldots ,k-1.$ The matrix

$$\begin{aligned} D\left( t\right) :=\left. \frac{\partial }{\partial \alpha }W\left( \hat{x}\left( t\right) \right) \right| _{\alpha =0}=\left[ \nabla _{\hat{x} }^{0}w_{ij}W^{t}\left( 0\right) \hat{a}\right] \end{aligned}$$

leads to

$$\begin{aligned} \partial _{\alpha }^{0}Q=\sum \limits _{t=0}^{k-2}W^{k-2-t}(\hat{0})D\left( t\right) W^{t}(\hat{0}). \end{aligned}$$

The entries in the matrix $D\left( t\right)$ are linear combinations of the derivatives $\partial _{x_{l}}^{0}w_{ij}$. It follows that the same is true of the entries in the matrix $\partial _{\alpha }^{0}Q$ and, as a result, the same is true of $\partial _{\alpha }^{0}r$. $\square$

The quantity $\partial _{\alpha }^{0}r$ for the gull model (17)–(19) with (18). We use the formula

$$\begin{aligned} \partial _{\alpha }^{0}r=\left. \hat{\nu }^{\tau }\partial _{\alpha }Q\left( p,\alpha \right) \hat{a}\right| _{\left( p,\alpha \right) =\left( p_{0},0\right) } \end{aligned}$$

where

$$\begin{aligned} \partial _{\alpha }Q\left( p,\alpha \right) =\partial _{\alpha }\prod \limits _{k-2}^{t=0}W\left( p,\hat{x}\left( t\right) \right) \end{aligned}$$

with matrix W defined by (17) and entries (18) and with the vectors $\hat{\nu }^{\tau }$ and $\hat{a}$ given by (20). By the product rule

$$\begin{aligned} \partial _{\alpha }^{0}Q=\sum \limits _{t=0}^{k-2}W^{k-2-t}(\hat{0})D\left( t\right) W^{t}(\hat{0}) \end{aligned}$$

where

$$\begin{aligned} D\left( t\right) :=\left[ \nabla _{\hat{x}}^{0}w_{ij}\left. \frac{d\hat{x}\left( i\right) }{d\alpha }\right| _{\alpha =0}\right] =\left[ \nabla _{\hat{x}}^{0}w_{ij}W^{t}\left( 0\right) \hat{a}\right] \end{aligned}$$

since

$$\begin{aligned} \hat{x}\left( i\right) =\left( \prod \limits _{t=0}^{i-1}W\left( \hat{x}\left( t\right) \right) \right) \alpha \hat{a} \end{aligned}$$

implies

$$\begin{aligned} \left. \frac{d\hat{x}\left( i\right) }{d\alpha }\right| _{\alpha =0}=W^{i}(\hat{0})\hat{a}. \end{aligned}$$

From the gull model matrix entries (18) we have

$$\begin{aligned} D\left( t\right) =\left( \begin{array}{cccc} 0 &{}\quad 0 &{}\quad p_{0}\nabla _{\hat{x}}^{0}\varphi W^{t}\left( 0\right) \hat{a} &{}\quad 0\\ \begin{array}{c} -s_{1}\nabla _{\hat{x}}^{0}\left( \pi _{3}\left( x_{1},x_{3}\right) x_{3}\right) W^{t}\left( 0\right) \hat{a} \\ \;-s_{1}\nabla _{\hat{x}}^{0}\left( \pi _{4}\left( x_{1},x_{4}\right) x_{4}\right) W^{t}\left( 0\right) \hat{a} \end{array} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad s_{4}\nabla _{\hat{x}}^{0}\left( \beta _{4}g\right) W^{t}\left( 0\right) \hat{a}\\ 0 &{}\quad 0 &{}\quad s_{3}\nabla _{\hat{x}}^{0}\beta _{3}W^{t}\left( 0\right) \hat{a} &{}\quad s_{4}\nabla _{\hat{x}}^{0}\left( \beta _{4}\left( 1-g\right) \right) W^{t}\left( 0\right) \hat{a} \end{array} \right) \end{aligned}$$

Let $M_{ij}$ be the $4\times 4$ matrices with all zero entries with the exception of a 1 in the $ij^{th}$ entry. Making use of these matrices, we write

$$\begin{aligned} D\left( t\right)&=-s_{1}\left( \begin{array}{cccc} 0&0&\pi _{3}\left( 0,0\right)&\pi _{4}\left( 0,0\right) \end{array} \right) W^{t}\left( 0\right) \hat{a}M_{21}+p_{0}\nabla _{\hat{x}}^{0}\varphi W^{t}\left( 0\right) \hat{a}M_{13} \\&\quad +s_{3}\nabla _{\hat{x}}^{0}\beta _{3}W^{t}\left( 0\right) \hat{a} M_{43}+s_{4}\nabla _{\hat{x}}^{0}\left( \beta _{4}g\right) W^{t}\left( 0\right) \hat{a}M_{34}\\&\quad +s_{4}\nabla _{\hat{x}}^{0}\left( \beta _{4}\left( 1-g\right) \right) W^{t}\left( 0\right) \hat{a}M_{44}. \end{aligned}$$

Then

$$\begin{aligned} \hat{\nu }^{\tau }W^{k-2-t}(\hat{0})D\left( t\right) W^{t}(\hat{0})\hat{a}&=-s_{1}c_{0}\left( t\right) \left( \begin{array}{cccc} 0&0&\pi _{3}\left( 0,0\right)&\pi _{4}\left( 0,0\right) \end{array}\right) W^{t}\left( 0\right) \hat{a} \\&\quad +p_{0}c_{1}\left( t\right) \nabla _{\hat{x}}^{0}\varphi W^{t}\left( 0\right) \hat{a}\\&\quad +s_{3}c_{2}\left( t\right) \nabla _{\hat{x}}^{0}\beta _{3}W^{t}\left( 0\right) \hat{a}+s_{4}c_{3}\left( t\right) \nabla _{\hat{x}}^{0}\left( \beta _{4}g\right) W^{t}\left( 0\right) \hat{a}\\&\quad +s_{4}c_{4}\left( t\right) \nabla _{\hat{x}}^{0}\left( \beta _{4}\left( 1-g\right) \right) W^{t}\left( 0\right) \hat{a} \end{aligned}$$

where we defined the nonnegative scalar coefficients

$$\begin{aligned} c_{0}\left( t\right)&:=\hat{\nu }^{\tau }W^{k-2-t}(\hat{0})M_{21} W^{t}(\hat{0})\hat{a},\quad c_{1}\left( t\right) =\hat{\nu }^{\tau } W^{k-2-t}(\hat{0})M_{13}W^{t}(\hat{0})\hat{a} \\ c_{2}\left( t\right)&=\hat{\nu }^{\tau }W^{k-2-t}(\hat{0})M_{43}W^{t} (\hat{0})\hat{a},\quad c_{3}\left( t\right) =\hat{\nu }^{\tau }W^{k-2-t} (\hat{0})M_{34}W^{t}(\hat{0})\hat{a}\\ c_{4}\left( t\right)&=\hat{\nu }^{\tau }W^{k-2-t}(\hat{0})M_{44}W^{t} (\hat{0})\hat{a}. \end{aligned}$$

This leads to

$$\begin{aligned} \partial _{\alpha }^{0}r&=\sum \limits _{t=0}^{k-2}\hat{\nu }^{\tau } W^{k-2-t}(\hat{0})D\left( t\right) W^{t}(\hat{0})\hat{a} \\&=-s_{1}\sum \limits _{t=0}^{k-2}c_{0}\left( t\right) \left( \begin{array}{cccc} 0&0&\pi _{3}\left( p_{0},0,0\right)&\pi _{4}\left( p_{0},0,0\right) \end{array} \right) W^{t}\left( 0\right) \hat{a} \\&\quad +\,p_{0}\sum \limits _{t=0}^{k-2} c_{1}\left( t\right) \left[ \nabla _{\hat{x}}^{0}\varphi W^{t}\left( 0\right) \hat{a}\right] \\&\quad +\,s_{3}\sum \limits _{t=0}^{k-2}c_{2}\left( t\right) \left[ \nabla _{\hat{x}}^{0}\beta _{3}W^{t}\left( 0\right) \hat{a}\right] +s_{4}\sum \limits _{t=0}^{k-2}c_{3}\left( t\right) \left[ \nabla _{\hat{x}}^{0} \beta _{4}W^{t}\left( 0\right) \hat{a}\right] \\&\quad +s_{4}\sum \limits _{t=0}^{k-2}\left( c_{3}\left( t\right) -c_{4}\left( t\right) \right) \left[ \nabla _{\hat{x}}^{0}gW^{t}\left( 0\right) \hat{a}\right] . \end{aligned}$$

Finally, making use of

$$\begin{aligned} \nabla _{\hat{x}}\left( \beta _{4}g\right)= & {} g\nabla _{\hat{x}}\beta _{4} +\beta _{4}\nabla _{\hat{x}}g\Rightarrow \nabla _{\hat{x}}^{0}\left( \beta _{4}g\right) =\nabla _{\hat{x}}^{0}\beta _{4}+\nabla _{\hat{x}}^{0}g\\ \nabla _{\hat{x}}\left( \beta _{4}\left( 1-g\right) \right)= & {} \left( 1-g\right) \nabla _{\hat{x}}\beta _{4}-\beta _{4}\nabla _{\hat{x}}g\Rightarrow \nabla _{\hat{x}}^{0}\left( \beta _{4}\left( 1-g\right) \right) =-\nabla _{\hat{x}}^{0}g \end{aligned}$$

we arrive at

$$\begin{aligned} \partial _{\alpha }^{0}r&=-s_{1}\sum \limits _{t=0}^{k-2}c_{0}\left( t\right) \left( \begin{array}{cccc} 0&0&\pi _{3}\left( p_{0},0,0\right)&\pi _{4}\left( p_{0},0,0\right) \end{array} \right) W^{t}\left( 0\right) \hat{a} \\&\quad +\varphi ^{\prime }\left( 0\right) p_{0}\sum \limits _{t=0}^{k-2}c_{1}\left( t\right) \left( \begin{array}{cccc} 0&0&c_{\varphi 3}&c_{j4} \end{array} \right) W^{t}\left( 0\right) \hat{a} \\&\quad +\sigma _{3}^{\prime }\left( 0\right) s_{3}\sum \limits _{t=0}^{k-2} c_{2}\left( t\right) \left( \begin{array}{cccc} \pi _{3}\left( p_{0},0,0\right)&0&0&0 \end{array} \right) W^{t}\left( 0\right) \hat{a} \\&\quad +\sigma _{4}^{\prime }\left( 0\right) s_{4}\sum \limits _{t=0}^{k-2} c_{3}\left( t\right) \left( \begin{array}{cccc} \pi _{4}\left( p_{0},0,0\right)&0&0&0 \end{array} \right) W^{t}\left( 0\right) \hat{a} \\&\quad +g^{\prime }\left( 0\right) s_{4}\sum \limits _{t=0}^{k-2}\left( c_{3}\left( t\right) -c_{4}\left( t\right) \right) \left( \begin{array}{cccc} 0&0&1&0 \end{array} \right) W^{t}\left( 0\right) \hat{a}. \end{aligned}$$

The first two terms, deriving from the adult density dependent fertility and the effect of cannibalism on egg survival, are negative and therefore contribute to a forward bifurcation. The third and fourth terms are positive, deriving from the positive density effect of cannibalism on adult survival. Finally the sign of the last term, which involves the synchrony term $g^{\prime }\left( 0\right) <0$, is ambiguous due to the difference $c_{3}\left( t\right) -c_{4}\left( t\right)$ whose sign is dependent on model parameters.