Skip to main content

Advertisement

SpringerLink
Log in

Kinetics of aggregation with a finite number of particles and application to viral capsid assembly

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

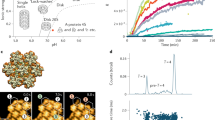
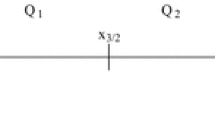
The formation of a viral capsid can be seen as a time-dependent process generated by the arrival of aggregates of various sizes at a nucleation site. Based on a model where aggregates arrive at a Poissonian rate to form a capsid particle, we develop kinetics assembly equations, that account for a finite size cluster and thus for rejection of too large aggregate. The model is derived under the assumption that the aggregate distribution has reached an exponential steady state. To account for the stochastic nature of the aggregates arrival, we also derive a stochastic equation to compute the mean time for a cluster to be formed. We find that this time has a minimum for a unique aggregate distribution. We obtain asymptotic expression for this time that we compare with numerically simulations. Finally, we find the mean size of the largest aggregate forming a viral capsid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Becker R, Döring W (1935) Kinetische Behandlung der Keimbildung in übersättigten Dämpfern. Ann Phys (Leipzig) 24:719–752

    Article  MATH  Google Scholar 

  • Chandrasekar S (1943) Stochastic problems in physics and astrophysics. Rev Mod Phys 15:1–89

    Article  Google Scholar 

  • Ding Y, Chuan YP, He L, Middelberg AP (2010) Modeling the competition between aggregation and self-assembly during virus-like particle processing. Biotechnol Bioeng 107(3):550–560

    Article  Google Scholar 

  • Doering CR, Ben-Avraham D (1989) Diffusion-limited coagulation in the presence of particle input: Exact results in one dimension. Phys Rev Lett 62:2563

    Article  MathSciNet  Google Scholar 

  • D’Orsogna MR, Lakatos G, Chou T (2012) Stochastic nucleation of incommensurate clusters. J Chem Phys 136:084110

    Article  Google Scholar 

  • Endres D, Zlotnick A (2002) Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys J 83(2):1217–1230

  • Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81(25):23402361

    Article  Google Scholar 

  • Gunzenhäuser J, Olivier N, Pengo T, Manley S (2012) Quantitative Super-resolution imaging reveals protein stoichiometry and nanoscale morphology of assembling HIV-Gag virions. Nano Lett 12(9):4705–4710

    Article  Google Scholar 

  • Hagan MF (2014) Modeling viral capsid assembly. Adv Chem Phys 155:1–42

  • Hoze N, Holcman D (2012) Coagulation-fragmentation for a finite number of particles and application to telomere clustering in the yeast nucleus. Phys Lett A 376(6–7):845–849

    Article  MATH  Google Scholar 

  • Hoze N, Holcman D (2013) Modeling capsid kinetics assembly from the steady state distribution of multi-sizes aggregates. Phys Lett A 376(6—-7):789–892

    Google Scholar 

  • Ivanchenko S et al. (2009) Dynamics of HIV-1 assembly and release. PLoS Pathog 5(11):e1000652

  • Knobler CM, Gelbart WM (2009) Physical chemistry of DNA viruses. Annu Rev Phys Chem 60:367–383

    Article  Google Scholar 

  • Kumar MS, Schwartz R (2010) A parameter estimation technique for stochastic self-assembly systems and its application to human papillomavirus self-assembly. Phys Biol 7(4):045005

  • Ono A, Demirov D, Freed EO (2000) Relationship between human immunodeficiency virus type 1 Gag multimerization and membrane binding. J Virol 74:51425150

    Google Scholar 

  • Schuss Z (2010) Diffusion and stochastic processes: an analytical approach. Springer, New York

    Google Scholar 

  • von Smoluchowski M (1916) Versuch einer mathematischen Theorie der Koagulationskinetik kolloider. Lösungen Phys Z 17:557

    Google Scholar 

  • Tritel M, Resh MD (2000) Kinetic analysis of human immunodeficiency virus type 1 assembly reveals the presence of sequential intermediates. J Virol 74:58455855

    Article  Google Scholar 

  • Twarock R (2006) Mathematical virology: a novel approach to the structure and assembly of viruses. Philos Transact A Math Phys Eng Sci 364(1849):3357–3373

    Article  MATH  MathSciNet  Google Scholar 

  • Wattis JAD (2006) An introduction to mathematical models of coagulation fragmentation processes: a discrete deterministic mean-field approach. Phys D : Nonlinear Phenomena 222(1):120

    MathSciNet  Google Scholar 

  • Yvenic R, D’Orsogna MR, Chou T (2012) First passage times in stochastic self-assembly. J Chem Phys 137(24):244107

  • Zandi R, Reguera D, Bruinsma RF, Gelbart WM, Rudnick J (2004) Origin of icosahedral symmetry in viruses. Proc Natl Acad Sci USA 101(44):15556–15560

    Article  Google Scholar 

Download references

Acknowledgments

N. Hoze is supported by a Labex MemoLife fellowship. D. H. research is supported by an ERC-starting-Grant

Author information

Authors and Affiliations

  1. Group of Computational Biology and Applied Mathematics, Ecole Normale Supérieure, Institute for Biology, IBENS, 46 rue d’Ulm, 75005 , Paris, France

    Nathanael Hoze & David Holcman

Authors
  1. Nathanael Hoze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Holcman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to David Holcman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hoze, N., Holcman, D. Kinetics of aggregation with a finite number of particles and application to viral capsid assembly. J. Math. Biol. 70, 1685–1705 (2015). https://doi.org/10.1007/s00285-014-0819-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-014-0819-2

Keywords

Mathematics Subject Classification

Search

Navigation