Skip to main content
SpringerLink
Log in

Casson towers and slice links

  • Published:
Inventiones mathematicae Aims and scope

Abstract

We prove that a Casson tower of height 4 contains a flat embedded disc bounded by the attaching circle, and we prove disc embedding results for height 2 and 3 Casson towers which are embedded into a 4-manifold, with some additional fundamental group assumptions. In the proofs we create a capped grope from a Casson tower and use a refined height raising argument to establish the existence of a symmetric grope which has two layers of caps, data which is sufficient for a topological disc to exist, with the desired boundary. As applications, we present new slice knots and links by giving direct applications of the disc embedding theorem to produce slice discs, without first constructing a complementary 4-manifold. In particular we construct a family of slice knots which are potential counterexamples to the homotopy ribbon slice conjecture.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Notes

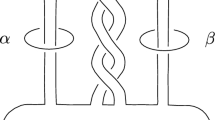
  1. In fact, Freedman showed that a two component link called “Whitehead\({}_3\)” bounds slicing discs in the 4-ball whose complement has free fundamental group. This link is associated to the simplest Casson tower T of height 3, as explained in our Sect. 6.1. It turns out that each of the two slicing discs is ambiently isotopic to the standard disc in the 4-ball by [20, 11.7 A]. It follows that the exterior of one slicing disc is T and the other slicing disc is bounded by C(T).

References

  1. Abe, T., Tange, M.: A construction of slice knots via annulus twists (2013). arXiv:1305.7492

  2. Bižaca, Ž.: A reimbedding algorithm for Casson handles. Trans. Am. Math. Soc. 345(2), 435–510 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bonahon, F.: Ribbon fibred knots, cobordism of surface diffeomorphisms and pseudo-Anosov diffeomorphisms. Math. Proc. Camb. Philos. Soc. 94(2), 235–251 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Casson, A.J.: Three lectures on new-infinite constructions in \(4\)-dimensional manifolds, À la recherche de la topologie perdue, Progr. Math., vol. 62, Birkhäuser, Boston, pp. 201–244 (1986) (with an appendix by L. Siebenmann)

  5. Casson, A.J., Freedman, M.H.: Atomic surgery problems. In: Durham, N.H. (ed.) Four-Manifold Theory, Contemp. Math., vol. 35. Amer. Math. Soc., Providence, pp. 181–199 (1982)

  6. Cochran, T.D., Friedl, S., Teichner, P.: New constructions of slice links. Comment. Math. Helv. 84(3), 617–638 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Casson, A.J., Gordon, C.McA.: A loop theorem for duality spaces and fibred ribbon knots. Invent. Math. 74(1), 119–137 (1983)

  8. Casson, A.J., Gordon, C.McA.: Cobordism of classical knots, À la recherche de la topologie perdue. Birkhäuser, Boston, pp. 181–199 (1986) (with an appendix by P. M. Gilmer)

  9. Cochran, T.D., Horn, P.D.: Structure in the bipolar filtration of topologically slice knots. Algebr. Geom. Topol. 15(1), 415–428 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cochran, T.D., Harvey, S., Horn, P.: Filtering smooth concordance classes of topologically slice knots. Geom. Topol. 17(4), 2103–2162 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cochran, T.D., Orr, K.E., Teichner, P.: Knot concordance, Whitney towers and \(L^2\)-signatures. Ann. Math. (2) 157(2), 433–519 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cochran, T.D., Orr, K.E., Teichner, P.: Structure in the classical knot concordance group. Comment. Math. Helv. 79(1), 105–123 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cappell, S.E., Shaneson, J.L.: The codimension two placement problem and homology equivalent manifolds. Ann. Math. (2) 99, 277–348 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  14. Cochran, T.D., Teichner, P.: Knot concordance and von Neumann \(\rho \)-invariants. Duke Math. J. 137(2), 337–379 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Davis, J.F.: A two component link with Alexander polynomial one is concordant to the Hopf link. Math. Proc. Cambr. Philos. Soc. 140(2), 265–268 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  16. Davis, J.F., Naik, S.: Alexander polynomials of equivariant slice and ribbon knots in \(S^3\). Trans. Am. Math. Soc. 358(7), 2949–2964 (2006, electronic)

  17. Edwards, R.D.: The solution of the \(4\)-dimensional annulus conjecture (after Frank Quinn), Four-manifold theory (Durham, N.H., 1982), Contemp. Math., vol. 35, pp. 211–264. Amer. Math. Soc., Providence (1984)

  18. Freedman, M.H., and Freedman, T.: Bing topology and Casson handles (2013). http://people.mpim-bonn.mpg.de/sbehrens/files/Freedman2013.pdf

  19. Freedman, M.H., Lin, X.-S.: On the \((A, B)\)-slice problem. Topology 28(1), 91–110 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  20. Freedman, M.H., Quinn, F.: Topology of 4-manifolds, Princeton Mathematical Series, vol. 39. Princeton University Press, Princeton (1990)

  21. Freedman, M.H.: A surgery sequence in dimension four; the relations with knot concordance. Invent. Math. 68(2), 195–226 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  22. Freedman, M.H.: The topology of four-dimensional manifolds. J. Differ. Geom. 17(3), 357–453 (1982)

    MathSciNet  MATH  Google Scholar 

  23. Freedman, M.H.: A new technique for the link slice problem. Invent. Math. 80(3), 453–465 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  24. Freedman, M.H.: White head\(_{3}\) is a “slice” link. Invent. Math. 94(1), 175–182 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  25. Freedman, M.H.: Link compositions and the topological slice problem. Topology 32(1), 145–156 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  26. Friedl, S.: Eta invariants as sliceness obstructions and their relation to Casson–Gordon invariants. Algebr. Geom. Topol. 4, 893–934 (2004, electronic)

  27. Freedman, M.H., Teichner, P.: \(4\)-manifold topology. I. Subexponential groups. Invent. Math. 122(3), 509–529 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  28. Michael, H., Teichner, P.: \(4\)-manifold topology. II. Dwyer’s filtration and surgery kernels. Invent. Math. 122(3), 531–557 (1995)

    MathSciNet  MATH  Google Scholar 

  29. Friedl, S., Peter, T.: New topologically slice knots. Geom. Topol. 9, 2129–2158 (2005, electronic)

  30. Gompf, R.E., Singh, S.: On Freedman’s reimbedding theorems, Four-manifold theory (Durham, N.H., 1982), Contemp. Math., vol. 35, pp. 277–309. Amer. Math. Soc., Providence (1984)

  31. Gompf, R.E., Stipsicz, A.I.: \(4\)-Manifolds and Kirby Calculus, Graduate Studies in Mathematics, vol. 20. American Mathematical Society, Providence (1999)

    MATH  Google Scholar 

  32. Gompf, R.E., Scharlemann, M., Thompson, A.: Fibered knots and potential counterexamples to the property 2R and slice-ribbon conjectures. Geom. Topol. 14(4), 2305–2347 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Garoufalidis, S., Teichner, P.: On knots with trivial Alexander polynomial. J. Differ. Geom. 67(1), 167–193 (2004)

    MathSciNet  MATH  Google Scholar 

  34. Hedden, M., Livingston, C., Ruberman, D.: Topologically slice knots with nontrivial Alexander polynomial. Adv. Math. 231(2), 913–939 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  35. Kervaire, M.A.: Les nœuds de dimensions supérieures. Bull. Soc. Math. Fr. 93, 225–271 (1965)

    MathSciNet  MATH  Google Scholar 

  36. Kirby, R.C.: Problems in low dimensional topology . In: Proceedings of Georgia Topology Conference, Part 2, pp. 35–473. Press (1995)

  37. Krushkal, V.S., Quinn, F.: Subexponential groups in 4-manifold topology. Geom. Topol. 4, 407–430 (2000, electronic)

  38. Krushkal, V.S.: On the relative slice problem and four-dimensional topological surgery. Math. Ann. 315(3), 363–396 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  39. Krushkal, V.S.: A counterexample to the strong version of Freedman’s conjecture. Ann. Math. (2) 168(2), 675–693 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  40. Krushkal, V.: “Slicing” the Hopf link. Geom. Topol. 19(3), 1657–1683 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  41. Kirby, R.C., and Taylor, L.R.: A survey of 4-manifolds through the eyes of surgery, Surveys on surgery theory, vol. 2, Ann. of Math. Stud., vol. 149. Princeton Univ. Press, Princeton, pp. 387–421 (2001)

  42. Levine, J.P.: Knot cobordism groups in codimension two. Comment. Math. Helv. 44, 229–244 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  43. Levine, A.S.: Slicing mixed Bing–Whitehead doubles. J. Topol. 5(3), 713–726 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  44. Levine, J.P., Orr, K.E.: A survey of applications of surgery to knot and link theory, Surveys on surgery theory, vol. 1, Ann. of Math. Stud., vol. 145, pp. 345–364. Princeton Univ. Press, Princeton (2000)

  45. Milnor, J.W.: Link groups. Ann. Math. (2) 59, 177–195 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  46. Miyazaki, K.: Nonsimple, ribbon fibered knots. Trans. Am. Math. Soc. 341(1), 1–44 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  47. Otto, C.: The \((n)\)-solvable filtration of link concordance and Milnor’s invariants. Algebr. Geom. Topol. 14(5), 2627–2654 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  48. Quinn, F.: Ends of maps. III. Dimensions \(4\) and \(5\). J. Differ. Geom. 17(3), 503–521 (1982)

    MathSciNet  MATH  Google Scholar 

  49. Ray, A.: Casson towers and filtrations of the knot concordance group. Algebr. Geom. Topol. (2013, preprint). arXiv:1309.7532

Download references

Acknowledgments

The authors would like to thank Kent Orr and Peter Teichner for some very helpful conversations and suggestions. Wojciech Politarczyk and Mark Powell worked together on the combinatorics chapter for the Freedman lecture notes, from which the proof of Lemma 3.7 is derived, and Mark Powell gained a great deal of understanding from this collaboration. We also thank the referees for their very useful comments. Jae Choon Cha was partially supported by NRF grants 2013067043 and 2013053914.

Author information

Authors and Affiliations

  1. Department of Mathematics, POSTECH, Pohang, 790-784, Republic of Korea

    Jae Choon Cha

  2. School of Mathematics, Korea Institute for Advanced Study, Seoul, 130-722, Republic of Korea

    Jae Choon Cha

  3. Départment de Mathématiques, UQAM, Montreal, QC, Canada

    Mark Powell

Authors
  1. Jae Choon Cha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark Powell
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jae Choon Cha.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cha, J.C., Powell, M. Casson towers and slice links. Invent. math. 205, 413–457 (2016). https://doi.org/10.1007/s00222-015-0639-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-015-0639-z

Mathematics Subject Classification

Search

Navigation