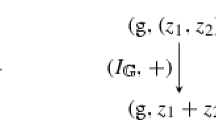Parseval Frames of Exponentially Localized Magnetic Wannier Functions

Abstract

Motivated by the analysis of gapped periodic quantum systems in presence of a uniform magnetic field in dimension $d \le 3$, we study the possibility to construct spanning sets of exponentially localized (generalized) Wannier functions for the space of occupied states. When the magnetic flux per unit cell satisfies a certain rationality condition, by going to the momentum-space description one can model m occupied energy bands by a real-analytic and ${{\mathbb {Z}}}^{d}$-periodic family $\left\{ P(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^{d}}$ of orthogonal projections of rank m. A moving orthonormal basis of ${{\,\mathrm{Ran}\,}}P(\mathbf{k})$ consisting of real-analytic and ${{\mathbb {Z}}}^d$-periodic Bloch vectors can be constructed if and only if the first Chern number(s) of P vanish(es). Here we are mainly interested in the topologically obstructed case. First, by dropping the generating condition, we show how to algorithmically construct a collection of $m-1$orthonormal, real-analytic, and ${{\mathbb {Z}}}^d$-periodic Bloch vectors. Second, by dropping the linear independence condition, we construct a Parseval frame of $m+1$ real-analytic and ${{\mathbb {Z}}}^d$-periodic Bloch vectors which generate ${{\,\mathrm{Ran}\,}}P(\mathbf{k})$. Both algorithms are based on a two-step logarithm method which produces a moving orthonormal basis in the topologically trivial case. A moving Parseval frame of analytic, ${{\mathbb {Z}}}^d$-periodic Bloch vectors corresponds to a Parseval frame of exponentially localized composite Wannier functions. We extend this construction to the case of magnetic Hamiltonians with an irrational magnetic flux per unit cell and show how to produce Parseval frames of exponentially localized generalized Wannier functions also in this setting. Our results are illustrated in crystalline insulators modelled by 2d discrete Hofstadter-like Hamiltonians, but apply to certain continuous models of magnetic Schrödinger operators as well.

Appendix A: Black Boxes

In this Appendix we will provide more details and appropriate references for a number of tools and “black boxes” employed in the paper.

1.1 A.1. Smoothing argument

We start by providing a smoothing argument that allows to produce real-analytic Bloch vectors from continuous ones.

Lemma A.1

(Smoothing argument). Let $\left\{ P(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^d}$ be a family of orthogonal projections admitting an analytic, ${{\mathbb {Z}}}^d$-periodic analytic extension to a complex strip around ${{\mathbb {R}}}^d \subset {{\mathbb {C}}}^d$. Assume that there exist continuous, ${{\mathbb {Z}}}^d$-periodic, and orthogonal Bloch vectors $\left\{ \xi _1,..., \xi _m \right\}$ for $\left\{ P(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^d}$. Then, there exist also real-analytic, ${{\mathbb {Z}}}^d$-periodic, and orthogonal Bloch vectors $\left\{ \widehat{\xi }_1,..., \widehat{\xi }_m \right\}$.

The same holds true if analyticity is replaced by $C^r$-smoothness for some $r \in {{\mathbb {N}}}\cup \left\{ \infty \right\}$.

Proof

(sketch). We sketch here the proof: more details can be found in [9, Sec. 2.3].

Define

$$\begin{aligned} g(\mathbf{k}) = g(k_1, \ldots , k_d) := \frac{1}{\pi ^d} \prod _{j=1}^{d} \frac{1}{1+k_j^2}. \end{aligned}$$

The function g is analytic over the strip $\left\{ {\mathbf {z}}=(z_1, \ldots , z_d) \in {{\mathbb {C}}}^d : \left| \mathrm {Im} \, z_j \right| < 1, \, j \in \right. \left. \left\{ 1,\ldots ,d \right\} \right\}$ and obeys $\int _{{{\mathbb {R}}}^d} g(\mathbf{k}) \, \mathrm {d}\mathbf{k}= 1$. For $\delta > 0$, define $g_\delta (\mathbf{k}) := \delta ^{-d} g(\mathbf{k}/\delta )$. Set

$$\begin{aligned} \psi _a^{(\delta )}(\mathbf{k}) := \int _{{{\mathbb {R}}}^d} g_\delta (\mathbf{k}- \mathbf{k}') \, \xi _a(\mathbf{k}') \, \mathrm {d}\mathbf{k}', \quad a \in \left\{ 1,...,m \right\} , \quad \mathbf{k}\in {{\mathbb {R}}}^d. \end{aligned}$$

The above define ${{\mathbb {Z}}}^d$-periodic vectors which admit an analytic extension to a strip of half-width $\delta$ around the real axis in ${{\mathbb {C}}}^d$, and moreover converge to $\xi _a$ uniformly as $\delta \rightarrow 0$. We note here that an alternative way of smoothing has been suggested to us by G. Panati: he proposed taking the convolution with the Fejér kernel, which has the advantage of integrating on $[-1/2,1/2]^d$ and not on the whole ${{\mathbb {R}}}^d$.

Now denote $\phi _a^{(\delta )}(\mathbf{k}) := P(\mathbf{k}) \, \psi _a^{(\delta )}(\mathbf{k})$, for $a \in \left\{ 1,...,m \right\}$ and $\mathbf{k}\in {{\mathbb {R}}}^d$. Then for any $\epsilon > 0$ there exists $\delta > 0$ such that $\phi _a^{(\delta )}(\mathbf{k})$ and $\xi _a(\mathbf{k})$ are uniformly at a distance less then $\epsilon$. Moreover, as the $\xi _a$’s are orthogonal, we can make sure that the Gram–Schmidt matrix $S^{(\delta )}(\mathbf{k})_{ab} := \left\langle \phi _a^{(\delta )}(\mathbf{k}), \phi _b^{(\delta )}(\mathbf{k}) \right\rangle$ is close to the identity matrix, uniformly in $\mathbf{k}$, possibly at the price of choosing an even smaller $\delta$. This implies that $S^{(\delta )}(\mathbf{k})^{-1/2}$ is real-analytic and ${{\mathbb {Z}}}^d$-periodic, and hence the vectors

$$\begin{aligned} \widehat{\xi }_a(\mathbf{k}) := \sum _{b=1}^{m} \phi _b^{(\delta )}(\mathbf{k}) \, \left[ S^{(\delta )}(\mathbf{k})^{-1/2}\right] _{ba} \end{aligned}$$

define the required real-analytic, ${{\mathbb {Z}}}^d$-periodic, and orthogonal Bloch vectors. $\quad \square$

1.2 A.2. Parallel transport

We recall here the definition of parallel transport associated to a smooth and ${{\mathbb {Z}}}^d$-periodic family of projections $\left\{ P(k_1,\ldots ,k_d) \right\} _{(k_1,\ldots ,k_d) \in {{\mathbb {R}}}^d}$ acting on an Hilbert space ${\mathcal {H}}$.

Fix $i \in \left\{ 1,\ldots , d \right\}$. For $(k_1,\ldots ,k_d) \in {{\mathbb {R}}}^d$, denote by $\mathbf{k}\in {{\mathbb {R}}}^D$, $D=d-1$, the collection of coordinates different from the i-th. We use the shorthand notation $(k_1,\ldots ,k_d) \equiv (k_i,\mathbf{k})$ throughout this Subsection.

Define

$$\begin{aligned} A_{\mathbf{k}}(k_i) := \mathrm {i}\left[ \partial _{k_i} P(k_i, \mathbf{k}), P(k_i, \mathbf{k}) \right] , \quad (k_i,\mathbf{k}) \in {{\mathbb {R}}}^d. \end{aligned}$$

(A.1)

Then $A_{\mathbf{k}}(k_i)$ defines a self-adjoint operator on ${\mathcal {H}}$. The solution to the operator-valued Cauchy problem

$$\begin{aligned} \mathrm {i}\, \partial _{k_i} T_{\mathbf{k}}(k_i, k_i^0) = A_{\mathbf{k}}(k_i) \, T_{\mathbf{k}} (k_i, k_i^0), \quad T_{\mathbf{k}}(k_i^0, k_i^0) = {\mathbf {1}}, \end{aligned}$$

(A.2)

defines a family of unitary operators on ${\mathcal {H}}$, called the parallel transport unitaries (along the i-th direction). In the following we will fix $k_i^0=0$. This notion coincides with the one in differential geometry of the parallel transport along the straight line from $(0,\mathbf{k})$ to $(k_i,\mathbf{k})$ associated to the Berry connection on the Bloch bundle. The parallel transport unitaries satisfy the properties listed in the following result.

Lemma A.2

Let $\left\{ P(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^d}$ be a smooth (respectively analytic) and ${{\mathbb {Z}}}^d$-periodic family of orthogonal projections acting on an Hilbert space ${\mathcal {H}}$. Then the family of parallel transport unitaries $\left\{ T_{\mathbf{k}}(k_i, 0) \right\} _{k_i \in {{\mathbb {R}}}, \, \mathbf{k}\in {{\mathbb {R}}}^D}$ defined in (A.2) satisfies the following properties:

• (1) the map ${{\mathbb {R}}}^d \ni \mathbf{k}= (k_i, \mathbf{k}) \mapsto T_{\mathbf{k}}(k_i, 0) \in {\mathcal {U}}({\mathcal {H}})$ is smooth (respectively real-analytic);

• (2) for all $k_i \in {{\mathbb {R}}}$ and $\mathbf{k}\in {{\mathbb {R}}}^D$

  $$\begin{aligned} T_{\mathbf{k}}(k_i+1, 1) = T_{\mathbf{k}}(k_i, 0) \end{aligned}$$

  and

  $$\begin{aligned} T_{\mathbf{k}+ {\mathbf {n}}}(k_i, 0) = T_{\mathbf{k}}(k_i, 0) \quad \text {for } {\mathbf {n}} \in {{\mathbb {Z}}}^D; \end{aligned}$$

• (3) the intertwining property

  $$\begin{aligned} P(k_i, \mathbf{k}) = T_{\mathbf{k}}(k_i, 0) \, P(0, \mathbf{k}) \, T_{\mathbf{k}}(k_i, 0)^{-1} \end{aligned}$$

  holds for all $k_i \in {{\mathbb {R}}}$ and $\mathbf{k}\in {{\mathbb {R}}}^D$ .

A proof of all these properties can be found for example in [19] or in [9, Sec. 2.6].

In (5.2), the parallel transport unitary ${\mathcal {T}}(\mathbf{k}) := T_{\mathbf{k}}(1,0)$ is employed to define the continuous, ${{\mathbb {Z}}}^D$-periodic family of unitary matrices $\left\{ \alpha (\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^D}$. Let $j \in \left\{ 1, \ldots , d \right\}$, $j \ne i$. The integrand in the formula (5.3) for $\deg _j(\det \alpha )$ can be expressed in terms of the parallel transport unitaries as

$$\begin{aligned} {{\,\mathrm{tr}\,}}_{{{\mathbb {C}}}^m} \left( \alpha (\mathbf{k})^* \partial _{k_j} \alpha (\mathbf{k}) \right) = {{\,\mathrm{Tr}\,}}_{{\mathcal {H}}} \left( P(0,\mathbf{k}) \, {\mathcal {T}}(\mathbf{k})^* \partial _{k_j} {\mathcal {T}}(\mathbf{k}) \right) \end{aligned}$$

(compare [11, Lemma 6.1]). Besides, by the Duhamel formula we have

$$\begin{aligned} \partial _{k_j} T_{\mathbf{k}}(k_i,0) = T_{\mathbf{k}}(k_i,0) \, \int _{0}^{k_i} \mathrm {d}s \, T_{\mathbf{k}}(s,0)^* \, \partial _{k_j} A_{\mathbf{k}}(s) \, T_{\mathbf{k}}(s,0), \end{aligned}$$

where $A_{\mathbf{k}}(s)$ is as in (A.1) (compare [11, Lemma 6.2]). On the other hand, one can also compute

$$\begin{aligned} P(k_i,\mathbf{k}) \, \partial _{k_j} A_{\mathbf{k}}(k_i) \, P(k_i,\mathbf{k}) = P(k_i,\mathbf{k}) \, [ \partial _{k_i} P(k_i,\mathbf{k}), \partial _{k_j} P(k_i,\mathbf{k}) ] \, P(k_i,\mathbf{k}) \end{aligned}$$

so that, denoting ${\mathbf {K}} := (k_i,\mathbf{k}) \in {{\mathbb {R}}}^d$,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}_{{\mathcal {H}}} \left( P(0,\mathbf{k}) \, {\mathcal {T}}(\mathbf{k})^* \partial _{k_j} {\mathcal {T}}(\mathbf{k}) \right) = \int _{0}^{1} \mathrm {d}k_i \, {{\,\mathrm{Tr}\,}}_{{\mathcal {H}}} \left( P({\mathbf {K}}) \, \left[ \partial _{k_i} P({\mathbf {K}}), \partial _{k_j} P({\mathbf {K}}) \right] \right) \end{aligned}$$

(compare [11, Eqn. (6.13)]). Putting all the above equalities together, we conclude that

$$\begin{aligned} \deg _j(\det \alpha ) = \frac{1}{2 \pi \mathrm {i}} \int _{0}^{1} \mathrm {d}k_j \int _{0}^{1} \mathrm {d}k_i \, {{\,\mathrm{Tr}\,}}_{{\mathcal {H}}} \left( P({\mathbf {K}}) \, \left[ \partial _{k_i} P({\mathbf {K}}), \partial _{k_j} P({\mathbf {K}}) \right] \right) = c_1(P)_{ij}, \end{aligned}$$

see (3.2). The above equality proves Proposition 5.3 as well as Equation (5.8).

1.3 A.3 Cayley transform

An essential tool to produce “good” logarithms for families of unitary matrices which inherit properties like continuity and ($\gamma$-)periodicity is the Cayley transform. We recall here this construction.

Lemma A.3

(Cayley transform). Let $\left\{ \alpha (\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^{D}}$ be a family of unitary matrices which is continuous and ${{\mathbb {Z}}}^{D}$-periodic. Assume that $-1$ lies in the resolvent set of $\alpha (\mathbf{k})$ for all $\mathbf{k}\in {{\mathbb {R}}}^{D}$. Then one can construct a family $\left\{ h(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^{D}}$ of self-adjoint matrices which is continuous, ${{\mathbb {Z}}}^{D}$-periodic and such that

$$\begin{aligned} \alpha (\mathbf{k}) = \mathrm {e}^{\mathrm {i}\, h(\mathbf{k})} \quad \text {for all } \mathbf{k}\in {{\mathbb {R}}}^{D}. \end{aligned}$$

If $D=2$ and $\left\{ \alpha (k_2,k_3) \right\} _{(k_2,k_3) \in {{\mathbb {R}}}^2}$ is $\gamma$-periodic (in the sense of Definition 6.1), then the above family of self-adjoint matrices can be chosen to be $\gamma$-periodic as well.

Proof

The proof adapts the one in [11, Prop. 3.5]. The Cayley transform

$$\begin{aligned} s(\mathbf{k}) := \mathrm {i}\, \left( {\mathbf {1}}- \alpha (\mathbf{k}) \right) \, \left( {\mathbf {1}}+ \alpha (\mathbf{k}) \right) ^{-1} \end{aligned}$$

is self-adjoint, depends continuously on $\mathbf{k}$, and is ${{\mathbb {Z}}}^D$-periodic (respectively $\gamma$-periodic) if $\alpha$ is as well. One also immediately verifies that

$$\begin{aligned} \alpha (\mathbf{k}) = \left( {\mathbf {1}}+ \mathrm {i}\, s(\mathbf{k}) \right) \, \left( {\mathbf {1}}- \mathrm {i}\, s(\mathbf{k}) \right) ^{-1}. \end{aligned}$$

Let ${\mathcal {C}}$ be a closed, positively-oriented contour in the complex plane which encircles the real spectrum of $s(\mathbf{k})$ for all $\mathbf{k}\in {{\mathbb {R}}}^D$. Let $\log (\cdot )$ denote the choice of the complex logarithm corresponding to the branch cut on the negative real semi-axis. Then

$$\begin{aligned} h(\mathbf{k}) := \frac{1}{2 \pi } \oint _{\mathcal {C}} \log \left( \frac{1 + \mathrm {i}\, z}{1 - \mathrm {i}\, z} \right) \left( s(\mathbf{k}) - z {\mathbf {1}}\right) ^{-1} \, \mathrm {d}z, \quad \mathbf{k}\in {{\mathbb {R}}}^D, \end{aligned}$$

obeys all the required properties. $\quad \square$

1.4 A.4 Generically non-degenerate spectrum of families of unitary matrices

The aim of this Subsection is to prove that

Proposition A.4

Let $D \le 2$. Consider a continuous and ${{\mathbb {Z}}}^D$-periodic family of unitary matrices $\left\{ \alpha (\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^D}$. Then, one can construct a sequence of continuous, ${{\mathbb {Z}}}^D$-periodic families of unitary matrices $\left\{ \alpha _n(\mathbf{k}) \right\} _{\mathbf{k}\in {{\mathbb {R}}}^D}$, $n \in {{\mathbb {N}}}$, such that

• $\sup _{\mathbf{k}\in {{\mathbb {R}}}^D} \left\| \alpha _n(\mathbf{k}) - \alpha (\mathbf{k}) \right\| \rightarrow 0$ as $n \rightarrow \infty$, and

• the spectrum of $\alpha _n(\mathbf{k})$ is completely non-degenerate for all $n \in {{\mathbb {N}}}$ and $\mathbf{k}\in {{\mathbb {R}}}^D$.

In $D=2$, the same conclusion holds if periodicity and homotopy are replaced by $\gamma$-periodicity and $\gamma$-homotopy, in the sense of Definition 6.1.

The periodic case for $D\le 2$ has already been treated in [9, 11, 12], but we will sketch below the main ideas and give details on the new, $\gamma$-periodic situation.

We will need two technical results, which we state here.

Lemma A.5

(Analytic approximation lemma). Consider a uniformly continuous family of unitary matrices $\alpha (k)$ where $k\in [a,b]\subset {{\mathbb {R}}}$. Let I be any compact set completely included in [a, b]. Then one can construct a sequence $\left\{ \alpha _n(k) \right\} _{k\in I}$, $n \in {{\mathbb {N}}}$, of families of unitary matrices which are real-analytic on I and such that

$$\begin{aligned} \sup _{k\in I} \left\| \alpha _n(k) - \alpha (k) \right\| \rightarrow 0 \quad \text {as } n \rightarrow \infty . \end{aligned}$$

If $\alpha$ is continuous and ${\mathbb {Z}}$-periodic, the same is true for $\alpha _n$ and the approximation is uniform on ${{\mathbb {R}}}$. This last statement can be extended to any $D\ge 1$.

Proof

(sketch). The proof proceeds in the same spirit of Lemma A.1 above. First, we take the convolution with a real-analytic kernel and obtain a smooth matrix $\beta (k)$ which is close in norm to $\alpha (k)$. Thus $\kappa :=\beta ^*\beta$ must be close to the identity matrix, it is self-adjoint and real-analytic, and the same holds true for $\kappa ^{1/2}$. Finally, we restore unitarity by writing $\alpha ':=\beta \kappa ^{1/2}$ and checking that $(\alpha ')^*\alpha '={\mathbf {1}}$. More details can be found in [11, Lemma A.2]. $\quad \square$

Lemma A.6

(Local splitting lemma). For $R > 0$ and $\mathbf{k}_0 \in {{\mathbb {R}}}^D$, denote by $B_R(\mathbf{k}_0)$ the open ball of radius R around $\mathbf{k}_0$. Let $\left\{ \alpha (\mathbf{k}) \right\} _{\mathbf{k}\in B_R(\mathbf{k}_0)}$ be a continuous family of unitary matrices. Then, for some $R' \le R$, one can construct a sequence $\left\{ \alpha _n(\mathbf{k}) \right\} _{\mathbf{k}\in B_{R'}(\mathbf{k}_0)}$, $n \in {{\mathbb {N}}}$, of continuous families of unitary matrices such that

• $\sup _{\mathbf{k}\in B_R(\mathbf{k}_0)} \left\| \alpha _n(\mathbf{k}) - \alpha (\mathbf{k}) \right\| \rightarrow 0$ as $n \rightarrow \infty$, and

• the spectrum of $\alpha _n(\mathbf{k})$ is completely non-degenerate for all $\mathbf{k}\in B_{R'}(\mathbf{k}_0)$.

The proof of the above Lemma can be found in [11, Lemma A.1] for $D=1$ and in [12, Lemma 5.1] for $D=2$.

Proof of Proposition  A.4

The main idea is to lift all the spectral degeneracies of $\alpha$ within the unit interval [0, 1] or the unit square $[0,1] \times [0,1]$, and then extend the approximants with non-degenerate spectrum to the whole ${{\mathbb {R}}}^D$ by either periodicity or $\gamma$-periodicity.

We start with $D=1$. By the analytic approximation Lemma we can find an approximant $\alpha ^{(1)}$ of $\alpha$ which depends analytically on k. If $\alpha ^{(1)}$ has degenerate eigenvalues, then they either cross at isolated points (a finite number of them in the compact interval [0, 1]) or they stay degenerate for all $k \in [0,1]$. Pick a point in [0, 1] which is not an isolated degenerate point. Applying the local splitting Lemma, find a continuous approximant $\alpha ^{(2)}$ of $\alpha ^{(1)}$ for which the second option is ruled out, so that its eigenvalues cannot be constantly degenerate.

Let now $\alpha ^{(3)}$ be an analytic approximation of $\alpha ^{(2)}$, obtained by means of the analytic approximation Lemma. The eigenvalues of $\alpha ^{(3)}$ can only be degenerate at a finite number of points $\left\{ 0< k_1< \cdots< k_S < 1 \right\}$ (we assume without loss of generality that no eigenvalue intersections occur at $k=0$: this can be achieved by means of small shift of the coordinate). By applying the local splitting Lemma to balls of radius 1 / n around each such point (starting from a large enough $n_0$), and extending the definition of the approximants from [0, 1] to ${{\mathbb {R}}}$ by periodicity, we obtain the required continuous and periodic approximants $\alpha _n$ with completely non-degenerate spectrum. Notice that, under the assumption of null-homotopy of $\alpha$, the rest of the argument of Theorem 5.2 applies: in particular, for n sufficiently large $\alpha _n$ admits a continuous and periodic logarithm, namely $\alpha _n(k) = \mathrm {e}^{\mathrm {i}\, h_n(k)}$.

Now we continue with $D=2$. We will only treat the $\gamma$-periodic setting, since the periodic case for $D\le 2$ has been already analyzed in [9, 11, 12].

We start by considering the strip $[0,1]\times {{\mathbb {R}}}$. The matrix $\alpha (0,k_3)$ is periodic, hence we may find a smooth approximation $\alpha _0(k_3)$ which is always non-degenerate and periodic.

The matrix $\alpha (k_2,k_3) \alpha (0,k_3)^{-1}$ is close to the identity near $k_2=0$, and so is $\alpha (k_2,k_3) \alpha _0(k_3)^{-1}$. Hence if $k_2$ is close to 0 we can write (using the Cayley transform)

$$\begin{aligned} \alpha (k_2,k_3)=\mathrm {e}^{\mathrm {i}H_0(k_2,k_3)}\alpha _0(k_3) \end{aligned}$$

where $H_0(k_2,k_3)$ is continuous, periodic in $k_3$, and uniformly close to zero. Due to the $\gamma$-periodicity of $\alpha$, we have that $\alpha (1,k_3)$ and $\gamma (k_3)\alpha _0(k_3)\gamma (k_3)^{-1}$ are also close in norm. Reasoning in the same way as near $k_2=0$ we can write

$$\begin{aligned} \alpha (k_2,k_3)=\mathrm {e}^{\mathrm {i}H_1(k_2,k_3)}\gamma (k_3)\alpha _0(k_3)\gamma (k_3)^{-1} \end{aligned}$$

where $H_1(k_2,k_3)$ is continuous, periodic in $k_3$, and uniformly close to zero near $k_2=1$.

Let $\delta <1/10$. Choose a smooth function $0\le g_\delta \le 1$ such that

$$\begin{aligned} g_\delta (k_2)= {\left\{ \begin{array}{ll} 1 &{} \text {if } k_2\in [0,\delta ]\cup [1-\delta ,1],\\ 0 &{} \text {if } 2\delta \le k_2\le 1-2\delta . \end{array}\right. } \end{aligned}$$

For $0\le k_2\le 1$ and $k_3\in {{\mathbb {R}}}$, define the matrix $\alpha _\delta (k_2,k_3)$ in the following way:

$$\begin{aligned} \alpha _\delta (k_2,k_3):= {\left\{ \begin{array}{ll} \mathrm {e}^{\mathrm {i}(1-g_\delta (k_2))H_0(k_2,k_3)} \, \alpha _0(k_3) &{} \text {if } 0\le k_2\le 3\delta ,\\ \alpha (k_2,k_3) &{} \text {if } 3\delta<k_2< 1-3\delta , \\ \mathrm {e}^{\mathrm {i}(1-g_\delta (k_2))H_1(k_2,k_3)} \, \gamma (k_3) \, \alpha _0(k_3)\, \gamma (k_3)^{-1} &{} \text {if } 1-3\delta \le k_2\le 1. \end{array}\right. } \end{aligned}$$

We notice that $\alpha _\delta$ is continuous, periodic in $k_3$ and converges in norm to $\alpha$ when $\delta$ goes to zero. Moreover,

$$\begin{aligned} \alpha _\delta (1,k_3)=\gamma (k_3)\,\alpha _\delta (0,k_3)\,\gamma (k_3)^{-1}, \end{aligned}$$

which is a crucial ingredient if we want to continuously extend it by $\gamma$-periodicity to ${{\mathbb {R}}}^2$.

We also note that $\alpha _\delta (k_2,k_3)$ is completely non-degenerate when $k_2$ is either 0 or 1, hence by continuity it must remain completely non-degenerate when $k_2\in [0,\epsilon ]\cup [1-\epsilon ,1]$ if $\epsilon$ is small enough.

Following [12], we will explain how to produce an approximation $\alpha '(k_2,k_3)$ of $\alpha _\delta (k_2,k_3)$ with the following properties:

• it coincides with $\alpha _\delta (k_2,k_3)$ if $k_2\in [0,\epsilon ]\cup [1-\epsilon ,1]$,

• it is continuous on $[0,1]\times {{\mathbb {R}}}$ and periodic in $k_3$,

• it is completely non-degenerate on the strip $[0,1]\times {{\mathbb {R}}}$.

Assuming for now that all this holds true, let us investigate the consequences. Because it coincides with $\alpha _\delta$ near $k_2=0$ and $k_2=1$, we also have:

$$\begin{aligned} \alpha '(1,k_3)=\gamma (k_3)\alpha '(0,k_3)\gamma (k_3)^{-1}. \end{aligned}$$

If $k_2>0$ we define recursively

$$\begin{aligned} \alpha '(k_2+1,k_3)=\gamma (k_3)\alpha '(k_2,k_3)\gamma (k_3)^{-1} \end{aligned}$$

and if $k_2<0$

$$\begin{aligned} \alpha '(k_2,k_3)=\gamma (k_3)^{-1}\alpha '(k_2+1,k_3)\gamma (k_3). \end{aligned}$$

Then $\alpha '$ has all the properties required in the statement, and the proof is complete.

Finally let us sketch the main ideas borrowed from [12] which are behind the proof of the three properties of $\alpha '$ listed above.

First, the construction of $\alpha '$ is based on continuously patching non-degenerate local logarithms, which is why the already non-degenerate region $k_2\in [0,\epsilon ]\cup [1-\epsilon ,1]$ is left unchanged.

Second, let us consider the finite segment defined by $k_2\in [\epsilon ,1-\epsilon ]$ and $k_3=0$. The family of matrices $\left\{ \alpha _\delta (k_2,0) \right\}$ is 1-dimensional, with a spectrum which is completely non-degenerate near $k_2=\epsilon$ and $k_2=1-\epsilon$. Reasoning as in the case $D=1$ we can find a continuous approximation $\alpha _2(k_2)$ which is completely non-degenerate on the whole interval $k_2\in [\epsilon ,1-\epsilon ]$. The matrix $\alpha _\delta (k_2,k_3)\alpha _2(k_2)^{-1}$ is close to the identity matrix if $|k_3|\ll 1$, hence we may locally perturb $\alpha _\delta$ near the segment $(\epsilon ,1-\epsilon )\times \{0\}$ so that the new $\alpha _\delta '$ is completely non-degenerate on a small tubular neighborhood of the boundary of the segment $(\epsilon ,1-\epsilon )\times \{0\}$. This perturbation must be taken small enough not to destroy the initial non-degeneracy near $k_2=\epsilon$ and $k_2=1-\epsilon$.

Third, since $\alpha _\delta$ is periodic in $k_3$, the local perturbation around the strip $(\epsilon ,1-\epsilon )\times \{0\}$ can be repeated near all the strips $(\epsilon ,1-\epsilon )\times {\mathbb {Z}}$. The new matrix, $\alpha _\delta ''$, will be non-degenerate near a small tubular neighborhood of any unit square of the type $[0,1]\times [p,p+1]$, with $p\in {\mathbb {Z}}$. The final step is to locally perturb $\alpha _\delta ''$ inside these squares, like in [12, Prop. 5.11]. The splitting method relies in an essential way on the condition $D\le 2$, since it uses the fact that a smooth map between ${{\mathbb {R}}}^D$ and ${{\mathbb {R}}}^3$ cannot have regular values. $\quad \square$

1.5 A.5 Resolvent estimates

In this final Appendix we will prove the estimates on the matrix elements of the resolvent of the Hamiltonian ${{\mathcal {H}}}_\epsilon$ that we used in Sect. 8.

Proposition A.7

(Combes–Thomas type estimate). Consider an operator $H_0$ in $\ell ^2({{\mathbb {Z}}}^2) \otimes {{\mathbb {C}}}^Q$ such that its matrix elements are localized along the diagonal, that is,

$$\begin{aligned} \left| H_0(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')\right| \le C\mathrm {e}^{-\beta _0\Vert \gamma -\gamma '\Vert } \qquad \forall \gamma ,\gamma ' \in {{\mathbb {Z}}}^2 , \quad {{\underline{x}}}, {{\underline{x}}}' \in \left\{ 1,\ldots ,Q \right\} \end{aligned}$$

for some positive constants C and $\beta _0$. Moreover fix a compact set $K\subset \rho ({{\mathcal {H}}}_0)$. Then, there exist two constants $C'$ and $0<\beta <\beta _0$ such that

$$\begin{aligned} \sup _{z\in K} \left\| (H_0-z)^{-1}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}') \right\| \le C' \mathrm {e}^{-\beta \Vert \gamma -\gamma '\Vert } , \quad \forall \, \gamma , \gamma '\in {{\mathbb {Z}}}^2, \, {{\underline{x}}}, {{\underline{x}}}' \in \left\{ 1,\ldots ,Q \right\} . \end{aligned}$$

Proof

Take $\gamma _0 \in {{\mathbb {Z}}}^2$. Consider the operator $H_\beta ^{(\gamma _0)}$ defined by the following matrix elements:

$$\begin{aligned} H^{(\gamma _0)}_\beta (\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}'):=\mathrm {e}^{\beta \Vert \gamma -\gamma _0\Vert }H_0(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')\mathrm {e}^{-\beta \Vert \gamma '-\gamma _0\Vert } , \end{aligned}$$

(A.3)

for all $\gamma , \gamma '\in {{\mathbb {Z}}}^2$, and $\, {{\underline{x}}}, {{\underline{x}}}' \in \left\{ 1,\ldots ,Q \right\}$. Using the inequality $|\mathrm {e}^{x}-1|\le |x| \mathrm {e}^{|x|}$, which holds for all $x\in {{\mathbb {R}}}$, together with the triangle inequality we have

$$\begin{aligned} \sup _{\gamma _0 \in {{\mathbb {Z}}}^2} \left| H^{(\gamma _0)}_\beta (\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')- H_0(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}') \right| \le C \beta \Vert \gamma -\gamma '\Vert \,\mathrm {e}^{-(\beta _0-\beta )\Vert \gamma -\gamma '\Vert }.\qquad \end{aligned}$$

(A.4)

Using a Schur–Holmgren estimate, as soon as $\beta <\beta _0$ we get from (A.4) that $\Vert H_\beta ^{(\gamma _0)}-H_0\Vert \le \beta C$ for all $\gamma _0$. If $z \in K\subset \rho (H_0)$, we can choose a $\beta$ small enough such that the operator

$$\begin{aligned} \left( {\mathbf {1}}+\left( H^{(\gamma _0)}_\beta -H_0 \right) \left( H_0-z\right) ^{-1}\right) \end{aligned}$$

is invertible uniformly in z and $\gamma _0$. Thus we obtain that

$$\begin{aligned} \big (H^{(\gamma _0)}_\beta -z\big )^{-1}=\left( H_0-z\right) ^{-1}\left( {\mathbf {1}}+ \left( H^{(\gamma _0)}_\beta -H_0\right) \left( H_0-z\right) ^{-1}\right) ^{-1}, \end{aligned}$$

which implies

$$\begin{aligned} \sup _{\gamma _0\in {{\mathbb {Z}}}^2}\sup _{z \in K } \left\| \big (H_\beta ^{(\gamma _0)}-z\big )^{-1} \right\| =: A<\infty . \end{aligned}$$

(A.5)

Also, $\beta$ only depends on the minimal distance between z and the spectrum of $H_0$.

We are now ready to prove the exponential localization of the resolvent of $H_0$. From the definition (A.3) of $H^{(\gamma _0)}_\beta$ we obtain that $\mathrm {e}^{-\beta \Vert \cdot -\gamma _0\Vert }H^{(\gamma _0)}_\beta =H_0 \mathrm {e}^{-\beta \Vert \cdot -\gamma _0\Vert }$. From this identity and from (A.5) we get that for every $z \in K$

$$\begin{aligned} \left( H_0-z\right) ^{-1} \mathrm {e}^{-\beta \Vert \cdot -\gamma _0\Vert } = \mathrm {e}^{-\beta \Vert \cdot -\gamma _0\Vert } \big (H^{(\gamma _0)}_\beta -z\big )^{-1} . \end{aligned}$$

(A.6)

Hence (A.6) shows that $\left( H_0-z\right) ^{-1} \mathrm {e}^{-\beta \Vert \cdot -\gamma _0\Vert }$ maps in the domain of the unbounded multiplication operator $\mathrm {e}^{\beta \Vert \cdot -\gamma _0\Vert }$. Finally, considering the vector $\delta _{\gamma _0,{{\underline{x}}}'}$ that is equal to 1 only in $(\gamma _0,{{\underline{x}}}')$, and using the fact that in the discrete setting the $\ell ^\infty$ norm is bounded by the $\ell ^2$ norm, (A.5) implies

$$\begin{aligned} \begin{aligned} \left| \mathrm {e}^{\beta \Vert \gamma -\gamma _0\Vert }\left( H_0-z\right) ^{-1} (\gamma ,{{\underline{x}}};\gamma _0,{{\underline{x}}}' )\right| =\left| \Big ( \big (H_\beta ^{(\gamma _0)}-z\big )^{-1} \delta _{\gamma _0,{{\underline{x}}}'} \Big ) (\gamma ,{{\underline{x}}})\right| \le A \, \end{aligned} \end{aligned}$$

which concludes the proof. $\quad \square$

For the next statement, recall that ${{\mathcal {H}}}_\epsilon$ was defined in (8.1).

Proposition A.8

Fix a compact set $K\subset \rho ({{\mathcal {H}}}_0)$. Then there exist $\epsilon _0>0$, $\alpha <\infty$ and $C<\infty$ such that for every $0\le \epsilon \le \epsilon _0$ we have that $K\subset \rho ({{\mathcal {H}}}_\epsilon )$ and:

$$\begin{aligned} \sup _{z\in K}\left| ({{\mathcal {H}}}_\epsilon -z)^{-1}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')-\mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma ,\gamma ')}({{\mathcal {H}}}_0-z)^{-1}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')\right| \le C\;\epsilon \;\mathrm {e}^{-\alpha \Vert \gamma -\gamma '\Vert }.\nonumber \\ \end{aligned}$$

(A.7)

Proof

By hypothesis we know that $|{{\mathcal {H}}}_0(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')| \le C' \mathrm {e}^{-\beta \Vert \gamma -\gamma '\Vert }$ and hence Proposition A.7 gives us that also $\left| ({{\mathcal {H}}}_0-z)^{-1}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}')\right| \le C'' \mathrm {e}^{-\beta \Vert \gamma -\gamma '\Vert }$, uniformly for every $z \in K$. Consider the operator $S_z^{(\epsilon )}$ defined by the following matrix elements:

$$\begin{aligned} S^{(\epsilon )}_z(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}'):=\mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma ,\gamma ')} ({{\mathcal {H}}}_0-z)^{-1}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}') , \end{aligned}$$

for all $\gamma , \gamma '\in {{\mathbb {Z}}}^2$, and ${{\underline{x}}}, {{\underline{x}}}' \in \left\{ 1,\ldots ,Q \right\}$. Then consider the matrix of $({{\mathcal {H}}}_{\epsilon }-z)S^{(\epsilon )}_z$. Exploiting the magnetic phase composition rule (9.8) and the fact that $\mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma ,\gamma )}=1$ we get

$$\begin{aligned} ({{\mathcal {H}}}_{\epsilon }-z)S^{(\epsilon )}_z=:\mathbf{1} + T_z^{(\epsilon )} , \end{aligned}$$

(A.8)

where $T_z^{(\epsilon )}$ is the operator associated with the matrix elements

$$\begin{aligned} \mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma ,\gamma ')}\sum _{{\widetilde{\gamma }}\in {{\mathbb {Z}}}^2}\sum _{{\widetilde{x}}=1}^{Q} \left( \mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma -{\widetilde{\gamma }},{\widetilde{\gamma }}-\gamma ')}-1\right) {{\mathcal {H}}}_0(\gamma ,{{\underline{x}}};{\widetilde{\gamma }},{\widetilde{x}}) ({{\mathcal {H}}}_0-z)^{-1}({\widetilde{\gamma }},{\widetilde{x}};\gamma ',{{\underline{x}}}') ,\nonumber \\ \end{aligned}$$

(A.9)

for all $\gamma , \gamma '\in {{\mathbb {Z}}}^2$, and ${{\underline{x}}}, {{\underline{x}}}' \in \left\{ 1,\ldots ,Q \right\}$. Now note that

$$\begin{aligned} \left| \mathrm {e}^{\mathrm {i}\epsilon \phi (\gamma -{\widetilde{\gamma }},{\widetilde{\gamma }}-\gamma ')}-1\right| \le \frac{\epsilon }{2} \Vert \gamma -{\widetilde{\gamma }}\Vert \Vert {\widetilde{\gamma }}-\gamma '\Vert . \end{aligned}$$

Considering the exponential localization of ${{\mathcal {H}}}_0$ and $({{\mathcal {H}}}_0-z)^{-1}$, a simple computation shows that, for every $\alpha <\beta$,

$$\begin{aligned} \mathrm {e}^{\alpha \Vert \gamma -\gamma '\Vert } \left| T_z^{(\epsilon )}(\gamma ,{{\underline{x}}};\gamma ',{{\underline{x}}}') \right| \le {\widetilde{C}} \epsilon , \end{aligned}$$

(A.10)

where ${\widetilde{C}}$ is some constant independent of z. Hence a Schur–Holmgren estimate now proves that $\Vert T_z^{(\epsilon )}\Vert \le {\tilde{C}}\epsilon$. So, fix an $\epsilon _0$ such that the norm of $T_z^{(\epsilon )}$ is less than 1, then for every $\epsilon \le \epsilon _0$ we can invert the operator $\mathbf{1}+T_z^{(\epsilon )}$. Due to the selfadjointness of ${{\mathcal {H}}}_{\epsilon }$ we know a priori that $({{\mathcal {H}}}_\epsilon -z)$ is invertible for every z such that $\mathrm {Im} \, z \ne 0$. So, from (A.8) we obtain that

$$\begin{aligned} ({{\mathcal {H}}}_\epsilon -z)^{-1}=S_z^{(\epsilon )}\left( { \mathbf 1}+T_z^{(\epsilon )}\right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Vert ({{\mathcal {H}}}_\epsilon -z)^{-1}\Vert \le \Vert S_z^{(\epsilon )}\Vert < C , \end{aligned} \end{aligned}$$

where C is a constant that depends only on K and does not depend on the imaginary part of z. So we can conclude that K is also in the resolvent set of ${{\mathcal {H}}}_{\epsilon }$ whenever $\epsilon \le \epsilon _0$. Finally, from (A.8) we have that $S_z^{(\epsilon )}-({{\mathcal {H}}}_\epsilon -z)^{-1} = ({{\mathcal {H}}}_\epsilon -z)^{-1} T_z^{(\epsilon )}$. Since K is in the resolvent set of ${{\mathcal {H}}}_\epsilon$, using Proposition A.7 we infer that $({{\mathcal {H}}}_\epsilon -z)^{-1}$ has matrix elements localized around the diagonal, hence (A.7) follows taking into account (A.10). $\quad \square$