1 Introduction

The chemistry of group 12 metals (M=Zn, Cd, Hg) is dominated by their + 2 oxidation state which is caused by the ease of loss of the outermost ns2 valence electrons [1]. A far less common oxidation state is + 1. Cp*Zn–ZnCp* (Cp* = pentamethylcyclopentadiene) [2, 3], Cd2[AlCl4]2 [4, 5] and Hg2Cl2 [6] are prominent examples of the latter category. The examples of molecular complexes having zero-valent oxidation state of the group 12 metals are very scarce. Scant examples of possible zero-valent Zn in complicated systems like Zn-encapsulated MFI-type zeolite [7] and [{Mo(CO)4}4(Zn)6(μ-ZnCp*)4] featuring a Mo4Zn6 tetrahedron [8] with Mo0–Zn0–Mo0 edges were reported. A set of comparatively simpler systems containing an M0 (M=Zn, Cd, Hg) center between two ZnI centers in (LZn)2M, where L is a sterically bulky amide, was reported by Jones et al. in 2015 [9]. Transient Zn(CO)n (n = 1, 2) and Cd(CO)2 molecules were also made in solid neon and characterized using matrix-isolation infrared spectroscopy [10, 11].

In 2006, Segawa et al. [12] synthesized {(HCNDipp)2B}Li(THF)2 (Dipp = 2,6-iPr2C6H3; henceforth {(HCNDipp)2B} is abbreviated as NHBDipp), where the anionic boron ligand acts as an excellent nucleophile, and consequently, a variety of stable complexes of NHBDipp ligand with main group and transition metal atoms were reported in the literature [13,14,15,16,17,18,19,20,21]. In 2008, Nozaki and co-workers prepared the Zn(NHBDipp)2 complex [22], and in 2014, Aldridge and co-workers synthesized its Cd and Hg homologues [23]. Given the fact that NHBDipp ligand is available in anionic form as Li salt, they were often treated as M(II) complexes [23, 24]. Very recently, it was theoretically shown that NHBMe facilitates the formation of an M0–M0 single bond in M2(NHBMe)2 (M=Zn, Cd, Hg) complexes [25].

On the other hand, M[Mn(CO)5]2 (M=Zn, Cd, Hg) complexes have been known synthetically for a long time. While Hg[Mn(CO)5]2 was first synthesized in 1960 by Hieber and Schropp [26], its lighter homologues, M[Mn(CO)5]2 (M=Zn, Cd), were prepared in 1968 by Burlitch [27]. Later on, some alternative procedures were also reported to synthesize these complexes [28,29,30,31,32]. They were characterized by IR and/or Raman spectroscopic studies which suggest that these complexes possess highly symmetric D4h or D4d structures. However, an X-ray structure is only available for Hg[Mn(CO)5]2 showing the molecule with an approximate D4h symmetry [33, 34] Since Mn(CO)5− is an 18-electron complex, these complexes are generally described with interaction between M2+ and two Mn(CO)5− ligands, giving the formal oxidation state + 2 for M [30]. But an in-depth bonding analysis for these complexes is missing which leads to the question about the correct oxidation state of the metal center in M(NHBDipp)2 and M[Mn(CO)5]2 (M=Zn, Cd, Hg).

We report in this work a theoretical analysis on M(NHBMe)2 and M[Mn(CO)5]2 (M=Zn, Cd, Hg) using state-of-the-art charge and energy decomposition methods, which shows that the title complexes are best described with dative bonds NHBMe⇆M0⇄NHBMe and Mn(CO)5⇆M0⇄Mn(CO)5, where M is in the electronic ground state with an ns2 electron configuration binding to with (NHBMe)2 and [Mn(CO)5]2 ligands via donor–acceptor interaction. It is suggested that the adducts are the first examples of mononuclear complexes of divalent group 12 metals with zero oxidation state that are stable at ambient condition.

2 Computational details

The geometry optimizations followed by the harmonic frequency calculations for all the systems presented here were carried out at the BP86-D3(BJ)/def2-TZVPP level [35,36,37,38,39] using the Gaussian 16 suit of program [40]. Scalar-relativistic effective core potentials were used for the 28 and 60 core electrons of Cd and Hg, respectively. Superfine integration grid is considered for all cases. QTAIM (Quantum Theory of Atoms in Molecules) analysis [41] was performed at the BP86-D3(BJ)/def2-TZVPP/x2C-TZVPall//BP86-D3(BJ)/def2-TZVPP level where all-electron x2C-TZVPall [42] basis set is used from Cd and Hg.

The energy decomposition analysis (EDA) [43] in combination with natural orbital for chemical valence (NOCV) [44] method was performed at the BP86-D3(BJ)-ZORA/TZ2P+//BP86-D3(BJ)/def2-TZVPP level using the ADF (2018.105) program package [45, 46]. The zeroth-order regular approximation (ZORA) [47] was used to include scalar relativistic effects for the metals. All electrons were considered in the computations.

In the EDA method, the interaction energy (ΔΕint) between two prepared fragments is divided into three energy terms, viz. the electrostatic interaction energy (ΔEelstat), which represents the quasiclassical electrostatic interaction between the unperturbed charge distributions of the prepared atoms, the Pauli repulsion (ΔEPauli), which is the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction that properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the product wavefunction, and the orbital interaction energy (ΔEorb), which is originated from the mixing of orbitals, charge transfer and polarization between the isolated fragments. Use of D3(BJ) gives additional dispersion interaction energy (ΔEdisp) between two interacting fragments. Therefore, the interaction energy (ΔΕint) between two fragments can be defined as:

$$\Delta {\rm E}_{{\text{int}}} = \Delta E_{{{\text{elstat}}}} + \Delta E_{{{\text{Pauli}}}} + \Delta E_{{{\text{orb}}}} + \Delta E_{{{\text{disp}}}}.$$
(1)

The orbital term may be further divided into contributions from each irreducible representation of the point group of the interacting system as follows:

$$\Delta E_{{{\text{orb}}}} = \mathop \sum \limits_{r} \Delta E_{r}.$$
(2)

The EDA–NOCV combination allows the partition of ΔEorb into pairwise contributions of the orbital interactions, which gives important information about bonding. The charge deformation Δρk(r) which is originated from the mixing of the orbital pairs ψk(r) and ψ-k(r) of the interacting fragments gives the size and the shape of the charge flow because of the orbital interactions (Eq. 3), and the corresponding ΔEorb reflects the amount of orbital interaction energy coming from such interaction (Eq. 4).

$$\Delta \rho_{{\text{orb }}} \left( r \right) = \mathop \sum \limits_{k} \Delta \rho_{k} \left( r \right) = \mathop \sum \limits_{K}^{N/2} \left[ { - \psi_{ - k}^{2} \left( r \right) + \psi _{k}^{2} \left( r \right)} \right]$$
(3)
$$\Delta E_{{{\text{orb}}}} = \mathop \sum \limits_{k} \Delta E_{k}^{{{\text{orb}}}} = \mathop \sum \limits_{k = 1}^{N/2} \nu_{k} \left[ { - F_{ - k}^{{{\text{TS}}}} + F_{k}^{{{\text{TS}}}} } \right].$$
(4)

This method is found to be excellent to analyze the intriguing bonding situation in several interesting complexes [48,49,50,51,52,53,54,55,56,57]. For further information about this method and its application, readers are referred to the related reviews [58,59,60,61].

3 Results and discussion

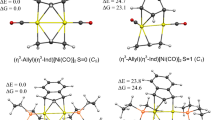
We calculated the model compounds M(NHBMe)2 (M=Zn, Cd, Hg) in place of M(NHBDipp)2 where the larger Dipp group linked to N centers is replaced by the Me group. The minimum energy geometries of the resulting complexes have a D2d symmetry and 1A1 electronic state (Fig. 1). The M–B bond lengths in M(NHBMe)2 match excellently with those of the experimental ones in M(NHBDipp)2. The B–M–B moiety in M(NHBMe)2 is perfectly linear, while due to the unsymmetrical structure of M(NHBDipp)2, the B–M–B angle in the experimental geometries ranges from 177.4° (Cd) to 179.1° (Hg). The only larger difference between the geometries of the model compounds and the experimental structures concerns the torsional angle t(N1B1B2N2) which is 90° in the model systems while it ranges from 41.8 (Cd) to 46.3 (Hg) in M(NHBDipp)2. This is most likely caused by the different steric interactions of the larger Dipp group compared with Me group. But the excellent matching in bond distances and B–M–B angles between the calculated and experimental values indicates that the model systems can be safely used to reflect the bonding situation in the experimental complexes.

Fig. 1
figure 1

The minimum energy geometries of M(NHBMe)2 and M[Mn(CO)5]2, M=Zn {Cd} [Hg] complexes at the BP86-D3(BJ)/def2-TZVPP level. The bond distances and angles are given in Å and in degree, respectively. The experimental parameters are given in italics. The computed BDE values at 298 K for ML2 → M + 2L are given in kcal/mol. Experimental bond distances correspond to M(NHBDipp)2 complexes which have two nonequivalent M–B bonds differed by only 0.001–0.002 Å

Full size image

The equilibrium geometries of M[Mn(CO)5]2 (M=Zn, Cd, Hg) have D4d symmetry at the BP86-D3(BJ)/def2-TZVPP level which is in contrast to the X-ray structure of Hg[Mn(CO)5]2 which has approximately a D4h symmetry. The calculated D4h symmetric structure has a small imaginary frequency which corresponds to the internal rotation of two Mn(CO)5 units with respect to each other (see Table S1). Very soft modes of rotation and small relative energies indicate very flat potential energy surface with respect to internal rotation, and the complexes are very floppy. Therefore, the D4h symmetry in Hg[Mn(CO)5]2 is more likely because of solid state effect in the crystal structure.

Figure 1 also shows the computed bond dissociation energy (BDE) for the most favorable dissociation pathway, ML2 → M + 2L, while the complete set of BDE values for three possible dissociations via homolytic bond cleavage (ML2 → M + 2L), heterolytic bond cleavage (ML2 → M2+  + 2L−) and a mixture of them (ML2 → M+  + L + L−) is given in Table S2, where L is NHBMe or Mn(CO)5. The BDE value at 298 K ranges from 69.4 kcal/mol to 81.6 kcal/mol for M(NHBMe)2 and from 31.7 kcal/mol to 51.9 kcal/mol for M[Mn(CO)5]2 showing the order Zn > Cd > Hg. The same order was earlier found for the methyl and phenyl compounds M(Me)2 and M(Ph)2 [62]. The calculations suggest that NHBMe is a much stronger ligand than Mn(CO)5. Note that the stability order contradicts the usual trend for transition metals which usually shows the heaviest (sixth row) element having the maximum BDE value [63]. The reason can be understood from the EDA–NOCV results (vide infra).

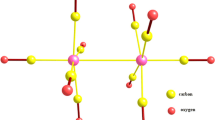
We employed the QTAIM method to analyze the electronic structure of the complexes. Figure 2 shows the contour plots of the Laplacian of electron density (∇2ρ(r)) at the Zn–B–N and Zn–Mn–C planes of Zn(NHBMe)2 and Zn[Mn(CO)5]2 complexes, respectively. The Laplacian distributions of the complete set of the systems are displayed in Figure S1. For a given type of systems, the distribution of ∇2ρ(r) looks very similar. However, there are significant differences in the Laplacian distribution between M(NHBMe)2 and M[Mn(CO)5]2 complexes. In the former systems, there is local electron density accumulation (indicated by a red dotted region) between B and M centers. Note that the bond critical point (BCP) is lying outside of the red region because of the polar nature of the bond. On the other hand, in the latter cases, there is no area of charge accumulation between Mn and M centers. There are only spherical areas of relative charge depletion (indicated by blue solid lines) around the metal atoms. Figure 2 also shows the values of ∇2ρ(rc) and local energy density (H(rc)) at the BCP of M–B and M–Mn bonds. ∇2ρ(rc) value is positive in all cases. But it does not mean that the interaction is noncovalent in nature. In fact, for such bonds where heavier elements are involved H(rc) is a more reliable descriptor to describe the nature of a bond than ∇2ρ(rc) [64]. For the M–B bonds, the polarized nature of the bond is also responsible for the positive ∇2ρ(rc) value. The H(rc) values at the BCP of M–B and M–Mn bonds are negative, indicating the covalent nature of the bond. The larger negative value in the former bond indicates larger covalent character in the M–B bond than in M–Mn bond. Note that there are no bond paths between M and CO groups. A similar situation was observed previously in the isoelectronic [M{Fe(CO)5}2]+ (M = Cu, Ag, Au) complexes [65,66,67]. This is in contrast to the recently reported hexacarbonyl cations [Ag{M(CO)6}2]+ (M = Cr, Mo, W) and the isoelectronic anions [Ag{M(CO)6}2]− (M = V, Nb, Ta) where bond paths and BCPs exist between Ag and tilted CO groups [68]. Figure 2 gives also the partial charges of the central atoms q(M) in the two sets of complexes. The group-12 metals carry a positive charge, which has the order Zn < Cd < Hg. The partial charges suggest that the [Mn(CO)5]2 ligands are stronger donor than (NHBMe)2.

Fig. 2
figure 2

The plot of Laplacian of electron density, ∇2ρ(r) at the Zn–B–N and Zn–Mn–C plane of Zn(NHBMe)2 and Zn[Mn(CO)5]2 complexes at the BP86-D3(BJ)/def2-TZVPP/x2C-TZVPall//BP86-D3(BJ)/def2-TZVPP level. Values of ∇2ρ(rc) in e/Å5 and H(rc) in Hartree/Å3 are given at BCP of M–B and M–Mn bonds. The values q(M) give the partial charge of the atom M. The blue solid lines indicate area of ∇2ρ(r) > 0, and red dotted lines represent the area of ∇2ρ(r) < 0. Blue spheres show the bond critical point

Full size image

More details about the nature of chemical bonding between M and NHBMe or Mn(CO)5 groups can be gained from the results of EDA–NOCV method. To get a reliable bonding situation in the complexes in the EDA–NOCV method, the selection of proper charge and electronic state of the interacting fragments is very crucial. One of the strengths of this method is that if there are more than one partitioning scheme available, one can choose the most suitable scheme to describe the bonding by using the size of ΔEorb as a probe. For a given interaction, those fragments, which give the lowest ΔEorb value, are the best one to describe the bonding situation as it indicates that the chosen fragments are most nearly prepared as those in the complex [69,70,71,72,73,74]. For both M(NHBMe)2 and M[Mn(CO)5]2 complexes, we have carried out EDA by considering M and (L)2 with different charges and electronic states as interacting fragments. Details about the results are given in Tables S3–S8. A comparison of the relative size of ΔEorb value indicates in all cases that the best description is provided using M in the ground state with (ns)2(np)0 valence electronic configuration and (L)2 in singlet spin state interacting through donor–acceptor type of bonding. Therefore, the complexes should be represented as NHBMe⇆M0⇄NHBMe and Mn(CO)5⇆M0⇄Mn(CO)5, where M is in the zero oxidation state.

Detailed numerical results of EDA–NOCV for the most favorable scheme are provided in Tables 1 and 2. Similar to the BDE values, the intrinsic interaction between M and (L)2 is the strongest for M=Zn followed by Cd and Hg, and for a given M, it is weaker for L = Mn(CO)5 than for NHBMe. Except for Zn(NHBMe)2, the M–L interaction is somewhat more electrostatic than covalent. Dispersion interaction is only responsible for 3–6% of total attraction. There are differences in the origin of obtained order in ΔEint between M(NHBMe)2 and M[Mn(CO)5]2 complexes. In the former case, increased Pauli repulsion and weakened ΔEorb values in going from Zn to Cd to Hg are responsible for the observed trend, whereas in the latter one, both weakened ΔEorb and ΔEelstat are accountable for this.

Table 1 EDA–NOCV results for M(NHBMe)2 complex at the BP86-D3(BJ)-ZORA/TZ2P+//BP86-D3(BJ)/def2-TZVPP level
Full size table
Table 2 EDA–NOCV results for M[Mn(CO)5]2 (M=Zn, Cd, Hg) complex at the BP86-D3(BJ)-ZORA/TZ2P+//BP86-D3(BJ)/def2-TZVPP level
Full size table

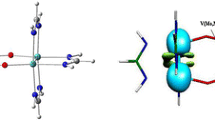
The breakdown of the ΔEorb into pairwise orbital interaction provides the most important information regarding the bonding between M and ligands. We have tabulated seven distinct pairwise contributions of ΔEorb for M(NHBMe)2 (Table 1) and nine such orbital terms for M[Mn(CO)5]2 (Table 2). Corresponding deformation densities Δρ for Zn complex are provided in Fig. 3 which help to understand the involved orbitals in the interaction. The Δρ plots for Cd and Hg homologues are very similar to the Zn complex. The results show that the strongest orbital contribution, ∆Eorb(1), is originated from the in-phase L←M(s)→L σ backdonation which accounts for 64–72% of total ΔEorb value. Note that because of relativistic contraction of 6s orbital in Hg, L←Hg(s)→L σ backdonation is the weakest one. The next strongest interaction, ∆Eorb(2), comes from the out-of-phase L→M(pσ)←L σ donation which is responsible for 17–22% of total ΔEorb. These two interactions together make the 81–94% of covalent interaction. There are two weak degenerate L→M(pπ)←L π donations ∆Eorb(3) and ∆Eorb(4), which only contribute 4–7% to ΔEorb. There is also some d orbital participation in the L←M(d)→L backdonation, albeit even weaker than the participation of the pπ orbitals. In case of M(NHBMe)2, the participation of only three d orbitals is found, whereas in M[Mn(CO)5]2, all five d orbitals are involved in the bonding where the CO groups also participate in the orbital interactions. Nevertheless, the combined effect of d orbitals provides only 3–5% to the covalent interaction. Interestingly, the present cases represent a rather rare scenario where L = NHBMe, Mn(CO)5 act as dominant acceptor and M=Zn, Cd, Hg act as donor centers. We have recently carried out EDA–NOCV calculations on [M{Fe(CO)5}2]+ (M=Cu, Ag, Au), the isoelectronic complexes of M[Mn(CO)5]2 (M=Zn, Cd, Hg), taking M+ as one fragment and (Fe(CO)5)2 as another [65]. The intrinsic interaction between coinage metal cation and (Fe(CO)5)2 is much stronger than that in the latter complex where both enhanced orbital and electrostatic interaction in the cationic complexes are responsible for this. Notably, despite cationic charge, [Fe(CO)5]←M+(d)→[Fe(CO)5] backdonation is much stronger (responsible for 13–24% of ΔEorb) than Mn(CO)5←M(d)→Mn(CO)5 backdonation.

Fig. 3
figure 3

The shape of the deformation densities, Δρ(n), which are associated with ∆Eorb(n) for Zn(NHBMe)2 and Zn[Mn(CO)5]2 complexes at the BP86-D3(BJ)-ZORA/TZ2P+//BP86-D3(BJ)/def2-TZVPP level. The isovalue is 0.0001 au. The direction of the charge flow of the deformation densities is red → blue

Full size image

The dominant orbital interaction ∆Eorb(1) coming from the L←M(s)→L σ backdonation is in agreement with the calculated partial charges q(M) given by the AIM method (Fig. 2). But the order of the donor strength of the group-12 atoms Zn > Cd > Hg given by ∆Eorb(1) is opposite to the order of the partial charges. Also, the [Mn(CO)5]2 ligands are more weakly bonded to the group-12 atoms than the (NHBMe)2 groups, although the charge donation of the former is larger compared with the latter. This shows that the size of the charge migration is not always a measure of the associated stabilization energy. This is a warning against premature correlations between charge migration and energy changes.

4 Summary and conclusions

Quantum chemical calculations are performed taking two sets of experimentally known complex of group 12 elements, M(NHBMe)2 and M[Mn(CO)5]2 (M=Zn, Cd, Hg), where the formal oxidation state of M was previously considered to be + 2 because of the anionic nature of the ligands. M(NHBMe)2 and M[Mn(CO)5]2 have D2d and D4d symmetry, respectively, with 1A1 electronic ground state. The bond dissociation energies of the ligands have the order of Zn > Cd > Hg. A thorough bonding analysis using charge and energy decomposition methods suggests that the title complexes are best represented as NHBMe⇆M0⇄NHBMe and Mn(CO)5⇆M0⇄Mn(CO)5, where M is in the electronic ground state with ns2 electron configuration binding to (NHBMe)2 and [Mn(CO)5]2 ligands through donor–acceptor interaction. The complexes are the first examples of mononuclear adducts with divalent group 12 metals with zero oxidation state that are stable at ambient condition. The complexes also represent a rare situation where the ligand acts as a strong acceptor and the metal center acts as strong donor. The relativistic effect of Hg leads to a weaker electron donor strength of the 6s orbital, which explains the trend of the bond dissociation energy. The present study shows that a thorough bonding analysis is needed to understand the actual bonding situation in the complex and the correct oxidation state of the metal.