Abstract
We recast the classical notion of “standard tableaux" in an alcove-geometric setting and extend these classical ideas to all “reduced paths" in our geometry. This broader path-perspective is essential for implementing the higher categorical ideas of Elias–Williamson in the setting of quiver Hecke algebras. Our first main result is the construction of light leaves bases of quiver Hecke algebras. These bases are richer and encode more structural information than their classical counterparts, even in the case of the symmetric groups. Our second main result provides path-theoretic generators for the “Bott–Samelson truncation" of the quiver Hecke algebra.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The symmetric group lies at the intersection of two great categorical theories: Khovanov–Lauda and Rouquier’s categorification of quantum groups and their knot invariants [8, 14] and Elias–Williamson’s diagrammatic categorification in terms of endomorphisms of Bott–Samelson bimodules. The purpose of this paper and its companion [2] is to construct an explicit isomorphism between these two diagrammatic worlds. The backbone of this isomorphism is provided by the “light-leaves" bases of these algebras.
The light leaves bases of diagrammatic Bott–Samelson endomorphism algebras were crucial in the calculation of counterexamples to the expected bounds of Lusztig’s and James’ conjectures [15]. These bases are structurally far richer than any known basis of the quiver Hecke algebra—they vary with respect to each possible choice of reduced word/path-vector in the alcove geometry—and this richer structure is necessary in order to construct a basis in terms of the “Soergel 2-generators" of these algebras. In this paper we show that the (quasi-hereditary quotients of) quiver Hecke algebras, \(\mathcal {H}_n^\sigma \) for \(\sigma \in {{\mathbb {Z}}}^\ell \), have analogues of the light leaves bases in the “non-singular" or “regular" case.
Without loss of generality, we assume that \(\sigma \in {{\mathbb {Z}}}^\ell \) is weakly increasing. We then let \({\underline{h}}= (h_0,\ldots ,h_{\ell -1}) \in {{\mathbb {N}}}^\ell \) be such that \(h_m\leqslant \sigma _{m+1}-\sigma _{m} \) for \(0\leqslant m< \ell -1\) and \(h_{\ell -1}< e+\sigma _0-\sigma _{\ell -1} \). The light leaves bases we construct are indexed by paths in an alcove geometry of type

for \(e> h= h_0+\cdots +h_{\ell -1} \), where each point in this geometry corresponds to an \(\ell \)-multipartition with at most \(h_m\) columns in the mth component (we denote the set of such \(\ell \)-multipartitions by \(\mathscr {P}_{{\underline{h}} }(n)\)). In this manner, we obtain cellular bases of the largest possible quasi-hereditary quotients of \(\mathcal {H}_n^\sigma \) controlled by non-singular Kazhdan–Lusztig theory (this is the broadest possible generalisation, in the context of cyclotomic quiver Hecke algebras, of studying the category of tilting modules of the principal block of the general linear group, \({\text {GL}}_h(\Bbbk )\), in characteristic \(p>h\)).
Theorem A
(Regular light leaves bases for quiver Hecke algebras) For each \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\) we fix a reduced path \(\mathsf {Q}_\lambda \in \,{{\text {Path}}}_{{\underline{h}}}(\lambda )\) and for each \({\textsf {S }}\in \,{{\text {Path}}}_{{\underline{h}}}(\lambda )\), we fix an associated reduced path vector \({{\underline{\mathsf {P }}}_{\textsf {S }}}\) terminating with \(\mathsf {Q}_\lambda \) (this notation is defined in Sects. 3 and 2). We have that
is a cellular basis of  where we quotient by the ideal generated by the element \( {\mathsf { y}}_{{\underline{h}} } \) which kills all simples indexed by \(\ell \)–partitions with more than \(h_m\) columns in the mth component.
where we quotient by the ideal generated by the element \( {\mathsf { y}}_{{\underline{h}} } \) which kills all simples indexed by \(\ell \)–partitions with more than \(h_m\) columns in the mth component.
We then consider the so-called “Bott–Samelson truncations" to the principal block
which we will show (in the companion paper [2]) are isomorphic to the (breadth enhanced) diagrammatic Bott–Samelson endomorphism algebras of Elias–Williamson [6]. The charm of this isomorphism is that it allows one to view the current state-of-the-art regarding p-Kazhdan–Lusztig theory (in type A) entirely within the context of the group algebra of the symmetric group, without the need for calculating intersection cohomology groups, or working with parity sheaves, or appealing to the deepest results of 2-categorical Lie theory. Furthermore, this isomorphism will allow us to prove (in a future paper) the beautiful “categorical blob” conjecture of Libedinsky-Plaza which brings together p-Kazhdan-Lusztig theory and statistical mechanics [11]. In this paper, we specialise Theorem A by making certain path-theoretic choices which allow us to reconstruct Elias–Williamson’s generators entirely within the quiver Hecke algebra itself, using our language of paths.
Theorem B
The Bott–Samelson truncation of the Hecke algebra  is generated by horizontal and vertical concatenation of the elements
is generated by horizontal and vertical concatenation of the elements

(this notation is defined in Sect. 4) for  such that
such that  and
and  label an arbitrary pair of non-commuting reflections and
label an arbitrary pair of non-commuting reflections and  and
and  label an arbitrary pair of commuting reflections.
label an arbitrary pair of commuting reflections.
The paper is structured as follows. In Sect. 2 we construct a “classical-type" cellular basis of \(\mathcal {H}^\sigma _n /\mathcal {H}^\sigma _n {\mathsf { y}}_{{\underline{h}}}\mathcal {H}^\sigma _n\) in terms of tableaux but using a slightly exotic dominance ordering—the proofs in this section are a little dry and can be skipped on the first reading. In Sect. 3, we upgrade this basis to a “light leaf type" construction and prove Theorem A. Finally, in Sect. 4 of the paper we illustrate how Theorem A allows us to reconstruct the precise analogue of the light leaves basis for the Bott–Samelson endomorphism algebras for regular blocks of quiver Hecke algebras (as a special case of Theorem A, written in terms of the generators of Theorem B). We do this in the exact language used by Elias, Libedinsky, and Williamson in order to make the construction clear for a reader whose background lies in either field.
This paper is a companion to [2], but the reader should note that the results here are entirely self-contained (although we refer to [2] for further development of ideas, examples, etc).
2 A tableaux basis of the quiver Hecke algebra
We let \(\mathfrak {S}_n\) denote the symmetric group on n letters and let \(\ell : \mathfrak {S}_n \rightarrow {{\mathbb {Z}}}\) denotes its length function. We let \(\leqslant \) denote the (strong) Bruhat order on \(\mathfrak {S}_n\). Given \(\underline{i}=(i_1,\ldots , i_n)\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n\) and \(s_r=(r,r+1)\in \mathfrak {S}_n\) we set \(s_r(\underline{i})= (i_1,\ldots , i_{r-1}, i_{r+1}, i_r ,i_{r+2}, \ldots ,i_n)\).
Definition 2.1
[3, 8, 14] Fix \(e > 2 \). The quiver Hecke algebra (or KLR algebra), \(\mathcal {H}_n \), is defined to be the unital, associative \({{\mathbb {Z}}}\)-algebra with generators

subject to the relations
for all \(r,s,{\underline{i}},{\underline{j}}\) and
for all permitted r, s, i, j. We identify such elements with decorated permutations and the multiplication with vertical concatenation, \(\circ \), of these diagrams in the standard fashion of [3, Section 1] and as illustrated in Fig. 1. We let \(*\) denote the anti-involution which fixes the generators.
Definition 2.2
Fix \(e > 2 \) and \(\sigma \in {{\mathbb {Z}}}^\ell \). The cyclotomic quiver Hecke algebra, \(\mathcal {H}_n^\sigma \), is defined to be the quotient of \(\mathcal {H}_n\) by the relation
As we see in Fig. 1, the \(y_k\) elements are visualised as dots on strands; we hence refer to them as KLR dots. Given \(p<q\) we set

and given an expression \({\underline{w}}=s_{i_1}\cdots s_{i_p}\in \mathfrak {S}_n\) we set \(\psi _{\underline{w}}= \psi _{i_1}\cdots \psi _{i_p}\in \mathcal {H}_n\). We let \(\boxtimes \) denote the horizontal concatenation of KLR diagrams. Finally, we define the degree as follows,
2.1 Box configurations, partitions, residues and tableaux
For a fixed \(n\in {{\mathbb {N}}}\) and \(\ell \geqslant 1\) we define a box-configuration to be a subset of
of n elements, which we call boxes, and we let \(\mathcal {B}_{ \ell }(n)\) denote the set of all such box-configurations. We refer to a box \([i,j,m]\in \lambda \in \mathcal {B}_{ \ell }(n)\) as being in the ith row and jth column of the mth component of \(\lambda \). Given a box, [i, j, m], we define the content of this box to be \({\mathsf { ct}}[i,j,m] = \sigma _m+ j-i\) and we define its residue to be \({\text {res}}[i,j,m]= {\mathsf { ct}}[i,j,m] \pmod e\). We refer to a box of residue \(r\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\) as an r-box.
We define a composition, \(\lambda \), of n to be a finite sequence of non-negative integers \( (\lambda _1,\lambda _2, \ldots )\) whose sum,  , equals n. We say that \(\lambda \) is a partition if, in addition, this sequence is weakly decreasing. An \(\ell \)-multicomposition (respectively \(\ell \)-multipartition)
, equals n. We say that \(\lambda \) is a partition if, in addition, this sequence is weakly decreasing. An \(\ell \)-multicomposition (respectively \(\ell \)-multipartition)  of n is an \(\ell \)-tuple of compositions (respectively partitions) such that
of n is an \(\ell \)-tuple of compositions (respectively partitions) such that  . We denote the sets of \(\ell \)-multipartitions and \(\ell \)-multi-compositions of n by \( \mathscr {P}_{\ell }(n)\) and \( \mathcal {C}_{\ell }(n)\), respectively. Given \(\lambda =(\lambda ^{(0)},\lambda ^{(1)},\ldots ,\lambda ^{(\ell -1)}) \in \mathscr {P}_{\ell }(n)\), the Young diagram of \(\lambda \) is defined to be the box configuration,
. We denote the sets of \(\ell \)-multipartitions and \(\ell \)-multi-compositions of n by \( \mathscr {P}_{\ell }(n)\) and \( \mathcal {C}_{\ell }(n)\), respectively. Given \(\lambda =(\lambda ^{(0)},\lambda ^{(1)},\ldots ,\lambda ^{(\ell -1)}) \in \mathscr {P}_{\ell }(n)\), the Young diagram of \(\lambda \) is defined to be the box configuration,
We do not distinguish between the multipartition and its Young diagram. We let \(\varnothing \) denote the empty multipartition. Given \(\lambda \in \mathcal {B}_\ell (n)\), we let
for \(\lambda \in \mathscr {P}_\ell (n)\subseteq \mathcal {B} _\ell (n)\) this coincides with the usual definition of addable and removable boxes. We let \({\text {Rem}}_r (\lambda )\subseteq {\text {Rem}} (\lambda )\) and \({\text {Add}}_r (\lambda )\subseteq {\text {Add}} (\lambda )\) denote the subsets of boxes of residue \(r\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\).
Given \(\lambda \in \mathcal {B}_{\ell }(n)\), we define a \(\lambda \)- tableau to be a filling of the boxes of \([\lambda ] \) with the numbers  . For \(\lambda \in \mathcal {B}_{\ell }(n)\), we say that a \(\lambda \)-tableau is row-standard, column-standard, or simply standard if the entries in each component increase along the rows, increase along the columns, or increase along both rows and columns, respectively. We say that a \(\lambda \)-tableau \(\mathsf {S }\) has shape \(\lambda \) and write \({\mathsf {Shape}}(\mathsf {S })=\lambda \). Given \(\lambda \in \mathcal {B}_{ \ell }(n)\), we let \({\text {Tab}}(\lambda )\) denote the set of all tableaux of shape \(\lambda \in \mathcal {B}_{ \ell }(n)\). Given \(\mathsf {T }\in {\text {Tab}}(\lambda )\) and \(1\leqslant k\leqslant n\), we let \(\mathsf {T }^{-1}(k)\) denote the box \(\square \in \lambda \) such that \(\mathsf {T }(\square )=k\). We let \({\text {RStd}}(\lambda ), {\text {CStd}}(\lambda ), {\text {Std}}(\lambda ) \subseteq {\text {Tab}}(\lambda ) \) denote the subsets of all row-standard, column-standard, and standard tableaux, respectively. We let \({\text {Std}}(n)=\cup _{\lambda \in \mathscr {P}_\ell (n)} {\text {Std}}(\lambda ) \) for \(n\in {{\mathbb {N}}}\).
. For \(\lambda \in \mathcal {B}_{\ell }(n)\), we say that a \(\lambda \)-tableau is row-standard, column-standard, or simply standard if the entries in each component increase along the rows, increase along the columns, or increase along both rows and columns, respectively. We say that a \(\lambda \)-tableau \(\mathsf {S }\) has shape \(\lambda \) and write \({\mathsf {Shape}}(\mathsf {S })=\lambda \). Given \(\lambda \in \mathcal {B}_{ \ell }(n)\), we let \({\text {Tab}}(\lambda )\) denote the set of all tableaux of shape \(\lambda \in \mathcal {B}_{ \ell }(n)\). Given \(\mathsf {T }\in {\text {Tab}}(\lambda )\) and \(1\leqslant k\leqslant n\), we let \(\mathsf {T }^{-1}(k)\) denote the box \(\square \in \lambda \) such that \(\mathsf {T }(\square )=k\). We let \({\text {RStd}}(\lambda ), {\text {CStd}}(\lambda ), {\text {Std}}(\lambda ) \subseteq {\text {Tab}}(\lambda ) \) denote the subsets of all row-standard, column-standard, and standard tableaux, respectively. We let \({\text {Std}}(n)=\cup _{\lambda \in \mathscr {P}_\ell (n)} {\text {Std}}(\lambda ) \) for \(n\in {{\mathbb {N}}}\).
Definition 2.3
We define the reverse cylindric ordering, \(\succ \), as follows. Let \(1\leqslant i,i',j,j' \leqslant n\) and \(0\leqslant m,m' < \ell \). We write \([i,j,m] \succ [i',j',m']\) if \(i<i'\), or \(i=i'\) and \(m<m'\), or \(i=i'\) and \(m=m'\) and \(j<j'\). For \(\lambda ,\mu \in \mathcal {B}_{\ell }(n)\), we write \(\lambda \succ \mu \) if the \(\succ \)-minimal box \(\square \in ( \lambda \cup \mu ) {\setminus } ( \lambda \cap \mu ) \) belongs to \(\mu \).
Definition 2.4
We define the dominance ordering, \(\rhd \), as follows. Let \(1\leqslant i,i',j,j' \leqslant n\) and \(0\leqslant m,m' < \ell \). We write \([i,j,m] \rhd [i',j',m']\) if \(m<m'\), or \(m=m'\) and \(i<i'\), or \(i=i'\) and \(m=m'\) and \(j<j'\). Given \(\lambda ,\mu \in \mathcal {B}_{\ell }(n)\), we write \(\lambda \rhd \mu \) if the \(\rhd \)-maximal box \(\square \in ( \lambda \cup \mu ) {\setminus } ( \lambda \cap \mu ) \) belongs to \(\lambda \).
Given \(\mathsf {S }\), we write \(\mathsf {S }{\downarrow }_{\leqslant k} \) or \(\mathsf {S }{\downarrow }_{\{1,\dots , k\}} \) (respectively \(\mathsf {S }{\downarrow }_{\geqslant k} \)) for the subtableau of \(\mathsf {S }\) consisting solely of the entries 1 through k (respectively of the entries k through n). Given \(\lambda \in \mathcal {B}_{\ell }(n)\), we let \(\mathsf {T }_\lambda \) denote the \(\lambda \)-tableau in which we place the entry n in the minimal \(\succ \)-node of \(\lambda \), then continue in this fashion inductively. Given \(\lambda \in \mathcal {B}_\ell (n)\), we let \({\textsf {S }}_\lambda \) denote the \(\lambda \)-tableau in which we place the entry n in the minimal \(\rhd \)-node of \(\lambda \), then continue in this fashion inductively. Finally, given \(\mathsf {S },\mathsf {T }\) two \(\lambda \)-tableaux, we let \(w^\mathsf {S }_ {\mathsf {T }} \in \mathfrak {S}_n\) be the permutation such that \(w^\mathsf {S }_ {\mathsf {T }}(\mathsf {T })=\mathsf {S }\).
Example 2.5
For \(\lambda =((2,1^2),(2^2,1),(1^3))\), we have that \(w^\mathsf {S }_{\mathsf {T }_\lambda }=(4,5)(2,6)\) for \(\mathsf {S }\) and \(\mathsf {T }_\lambda \) the tableaux

Definition 2.6
Given any box, [r, c, m] , we define the associated (\(\succ \))-Garnir belt to be the collection of boxes, \( {\mathsf { Gar}}_{\succ }([r,c,m])\), as follows

with the convention that we ignore any box from the “zeroth" row. We define \( {\mathsf { Gar}}_{\rhd }([r,c,m]) \) to be the intersection of \({\mathsf { Gar}}_{\succ }([r,c,m]) \) with the mth component and refer to this as the (\(\rhd \))-Garnir belt.
Example 2.7
Let \(\sigma =(0,3,8)\in {{\mathbb {Z}}}^3\) and \(e=14\). Given \(\lambda = ((3^2,2^2,1 ),(5^2,3,2,1 ),(4^2,3,1^2 ))\) and the box \([3,3,1]\in \lambda \), we colour \({\mathsf { Gar}}_{\succ }([3,3,1]) \cap \lambda \) below

The \((\rhd )\)-Garnir belt is the subset of boxes coloured in orange.
Given \({\underline{h}}\in {{\mathbb {N}}}^\ell \), we let \(\mathscr {P}_{{\underline{h}}}(n)\) (respectively \(\mathscr {C}_{{\underline{h}}}(n)\)) denote the subsets of \(\ell \)-multipartitions (respectively \(\ell \)-multicompositions) with at most \(h_m\) columns in the mth component.
Lemma 2.8
Let \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). For any box [i, j, m], the multiset of residues of the boxes in \(\lambda \cap {{\text {Gar}}}_{\succ }[i,j,m] \) is multiplicity-free (i.e. no residue appears more than once).
Proof
This follows immediately from the definitions since \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). \(\square \)
Let \(\geqslant \) be an ordering on \( \mathcal {B}_\ell (n)\). Given \(1\leqslant k\leqslant n\), we let \({{\mathcal {A}}}^{\geqslant }_\mathsf {T }(k)\), (respectively \({{\mathcal {R}}}^{\geqslant }_\mathsf {T }(k)\)) denote the set of all addable \(\text {res}(\mathsf {T }^{-1}(k))\)-boxes (respectively all removable \(\text {res}(\mathsf {T }^{-1}(k))\)-boxes) of the box-configuration \({\text {Shape}}(\mathsf {T }{\downarrow }_{\{1,\ldots ,k\}})\) which are less than \(\mathsf {T }^{-1}(k)\) in the \(\geqslant \)-order. We define the \((\geqslant )\)-degree of \(\mathsf {T }\in {\text {Std}}(\lambda )\) for \(\lambda \in \mathscr {P}_\ell (n)\) as follows,
We let \({{\text {res}} (\mathsf {T })}\) denote the residue sequence consisting of \(\text {res}(\mathsf {T }^{-1}(k))\) for \(k=1,\ldots , n\) in order. We set \(e_\mathsf {T }:= e_{{\text {res}} (\mathsf {T })}\in \mathscr {H}_n^\sigma \). We set
For \(\lambda \in \mathscr {P}_\ell (n)\), the element \({y }_\lambda ^{\rhd } \) was first defined in [7, Definition 4.15]. We remark that \({y }^\succ _\lambda = e_{\mathsf {T }_\lambda }\) for \(\lambda \in \mathscr {P}_{{\underline{h}}} (n)\). Given \({\textsf {S }}, \mathsf {T }\in {\text {Std}}(\lambda )\) and \({\underline{w}}\) any fixed reduced word for \(w^{\textsf {S }}_\mathsf {T }\) we let \(\psi ^{\textsf {S }}_\mathsf {T }:=e_{\textsf {S }}\psi _{\underline{w}}e_\mathsf {T }\).
Definition 2.9
We set \(\mathcal {Y}_n=\langle e_{\underline{i}}, y_k \mid \underline{i}\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n, 1\leqslant k \leqslant n\rangle \).
2.2 The quotient
A long-standing belief in modular Lie theory is that we should (first) restrict our attention to fields whose characteristic, p, is greater than the Coxeter number, h, of the algebraic group we are studying. This allows one to consider a “regular block" of the algebraic group in question. What does this mean on the other side of the Schur–Weyl duality relating \({\text {GL}}_h(\Bbbk )\) and \(\Bbbk \mathfrak {S}_n\)? By the second fundamental theorem of invariant theory, the kernel of the group algebra of the symmetric group acting on n-fold h-dimensional tensor space is the 2-sided ideal generated by the element
Modulo “more dominant terms" this element can be rewritten in the form we introduced in Eq. (2.2), as follows
by [7, 4.16 Corollary]. The simples of this algebra are indexed by partitions with at most h columns. Given \(\sigma \in {{\mathbb {Z}}}^\ell \), we let \({\underline{h}}= (h_0,\ldots ,h_{\ell -1}) \in {{\mathbb {N}}}^\ell \) be such that \(h_m\leqslant \sigma _{m+1}-\sigma _{m} \) for \(0\leqslant m< \ell -1\) and \(h_{\ell -1}< e+\sigma _0-\sigma _{\ell -1} \). We define

to be the higher level analogue of the element in (2.3).
Definition 2.10
Given weakly increasing \(\sigma \in {{\mathbb {Z}}}^\ell \), we let \({\underline{h}}= (h_0,\ldots ,h_{\ell -1}) \in {{\mathbb {N}}}^\ell \) be such that \(h_m\leqslant \sigma _{m+1}-\sigma _{m} \) for \(0\leqslant m< \ell -1\) and \(h_{\ell -1}< e+\sigma _0-\sigma _{\ell -1} \). We define \( {\mathscr {H}^\sigma _n}:= \mathcal {H}^\sigma _n /\mathcal {H}^\sigma _n {\mathsf { y}}_{{\underline{h}}}\mathcal {H}^\sigma _n\).
In level \(\ell =1\), the condition of Definition 2.10 is equivalent to \(h_0< e\) (and \(\mathscr {P}_{{\underline{h}}}(n)\) is the set of partitions of n with strictly fewer than e columns).
2.3 Generator/partition combinatorics
Our cellular basis will provide a stratification of \({\mathscr {H}^\sigma _n}\) in which each layer is generated by an idempotent correspond to some multipartition. Whence we wish to understand the effect of multiplying a generator of a given layer in the cell-stratification by a KLR “dot generator". This leads us to define combinatorial analogues of the dot generators as maps on the set of box configurations.
Definition 2.11
Let \(\lambda \in \mathcal {B}_{ \ell }(n)\) and let \([i,j,m]\in \lambda \). We say that [i, j, m] is left-justified if either \(j\leqslant e\) or there exists some \([i,j-p,m]\in \lambda \) for \(1\leqslant p \leqslant e\).
Definition 2.12
Let \(\lambda \in \mathcal {B}_{ \ell }(n)\). For \(\alpha \in \lambda \) an r-box, we define  where the r-box \(\beta \not \in \lambda \) is such that \(\beta \succ \alpha \), it is left-justified, and is minimal in \(\succ \) with respect to these properties (if such a box exists). If such a box does not exist then we say that \(Y_\alpha (\lambda )\) and \(\beta \) are both undefined.
where the r-box \(\beta \not \in \lambda \) is such that \(\beta \succ \alpha \), it is left-justified, and is minimal in \(\succ \) with respect to these properties (if such a box exists). If such a box does not exist then we say that \(Y_\alpha (\lambda )\) and \(\beta \) are both undefined.
We write  if \( \lambda = Y_\alpha (\mu ) \) for some \(\alpha \in \mu \) and we then extend
if \( \lambda = Y_\alpha (\mu ) \) for some \(\alpha \in \mu \) and we then extend  to a partial ordering on \( \mathcal {B}_{ \ell }(n)\) by taking the transitive closure. Suppose that \(\{[i_k,j_k,m_k]\mid {0< k\leqslant p} \} \) is a set of r-boxes and that \(Y_{[i_k,j_k,m_k]}(\lambda \cup [i_k,j_k,m_k]) = \lambda \cup [i_{k+1},j_{k+1},m_{k+1}] \) for \(k\geqslant 1\). We define
to a partial ordering on \( \mathcal {B}_{ \ell }(n)\) by taking the transitive closure. Suppose that \(\{[i_k,j_k,m_k]\mid {0< k\leqslant p} \} \) is a set of r-boxes and that \(Y_{[i_k,j_k,m_k]}(\lambda \cup [i_k,j_k,m_k]) = \lambda \cup [i_{k+1},j_{k+1},m_{k+1}] \) for \(k\geqslant 1\). We define
We remark that  implies that \(\lambda \succ \mu \) and so
implies that \(\lambda \succ \mu \) and so  is a coarsening of \(\succ \).
is a coarsening of \(\succ \).
Example 2.13
Let \(e=5\) and \(\ell =1\). For \(\lambda =(3,2^2,1^6) \in \mathscr {P}_{1}(13)\), we have that \(Y_{[3,2,0]} (\lambda ) = (3,2,1^7) \cup [2,6,0] \). We have that \(Y^2_{[3,2,0]} (\lambda ) = Y_{[2,6,0]}((3,2,1^7) \cup [2,6,0]) = (3,2,1^7) \cup [1,5,0] \).
Example 2.14
Let \(e=5\) and \(\ell =1\) and \(r=2\). For \(\lambda =(3,2^2,1^6) \in \mathscr {P}_{1}(13)\), we have \(Y^1_{[4,1,0]} (\lambda ) = (3,2^2,1^6) \cup [3,5,0] - [4,1,0] \) and \(Y^2_{[4,1,0]} (\lambda ) = (3,2^2,1^6) \cup [2,4,0] - [4,1,0] \) (see Fig. 2).
Given an idempotent generator, \(e_{\underline{j} }\) for \(\underline{j} \in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n\), of the KLR algebra, we wish to identify to which layer of our stratification our idempotent belongs. To this end we make the following definition.
Definition 2.15
Associated to any \(\underline{j} = (j_1,\ldots , j_n) \in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n\), we have an element \({\mathsf { J}} \in {\text {Std}}(n) \cup \{0\}\) given by placing the entry \(k= 1,2,\ldots ,n+1\) in the lowest addable \(j_k\)-box under \(\succ \) of the partition \({\text {Shape}}({\mathsf { J}}_{\leqslant k-1})\), and formally setting \({\mathsf { J}}=0\) and \({\text {Shape}}({\mathsf { J}})=0\) if no such box exists for some \(1\leqslant k\leqslant n\).
2.4 A tableaux theoretic basis
We are now ready to construct our first basis of \(\mathscr {H}^\sigma _n \). This basis will serve as the starting point for our light-leaves bases of Theorem A. The combinatorics of this basis will be familiar to anyone who has studied symmetric groups and cyclotomic Hecke algebras (but with respect to the, less familiar, \((\succ )\)-ordering).
Definition 2.16
Let \( \lambda \in \mathscr {P}_{{\underline{h}}}(n )\). We define the Garnir adjacency set of an r-box \(\alpha =[i,j,m]\not \in \lambda \) to be the set of boxes, \(\gamma \in \lambda \cap {\mathsf {{Gar}}_{\succ }}(\alpha )\) such that \(|{\text {res}}(\gamma ) - r |\leqslant 1\) and denote this set by \({\mathsf {{Adj}}}\text {-}\mathsf {{Gar}}_{\succ }(\alpha )\). We set \({\text {res}}( \mathsf {Adj}\text {-}\mathsf {Gar}_{\succ }(\alpha ))=\{ \text {res}(\gamma ) \mid \gamma \in {\mathsf {Adj}\text {-}\mathsf {Gar}}_{\succ }(\alpha ) \}\).
Example 2.17
Continuing with Example 2.7, we have that \( {\mathsf { Adj}\text {-}\mathsf {Gar}}_{\succ }([3,3,1]) =\{[3,2,1], [2,3,1]\}\).
Remark 2.18
We are endeavouring to construct a 2-sided chain of ideals of \(\mathscr {H}_n^\sigma \), ordered by  , in which each 2-sided ideal is generated by an idempotent \(e_{\mathsf {T }_\lambda }\) for \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). Equations (2.6) and (2.7) of Theorem 2.19 will allow us to rewrite any element of \(\mathcal {Y}_n \) in the required form by moving a given box \(\square \) through the partition \(\lambda \) one row at a time along the
, in which each 2-sided ideal is generated by an idempotent \(e_{\mathsf {T }_\lambda }\) for \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). Equations (2.6) and (2.7) of Theorem 2.19 will allow us to rewrite any element of \(\mathcal {Y}_n \) in the required form by moving a given box \(\square \) through the partition \(\lambda \) one row at a time along the  ordering until it comes to rest at some point \(\lambda \cup \square '\in \mathscr {P}_{{\underline{h}}}(n )\). For \({\mathsf {J}}\) the tableau in Fig. 3, then the eight steps involved in rewriting \(e_{\mathsf {J}}\) as an element of \({\mathscr {H}}^{\succeq (3,2^2,1^6)}\) are illustrated in Fig. 4.
ordering until it comes to rest at some point \(\lambda \cup \square '\in \mathscr {P}_{{\underline{h}}}(n )\). For \({\mathsf {J}}\) the tableau in Fig. 3, then the eight steps involved in rewriting \(e_{\mathsf {J}}\) as an element of \({\mathscr {H}}^{\succeq (3,2^2,1^6)}\) are illustrated in Fig. 4.
The following theorem is the technical heart of this section. We define \(\mathscr {H}^ {\geqslant \lambda }= \mathscr {H}^\sigma _n\langle e_{\mathsf {T }_\nu } \mid \nu \geqslant {\lambda }\rangle \mathscr {H}^\sigma _n\) (respectively \(\mathcal {H}^ {\geqslant \lambda }= \mathcal {H}^\sigma _n\langle e_{\mathsf {T }_\nu } \mid \nu \geqslant {\lambda }\rangle \mathcal {H}^\sigma _n\)) for \(\geqslant \) any ordering on \( \mathscr {P}_{{\underline{h}}}(n)\) (respectively \(\mathscr {P} _\ell (n)\)). Given \(\geqslant \) a total order on \( \mathscr {P}_{{\underline{h}}}(n)\), we let \( \lambda ^{[0]}> \lambda ^{[1]}>\cdots >\lambda ^{[m]} \) denote the complete set of elements of \( \mathscr {P}_{{\underline{h}}}(n)\) enumerated according to the total ordering >. Given \(\lambda \in \mathcal {B}_\ell (n-1)\) and \(\alpha \not \in \lambda \), we define

Theorem 2.19
Let \(\lambda \in \mathscr {P}_{{\underline{h}}}(n-1 )\) and assume \( \alpha = [i,j,m] \not \in \lambda \) is left-justified. We set \(a= \mathsf {T }_{\lambda \cup \alpha }(\alpha ) \).
- (a):
-
If \(\alpha = [1,j,0] \) for some \(j\geqslant 1\) then (i) \( {y }_{\mathsf {T }_{\lambda \cup \alpha }} =0\) if \(\lambda \cup \alpha \not \in \mathscr {P}_{{\underline{h}}}(n)\) and (ii) \( y_{a} {y }_{\mathsf {T }_{\lambda \cup \alpha }} =0\) if \(\lambda \cup \alpha \in \mathscr {P}_{{\underline{h}}}(n)\).
- (b):
-
For \(\alpha \ne [1,j,0] \) for some \(j\geqslant 1\), we set \(\beta \) to be the box determined by
$$\begin{aligned} {\left\{ \begin{array}{ll} Y^{\ell +1}_\alpha (\lambda \cup \alpha ) = \lambda \cup \beta &{}\text { if }{res }( {\mathsf { Adj }\text {-}\mathsf {Gar }}(\alpha ))=\{r-1\} ; \\ Y^1_\alpha (\lambda \cup \alpha ) = \lambda \cup \beta &{}\text { otherwise } \end{array}\right. } \end{aligned}$$(2.5)and we set \(b= \mathsf {T }_{\lambda \cup \beta } (\beta ) \).
Let \(e=5\) and \(\ell =1\). On the left, we have the residues for the partition \(\lambda =(3,2^2,1^6)\). On the right, we have the tableau \({\mathsf { J}} \in {\text {Std}}(3,2^2,1^6)\) for \(\underline{j}=(0,1,4,0,3,4,2,1,0,4,3,2,2)\) as in Definition 2.15
For \(n=13\) and \(\lambda =(2^3,1^6)\), we illustrate how the idempotent, \(e_{(0,1,4,0,3,4,2,1,0,4,3,2,2)}\), labelled by \({\mathsf {J}}\) in Fig. 3 is rewritten in the form (2.8). The box moves through each row until it comes to rest at the point \({\mathsf {J}}^{-1}(13)=[1,3,0]\). This involves repeated applications of Eq. (2.6) to deduce (2.8). For the purposes of later referencing, we label the 9 boxes from bottom-to-top by \(\alpha _1=[9,6,0],\alpha _2=[8,5,0] , \ldots , \alpha _9=[1,3,0]\). This visualisation is explained in Remark 2.18
-
If \(\lambda \cup \alpha \not \in \mathscr {P}_{{\underline{h}}}(n)\), then we have that
 (2.6)
(2.6)(the cases are detailed in the proof).
-
If \(\lambda \cup \alpha \in \mathscr {P}_{{\underline{h}}}(n)\), then we have that
 (2.7)
(2.7)
- (c):
-
For \(\underline{j}\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^{n }\), using the notation of Definition 2.15, we have that:
 (2.8)
(2.8)where \({\tilde{\psi }}_{\mathsf {T }_{\nu }}^{\mathsf {J}} \) is obtained from \( {\psi }_{\mathsf {T }_{\nu }}^{\mathsf {J}} \) by possibly adding some dot decorations along the strands. Thus if \(\geqslant \) is any total refinement of
 then the \({{\mathbb {Z}}}\)-algebra \(\mathscr {H}^\sigma _n\) has a chain of two-sided ideals $$\begin{aligned} 0 \subset \mathscr {H}^{\geqslant \lambda ^{[0]}}_n \subset \mathscr {H}^{\geqslant \lambda ^{[1]}}_n \subset \cdots \subset \mathscr {H}^{\geqslant \lambda ^{[m]}}_n= \mathscr {H}^\sigma _n .\end{aligned}$$(2.9)
then the \({{\mathbb {Z}}}\)-algebra \(\mathscr {H}^\sigma _n\) has a chain of two-sided ideals $$\begin{aligned} 0 \subset \mathscr {H}^{\geqslant \lambda ^{[0]}}_n \subset \mathscr {H}^{\geqslant \lambda ^{[1]}}_n \subset \cdots \subset \mathscr {H}^{\geqslant \lambda ^{[m]}}_n= \mathscr {H}^\sigma _n .\end{aligned}$$(2.9)
Remark 2.20
In the proof, we will often relate ideals in smaller and larger algebras using horizontal concatenation of diagrams, this is made possible by the definition of the reverse cylindric ordering \(\succ \) (which distinguishes between box configurations based on the first discrepancy upon reading a pair of box configurations backwards).
Remark 2.21
If \(\lambda \cup \alpha \in \mathscr {P}_{{\underline{h}}}(n)\), then \({y }^{{\succ }}_{{{\mathsf {T }_{\lambda \cup \alpha }}}}=e_{\mathsf {T }_{\lambda \cup \alpha }}\) by Lemma 2.8.
Proof of Theorem 2.19
Part (a), let \(\alpha = [1,j,0] \) for some \(j\geqslant 1\). Claim (ii) follows by applying case 3 of R4a times, followed by the commuting KLR relations and the cyclotomic relation. The proof of claim (i) is similar. Thus (a) follows.
For parts (b) and (c), we assume that Eqs. (2.6)–(2.9) all hold for rank \(n-1\). We further assume that Eqs. (2.7) and (2.6) have been proven for all \(\nu =\mu \cup \alpha \) with \(\mu \in \mathscr {P}_{{\underline{h}}}(n-1)\) such that  ; thus leaving us to prove Eqs. (2.7) and (2.6) for \(\nu =\lambda \cup \alpha \) for \( \lambda \in \mathscr {P}_{{\underline{h}}}(n-1)\) and Eq. (2.8) for all \(\underline{j}\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^{n }\). Equation (2.9) follows immediately from Eq. (2.8) and the idempotent decomposition of the identity in relation R1. By Definition 2.12, \(\text {res}(\alpha )=\text {res}(\beta )\) and we set this residue equal to \(r \in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\).
; thus leaving us to prove Eqs. (2.7) and (2.6) for \(\nu =\lambda \cup \alpha \) for \( \lambda \in \mathscr {P}_{{\underline{h}}}(n-1)\) and Eq. (2.8) for all \(\underline{j}\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^{n }\). Equation (2.9) follows immediately from Eq. (2.8) and the idempotent decomposition of the identity in relation R1. By Definition 2.12, \(\text {res}(\alpha )=\text {res}(\beta )\) and we set this residue equal to \(r \in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\).
Proof of Eq. (2.6) for a given \(\lambda \) and \(\alpha \). We include a running example for \(e=5\) and \(\ell =1\) and \(\lambda =(2^3,1^6)\). We assume that \(\lambda \cup \alpha \not \in \mathscr {P}_{\underline{h}}(n)\). There are four cases to consider, depending on the residue of \(\alpha ':=\mathsf {T }_{\lambda \cup \alpha }^{-1}(a-1)\). We assume that \(\alpha '\) is in the same row of the same component as \(\alpha \) (as otherwise \(y_{\mathsf {T }_{\lambda \cup \alpha }}=y_{\mathsf {T }_{\lambda \cup \beta }}\) by definition). We let \(\beta '\) be the box determined by
- (i):
-
Suppose \(\alpha ' \) has residue \(r\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\) and so \( {y }^{{\succ }}_{\mathsf {T }_{\lambda \cup \alpha }}=e_{\mathsf {T }_{\lambda \cup \alpha }}\) by Lemma 2.8. By application of relations R3 and R4, we have that
$$\begin{aligned} e_{\mathsf {T }_{\lambda \cup \alpha }}&=\psi _{a-1} y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha }}\psi _{a} y_{a-1} - y_{a} \psi _{a-1}y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha }}\psi _{a-1} . \end{aligned}$$(2.10)An example of the visualisation of the idempotents on the righthand-side of Eq. (2.10) is given in the first step of Fig. 4; the corresponding righthand-side of Eq. (2.10) is depicted in Fig. 5. Now, we have that
$$\begin{aligned} y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha }} = (y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha } \downarrow _{\leqslant a-1} }) \boxtimes e_r \boxtimes e_{\mathsf {T }_{\lambda \cup \alpha } \downarrow _{> a} } \end{aligned}$$and so by our inductive assumption for Eq. (2.7) for rank \(a-1<n\), we have that

where we have implicitly used the following facts: (i) \(Y_{\alpha '} (\lambda \cup \alpha )=\lambda \cup \alpha \cup \beta -\alpha ' \) (ii) \({\mathsf {T }_{\lambda \cup \alpha } {\downarrow }_{> a} }= {\mathsf {T }_{\lambda \cup \beta } {\downarrow }_{> a} } \) and (iii) \(e_{\mathsf {T }_{\lambda \cup \beta \cup \alpha -\alpha '}}= e_{\mathsf {T }_{\lambda \cup \beta }}\). Substituting this back into Eq. (2.10), we obtain
 (2.11)
(2.11)as required (as in the second case in Eq. (2.6)). An example is depicted in Fig. 5 (although we remark that the error terms belonging to
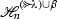 are actually all zero in this case).
are actually all zero in this case). - (ii):
-
Now suppose \(\alpha '=[x,y,z]\) has residue \(r+1\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\). We have two subcases to consider. We first consider the easier subcase, in which \( [x,y,z]=[i,1,m]\) and so \(b=a-1\). We have that \( [i+1,1,m] \in {\text {Add}}_r (\mathsf {T }_{\lambda \cup \alpha }{\downarrow }_{\leqslant a})\) whereas \( {\text {Add}}_r (\mathsf {T }_{\lambda \cup \beta }{\downarrow }_{\leqslant b})=\emptyset \). By relation R4, we have that
$$\begin{aligned} {y }^{{\succ }}_{\mathsf {T }_{\lambda \cup \alpha }}= y_a e_{\mathsf {T }_{\lambda \cup \alpha }} = y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha }} - e_{\mathsf {T }_{\lambda \cup \alpha }}\psi _{a-1} e_{\mathsf {T }_{\lambda \cup \beta }} \psi _{a-1} e_{\mathsf {T }_{\lambda \cup \alpha }} = y_{a-1}e_{\mathsf {T }_{\lambda \cup \alpha }} - \psi ^a_b y^{\succ }_{\mathsf {T }_{\lambda \cup \beta }} \psi ^b_{a}. \end{aligned}$$We have that
 and so the former term is of the required form by our assumption for
and so the former term is of the required form by our assumption for  . Now, if \(y>1\) then the \((a-2)\)th, \((a-1)\)th and \(a\)th strands have residues r, \(r+1\), and r respectively. We have that $$\begin{aligned} {y }^{\succ }_{\mathsf {T }_{\lambda \cup \alpha }}=e_{\mathsf {T }_{\lambda \cup \alpha }}&= e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-2} \psi _{a-1} \psi _{a-2} e_{\mathsf {T }_{\lambda \cup \alpha }} - e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-1} \psi _{a-2} \psi _{a-1} e_{\mathsf {T }_{\lambda \cup \alpha }} \nonumber \\&= - e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-2} \psi _{a-1}y_{a-1} \psi _{a-1} \psi _{a-2} e_{\mathsf {T }_{\lambda \cup \alpha }} + e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-1} \psi _{a-2} y_{a-2} \psi _{a-2} \psi _{a-1} e_{\mathsf {T }_{\lambda \cup \alpha }}. \end{aligned}$$(2.12)
. Now, if \(y>1\) then the \((a-2)\)th, \((a-1)\)th and \(a\)th strands have residues r, \(r+1\), and r respectively. We have that $$\begin{aligned} {y }^{\succ }_{\mathsf {T }_{\lambda \cup \alpha }}=e_{\mathsf {T }_{\lambda \cup \alpha }}&= e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-2} \psi _{a-1} \psi _{a-2} e_{\mathsf {T }_{\lambda \cup \alpha }} - e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-1} \psi _{a-2} \psi _{a-1} e_{\mathsf {T }_{\lambda \cup \alpha }} \nonumber \\&= - e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-2} \psi _{a-1}y_{a-1} \psi _{a-1} \psi _{a-2} e_{\mathsf {T }_{\lambda \cup \alpha }} + e_{\mathsf {T }_{\lambda \cup \alpha }} \psi _{a-1} \psi _{a-2} y_{a-2} \psi _{a-2} \psi _{a-1} e_{\mathsf {T }_{\lambda \cup \alpha }}. \end{aligned}$$(2.12)where the first equality follows from Lemma 2.8, the second from relation R5 and the third follows from relations R3 and R4. We set \(\xi ={\text {Shape}}(\mathsf {T }_\lambda {\downarrow }_{<a-2})\). The two terms in Eq. (2.12) factor through the elements
$$\begin{aligned} \underbrace{e_{\mathsf {T }_\lambda {\downarrow }_{<a-2}} \boxtimes e_{r+1}}_{\xi \cup [x,y,z] } \boxtimes y_1e_{r,r} \boxtimes e_{\mathsf {T }_{\lambda \cup \alpha } {\downarrow }_{> a}} \qquad \underbrace{ e_{\mathsf {T }_\lambda {\downarrow }_{<a-2}} \boxtimes y_1 e_r }_{\xi \cup [x,y-1,z]} \boxtimes e_{r,r+1} \boxtimes e_{\mathsf {T }_{\lambda \cup \alpha } {\downarrow }_{> a}}\nonumber \\ \end{aligned}$$(2.13)respectively.
-
We first consider the latter term on the righthand-side of Eq. (2.12) (which we will see, is the required non-zero term). We note that \([x,y-1,z]\) and \(\alpha \) have the same residue and so \(Y_{[x,y-1,z]} (\xi \cup {[x,y-1,z]})= \xi \cup \beta \). By our inductive assumption that Eq. (2.7) holds for rank \(a-2<n\), we have that
 (2.14)
(2.14)Substituting this back into the second term of Eq. (2.13) we obtain

and then substituting into the second term of Eq. (2.12) we obtain

as required.
-
We now consider the former term of Eq. (2.12) (which, we will see, is zero modulo the ideal). We have that
 for \(\gamma \) a box of residue \(r+1\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\). We set \(c=\mathsf {T }_{\xi \cup \gamma }^{-1}(\gamma )\). We have that
for \(\gamma \) a box of residue \(r+1\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\). We set \(c=\mathsf {T }_{\xi \cup \gamma }^{-1}(\gamma )\). We have that 
by our inductive assumption that Eq. (2.6) holds for rank \(a-2<n\). Concatenating, we have that

and we note that the idempotent on the righthand-side belongs to the ideal
 and so the result follows by our assumption for
and so the result follows by our assumption for  .
.
- (iii):
-
Now suppose \(\alpha ' \) has residue \(d\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\) such that \(|d-r|>1\). We set \(\xi ={\text {Shape}}(\mathsf {T }_\lambda {\downarrow }_{< a-1})\). By case 2 of relation R4, we have that
$$\begin{aligned} y_a^k e_{\mathsf {T }_{\lambda \cup \alpha }}&= \psi _{a-1} \big ( \underbrace{e_{\mathsf {T }_\lambda {\downarrow }_{<a-1}}\boxtimes y_1^k e_{r } }_{\xi \cup \alpha }\boxtimes e_{d} \boxtimes e_{\mathsf {T }_{\lambda \cup \alpha }{\downarrow }_{>a}} \big )\psi _{a-1} \end{aligned}$$(2.15)for \(k\in \{0,1\}\). By the inductive assumption for rank \(a-1<n\) of Eq. (2.6), we have that

As in the case (ii) above, we concatenate to deduce the result. Two examples of the visualisation of the righthand-side of Eq. (2.15) are given in the third and fourth steps of Fig. 4; the corresponding elements are depicted in Fig. 6.
- (iv):
-
Suppose \(\alpha '=[x,y,z]\) has residue \(r-1\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\) (thus \([x,y,z]= [i,j-1,m]\) by residue considerations) and that \( [i-1,j,m]\not \in \lambda \) (if \([i-1,j,m]\in \lambda \), this implies that \(\lambda \cup \alpha \in \mathscr {P}_{{\underline{h}}}(n)\) and so the process would terminate). We remark that \({\text {res}}( {\mathsf {Adj}\text {-}\mathsf {Gar}}(\alpha ))=\{r-1\} \) and this is the unique case of the proof for which this holds. Let \(\gamma = [i-1,j-1,m]\) and we set \(c=\mathsf {T }_{\lambda \cup \alpha } (\gamma ) \) and let \(\xi = {\text {Shape}}(\mathsf {T }_\lambda {\downarrow }_{<a-1}) \) (see Fig. 7 for an example). By Lemma 2.8, \( e_{{\mathsf {T }_ {\lambda \cup \alpha }}}= {y }^{\succ }_{{\mathsf {T }_ {\lambda \cup \alpha }}}\). We have that
 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20)where the first and third equalities follow from the commuting case 2 of relation R4 and Lemma 2.8, and the second equality follows from case 1 of relation R5; the fourth equality follows from R3; the fifth is either trivial or follows from case (3) of R4 (in the latter case, the error term is zero by our inductive assumption for rank \(c-1<n\) of Eq. (2.7)). For our continuing example, the righthand-side of Eq. (2.19) is depicted in Fig. 9; the box-configurations labelling the idempotents on the left and righthand-sides of Eq. (2.18) are depicted in Fig. 7. We now consider the second term on the righthand-side of Eq. (2.18). We have that
$$\begin{aligned} e_{\mathsf {T }_{\xi -\gamma } } \boxtimes e_{r-1,r,r} =e_{\mathsf {T }_{ \xi -\gamma \cup [i,j-1,m] \cup \alpha \cup [i,j+e,m]}} \end{aligned}$$By our inductive assumption for ranks \(a-2,a-1<n\) for Eq. (2.6), we have that:

for \(\rho = Y^{\ell +1}_{[i,j-1,m]}(\xi -\gamma \cup [i,j-1,m]) \). Given
 , we can left justify \(\pi \cup [i,j+e,m]\) to obtain \(\pi \cup \alpha \). We note that \({\mathsf {Gar}}_{\succ }(\alpha )\cap \pi \) contains no nodes of residue r or \(r\pm 1\). Therefore
, we can left justify \(\pi \cup [i,j+e,m]\) to obtain \(\pi \cup \alpha \). We note that \({\mathsf {Gar}}_{\succ }(\alpha )\cap \pi \) contains no nodes of residue r or \(r\pm 1\). Therefore 
as required. (Note that \(\gamma ,\beta \not \in \pi \) by Lemma 2.8.) See Fig. 8 for an example.
The righthand-side of Eq. (2.15) for \(\lambda =(2^6,1^3)\) and \(\alpha =\alpha _3\) and \(\alpha _4\) respectively
Rewriting the first term after the equality in Eq. (2.18). We have moved the 1-box using case (iii) and this leaves us free to move the 2-boxes up their corresponding diagonals. The righthand-side is a box configuration which is strictly higher than \(\lambda \cup \beta \) in the \(\succ \)-ordering
Proof of Eq. (2.7) for a given \(\lambda \) and \(\alpha \). We assume that Eq. (2.7) holds for all \(\lambda \in \mathscr {P}_{{\underline{h}}}(n-1)\). We set \(\nu =\lambda \cup \alpha \in \mathscr {P}_{{\underline{h}}}(n)\) and we assume that \(\alpha \) is of residue \(r\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\). We have that \(e_{\mathsf {T }_{\lambda \cup \alpha }}={y }^{\succ }_{\mathsf {T }_{\lambda \cup \alpha }}\). We have that
In the first case, this follows from case 3 of relation R4 and the commutativity relations, to see this note that the \( (a-1)\)th strand has residue \(r-1\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\). In the second case, the statement follows from Lemma 2.8 and the fact that \(b=a\). Letting \(\beta '\) be as in Sect. 2.4, we note that  and so the first case of Eq. (2.21) is of the required form by our assumption for
and so the first case of Eq. (2.21) is of the required form by our assumption for  .
.
Proof of Eq. (2.8). Let \(\underline{j}= (j_1,\ldots , j_{n-1},r)\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^{n }\). We can assume that \({\text {Shape}}({\mathsf {J}}_{\leqslant n-1}) = \lambda \in \mathscr {P}_h(n-1) \) as otherwise \(e_{\underline{j}} \boxtimes e_{j_n} = 0 \boxtimes e_{r} = 0\) by induction. Thus it remains to show that

We can associate this rightmost r-strand to the (unique) left-justified r-box \(\alpha \) such that \(\square \succ \alpha \) for all \(\square \in \lambda \). (For example, \(\square =[9,6,0]\) for \(\lambda =(2^3,1^6)\), see Fig. 4.) Thus every strand in the diagram is labelled by a box. We pull the strand labelled by \(\alpha \) through the centre of the diagram (which is equal to the idempotent \(e_{\mathsf {T }_\nu }\)) one row at a time using Eq. (2.6). We can utilise Eq. (2.6) precisely when \(\lambda \cup \alpha \not \in \mathscr {P}_h(n)\). Therefore this process terminates when we reach the smallest addable r-box of \(\lambda \) under the \(\succ \)-ordering, namely \( {\mathsf {J}}^{-1}(n )\). Thus Eq. (2.8) follows. \(\square \)
Proposition 2.22
[4, Lemma 2.4 and Proposition 2.5] We let \({\underline{w}}\), \({\underline{w}}'\) be any two choices of reduced expression for \(w\in \mathfrak {S}_n \) and let \({\underline{v}}\) be any non-reduced expression for w. We have that



for some \( f_{{\underline{x}}}(y), g_{{\underline{x}}}(y)\in \mathcal {Y}_n\).
Proposition 2.23
Let \(\Bbbk \) be an integral domain. The \(\Bbbk \)-algebra \( \mathscr {H}^\sigma _n\) has spanning set
Proof
Let \(d \in e_{\underline{i}} \mathscr {H}^\sigma _n e_{\underline{j}}\) for some \(\imath ,\jmath \in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n\). By Eq. (2.8), we can rewrite \(e_{\underline{j}}\) (or equivalently \(e_{\underline{i}}\)) so that \(d=\sum _{x,y\in \mathfrak {S}_n} e_{\underline{i}} a_x e_{\mathsf {T }_\lambda }a _y e_{\underline{j}}\) for some \(a_x, a_y \) which are linear combinations of KLR elements tracing out some bijections \(x,y\in \mathfrak {S}_n\) respectively (but are possibly decorated with dots and need not be reduced). It remains to show that \(a_x, a_y\in \mathscr {H}_n^\sigma \) can be assumed to be reduced and undecorated. We establish this by induction along the Bruhat order, by working modulo the span of elements

If \({\underline{x}}\) is not reduced \(\psi _{\underline{x}}e_{\mathsf {T }_\lambda } a_y\) is zero modulo (2.26) by Eq. (2.23). Given two choices \({\underline{x}},{\underline{x}}' \) of reduced expression for \(x \in \mathfrak {S}_n\) we have that \( ( \psi _{\underline{x}}- \psi _{{\underline{x}}'}) e_{\mathsf {T }_\lambda }a_{\underline{y}}\) belongs to (2.26) by Eq. (2.22) followed by Eq. (2.7). Finally, if \(a_x\) is obtained from \(\psi _{\underline{x}}\) by adding a linear combination of dot decorations (at any points within the expression \(\psi _{{\underline{x}}}=\psi _{s_{i_1}}\ldots \psi _{s_{i_k}}\)) then \(\psi _{\underline{x}}e_{\mathsf {T }_\lambda } a_y\) is zero modulo (2.26) by Eq. (2.24) followed by Eq. (2.7). Thus  is spanned by elements of the form
is spanned by elements of the form

It remains to show that a spanning set is given by the elements \( x= w^\mathsf {S }_{\mathsf {T }_\lambda } \), \( y= w _\mathsf {T }^{\mathsf {T }_\lambda } \) for \( \mathsf {S },\mathsf {T }\in {\text {Std}}(\lambda ) \).
Given \(\mathsf {T }\in {\text {CStd}}(\lambda ){\setminus } {\text {Std}}(\lambda )\), we have that \(w_\mathsf {T }^{\mathsf {T }_\lambda }\) has a pair of crossing strands from \(1\leqslant i<j\leqslant n\) to \(1\leqslant w_\mathsf {T }^{\mathsf {T }_\lambda }(j)<w_\mathsf {T }^{\mathsf {T }_\lambda }(i)\leqslant n\) such that \(\mathsf {T }_\lambda ^{-1}(i)=[r,c,m]\) and \(\mathsf {T }_\lambda ^{-1}(j)=[r,c+1,m]\) are in the same row and in particular so that \(i=j-1\). It suffices to show that \( \psi _{\underline{x}} e_{\mathsf {T }_\lambda } \psi _{\underline{y}} \) belongs to the ideal  for a preferred choice of \({\underline{y}}\); we choose \({\underline{y}}= s_{i} {\underline{w}}\) (for some \(w\in \mathfrak {S}_n\) such that \(s_i w =y\)). Thus it remains to show that
for a preferred choice of \({\underline{y}}\); we choose \({\underline{y}}= s_{i} {\underline{w}}\) (for some \(w\in \mathfrak {S}_n\) such that \(s_i w =y\)). Thus it remains to show that  . However, this immediately follows from Eq. (2.6) because \(e_{\mathsf {T }_\lambda }\psi _{s_{i} } =\psi _{s_{i} } e_{s_i(\mathsf {T }_\lambda )} \) and we have that
. However, this immediately follows from Eq. (2.6) because \(e_{\mathsf {T }_\lambda }\psi _{s_{i} } =\psi _{s_{i} } e_{s_i(\mathsf {T }_\lambda )} \) and we have that  for
for  .
.
Given any \(\mathsf {T }\in {\text {RStd}}(\lambda ){\setminus } {\text {Std}}(\lambda )\) we let k be minimal such that \(\mathsf {T }{\downarrow }_{<k}\in {\text {Std}}(\mu )\) for some \(\mu \in \mathscr {P}_{{\underline{h}}}(k-1)\) and \({\text {Shape}}(\mathsf {T }{\downarrow }_{\leqslant k})=\nu \) for some \(\nu \not \in \mathscr {P}_{{\underline{h}}}(k)\). We have that \(e_{\mathsf { T}}= e_{\mathsf {T }_{\leqslant k}}\boxtimes e_{\mathsf {T }_{> k}}\) where \({\text {Shape}}(e_{\mathsf {T }_{\leqslant k}}) =\nu \in \mathscr {C}_{{\underline{h}}}(k) {\setminus } \mathscr {P}_{{\underline{h}}}(k)\) and so  by Eq. (2.6) and so
by Eq. (2.6) and so  by concatenation and the definition of
by concatenation and the definition of  . This implies that
. This implies that  , as required. \(\square \)
, as required. \(\square \)
Theorem 2.24
Let \(\Bbbk \) be an integral domain. The \(\Bbbk \)-algebra \( \mathscr {H}^\sigma _n\) is graded cellular with basis
anti-involution \(*\) and the degree function  . For \(\Bbbk \) a field, \( \mathscr {H}^\sigma _n\) is quasi-hereditary.
. For \(\Bbbk \) a field, \( \mathscr {H}^\sigma _n\) is quasi-hereditary.
Proof
We first prove that the spanning set of Proposition 2.23 is a \(\Bbbk \)-basis. We will show that the rank, as a \(\Bbbk \)-module, of \(\mathcal {H}^\sigma _n {\mathsf { y}}_{{\underline{h}}}\mathcal {H}^\sigma _n \) is less than or equal to \(\sum _{\lambda \in \mathscr {P}(n) {\setminus } \mathscr {P}_{{\underline{h}}}(n)}|{\text {Std}}(\lambda )|^2\). The ( )-ordering does not give us an easily constructible basis of \( \mathcal {H}^\sigma _n\) (see [5]). Hu and Mathas [7, Main Theorem] have shown that the classical ordering \(\rhd \) does give us an easily constructible basis \(\{\psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_{{\textsf {S }}_\lambda }\psi _ \mathsf {T }^{{\textsf {S }}_\lambda } \mid \mathsf {S },\mathsf {T }\in {\text {Std}}(\lambda )\}\) and presentations of all these cell-modules are given in [9, Definition 5.9]. We claim that \({\mathsf {y}}_{{\underline{h}}}\) annihilates any (\(\rhd \))-cell-module labelled by a \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\); in other words \({\mathsf {y}}_{{\underline{h}}} \psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_{{\textsf {S }}_\lambda } \in \mathcal {H}^{\rhd \lambda }_n\) for \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). Once we have proven the claim, we will deduce that the ideal is of the required rank, thus the spanning set is linearly independent (and hence a basis) as required. The algebra is then cellular (by its construction via idempotent ideals) with the stated basis (since we have a spanning set of the required rank). Finally, we note that each layer of the cell chain contains an idempotent \(e_{\mathsf {T }_\lambda }\) and so the algebra is quasi-hereditary, as required. We now turn to the proof of the claim. If \(m<\ell -1\) and \(h_m<\sigma _{m+1}-\sigma _{m}\), or if \(m=\ell -1\) and \(h_{\ell -1}<e+\sigma _{0}-\sigma _{\ell -1}\) then the mth summand
)-ordering does not give us an easily constructible basis of \( \mathcal {H}^\sigma _n\) (see [5]). Hu and Mathas [7, Main Theorem] have shown that the classical ordering \(\rhd \) does give us an easily constructible basis \(\{\psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_{{\textsf {S }}_\lambda }\psi _ \mathsf {T }^{{\textsf {S }}_\lambda } \mid \mathsf {S },\mathsf {T }\in {\text {Std}}(\lambda )\}\) and presentations of all these cell-modules are given in [9, Definition 5.9]. We claim that \({\mathsf {y}}_{{\underline{h}}}\) annihilates any (\(\rhd \))-cell-module labelled by a \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\); in other words \({\mathsf {y}}_{{\underline{h}}} \psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_{{\textsf {S }}_\lambda } \in \mathcal {H}^{\rhd \lambda }_n\) for \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). Once we have proven the claim, we will deduce that the ideal is of the required rank, thus the spanning set is linearly independent (and hence a basis) as required. The algebra is then cellular (by its construction via idempotent ideals) with the stated basis (since we have a spanning set of the required rank). Finally, we note that each layer of the cell chain contains an idempotent \(e_{\mathsf {T }_\lambda }\) and so the algebra is quasi-hereditary, as required. We now turn to the proof of the claim. If \(m<\ell -1\) and \(h_m<\sigma _{m+1}-\sigma _{m}\), or if \(m=\ell -1\) and \(h_{\ell -1}<e+\sigma _{0}-\sigma _{\ell -1}\) then the mth summand
in Eq. (2.4) is an idempotent whose residue sequence is not equal to that of any tableau \({\textsf {S }}\in {\text {Std}}(\lambda )\) for \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\) and therefore the claim is immediate. If \(h_m=\sigma _{m+1}-\sigma _{m}\), then the term in (2.29) is nilpotent and equal to
The idempotent in (2.30) annihilates \(\psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_\lambda \) unless \({\textsf {S }}{\downarrow }_{\{1,\ldots ,h_m+1\}}\) is equal to \(\mathsf {T }_{ (\emptyset ,\ldots ,\emptyset ,(h_m), (1), \emptyset ,\ldots ,\emptyset )} \). We now suppose that \({\textsf {S }}{\downarrow }_{\{1,\ldots ,h_m+1\}}\) is of this form and we set \(s_{m+1}\equiv \sigma _{m+1} \; {\text {mod}}\; e\).
Since \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\), we observe that \([1,1,m+1]\) is the unique box in \(\lambda \) of residue \(s_{m+1}\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}\) in which we can place the integer \(h_m+1\) (or any integer smaller than \(h_m+1\)) without violating the standard condition, by Lemma 2.8. The presentation of the Specht module in [9, Definition 5.9] implies that (i) \(\psi _{\underline{w}}y^{\rhd }_\lambda \in \mathcal {H}^{\rhd \lambda }_n\) for any \(w \ne w^{\textsf {S }}_{{\textsf {S }}_\lambda }\) for some \({\textsf {S }}\in {\text {Std}}(\lambda )\) with \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\) (since every (\(\rhd \))-Garnir belt has fewer than e boxes) and (ii) \(y_k y^{\rhd }_\lambda \in \mathcal {H}^{\rhd \lambda }_n\) for any \(1\leqslant k \leqslant n\).
We are now ready to prove the claim. Using Eq. (2.24), we move the dot at the top of \(y_{h_m+1}\psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_\lambda \) down the \((h_m+1)\)th strand to obtain a linear combination of undecorated diagrams (in which we have undone some number of crossings \(s_m\)-strands) and \( \psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y_{{\textsf {S }}_\lambda (1,1,m+1) } y^{\rhd }_\lambda \). By our above observation, all of these undecorated diagrams are labelled by non-standard \(\lambda \)-tableaux. Therefore all of these terms (and hence \(y_{h_m+1}\psi ^ {\textsf {S }}_{{\textsf {S }}_\lambda } y^{\rhd }_\lambda \)) are zero, by (i) and (ii). The claim and result follow. \(\square \)
Let \(\Bbbk \) be an integral domain. We define the standard or Specht modules of \( \mathscr {H}^\sigma _n \) as follows,
for \(\lambda \in {{\mathscr {P}}}_{{\underline{h}}}(n) \). We immediately deduce the following corollary of Theorem 2.24.
Corollary 2.25
The module \( \mathbf{S}_\Bbbk (\lambda ) \) is the module generated by \(e_{\mathsf {T }_\lambda }\) subject to the following relations:
-
\(e_{\underline{i}}e_{\mathsf {T }_\lambda }=\delta _{\underline{i},{{\text {res}}}({\mathsf {T }_\lambda })}e_{\mathsf {T }_\lambda }\) for \(\underline{i}\in ({{\mathbb {Z}}}/e{{\mathbb {Z}}})^n\);
-
\(y_k e_{\mathsf {T }_\lambda }=0\) for \(1\leqslant k \leqslant n\);
-
\(\psi _k e_{\mathsf {T }_\lambda }=0\) for any \(1\leqslant k< n\) such that \(s_k(\mathsf {T }_\lambda )\) is not row standard;
-
\(\psi ^{\mathsf { S}}_{\mathsf {T }_\lambda }e_{\mathsf {T }_\lambda }=0\) for \({\mathsf {S}} \in {RStd } (\lambda ){\setminus } {Std } (\lambda )\).
Proof
We have already checked that all of these relations hold (and so one can define a homomorphism from the abstractly defined module with this presentation to \( \mathbf{S}_\Bbbk (\lambda )\)) it only remains to check that these relations will suffice (i.e. the homomorphism is surjective). We know that \( \mathbf{S}_\Bbbk (\lambda )\) has a basis indexed by standard tableaux and so the result follows. \(\square \)
We now recall that the cellular structure allows us to define bilinear forms, for each \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\), there is a bilinear form \( \langle \ ,\ \rangle ^{ \lambda }\) on \( \mathbf{S}_\Bbbk (\lambda ) \), which is determined by
for any \(\mathsf {S },\mathsf {T }\in {\text {Std}}(\lambda )\). Let \(\Bbbk \) be a field of arbitrary characteristic. Factoring out by the radicals of these forms, we obtain a complete set of non-isomorphic simple \( \mathscr {H}^\sigma _n\)-modules
Proposition 2.26
Let \(\lambda \in \mathscr {P}_{{\underline{h}}} (n)\) and let \(A_1\succ A_2 \succ \cdots \succ A_z\) denote the removable boxes of \(\lambda \), totally ordered according to the \(\succeq \)-ordering. The restriction of \(\mathbf{S}_\Bbbk (\lambda )\) has an \(\mathscr {H}_{n-1} ^\sigma \)-module filtration
given by
For each \(1\leqslant r\leqslant z\), we have that
Proof
On the level of \(\Bbbk \)-modules, this is clear. Lifting this to \(\mathscr {H}_{n-1}^\sigma \)-modules is a standard argument which proceeds by checking the relations of Corollary 2.25 in a routine manner. \(\square \)
3 General light leaves bases for quiver Hecke algebras
The principal idea of categorical Lie theory is to replace existing structures (combinatorics, bases, and presentations of Hecke algebras) with richer structures which keep track of more information. In this section, we replace the classical tableaux combinatorics of symmetric groups (and quiver Hecke algebras) with that of paths in an alcove geometry. This will allow us to construct “light leaves" bases of these algebras, for which p-Kazhdan–Lusztig is baked-in to the very definition. The light leaves bases of \(\mathbf{S}_\Bbbk (\lambda )\) are constructed in such a way as to keep track of not just the point \(\lambda \in \mathbb {E}_{{\underline{h}}}\) (or rather the single path, \(\mathsf {T }_\lambda \), to the point \(\lambda \)) but of the many different ways we can get to the point \(\lambda \) by a reduced path/word in the alcove geometry. This extra generality is essential when we wish to write bases in terms of “2-generators" of the algebras of interest.
3.1 The alcove geometry
For ease of notation, we set \(H_m=h_0+\cdots +h_m\) for \(0\leqslant m <\ell \), and \(h=h_0+\cdots +h_{\ell -1}\). For each \( 1\leqslant i\leqslant n\) and \( 0\leqslant m< \ell \) we let \( \varepsilon _{i,m}:= \varepsilon _{(h_0+\cdots +h_{m-1}) + i}\) denote a formal symbol, and define an \(h\)-dimensional real vector space

and \(\overline{{\mathbb {E}}}_{{\underline{h}}}\) to be the quotient of this space by the one-dimensional subspace spanned by
We have an inner product \(\langle \; , \; \rangle \) on \({{\mathbb {E}}}_{{\underline{h}}}\) given by extending linearly the relations
for all \(1\leqslant i, j\leqslant n\) and \(0 \leqslant p,q< \ell \), where \(\delta _{i,j}\) is the Kronecker delta. We identify \(\lambda \in {{\mathcal {C}}}_{{\underline{h}}}(n)\) with an element of the integer lattice inside \(\mathbb {E}_{{\underline{h}}} \) via the map
where \(({-})^T\) is the transpose map. We let \(\Phi \) denote the root system of type \(A_{h-1}\) consisting of the roots
and \(\Phi _0\) denote the root system of type \(A_{h_0-1}\times \cdots \times A_{h_{\ell -1}-1}\) consisting of the roots
We choose \(\Delta \) (respectively \(\Delta _0\)) to be the set of simple roots inside \(\Phi \) (respectively \(\Phi _0\)) of the form \(\varepsilon _t-\varepsilon _{t+1}\) for some t. Given \(r\in {{\mathbb {Z}}}\) and \(\alpha \in \Phi \) we define \(s_{\alpha ,re}\) to be the reflection which acts on \({{\mathbb {E}}}_{{\underline{h}}}\) by
The group generated by the \(s_{\alpha ,0}\) with \(\alpha \in \Phi \) (respectively \(\alpha \in \Phi _0\)) is isomorphic to the symmetric group \(\mathfrak {S}_{{h}}\) (respectively to \(\mathfrak {S}_f:=\mathfrak {S}_{h_0}\times \cdots \times \mathfrak {S}_{h_{\ell -1}}\)), while the group generated by the \(s_{\alpha ,re}\) with \(\alpha \in \Phi \) and \(r\in {{\mathbb {Z}}}\) is isomorphic to \(\widehat{\mathfrak {S}}_{{h}}\), the affine Weyl group of type \(A_{{h}-1}\). We set \(\alpha _0=\varepsilon _{{h}}-\varepsilon _1\) and \(\Pi =\Delta \cup \{\alpha _0\}\). The elements \(S= \{s_{\alpha ,0}:\alpha \in \Delta \}\cup \{s_{\alpha _0,-e}\} \) generate \(\widehat{{\mathfrak {S}}}_{{h}}\).
Notation 3.1
We shall frequently find it convenient to refer to the generators in S in terms of the elements of \(\Pi \), and will abuse notation in two different ways. First, we will write \(s_{\alpha }\) for \(s_{\alpha ,0}\) when \(\alpha \in \Delta \) and \(s_{\alpha _0}\) for \(s_{\alpha _0,-e}\). This is unambiguous except in the case of the affine reflection \(s_{\alpha _0,-e}\), where this notation has previously been used for the element \(s_{\alpha ,0}\). As the element \(s_{\alpha _0,0}\) will not be referred to hereafter this should not cause confusion. Second, we will write \(\alpha = \varepsilon _i- \varepsilon _{i+1}\) in all cases; if \(i={h}\) then all occurrences of \(i+1\) should be interpreted modulo \({h}\) to refer to the index 1.
We shall consider a shifted action of the affine Weyl group \(\widehat{\mathfrak {S}}_{h}\) on \({{\mathbb {E}}}_{h,l}\) by the element
that is, given an element \(w\in \widehat{\mathfrak {S}}_{h} \), we set \( w\cdot x=w(x+\rho )-\rho . \) This shifted action induces a well-defined action on \(\overline{{\mathbb {E}}}_{{\underline{h}}}\); we will define various geometric objects in \({{\mathbb {E}}}_{{\underline{h}}}\) in terms of this action, and denote the corresponding objects in the quotient with a bar without further comment. We let \({{\mathbb {E}}} ({\alpha , re})\) denote the affine hyperplane consisting of the points
Note that our assumption that \(e>h_0+\cdots +h_{\ell -1}\) implies that the origin does not lie on any hyperplane. Given a hyperplane \({{\mathbb {E}}} ( \alpha ,re)\) we remove the hyperplane from \({{\mathbb {E}}}_{{\underline{h}}}\) to obtain two distinct subsets \({\mathbb E}^{>}(\alpha ,re)\) and \({{\mathbb {E}}}^{<}(\alpha ,re)\) where the origin lies in \( {{\mathbb {E}}}^{< }(\alpha ,re)\). The connected components of
are called chambers. The dominant chamber, denoted \(\overline{{\mathbb {E}}}_{{\underline{h}}}^+ \), is defined to be

The connected components of
are called alcoves, and any such alcove is a fundamental domain for the action of the group \( \widehat{\mathfrak {S}}_{h}\) on the set \(\mathbf{Alc} \) of all such alcoves. We define the fundamental alcove \(A_0\) to be the alcove containing the origin (which is inside the dominant chamber). We have a bijection from \(\widehat{\mathfrak {S}}_{h}\) to \(\mathbf{Alc} \) given by \(w\longmapsto wA_0\). Under this identification \(\mathbf{Alc} \) inherits a right action from the right action of \(\widehat{\mathfrak {S}}_{h}\) on itself. Consider the subgroup
The dominant chamber is a fundamental domain for the action of \(\mathfrak {S}_f\) on the set of chambers in \({\overline{\mathbb {E}}}_{{\underline{h}}}\). We let \( \mathfrak {S}^f\) denote the set of minimal length representatives for right cosets \(\mathfrak {S}_f \backslash \widehat{\mathfrak {S}}_{h}\). So multiplication gives a bijection \(\mathfrak {S}_f\times \mathfrak {S}^f \rightarrow \widehat{\mathfrak {S}}_{h}\). This induces a bijection between right cosets and the alcoves in our dominant chamber. Under this identification, alcoves are partially ordered by the Bruhat-ordering on \(\widehat{ \mathfrak {S}}_h\) which is a coarsening of the opposite of the order  .
.
If the intersection of a hyperplane \(\overline{{\mathbb {E}}}(\alpha ,re)\) with the closure of an alcove A is generically of codimension one in \(\overline{{\mathbb {E}}}_{{\underline{h}}}\) then we call this intersection a wall of A. The fundamental alcove \(A_0\) has walls corresponding to \(\overline{{\mathbb {E}}}(\alpha ,0)\) with \(\alpha \in \Delta \) together with an affine wall \(\overline{{\mathbb {E}}}(\alpha _0,-e)\). We will usually just write \(\overline{{\mathbb {E}}}(\alpha )\) for the walls \(\overline{{\mathbb {E}}}(\alpha ,0)\) (when \(\alpha \in \Delta \)) and \(\overline{{\mathbb {E}}}(\alpha ,-e)\) (when \(\alpha =\alpha _0\)). We regard each of these walls as being labelled by a distinct colour (and assign the same colour to the corresponding element of S). Under the action of \(\widehat{\mathfrak {S}}_{h}\) each wall of a given alcove A is in the orbit of a unique wall of \(A_0\), and thus inherits a colour from that wall. We will sometimes use the right action of \(\widehat{\mathfrak {S}}_{h}\) on \(\mathbf{Alc} \). Given an alcove A and an element \(s\in S\), the alcove As is obtained by reflecting A in the wall of A with colour corresponding to the colour of s. With this observation it is now easy to see that if \(w=s_{1}\ldots s_{t}\) where the \(s_i\) are in S then \(wA_0\) is the alcove obtained from \(A_0\) by successively reflecting through the walls corresponding to \(s_1\) up to \(s_h\). We will call a multipartition regular if its image in \(\overline{{\mathbb {E}}}_{h,l}\) lies in some alcove; those multipartitions whose images lies on one or more walls will be called singular.
3.2 Paths in the geometry
We now develop a path combinatorics inside our geometry. Given a map  we define points \(\mathsf {P }(k)\in {{\mathbb {E}}}_{{\underline{h}}}\) by
we define points \(\mathsf {P }(k)\in {{\mathbb {E}}}_{{\underline{h}}}\) by
for \(1\leqslant i \leqslant n\). We define the associated path of length n by
and we say that the path has shape \(\pi = \mathsf {P }(n) \in {{\mathbb {E}}}_{{\underline{h}}}\). We also denote this path by
Given \(\lambda \in \mathscr {C}_{h}(n)\) we let \({\text {Path}}(\lambda )\) denote the set of paths of length n with shape \(\lambda \). We define \({\text {Path}}_{{\underline{h}}}(\lambda )\) to be the subset of \({\text {Path}}(\lambda )\) consisting of those paths lying entirely inside the dominant chamber; i.e. those \(\mathsf {P }\) such that \(\mathsf {P }(i)\) is dominant for all \(0\leqslant i\leqslant n\). We let \({\text {Path}}_{{\underline{h}}}(n) = \cup _{\lambda \in \mathscr {P}_{{\underline{h}}}(n)}{\text {Path}}_{{\underline{h}}}(\lambda )\).
Given a path \(\mathsf {T}\) defined by such a map p of length n and shape \(\lambda \) we can write each p(j) uniquely in the form \( \varepsilon _{p(j)}= \varepsilon _{m_j,c_j}\) where \(0\leqslant m_j<\ell \) and \(1\leqslant c_j\leqslant h_j\). We record these elements in a tableau of shape \(\lambda ^T\) by induction on j, where we place the positive integer j in the first empty box in the \(c_j\)th column of component \(m_j\). By definition, such a tableau will have entries increasing down columns; if \(\lambda \) is a multipartition then the entries also increase along rows if and only if the given path is in \({\text {Path}}_{{\underline{h}}}(\lambda )\), and hence there is a bijection between \({\text {Path}}_{{\underline{h}}}(\lambda )\) and \({\text {Std}}(\lambda )\). For this reason we will sometimes refer to paths as tableaux, to emphasise that what we are doing is generalising the classical tableaux combinatorics for the symmetric group.
Example 3.2
Let \(\sigma =(0,3,6)\in {{\mathbb {Z}}}^3\) and \(e=9\). For \(\lambda =((2,1),(2,1),(1^3))\), the standard \(\lambda \)-tableaux of Example 2.5 correspond to the paths
Given a path \(\mathsf {P }\) we define
where \(\text {res}_\mathsf {P }(i)\) denotes the residue of the box labelled by i in the tableau corresponding to \(\mathsf {P }\).
Given paths \(\mathsf {P }=(\varepsilon _{p(1)},\ldots ,\varepsilon _{p(n)})\) and \(\mathsf {Q}=(\varepsilon _{q(1)},\ldots ,\varepsilon _{q(n)})\) we say that \(\mathsf {P }\sim \mathsf {Q}\) if there exists an \(\alpha \in \Phi \) and \(r\in {{\mathbb {Z}}}\) and \(s\leqslant n\) such that
In other words the paths \(\mathsf {P }\) and \(\mathsf {Q}\) agree up to some point \(\mathsf {P }(s)=\mathsf {Q}(s)\) which lies on \({{\mathbb {E}}}(\alpha ,re)\), after which each \(\mathsf {Q}(t)\) is obtained from \(\mathsf {P }(t)\) by reflection in \({{\mathbb {E}}}(\alpha ,re)\). We extend \(\sim \) by transitivity to give an equivalence relation on paths, and say that two paths in the same equivalence class are related by a series of wall reflections of paths and given \({\textsf {S }}\in {\text {Path}}_{{\underline{h}}}(n)\) we set \([{\textsf {S }}] = \{ \mathsf {T }\in {\text {Path}}_{{\underline{h}}}(n) \mid {\textsf {S }}\sim \mathsf {T }\}\).
We recast the degree of a tableau in the path-theoretic setting as follows.
Definition 3.3
Given a path \(\mathsf {S }=(\mathsf {S }(0),\mathsf {S }(1),\mathsf {S }(2), \ldots , \mathsf {S }(n))\) we set \(\deg (\mathsf {S }(0))=0\) and define
where \(d(\mathsf {S }(k),\mathsf {S }(k-1))\) is defined as follows. For \(\alpha \in \Phi \) we set \(d_{\alpha }(\mathsf {S }(k),\mathsf {S }(k-1))\) to be
-
\(+1\) if \(\mathsf {S }(k-1) \in {{\mathbb {E}}}(\alpha ,re)\) and \(\mathsf {S }(k) \in {{\mathbb {E}}}^{<}(\alpha ,re)\);
-
\(-1\) if \(\mathsf {S }(k-1) \in {{\mathbb {E}}}^{>}(\alpha ,re)\) and \(\mathsf {S }(k) \in {{\mathbb {E}}}(\alpha ,re)\);
-
0 otherwise as illustrated in (Fig. 12).
We let
We say that \(\mathsf {P }=(\varepsilon _{p(1)},\ldots ,\varepsilon _{p(n)})\) is a reduced path if \(d_\alpha (\mathsf {P }(k-1),\mathsf {P }(k ))=0 \) for \(1\leqslant k \leqslant n\) and \(\alpha \in \Pi \).
This definition of a reduced path is easily seen to be equivalent to that of [2, Section 2.3] .
There exist a unique reduced path in each \(\sim \)-equivalence class (and, of course, each reduced path belongs to some \(\sim \)-equivalence class and so \(\sim \)-classes and reduced paths are in bijection). We remark that \(\mathsf {T }_\mu \), the maximal path in the reverse cylindric ordering \(\succ \), is an example of a reduced path. Given \({\textsf {S }}\in {\text {Path}}_{{\underline{h}}}(n)\), we let \(\min [{\textsf {S }}]\) denote the minimal path in the \(\sim \)-equivalence class containing \({\textsf {S }}\). Given a reduced path \(\mathsf {P }_\lambda \in {\text {Path}}_{{\underline{h}}} (\lambda )\), we have that
decomposes (in a unitriangular fashion) as a sum of projective indecomposable modules for some generalised p-Kostka coefficients \(k^\mu _{\mathsf {P }_\lambda }\in \Bbbk \). In general, we have
for reduced paths \( \mathsf {P }_\lambda , \mathsf {Q}_\lambda \in {\text {Path}}_{{\underline{h}}} (\lambda )\) and so the choice of reduced path does matter. (This is not surprising, the auxiliary steps in Soergel’s algorithm for calculating Kazhdan–Lusztig polynomials produces a different pattern depending on the choice of reduced expression.) However, they do agree modulo higher terms under  , as we shall soon see (and indeed, after the cancellations in Soergel’s algorithm one obtains that the Kazhdan–Lusztig polynomials are independent of choices of reduced expressions).
, as we shall soon see (and indeed, after the cancellations in Soergel’s algorithm one obtains that the Kazhdan–Lusztig polynomials are independent of choices of reduced expressions).
Lemma 3.4
Given \(\lambda \in \mathscr {P}_ {{\underline{h}}}(n)\), let \(\mathsf {P }_\lambda \), \(\mathsf {Q}_\lambda \), \({\textsf {S }}_\lambda \) be any triple of reduced paths in \({\text {Path}}_{{\underline{h}}}(\lambda )\). The element \(e_{\mathsf {P }_\lambda }\) generates \(\mathcal {H}^{\succeq \lambda }/\mathcal {H}^{\succ \lambda }\) and moreover
for some \(k\in \Bbbk {\setminus } \{0\}\).
Proof
Let \({{\mathsf { R}}_\lambda } \) be any reduced path in \( {\text {Path}}_{{\underline{h}}}(\lambda )\). Two paths have the same residue sequence if and only if they belong to the same \(\sim \)-class. If \({\textsf {S }}\sim {{\mathsf {R}}_\lambda }\) then either \({\textsf {S }}={{\mathsf {R}}_\lambda }\) or \({\textsf {S }}\) terminates at a point \(\mu \succ \lambda \). Thus, we have that

This implies that \(e_{{\mathsf {R}}_\lambda }\in \mathcal {H}^{\succeq \lambda }/\mathcal {H}^{\succ \lambda }\) and therefore generates \( \mathcal {H}^{\succeq \lambda }/\mathcal {H}^{\succ \lambda }\) and belongs to the simple head of the Specht module; the result follows. \(\square \)
Definition 3.5
Given two paths
we define the naive concatenated path
3.3 Branching coefficients
We now discuss how one can think of a permutation as a morphism between pairs of paths in the alcove geometries of Sect. 3.1. Let \(\lambda \in \mathcal {C}_{{\underline{h}}}(n)\). Given a pair of paths \({\textsf {S }},\mathsf {T }\in {\text {Path}}(\lambda )\) we write the steps in \({\textsf {S }}\) and \(\mathsf {T }\) in sequence along the top and bottom edges of a frame, respectively. We can now reinterpret the element \(w^{{\textsf {S }}}_{\mathsf {T }}\in \mathfrak {S}_n\) (of Sect. 2) as the unique step-preserving permutation with the minimal number of crossings.
In the following (running) example we label our paths by  and
and  . For this section, we do not need to know what inspires this notation; however, all will become clear in Sect. 4.
. For this section, we do not need to know what inspires this notation; however, all will become clear in Sect. 4.
Example 3.6
We consider \(\Bbbk \mathfrak {S}_9\) for \(\Bbbk \) a field of characteristic 5; the characteristic is unimportant now, but inspires the notation and will be needed when we refer back to this example later. We set  . Here we have
. Here we have

are two examples of paths of shape \((3^3\)). The unique step-preserving permutation of minimal length is given by

Notice that if two strands have the same step-label, then they do not cross. This is, of course, exactly what it means for a step-preserving permutation to be of minimal length.
Definition 3.7
Fix \(({\textsf {S }},\mathsf {T })\) an ordered pair of paths which both terminate at some point \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\). We now inductively construct a reduced expression for \(w^{\textsf {S }}_\mathsf {T }\). We define the branching coefficients
and
for \(1\leqslant p \leqslant n\). These allow us to fix a distinguished reduced expression, \({\underline{w}}^{\textsf {S }}_\mathsf {T }\), for \(w^{\textsf {S }}_\mathsf {T }\) as follows,
and we set
Example 3.8
We continue with the assumptions of Example 3.6. We have that

for each \(p=1,2,3,4,5,6,9\) because  for all \(1\leqslant i \leqslant p\). We have that
for all \(1\leqslant i \leqslant p\). We have that

and so our reduced word is depicted in Fig. 13.
We can think of the branching coefficients as “one step morphisms" which allow us to mutate the path \({\textsf {S }}\) into \(\mathsf {T }\) via a series of n steps (as each branching coefficient moves the position of one step in the path) and so this mutation proceeds via \(n+1\) paths
see Fig. 13 for an example. We now lift these branching coefficients to the KLR algebra.
Remark 3.9
The “sign twist" in Definition 3.7 is of no consequence in this paper as we are mostly concerned with constructing generators and bases of quiver Hecke algebras and their truncations. However, in order to match-up our relations with those of Elias–Williamson, this sign twist will be necessary and so we introduce it here for the purposes of consistency with [2].
Now, let’s momentarily restrict our attention to pairs of paths of the form \(({\textsf {S }},\mathsf {T }_\lambda )\). In this case, the branching coefficients actually come from the “branching rule" for restriction along the tower \(\cdots \subset \mathscr {H}_{n-1}^\sigma \subset \mathscr {H}_{n}^\sigma \subset \cdots \). To see this, we note that
where \(w_n({{\textsf {S }}},{\mathsf {T }_\lambda })= w^n_{\mathsf {T }_\lambda (\square )}\) for some removable box \(\square \in {\text {Rem}}(\lambda )\) and where
By Proposition 2.26, we have that
Thus the branching coefficients above provide a factorisation of the cellular basis of Theorem 2.24 which is compatible with the restriction rule.
Example 3.10
Continuing with Examples 3.6 and 3.8, the lift of the path-morphism to the KLR algebra is as follows,

At each step in the restriction along the tower, there is precisely one removable box of any given residue and so the restriction is, in fact, a direct sum of Specht modules.
We wish to modify the branching coefficients above so that we can consider more general (families of) reduced paths \(\mathsf {P }_\lambda \) in place of the path \(\mathsf {T }_\lambda \). Given \({\textsf {S }}\in {\text {Path}}_{{\underline{h}}} (\lambda ), \) we can choose a reduced path vector as follows
such that \({\text {Shape}}({ \mathsf {P }}_{{\textsf {S }},k})={\text {Shape}}({ {\textsf {S }}} _{\leqslant k})\) for each \(0\leqslant k \leqslant n\). In other words, we choose a reduced path \({ \mathsf {P }}_{{\textsf {S }},p}\) for each and every point in the path \({\textsf {S }}\). For \(0\leqslant p \leqslant n\) and \({\text {Shape}}({\textsf {S }}_{< p}) + \varepsilon _{i_p} = {\text {Shape}}({\textsf {S }}_{\leqslant p })\), we define the modified branching coefficient,
and we hence define
Here we have freely identified elements of algebras of different sizes using the usual embedding \(\mathscr {H}_{n-1}^\sigma \hookrightarrow \mathscr {H}_{n}^\sigma \) given by \(d\mapsto d \boxtimes (\sum _{i\in {{\mathbb {Z}}}/e{{\mathbb {Z}}}} e(i) )\). We set \(\Upsilon _{\textsf {S }}^ {{\underline{\mathsf {P }}}_{{\textsf {S }}}}:=(\Upsilon ^{\textsf {S }}_ {{\underline{\mathsf {P }}}_{{\textsf {S }}}})^*\).
Remark 3.11
For symmetric groups there is a canonical choice of reduced path vector coming from the coset-like combinatorics which has historically been used for studying these groups. For the light leaves construction of Bott–Samelson endomorphism algebras, Libedinsky and Elias–Williamson require very different families of reduced path vectors whose origin can be seen as coming from a basis which can be written in terms of their 2-generators [6, 10].
Example 3.12
Continuing with Example 3.10 we have already noted that  . We choose to take the sequence \( \mathsf {T }_\mu \) for
. We choose to take the sequence \( \mathsf {T }_\mu \) for  for \(k\geqslant 0\) as our reduced path vector \( {{\underline{\mathsf {P }}}_{{\textsf {S }}}} \). Having made this choice, we have that
for \(k\geqslant 0\) as our reduced path vector \( {{\underline{\mathsf {P }}}_{{\textsf {S }}}} \). Having made this choice, we have that  (this holds more generally, see the Corollary 3.14 and the discussion immediately prior). We record this in tableaux format to help the reader transition between the old and new ways of thinking.
(this holds more generally, see the Corollary 3.14 and the discussion immediately prior). We record this in tableaux format to help the reader transition between the old and new ways of thinking.

The light leaves basis will be given in terms of products \( \Upsilon ^{\textsf {S }}_ {{\underline{\mathsf {P }}}_{\textsf {S }}} \Upsilon _\mathsf {T }^ {{\underline{\mathsf {P }}}_\mathsf {T }} \) for \( {\textsf {S }},\mathsf {T }\in {\text {Path}}_{{\underline{h}}} (\lambda )\) and “compatible choices" of \({{\underline{\mathsf {P }}}_{\textsf {S }}}\) and \({{\underline{\mathsf {P }}}_\mathsf {T }}\). Here the only condition for compatibility is that \(\mathsf {P }_{{\textsf {S }},n}=\mathsf {Q}_\lambda =\mathsf {P }_{\mathsf {T },n}\) for some fixed choice of reduced path \(\mathsf {Q}_\lambda \in {\text {Path}}_{{\underline{h}}} (\lambda )\), in other words the final choices of reduced path for each of \({\textsf {S }}\) and \(\mathsf {T }\) coincide. We remark that if \(\mathsf {P }_{{\textsf {S }},n}\ne \mathsf {P }_{\mathsf {T },n}\) then the product is clearly equal to zero (by idempotent considerations) and so this is the only sensible choice to make for such a product. In light of the above, we let \(\mathsf {Q}_\lambda \) be a reduced path and we say that a reduced path vector \({{\underline{\mathsf {P }}}_{\textsf {S }}}\) terminates at \(\mathsf {Q}_\lambda \) if \({{\underline{\mathsf {P }}}_{{\textsf {S }},n}}=\mathsf {Q}_\lambda \).
Theorem 3.13
(The light leaves basis) Let \(\Bbbk \) be an integral domain and \({\underline{h}}= (h_0,\ldots ,h_{\ell -1}) \in {{\mathbb {N}}}^\ell \) be such that \(h_m\leqslant \sigma _{m+1}-\sigma _{m} \) for \(0\leqslant m< \ell -1\) and \(h_{\ell -1}< e+\sigma _0-\sigma _{\ell -1} \). For each \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\) we fix a reduced path  and for each \({\textsf {S }}\in {Path }_{{\underline{h}}}(\lambda )\), we fix an associated reduced path vector \({{\underline{\mathsf {P }}}_{\textsf {S }}}\) terminating with
and for each \({\textsf {S }}\in {Path }_{{\underline{h}}}(\lambda )\), we fix an associated reduced path vector \({{\underline{\mathsf {P }}}_{\textsf {S }}}\) terminating with  . The \(\Bbbk \)-algebra \( \mathscr {H}^\sigma _n\) is a graded cellular algebra with basis
. The \(\Bbbk \)-algebra \( \mathscr {H}^\sigma _n\) is a graded cellular algebra with basis
anti-involution \(*\) and the degree function  .
.
Proof
By Theorem 2.24, we have that
provides a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\). By Lemma 3.4, we have that \( \Upsilon ^{\mathsf {T }_\lambda } _{\mathsf {Q}_\lambda } e_{\mathsf {Q}_\lambda } \Upsilon _{\mathsf {T }_\lambda } ^{\mathsf {Q}_\lambda } = k e_{\mathsf {T }_\lambda }\) for some \(k\in \Bbbk {\setminus } \{0\}\) modulo higher terms under \(\succ \) and so
provides a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\). By Eq. (3.3) and (3.4), we have that
provides a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\). By Proposition 2.26, we have that
generates a left subquotient of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\) which is isomorphic to \(\mathbf{S}_\Bbbk (\lambda -{ \varepsilon _i})\). Now, for each pair \( \varepsilon _i \in {\text {Rem}}(\lambda )\) and \({\mathsf {s}} \in {\text {Std}}(\lambda - \varepsilon _i)\), we fix a corresponding choice of reduced path \({\mathsf {P}}_{{\textsf {S }},n-1} \in {\text {Path}}_{{\underline{h}}}(\lambda -{ \varepsilon _i})\). By Lemma 3.4 and Proposition 2.26, we have that the set of all
as we vary over all \( {\mathsf {s}} \in {\text {Path}}_{{\underline{h}}}(\lambda -{ \varepsilon _i}), { \varepsilon _i} \in {\text {Rem}}(\lambda ), \) and \( \mathsf {T }\in {\text {Path}}_{{\underline{h}}}(\lambda ) \) provides a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\). Re-bracketing the above, we have that the set of all
as we vary over all \( {{\mathsf {s}}} \in {\text {Path}}_{{\underline{h}}}(\lambda -{ \varepsilon _i}), { \varepsilon _i} \in {\text {Rem}}(\lambda ),\) and \( \mathsf {T }\in {\text {Path}}_{{\underline{h}}}(\lambda ) \) provides a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\). Finally, simplifying using Proposition 2.22 we obtain that
is a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\) where we note that the middle term in the KLR-product is our modified branching coefficient. Repeating n times, we have that
is a \(\Bbbk \)-basis of \(\mathscr {H}^{\succeq \lambda }/\mathscr {H}^{\succ \lambda }\); repeating the above for the righthand-side, the result follows. \(\square \)
In particular, we can set \( {\underline{\mathsf {P }}}_{\textsf {S }}= (\mathsf {Q}_\lambda {\downarrow }_{\leqslant k})_{k\geqslant 0}\) and obtain the following corollary, which specialises to Theorem 2.24 for \(\mathsf {Q}_\lambda =\mathsf {T }_\lambda \).
Corollary 3.14
For each \(\lambda \in \mathscr {P}_{{\underline{h}}}(n)\) we fix a reduced path \({{\text {Q}}}_\lambda \in {{\text {Path}}}_{{\underline{h}}}(\lambda )\). The \(\Bbbk \)-algebra \( \mathscr {H}^\sigma _n\) is a graded cellular algebra with basis
anti-involution \(*\) and the degree function  .
.
4 Light leaf generators for the principal block
We now restrict our attention to the principal block and illustrate how the constructions of previous sections specialise to be familiar ideas from Soergel diagrammatics. In particular, we provide an exact analogue of Libedinsky’s and Elias–Williamson’s algorithmic construction of a light leaves basis for such blocks. In order to do this, we provide a short list of path-morphisms which we will show generate the algebra \({\mathsf {f}}_{n,\sigma }(\mathcal {H}^\sigma _n /\mathcal {H}^\sigma _n {\mathsf {y}}_{{\underline{h}}}\mathcal {H}^\sigma _n) {\mathsf {f}}_{n,\sigma } \) (thus proving Theorem B).
4.1 Alcove paths
When passing from multicompositions to our geometry \(\overline{{\mathbb {E}}}_{h,l}\), many non-trivial elements map to the origin. One such element is  . (Recall our transpose convention for embedding multipartitions into our geometry.) We will sometimes refer to this as the determinant as (for the symmetric group) it corresponds to the determinant representation of the associated general linear group. We will also need to consider elements corresponding to powers of the determinant, namely
. (Recall our transpose convention for embedding multipartitions into our geometry.) We will sometimes refer to this as the determinant as (for the symmetric group) it corresponds to the determinant representation of the associated general linear group. We will also need to consider elements corresponding to powers of the determinant, namely  . We now restrict our attention to paths between points in the principal linkage class, in other words to paths between points in \(\widehat{\mathfrak {S}}_{h}\cdot 0\). Such points can be represented by multicompositions \(\mu \) in \(\widehat{\mathfrak {S}}_{h}\cdot \delta _k\) for some choice of k.
. We now restrict our attention to paths between points in the principal linkage class, in other words to paths between points in \(\widehat{\mathfrak {S}}_{h}\cdot 0\). Such points can be represented by multicompositions \(\mu \) in \(\widehat{\mathfrak {S}}_{h}\cdot \delta _k\) for some choice of k.
Definition 4.1
We will associate alcove paths to certain words in the alphabet
where \(s_\emptyset =1\). That is, we will consider words in the generators of the affine Weyl group, but enriched with explicit occurrences of the identity in these expressions. We refer to the number of elements in such an expression (including the occurrences of the identity) as the degree of this expression. We say that an enriched word is reduced if, upon forgetting occurrences of the identity in the expression, the resulting word is reduced.
Given a path \(\mathsf {P }\) between points in the principal linkage class, the end point lies in the interior of an alcove of the form \(wA_0\) for some \(w\in \widehat{{\mathfrak {S}}}_{h}\). If we write w as a word in our alphabet, and then replace each element \(s_{\alpha }\) by the corresponding non-affine reflection \(s_{\alpha }\) in \({{\mathfrak {S}}}_{h}\) to form the element \({\overline{w}}\in {{\mathfrak {S}}}_{h}\) then the basis vectors \(\varepsilon _i\) are permuted by the corresponding action of \({\overline{w}}\) to give \(\varepsilon _{{\overline{w}}(i)}\), and there is an isomorphism from \(\overline{{\mathbb {E}}}_{h,l}\) to itself which maps \(A_0\) to \(wA_0\) such that 0 maps to \(w\cdot 0\), coloured walls map to walls of the same colour, and each basis element \(\varepsilon _i\) map to \(\varepsilon _{{\overline{w}}(i)}\). Under this map we can transform a path \(\mathsf {Q}\) starting at the origin to a path starting at \(w\cdot 0\) which passes through the same sequence of coloured walls as \(\mathsf {Q}\) does.
Definition 4.2
Given two paths \(\mathsf {P }=( \varepsilon _{i_1}, \varepsilon _{i_2},\ldots , \varepsilon _{i_p}) \in {\text {Path}}(\mu )\) and \( \mathsf {Q}=( \varepsilon _{j_1}, \varepsilon _{j_2},\ldots , \varepsilon _{j_q}) \in {\text {Path}}(\nu )\) with the endpoint of \(\mathsf {P }\) lying in the closure of some alcove \(wA_0\) we define the contextualised concatenated path
If there is a unique such w then we may simply write \(\mathsf {P }\otimes \mathsf {Q}\). If  we will simply write
we will simply write  .
.
We now define the building blocks from which all of our distinguished paths will be constructed. We begin by defining certain integers that describe the position of the origin in our fundamental alcove.
Definition 4.3
Given  we define
we define  to be the distance from the origin to the wall corresponding to
to be the distance from the origin to the wall corresponding to  , and let \(b_\emptyset =1\). Given our earlier conventions this corresponds to setting
, and let \(b_\emptyset =1\). Given our earlier conventions this corresponds to setting
for \(1\leqslant i <h_{m+1}\) and \(0 \leqslant m <\ell \) and that
for \(0\leqslant m<\ell -1\). We sometimes write  for the element
for the element  . Given
. Given  we set
we set  .
.
Example 4.4
Let \(e=5\), \(h=3\) and \(\ell =1\) as in Fig. 11. Then  and
and  both equal 1, while
both equal 1, while  and \(b_{\emptyset }=1\).
and \(b_{\emptyset }=1\).
Example 4.5
Let \(e=7\), \(h=2\) and \(\ell =2\) and \(\sigma =(0,3)\in {{\mathbb {Z}}}^2\). Then  and
and  both equal 1, while
both equal 1, while  ,
,  , and \(b_{\emptyset }=1\).
, and \(b_{\emptyset }=1\).
We can now define our basic building blocks for paths.
Definition 4.6
Given  , we consider the multicomposition
, we consider the multicomposition  with all columns of length
with all columns of length  , with the exception of the ith and \((i+1)\)st columns, which are of length 0 and
, with the exception of the ith and \((i+1)\)st columns, which are of length 0 and  , respectively. We set
, respectively. We set

where \(\widehat{.}\) denotes omission of a coordinate. Then our distinguished path corresponding to  is given by
is given by

The distinguished path corresponding to \(\emptyset \) is given by

and set  .
.
Given all of the above, we can finally define our distinguished paths for general words in our alphabet. There will be one such path for each word in our alphabet, and they will be defined by induction on the degree of the word, as follows.
Definition 4.7
We now define a distinguished path \(\mathsf {P }_{{\underline{w}}}\) for each word \({\underline{w}}\) in our alphabet \(S\cup \{1\}\) by induction on the degree of \({\underline{w}}\). If \({\underline{w}}\) is \(s_\emptyset \) or a simple reflection \(s_\alpha \) we have already defined the distinguished path in Definition 4.6. Otherwise if \({\underline{w}}=s_\alpha {\underline{w}}'\) then we define

If \({\underline{w}}\) is a reduced word in \(\widehat{{\mathfrak {S}}}_{hl}\), then the corresponding path \(\mathsf {P }_{{\underline{w}}}\) is a reduced path.
Remark 4.8
Contextualised concatenation is not associative (if we wish to decorate the tensor products with the corresponding elements w). As we will typically be constructing paths as in Definition 4.7 we will adopt the convention that an unbracketed concatenation of n terms corresponds to bracketing from the right:
We will also need certain reflections of our distinguished paths corresponding to elements of \(\Pi \).
Definition 4.9
Given  we set
we set

the path obtained by reflecting the second part of  in the wall through which it passes.
in the wall through which it passes.
Example 4.10
We illustrate these various constructions in a series of examples. In the first two diagrams of Fig. 14, we illustrate the basic path  and the path
and the path  and in the rightmost diagram of Fig. 14, we illustrate the path \(\mathsf {P }_\emptyset \). A more complicated example is illustrated in Fig. 11, where we show the distinguished path \(\mathsf {P }_{\underline{w}}\) for
and in the rightmost diagram of Fig. 14, we illustrate the path \(\mathsf {P }_\emptyset \). A more complicated example is illustrated in Fig. 11, where we show the distinguished path \(\mathsf {P }_{\underline{w}}\) for  as in Fig. 11. The components of the path between consecutive black nodes correspond to individual
as in Fig. 11. The components of the path between consecutive black nodes correspond to individual  s.
s.
The leftmost two diagrams picture the path  walking through an
walking through an  -hyperplane in \(\overline{{\mathbb {E}}}_{1,3}^+\), and the path
-hyperplane in \(\overline{{\mathbb {E}}}_{1,3}^+\), and the path  which reflects this path through the same
which reflects this path through the same  -hyperplane. The rightmost diagram pictures the path \(\mathsf {P }_\emptyset \) in \(\overline{{\mathbb {E}}}_{1,3}^+\). We have bent the paths slightly to make them clearer
-hyperplane. The rightmost diagram pictures the path \(\mathsf {P }_\emptyset \) in \(\overline{{\mathbb {E}}}_{1,3}^+\). We have bent the paths slightly to make them clearer
4.2 The principal block of \({\mathscr {H}^\sigma _n}\)
We now restrict our attention to regular blocks of \({\mathscr {H}^\sigma _n}\). In order to do this, we first recall that we consider an element of the quiver Hecke algebra to be a morphism between paths. The easiest elements to construct are the idempotents corresponding to the trivial morphism from a path to itself. Given  a simple reflection or
a simple reflection or  , we have an associated path
, we have an associated path  , a trivial bijection
, a trivial bijection  , and an idempotent element of the quiver Hecke algebra
, and an idempotent element of the quiver Hecke algebra

More generally, given any \({\underline{w}}=s_{ \alpha ^{(1)}}s_{ \alpha ^{(2)}}\ldots s_{ \alpha ^{(k)} }\), we have an associated path \(\mathsf {P }_{\underline{w}}\), and an element of the quiver Hecke algebra
We let \({\text {Std}}_{n,\sigma } (\lambda )\) be the set of all standard \(\lambda \)-tableaux which can be obtained by contextualised concatenation of paths from the set

We let \(\mathscr {P}_{{\underline{h}}}(n,\sigma )=\{ \lambda \in \mathscr {P}_{{\underline{h}}}(n) \mid {\text {Std}}_{n,\sigma } (\lambda )\ne \emptyset \}\). We let \({\text {Std}}_{n,\sigma } = \cup _{\lambda \in \mathscr {P}_{{\underline{h}}}(n ,\sigma )}{\text {Std}}_{n,\sigma } (\lambda )\). For example, the path in Fig. 11 is equal to  We define
We define
and the remainder of this paper will be dedicated to understanding the algebra
In fact, we will provide a concise list of generators for this truncated algebra (in the spirit of [6]) and rewrite the basis of Theorem 3.13 in terms of these generators.
In this section, we use our concrete branching coefficients to define the “Soergel 2-generators" of \( {\mathsf {f}}_{n,\sigma } (\mathcal {H}^\sigma _n/ \mathcal {H}^\sigma _n {\mathsf {y}}_{{\underline{h}} }\mathcal {H}^\sigma _n ) {\mathsf { f}}_{n,\sigma }\) explicitly. In the companion paper [2], we will show that these generators are actually independent of these choices of reduced expressions (however, this won’t be needed here—we simply make a note, again, for purposes of consistency with [2]).
4.3 Generator morphisms in degree zero
We first discuss how to pass between paths \( {\mathsf {P }_{\underline{w}}} \) and \( {\mathsf {P }_{{\underline{w}}'} } \) which are in different linkage classes but for which \({\underline{w}}\) and \({\underline{w}}'\) have the same underlying permutation. Fix two such paths
with \(\alpha ^{(1)} ,\ldots , \alpha ^{(k)} , \beta ^{(1)} ,\ldots , \beta ^{(k)} \in \Pi \cup \{\emptyset \}\). We suppose, only for the purposes of this motivational discussion, that both paths are reduced. In which case, we have that \(w \in \widehat{\mathfrak {S}}_{h}\) and so the expressions \({\underline{w}}\) and \({\underline{w}}'\) differ only by applying Coxeter relations in of \( \widehat{\mathfrak {S}}_{h}\) and the trivial “adjustment" relation \(s_i 1 = 1 s_i\) (made necessary by our augmentation of the Coxeter presentation). Moreover, \({\underline{w}}\) and \({\underline{w}}'\) are both reduced expressions and so we need only apply the “hexagon" relation \(s_i s_{i+1} s_i= s_{i+1} s_is_{i+1}\) and the “commutation" relation \(s_i s_j = s_j s_i\) for \(|i-j|>1\). The remainder of this subsection will be dedicated to lifting these path-morphisms to the level of generators of the KLR algebra. We stress that one can apply these adjustment/hexagon/commutator path-morphisms to any paths (not just reduced paths) but the reduced paths provide the motivation.
4.3.1 Adjustment generator
We will refer to the passage between alcove paths which differ only by occurrences of \(s_\emptyset =1\) (and their associated idempotents) as “adjustment". We define the KLR-adjustment generator to be the element

Examples of the paths  ,
,  , and adjustment generators are given in Figs. 15 and 16.
, and adjustment generators are given in Figs. 15 and 16.
4.3.2 The KLR hexagon diagram
We wish to pass between the two distinct paths around a vertex in our alcove geometry which lies at the intersection of two hyperplanes labelled by non-commuting reflections. To this end, we let  label a pair of non-commuting reflections. Of course, one path around the vertex may be longer than the other. Thus, we have two cases to consider: if
label a pair of non-commuting reflections. Of course, one path around the vertex may be longer than the other. Thus, we have two cases to consider: if  then we must pass between the paths
then we must pass between the paths  and
and  and if
and if  then we pass between the paths
then we pass between the paths  and
and  , where here
, where here  .
.
We define the KLR-hexagon to be the element

for  or
or  respectively. Two such pairs of paths are despited in Fig. 17. For the latter pair, the corresponding KLR-hexagon element is depicted in Fig. 18.
respectively. Two such pairs of paths are despited in Fig. 17. For the latter pair, the corresponding KLR-hexagon element is depicted in Fig. 18.
4.3.3 The KLR commutator
Let  be roots labelling commuting reflections. We wish to understand the morphism relating the paths
be roots labelling commuting reflections. We wish to understand the morphism relating the paths  to
to  . We define the KLR-commutator to be the element
. We define the KLR-commutator to be the element

as illustrated in Fig. 19.
We let \(h=1\), \(\ell =4\), \(\kappa =(0,2,4,6)\in ({{\mathbb {Z}}}/8{{\mathbb {Z}}})^4\) and  and
and  . We picture the element
. We picture the element  , the corresponding paths are depicted in Fig. 20
, the corresponding paths are depicted in Fig. 20
We let \(h=1\), \(\ell =4\), \(\kappa =(0,2,4,6)\in ({{\mathbb {Z}}}/8{{\mathbb {Z}}})^4\) and  and
and  . We picture the element
. We picture the element  , the corresponding paths are depicted in Fig. 19
, the corresponding paths are depicted in Fig. 19
4.4 Generator morphisms in non-zero degree
We have already seen how to pass between \({\textsf {S }},\mathsf {T }\in {\text {Std}}_{n,\sigma }(\lambda )\) any two reduced paths. We will now see how to inflate a reduced path to obtain a non-reduced path. Given \({\textsf {S }},\mathsf {T }\in {\text {Std}}_{n,\sigma }(\lambda )\), we suppose that the former is obtained from the latter by inflating by a path through a single hyperplane  . Of course, since \({\textsf {S }}\) and \(\mathsf {T }\) have the same shape, this inflation must add an
. Of course, since \({\textsf {S }}\) and \(\mathsf {T }\) have the same shape, this inflation must add an  at some point (and will involve removing an occurrence of
at some point (and will involve removing an occurrence of  in order to preserve n). There are two ways which one can approach a hyperplane: from above or from below. Adding an upward/downward occurrence of
in order to preserve n). There are two ways which one can approach a hyperplane: from above or from below. Adding an upward/downward occurrence of  corresponds to the spot/fork Soergel generator.
corresponds to the spot/fork Soergel generator.
4.4.1 The spot morphism
We now define the morphism which corresponds to reflection towards the origin through the hyperplane labelled by  . We consider the paths
. We consider the paths

examples of these paths are depicted in Fig. 21. We define the KLR-spot to be the element

which is of degree \(+1\) (corresponding to the unique step of off the  -hyperplane). We have already constructed an example of an element
-hyperplane). We have already constructed an example of an element  in great detail over the course of Examples 3.6, 3.8 and 3.10 and Fig. 13.
in great detail over the course of Examples 3.6, 3.8 and 3.10 and Fig. 13.
4.4.2 The fork morphism
We wish to understand the morphism from  to
to  . We define the KLR-fork to be the elements
. We define the KLR-fork to be the elements

as illustrated in Fig. 22. The element  is of degree \(-1\).
is of degree \(-1\).
Fix \(\ell =1\) and \(h=3\) and \(e=5\) and  (so that
(so that  ). We picture the element
). We picture the element  . The first 9 and final 4 of the branching coefficients are trivial and so we do not waste trees by picturing all of them. The corresponding paths are pictured in Fig. 23
. The first 9 and final 4 of the branching coefficients are trivial and so we do not waste trees by picturing all of them. The corresponding paths are pictured in Fig. 23
Fix \(\ell =1\) and \(h=3\) and \(e=5\) and  (so that
(so that  ). We depict the paths
). We depict the paths  and
and  (although we do not depict the determinant path). The corresponding fork generator is pictured in Fig. 22
(although we do not depict the determinant path). The corresponding fork generator is pictured in Fig. 22
4.5 Light leaves for the Bott–Samelson truncation
We now rewrite the truncated basis of Theorem 3.13 in terms of the Bott–Samelson generators (thus showing that these are, indeed, generators of the truncated algebra). Of course, the idempotent of Eq. (4.1) is specifically chosen so that the truncated algebra
has basis indexed by the (sub)set of alcove-tableaux (and this basis is simply obtained from that of Theorem 2.24 by truncation). It only remains to illustrate how the reduced-path-vectors can be chosen to mirror the construction of paths in \({\text {Std}}_{n,\sigma }(\lambda )\) via concatenation.
We can extend a path \(\mathsf {T }'\in {\text {Std}}_{n,\sigma }(\lambda )\) to obtain a new path \(\mathsf {T }\) in one of three possible ways

for some  . The first two cases each subdivide into a further two cases based on whether
. The first two cases each subdivide into a further two cases based on whether  is an upper or lower wall of the alcove containing \(\lambda \). These four cases are pictured in Fig. 24 (for \({\textsf {S }}_\emptyset \) we refer the reader to Fig. 14). Any two reduced paths \( \mathsf {P }_{{\underline{w}}} , \mathsf {P }_{\underline{v}}\in {\text {Std}}_{n,\sigma } (\lambda )\) can be obtained from one another by some iterated application of hexagon, adjustment, and commutativity permutations. We let
is an upper or lower wall of the alcove containing \(\lambda \). These four cases are pictured in Fig. 24 (for \({\textsf {S }}_\emptyset \) we refer the reader to Fig. 14). Any two reduced paths \( \mathsf {P }_{{\underline{w}}} , \mathsf {P }_{\underline{v}}\in {\text {Std}}_{n,\sigma } (\lambda )\) can be obtained from one another by some iterated application of hexagon, adjustment, and commutativity permutations. We let
denote the corresponding path-morphism in the algebras \(\mathcal {H}_n^\sigma /\mathcal {H}_n^\sigma {\mathsf {y}}_{\underline{h}}\mathcal {H}_n^\sigma \) (so-named as they permute reduced expressions). In the following construction, we will assume that the elements \(c^{{\textsf {S }}'}_{\mathsf {T }'}\) exist for any choice of reduced path \({\textsf {S }}'\). We then extend \({\textsf {S }}'\) using one of the \( U_0, U_1, D_0, \) and \(D_1\) paths (which puts a restriction on the form of the reduced expression) but then use a “rex move" to obtain cellular basis elements “glued together” along an idempotent corresponding to an arbitrary reduced path.
The first (respectively last) two paths are  and
and  originating in an alcove with
originating in an alcove with  labelling an upper (respectively lower) wall. Here we take the convention that the origin is below the pink hyperplane. The degrees of these paths are \( 1, 0, 0, -1\) respectively. We call these paths \( U_0, U_1, D_0, \) and \(D_1\) respectively
labelling an upper (respectively lower) wall. Here we take the convention that the origin is below the pink hyperplane. The degrees of these paths are \( 1, 0, 0, -1\) respectively. We call these paths \( U_0, U_1, D_0, \) and \(D_1\) respectively
Definition 4.11
Suppose that \(\lambda \) belongs to an alcove which has a hyperplane labelled by  as an upper alcove wall. Let \(\mathsf {T }'\in {\text {Std}}_{n,\sigma }(\lambda )\). If
as an upper alcove wall. Let \(\mathsf {T }'\in {\text {Std}}_{n,\sigma }(\lambda )\). If  then we inductively define
then we inductively define

If  then we inductively define
then we inductively define

Now suppose that \(\lambda \) belongs to an alcove which has a hyperplane labelled by  as a lower alcove wall. Thus we can choose
as a lower alcove wall. Thus we can choose  . For
. For  , we inductively define
, we inductively define

and if  then then we inductively define
then then we inductively define

Theorem 4.12
(The Libedinsky–Williamson light leaves basis) Given weakly increasing \(\sigma \in {{\mathbb {Z}}}^\ell \), we let \({\underline{h}}= (h_0,\ldots ,h_{\ell -1}) \in {{\mathbb {N}}}^\ell \) be such that \(h_m\leqslant \sigma _{m+1}-\sigma _{m} \) for \(0\leqslant m< \ell -1\) and \(h_{\ell -1}< e+\sigma _0-\sigma _{\ell -1} \). Suppose that n is divisible by \(h\). For each \(\lambda \in \mathscr {P}_{{\underline{h}}}(n,\sigma )\) we fix an arbitrary reduced path \( \mathsf {P }_\lambda \in {{\text {Std}}}_{n,\sigma }(\lambda ) \). The algebra  is quasi-hereditary with graded integral cellular basis
is quasi-hereditary with graded integral cellular basis
with respect to the ordering  on \( \mathscr {P}_{{\underline{h}}} (n )\), the anti-involution \(*\) given by flipping a diagram through the horizontal axis and the map \(\deg : {{\text {Std}}}_{n,\sigma } (\lambda ) \rightarrow {{\mathbb {Z}}}\).
on \( \mathscr {P}_{{\underline{h}}} (n )\), the anti-involution \(*\) given by flipping a diagram through the horizontal axis and the map \(\deg : {{\text {Std}}}_{n,\sigma } (\lambda ) \rightarrow {{\mathbb {Z}}}\).
Proof
Suppose that \(\mathsf {Q}, \textsf {U}\in {\text {Std}}_{k,\sigma }( \nu )\) with \(\mathsf {Q}\) reduced and \(k<n\) divisible by h. By induction, we may assume that \(c^{\mathsf {Q}}_{\textsf {U}} =\Upsilon ^{{\underline{\mathsf {P }}}_{\textsf {U}}}_{\textsf {U}} \) for some reduced path vector \({{\underline{\mathsf {P }}}_{\textsf {U}}}\) such that \({{\underline{\mathsf {P }}}_{\textsf {U}}}=(\mathsf {P }_{\textsf {U},0},\mathsf {P }_{\textsf {U},1},\ldots , \mathsf {P }_{\textsf {U},k})\) with \( \mathsf {P }_{\textsf {U},k}=\mathsf {Q}\). By Theorem 3.13 and our inductive assumption, the result holds for all \(k<n\) divisible by h. Now suppose that \(\lambda \in \mathscr {P}_{\underline{h}}(n,\sigma )\) and that \(\lambda \) belongs to an alcove, \(A_\lambda \), which has a hyperplane labelled by  and that
and that  . We now reconstruct the element \(c^{\mathsf {P }}_{\mathsf {T }}\) in terms of the basis of modified branching coefficients (as in Theorem 3.13) with \(\mathsf {P }:=\mathsf {P }_\lambda \) reduced and \(\mathsf {T }\) equal to either
. We now reconstruct the element \(c^{\mathsf {P }}_{\mathsf {T }}\) in terms of the basis of modified branching coefficients (as in Theorem 3.13) with \(\mathsf {P }:=\mathsf {P }_\lambda \) reduced and \(\mathsf {T }\) equal to either  or
or  . This amounts to defining a reduced path vector,
. This amounts to defining a reduced path vector,
for which \(c^{\mathsf {P }}_{\mathsf {T }} =\Upsilon ^{{\underline{\mathsf {P }}}_{\mathsf {T }}}_{\mathsf {T }} \). To do this, we simply set

To summarise: we incorporate the “rex" move into the final branching coefficient (and all other branching coefficients are left unmodified). Choosing the reduced path vectors in this fashion, we obtain the required basis as a special case of Theorem 3.13 . \(\square \)
We have shown that we can write a basis for our algebra entirely in terms of the elements

for  such that
such that  and
and  label an arbitrary pair of non-commuting reflections and
label an arbitrary pair of non-commuting reflections and  and
and  label an arbitrary pair of commuting reflections. Thus we deduce the following:
label an arbitrary pair of commuting reflections. Thus we deduce the following:
Corollary 4.13
Theorem B of the introduction holds.
References
Bowman, C., Cox, A. G.:Modular decomposition numbers of cyclotomic Hecke and diagrammatic Cherednik algebras: A path theoretic approach, Forum Math. Sigma 6, no. e11 (2018)
Bowman, C., Cox, A., Hazi, A.: Path isomorphisms between quiver Hecke and diagrammatic Bott–Samelson endomorphism algebras, arXiv: 2005.02825, preprint
Brundan, J., Kleshchev, A.:Blocks of cyclotomic Hecke algebras and Khovanov-Lauda algebras, Invent. Math. 178, no. 3, 451–484. MR2551762 (2009)
Brundan, J., Kleshchev, A., Wang, W.: Graded Specht modules. J. Reine Angew. Math. 655, 61–87 (2011). https://doi.org/10.1515/CRELLE.2011.033
Bowman, C.:dThe many graded cellular bases of Hecke algebras, arXiv: 1702.06579
Elias, B., Williamson, G. : Soergel calculus, Represent. Theory 20, 295–374. MR3555156 (2016)
Hu, J., Mathas, A.: Graded cellular bases for the cyclotomic Khovanov-Lauda-Rouquier algebras of type \(A\). Adv. Math. 225(2), 598–642 (2010). https://doi.org/10.1016/j.aim.2010.03.002
Khovanov, M., Lauda, A.: A diagrammatic approach to categorification of quantum groups. I, Represent. Theory 13, 309–347. MR2525917 (2009)
Kleshchev, A. S., Mathas, A., Ram, A.: Universal graded Specht modules for cyclotomic Hecke algebras, Proc. Lond. Math. Soc. (3) 105, no. 6, 1245–1289. MR3004104 (2012)
Libedinsky,N.: Sur la catégorie des bimodules de Soergel, J. Algebra 320, no. 7, 2675–2694. MR2441994 (2008)
Libedinsky, N., Plaza, D. :Blob algebra approach to modular representation theory, arXiv: 1801.07200, preprint
Lobos, D., Plaza, D., Ryom-Hansen,S.: The nil-blob algebra: An incarnation of type \({\tilde{A}}_1\)soergel calculus and of the truncated blob algebra, arXiv: 2001.00073
Mathas, A. :Iwahori–Hecke Algebras and Schur Algebras of the Symmetric Group, University Lecture Series, vol. 15, Am. Math. Soc. Providence, RI (1999). https://doi.org/10.1090/ulect/015
Rouquier, R.: \(2\)-Kac–Moody algebras, arXiv: 0812.5023, preprint
Williamson, G.: Schubert calculus and torsion explosion, J. Amer. Math. Soc. 30, no. 4, 1023–1046, With a joint appendix with Kontorovich, A., McNamara, P.J.: MR3671935 (2017)
Acknowledgements
The first and third authors thank the Institut Henri Poincaré for hosting us during the thematic trimester on representation theory. The first author was funded by EPSRC grant EP/V00090X/1 and the third author was funded by the Royal Commission for the Exhibition of 1851. The authors would like to express their gratitude to the referee for their incredibly helpful comments and careful reading of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bowman, C., Cox, A., Hazi, A. et al. Path combinatorics and light leaves for quiver Hecke algebras. Math. Z. 300, 2167–2203 (2022). https://doi.org/10.1007/s00209-021-02829-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02829-0











 then the
then the 


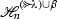 are actually all zero in this case).
are actually all zero in this case). and so the former term is of the required form by our assumption for
and so the former term is of the required form by our assumption for  . Now, if
. Now, if 


 for
for 

 and so the result follows by our assumption for
and so the result follows by our assumption for  .
.






 , we can left justify
, we can left justify 








 (see also Examples
(see also Examples 

 . The adjustment term
. The adjustment term  is illustrated
is illustrated
 . We picture the paths
. We picture the paths  and
and 

 and
and  and
and  . The paths
. The paths  ,
,  ,
,  and
and  are pictured
are pictured
 and
and  . We picture
. We picture 



 and we depict the paths
and we depict the paths  and
and  (we actually only depict
(we actually only depict  ). We have already constructed the corresponding element
). We have already constructed the corresponding element  in great detail over the course of Examples
in great detail over the course of Examples 

