Learning and market clearing: theory and experiments

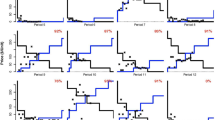
Abstract

This paper investigates theoretically and experimentally whether traders learn to use market-clearing trading institutions or whether other (inefficient) market institutions can survive in the long run. Using a framework with boundedly rational traders, we find that market-clearing institutions are always stable under a general class of learning dynamics. However, we show that there exist other, non-market-clearing institutions that are also stable. Therefore, in the long run, traders may fail to coordinate exclusively on market-clearing institutions. Using a replica-economies approach, we find the results to be robust to large market size. The theoretical predictions were confirmed in a series of platform choice experiments. Traders coordinated on platforms predicted to be stable, including market-clearing as well as non-market-clearing ones, while platforms predicted to be unstable were avoided in the long run.

Appendices

Appendix 1: Proofs

Proof

(Proof of Lemma 1) Suppose $\beta _z(n_z,m_z)<1$. Then, buyers, but not sellers, are rationed at institution z. We have that $q_S^0=s(p_0)$ and $q_S^z=s(p_z)$. Suppose now that $v_S(q_S^0,p_0)\le v_S(q_S^z,p_z)$. By A1, we must have that $p_0\le p_z$.

Then, again by A1, $v_B(q_B^0,p_0)\ge v_B(d(p_z),p_z)$. Since $d(p_z)>q_B^z$ (buyers are rationed), A2 implies that $v_B(d(p_z),p_z)>v_B(q_B^z,p_z)$.

The case $\beta _z(n_z,m_z)>1$ is analogous.

If $\beta _{z}(n_{z},m_{z})=1$, no traders are rationed, and the analogous arguments follow with weak inequalities (A2 does not apply since there is no rationing). $\square$

We now prove some auxiliary lemmata. The first shows that traders in an inactive institution will always prefer any active institution.

Lemma 2

Suppose that institution z is inactive and institution $z'$ is active. If traded quantities are not zero at $z'$, any trader in z or $z'$ strictly prefers the outcome of institution $z'$ to that of z. If traded quantities are zero at $z'$, traders in z or $z'$ are indifferent between the two institutions.

Proof

Since $m_z=0$ or $n_z=0$, traded quantities are zero at z. Since both the bias $\beta _{z'}(n_{z'},m_{z'})$ and the market-clearing price $p^{*}(n_{z'},m_{z'})$ are strictly positive, it follows that $p_{z'}(n_{z'},m_{z^{\prime }})>0$. If $d( p_{z'}(n_{z'},m_{z'})) >0$, the claim then follows from assumption A3. If $d\left( p_{z'}(n_{z'},m_{z'})\right) =0$, the claim follows from our explicit assumption as part of A3 that evaluations do not depend on hypothetical prices. $\square$

Lemma 3

Assume A1–A3. Under D0–D2, given any state $\omega$ with $n_0\left( \omega \right) \ge 1$ and $m_0\left( \omega \right) \ge 1$, there exists a finite, positive probability path of the unperturbed dynamics leading from $\omega$ to the state $\omega _0$ with $n_0\left( \omega _0\right) =n$ and $m_0\left( \omega _0\right) =m$.

Proof

Consider any institution $z\ne 0,$ which is chosen by some traders in state $\omega$. If $n_z\left( \omega \right) =0$ or $m_z\left( \omega \right) =0$, by Lemma 2, we can build a positive-probability path to a new state where no trader is at institution z. Hence, without loss of generality, suppose that $n_z=n_z\left( \omega \right) >0$ and $m_z=m_z\left( \omega \right) >0$.

If $\beta _z(n_z,m_z)\ne 1$, it follows from Lemma 1 that in state $\omega$, at least one of the two types of traders strictly prefers the market-clearing institution. Let k be a trader of that type who is at the non-market-clearing institution z. It might happen that k prefers a third institution to the market-clearing one, but certainly will not stay in z if given revision opportunity. Further, by Assumption D1, there is strictly positive probability that k is the only trader of his type obtaining revision opportunity. Consider the paths where this event happens, and let $k'$ denote a trader of the other type (i.e., not of the same type as k) who, in state $\omega ,$ is in the same non-market-clearing institution z. Consider now the event that only k and $k'$ get revision opportunity.

If this event has positive probability, then (if it occurs) $k'$ may or may not change institution, but k will, switching to the market-clearing or another institution. If the probability of k and $k'$ being the only revising traders is zero, by Assumption D2, no agent of the same type as $k'$ will revise this period, and hence k will change institution but no other agent will. In any case, the process reaches a state with strictly less traders at institution z than there were in $\omega$, but at least the same traders in the other institutions (and, in particular, the market-clearing one). If $\beta _z(n_z,m_z)=1$, Lemma 1 yields weak preferences. The argument above applies again, because by Assumption D0 ties are broken randomly, i.e., if a trader weakly prefers another institution to his current one, there is a maybe small but positive probability that he switches away.

Repeating this argument, we will reach a state $\omega '$ with either $n_z( \omega ') =0$ or $m_z( \omega ^{\prime }) =0$. From this state, all remaining traders will leave institution z as above (by Lemma 2). Hence, we reach a state where strictly less institutions are chosen than in $\omega$.

Repeating this procedure, we will reach a state where only two institutions are chosen by traders, and one of them will necessarily be the market-clearing one. Applying again the same argument (using Lemma 1) shows that we can construct a positive-probability path to $\omega _0$, where 0 is the only active institution. $\square$

Proof

(Proof of Proposition 1) The states given in (i) are obviously absorbing because, in the absence of experimentation, traders will never switch to unobserved institutions. To see that there are no other absorbing states, suppose that there are traders of the same type in at least two different institutions. Since necessarily one of those institutions is yielding (weakly) higher payoffs than the other, and under Assumption D1 there is positive probability that one of the traders not in that institution is given revision opportunity, there is a positive probability transition to a different state, a contradiction. Finally, if there is only one active institution but the state is not monomorphic, the result follows from Lemma 2. Part (ii) follows immediately from Lemma 3. $\square$

The remaining proofs rely on the characterization of the set of stochastically stable states introduced by Kandori et al. (1993) and Young (1993), and on the concept of radius and coradius developed by Ellison (2000). Given two absorbing sets A and B, let $c(A,B)>0$ (referred to as the transition cost from A to B) denote the minimal number of mistakes in a positive-probability path starting in an element of A and leading to an element in B. The following lemma contains all the results on stochastic stability that we require for the analysis. Its proof is a straightforward application of Ellison (2000, Theorems 1 and 3) and is analogous to the proof of Lemma 2 in Alós-Ferrer and Kirchsteiger (2010); hence, we omit it here.

Lemma 4

Let A be an absorbing set and define the Radius of A by

$$\begin{aligned} R(A)=\min \left\{ c(A,B)\left| B\text { is an absorbing set, }B\ne A\right. \right\} \end{aligned}$$

and the Coradius of A by

$$\begin{aligned} CR(A)=\max \left\{ c(B,A)\left| B\text { is an absorbing set, }B\ne A\right. \right\} \end{aligned}$$

Then:

• (i) If $R(A)\ge CR(A)$, the states in A are stochastically stable.

• (ii) If $R(A)>CR(A)$, the only stochastically stable states are those in A.

• (iii) If the states in an absorbing set B are stochastically stable and $R(A)=c(B,A)$, the states in A are also stochastically stable.

Proof

(Proof of Theorem 1) We have to show the stochastic stability of the state $\omega _{0}$. If there is any other market-clearing institution, the conclusion follows by renaming. First, notice that, by Lemma 2, no monomorphic state can be left with less than two mutations unless the traded quantity is zero. Since traded quantities at a market-clearing institution are never zero, it follows that $R(\left\{ \omega _{0}\right\} )\ge 2$.

Consider any state in any absorbing set other than $\left\{ \omega _0\right\}$. Notice that two mutations (to the market-clearing institution) suffice to reach a state $\omega$ with $n_0\left( \omega \right) \ge 1$ and $m_0\left( \omega \right) \ge 1$. By Lemma 3, there is a positive-probability path of the unperturbed dynamics (i.e., requiring no further mutations), leading to $\omega _0$. This shows that $CR(\left\{ \omega _0\right\} )=2$ (the equality follows because two mutations are required to leave any other monomorphic state). The result follows from Lemma 4(i). $\square$

Proof

(Proof of Theorem 2) Let $\omega _z$ denote the monomorphic state corresponding to coordination on institution z. We know from Theorem 1 that $\omega _0$ is stochastically stable. By definition of a favored institution, we see that if exactly two mutations to institution z occur at state $\omega _0$, we reach a state where at least one type of traders strictly prefer that institution. Analogously to the proof of Lemma 3 (through repeated application of Definition 3), from this state, there exists a positive-probability path involving no further mutations which leads to state $\omega _z$. From the proof of Theorem 1, we already know that it is possible to make the opposite transition with exactly two mutations (but no less). Thus, we obtain that $c(\left\{ \omega _0\right\} ,\left\{ \omega _z\right\} )=2=R(\left\{ \omega _z\right\} )$, and the result follows from Lemma 4(iii). $\square$

Proof

(Proof of Theorem 3) For any given n, m, let

$$\begin{aligned} R(n,m)=\left\{ \frac{a}{b}\left| a=1,\ldots ,n,\text { and }b=1,\ldots ,m\right. \right\} \end{aligned}$$

be the set of feasible buyers–sellers ratios and define

$$\begin{aligned} \underline{\beta }(n,m)=\max _{r\in R(n,m)}\underline{\beta }(r)\qquad \text { and}\qquad \overline{\beta }(n,m)=\min _{r\in R(n,m)}\overline{\beta }(r). \end{aligned}$$

Note that for any given number of buyers and sellers, there exists only a finite number of values r can take. Hence, by A4, $\underline{ \beta }(n,m)<1<\overline{\beta }(n,m)$. For any given n, m, define T(n, m) as the set of all pairs $\left( r_0,r_z\right)$ such that $r_0=\frac{n_0}{ m_0}$ and $r_z=\frac{n_z}{m_z}$ with $n_0,n_z\in \left\{ 1,\ldots ,n\right\}$ and $m_0,m_z\in \left\{ 1,\ldots ,m\right\}$ such that $n_0+n_z=n$ and $m_0+m_z=m$. In other words, T(n, m) is the set of all pairs of buyer–seller ratios which are feasible when exactly two institutions are simultaneously active. Finally, define

$$\begin{aligned} \underline{\beta }^{*}(n,m)= & {} \max \left\{ \underline{\beta }(n,m),\max \left\{ \frac{p(r_0)}{p(r_z)}\left| \left( r_0,r_z\right) \in T(n,m)\text { and }r_0<r_z\right. \right\} \right\} \\ \overline{\beta }^{*}(n,m)= & {} \min \left\{ \overline{\beta }(n,m),\min \left\{ \frac{p(r_0)}{p(r_z)}\left| \left( r_0,r_z\right) \in T(n,m)\text { and }r_0>r_z\right. \right\} \right\} \end{aligned}$$

Notice that $\underline{\beta }^{*}(n,m)$ (and analogously $\overline{\beta } ^{*}(n,m)$) is well defined because T(n, m) is finite and $r_0<r_z$ implies $\frac{p(r_0)}{p(r_z)}<1$. Clearly,$\underline{\text { }\beta }(n,m)\le \underline{\beta }^{*}(n,m)<1<\overline{\beta }^{*}(n,m)\le \overline{\beta }(n,m)$.

Consider an institution F such that $\underline{\beta }^{*}(n,m)<\beta _F(n_z,m_z)<\overline{\beta }^{*}(n,m)$ for all feasible $n_z,m_z$. We prove that F is favored.

We want to show that, whenever $v_S\left( q_S^0,p_0\right) \ge v_S\left( q_S^F,p_F\right)$, then $v_B\left( q_B^0,p_0\right) <v_B\left( q_B^F,p_F\right)$. Let $\beta _F=\beta _F(n_z,m_z)$ be the realized bias at institution F. Suppose $\beta _F<1$. Then, buyers, but not sellers, are rationed at F. We have that $q_S^0=s(p_0)$ and $q_S^F=s(p_F)$. Suppose now that $v_S(q_S^0,p_0)\ge v_S(q_S^F,p_F)$. By A1, and we must have that $p_0\ge p_F$.

Suppose that $r_0\ge r_F$. Then, $p_0=p(r_0)\ge p(r_F)$ and, by A1, $v_B(q_B^0,p_0)=V_B(1,r_0)\le V_B(1,r_F)$. By A4, $V_B(1,r_F)<V_B(\beta _F,r_F)=v_B\left( q_B^F,p_F\right)$ and the claim follows.

Suppose now that $r_0<r_F$. Then, $p_0=p(r_0)<p(r_F)$. If, as assumed, $v_S\left( q_S^0,p_0\right) \ge v_S\left( q_S^F,p_F\right)$, then $p_0\ge p_F=\beta _F\cdot p(r_F)$ by A1. It follows that $\beta _F\le \frac{p(r_0)}{p(r_F)}$, a contradiction with $\beta _F>\underline{\beta }^{*}(n,m)$. Hence, $v_S\left( q_S^0,p_0\right) <v_S\left( q_S^F,p_F\right)$.

The case $\beta _F>1$ is analogous. $\square$

The following Lemma is used in the proof of Theorem 4.

Lemma 5

Assume A1 and A4. If $\underline{\beta }(1)<\beta _B<1<\beta _S<\overline{\beta }(1)$, then

• (i) if $m\le n$ (more buyers than sellers), in a state where an equal, strictly positive number of sellers and buyers are at an institution z with constant $\beta _z=\beta _B$ and the remaining traders are at a market-clearing institution (and there are traders of both types in the latter), buyers strictly prefer z;

• (ii) if $m\ge n$ (more sellers than buyers), in a state where an equal, strictly positive number of sellers and buyers are at an institution z with constant $\beta _z=\beta _S$ and the remaining traders are at a market-clearing institution (and there are traders of both types in the latter), sellers strictly prefer z.

Proof

We will show part (i). Part (ii) is analogous. Let $0<\ell <\max (m,n)$ be the number of sellers and buyers at the alternative institution z. Since $m\le n$, we have that $m-\ell \le n-\ell$ and hence

$$\begin{aligned} r=\frac{n-\ell }{m-\ell }\ge 1 \end{aligned}$$

That is, there are (weakly) more buyers than sellers at the market-clearing institution. By A4, since $\underline{\beta }(1)<\beta _{B}<1$,

$$\begin{aligned} V_{B}(\beta _{B},1)>V_{B}(1,1) \end{aligned}$$

and, by A1,

$$\begin{aligned} V_{B}(1,1)=v_{B}\left( q_{B}^{z}(1,1),p(1)\right) \ge v_{B}\left( d(p(r)),p(r)\right) \end{aligned}$$

because $q_{B}^{z}(1,1)=d(p(1))$ and $p(1)\le p(r)$ since $r\ge 1$ and p is increasing in r. Hence,

$$\begin{aligned} V_{B}(\beta _{B},1)>v_{B}\left( d(p(r)),p(r)\right) \end{aligned}$$

which proves the claim, because $v_{B}\left( d(p(r)),p(r)\right)$ is the buyers’ payoff at the market-clearing institution, and $V_{B}(\beta _{B},1)$ is the payoff of the buyers at the non-market-clearing institution with $\beta _{z}=\beta _{B}$. $\square$

Proof

(Proof of Theorem 4) We will show part (i). Part (ii) is analogous, and part (iii) follows from (i) and (ii). Let $\omega _1$ denote the monomorphic state corresponding to coordination on the buyers’ institution z. By hypothesis, z is a favored institution for the economy with $K=1$. Further, we know from Theorem 1 that $\omega _0$ is stochastically stable. In order to show stochastic stability of $\omega _1$ for large K, by Lemma 4(iii), it is enough to show that two mutations at $\omega _0$ from the market-clearing institution 0 to z suffice for a transition.

Let a buyer and a seller mutate from 0 to z. Then, $r_z=1$ and $r_0=\frac{Kn-1}{Km-1}\ge 1$. By Lemma 5(i), the mutant buyer is strictly better off. By $\mathbf{D3}_K$, let K buyers revise, including the mutant, and follow him to z (so exactly $K-1$ buyers switch). Now, $r_z=\frac{K}{1}$ and $r_0=\frac{(n-1)K}{Km-1}$.

Since $\lim _{r\rightarrow \infty }p(r) = +\infty$ under M1 $^{\prime }$–M2 $^{\prime }$, $r_z\rightarrow \infty$ as $K\rightarrow \infty$, and $r_0\rightarrow \frac{n-1}{m}$ (finite), even though $\beta _z<1$ it follows that there exists $K^*$ such that, for all $K\ge K^*$, $p_z=\beta _z p^ *(r_z) > p^*(r_0)=p_0$.

Sellers are not rationed at 0 (by definition), and they are not rationed at z either since $\beta _z<1$. Hence, by A1, sellers are strictly better off at z since they face a higher price. By $\mathbf{D3}_K$, there is positive probability that K sellers, including the lone seller already in z, revise and move to z from 0, while no other trader receives revision opportunity. In the new state, we have $r_z=\frac{K}{K}=1$ and $r_0=\frac{(n-1)K}{(m-1)K} =\frac{(n-1)}{(m-1)}$. By Lemma 5(i), $V_B(\beta _z,r_z)>V_B(1,r_0)$ and buyers at z are strictly better off. By $\mathbf{D3}_K$, there is positive probability that K buyers from 0 revise and follow them to z.

We know that the market institution z is favored for the economy with $K=1$. That means that one market side is better off at z for all prices resulting from population proportions which are feasible in the economy with $K=1$ (recall the construction of the set T(m, n) in the proof of Theorem 3). In the state we have just reached, we have $r_z=\frac{2K}{K}=2$ and $r_0=\frac{(n-2)K}{(m-1)K}=\frac{n-2}{m-1}$, which are feasible population proportions in the economy with $K=1$.

We conclude that one market side is better off at z. Let K traders of the appropriate market side switch (using $\mathbf{D3}_K$). The new population distribution is always a multiple of K for each trader type and each institution; hence, we can apply the fact that z is favored in the economy with $K=1$ again. Proceeding iteratively, eventually we reach a state where a complete market side is at institution z. By A3, we can complete the transition by moving groups of K traders of the other market side to z until the market-clearing institution becomes empty. $\square$

Appendix 2: Experimental instructions and payoff matrices

The instructions and the control questionnaire below are translated from German into English as literally as possible. These instructions were distributed to Type I traders (i.e., sellers) of treatment 3 (choice between three platforms). The instructions for Type II traders (buyers) were symmetric (of course with the appropriate payoffs in the examples). The instructions for T1 and T2 were similar, with the only difference that all the references to choice C were deleted.

Each participant was provided with the appropriate payoff tables for the institutions used in the experiment. Table 5 displays the payoffs obtained by buyers and sellers at each of the three institutions used in the experiments. Within each table, each row corresponds to the number n of buyers present at the institution, each column to the number m of sellers.

Table 5 Experimental payoff tables

Instructions: Type I

The experiment you are about to participate in is part of a research project on decision behavior. The instructions are simple, and if you read them carefully and make appropriate decisions, you can earn a considerable amount of money.

The revenues made during the experiment are counted in ECU (“experimental currency units”). After the end of the experiment all the revenues you made during the experiment will be added up and paid to you in cash. For every ECU you will receive 0.7 Eurocent.

Any communication between the participants is strictly forbidden.

In every round of the experiment you have to choose between three different options, A, B, or C. To do so you click on the appropriate button for decision A, B, or C. Then you confirm your decision by clicking on the OK button. In each round you have half a minute to make this decision.

In this experiment there are two types of participants, participants of Type I and participants of Type II. You are of Type I. All in all, there are 7 participants of Type I and 7 participants of Type II within the group relevant for you. You will not be informed about the identity of the other group members, and the other group members will not be informed about your identity.

The revenues you make in a round depend on the number of other group members of each type who make the same decision as you. Assume that you have made decision A, three other Type I participants have made the same decision, and 5 Type II participants have chosen A, too. In this case 4 Type I participants and 5 Type II participants have chosen A. As you can see from the attached revenue matrix, your revenues are 21 ECU in this case.

Another example: You have chosen B, one other Type I participant has made the same decision, and 3 Type II participants have chosen B, too. In this case your revenues are 20 ECU.

After all members of your group have made a decision, you will be informed about the number of participants of each type that have chosen A, B, and C. You will also be informed about their revenues, and about the sum of revenues you have earned so far in the whole experiment.

After that, a new round will start, in which you will have to decide between A, B, and C, again. Overall there will be 90 rounds.

Control Questionnaire

• 1. Suppose that you have made decision B, 2 other Type I participants have made the same decision, and 2 Type II participants have also chosen B. What are your revenues?

  Suppose that 2 Type I participants and 3 Type II participants have chosen A. What are the revenues of those Type I participants who have chosen A?

  Suppose the remaining 2 Type I participants and the remaining 2 Type II participants have chosen C. What are the revenues of those Type I participants who have chosen C?

• 2. Suppose that you have made decision C, 3 other Type I participants have made the same decision, and 2 Type II participants have also chosen C. What are your revenues?

  Suppose that 1 Type I participant and 2 Type II participants have chosen B. What are the revenues of the Type I participant who has chosen B?

  Suppose the remaining 2 Type I participants and the remaining 3 Type II participants have chosen A. What are the revenues of those Type I participants who have chosen A?