Generalization techniques to reduce the number of volume elements for terrain effect calculations in fully analytical gravitational modelling

Abstract

Beyond rectangular prism polyhedron, as a discrete volume element, can also be used to model the density distribution inside 3D geological structures. The calculation of the closed formulae given for the gravitational potential and its higher-order derivatives, however, needs twice more runtime than that of the rectangular prism computations. Although the more detailed the better principle is generally accepted it is basically true only for errorless data. As soon as errors are present any forward gravitational calculation from the model is only a possible realization of the true force field on the significance level determined by the errors. So if one really considers the reliability of input data used in the calculations then sometimes the “less” can be equivalent to the “more” in statistical sense. As a consequence the processing time of the related complex formulae can be significantly reduced by the optimization of the number of volume elements based on the accuracy estimates of the input data. New algorithms are proposed to minimize the number of model elements defined both in local and in global coordinate systems. Common gravity field modelling programs generate optimized models for every computation points (dynamic approach), whereas the static approach provides only one optimized model for all. Based on the static approach two different algorithms were developed. The grid-based algorithm starts with the maximum resolution polyhedral model defined by 3–3 points of each grid cell and generates a new polyhedral surface defined by points selected from the grid. The other algorithm is more general; it works also for irregularly distributed data (scattered points) connected by triangulation. Beyond the description of the optimization schemes some applications of these algorithms in regional and local gravity field modelling are presented too. The efficiency of the static approaches may provide even more than 90% reduction in computation time in favourable situation without the loss of reliability of the calculated gravity field parameters.

1 Introduction: a short trip around a cubic and a polyhedral globe

As a solution of the regional forward gravitational potential modelling problem the 3D model of the density distribution of the lithosphere in the Alps–Carpathians–Pannonian basin (ALCAPA) region has been used to determine different parameters of the gravity field analytically. Gravity acceleration, geoid undulation, gravity potential and gravity anomaly, generated partly by the Newtonian attraction of masses discretized by the model, were calculated by Papp (1996a, b), Papp and Kalmár (1995, 1996), Papp and Benedek (2000), Benedek (2001) and Papp et al. (2004, 2009). The consistency of the parameters is provided by the rigorous functional relations existing between the gravitational field and its source represented by such a discrete volumetric model. The building block of the ALCAPA model was the right rectangular parallelepiped (prism) the gravitational field parameters of which can be calculated by closed, analytical formulae. Prisms are mainly used for local modelling if flat earth approximation based on planar geodetic coordinates is allowed. For an extended reference of the earliest applications of prisms in modelling (e.g. Zach 1811) see the paper by Nagy et al. (2000). Consequently it gives an exact way to test the accuracy of numerical methods transforming one kind of gravity field-related parameter to another (see e.g. solutions of the Stokes integral) in closed-loop test way (Benedek 2001). The analytical approach makes the referencing procedure hypothesis free, so any numerical approximation used in the calculations can be investigated rigorously.

The polyhedron is a relatively new volume element (Okabe 1979; Cady 1980). Its application improves the realism of geometrical description of the bounding surfaces (density interfaces) related to flat-topped rectangular prisms because it is able to provide continuity where it is reasonable. The spatial resolution of the model can be arbitrarily synchronized to the resolution of the available geometrical data (points of the interfaces) and physical parameters (e.g. mass density distribution). Furthermore the effect of the Earth’s curvature can easily be taken into account in the computations (Benedek and Papp 2009), because the polyhedral geometry allows the description of any density model not only in local (planar) but also in global geodetic coordinate system (e.g. WGS84) too. Analytical expressions for the gravitational field of a polyhedral body with either linearly or nonlinearly varying density are also available (Garcia-Abdealem 1992, 2005; Pohánka 1998; Hansen 1999; Holstein 2003; Zhou 2009). This improvement enables the modelling of the continuous density variation inside the volume element if geology justifies its existence.

The time for computing the gravitational potential and its higher-order derivatives of a single, triangle-based polyhedron is twice more than that of a single rectangular prism. It, however, can be reduced by about 30% using carefully optimized analytical formulae (Benedek 2001) selected from a variety of available expressions (Götze and Lahmeyer 1988; Pohánka 1998; Petrovič 1996; Holstein et al. 1999; Holstein 2002a, b; Werner and Scheeres 1997; Guptasarma and Singh 1999; Singh and Guptasarma 2001; Holstein and Ketteridge 1996). It is nearly a linear function of the number of volume elements. One, however, should note that two triangle-based polyhedrons¹ are needed for the substitution of a single rectangular prism, so the time factor is even 4. If a model contains about 10$^{6}$ polyhedrons the calculation of its gravitational potential on a grid consisting of 10$^{4}$ points needs approximately 40 h on a 15-year-old HP A500 platform running in parallel mode (PA-8500 440-MHz processors). The runtime, of course, is strongly platform and processor dependent, so if the same model is processed, e.g. on a HP rx2800 system on a single core of an Itanium processor, it is eight times less as it was experienced.

With the optimization of the number of volume elements defined in the input model the computational time outlined above can be further reduced. The measure of reduction depends on (1) the complexity of the density distribution defined by the known geometrical and physical parameters and (2) the accuracy of these parameters. The questions related to these two factors are discussed in the next chapters in details. Some examples of how these factors influence the efficiency of generalization are also provided.

2 A short review of dynamic and static model generalizations

In the dynamic approach (Tscherning et al. 1991; Holzrichter et al. 2014) a new model is derived for each computation point P from the available DTM data supposing that the closest vicinity of P needs much higher spatial resolution (i.e. small volume elements) than what the far zones described by large elements admit. This assumption is in accordance with the inverse distance law of gravitation and the advantage of its application considering computation time is straightforward. As far as the authors know the existing algorithms, however, neglect the uncertainties of the input data so if those are erroneous the errors propagate certainly into the computed field parameters regardless of the systematically (or in the sense of calculation time, optimally) changing resolution.

Based on the static approach two different algorithms were developed. The grid-based algorithm (GBA) starts with a set of surface points defined on a uniform grid representing maximum available spatial resolution and generates a polyhedral surface so that the differences along the Z axis between the two surfaces do not exceed the threshold ${\delta } H$ defined in advance. The value of the threshold depends on either local or global a priori error statistics of the input data (e.g. $\delta H=\mu _z )$. The algorithm is fast, but it does not guarantee the best optimum (i.e. the smallest number of volume elements). It was implemented in Fortran language and developed for both in the local (planar) and global rectangular (WGS84) coordinate systems.

Fig. 1

The main steps of volumetric model generation and their related errors. a Reality (e.g. the topographic surface $z=f(x, y)$ and the density distribution $\rho =\rho (x, y, z)$ below it), b irregularly sampled version of the reality and the position errors $\sigma _{x}$, $\sigma _{y}$ and $\sigma _{z}$ at A, B, C and D points defined by x, y, z coordinates, c regularization of the mesh defined by $A'$, $B'$, $C'$ and $D'$ by interpolation to an equidistant grid of points $G_{i,j}$-s. Here $\sigma _{z}$ is the regularization (interpolation) error. d Generation of a flat-topped prism utilizing e.g. the mean height derived from the z coordinates of points $G_{i,j}$-s (top), generation of two joining polyhedral volume elements with triangular base faces defined by $G_{i,j}$-s (bottom), e assigning density value $\rho$ and its error $\sigma _{\rho }$ to the prism (top) and to the polyhedrons (bottom)

The other, triangle-based algorithm (TBA) is more general; it works for irregularly distributed data (points) connected by triangulation. It starts from this Delaunay-triangulated mesh and provides the minimum number of volume elements. It, however, is highly time-consuming; the computational time is an exponential function of the number of input elementary triangles and $\delta H$ chosen.

3 The error budget of a DTM-based volume model and its propagation to gravitational field parameters

3.1 General considerations

Obviously both the geometrical and the physical parameters used in the process of volume element model generalization are affected by uncertainties, since those are usually derived from heterogeneous, partly measured, partly estimated data using interpolation methods and/or general rules of (geo)physics. One should note that even most of these rules are just formulated from numerical experiments and based on statistical correlations (e.g. mass density—seismic velocity law, depth—density law for the sediments) discussed by e.g. Strykowski (1996) in details.

As Fig. 1 shows the overall accuracy of a specific volume element model depends on several elementary components. The first one is the position error (or sampling error) of those discrete points (e.g. the error of topographic height) which provide a set of samples for the discretization of the surface/volume to be modelled.

Table 1 Normal and Laplacian distribution statistics of $\Delta H$ residuals

The next component is the so-called geometrical regularization error which is related to the chosen regularized geometrical representation of the real density interfaces e.g. the surface separating the topographic masses from the air. It is mainly caused by interpolation which is a necessary step to define that specific volume over which the Newtonian integral will be analytically computed in a selected coordinate system. If sampling and regularization is integrated in one process (e.g. scanning of the target surface on a predefined equidistant grid) and no further regularization of the samples is required then sampling error cannot be distinguished from regularization error.

The third component is the geometrical discretization error (or volumetric representation error) which comes from the differences between the geometry of the possible volume elements applicable for the same regularized samples. For instance a model consisting of either flat-topped prisms or polyhedrons can be applied to represent the volume defined by the same set of grid (i.e. regularized) points.

The last component is the discretization error of the density distribution inside the volume of modelled masses. Basically it is defined by the elaboration of knowledge about the geology of the structure under consideration. Although sophisticated geophysical exploration methods (seismic and geoelectric soundings, borehole drillings, etc.) provide a huge amount of petrophysical data most of them cannot be used directly in gravitational modelling (Strykowski 1996). On the one hand the volume density is the least important rock parameter for exploration purposes; therefore, in situ determinations are very rare usually. On the other hand the penetration depth of these methods is limited since the target structures (e.g. oil and gas traps) are located in shallow geological structures, hidden in and directly below the sedimentary deposits, maximum at a few km depth.

The most obvious example for the complexity of sampling and regularization is the workflow of the creation of a digital terrain model (DTM). It is usually the result of compilation of data (1) supplied by traditional geodetic measurements, modern remote sensing techniques and digitization of old printed contour maps, (2) processed by interpolation methods and (3) transformed from and to the respective coordinate systems. The integrated effect of sampling and regularization errors (cited as DTM error in the following) was analysed by Zahorec et al. (2010). They showed that the quality of the used digital terrain model is the most critical factor in the accuracy of the calculated terrain-related gravitational potential and its derivatives.

The effect of geometrical discretization error was investigated in details in Tsoulis et al. (2003, 2009) and Tsoulis (2001) using different representations of the reference terrain (i.e. some selected specific realizations of the real terrain). These representations were based on (1) the tessellated system of the upper horizontal bounding faces of rectangular prisms forming a step-like mosaic surface, (2) continuous triangular coverage provided by the application of polyhedrons, (3) tessellations of bilinear continuous surfaces between the grid points and (4) tessellations of the upper bounding spherical caps defined by tesseroids. The results indicate a convergence of all investigated methods as the resolution of DTM-s increases, no matter what type of computational strategy or geometrical representation of the terrain is used.

3.2 Analysis of DTM errors on the area of Hungary

Due to the above-mentioned complexity of DTM generation and its overall error budget the accuracy estimates of the new, high-resolution ($\Delta x,\Delta y<100\hbox { m})$ global (e.g. SRTM3) and local (e.g. HU-DTM30) DTM-s, regardless of whether those are surface or terrain models, are sometimes disappointing. Papp and Szűcs (2011) showed that SRTM3, since it is a surface model, cannot describe the topographic surface better than $8.8\pm 5.4\hbox { m }$ and $8.1\pm 5.9\hbox { m }$ if the SRTM heights are compared to the reference heights $H_{\mathrm{{geod}}}$ of the horizontal and vertical geodetic control network points, respectively, on the area of a so flat country like Hungary. But even the HU-DTM30, which is a version of the $10\hbox { m }\times 10\hbox { m}$ DTM of Hungary (generated by the Institute of Geodesy, Cartography and Remote Sensing operated by the Ministry of Agriculture, Department of Land Administration) interpolated on a $30\hbox { m }\times 30\hbox { m }$ grid cannot provide much better accuracy of residual heights defined by:

$$\begin{aligned} \Delta H=H_{\mathrm{{geod}}} -H_{\mathrm{HU}\hbox {-}\mathrm{DTM30}} \end{aligned}$$

(1)

in terms of standard deviation (see SD in Table 1). The dispersion estimate in Table 1 based on ${H}_{0}$: normal distribution, however, is not correct considering the empirical distribution of residual heights (Fig. 2).

Fig. 2

The histogram of $\Delta H$ height differences defined by (1) and the theoretical distributions computed by the estimated statistics for full data set in Table 1

According to earlier experience (e.g. Papp 1993; Zahorec et al. 2010; Wang et al. 2015) the estimation procedure of statistical parameters (expected value, deviation) of residual data has to be selected according to the real distribution of those in order to obtain realistic error estimates. Since the distribution of $\Delta H$ is obviously not normal, Laplacian distribution was probed by ${\upchi }^{2}$-test. For Laplacian distribution the expected value and the deviation have to be estimated by the median and the mean absolute deviation (MAD), respectively, which are also listed in Table 1. As one can see MAD is significantly less than SD, but even if it is much closer to the characteristics (more than 60% concentration of $\Delta H$ data in the interval defined by $\pm \,\hbox {MAD}$) of the histogram ${H}_{0}$: Laplacian distribution is also false (c.f. the theoretical frequencies to the empirical ones in Fig. 3). One has to note that gross errors also influence significantly the value of SD so those have to be identified and removed prior to parameter estimation (Table 1).

3.3 Error estimation based on the law of error propagation

3.3.1 Case of rectangular prism

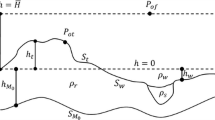
The general law of error propagation can be applied for the investigation of the modelling errors. If e.g. the vertical component $g_z$ of $\hbox {grad}U=\left( {g_x ,g_y ,g_z } \right)$ defined by Nagy et al. (2000)

$$\begin{aligned} g_z \left( P \right)= & {} \left. G\rho _\mathrm{topo} \left( {\frac{\partial u}{\partial z}} \right) \right| _P =G\rho _\mathrm{topo} \left( \Bigg |\Bigg \Vert x\ln (y+r)\right. \nonumber \\&\left. +y\ln (x+r)-z\tan ^{-1}\frac{xy}{zr}\Bigg |_{x_1 }^{x_2 }\Bigg |_{y_1 }^{y_2 } \Bigg |_{z_1 }^{z_2 } \right) \end{aligned}$$

(2)

is computed from a DTM composed of rectangular prisms the analytical formula of ${\partial g_z }/{\partial z}$ (the second vertical derivative of the gravitational potential U) can be used to derive the error $\mu _{g_z }$, i.e. the uncertainty of $g_z$ due to the error $\mu _z$ of the height z:

$$\begin{aligned} \mu _{g_z }= & {} \left. {\left( {\frac{\partial g_z }{\partial z}} \right) } \right| _P \mu _z =G\rho _\mathrm{topo} \left. {\left( {\frac{\partial ^{2}u}{\partial z^{2}}} \right) } \right| _P \mu _z\nonumber \\= & {} G\rho _\mathrm{topo} \left( \Bigg |{\Bigg \Vert {-\tan ^{-1}\frac{xy}{zr}} \Bigg |_{x_1 }^{x_2 } } \Bigg |_{y_1 }^{y_2 } \Bigg |_{z_1 }^{z_2 } \right) \mu _z . \end{aligned}$$

(3)

In (2) and (3) G is the gravitational constant, r is the distance between the computation point P and the respective corner of the prism, $x_1 ,x_2 ,y_1 ,y_2 ,z_1$ and $z_2$ define the prism in a rectangular coordinate system the origin of which is shifted to the computation point, and its axes are parallel to the respective edges of the prism and u is the primitive function of 1 / r over the integration domain $\left[ {x_1 ,x_2 } \right] \times \left[ {y_1 ,y_2 } \right] \times \left[ {z_1 ,z_2 } \right]$ (Nagy et al. 2000). Obviously (3) gives the error contribution of a single prism, not that of the whole model. It is defined by:

$$\begin{aligned} \sigma _{g_z }^2 =\left( {\mu _{g_z } } \right) _1^2 +\left( {\mu _{g_z } } \right) _2^2 +\cdots +\left( {\mu _{g_z } } \right) _i^2 +\cdots +\left( {\mu _{g_z } } \right) _N^2 , \end{aligned}$$

(4)

where N is the number of prisms. But if P is just above a specific prism, located on its vertical axis where $\left. {\left( {{\partial g_z }/{\partial z}} \right) } \right| _{z=\mathrm{const}}$ has a local maximum, the computation of $\mu _{g_z }$ is a kind of minimum estimation due to the omission of the contribution of other prisms.

Computing (3) for different $\mu _z$ values (0–10 m) and for variable heights (80–1000 m) simulating real situations referring to the reliability of available DTM-s (Table 1) and topographic heights of Hungary (Papp and Kalmár 1996), respectively, one can see from Fig. 3 how the minimum estimation is influenced by $\mu _z$ and $z_2$ when $z_1 =0\hbox { m}$, $x_2 -x_1 =y_2 -y_1 =30\hbox { m}$ and $\rho _\mathrm{topo} =2670\hbox { kg/m}^{\mathrm{3}}$. In the height range investigated no influence of $z_{2}$ can be detected and $\mu _{g_z}$ is a strongly linear function of $\mu _z$. One should notice that (3) is formally identical with the Bouguer plate effect:

$$\begin{aligned} \delta g_B= & {} 2\pi G\rho _\mathrm{topo} H_\mathrm{topo} =\frac{\partial g}{\partial H}H_\mathrm{topo} \nonumber \\= & {} 0.1119H_\mathrm{topo} \left[ {\frac{\hbox {mGal}}{\hbox {m}}} \right] \left[ \hbox {m} \right] \end{aligned}$$

(5)

where $\rho _\mathrm{topo} =2670\hbox { kg/m}^{3}$ and 1 $\hbox {mGal}=10^{-5}\hbox { m/s}^{2}$. So if $H_\mathrm{topo}$ is substituted by $\mu _z$ in (5) then (3) can be well approximated by (5) indicating that there is not much difference between the Bouguer plate effect and the exact solution given by (3) when $\mu _z \le$ 10 m, $x_2 -x_1 =y_2 -y_1 =30\hbox { m}$ and the computation point is on the vertical axis of symmetry of the prism.

Fig. 3

The error of $g_{z}$ generated by a single $30\hbox { m}\times \hbox {30 m}\times \hbox {z}_{2}$ prism in a point located on its vertical axis of symmetry at heights of 0.01 m (a) and 0.50 m (b) above $z_2$ as a function of topographic height $z_2$ and its error $\mu _z$. Contour interval is 0.1 mGal

Taking the MAD values from Table 1 as the best estimations of $\mu _z$ the error of the vertical component of the $\hbox {grad} U$ cannot be less than 0.1 mGal regarding the horizontal variation of surface mass density $(1900 \hbox { kg/m }^{3} \le \rho _\mathrm{topo} \le 2900\hbox { kg/ m}^{3})$ on the area of Hungary indicated by geological maps² (Fig. 4). This result is in a good accordance with the case studies published by Papp et al. (2009) and Papp and Szűcs (2011).

Fig. 4

Distribution of surface densities on the area of Hungary (Rónai et al. 1984)

3.3.2 Case of polyhedron

The analytical formulae of the first and second derivatives of the gravitational potential generated by a polyhedron volume element are derived based on the paper of Pohánka (1998), using notation analogous to that used by Holstein (2002a, b). The following expressions were coded in Fortran for the analysis of error propagation:

$$\begin{aligned} g_z= & {} \frac{\partial U}{\partial z}=-G\rho _\mathrm{topo} \sum _{i=1}^n {n_{i,z} \left( {\sum _{j=1}^{l(i)} {\left( {h_{ij} C_{ij\varepsilon } -z_{i\varepsilon } \Omega _{ij\varepsilon } } \right) } } \right) }\nonumber \\ \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial g_z }{\partial z}= & {} \frac{\partial ^{2}U}{\partial z^{2}} \nonumber \\= & {} G\rho _\mathrm{topo} \sum _{i=1}^n n_{i,z} \sum _{j=1}^{l\left( i \right) } {\left( {\nu _{ij,z} C_{ij\varepsilon } -n_{i,z} \hbox {sign}(h_i )\Omega _{ij\varepsilon } } \right) }\nonumber \\ \end{aligned}$$

(7)

The definition of $C_{ij\varepsilon }$, $\Omega _{ij\varepsilon }$ functions is:

$$\begin{aligned} C_{ij\varepsilon }= & {} C_{ij\varepsilon } \left( {l_{1ij} ,l_{2ij} ,h_{ij} ,h_i ,\varepsilon } \right) =\hbox {sign}\left( {l_{2ij} } \right) \nonumber \\&\times \cdot \ln \left( {\frac{V_{ij\varepsilon } +\left| {l_{2ij} } \right| }{W_{ij\varepsilon } }} \right) \nonumber \\&-\hbox {sign}\left( {l_{1ij} } \right) \cdot \ln \left( {\frac{Q_{ij\varepsilon } +\left| {l_{1ij} } \right| }{W_{ij\varepsilon } }} \right) \nonumber \\ \Omega _{ij\varepsilon }= & {} \Omega _{ij\varepsilon } \left( {l_{1ij} ,l_{2ij} ,h_{ij} ,z_i ,\varepsilon } \right) \nonumber \\= & {} 2\tan ^{-1}\frac{2h_{ij} l_{ij} }{\left( {T_{ij\upvarepsilon } +l_{ij} } \right) \cdot \left| {T_{ij\upvarepsilon } -l_{ij} } \right| +2T_{ij\upvarepsilon } z_{i\upvarepsilon }} \end{aligned}$$

(8)

where

$$\begin{aligned}&z_{i\upvarepsilon } =z_i +\varepsilon , W_{ij\upvarepsilon } =\sqrt{h_{ij}^2 +z_\upvarepsilon ^2 }, Q_{ij\varepsilon } =\sqrt{l_{1ij}^2 +W_{ij\varepsilon }^2 },\nonumber \\&V_{ij\upvarepsilon } =\sqrt{l_{2ij}^2 +W_{ij\varepsilon }^2 }, T_{ij\upvarepsilon } =Q_{ij\upvarepsilon } +V_{ij\upvarepsilon }\nonumber \\&{} \mathbf{l}_{ij} =\mathbf{a}_{ij+1} -\mathbf{a}_{ij} , \quad l_{ij} =\left| {\mathbf{a}_{ij+1} -\mathbf{a}_{ij} } \right| ,\nonumber \\&{{\varvec{\upmu }} }_{ij} =\frac{\mathbf{a}_{ij+1} -\mathbf{a}_{ij} }{\left| {\mathbf{a}_{ij+1} -\mathbf{a}_{ij} } \right| },\nonumber \\&{} \mathbf{n}_i =\left( {n_{i,x} ,n_{i,y} ,n_{i,z} } \right) =\frac{\mathbf{l}_{i1} \times \mathbf{l}_{i2} }{\left| {\mathbf{l}_{i1} \times \mathbf{l}_{i2} } \right| },\nonumber \\&{{\varvec{\nu }}}_{ij} =\left( {\nu _{ij,x} ,\nu _{ij,y} ,\nu _{ij,z} } \right) ={{\varvec{\upmu }} }_{ij} \times \mathbf{n}_i ,\nonumber \\&{} \mathbf{r}_{1ij} =\mathbf{a}_{ij} -\mathbf{r}_M , \quad \mathbf{r}_{2ij} =\mathbf{a}_{ij+1} -\mathbf{r}_M ,\nonumber \\&l_{1ij} =\mathbf{r}_{1ij} \cdot {{\varvec{\upmu }} }_{ij} , \quad {h_{ij}} = {\mathbf{{r}}_{1ij}} \cdot {{\varvec{\upnu }}}_{ij} \nonumber \\&z_i =\left| {h_i } \right| =\left| {\mathbf{r}_{1ij} \cdot \mathbf{n}_i } \right| , \quad l_{2ij} =l_{1ij} +l_{ij} . \end{aligned}$$

(9)

The number of polyhedron faces is denoted by n, $l\left( i \right)$ is the number of the vertex of ith face, i is the face index, and j is the index of vertices, ($\mathbf{e}_{1}$, $\mathbf{e}_{2}$, $\mathbf{e}_{3})$ are the unit vectors of the input coordinate system. The normal vector of the ith face is $\mathbf{n}_i$, ${{\varvec{\upmu }} }_{i,j}$ is unit vector belonging to the jth edge (connecting the j and $j+1$ vertices, where the direction defined by the $j,j+1,j+2,\ldots$ points is counter clockwise) of the ith face, ${{\varvec{\upnu }}}_{i,j}$ is the cross-product of these two unit vectors so that $\left( {{\varvec{\upmu }}}_{i,j} ,\mathbf{n}_i ,{ {\varvec{\upnu }} }_{i,j} \right)$ is a right-handed system belonging to the jth vertex (Fig. 5). $\varepsilon$ is an arbitrarily small (e.g. 10$^{-25})$ constant applied to avoid numerical singularities.

Fig. 5

The illustration of vector quantities used in formula (9)

The test polyhedron volume element used for the computation of $\mu _{g_z }$ was derived from a prism by halving it vertically along two opposite vertical edges. However, in Eq. (3) the second vertical derivative $\partial g_z /\partial z$ of gravitational potential was replaced by (7). The error $\mu _{g_z }$ determined by the height error ($\mu _z$) was investigated in terms of inclination angle $\alpha$ of the top face (Fig. 6). For each $\alpha$ the maximum value was selected from the derivatives computed at 28 points evenly distributed above the triangular top face of the polyhedron at a height of 0.5 m. This height was measured along the vertical lines connecting the computation points and their vertical projections on the top face. The height $z_2$ of the test polyhedron was 100 m for $\alpha =0^{\circ }$, and this value was fixed for all $\alpha$ as Fig. 6 shows. Consequently $z_2$ was the height of the rotation axis $AA'$ in horizontal position around which the top face of the test polyhedron was tilted incrementally. Actually $AA'$ is identical with the axis of symmetry of the top face which is a right isosceles triangle in this case.

Fig. 6

a Polyhedron volume element with triangular top and bottom faces. The triangular face of the top of the polyhedron is tilted with angle $\alpha \in \{0{^{\circ }},5{^{\circ }},10{^{\circ }},\ldots ,60{^{\circ }}\}$ along the median $AA'$ of the triangle. b The contour map of the error of $g_{z}$ generated by a polyhedron with 30 m $\times$ 30 m $\times$ 100 m dimensions as a function of the tilt of the top face $\alpha$ and the height error ($\mu _z )$. $\mu _{g_z }$ is computed at the height of 0.5 m above the top triangular face. Contour interval is 0.05 mGal

It can be clearly seen from Figs. 3 and 6 that the maximum errors of $g_z$ generated by a prism and a polyhedron (even if the mass of the latter is just half of the former) at the same computation point are nearly identical and both agree well with the Bouguer plate effect for $0^{\circ }\le \alpha \le 10^{\circ }$. It is, however, interesting that the $\mu _{g_z }$ for a given $\mu _z$ is significantly decreasing as $\alpha$ is increasing so formally the same DTM error generates smaller error of $g_z$ in case of a steep terrain than in case of a flat terrain. But this tendency, indicated by the contour lines in Fig. 6, dominates in the very rare situation of extremely rugged topography (Ramsayer 1963; Levallois 1964). As it was shown in the subsections above the height errors of the recent high-resolution DTMs are still in the order of a few metres, so eventually not less than a few tenth of mGal uncertainty of the gravitational effect $g_z$ computed from them can be expected.

Consequently a “blind” application of the dynamic generalization does not provide physically significant short-wave signal content at P necessarily, but it certainly produces noise. Moreover the input model is not the same for all the computation points (i.e. the model is slowly changing as the computation point moves from one place to the next one), so it is also a usually unknown and probably terrain-dependent error source among the uncertainties. In the static approach described in Sect. 4 only one model is derived from the input data taking into account the reliability of them. This is usually not so effective in terms of computation speed but much more self-consistent.

3.4 Estimation of the geometrical discretization error using a high-resolution DTM

In this section the statistics of differences between gravitational fields ($g_z$) generated by prism- and polyhedron-based representations of a subset of the available highest resolution (10 m $\times$ 10 m) DTM of Hungary (HU-DTM10) was investigated numerically using Eqs. (2) and (6), respectively. The selected area is a small region with a horizontal extension of 6.99 km $\times$ 6.99 km where the topographic surface is defined by $700 \times 700 = 490{,}000$ grid points. It is located on the northern part of the Great Hungarian Plain (Fig. 7) and is defined by the geographical coordinates $19^{\circ }40'32''\le \lambda \le 19^{\circ }4{6}'{8}''$ and $47^{\circ }1{7}'5{9}''\le \varphi \le 47^{\circ }2{1}'4{4}''$. A constant density value of $2.67\hbox { g/cm}^{3}$ was used to scale the gravitational effect of topographic masses.

The prism model is composed of 490,000 elementary volume elements with $10\hbox { m }\times 10\hbox { m}$ horizontal extension, whereas the heights of the prisms were defined by the respective grid points. It covers an area of $6.995\hbox { km }\times 6.995\hbox { km}$ since one grid point represents one prism.

Fig. 7

The grey-shaded relief map of the test area in the northern part of the Great Hungarian Plain drawn from HU-DTM10. The coordinates are given in the local planar geodetic projection system (central EOV) of Hungary. The contour interval is 5 m. The statistics of height values in grid points: $H_\mathrm{mean} =120.65\hbox { m}$, $\mathrm{SD}_{H}=\pm 16.86\hbox { m}$, $H_{\min } =101\hbox { m}$, $H_{\max } =175\hbox { m}$

The polyhedron model is composed of nearly 1 million elementary volume elements defined by three neighbouring grid points of HU-DTM10 forming a flat triangle on the $z = 0$ plane (bottom triangle) and a tilted triangle defined by the heights of the respective grid points on the topographic surface (top triangle). Since it covers an area of $6.99\hbox { km }\times 6.99\hbox { km}$ there is a systematic volumetric difference near to the edges of the models which must be considered in the comparison of calculation results.

Fig. 8

a The difference $\Delta g_z =\left( {g_z } \right) _\mathrm{ph} -\left( {g_z } \right) _\mathrm{pr}$ of the first vertical derivatives of gravitational potentials $\left( {g_z } \right) _\mathrm{ph}$ and $\left( {g_z } \right) _\mathrm{pr}$ computed from the elementary models built from polyhedrons and prisms, respectively. Both models were generated from a subset of HU-DTM10 having a horizontal extension of 6.99 km $\times$ 6.99 km and 10 m $\times$ 10 m horizontal resolution. The relative distance (i.e. the height difference) between the computation points (P) and their vertical projection points on the top faces of the polyhedron volume elements (${{P}'}$) was 0.5 m. The grid defined by this way was applied for the calculation of the effect of prism-based model too. The constant value of $2.67\hbox { g/cm}^{3}$ was used to scale the gravitational effect of topographic masses. b The variation of $\Delta g_z$ differences as a function of the height differences $\Delta H_M =z_\mathrm{ph} \left( {{P}'} \right) -z_\mathrm{pr}$ of the top surfaces of the two elementary models and the relevant statistics. The grey stripe shows $-0.7\hbox { m}\le \varDelta H_M \le 0.7\hbox { m}$ range of differences where $\Delta g_z$ is nearly zero

Fig. 9

The scheme of the three typical set-up of the computation point (P) related to the top of the prism and polyhedron. The computation point (P) is at 0.5 m above the surface of polyhedron model (i.e. ${ PP}' = 0.5$ m) so $z_P =z_\mathrm{ph} \left( {{P}'} \right) +0.5$. a The computation point is inside the prism where $\Delta H_M =z_\mathrm{ph} -z_\mathrm{pr} <-0.7\hbox { m}$. b The computation point is near to both of the top faces where $-0.7\hbox { m}<\Delta H_M <0.7\hbox { m}$. c The computation point is above both of the volume elements, but it is located closer to the top face of the polyhedron than that of the prism where $\Delta H_M <0.7\hbox { m}$. The grey stripe shows $-0.7\hbox { m}<\Delta H_M <0.7\hbox { m}$ range of differences where $\Delta g_z$ is nearly zero (Fig. 8)

The effect of the geometrical discretization error of the DTM on $g_z$ can be analysed by the statistics of the difference $\Delta g_z =\left( {g_z } \right) _\mathrm{ph} -\left( {g_z } \right) _\mathrm{pr}$, where $\left( {g_z } \right) _\mathrm{ph}$ and $\left( {g_z } \right) _\mathrm{pr}$ are the vertical gravitational attractions generated by polyhedrons and prisms, respectively (Fig. 8). The data were computed in 128 $\times$ 128 grid points. The height of a grid point $H_P$ was determined by the continuous surface formed by the joining top faces of the polyhedrons so that the vertical distance $\varDelta H_P =\overline{PP'}$(see Fig. 9) was always 0.5 m, regardless of the horizontal location of the respective grid point defined by $x_P,y_P$:

$$\begin{aligned} {H_P}= & {} {H_{P'}} + 0.5~\left[ m \right] = ~{z_\mathrm{ph}}\left( {P'} \right) + 0.5~\left[ m \right] \nonumber \\= & {} ~{z_\mathrm{ph}}\left( {{x_P},{y_P}} \right) + 0.5~\left[ m \right] , \end{aligned}$$

(10)

where ${P}'$ is the vertical projection point of P on the top face of the polyhedron and $z_\mathrm{ph} \left( {x_P ,y_P } \right)$ is the actual height of the (generally tilted) top face at $x_P,y_P$. The same grid with $H_{{P}'}$ grid point heights was applied for the calculations of $\left( {g_z } \right) _\mathrm{pr}$.

Due to the edge effect mentioned above the data in a 0.4-km-wide band around the models were omitted from the calculations of statistics. The mean of $\Delta g_z$ difference is -0.001 mGal, the standard deviation is ± 0.002 mGal, and the maximum deviation is about 0.060 mGal (Fig. 8). So the geometrical discretization error is negligible in most cases of practical applications (e.g. gravity reductions) if the terrain is as flat as in this example. The variation of the $\Delta g_z$ difference was also investigated as a function of the deviation between the two surfaces defined by the top faces of polyhedron- and prism-based models:

$$\begin{aligned} \Delta {H_M} = {\text {~}}{z_\mathrm{ph}}\left( {P'} \right) - {z_\mathrm{pr}}\left( {{x_P},{y_P}} \right) . \end{aligned}$$

(11)

Figure 8 shows that $\Delta g_z$ data concentrated mainly in the range $-0.7\hbox { m}\le \varDelta H_M \le 0.7\hbox { m}$ are nearly zero or slightly negative, whereas $\Delta g_z$ is positive outside of it regardless of the sign of $\Delta H_M$. This interesting attribute of $\Delta g_z$ can be explained if the relative position between the location of the computation point and the heights of both the prisms and polyhedron top faces is analysed in three classified groups (Fig. 9). If $\Delta H_M <-0.7\hbox { m}$ (Fig. 9a) then the computation point is situated inside the prism and outside the polyhedron since $\overline{PP'}$ was 0.5 m. The mass of the prism located directly above P diminishes $\left( {g_z } \right) _\mathrm{pr}$, so $\Delta g_z >0$ dominantly. If $-0.7\hbox { m}\le \varDelta H_M \le 0.7\hbox { m}$ (Fig. 9b) then the gravitational effect of the two volume elements will be nearly the same, so $\Delta g_z \approx 0$ or slightly negative according to the well-known characteristics of the gravimetric terrain correction. One should recall that the difference between the gravitational effect of the real terrain and a Bouguer plate is always negative if P is located on the topographic surface. In this simplified model (Fig. 9b) the prism and the polyhedron play the role of the Bouguer plate and the real terrain, respectively. If $\Delta H_M >0.7\hbox { m}$, then P is farer from the top face of the prism than from that of the polyhedron. Consequently $\left( {g_z } \right) _\mathrm{ph} >\left( {g_z } \right) _\mathrm{pr}$. One should note that the range limits (defined by eye and displayed as light grey stripes in Figs. 8 and 9) used above to separate typical cases are strongly dependent from the value of $\overline{PP'}$ and probably the locations of the sampling test points have also some slight effect on the statistics.

Fig. 10

Explanation of the processing of a grid containing $17 \times 17$ points ($N = 4$). a The structure of the block systems at different levels of the evaluation process of the grid and their hierarchical connection. b The hierarchy defined by the connectivity relation between the blocks determined at different levels. The first level contains $8 \times 8$ block values (0 or 1) defining the $\mathbf{A}_{1}$ matrix. At this level each block represents $3 \times 3$ grid points. The second level contains $4 \times 4$ block values defining the $\mathbf{A}_{2}$ matrix, the third level contains $2 \times 2$ block values defining $\mathbf{A}_{3}$, and the last level contains 1 $\times$ 1 block defining $\mathbf{A}_{4}$. c C(k, l) matrix elements are the integrated connectivity indices. The mesh drawn in grey colour shows the processed grid

4 Detailed descriptions of the proposed static generalization techniques

The input grid of GBA algorithm must contain $\left( {2^{N}+1} \right) \times \left( {2^{N}+1} \right)$ points where N is an integer. One should note that it is the weakest point of the algorithm since this requirement increases the necessary allocated memory with dummy matrix elements. Obviously a generalization of GBA for $\left( {2^{N}+1} \right) \times \left( {2^{M}+1} \right)$ nodes (where $N\ne M)$ may diminish this problem if the data grid has no square envelope.

Fig. 11

a The block system of the GBA with the fixed corner points (black dots) and the reference planes defined for the investigation of co-planarity. b The final triangles fixed to the corner points and the new point $B^{\prime }$ (white dot) interpolated along facet $\overline{AC}$. GBA grid-based algorithm

In the first step the extended model is divided into quadratic blocks with dimension of 2 so any block contains 2 $\times$ 2 grid cells i.e. 3 $\times$ 3 grid points. In case of each block of this level of evaluation (i.e. first level of evaluation) the co-planarity of the nine facets belonging to a certain block is checked and block value 1 or 0 is assigned in confirmed case or otherwise, respectively. Co-planarity is fulfilled if

$$\begin{aligned} \left| {H_j -\hat{H} _j } \right| < \delta H \left( {j=1,\ldots ,L} \right) \end{aligned}$$

(12)

holds for every j. L is the number of grid points in the block investigated, $H_j$ and $\hat{H}_j$ are the height of the jth grid point and the height of the plane fitted over the block at this point, respectively. Consequently the number of blocks in the first, second, ... and the Nth level is $2^{N-1}\times 2^{N-1}$, $2^{N-2}\times 2^{N-2}$, ... and one, respectively. The block values of the ith level define the $\mathbf{A}_i$ square matrix of order $2^{i-1}$ with 0 and 1 elements (Fig. 10). These elements determine a kind of connectivity relation existing between the corresponding blocks of levels i and $i-1$. If its value, i.e. the connectivity index, is 1 then the grid points represented by the four corresponding blocks (i.e. a square submatrix of $\mathbf{A}_{i-1} )$ of the preceding level $i-1$ are co-planar.

In case of $N=4$, the number of grid points is 17 $\times$ 17. This grid defines 16 $\times$ 16 blocks (grid cells) defined by 2 $\times$ 2 grid points (Fig. 10). After the first turn of evaluation of co-planarity the first level contains 8 $\times$ 8 = 64 = 4$^{3}$ blocks and each block represents 3 $\times$ 3 grid points of the original grid. In the second and the further turns the second level contains $4 \times 4 = 16 = 4^{2}$ blocks representing $5 \times 5$ grid points, the third level contains $2 \times 2 = 4 = 4^{1}$ blocks representing 9 $\times$ 9 grid points, and the last level contains $1 \times 1 = 1 = 4^{0}$ block representing the initial $17 \times 17$ grid points, respectively. In a specific case when the block value of the last level ($i=4$) is 1 then all the $17 \times 17$ evaluated grid points define a plane fulfilling (12). At any level the occurrence of a block having 0 value means that the grid points belonging to the four adjacent blocks defined by the previous level do not satisfy (12) above the domain determined by them.

Fig. 12

The optimized models created by the two algorithms and represented as triangular meshes in case of a $\delta H = 1 \,\mathrm{m}, \mathbf{b } \ \delta H = 0.5$ m and c $\delta H = 0.1$ m thresholds. ${ TBA}$ triangle-based algorithm, ${ GBA}$ grid-based algorithm

An integrated connectivity index $c (c\le N)$ can be derived for each block of level 1 by summing up the connectivity indices determined for the consecutive levels ($i=1,\ldots ,N)$. Its value is proportional to the number of grid points $\left( {2^{c}+1} \right) ^{2}$ satisfying co-planarity relation (12) on a specific quadratic subset of the original grid. The hierarchy of the levels and the rigorous quad-tree structure implemented by the evaluation algorithm ensure that the position and dimension of c can be unambiguously identified. The properly ordered integrated connectivity indices define matrix C (Fig. 10) of order $2^{N-1}$. Figure 10b shows an example for $c=C(1,1)=1+1+1+0=3.$

Table 2 The comparison of the efficiency of the two algorithms

Table 3 The statistics of the residual heights are given in m unit

Fig. 13

Histograms of $\Delta H$ height differences for a $\delta H = 1$ m and b $\delta H = 0.5$ m thresholds. Left column: ${ GBA}$, right column: ${ TBA}$. ${ TBA}$ triangle-based algorithm, ${ GBA}$ grid-based algorithm

If any element of C is zero then the four corresponding elementary square faces defined by $3 \times 3$ grid points on level 1 cannot be merged to one surface element without violating (12). In this case eight triangular faces (right isosceles triangles) are formed, which define eight polyhedron volume elements having constant densities in the output volumetric model.

Depending on the value of c ($c>0) \quad 4^{c}$ elementary grid cells can be merged to one larger block so that (12) is satisfied for all of the corresponding $\left( {2^{c}+1} \right) ^{2}$ grid points. Eventually all the square blocks fixed at any level are divided into two triangles forming the upper planes of the corresponding polyhedrons. These two triangles are defined by the four corner points of the specific block regardless of its level.

It is obvious from the scheme above that the co-planarity of the grid points in any single square-shaped block is investigated independently from its neighbours since the vicinity relation is defined by a rigorous quad-tree structure fixed to the grid geometry of input data. So this method cannot automatically provide a continuous joining of the facets of tilted planes defined by block corners. Consequently, a final correction is needed to provide continuity (i.e. stepless joining of the neighbour triangles having usually different dimensions) of the optimized surface (Fig. 11). This correction process starts at the highest block level (i.e. at squares of largest size) containing nonzero element (Fig. 10). The heights of the four corner points of a square block considered are fixed to their original value. The heights of the grid points along the block boundaries (facets) are, however, adjusted to those defined by the equations of the specific facets (applying linear interpolation), so when neighbour blocks at lower level are considered, their corner points, if those are aligned on a joining block facet, inherit the new interpolated height. This process is repeated from level to level resulting in a set of blocks of varying size.

Eventually all the square blocks at any level are divided into two triangles representing the upper planes of the two corresponding polyhedrons.

The TBA investigates co-planarity in the closest vicinity of the specific point P (where the height $H_{P}$ is known) defined by the so-called Dirichlet cell the central point of which is P itself. For this a least-squares height interpolation is done at P from its Dirichlet neighbours by calculating the normal vectors of the triangles connecting the neighbours with P (Kalmár et al. 1995). The variation of $H_P$ obviously changes the tilts of the corresponding triangles, the common vertex of which is P itself. Therefore a suitable $\hat{H}_P$ can be found where the squared sum of the deviations of the normal vectors from their average gives a minimum. If $\left| {H_P -\hat{H}_P } \right| < \delta H$ holds then P is flagged and the process can be repeated on all the Dirichlet cells formed by tessellation on the whole set of irregularly distributed points. The flagged points are skipped from the set of points being investigated in the next loop until no more points can be flagged. Obviously before each and every loop of co-planarity investigation a new tessellation has to be done. The final triangulation defines a continuous tessellated surface composed by general triangles which can straightforwardly be used to form polyhedrons.

Fig. 14

The grey-shaded maps of the $\Delta H$ differences for the GBA (left column) and TBA (right column) solutions using a $\delta H = 1$ m and b $\delta H = 0.5$ m thresholds. ${ TBA}$ triangle-based algorithm, ${ GBA}$ grid-based algorithm

Fig. 15

The differences of the first derivatives of potential $\Delta g_z =\left( {g_z } \right) _\mathrm{elementary} -\left( {g_z } \right) _\mathrm{GBA}$ generated by the elementary model and the model derived by GBA with a $\delta H = 1$ m and b $\delta H = 0.5$ m thresholds computed in 128 $\times$ 116 grid points at 0.5 m above the models. $1\hbox { mGal}=10^{-5} \hbox { m/s}^{2}$. ${ GBA}$ grid-based algorithm

Fig. 16

The areal distribution of the differences (left) of the second derivatives of the potential $\Delta \left( {{\partial g_z }/{\partial z}} \right) =\left( {{\partial g_z }/{\partial z}} \right) _{\mathrm{{elementary}}} -\left( {{\partial g_z }/{\partial z}} \right) _{\mathrm{{GBA}}}$ generated by the elementary model and the model optimized by GBA and their histograms (right) with a) 1-m b) 0.5-m thresholds computed in $128 \times 116$ grid points at 0.5 m above the models. 1 Eötvös unit $=\,10^{-9}\hbox { s}^{-2}$. ${ GBA}$ grid-based algorithm

5 Local and regional case studies for static generalization

The effect of generalization (or optimization) can be studied with respect to heights and gravitation. In the first case the original grid point values (topographic elevations) are compared to those heights which are determined by the surface of joining triangular faces provided by the generalization process. In the second case gravitational effects (Eqs. 6 and 7) of the optimized model are calculated and compared to those computed from the elementary polyhedral volumetric model serving as input for generalization. Both aspects were considered and discussed in details in the next paragraphs.

The description of the local, high-resolution DTM data used to demonstrate the capabilities of the proposed static methods can be found in Sect. 3.4. The optimized volumetric models of the topography were created by the two algorithms described in Sect. 4 using three different threshold values (Fig. 12). The efficiency of the algorithms can be classified by (1) the reduction factor of the model elements and by (2) the computational time (Table 2). The overall geometrical correctness of the process can be checked by the statistics of

$$\begin{aligned} \Delta H=H_\mathrm{grid} -H_\mathrm{optimized} \end{aligned}$$

(13)

difference which is the deviation between the surface topography described by the original grid points and the surface generated by the presented algorithms. It was determined in all the 490,000 grid points of the model and analysed statistically (Table 3) in case of $\delta H =1$ m and $\delta H = 0.5$ m thresholds (Figs. 13, 14) in accordance with the MAD statistics of DTM errors given in Table 1.

One should note that the maximum and minimum values of $\Delta H$ differences are somewhat larger than the predefined $\delta H$ for both methods (Table 3). The reason of the outliers, however, is different.

For GBA two sources of accuracy degradation exist. Although condition (12) is strictly considered during the examination of the co-planarity of points located in the individual blocks, when the block corners are fixed, then their original height is kept. Even if this is a violation of (12) when a square block is finally divided into two triangles the regression plane defined virtually on it is substituted by two joining triangular faces (Fig. 11). And if there is a small (i.e. not “seen” by Eq. 12) but systematic change of slope on the area of the block considered then two surface elements may give a better approximation than one diminishing the unfavourable effect of this simplification eventually. The other source is the last step i.e. the fitting of the edges of the final triangles providing continuous surface approximation. It adjusts the heights of the corner points of lower level (smaller) blocks based on the original DTM heights given in the largest block corners along the joining edges as it is shown in Fig. 11.

For TBA the gross errors come from the combination of the method of co-planarity investigation and the reprocessing of the set of points updated by thinning/decimation in each loop. As it is detailed already the co-planarity is checked very locally (from one Dirichlet cell to the next one) and if a point (i.e. the centre of a specific cell) can be skipped from the full set of points it means a loss of information in the next loop when the same process is repeated on the Dirichlet cells regenerated from the remaining points around it. This way the domain of evaluation is enlarged (if possible) from loop to loop but more or less the same number of data forming larger and larger Dirichlet cells is used as the process advances.

The histograms in Fig. 13, however, indicate that the number of $\Delta H$ values greater than threshold $\delta H$ is very small and those are negligible considering the overall accuracy of the optimized models. The dispersions regardless of their estimation method are well below $\delta H$, and the mean values of the residual heights indicate no systematic distortions (Table 3).

To see the influence of generalization on the computed gravity-related parameters both $g_z ={\partial U}/{\partial z}$ (Fig. 15) and ${\partial g_z }/{\partial z}={\partial ^{2}U}/{\partial z^{2}}$ (Fig. 16) were computed in $128 \times 116$ grid points at 0.5 m height above either the initial elementary or the GBA-optimized models. The statistics of the residuals of first vertical derivatives of the potential $\left( {\Delta g_z =\left( {g_z } \right) _\mathrm{elementary} -\left( {g_z } \right) _\mathrm{GBA} } \right)$ show that the difference between the models has a very small influence on the gravitational acceleration and even the extrema of $\Delta g_z$ hardly reach $\pm \,0.1$ mGal value (Table 4).

In case of the second derivatives (gravity gradients) the range of residual $(\Delta (\partial g_{z}/\partial _{z})=(\partial g_{z}/\partial _{z})_{elementary}-(\partial g_{z}/\partial _{z})_\mathrm{GBA})$ is quite large (Table 4). It is well known both from field practice (e.g. Völgyesi 2012) and from simulation studies (e.g. Papp and Szűcs 2011) that gravity gradients are very sensitive for terrain variability as small as a few decimetres in the close vicinity ($\le$ 10 m) of the point of observation or computation, respectively. So it is expected that for local modelling of the gravity gradients when the computation point is close to the topographic surface, even a volume element model based on a $10\hbox { m} \times 10\hbox { m}$ grid is not sufficient. The histograms (Fig. 16), however, indicate a significant concentration ($\ge$ 50%) of data in a ± 5 E (1 Eötvös unit = $10^{-9}\hbox { s}^{-2})$ interval around zero mean value for both threshold parameters, and the numbers of residuals having a value larger or smaller than $\pm \,3\upsigma$ are less than 2%. The formally computed standard deviations (SD) are certainly underestimations of the real dispersions because ${\upchi }^{2}$ tests fail for ${H}_{0}$: normal distribution. MAD values are tendentiously and significantly smaller, ± 8.5 E and ± 6.7 E for $\delta H=1\hbox { m}$ and $\delta H=0.5\hbox { m}$ thresholds, respectively.

GBA can be easily generalized for the application in a global rectangular coordinate system. As an example the regional model of the Moho interface of the European plate (Grad and Tiira 2009) given in WGS84 with $0.1^{\circ }(\sim \,11\hbox { km}$) horizontal resolution was processed by GBA. The initial model (i.e. the $0.1^{\circ }\times 0.1^{\circ }$ grid of Moho depths) contains 301,602 elementary polyhedrons. The generalized model computed with very optimistic (i.e. overestimated in the sense of accuracy) 100-m threshold consists of 29,442 polyhedrons, which means a 90% rate of reduction (Fig. 17). It indicates that the variability (defined by e.g. the average height change per distance unit) of the Moho surface is very low.

Table 4 The statistics of residual first $(\Delta g_z)$ and second derivatives $(\Delta ( {{\partial g_z }/{\partial z}} ))$ obtained as differences between the gravitational effect of the elementary and optimized (GBA) volume element models

Fig. 17

a The colour shaded depth map of Moho of the European plate (Grad and Tiira 2009), b GBA-generated model. Coordinates are given in arc degrees. The dashed white line shows the state border of Hungary. GBA grid-based algorithm

The second application is a counterexample. It considers the topography of Central-East Europe (Fig. 18). The specific subset of ETOPO1 model (Amante and Eakins 2009) with $0.033^{\circ }(\sim 3.7\hbox { km}$) degraded horizontal resolution leads to an initial model consisting of 638,684 elementary polyhedrons defined in a global geocentric Cartesian coordinate system connected to WGS84 system. In order to check the correctness of the result of elementary volume element model generation by applying polyhedrons the volumes of all the elements were computed from the respective Cartesian coordinates. If the respective element represents a topographic mass column it has a positive volume, and when it represents a water mass column (bathymetry) it has a negative volume. These volumes were ordered to the grid points of the initial model and finally plotted in Fig. 18. From this elementary model GBA produces 323,424 and 288,244 volume elements applying 15 and 20-m thresholds, respectively. The low rate of reduction (only about 50%) is in a good accordance with the low horizontal resolution of the degraded ETOPO1 which means strong height averaging in a grid cell obviously. So the relation between the model resolution and the variability of the surface to be approximated has a significant influence on the efficiency of generalization.

Fig. 18

a The colour shaded volumetric map of the topography of Central-East Europe based on ETOPO1 model. Volumes are computed from elementary polyhedron model so those are nearly linear functions of height. Positive and negative volumes mean topography and bathymetry, respectively. The black line shows the location of those volume elements the volume of which is nearly zero i.e. those are at the coast line. b The triangular mesh of the upper faces of the polyhedron system derived by GBA in and around the Pannonian basin. GBA grid-based algorithm

6 Conclusions and future applications

Currently available high-resolution digital elevation models permit computations of terrain-related gravitational parameters with an unprecedented accuracy. It is $\pm \,0.1\hbox { mGal }(10^{-6}\hbox { m/s}^{2})$ and ± 10 E unit ($10^{-8}\hbox { s}^{-2})$ in terms of the first and second derivatives of the gravitational potential, respectively. These grid models, however, mean a huge number of elementary polyhedron volume elements (even $\sim$ 100 million polyhedrons in case of a country as small as Hungary) the computation of the gravitational effect of which is a real challenge when fully analytical solution is preferred. If the characteristic number, i.e. the number of volume elements times the number of computational points, is around 10$^{12}$ the runtime may take a few months on a single processor (core) designed for general IT purposes. The proposed and presented static generalization techniques, however, may reduce the number of volume elements efficiently by a factor of 5–10 if the known/estimated accuracy of the terrain data is interpreted as a threshold parameter. In the range of the threshold all the possible realizations of the real topography may give statistically equivalent results in gravitational forward modelling. In these contexts the presented examples and the results of their statistical evaluations are in a good accordance with the accuracy estimations obtained from the simplified application of the error propagation law demonstrated in this paper.

The detailed analysis of the methods and the results provided by them recovered those points where further developments are possible. In GBA a generalization of the method by changing the initial grid for a $2^{N}\times 2^{M}$ nodes is possible which may reduce the required memory allocation. Also a more sophisticated calculation can be applied to fix the corner points of the blocks created at any level of the optimization process to the reference planes used for the investigation of co-planarity of points of the block considered. The method of the final division of the block into two triangles, the solution of which is not unique, can be developed by investigating the statistics of the fit between block points and the faces defined by the triangles joining along one diagonal of the block or the other. Moreover the algorithm can be easily parallelized for multiprocessor/core systems.

TBA can also be developed methodologically if the flagged centre points of the Dirichlet cells tessellated in a loop are reused in the next loop to make a triangular mesh of points inside the new (usually larger) cells, and height interpolation to its central point is done from all the triangles defined by both flagged and un-flagged points. The runtime required for such a process probably does not make its application possible for large number of points ($> 10^{6}$) and low threshold ($< 1\hbox { m}$).

The efficiency of the methods can be evaluated by the GGMplus model (Hirt et al. 2013) providing data of Earth’s gravity at 200-m grid resolution with near-global coverage. By the application of the proposed generalization technique the agreement between gravity data synthetically computed from the local model HU-DTM30 and GGMplus gravity can be analysed up to the ultra-high-frequency components provided by SRTM3 global elevation model for GGMplus. If the discrepancy is not significant the use of SRTM3 surface model instead of HU-DTM30 in the geodetic computations can also be feasible, but at the same time it reduces the computational time by a factor of 10 due to the resolution differences. In this case even a global model can be applied for local/regional modelling of the gravitational effect of the topographic masses in the ALCAPA region. Otherwise the merging of the local terrain model (HU-DTM30) and the regional surface model (SRTM3) will be necessary to generate a suitable topographic model which can describe the local gravity field with sufficient accuracy.