Abstract
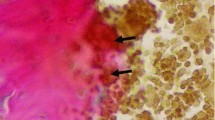
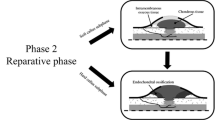
In case of the secondary bone fracture healing, four characteristic steps are often distinguished. The first stage, hematoma and clot formation, which is an object of our study, is important because it prepares the environment for the following stages. In this work, a new mathematical model describing basic effects present short after the injury is proposed. The main idea is based on the assumption that blood leaking from the ruptured blood vessels propagates into a poroelastic saturated tissue close to the fracture and mixes with the interstitial liquid present in pores. After certain time period from the first contact with surrounding tissue, the solidification of blood in the fluid mixture starts. This results in clot formation. By assuming the time necessary to initiate solidification and critical saturation of blood in the mixture, the shape and the structure of blood clot could be determined. In numerical example, proposed mathematical formulas were used to study the size of the gap between fractured parts and its effect in blood clot formation.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Bear J., Bachmat Y.: Introduction to Modeling of Transport Phenomena in Porous Media. Kluwer, Dordrecht (1990)
Blaž M., Vane A.: Optimal mechanical environment of the healing bone fracture/osteotomy. Int. Orthop. 36, 689–695 (2012)
Carter D.R., Beaupré G.S., Giori N.J. et al.: Mechanobiology of skeletal regeneration. Clin. Orthop. Relat. Res. 355, 41–55 (1998)
Checa S., Prendergast P.J.: A mechanobiological model for tissue differentiation that includes angiogenesis: a lattice-based modeling approach. Ann. Biomed. Eng. 37, 129–145 (2009)
Chen, G., Niemeyer, F., Wehner, T., et al.: Simulation of the nutrient supply in fracture healing. J. Biomech. (2009). doi:10.1016/j.jbiomech.2009.07.010
Claes L.E., Wilke H.J., Augat P. et al.: Effect of dynamization on gap healing of diaphyseal fractures under external fixation. Clin. Biomech. 10(5), 227–234 (1995)
Claes L.E., Heigele C.A.: Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J. Biomech. 32(3), 255–266 (1999)
Claes L.E., Eckert K., Augat P.: The fracture gap size influences the local vascularization and tissue differentiation in callus healing. Langenbecks Arch. Surg. 388(5), 316–322 (2003)
Dell’Isola F., Batra R.C.: Saint-Venant’s problem for porous linear elastic materials. J. Elast. 47(1), 73–81 (1997)
Dell’isola F., Romano A.: A phenomenological approach to phase transition in classical field theory. Int. J. Eng. Sci. 25(11–12), 1469–1475 (1987)
Dell’isola F., Romano A.: On the derivation of thermomechanical balance equations for continuous systems with a nonmaterial interface. Int. J. Eng. Sci. 25(11–12), 1459–1468 (1987)
Dell’Isola, F., Hutter, K.: What are the dominant thermomechanical processes in the basal sediment layer of large ice sheets? Proc. R. Soc. A Math. Phys. 454, 1169–1195 (1998)
Dell’Isola F., Guarascio M., Hutter K.: A variational approach for the deformation of a saturated porous solid. A second-gradient theory extending Terzaghi’s effective stress principle. Arch. Appl. Mech. 70(5), 323–337 (2000)
Dietrich L., Lekszycki T., Lekszycki T.: Problems of identification of mechanical characteristics of viscoelastic composites. Acta Mech. 126(1-4), 153–167 (1998)
Dimitriou R., Tsiridis E., Giannoudis P.V.: Current concepts of molecular aspects of bone healing. Injury 36(12), 1392–1404 (2005)
Doblaré M., García J.M., Gómez M.J.: Modeling bone tissue fracture and healing: a review. Eng. Fract. Mech. 71, 1809–1840 (2004)
Einhorn T.A.: The cell and molecular biology of fracture healing. Clin. Orthop. Relat. Res. 355(Suppl), S7–S21 (1998)
Federico S., Grillo A., Giaquinta G., Herzog W.: A semi-analytical solution for the confined compression test of hydrated soft tissue. Meccanica 44, 197–205 (2009). doi:10.1007/s11012-008-9165-z
Frischmuth K., Kosiński W., Lekszycki T.: Free Vibrations of Finite-Memory Material Beams. Int. J. Eng. Sci. 31(3), 385–395 (1993)
García J.M., Kuiper J.H., Gómez M.J. et al.: Computational simulation of fracture healing: influence of interfragmentary movement on the callus growth. J. Biomech. 40(7), 1467–1476 (2007)
Geris, L., Sloten, V.J., Oosterwyck, H.V.: Mathematical modeling of fracture healing: coupling between mechanics, angiogenesis and osteogenesis. ECIFMBE 2008, IFMBE Proceedings 22, pp. 2651–2654 (2009)
Gómez M.J., García J.M., Kuiper J.H. et al.: Influence of fracture size on the pattern of long bone healing: a computational study. J. Theor. Biol. 235(1), 105–119 (2005)
González, L.A., Gómez, M.J., Doblaré, M., et al.: Influence of the frequency of the external mechanical stimulus on bone healing: a computational study. Med. Eng. Phys. (2010). doi:10.1016/j.medengphy.2010.01.010
Grillo A., Federico S., Wittum G.: Growth, mass transfer, and remodeling in fiber-reinforced, multi-constituent materials. Int. J. Non-Linear Mech. 47, 388–401 (2012)
Hollinger J., Wong M.E.K.: The integrated process of hard tissue regeneration with special emphasis on fracture healing. Oral Surg. Med. Oral Pathol. 82, 594–606 (1996)
Lacroix D., Prendergast P.J.: A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J. Biomech. 35(9), 1163–1171 (2002)
Lekszycki T., Mróz Z.: Variational Principles on Analysis and Synthesis of Elastic Systems with Damping. Solid Mech. Arch. 14(3–4), 181–201 (1989)
Lekszycki T.: Modeling of bone adaptation based on an optimal response hypothesis. Meccanica 37, 343–354 (2002)
Lekszycki T., Dell’Isola F.: A mixture model with evolving mass densities for describing synthesis and resorption phenomena in bones reconstructed with bio-resorbable materials. ZAMM-Z. Angew. Math. Mech. 92(6), 426–444 (2012)
Luongo, A.: Perturbation methods for nonlinear autonomous discrete-time dynamical systems. Nonlinear Dyn. 10(4), 317–331 (1996)
Luongo A., Paolone A.: On the reconstruction problem in the multiple time-scale method. Nonlinear Dyn. 19(2), 133–156 (1999)
Luongo, A., Di Egidio, A., Paolone, A.: Multiscale analysis of defective multiple-Hopf bifurcations. Comput. Struct. 82(31–32), 2705–2722 (2004)
Marsell R., Einhorn T.A.: The biology of fracture healing. Injury 42(6), 551–555 (2011)
Madeo A., George D., Lekszycki T., Nierenberger M., Rémond Y.: A second gradient continuum model accounting for some effects of micro-structure on reconstructed bone remodeling. CR Mec. 340(8), 575–589 (2012)
Manjubala, I., Liu, Y., Epari, D.R., et al.: Spatial and temporal variations of mechanical properties and mineral content of the external callus during bone healing. Bone (2009). doi:10.1016/j.bone.2009.04.249
Mavčič, B., Antolič, V.: Optimal mechanical environment of the healing bone fracture/osteotomy. Int. Orthop. (2012). doi:10.1007/s00264-012-1487-8
Nagel T., Kelly D.J.: Mechano-regulation of mesenchymal stem cell differentiation and collagen organisation during skeletal tissue repair. Biomech. Model Mechanobiol. 9(3), 359–372 (2010)
Phillips A.M.: Overview of the fracture healing cascade. Injury 36(3), S5–7 (2005)
Prendergast P.J., Huiskes R., Soballe K.: Biophysical stimuli on cells during tissue differentiation at implant interfaces. J. Biomech. 6, 539–548 (1997)
Sandino, C., Checa, S., Prendergast, P.J., et al.: Simulation of angiogenesis and cell differentiation in a CaP scaffold subjected to compressive strains using a lattice modeling approach. Biomaterials (2010). doi:10.1016/j.biomaterials.2009.11.063
Sciarra,G., Dell’Isola, F.K., Hutter: A solid-fluid mixture model allowing for solid dilatation under external pressure. Contin. Mech. Therm. 13(5), 287–306 (2001)
Vetter A., Witt F., Sander O. et al.: The spatio-temporal arrangement of different tissues during bone healing as a result of simple mechanobiological rules. Biomech. Model Mechanobiol. 11(1–2), 147–160 (2012)
Webb J.C.J., Tricker J.: A review of fracture healing. Curr. Orthop. 14, 457–463 (2000)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Francesco dell'Isola and Giuseppe Piccardo.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Lu, Y., Lekszycki, T. Modeling of an initial stage of bone fracture healing. Continuum Mech. Thermodyn. 27, 851–859 (2015). https://doi.org/10.1007/s00161-014-0380-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-014-0380-7