The Milky Way’s stellar disk

Abstract

A suite of vast stellar surveys mapping the Milky Way, culminating in the Gaia mission, is revolutionizing the empirical information about the distribution and properties of stars in the Galactic stellar disk. We review and lay out what analysis and modeling machinery needs to be in place to test mechanism of disk galaxy evolution and to stringently constrain the Galactic gravitational potential, using such Galactic star-by-star measurements. We stress the crucial role of stellar survey selection functions in any such modeling; and we advocate the utility of viewing the Galactic stellar disk as made up of ‘mono-abundance populations’ (MAPs), both for dynamical modeling and for constraining the Milky Way’s evolutionary processes. We review recent work on the spatial and kinematical distribution of MAPs, and point out how further study of MAPs in the Gaia era should lead to a decisively clearer picture of the Milky Way’s dark-matter distribution and formation history.

1 Introduction

In the world of galaxies, the Milky Way is in many ways as typical as it gets: half of the Universe’s present-day stars live in galaxies that match our Milky Way in stellar mass, size, chemical abundance, etc. within factors of a few (e.g., Mo et al. 2010). But for us, it is the only galaxy whose stellar distribution we can see in its full dimensionality: star-by-star we can obtain 3D positions and 3D velocities (v _los,μ _ℓ ,μ _b ), coupled with the stars’ photospheric element abundances and constraints on their ages. We know that in principle this enormous wealth of information about the stellar body of our Galaxy holds a key to recognizing and understanding some of the mechanisms that create and evolve disk galaxies. And it holds a key to mapping the three-dimensional gravitational potential and by implication the dark-matter distribution in the Milky Way. A sequence of ongoing photometry and spectroscopy surveys has recently hundred-folded the number of stars with good distances, radial and transverse velocities, and abundance estimates; this only forebodes the data wealth expected from ESA’s flagship science Mission Gaia to be launched next year.

Yet, practical approaches to extract the enormous astrophysical information content of these data remain sorely underdeveloped. It is not even qualitatively clear at this point what will limit the accuracy of any galaxy-formation or dark-matter inferences: the sample sizes, the fraction of the Milky Way’s stellar body covered (cf. Fig. 1), the precision of the x–v phase-space measurements, the quality and detail of the abundance information, or the (lack of) stellar age estimates. Are dynamical analyses limited by the precision with which sample selection functions can be specified, or by the fact that dust obscuration and crowding will leave the majority (by stellar-mass-weighted volume) of Milky Way stars unobserved even if all currently planned experiments worked our perfectly? Or are dynamical inferences limited by the fact that the symmetry and equilibrium assumptions, which underlie most dynamical modeling, are only approximations?

Fig. 1

A view of our Galaxy and the effective volume that Gaia will survey (courtesy X. Luri and A. Robin), based on current simulations of Gaia mock catalogs. Even in the age of Gaia, dust extinction and image crowding will limit the exploration of the Disk to only a quadrant with optical surveys

The ongoing data deluge and the continuing recognition how much our Milky Way, despite being ‘just one galaxy’, may serve as a Rosetta Stone for galaxy studies, have triggered a great deal of preparatory work on how to analyze and model these data. Many of the scientific and practical issues have been laid out, e.g., in Turon et al. (2008) or Binney (2011). Yet, it appears (at least to the authors) that the existing survey interpretation and modeling approaches are still woefully inadequate to exploit the full information content of even the existing Galactic stellar surveys, let alone the expected information content of Gaia data.

And while the science theme of ‘understanding the current structure of the Galaxy and reconstructing its formation history’ remains of central interest to astrophysics, the specific questions that should be asked of the data have evolved since the original Gaia mission science case was laid out, through advances in our understanding of galaxy formation in the cosmological framework and recent work on secular galaxy evolution. The aim of simply ‘reconstructing’ the formation history of the Galaxy in light of even idealized Gaia data, now seems naive.

The review here will restrict itself to the Galactic stars (as opposed to the Galactic interstellar medium), and in particular to the Milky Way’s dominant stellar component, its Disk, which contains about three quarters of all Galactic stars. As a shorthand, we will use the term Disk (capitalized) to refer to the ‘Milky Way’s stellar disk’. All other disks will be labeled by qualifying adjectives. The discussion will focus on the stellar disk of our Galaxy and dark matter in the central parts of the overall Milky Way halo (≤0.05×R _virial∼12 kpc), with only cursory treatment of the other stellar components, the gas and dust in the Milky Way, and the overall halo structure. Perhaps our neglect of the Galactic bar is most problematic in drawing scope boundaries for this review, as the interface between disk and bar is both interesting and unclear, and because it is manifest that the present-day Galactic bar has an important dynamical impact on the dynamics and evolution of the Disk; yet, the Galactic bar’s role and complexity warrants a separate treatment.

The questions about galaxy disk formation that a detailed analysis of the Milky Way may help answer are manyfold. What processes might determine galaxy disk structure? In particular, what processes set the exponential radial and vertical profiles seen in the stellar distributions of galaxy disks? Were all or most stars born from a well-settled gas disk near the disk plane and acquired their vertical motions subsequently? Or was some fraction of disk stars formed from very turbulent gas early on (e.g., Bournaud et al. 2009; Ceverino et al. 2012), forming a primordial thick disk? Are there discernible signatures of the stellar energy feedback to the interstellar medium that global models of galaxy formation have identified as a crucial ‘ingredient’ of (disk) galaxy formation (Nath and Silk 2009; Hopkins et al. 2012)? What was the role of internal heating in shaping galaxy disks? What has been the role of radial migration (Sellwood and Binney 2002; Roškar et al. 2008a, 2008b; Schönrich and Binney 2009a; Minchev et al. 2011), i.e., the substantive changes in the stars’ mean orbital radii that are expected to occur without boosting the orbits’ eccentricity? What was the disk-shaping role of minor mergers (e.g., Abadi et al. 2003), which are deemed an integral part of the ΛCDM cosmogony? How much did in-falling satellites impulsively heat the Milky Way’s disk, potentially leading to a distinct thick disk (Villalobos and Helmi 2008)? How much stellar debris did they deposit in this process? Is the radial orbit migration induced by satellite infall (Bird et al. 2012) distinguishable from purely internal processes? All of these questions are not only relevant for the Milky Way in particular, but lead generically to the question of how resilient stellar disks are to tidal interactions; it has been claimed (e.g., Kormendy et al. 2010; Shen et al. 2010) that the existence of large, thin stellar disks poses a challenge to the merger-driven ΛCDM picture.

In the end, answers to these questions require a multi-faceted comparison of the Disk’s observable status quo to the expectations from ab initio formation models (see e.g. Fig. 2), in practice for the most part hydrodynamical simulations. However, the current generation of ‘cosmological’ disk galaxy formation models is more illustrative than exhaustive in their representation of possible disk galaxy formation histories; therefore the question of how to test for the importance of galaxy formation ingredients through comparison with observational data is actively under way.

Fig. 2

Output of the ERIS disk galaxy formation simulation aimed at following the formation history of a Milky-Way-like galaxy ab initio. The figure shows a projection resembling the 2MASS map of the Galaxy, and shows that simulations have now reached a point where, with very quiescent merging histories, disk-dominated galaxies can result

The maximal amount of empirical information about the Disk that one can gather from data is a joint constraint on the gravitational potential in which stars orbit Φ(x,t) and on the chemo-orbital distribution function of the Disk’s stars. How to best obtain such a joint constraint is a problem solved in principle, but not in practice (see Sects. 2.3 and 5).

It is in this context that this review sets out to work towards three broad goals:

• Synthesize what the currently most pertinent questions about dark matter, disk galaxy formation, and evolution are that may actually be addressed with stellar surveys of the Galactic disk.

• Lay out what ‘modeling’ of large stellar samples means and emphasize some of the practical challenges that we see ahead.

• Describe how recent work may change our thinking about how to best address these questions.

Compared to Turon et al. (2008) and Ivezić et al. (2012) for an empirical description of the Milky Way disk, and compared to a series of papers by Binney and collaborators on dynamical modeling of the Galaxy (Binney 2010, 2012a; Binney and McMillan 2011; McMillan and Binney 2012), we place more emphasis two aspects that we deem crucial in Galactic disk modeling:

• The consideration of ‘mono-abundance’ stellar sub-populations (MAPs), asking the question of ‘what our Milky Way disk would look like if we had eyes for stars of only a narrow range of photospheric abundances’. The importance of ‘mono-abundance components’ arises from the fact that in the presence of significant radial migration, chemical abundances are the only lifelong tags (see Freeman and Bland-Hawthorn 2002) that stars have, which can be used to isolate sub-groups independent of presuming a particular dynamical history. In a collisionless system, such populations can be modeled completely independently; yet they have to ‘feel’ the same gravitational potential.

• The central importance of the (foremost spatial) selection function of any stellar sample that enters modeling. Dynamical modeling links the stars’ kinematics to their spatial distribution. Different subsets of Disk stars (differing e.g. by abundance) have dramatically different spatial and kinematical distributions. If the spatial selection function of any subset of stars with measured kinematics is not known to better than some accuracy, this will pose a fundamental limitation on the dynamical inferences, irrespective of how large the sample is; with ever larger samples emerging, understanding the selection function is increasingly probably to be a limiting factor in the analysis.

The remainder of the review is structured as follows: in Sect. 2 we discuss in more detail the overall characterization of the Milky Way’s disk and treat in detail the open questions of stellar disk formation and evolution in a cosmological context. In Sect. 3 we provide an overview of the existing and emerging stellar Galactic surveys, and in Sect. 4 we describe how the survey selection function can and should be rigorously handled in modeling. In Sects. 5 and 6 we present recent results in dynamical and structural modeling of the Disk, and their implications for future work. In the closing Sect. 7, we discuss what we deem the main practical challenges and promises for this research direction in the next years.

2 Galactic Disk studies: an overview

‘Understanding’ the Disk could mean having a comprehensive empirical characterization for it and exploring which—possibly competing—theoretical concepts that make predictions for these characteristics match, or do not. As the Milky Way is only one particular galaxy and as disk galaxy formation is a complex process that predicts broad distributions for many properties, it may be useful to consider which Disk characteristics generically test formation concepts, rather than simply representing one of many possible disk formation outcomes.

2.1 Characterizing the current structure of the Disk

In a casual, luminosity or mass-weighted average, the Disk can be characterized as a highly flattened structure with an (exponential) radial scale length of 2.5–3 kpc and scale height of ≃0.3 kpc (e.g., Kent et al. 1991; López-Corredoira et al. 2002; McMillan 2011), which is kinematically cold in the sense that the characteristic stellar velocity dispersions near the Sun of σ _z ≃σ _ϕ ≃σ _R /1.5≃25 km s⁻¹ are far less than v _circ≃220 km s⁻¹. Current estimates for the overall structural parameters of the Milky Way are compiled in Table 1.2 of Binney and Tremaine (2008); more specifically estimates for the mass of the Disk are ≃5×10¹⁰ M_⊙ (Flynn et al. 2006; McMillan 2011), though the most recent data sets have not yet been brought to bear on this basic number. No good estimates for the globally averaged metallicity of the Disk exist, though 〈[Fe/H]〉, being about the solar value, seems likely.

With these bulk properties, the Milky Way and its Disk are very ‘typical’ in the realm of present-day galaxies: comparable numbers of stars in the low-redshift Universe live in galaxies larger and smaller (more and less metal-rich) than the Milky Way. For its stellar mass, the structural parameters of the Disk are also not exceptional (e.g., van der Kruit and Freeman 2011). Perhaps the most unusual aspect of the Milky Way is that its stellar disk is so dominant, with a luminosity ratio of bulge-to-disk of about 1:5 (Kent et al. 1991): most galaxies of M_∗>5×10¹⁰ M_⊙ are much more bulge dominated (Kauffmann et al. 2003).

But describing the Disk by ‘characteristic’ numbers, as one is often forced to do in distant galaxies, does not even begin to do justice to the rich patterns that we see in the Disk: it has been long established that positions, velocities, chemical abundances, and ages are very strongly and systematically correlated. This is in the sense that younger and/or more metal-rich stars tend to be on more nearly circular orbits with lower velocity dispersions. Of course, stellar populations with lower (vertical) velocity dispersions will form a thinner disk component. This has led to the approach of defining subcomponents of the Disk on the basis of the spatial distribution, kinematics, or chemical abundances. Most common has been to describe the Disk in terms of a dominant thin disk and a thick disk, with thin–thick disk samples of stars defined spatially, kinematically, or chemically. While these defining properties are of course related, they do not isolate identical subsets of stars. Whether it is sensible to parse the Disk structure into only two distinct components is discussed below.

Much of what we know about these spatial, kinematical, and chemical correlations within the Disk has come until very recently from very local samples of stars, either from studies at R≃R _⊙ or from the seminal and pivotal Hipparcos/Geneva–Copenhagen sample of stars drawn from within ≃100 pc (ESA 1997; Nordström et al. 2004). As dynamics links local and global properties, it is perfectly possible and legitimate to make inferences about larger volumes than the survey volume itself; yet, it is important to keep in mind that the volume-limited Geneva–Copenhagen sample encompasses a volume that corresponds to two-millionths of the Disk’s half-mass volume. Only recently have extensive samples beyond the solar neighborhood with $p(\boldsymbol{x},\boldsymbol{v},[\overrightarrow{\mathrm{X}/\mathrm{H}}])$ become available.

While a comprehensive empirical description of the Disk (spatial, kinematical, and as regards abundances) in the immediate neighborhood of the Sun has revealed rich correlations that need explaining, an analogous picture encompassing a substantive fraction of the disk with direct observational constraints is only now emerging.

But the Disk is neither perfectly smooth nor perfectly axisymmetric, as the above description implied. This is most obvious for the youngest stars that still remember their birthplaces in star clusters and associations and in spiral arms. But is also true for older stellar populations. On the one hand, the spiral arms and the Galactic bar are manifest non-axisymmetric features, with clear signatures also in the Solar neighborhood (e.g., Dehnen 1998, 2000; Fux 2001; Quillen 2003; Quillen and Minchev 2005), as shown in Fig. 3. By now the strength of the Galactic bar and its pattern speed seem reasonably well established, both on the basis of photometry (Binney et al. 1997; Bissantz and Gerhard 2002) and on the basis of dynamics (Dehnen 1999; Minchev et al. 2007). But we know much less about spiral structure in the stellar disk. While the location of the nearby Galactic spiral arms have long been located on the bases of the dense gas geometry and distance measurements to young stars, the existence and properties of dynamically important stellar spiral structure is completely open: neither has there been a sound measure of a spiral stellar over-density that should have dynamical effects, nor has there been direct evidence for any response of the Disk to stellar spirals. Clarifying the dynamical role of spiral arms in the Milky Way presumably has to await Gaia.

Fig. 3

Distribution in v _x –v _z -space of very nearby stars in the Disk with distances from Hipparcos (≃100 pc; Dehnen 1998). The sample shows rich substructure of ‘moving groups’, some of which reflect stars of common birth origin, others are the result of resonant orbit trapping

In addition there is a second aspect of non-axisymmetric substructure, which is known to be present in the Disk, but which is far from being sensibly characterized: there are groups of chemically similar stars on similar but very unusual orbits (streams, e.g., Helmi et al. 1999; Navarro et al. 2004; Klement et al. 2008, 2009) that point towards an origin where they were formed in a separate satellite galaxy and subsequently disrupted in a (minor) merger, spending now at least part of their orbit in the disk. The process of Disk heating and Disk augmentation through minor mergers has been simulated extensively, both with collisionless and with hydrodynamical simulations (e.g., Velazquez and White 1999; Abadi et al. 2003; Kazantzidis et al. 2008; Moster et al. 2010): these simulations have shown that galaxy disks can absorb considerably more satellite infall and debris than initial estimates had suggested (Toth and Ostriker 1992). However, these simulations also indicated that—especially for prograde satellite infall—it is not always easy to distinguish satellite debris by its orbit from ‘disk groups’ formed in situ, once the satellite debris has been incorporated into the disk.

2.2 The formation and evolution of the Disk

Explaining the formation and evolution of galaxy disks has a 50-year history, gaining prominence with the seminal papers by Mestel (1963) and Eggen et al. (1962). Yet, producing a galaxy through ab initio calculations that in its disk properties resembles the Milky Way has remained challenging to this day.

Exploring the formation of galaxy disks through simplified (semi-)analytic calculations has yielded seemingly gratifying models, but at the expense of ignoring ‘detail’ that is known to play a role. Milestones in this approach were in particular the work by Fall and Efstathiou (1980) that put Mestel’s idea of gas collapse under angular momentum conservation into the cosmological context of an appropriately sized halo that acquired a plausible amount of angular momentum through interactions with its environment: this appeared as a cogent explanation for galactic disk sizes. These concepts were married with the Press and Schechter (Press and Schechter 1973; Bond et al. 1991) formalism and its extensions by Mo et al. (1998), to place disk formation in the context of halos that grew by hierarchical merging. This approach performed well in explaining the overall properties of the present-day galaxy disk population and also its redshift evolution (e.g., Somerville et al. 2008).

Yet, trouble in explaining disks came with the efforts to explain galaxy disk formation using (hydrodynamical) simulations in a cosmological context. The first simulations (Katz and Gunn 1991), which started from unrealistically symmetrical and quiescent initial conditions, yielded end-products that resembled observed galaxy disks. But then the field entered a 15 year period in which almost all simulations produced galaxies that were far too bulge-dominated and whose stellar disks were either too small, or too anemic (low mass fraction), or both. Of course, it was clear from the start that this was a particularly hard problem to tackle numerically: the initial volume from which material would come (≃500 kpc) and the thinness of observed disks (≃0.25 kpc) implied very large dynamic ranges, and the ‘sub-grid’ physics issue of when to form stars from gas and how this star-formation would feed back on the remaining gas played a decisive role.

As of 2012, various groups (Agertz et al. 2011; Guedes et al. 2012; Martig et al. 2012; Stinson et al. 2013) have succeeded in running simulations that can result in large, disk-dominated galaxies, resembling the Milky Way in many properties (cf. Fig. 2). This progress seems to have—in good part—arisen from the explicit or implicit inclusion of physical feedback processes that had previously been neglected. In particular, ‘radiative feedback’ or ‘early stellar feedback’ from massive stars before they explode as Supernovae seems to have been an important missing feedback ingredient and must be added in simulations to the well-established supernovae feedback (Nath and Silk 2009; Hopkins et al. 2012; Brook et al. 2012). With such—physically expected—feedback implemented, disk dominated galaxies can be made in ab initio simulations that have approximately correct stellar-to-halo mass fractions for a wide range of mass scales. In some of the other cases, cf. Guedes et al. (2012), the radiative feedback is not implemented directly, but cooling-suppression below 10⁴ K has a similar effect. It appears that the inclusion of this additional feedback not only makes disk dominated galaxies a viable simulation outcome, but also improves the match to the galaxy luminosity function and Tully–Fisher relations.

This all constitutes long-awaited success, but is certainly far from having any definitive explanation for the formation of any particular galaxy disk, including ours. In particular, a very uncomfortable dependence of the simulation outcome on various aspects of the numerical treatment remains, which has recently been summarized by Scannapieco et al. (2012).

In addition to the fully cosmological simulations, a large body of work has investigated processes relevant to disk evolution from an analytic or numerical perspective, with an emphasis on chemical evolution and the formation and evolution of thick-disk components. The chemical evolution of the Milky Way has been studied with a variety of approaches (e.g., Matteucci and Francois 1989; Gilmore et al. 1989; Chiappini et al. 2001) mostly with physically motivated but geometrically simplified models (not cosmological ab initio simulations): these studies have aimed at constraining the cosmological infall of ‘fresh’ gas (e.g., Fraternali and Binney 2008; Colavitti et al. 2008), explain the origin of radial abundance gradients (e.g., Prantzos and Aubert 1995), and explore the role of ‘galactic fountains’, i.e. gas blown from the disk, becoming part of a rotating hot corona, and eventually returning to the disk (e.g., Marinacci et al. 2011). Recent work by Minchev et al. (2012b) has introduced a new approach to modeling the evolution of the Disk by combining detailed chemical evolution models with cosmological N-body simulations.

To explain in particular the vertical disk structure qualitatively different models have been put forward, including cosmologically motivated mechanisms where stars from a disrupted satellite can be directly accreted (Abadi et al. 2003), or the disk can be heated through minor mergers (Toth and Ostriker 1992; Quinn et al. 1993; Kazantzidis et al. 2008; Villalobos and Helmi 2008; Moster et al. 2010) or experience a burst of star formation following a gas-rich merger (Brook et al. 2004). Alternatively, the disk could have been born with larger velocity dispersion than is typical at z≈0 (Bournaud et al. 2009; Ceverino et al. 2012); or purely internal dynamical evolution due to radial migration may gradually thicken the disk (Schönrich and Binney 2009b; Loebman et al. 2011; Minchev et al. 2012a). It is likely that a combination of these mechanisms is responsible for the present-day structure of the Disk, but what relative contributions of these effects should be expected has yet to be worked out in detail, and none of these have been convincingly shown to dominate the evolution of the Disk.

Radial migration is likely to have a large influence on the observable properties of the Disk, if its role in shaping the bulk properties of the disk were sub-dominant. The basic process as described by Sellwood and Binney (2002) consists of the scattering of stars at the corotation radius of transient spiral arms; at corotation such scattering changes the angular momentum, L _z , of the orbit (≃mean radius) without increasing the orbital random energy. A similar—and potentially more efficient—process was later shown to happen when the bar and spiral structure’s resonances overlap (Minchev and Famaey 2010; Minchev et al. 2011). Such changes in the mean orbital radii are expected to be of order unity within a few Gyrs, and to have a profound effect on the interpretation of the present-day structure of the Disk: e.g. present-day L _z can no longer be used as a close proxy for the birth L _z , even for stars on near-circular orbits. Quantifying the strength of radial migration in the Milky Way is one of the most pertinent action items for the next-generation of Milky Way surveys.

A brief synthesis of the predictions from all these efforts is as follows:

• Stellar disks should generically form from the inside out. More specifically, it is the low angular momentum gas that settles first near the centers of the potential wells forming stars at small radii.

• Disk-dominated galaxies with disk sizes in accord with observations can emerge, if, and only if, there is no major merger since z≃1.

• The luminosity- or mass-weighted radial stellar density profiles at late epochs resemble exponentials.

• Stars that formed at earlier epochs (z≥1), when the gas fraction was far higher, do not form from gas disks that are as well-settled and thin as they are at z≃0 with dispersions of ≤10 km s⁻¹.

• Characteristic disk thicknesses or vertical temperatures of 400 pc and σ _z ≃25 km s⁻¹ are plausible.

• Material infall, leading to fresh gas supply and dynamical disk heating, and star formation is not smooth but quite variable, even episodic, with a great deal of variation among dark-matter halos with the same overall properties. It is rare that one particular infall or heating event dominates.

• Throughout their formation histories galaxies exhibit significant non-axisymmetries, which at epochs later than z≃1 resemble bars and spiral arms. Through resonant interactions, these structures may have an important influence on the evolution of stellar disks.

2.3 The Disk and the Galactic gravitational potential

Learning about the orbits of different Disk stellar sub-populations as a galaxy formation constraint and learning from these stars about the gravitational potential, Φ(x,t), are inexorably linked. Those orbits are generally described by a chemo-orbital distribution function, $p(\boldsymbol{J},\boldsymbol{\phi},[\overrightarrow {\mathrm{X}/\mathrm{H}}], t_{\mathrm{age}}| \varPhi (\boldsymbol{x}))$ that quantifies the probability of being on an orbit labeled by J,ϕ for each subset of stars (characterized by, e.g., by their ages t _age or their chemical abundances $[\overrightarrow{\mathrm{X}/\mathrm{H}}]=[\mathrm{Fe}/\mathrm{H}], [\alpha/\mathrm{Fe}], \ldots$). Here, we chose to characterize the orbit (the argument of the distribution function) by J, actions or integrals of motion (which depend on both its observable instantaneous phase-space coordinates p(x,v) and on Φ(x,t)). Each star then also has an orbital phase (or angle), ϕ, whose distribution is usually assumed to be uniform in [0,2π].

Unless direct accelerations are measured for stars in many parts of the Galaxy, many degenerate combinations of Φ(x,t) and $p(\boldsymbol{J},\boldsymbol{\phi},[\overrightarrow{\mathrm{X}/\mathrm{H}}], t_{\mathrm {age}})$ exist, unless astrophysically plausible constraints and/or assumptions are imposed: time-independent steady-state solutions, axisymmetric solutions, uniform phase distributions of stars on the same orbit, etc. This is the art and craft of stellar dynamical modeling (Binney and Tremaine 2008; Binney and McMillan 2011).

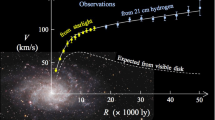
Learning about the Galactic potential is one central aspect of such dynamical modeling. On scales larger than individual galaxies, the so-called standard ΛCDM cosmology has been tremendously successful in its quantitative predictions. If certain characteristics for dark energy and dark matter are adopted the large-scale matter and galaxy distribution can be well explained (including baryon acoustic oscillations) and be linked to the fluctuations in the cosmic microwave background. On the scales of galaxies and smaller, theoretical predictions are more complex, both because all of these scales are highly non-linear and because the cooling baryons constitute an important, even dominant mass component. Indeed, the ΛCDM paradigm seems to make at least two predictions that are unsubstantiated by observational evidence, or even in seeming contradiction. Not only are numerous low-mass dark-matter halos predicted, almost completely devoid of stars (Kauffmann et al. 1993; Klypin et al. 1999; Moore et al. 1999), but ΛCDM simulations also predict that dark-matter profiles are cuspy, i.e., have divergent dark-matter densities towards their centers (Dubinski and Carlberg 1991; Navarro et al. 1996). In galaxies as massive as our Milky Way, baryonic processes could not easily turn the dark-matter cusp into a core, as seems viable in low mass galaxies (e.g., Flores and Primack 1994; Pontzen and Governato 2012). Therefore, we should expect for the Milky Way that more than half of the mass within a sphere of ≃R ₀ should be dark matter. Yet microlensing towards the Milky Way bulge (Popowski et al. 2005; Hamadache et al. 2006; Sumi et al. 2006) indicates that in our own Galaxy most of the in-plane column density is made up of stars (e.g., Binney and Evans 2001). Measurements in individual external galaxies remain inconclusive, because dynamical tracers only measure the total mass, but cannot separate the stellar and DM contributions. In the Milky Way, almost all stellar mass beyond the bulge is in a stellar disk and hence very flat, while the DM halos emerging from ΛCDM simulations are spheroidal or ellipsoidal. So, mapping the Milky Way’s mass near the disk plane as a function of radius through the vertical kinematics will break the so-called disk—halo degeneracy, when combined with the rotation curve and the outer halo mass profile: one can then separate the flat from the round-ish mass contributions.

Perhaps the most immediate goal of dynamical Disk modeling is to determine how much DM there is within the Solar radius: as little as implied by the microlensing results, or as much as predicted by ΛCDM cosmology. A second goal for the Galactic potential is to determine whether the disk-like total mass distribution is as thin as the stellar counts imply; this is interesting, because the possibility of a thick dark-matter disk has been raised (Read et al. 2008). Finally, we can combine precise constraints from near the Galactic disk with constraints from stellar halo streams (e.g., Koposov et al. 2010) to get the shape of the potential as a function of radius. This can then be compared to the expectations, e.g., of alternative gravity models, and provide another, qualitatively new test for the inevitability of some form of dark matter.

On the other hand, the best possible constraints on Φ(x) are necessary to derive the (chemo-)orbital distribution of stars (the ‘distribution function’, DF), as the orbit characteristic, such as the actions depend of course on both (x,v) of the stars and on Φ(x).

3 Stellar surveys of the Milky Way

3.1 Survey desiderata

The ideal survey would result in an all-encompassing catalog of stars throughout the Disk, listing their 3-D positions and 3-D velocities (x,v), elemental abundances $([\overrightarrow{\mathrm {X/H}}])$, individual masses (M _∗), ages (t _age), binarity, and line-of-sight reddening (A _V ), along with the associated uncertainties. Furthermore, these uncertainties should be ‘small’, when compared to the scales on which the multi-dimensional mean number density of stars $n(\boldsymbol{x}, \boldsymbol{v}, [\overrightarrow{\mathrm{X}/\mathrm{H}}], M_{*}, t_{\mathrm{age}})$ has structure. In practice, this is neither achievable in the foreseeable future, nor is it clear that a ‘fuller’ sampling of $n(\boldsymbol{x}, \boldsymbol{v}, [\overrightarrow{\mathrm{X}/\mathrm{H}}], M_{*}, t_{\mathrm{age}})$ is always worth the additional effort. Such an all-encompassing survey would imply that the probability of entering the catalog is $p_{\mathrm {complete}}(\boldsymbol{x}, \boldsymbol{v}, [\overrightarrow{\mathrm{X}/\mathrm{H}}], M_{*}, t_{\mathrm{age}})\simeq1$ across the entire relevant domain¹ of x, v, $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$, M _∗, and t _age.

Any realistic survey is a particular choice of compromise in this parameter space. Fundamentally, p _complete of any survey, i.e., the probability of any given star having ended up in the catalog, is always limited by quantities in the space of ‘immediate observables’, foremost by the stars’ fluxes (or signal-to-noise) vis-à-vis a survey’s flux limit or image-crowding limit. But these ‘immediate observables’ are usually not the quantities of foremost astrophysical interest, say $\boldsymbol{x}, \boldsymbol{v}, [\overrightarrow {\mathrm{X}/\mathrm{H}}], m, t_{\mathrm{age}}$. While full completeness is practicable with respect to some quantities, e.g., the angular survey coverage (ℓ,b) and the velocities v, it is not in other respects. The effective survey volume will always be larger for more luminous stars, the survey’s distance limit will always be greater in directions of lower dust extinction at the observed wavelength; and an all-sky survey at fixed exposure time will go less deep towards the bulge because of crowding.

So, in general, ‘completeness’ is an unattainable goal. And while samples that are ‘complete’ in some physical quantity such as volume or mass are immediately appealing and promise easy analysis, their actual construction in many surveys comes at the expense of discarding a sizable (often dominant) fraction of the pertinent catalog entries. With the right analysis tools, understanding the survey (in-)completeness and its mapping into the physical quantities of interest are more important than culling ‘complete’ samples. We will return to this in Sect. 4.

3.2 Observable quantities and physical quantities of interest

The physical attributes about a star ($\boldsymbol{x}, \boldsymbol{v}, [\overrightarrow{\mathrm{X}/\mathrm{H}}], m, t_{\mathrm{age}}$) that one would like to have for describing and modeling the Disk are in general not direct observables. This starts out with the fact that the natural coordinates for (x, v) in the space of observables are (ℓ,b,D) and (v _los,μ _ℓ ,μ _b ), respectively, with a heliocentric reference system in position and velocity.

In general, Galactic star surveys fall into two seemingly disjoint categories: imaging and spectroscopy. Imaging surveys get parsed into catalogs that provide angular positions and fluxes (typically in 2 to 10 passbands) for discrete sources, once photometric solutions (e.g., Schlafly et al. 2012) and astrometric solutions (Pier et al. 2003) have been obtained. Multi-epoch surveys, or the comparison of different surveys from different epochs, then provide proper motions, and—with sufficient precision—useful parallaxes (e.g., Perryman et al. 1997; Munn et al. 2004). Spectroscopic surveys are carried out with different instrumentation or even as disjoint surveys, usually based on a pre-existing photometric catalog. These spectra, usually for vastly fewer objects, provide v _los on the one hand and the spectra that allow estimates of the ‘stellar parameters’, T _eff, logg, and $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ (e.g., Nordström et al. 2004; Yanny et al. 2009). But ‘imaging’ and ‘spectroscopic’ surveys are only seemingly disjoint categories, because multi-band photometry may be re-interpreted as a (very) low resolution spectrum and some stellar parameters (e.g., T _eff and [Fe/H]) can be constrained by photometry and/or spectra (e.g., Ivezić et al. 2008).

The practical link between ‘observables’ and ‘quantities of interest’ warrants extensive discussion: along with the survey selection function (Sect. 4) it is one of the two key ingredients for any rigorous survey analysis. For some quantities, such as (ℓ,b) and v _los this link is quite direct; but even there a coordinate transformation is required, which involves R _⊙, v _LSR and of course the distances, as most dynamical or formation models are framed in some rest-frame system with an origin at the Galactic center. Similarly, converting estimates of μ _ℓ ,μ _b to two components of v (and δ v) requires knowledge of the distance. In Fig. 4, we show a graphical model overview over the task of ‘astrophysical parameter determination’ in Galactic surveys. In the subsequent subsections, we discuss different aspects of this model.

Fig. 4

Constraining Stellar Parameters from Observables in Milky Way Surveys: this figure provides a schematic overview, in the form of a simplified graphical model, of the logical dependencies between the stellar observables in Galactic surveys (thick dotted ovals) and the main desiderata for each star (thin dashed ovals), its stellar parameters and distance, given various prior expectations about galaxy formation, star formation and the Galactic dust distribution (top). The basic observables are: line-of-sight-velocity, v _los, proper motions, μ, parallax π, multi-band photometry $m_{\lambda_{i}}$ and photospheric parameters derived from spectra (T _eff, logg, abundances, Z); most of them depend on the Sun’s position x _⊙ through, Δx. The main desiderata are the star’s mass M _∗, age t _age and abundances Z, along with its distance D from the Sun and the (dust) extinction along the line of sight, A _V . The prior probabilities of M _∗, age t _age, Z, D, and A _V are informed by our notions about star formation (the IMF) the overall structure of the Galaxy and various constraints on the dust distribution. Overall the goal of most survey analysis is to determine the probability of the stellar observables for a given set of desiderata, which requires both isochrones and stellar atmospheric models (see Burnett and Binney 2010). In practice, most existing Galactic surveys analyses can be mapped onto this scheme, with logical dependencies often replaced by assumed logical conditions (e.g. ‘using dereddened fluxes’, ‘presuming the star is on the main sequence’, etc.). This graphical model still makes a number of simplifications on the velocities

3.2.1 Distance estimates

Clearly, a ‘direct’ distance estimate, one that is independent of any intrinsic property of the stars, such as parallax measurements, is to be preferred. At present, good parallax distance estimates exist for about 20,000 stars within ≃100 pc from Hipparcos (Perryman et al. 1997; ESA 1997). And a successful Gaia mission will extend this to ≃10⁹ stars within ≃10 kpc (de Bruijne 2012). However, a widely usable catalog with Gaia parallaxes is still 5 years away as of this writing, and even after Gaia most stars in the already existing wide-field photometric surveys (e.g., SDSS or PS1) will not have informative Gaia parallax estimates, simply because they are too faint.

Therefore, it is important to discuss the basics and the practice of (spectro-) photometric distance estimates to stars, which has turned out to be quite productive with the currently available data quality. Such distance estimates, all based on the comparison of the measured flux to an inferred intrinsic luminosity or absolute magnitude, have a well-established track record in the Galaxy, when using so-called standard candles, such as BHB stars (Sirko et al. 2004; Xue et al. 2008) or ‘red clump stars’ in near-IR surveys (e.g., Alves et al. 2002). But, of course, as the ‘physical HR diagram’ (L vs. T _eff) in Fig. 5 shows, the distance-independent observables greatly constrain luminosity and hence distance for basically all stars. Foremost, these distance-independent observables are T _eff or colors as well $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$, potentially augmented by spectroscopic logg estimates.

Fig. 5

‘Physical’ color–magnitude diagram, shown by BaSTI isochrones for two metallicities, which are spaced 0.2 dex in age between 10⁹ and 10¹⁰ yr. This diagram serves as a reference for the discussion of how to derive physical parameters (distances, ages, abundances) for stars from observables (cf. Sect. 3.2): the age-independence of the luminosity on the MS makes for robust photometric distance estimates; the age and abundance sensitivity of L and T _eff near the turn-off and on the (sub-)giant branch makes for good age determinations, but only if parallax-based distances exist; etc.

A general framework for estimating distances in the absence of parallaxes is given in Burnett et al. (2011) or Breddels et al. (2010), and captured by the graphical model in Fig. 4. Basically, the goal is to determine the distance modulus likelihood

(1)

where the m _i are the apparent magnitudes of the star in various passbands (i.e., also the ‘colors’) and M _∗ is its stellar mass, which predicts the star’s luminosity and colors (at a given [Fe/H] and t _age, see Fig. 4). Note that [Fe/H] appears both as an observational constraint and a model parameter, which determines isochrone locations. The prior on ([Fe/H],t _age) may depend on the distance modulus to use the different spatial distribution of stars of different metallicities (in this case, the position of the sky would also be included to compute the 3D position).

To get distance estimates, one needs to marginalize over the nuisance parameters (M _∗, [Fe/H], and t _age in the case above), and one needs to spell out the external information (i.e. priors) on the relative probability of these nuisance parameters (e.g., Bailer-Jones 2011). As Fig. 5 makes obvious, the precision of the resulting distance estimates depends on the evolutionary phase, the quality of observational information, and any prior information. To give a few examples: for stars on the lower main sequence, the luminosity is only a function of T _eff or color, irrespective of age; hence it can be well determined (≃5–10 %) if the metallicity is well constrained (δ[Fe/H]≤0.2) and if the probability of the object being a (sub-)giant is low, either on statistical grounds or through an estimate of logg. Jurić et al. (2008) showed that such precisions can be reached even if the metallicity constraints only come from photometry. On the giant branch, colors reflect metallicity (and also age) as much as they reflect luminosity; therefore photometric distances are less precise. Nonetheless, optical colors good to ≃0.02 mag and metallicities with δ[Fe/H]≤0.2 can determine giant star distances good to ≃15 %, if there is a prior expectation that the stars are old (Xue et al. 2012, in preparation). The power of spectroscopic data comes in determining logg, T _eff especially in the case of significant reddening, and in constraining the abundances, especially [Fe/H]. While only high-dispersion and high-S/N spectra will yield tight logg estimates, even moderate-resolution and moderate-S/N spectra (as for the SEGUE and LAMOST surveys; see Sect. 3.3.2) suffice to separate giants from dwarfs (e.g., Yanny et al. 2009), thereby discriminating the multiple branches of L(color,[Fe/H]) in the isochrones. While main-sequence turn-off stars have been widely used to make 3D maps of the Milky Way (Fig. 4; e.g., Belokurov et al. 2006; Jurić et al. 2008; Bell et al. 2008), they are among the stellar types abundantly found in typical surveys, the ones for which precise (<20 %) spectrophotometric distances are hardest to obtain (e.g., Schönrich et al. 2011).

The absolute scale for such spectrophotometric distance estimates is in most cases tied to open or globular clusters, which are presumed to be of known distance, age and metallicity (e.g., Pont et al. 1998; An et al. 2009). Because the number of open and globular clusters is relatively small and, in particular, old open clusters are rare, the sampling in known age and metallicity is sparse and non-uniform. Therefore, care is necessary to make this work for Disk stars of any age or metallicity. Interestingly, the panoptic sky surveys with kinematics offer the prospect of self-calibration of the distance scale (Schönrich et al. 2012) through requiring dynamical consistency between radial velocities and proper motions.

3.2.2 Chemical abundances

Chemical abundances are enormously important astrophysically, as they are witnesses of the Disk’s enrichment history and as they are lifelong tags identifying various stellar sub-populations. Broadly speaking, metals are produced in stars as by-products of nuclear burning and are dispersed into the interstellar medium by supernova explosions and winds. This leads to a trend toward higher metallicity as time goes on, with inside-out formation leading to faster chemical evolution or metal-enrichment in the inner part of the Disk. While all supernovae produce iron, α-element enrichment occurs primarily through type II supernovae of massive stars with short lifetimes. Therefore, until type Ia supernovae, with typical delay times of 2 Gyr (e.g., Matteucci and Recchi 2001; Dahlen et al. 2008; Maoz et al. 2011), start occurring, the early disk’s ISM, and stars formed out of it, has [α/Fe] that is higher than it is today. For a temporally smooth star-formation history, [α/Fe] decreases monotonically with time. However, a burst of star formation, e.g., following a gas-rich merger, could re-instate a higher [α/Fe], such that the relation between [α/Fe] and age is dependent on the star-formation history (e.g., Gilmore and Wyse 1991).

Beyond the astrophysical relevance of abundance information, it is also of great practical importance in obtaining distances (Sect. 3.2.1) and ages (Sect. 3.2.3). Among the ‘abundances’ $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$, the ‘metallicity’ [Fe/H] is by far of the greatest importance for distance estimates. Practical determinations of $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ fall into three broad categories: estimates (usually just [Fe/H], or [M/H] as a representative of the overall metal content) from either broad- or narrow-band photometry; estimates based on intermediate-resolution spectra (R=2000 to 3000); or estimates from high-resolution spectra (R=10,000 and higher) that enable individual element abundance determinations. We discuss here briefly abundances obtained in these three different regimes.

• Stellar Abundances from Photometry: That abundances can be constrained through photometry—at least for some stellar types—has been established for half a century (Wallerstein 1962; Strömgren 1966). The level of overall metal-line blanketing or the strength of particular absorption features varies with [Fe/H] (e.g., Böhm-Vitense 1989), which appreciably changes the broad-band fluxes and hence colors. How well this can be untangled from changes in T _eff or other stellar parameters, depends of course on the mass and evolutionary phase of the star. The most widely used applications are the ‘color of the red giant branch’, which is a particularly useful metallicity estimate if there are priors on age and distance (e.g. McConnachie et al. 2010 for the case of M31). In the Galaxy, variants of the ‘UV excess method’ (Wallerstein 1962) have been very successfully used to estimate [Fe/H] for vast numbers of stars. In particular, Ivezić et al. (2008) calibrated the positions of F & G main sequence stars in the SDSS (u−g)–(g−r) color plane against spectroscopic metallicity estimates. Based on SDSS photometry, they showed that metallicity precisions of δ[Fe/H]≃0.1 to 0.3 can be reached, depending on the temperature and metallicity of the stars: in this way they determined [Fe/H] for over 2,000,000 stars.

  Some narrow- or medium-band photometric systems (foremost Strömgren filters; Strömgren 1966; Bessell et al. 2011) can do even better in estimating chemical abundances, foremost [Fe/H], by placing filters on top of strong absorptions features. Recently, this has been well illustrated by Árnadóttir et al. (2010) and Casagrande et al. (2011), who compared Strömgren photometry to abundances from high-resolution spectra, showing that [Fe/H] precisions of ≤0.1 dex are possible in some T _eff regimes. Casagrande et al. (2011) also showed that precise Strömgren photometry can constrain [α/Fe] to ≃0.1 dex. In addition, narrow band photometry can provide good metallicity estimates (δ[Fe/H]≃0.2) for a wider range of stellar parameters than SDSS photometry.

  Indeed, the literature is scattered with disputes that a certain photometric abundance determination precision is untenable, because the same approach yields poor [Fe/H] estimates for a sample at hand. In many cases, this seeming controversy can be traced back to the fact that different approaches vary radically in their accuracy across the T _eff, logg, t _age parameter plane.

  The abundance information from Gaia will be based on a spectral resolution of only R=15 to 80 for most stars; and while these data are produced through a dispersive element, they are probably best thought of as many-narrow-band photometry; for FGKM stars with g<19 Gaia data are expected to yield δ[Fe/H]≤0.2 (Liu et al. 2012).

• Stellar Abundances from High-Resolution Spectroscopy: High-resolution spectroscopy (R≥10,000), either in the optical or in the near-IR, is an indispensable tool to obtain individual element abundances and to anchor any abundance scale in physically motivated models of stellar photospheres (e.g., Asplund et al. 2009; Edvardsson et al. 1993; Reddy et al. 2003; Bensby et al. 2005; Allende Prieto et al. 2008). The abundances are then fit by either modeling the spectrum directly in pixel or flux space, or more commonly by parsing the observed and the model spectrum into a set of line equivalent widths which are compared in a χ ²-sense. From typical existing spectra, about 10 to 20 individual abundances are derived, with relative precisions of 0.05 to 0.2 (e.g., Reddy et al. 2003; Boeche et al. 2011). High resolution spectroscopy has remained the gold standard for investigating chemo-dynamical patterns in the Milky Way in detail.

• Stellar Abundances from Moderate-Resolution Spectroscopy: In recent years, large data sets at moderate spectral resolution² have become available, foremost by SDSS/SEGUE (Yanny et al. 2009) in the last years, but in the future also from LAMOST data (Deng et al. 2012). Such data can provide robust metallicities [Fe/H], good to δ[Fe/H]≤0.2, and constrain [α/Fe] to δ[α/Fe]≤0.15 (Lee et al. 2008a, 2011), for F, G and K stars. The accuracy of these data has been verified against high-resolution spectroscopy and through survey spectra in globular clusters of known metallicity (Lee et al. 2008b, 2011). Recently, Bovy et al. (2012c) have pursued an alternate approach to determine the precision (not accuracy) of abundance determinations [Fe/H], [α/Fe], through analyzing the abundance-dependent kinematics of Disk stars. They found that for plausible kinematical assumptions, the SDSS spectra of G-dwarfs must be able to rank stars in [Fe/H] and [α/Fe] at the (0.15,0.08) dex level, respectively. These precisions should be compared to the range of [Fe/H] (about 1.5 dex) and [α/Fe] (about 0.45 dex) of abundances found in the Disk, which illustrates that moderate resolution spectroscopy is very useful for isolating abundance-selected subsamples of stars in the Disk.

3.2.3 Stellar ages

Constraints on stellar ages are of course tremendously precious information for understanding the formation of the Disk, yet are very hard to obtain in practice. The review by Soderblom (2010) provides an excellent exposition of these issues, and we only summarize a few salient points here. For the large samples under discussion here, the absolute age calibration is not the highest priority, but the aim is to provide age constraints, even if only relative-age constraints, for as many stars as possible. In the terminology of Soderblom (2010), it is the ‘model-based’ or ‘empirical’ age determinations that are relevant here: three categories of them matter most for the current context (0.5 Gyr≤t _age≤13 Gyr), depending on the type of stars and the information available. First, the chromospheric activity or rotation decays with increasing age of stars, leading to empirical relations that have been calibrated against star clusters (e.g., Baliunas et al. 1995), especially for stars younger than a few Gyr. Soderblom et al. (1991) showed that the expected age precision for FGK stars is about 0.2 dex. Second, stellar seismology, probing the age-dependent internal structure can constrain ages well; the advent of superb light-curves from the Kepler mission, has just now enabled age constraints—in particular for giant stars—across sizable swaths of the Disk (Van Grootel et al. 2010).

The third, and most widely applicable approach in the Disk context, is the comparison between isochrones and the position of a star in the observational or physical Hertzsprung–Russell diagram, i.e., the L (or logg)–T _eff,[Fe/H] plane (see Fig. 5). Ideally, the set of observational constraints for a star, {data}_obs, would be precise determinations of {data}_obs={L,T _eff,[Fe/H]}, or perhaps precise estimates of logg,T _eff,[Fe/H]. But until good parallaxes to D≥1 kpc exist, L is poorly constrained (without referring to T _eff and [Fe/H] etc.) and the error bars on logg are considerable (≃0.5 dex), leaving T _eff,[Fe/H] as the well-determined observables.

All these observable properties of a star depend essentially only on a few physical model parameters for the star M _∗,[Fe/H],t _age (Fig. 4), and the observables (at a given age) can be predicted through isochrones (e.g., Girardi et al. 2002; Pietrinferni et al. 2004). For any set of observational constraints, the probability of a star’s age is then given by a similar expression as that for photometric distances in Eq. (1) (cf. Takeda et al. 2007; Burnett and Binney 2010):

(2)

where p({data}_obs|M _∗,[Fe/H],t _age) is the probability of the data given the model parameters (i.e., the likelihood); the shape of that distribution is where the uncertainties on the observables are incorporated. Further, not all combinations of M _∗,[Fe/H],t _age are equally likely, since we have prior information on p _p (M _∗|t _age) and p _p ([Fe/H]|t _age). Those prior expectations come from our overall picture of Galaxy formation or from our knowledge of the stellar mass function; also they may reflect the sample properties, when analyzing any one individual star. To be specific, p _p (M _∗|t _age) simply reflects the mass function, truncated at M _∗,max(t _age), if one accepts that there has been an approximately universal initial mass function in the Disk.

The integration, or marginalization, over M _∗ and [Fe/H], of course involves the isochrone-based prediction of observables {params}_ic, as illustrated in Fig. 4, so that

$$ p\bigl(\{\mathrm{data}\}_{\mathrm{obs}}| M_*,[\mathrm{Fe}/\mathrm {H}],t_{\mathrm{age}}\bigr )\rightarrow p\bigl(\{\mathrm{data}\}_{\mathrm{obs}}| \{\mathrm{params}\} _{\mathrm {ic}}\bigl(M_*,[\mathrm{Fe}/\mathrm{H}],t_{\mathrm{age}}\bigr)\bigr), $$

(3)

where {params}_ic could for example be {L,T _eff,[Fe/H]}_ic(M _∗,[Fe/H],t _age).

To get the relative probabilities of different presumed ages, $\mathcal{L}(\{\mathrm{data}\}_{\mathrm{obs}}|t_{\mathrm{age}})$, one simply goes over all combinations of M _∗ and [Fe/H] at t _age and one integrates up how probable the observations are for each combination of M _∗ and [Fe/H]. This has been put into practice for various large samples, where luminosity constraints either come from parallaxes or from logg (see Nordström et al. 2004; Takeda et al. 2007; Burnett and Binney 2010).

The quality of the age constraints depends dramatically both on the stellar evolutionary phase and on the quality of the observational constraints. It is worth looking at a few important regimes, using the isochrones for two metallicities in Fig. 5 as a guide. Note that stars with ages >1 Gyr, which make up over 90 % of Disk, correspond to the last four isochrones in this figure.

(1) For stars on the lower main sequence (where main sequence lifetimes exceed 10 Gyr; L≤L _⊙), isochrone fitting provides basically no age constraints at all; in turn, photometric distance estimates are most robust there. For stars on the upper main sequence, Eq. (2) ‘automatically’ provides a simple upper limit on the age, given by the main sequence lifetime.

(2) For stars near the main-sequence turn-off and on the horizontal branch, the isochrones for a given metallicity are widely spread enabling good age determinations: Takeda et al. (2007) obtained a relative age precision for their stars with logg<4.2 of ≃15 %. Similarly, the parallax-based luminosities of the stars in the Geneva–Copenhagen Survey (GCS) provide age estimate for stars off the main sequence of ≃20 %. Note that the [Fe/H] marginalization in Eq. (2) and the strong metallicity dependence of the isochrones in Fig. 5 illustrate how critical it is to have good estimates of the metallicity: without very good metallicities, even perfect Gaia parallaxes (and hence perfect luminosities) will not yield good age estimates across much of the color–magnitude diagram.

(3) On the red giant branch, there is some L–T _eff spread in the isochrones of a given metallicity; but for ages >1 Gyr the metallicity dependence of T _eff is so strong as to preclude precise age estimates.

Note that the formalism of Eq. (2) provides at least some age constraints even in the absence of good independent L constraints (e.g., Burnett and Binney 2010), as the different stellar phases vary vastly in duration, which enters through the strong M _∗ dependence in Eq. (2).

3.2.4 Interstellar extinction

The complex dust distribution in the Galaxy is of course very interesting in itself (e.g., Jackson et al. 2008), delineating spiral arms, star formation locations, and constraining the Galactic matter cycle. For the study of the overall stellar distribution of the Milky Way, it is foremost a nuisance and in some regimes, e.g., at very low latitudes, a near-fatal obstacle to seeing the entire Galaxy in stars (e.g., Nidever et al. 2012). Unlike in the analysis of galaxy surveys, where dust extinction is always in the foreground and can be corrected by some integral measure A _λ (ℓ,b) (from, e.g., Schlegel et al. 1998), one needs to understand the 3D dust distribution in the Galaxy, A _λ (ℓ,b,D). On the one hand, one needs to know, and marginalize out, the extinction to each star in a given sample, foremost to get its intrinsic properties. On the other hand, for many modeling applications one needs the full 3D extinction information A _λ (ℓ,b,D), also in directions where there are no stars, e.g., in order to determine the ‘effective survey volume’ (see below): it obviously makes a difference whether there are no stars in the sample with a given (ℓ,b,D) because they are truly absent or because they have been extinguished below some sample flux threshold.

Practical ways to constrain the extinction to any given star, given multi-band photometry or spectra, have recently been worked out by, e.g., Bailer-Jones (2011) and Majewski et al. (2011) for different regimes of A _v . In the absence of parallax distances or spectra for the stars, estimates of A _λ (ℓ,b) inevitably involve mapping the stars’ SED back to a plausible unreddened SED, the so-called stellar locus. This de-reddening constrains the amount of extinction, but only through the wavelength variation of the extinction, the reddening.

Estimates of T _eff or L from spectra or from well-known parallax distances, allow of course far tighter constraints, because the dereddened colors are constrained a priori and because also the ‘extinction’ not just the ‘reddening’ appears as constraints.

How to take that star-by-star extinction information, potentially combine it with maps of dust emissivity (e.g., Planck Collaboration et al. 2011), to get a continuous estimate of A _λ (ℓ,b,D) has not yet been established. This task is not straightforward, as emission line maps indicate that the fractal nature of dust (and hence) extinction distribution continues to very small scales. Presumably, some form of interpolation between the A _λ (ℓ,b,D) to a set of stars, exploiting the properties of Gaussian processes, is a sensible way forward.

3.2.5 Towards an optimal Disk survey analysis

The task ahead is now to lay the foundation for an optimal survey analysis that will allow optimal dynamical modeling, by rigorously constructing the PDF for the physical quantities of interest, $\boldsymbol{x}, \boldsymbol{v}, t_{\mathrm{age}}, [\overrightarrow{\mathrm{X}/\mathrm{H}}], M_{*}$ from the direct observables. The preceding subsections show that many sub-aspects of the overall approach (Fig. 4) have been carried out and published; and a general framework has been spelled out by Burnett and Binney (2010). What is still missing is a comprehensive implementation that uses the maximal amount of information and accounts for all covariances, especially one that puts data sets from different surveys on the same footing.

3.3 Existing and current Disk surveys

There is a number of just-completed, ongoing, and imminent surveys of the stellar content of our Galaxy, all of which have different strengths and limitations. Tables 1 and 2 provide a brief overview of the most pertinent survey efforts. The (ground-based) surveys fall into two categories: wide-area multi-color imaging surveys and multi-object, fiber-fed spectroscopy. Broadly speaking, the ground-based imaging surveys provide the angular distribution of stars with complete (magnitude-limited) sampling, proper motions at the ≃3 mas yr⁻¹ level (in conjunction with earlier imaging epochs), and photometric distances; for stars of certain temperature ranges (F through K dwarfs) they can also provide metallicity estimates.

Table 1 Stellar photometric surveys of the Milky Way

Table 2 Stellar spectroscopy surveys of the Milky Way

The ground-based spectroscopic surveys have all been in ‘follow-up’ mode, i.e., they select their spectroscopic targets from one of the pre-existing photometric surveys, using a set of specific targeting algorithms. In most cases, the photometric samples are far larger than the number of spectra that can be taken, so target selection is a severe downsampling, in sky area, in brightness or in color range. The survey spectra provide foremost radial velocities, along with good stellar photospheric parameters, including more detailed and robust elemental abundances.

In this section we restrict ourselves to surveys that have started taking science-quality data as of Summer 2012, with the exception of Gaia.

3.3.1 Individual photometric surveys

• 2MASS (Skrutskie et al. 2006): Designed as an ‘all purpose’ near-infrared (JHK) imaging survey, it has produced the perhaps most striking and clearest view of the Milky Way’s stellar distribution to date with half a Billion stars, owing to its ability to penetrated dust extinction better than optical surveys. Its imaging depth is sufficient to see, albeit not necessarily recognize, modestly extinct giant stars to distances >10 kpc. It has been very successfully used to map features in the Milky Way’s outskirts, e.g., the Sagittarius stream (Majewski et al. 2003) and the Monoceros feature in the outer Disk (Rocha-Pinto et al. 2003). Looking towards the Galactic center, 2MASS has been able to pin down the geometry of the extended stellar bar (e.g., Cabrera-Lavers et al. 2007; Robin et al. 2012b). 2MASS has also provided constraints on the scale heights and lengths of the Disk components (Cabrera-Lavers et al. 2005). It has been the photometric basis for several spectroscopic surveys, in the Disk-context most notably RAVE and APOGEE (see below). However, as a stand-alone survey, 2MASS has been hampered in precise structural analyses of the disk by the difficulties to deriving robust distances and abundances from its data. But 10 years after its completion, it is still the only all-sky survey in the optical/near-IR region of the electromagnetic spectrum. In imaging at ≥10,000 square degree coverage, 2MASS is now being surpassed (by 4 magnitudes) by the Vista Hemisphere Survey (VHS) (McMahon et al., 2012, in preparation).

• SDSS (e.g., York et al. 2000; Stoughton et al. 2002; Abazajian et al. 2009): The primary science goals of the (imaging & spectroscopy) Sloan Digital Sky Survey were focused on galaxy evolution, large-scale structure and quasars, and the 5-band imaging survey ‘avoided’ much of the Milky Way by largely restricting itself to |b|>30^∘. Nonetheless, SDSS imaging has had tremendous impact on mapping the Galaxy (see Fig. 6). Like 2MASS, its impact has been most dramatic for understanding the outskirts of the Milky Way, where its imaging depth (giant stars to 100 kpc, old main-sequence turn-off stars to 25 kpc), its precise colors and its ability to get photometric metallicity constraints (Ivezić et al. 2008) have been most effective. On this basis, SDSS has drawn up a state-of the art picture of the overall stellar distribution (Jurić et al. 2008), drawn the clearest picture of stellar streams in the Milky Way halo (Belokurov et al. 2006), and expanded the known realm of low-luminosity galaxies by two orders of magnitude (e.g., Willman et al. 2005). SDSS photometry and proper motions (δ μ≃3 mas yr⁻¹ through comparison with USNOB, Munn et al. (2004) have allowed a kinematic exploration of the Disk (Fuchs et al. 2009; Bond et al. 2010). However, the bright flux limit of SDSS (g≃15) makes an exploration of the Solar neighborhood within a few 100 pc actually difficult with these data.

  Fig. 6

  

  Stellar number density map of the Disk and halo from Jurić et al. (2008), for K-stars with colors 0.6≤r−i≤0.65. The map, averaged over the ϕ-direction was derived drawing on SDSS photometry, and applying photometric distance estimates that presume (sensibly) that the vast majority of stars are on the main sequence, not giants. Note that for these colors the main sequence stars will sample all ages fairly, as their MS luminosity remains essentially unchanged. With increasing |z| and R, however, the mean metallicity of the stars changes, and the stars within that color range represent different masses and luminosities

• PanSTARRS1 (Kaiser et al. 2010): PanSTARRS 1 (PS1) is carrying out a time-domain imaging survey that covers 3/4 of the sky (δ>−30^∘) in five bands to an imaging depth and photometric precision comparable to SDSS (e.g., Schlafly et al. 2012). PS1 has imaging in the y band, but not in the u band, which limits its ability to determine photometric metallicities. However, it is the first digital multi-band survey in the optical to cover much of the Disk, including at b=0 both the Galactic Center and the Galactic Anticenter.

• SkyMapper (Keller et al. 2007): The Southern Sky Survey with the SkyMapper telescope in Australia is getting under way, set to cover the entire Southern celestial hemisphere within 5 years to a depth approaching that of SDSS. Through the particular choice of its five filters, SkyMapper is a survey designed for stellar astrophysics, constraining metallicities and surface gravities through two blue medium band filters (u,v). Together with PanSTARRS 1, SkyMapper should finally provide full-sky coverage in the optical to g≤21.

• UKIDSS (Lawrence et al. 2007; Lucas et al. 2008; Majewski 1994): A set of near-IR sky surveys, of which the Galactic Plane Survey (GPS) has covered a significant fraction in Galactic latitude at |b|<5^∘ in JHK, 3 magnitudes deeper than 2MASS. It has not yet been used for studies of the overall Disk structure.

3.3.2 Spectroscopic surveys

• Geneva–Copenhagen Survey (GCS) (Nordström et al. 2004): This has been the first homogeneous spectroscopic survey of the Disk that encompasses far more than 1000 stars. For ≃13,000 stars in the Galactic neighborhood (within a few 100 pc) that have Hipparcos parallaxes, it obtained Strömgren photometry and radial velocities through cross-correlation spectrometry, and derived T _eff, [Fe/H], logg, ages, and binarity information from them. It has been the foundation for studying the Galactic region around the Sun for a decade.

• SEGUE (Yanny et al. 2009): Over the course of its first decade, the SDSS survey facility has increasingly shifted its emphasis towards more systematically targeting stars, resulting eventually in R≈2000 spectra from 3800 Å to 9200 Å for ≃350,000 stars. This survey currently provides the best extensive sample of Disk stars beyond the Solar neighborhood with good distances (≃10 %) and good abundances ([Fe/H],[α/Fe]), see Fig. 7.

  Fig. 7

  

  The geometry of ‘mono-abundance populations’ (MAPs), as derived from SDSS/SEGUE data in Bovy et al. (2012d). The figure shows lines of constant stellar number density (red, green and blue) for MAPs of decreasing chemical age (i.e. decreasing [α/Fe] and increasing [Fe/H], with color coding analogous to Fig. 10), illustrating the sequence of MAPs from ‘old, thick, centrally concentrated’ to ‘younger, thin, radially extended’. The figure also puts the SDSS/SEGUE survey geometry into perspective of the overall Galaxy (here represented by an image of NGC 891)

• RAVE (Steinmetz et al. 2006): RAVE is a multi-fiber spectroscopic survey, carried out at the AAO 1.2 m Schmidt telescope, which, as of 2012, has obtained R≈7000 spectra in the red CaII-triplet region (8410 Å<λ<8795 Å) for nearly 500,000 bright stars (9<I<13). RAVE covers the entire Southern celestial hemisphere except, regions at low |b| and low |ℓ|. The spectra deliver velocities to ≤2 km s⁻¹, T _eff to ≃200 K, logg to 0.3 dex, and seven individual element abundances to 0.25 dex (Boeche et al. 2011). At present, precise distance estimates, even for main-sequence stars, are limited by the availability of precise (at the 1–2 %-level) optical colors.

• APOGEE (Allende Prieto et al. 2008): The APO Galactic Evolution Experiment (APOGEE), is the only comprehensive near-IR spectroscopic survey of the Galaxy; it started in the Spring of 2011 taking R≈22,500 spectra in the wavelength region 1.51 μm<λ<1.70 μm for stars preselected to likely be giants with H<13.8 mag. It aims to obtain spectra for eventually 100,000 stars that yield velocities to better than 1 km s⁻¹, individual element abundances and logg; the APOGEE precisions for $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ and logg have yet to be verified. The lower extinction in the near-IR A _H ≃A _V /6 enables APOGEE to focus on low latitude observations, with the majority of spectra taken with |b|<10^∘.

• Gaia-ESO (Gilmore et al. 2012): The Gaia-ESO program, is a 300-night ESO public survey, which commenced in early 2012, and will obtain 100,000 high-resolution spectra with the GIRAFFE and UVES spectrographs at the VLT. It will sample all Galactic components, and in contrast to all the other surveys, will obtain an extensive set of analogous spectra for open clusters with a wide rage of properties; this will constitute the consummate calibration data set for ‘field’ stars in the Disk. The stars targeted by Gaia-ESO will typically be 100-times fainter than those targeted by APOGEE, including a majority of stars on the main sequence; however, taking spectra at ≈0.5 μm, Gaia-ESO will not penetrate the dusty low-latitude parts of the Disk.

• LAMOST (Deng et al. 2012): The most extensive ground-based spectroscopic survey of the Galaxy currently under way is being carried out with the LAMOST telescope. The Galactic Survey, LEGUE, has just started towards obtaining moderate-resolution spectra (R≈2000) for 2.5 million stars with r≤18. In the context of the Disk, LEGUE is expected to focus on the Milky Way’s outer disk, carrying out the majority of its low-latitude observations towards the Galactic anticenter.

3.3.3 The survey road ahead: Gaia

Gaia is an astrometric space mission currently scheduled to launch in September 2013 that will survey the entire sky down to 20th magnitude in a broadband, white-light filter, G. A recent overview of the spacecraft design and instruments, and the expected astrometric performance is given in de Bruijne (2012); the expected performance of Gaia’s stellar parameters and extinction measurements is given in Liu et al. (2012). For Disk studies in particular, Gaia will obtain 10 percent measurements of parallaxes and proper motions out to about 4 kpc for F- and G-type dwarfs, down to (non-extinguished) G≃V=15, for which the Gaia spectro-photometry also provides line-of-sight velocities good to ≃5 to 10 km s⁻¹ and logg and [M/H] good to 0.1 to 0.2 dex. Overall, Gaia will observe approximately 400 million stars with G _RVS<17—where G _RVS is the integrated flux of the Radial Velocity Spectrometer (RVS)—for which line-of-sight velocities and stellar parameters can be measured (Robin et al. 2012a).

While high-precision samples from Gaia will provide an enormous improvement over current data, it is important to realize that most Gaia projections are in the non-extinguished, non-crowded limit and Gaia’s optical passbands will be severely hampered by the large extinctions and crowding in the Galactic plane. In practice, this will limit most Disk tracers to be within a few kpc from the Sun, and Gaia will in particular have a hard time constraining large-scale Disk asymmetries that are only apparent when looking beyond the Galactic center (the ‘far side’ of the Galaxy, D≥10 kpc,|ℓ|<45^∘). Gaia’s lack of detailed abundance information beyond [M/H] also means that it probably will need to be accompanied by spectroscopic follow-up to reach its full potential for constraining Disk formation and evolution. Some follow-up is being planned (e.g., 4MOST; de Jong 2011), but no good studies of the trade-offs between, for example, sample size and abundance-precision have been performed to date.

4 From surveys to modeling: characterizing the survey selection functions

Spectroscopic surveys of the Milky Way are always affected by various selection effects, commonly referred to as ‘selection biases’.³ In their most benign form, these are due to a set of objective and repeatable decisions of what to observe (necessitated by the survey design). Selection biases typically arise in three forms: (a) the survey selection procedure, (b) the relation between the survey stars and the underlying stellar population, and (c) the extrapolation from the observed (spatial) volume and the ‘global’ Milky Way volume. Different analyses need not be affected by all three of these biases.

In many existing Galactic survey analyses emphasis has been given—in the initial survey design, the targeting choices, and the subsequent sample culling—to getting as simple a selection function as possible, e.g. Kuijken and Gilmore (1989a), Nordström et al. (2004), Fuhrmann (2011), Moni Bidin et al. (2012). This then lessens, or even obviates the need to deal with the selection function explicitly in the subsequent astrophysical analysis. While this is a consistent approach, it appears not viable, or at least far from optimal, for the analyses of the vast data sets that are emerging from the current ‘general purpose’ surveys. In the context of Galactic stellar surveys, a more general and rigorous way of guarding against these biases and correcting for them has been laid our perhaps most explicitly and extensively in Bovy et al. (2012d), and in the interest of a coherent exposition we focus on this case.

Therefore, we use the example of the spectroscopic SEGUE G-dwarf sample used in Bovy et al. (2012d)—a magnitude-limited, color-selected sample part of a targeted survey of ≃150 lines of sight at high Galactic latitude (see Yanny et al. 2009). We consider the idealized case that the sample was created using a single g−r color cut from a sample of pre-existing photometry and that objects were identically and uniformly sampled and successfully observed over a magnitude range r _min<r<r _max. We assume that all selection is performed in dereddened colors and extinction-corrected magnitudes. At face value, such a sample suffers from the three biases mentioned in the previous paragraph: (a) the survey selection function (SSF) is such that only stars in a limited magnitude range are observed spectroscopically, and this range corresponds to a different distance range for stars of different metallicities; (b) a g−r color cut selects more abundant, lower-mass stars at lower metallicities, such that different ranges of the underlying stellar population are sampled for different metallicities; (c) the different distance range for stars of different metallicities combined with different spatial distributions means that different fractions of the total volume occupied by a stellar population are observed.

We assume that a spectroscopic survey is based on a pre-existing photometric catalog, presumed complete to potential spectroscopic targets. The survey selection procedure can then ideally be summarized by (a) the cuts on the photometric catalog to produce the potential spectroscopic targets, (b) the sampling method, and (c) potential quality cuts for defining a successfully observed spectrum (for example, a signal-to-noise ratio cut on the spectrum). We will assume that the sampling method is such that targets are selected independently from each other. If targets are not selected independently from each other (such as, for example, in systematic sampling techniques where each ‘N’th item in an ordered list is observed), then correcting for the SSF may be more complicated. For ease of use of the SSF, spectroscopic targets should be sampled independently from each other.

The top panel of Fig. 8 shows the relation between the underlying, complete photometric sample and the spectroscopic sample for the SEGUE G-dwarf sample. While the sampling in color is close to unbiased, the sampling in r-band magnitude is strongly biased against faint targets because of the signal-to-noise ratio cut (>15 in this case).

Fig. 8

Spectroscopic survey selection functions: this figure illustrates two essential elements of the selection functions in spectroscopy surveys that must be accounted for rigorously in analyses of spectroscopic surveys of stars in the Galaxy. The specific case is taken from Bovy et al. (2012d) and discussed in Sect. 6.3. The left panel shows in grayscale the number density of stars with SDSS photometry (presumed to be complete) within the G-dwarf target selection box in (r,g−r) space; the contours show the distribution of stars that resulted in successful spectroscopic catalog entries (the spectroscopic completeness), after ‘bright’ and ‘faint’ plates were taken (see Bovy et al. 2012d) obviously the distributions differ distinctly, as also the marginalized histograms show. The right panel shows the fraction of ‘available’ G-dwarf targets that were assigned fibers; clearly that fraction varies dramatically with Galactic coordinates

The selection function can then be expressed as a function S(r) of the relevant quantities r from the photometric catalog; this function expresses the relative fraction of entries in the spectroscopic catalog with respect to the complete photometric catalog, as a function of r. We will not concern ourselves here with how this function is derived for the spectroscopic survey in question; an example is given in Appendix A of Bovy et al. (2012d) and Fig. 8. We assume that the SSF is unbiased in velocity space, that is, that all velocities have equal probability of being observed, such that the SSF only affects analyses concerned with the spatial densities of objects. If we then want to infer the spatial density in x≡(R,z,ϕ) of a set of spectroscopic objects, we need to constrain the joint distribution λ(θ) of r, x, and whichever other parameters f are necessary to relate x to r (for example, when photometric distances are used, the metallicity can be used in addition to purely photometric properties to calculate x); we denote all arguments of λ as θ≡(r,x,f). The joint distribution can be written as

$$ \lambda(\boldsymbol{r},\boldsymbol{x},\boldsymbol{f}) = \rho(\boldsymbol{r},\boldsymbol{f}|\boldsymbol{x})\nu_*(\boldsymbol{x})|J| S(\boldsymbol{r} ), $$

(4)

where ρ(r,f|x) is the distribution of r and f as a function of x, and |J| is a Jacobian, transforming from the heliocentric frame to the Galactocentric one. As discussed in Bovy et al. (2012d), the correct likelihood to fit is

$$ \mathcal{L} = \prod_i \frac{\lambda(\theta_i)}{\int\mathrm {d}\theta \lambda(\theta)}, $$

(5)

where the product is over all spectroscopic data points. This likelihood simply states that the observed rate is normalized over the volume in θ space that could have been observed within the survey selection constraints as expressed by the SSF.

For example, in the SEGUE example discussed above, we may further assume for simplicity that the distance is obtained simply as d(r,g−r) (that is, ignoring the metallicity, such that there are no f) with no uncertainty, and that the distribution of colors g−r is uniform over the observed color range, then λ(θ) can be written as

$$ \lambda(r,g-r,\boldsymbol{x}) = \delta\bigl(r-r[\boldsymbol{x},g-r,\ell,b]\bigr)\nu _*(\boldsymbol{x})|J|S(r,g-r,\ell,b), $$

(6)

where l and b are Galactic longitude and latitude, respectively; δ(r−r[x,g−r,ℓ,b]) is a Dirac delta function that expresses the photometric distance. The likelihood then reduces to

$$ \mathcal{L} \propto\prod_i \frac{\nu_*(\boldsymbol{x}_i)}{\int \mathrm{d}d \,\mathrm{d}(g-r) \mathrm{d} l\,\mathrm{d}b\nu_*(\boldsymbol{x}(r,g-r,\ell,b))|J|S(r,g-r,\ell ,b)}, $$

(7)

where we have assumed that we only want to fit parameters of ν _∗ (such that the SSF can be dropped from the numerator). For a survey of a limited number of lines of sight such as SEGUE, the integral over l and b can be re-written as a sum over the lines of sight.

Assuming that the SSF does not depend on the velocity, fitting a joint distribution function model for the positions and velocity, for example when fitting dynamical models to data, uses a similar expression, with the density ν _∗ simply getting replaced by the distribution function, and the integral in the denominator in Eq. (5) includes an additional integration over velocities v. For example, in the context of the simplified SEGUE example, we fit a DF f(x,v|p) with parameters p using the likelihood

$$ \mathcal{L}(\boldsymbol{p}) = \prod_i \frac{\boldsymbol{f}(\boldsymbol{x}_i,\boldsymbol{v}_i|\boldsymbol{p})}{\int \mathrm{d}r\, \mathrm{d}(g-r) \mathrm{d} l\,\mathrm{d}b\,\mathrm{d}\boldsymbol{v}\boldsymbol{f}(\boldsymbol{x}(r,g-r,\ell ,b),\boldsymbol{v}|\boldsymbol{p})|J|S(r,g-r,\ell,b)}. $$

(8)

Correcting for selection bias (b) requires stellar-population synthesis models, to connect the number of stars observed in a given color range to the full underlying stellar population. An example where this correction is performed by calculating the total stellar mass in a stellar population given the number of stars in a given color range is given in Appendix A of Bovy et al. (2012b). The total stellar mass is calculated as

$$ M_* = N \langle M \rangle f_\mathrm{M}^{-1}, $$

(9)

where N is the number of stars and 〈M〉 is the average mass in the observed color range, and f _M is the ratio of the total mass of a stellar population to the mass in the observed range. All of these can be easily calculated from stellar-population synthesis models (see Appendix A of Bovy et al. 2012b).

The correction for bias (c) above involves extrapolating the densities of stars in the observed volume to a ‘global’ volume. This is useful when comparing the total number of stars in the Milky Way in different components. For example, Bovy et al. (2012b) calculated for different MAPs the total stellar surface density at the solar radius as the ‘global’ quantity—also correcting biases (a) and (b) above—extrapolating from the volume observed by SEGUE (see below). This extrapolation requires the spatial density of each component to calculate the fraction of stars in the observed volume with respect to the ‘global’ volume. Correcting for this bias is then as simple as multiplying the number of stars in the observed volume by this factor.

5 Dynamical modeling of the Disk

5.1 Goals

To recall from the Introduction, the goals of dynamical modeling in the context of the Disk are two-fold: learn about the gravitational potential, $p(\varPhi(\boldsymbol{x}, t)| \{\overrightarrow{\mathrm{data}}\})$, and learn about the chemo-orbital distribution of Disk stars, $p(\boldsymbol{J},\boldsymbol{\phi},[\overrightarrow{\mathrm{X}/\mathrm{H}}], t_{\mathrm{age}}| \varPhi(\boldsymbol{x},t ))$. The lengthy, explicit notation makes it clear that we need to evaluate the gravitational potential in light of all the data, and that we need to marginalize over the different Φ(x,t) to learn about the orbital distribution. That is, a simultaneous solution for potential and orbits is needed (e.g., Binney and McMillan 2011). This is a challenge that much of the existing dynamical analyses of the Disk have bypassed: when focusing on orbital structure, they have assumed a ‘fiducial potential’ (e.g., Helmi et al. 1999; Klement et al. 2008; Dierickx et al. 2010), or have simplified the treatment of the orbital structure, e.g., by the use of the Jeans Equation (e.g., Just and Jahreiß 2010) or an ad hoc simplified distribution function. Also, basically all dynamical models have focused on steady state models, $\varPhi(\boldsymbol{x}, \not t)$, or Φ(x), an assumption that seems wise to retain until comprehensive equilibrium modeling has actually been implemented.

The gravitational potential near the Disk has conventionally been characterized separately by the ‘rotation curve’, v _c (R) and by the ‘vertical force’ $K_{z}\equiv\frac{\partial\varPhi}{\partial z} (R_{0}, z)$ at the Solar radius, which describes the surface mass density near the mid-plane, Σ(≤z,R ₀). Good basic estimates for both quantities have been in place for two decades, v _c (R)≃225 km s⁻¹ and Σ(<1.1 kpc,R ₀)≃75 M_⊙ pc⁻², with quoted uncertainties at the 10 % to 15 % level. The challenge therefore is to exploit the emerging wealth of data to take this to the next precision level, to obtain analogous constraints over a wider portion of the Disk and to eventually make statements about the non-(axi-) symmetric aspects of the potential. At the same time, one would like to eliminate uncertainties in Φ(x) as a factor in analyzing the stellar orbit (sub-) structure.

These aspects alone imply that a methodology has to be in place to constrain the potential to δΦ/Φ≤0.1. In addition, one should expect that the ability of data sets to discriminate models grows as $\sqrt{N_{\mathrm{data}}}$, where N _data is the number of data points with useful (x,v) information. By now, N _data has reached 10⁵, with Gaia, it will be >10⁷–10⁸: this puts enormous demands on the ‘modeling’ if the information content of the data is to be exploited. As even the Jeans Equation in its simplest (1D) form illustrates, dynamical modeling always involves the link between the gravitational potential, the kinematics of tracers and the (gradients of the) spatial density (ν) of tracers,

$$\frac{\partial(\nu_{\mathrm{tracer}}\sigma_{\mathrm {tracer}}^2)}{\partial r} = -\nu_{\mathrm{tracer}} \frac{\partial \varPhi }{\partial r}; $$

this illustrates the paramount importance of knowing the selection function of any survey, which enters the determination of ν _tracer.

It this context it then also becomes no longer tenable to view the stellar Disk in isolation, as the mass contributions from the dark matter and the ISM must be taken into account.

5.2 Approaches

To date, the majority of constraints on the Galactic potential from Disk stars have been derived through the Jeans Equation (cf. Binney and Tremaine 2008; e.g., Holmberg and Flynn 2004; Bovy and Tremaine 2012; Zhang et al. 2012; see also Sect. 5.3). This approach has been sensible, because for a relatively cold and thin disk, one has a clear prior on the orbital structure: most orbits should be ‘nearly circular’, and the deviations from this can be treated as vertical or in-plane oscillations around a guiding center.

However, solving the Jeans Equations neither delivers a distribution function for the stars, nor can it provide constraints on Φ marginalized over the possible distribution functions; it only can provide a Φ-constraint conditioned on a particular (yet ill-specified) distribution function. Hence, more rigorous modeling approaches that explicitly account for the orbit-nature of the stars are needed in the Disk context, both given the quality of the data and the subtlety of the questions one would like to address. Mostly in the context of modeling external galaxies or star clusters, three ultimately related approaches have been developed over the last decades.

• Methods based on distribution functions: Assuming families of analytic distribution functions, for which p(x,v) can be predicted in a given potential Φ(x) and compared to the data {x,v}. By varying Φ(x) and finding the distribution function whose prediction matches the data in each case, one obtains $\mathcal{L}( \{\boldsymbol{x}, \boldsymbol{v}\}| \varPhi (\boldsymbol{x}) )$; this approach also yields the distribution function, DF_best(Φ _best).

• Orbit-based methods: This entails the prediction of p(x,v|orbit) by explicit calculation of these orbits (‘Schwarzschild method’), where the best potential is found again by varying Φ(x) and optimizing the ‘weights’ of all calculated orbits to match the data. Among the advantages of this approach are that no explicit distribution function needs to be spelled out, which is difficult to do in, e.g., non-axisymmetric potentials; among the disadvantages is that it is difficult to ensure that the distribution function-space has been well-sampled by the discrete orbits. This approach has been implemented by Rix et al. (1997), Gebhardt et al. (2003), and van den Bosch et al. (2008).

• Particle-based methods: Iteratively modifying a self-consistent N-body model, so that its predictions increasingly better match a set of given observations (‘made-to-measure’). This approach has the advantage that no orbit library needs to be stored and that it makes no explicit symmetry assumptions; at least in simple cases, it is shown to recover the correct distribution function. However, by its particle nature, its outcome is only one specific particle sampling of the underlying distribution function. This approach has been originally devised by Syer and Tremaine (1996), and its practical applications for galaxy modeling have been pursued foremost by Gerhard and collaborators (e.g., Morganti and Gerhard 2012).

5.2.1 Data-model comparison in dynamical modeling

Modeling the Disk also calls for data vs. model comparisons that differ from those most commonly used in stellar dynamical modeling. Usually, the data-model comparison is presented by comparing the surface-brightness, mean-velocity and velocity dispersion profiles with data that have been binned or never been resolved into individual stars. The case of the Disk, or most other parts of the Milky Way, is of course different, in at least two respects: first, the data are obtained star-by-star, where each star has uncertainty estimates for each of its phase-space coordinates; second, our position within the disk means that the direct dynamical observables $\{\overrightarrow{\mathrm{data}}\}\equiv p(v_{\mathrm{los}}, \boldsymbol{\mu},\ell,b,D)$ map into very different components of (x,v)_GC. Further, the Sun’s motion with respect to the Galactic rest-frame system and with respect to any sensible local corotating reference frame (‘standard of rest’) is still under considerable debate (e.g., Schönrich et al. 2010; Bovy et al. 2012a). This enters into the (v _los,μ,ℓ,b,D)↦(x,v)_GC transformation, Finally, the size of the uncertainties in (v _los,μ,ℓ,b,D) will vary dramatically among sample members, e.g., if some sample stars have v _los measurements and others do not.

While this calls for an approach beyond comparing tracer density and dispersion profiles, a data-model comparison is still straightforward for any model that predicts n _∗(x,v), or ν _∗(x) and p(v|x), for a given Φ(x). Rather than asking models to match binned moments of the observables, ν _∗(R,z) and σ _R/ϕ/z (R,z), one simply calculates the likelihood of the individual data $\mathcal{L}(\{\mathrm{data}\}^{N_{*}}_{i=1}|\mathrm {model})$, see Bovy et al. (2012d).

5.3 Recent results

In light of the vastly better data, the recent progress in understanding the dynamical properties of the Milky Way and the local (few kpc) Galactic potential may seem disappointing: the debate around the ‘circular velocity at R ₀’ has not abated, nor have the constraints on the stellar and DM mass distribution near R ₀ been tightened by significant factors. Before sketching the road towards comprehensive dynamical modeling (Sect. 7), it is worth looking at some of the recent results to describe the status quo, first for v _circ(R) then for K _z (z|R ₀).

5.3.1 The Disk’s ‘circular velocity’

Characterizing the Milky Way’s central mass distribution by its circular velocity has tradition and is (operationally) sensible. For an axisymmetric galaxy, v _circ(R) is simply $\sqrt{R \partial\varPhi / \partial R (R,z=0)}$. The ‘rotation curve’, especially v _circ(≃R ₀), can be constrained in many different ways: by considering the reflex motion of the Galactic Center (e.g., Ghez et al. 2008; Reid and Brunthaler 2004), by measuring the velocities of globular clusters or halos stars (e.g., Sirko et al. 2004; Deason et al. 2011), considering them to be a non-rotating component, by measuring line-of-sight or 3D velocities to ISM tracers (Fich et al. 1989; Reid et al. 2009), presumed to be on near-circular orbits, by determining an overall mass model for the Galaxy and its halo and interpolating inferences to (R ₀,z=0) (e.g., Xue et al. 2008; Koposov et al. 2010; McMillan 2011), or by mapping and modeling the stellar velocities across a sufficiently large portion of the Disk (Bovy et al. 2012a; Schönrich 2012). Over the last years, this has led to (published) estimates of v _circ(≃R ₀), ranging from 215 to 255 km s⁻¹, with seemingly little progress since the IAU recommended a value of 220 km s⁻¹, nearly 30 years ago (Kerr and Lynden-Bell 1986).

This range of values, given the precision that the data seemingly can offer, can be traced to the fact (a) that the Sun’s motion with respect to v _circ(R ₀) is uncertain at the ≃10 km s⁻¹ level, (b) that the Galactic potential is not axisymmetric presumably at the ≃5 % level, and (c) that (hence) cold tracers do not move on circular orbits. Judging from external galaxies (e.g., Rix and Zaritsky 1995), non-axisymmetries in the gravitational potential at R ₀ in a Milky-Way-like galaxy are expected to be at the 5 to 10 % level, with causes ranging from lopsidedness (m=1), to spiral arms in the stellar disk mass distribution, to bars in the center, and potentially asymmetric dark-matter halos. This leads to smooth azimuthal variations in v _ϕ of closed orbits, the closest equivalent to v _circ. As of now, the majority of the analyses have focused on the nearby half of the Disk, or the local quadrant. This makes analyses susceptible to such asymmetries and makes it hard to test for them. The observability of ISM tracers, such as masers (Reid et al. 2009), depends potentially strongly on their orbital phase. Therefore the assumption that the orbital phases are random, underlying most analyses, is poorly justified. In principle, stars are better tracers of a ‘smooth rotation curve’, as their finite kinetic temperature reduces their response to non-axisymmetric potential perturbations. For them, however, a model accounting for their velocity dispersion, and corresponding lag in v _ϕ , the asymmetric drift must be made (see Bovy et al. 2012a).

In the context of axisymmetric models, Bovy et al. (2012a) has analyzed new stellar radial velocities and approximate distances from the APOGEE survey, and has extensively explored and accounted for a wide range of uncertainties and model assumptions. They find a rotation curve that is very close to flat and has v _circ=218±6 km s⁻¹. They show that this result is consistent with all other existing determinations. The analysis, however, implies two perhaps surprising results: first, that the radial velocity of the stars does not decline towards greater galacto-centric distances; second, that the Sun’s azimuthal velocity, v _ϕ , is 24 km s⁻¹ higher than v _circ(R ₀). The main remaining model limitation in Bovy et al. (2012a)’s approach is that the possible consequences of non-axisymmetries have not been thoroughly explored, not even the known ones that must arise from the Galactic bar.

5.3.2 The potential perpendicular to the Disk

The second focus of dynamical Disk modeling has been the study of the gravitational potential perpendicular to the Disk at ≃R ₀. Broadly speaking, K _z (z)≡|∂Φ/∂z(R ₀,z)| is expected to vary linearly for small z (≃200 pc), as the enclosed (presumably) stellar surface mass density Σ _∗(<|z|) grows linearly; for |z| above the dominant layer of Disk mass, the K _z -profile is expected to flatten, as for plane parallel geometry one has K _z (z)→ const. for Σ _∗(<|z|)= const. Once, or if, a spheroidal dark-matter distribution becomes dominant while |z|≪R ₀ still approximately holds, one expects again K _z (z)∝z; for a given radial dark-matter profile, ρ _DM(r), the relation K _z (z)∝ρ _DM(R ₀,z=0)×z provides a constraint on the local dark-matter density.

Building on the seminal work of Kapteyn (1922) and Oort (1932), who coined the term K _z -force, the analysis of Kuijken and Gilmore (1989a, 1989b) has set the standard for such an analysis for decades. They adopted a parameterized 1D vertical force law of the form

$$ K_z(z)= 2\pi G \biggl( \varSigma_{0}\times\frac{z}{\sqrt{z^2+z_h^2}} \biggr) + 4\pi G \rho_{\mathrm{DM}}\times z, $$

(10)

where Σ ₀ is the integrated disk surface mass density at the Sun’s radius (including the contribution from the cold interstellar medium). The thickness of the stellar distribution is described by z _h and the DM density at (R ₀,0) is described by ρ _DM. In order to break the degeneracy between the two K _z -terms that scale linearly with z, it is necessary that 2Σ _0,∗/h _z is substantially larger than ρ _DM, which turns out to be the case.

One the one hand, it is therefore necessary to have observational constraints with |z|≫h _z ; on the other hand the present analysis context is limited by the requirement that a one-dimensional analysis in cylindrical coordinates makes sense: taken together this leads to a vertical range over which constraints are needed of |z _max|≃1 to 4 kpc.

Kuijken and Gilmore (1989a) laid out how to link the observables—the vertical density distribution of tracer particles, ν _∗(z) and their vertical velocity dispersion profile, σ _z (z)—to K _z (z). Their approach and all subsequent ones have exploited variants of the Jeans Equation, where—of course—it is crucial that the radial dependence of all properties is correctly taken into (e.g., Kuijken and Gilmore 1989a; Bovy and Tremaine 2012). These radial terms matter least in the case of a perfectly flat rotation curve near R ₀, which fortunately or fortuitously seems to be an excellent approximation (e.g., Bovy et al. 2012a).

Based on an approximately volume-complete sample of K stars towards the Galactic pole, Kuijken and Gilmore (1989b, 1991) found at the time that the best determined quantity was Σ _<1.1 kpc=71±6 M_⊙ pc⁻², with a likely baryonic disk mass of 48±8 M_⊙ pc⁻², and no evidence, or at least no data-driven need, for disk dark matter near the Sun. A number of conceptually similar analyses have been carried out since (e.g., Flynn and Fuchs 1994; Siebert et al. 2003; Holmberg and Flynn 2004): these confirmed the approximate values for Σ _<1 kpc, and Siebert et al. (2003) obtained a first constraint on the dynamical thickness of the stellar disk layer. All of these studies were inconclusive on estimating local dark matter, as the data could neither rule out ρ _DM=0 nor ρ _DM≃0.06–0.12 M_⊙ pc⁻³, the value expected for the inward extrapolation of global dark matter halo fits (e.g., Xue et al. 2008; Deason et al. 2012).

This has recently changed, as three studies have claimed significantly non-zero ρ _DM estimates from K _z -type experiments. Garbari et al. (2012) reanalyzed literature data, but properly marginalized over a number of assumptions and parameters in previous analyses, and inferred $\rho_{\mathrm{DM}}=0.025^{+0.013}_{-0.014}~\mathrm{M}_{\odot }~\mathrm{pc}^{-3}$, potentially indicating a flattened halo. Bovy and Tremaine (2012) reanalyzed a set velocity measurements and errors for ≃400 stars with distances and kinematics assembled by Moni Bidin et al. (2012), and obtained an estimate of 0.008±0.003 M_⊙ pc⁻³ (where the uncertainties should also incorporate a systematic component); despite the modestly sized sample this local dark-matter constraint was enabled by the large vertical extent of the tracer stars (≃4 kpc), which sample high above the disk.

All of these analyses had to carefully model the metallicity (selection) distribution of the stars, as the vertical density profile and effective σ _z dispersion depend sensitively on the abundance mix of the sample stars (see Sect. 6.2). Zhang et al. (2012) tackled this limitation, by analyzing the K _z (z)-force problem considering and fitting abundance-selected, nearly isothermal subsamples separately. Using ≃9000 K-type dwarfs from SDSS/SEGUE, they found 0.0065±0.0025 M_⊙ pc⁻³, which in conjunction with Bovy and Tremaine (2012) yields ρ _DM=0.0075±0.0021 M_⊙ pc⁻³, or 0.28±0.08 GeV cm⁻³.

They also obtained Σ _<1.1 kpc=68±6 M_⊙ pc⁻², consistent with Kuijken and Gilmore (1991) and other previous results. It may seem startling that the error bars have not become substantially smaller. However, recent determinations have fitted directly for many more aspects of the model, rather than simply assuming a prior value, which broadens their confidence limits, even with larger samples. For example, Zhang et al. (2012) determined not only the tracer scale-heights consistently, but also fitted the Disk’s effective mass scale height, finding 100 pc<z _h<350 pc.

To date, the dark-matter constraints from K _z (z) analyses corroborate other evidence (see Fig. 9), but are not yet better than other approaches. This should to change in the near future, as we outline below.

Fig. 9

The (vertical) Galactic potential at the Solar radius. This figure, taken from Zhang et al. (2012) summarizes various estimates for Φ(z|R _⊙): the left panel shows various estimates of K _z (z), where the initial steep rise of K _z (z) reflects the stellar and gaseous disk mass, and the slope beyond ≃1 kpc reflects the local dark-matter density: the red lines show the results from Zhang et al. (2012) with the best fitting ρ _DM (solid line) and with ρ _DM≡0.008 M_⊙ pc⁻³ from Bovy and Tremaine (2012) (dashed line); the fat portions of the red lines show the |z|-range that are directly constrained by the SEGUE data. The dashed line shows the result from Kuijken and Gilmore (1991), the gray dash-dotted line for z<1.5 kpc the result from Holmberg and Flynn (2004), and the dash dotted line beyond z≃1.5 kpc the result from Bovy and Tremaine (2012). The right panel illustrates recent estimates of the implied local dark-matter density: Garbari et al. (2012) in blue, Bovy and Tremaine (2012) in black, and Zhang et al. (2012) in red; the open histogram shows the joint probability of these estimates

6 New ways of looking at the Milky Way’s stellar Disk

6.1 Mono-abundance sub-populations

We now lay out in more detail why we believe that dissecting the Disk in terms of ‘mono-abundance stellar populations’ (MAPs), i.e. in terms of stellar subcomponents with very similar abundances (e.g. [Fe/H] and [α/Fe]), is a productive way forward, both for studying galaxy evolution and for dynamical modeling. We do so by synthesizing a number of recent results. We also show that for the most part this new (or, newly implemented) way of looking at the Disk is largely consistent with a range of earlier results when properly compared.

Work over the last 30 years has shown that the Disk is complex, with stars of different ages and abundances showing a different dynamical structure (e.g., Gilmore et al. 1989). To simplify the problem of understanding the Disk, it is sensible to dissect it into different components. A dissection into a thin and a thick disk, either by spatial or by kinematical criteria seems obvious. But the hierarchical assembly and secular evolution processes erase, or at least diffuse, dynamical memory with time (Wielen 1977; Sellwood and Binney 2002; Kormendy and Kennicutt 2004; Schönrich and Binney 2009a; see Sect. 7). Further, any (sub-)sample selection based on spatial or kinematic criteria feeds back into the inferred structure of that component in very complex ways. This leaves ‘age’ and ‘chemical abundances’ $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ as lifelong tags to mark sub-populations (Bland-Hawthorn et al. 2010), and disk subcomponents have long been defined that way (Fuhrmann 2011). Because good age determinations, spanning 1 to 12 Gyrs, are at present only available for tiny volumes (≃10⁻³ kpc³; where parallaxes exist), this leaves ‘mono-abundances’ criteria as the sub-population marker of choice for the near future. Of course, abundances and ages are linked through chemical enrichment, making ‘mono-abundances’ a sensible, albeit qualitative, proxy for mono-age populations, an issue which we explore in Sect. 7. The concept of MAPs is different from a mere abundance-based thin–thick disk distinction on the basis of abundances: it presumes nothing about the spatial or kinematic properties of stars at a given $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$, nor does it presume that there is a small number of distinct components.

As we will see, the consideration of MAPs allows quite direct inferences about galaxy formation, but it has also two advantages for dynamical modeling: first, in dynamical modeling it is convenient to have tracer populations that have simple orbit distribution function properties, which MAPs turn out to have. Second, all MAPs live in the same gravitational potential, and hence provide opportunities to cross-check dynamical inferences (cf. Sect. 5.3.2).

6.2 Properties of the Disk’s mono-abundance sub-populations

Following Bovy et al. (2012b, 2012c, 2012d) we now lay out the results of analyzing MAPs in the Disk, drawing on spectra from SDSS/SEGUE.⁴ Again, qualitatively we are asking “What would the spatial, kinematical, and dynamical structure of the Disk look like, if we had eyes only for stars of a particular abundance?” In the present context ‘abundances’ refer to [Fe/H] and [α/Fe] only, both because such data are available from SDSS, and because they describe the bulk of the variation of individual abundances (e.g., Ting et al. 2012a). While the Bovy et al. (2012d) analysis goes well beyond the solar neighborhood (thoroughly probed by the GCS, but it still covers only 6 kpc<R<10 kpc and 0.3 kpc<|z|<2 kpc (see Fig. 7), not the entire Disk). In practical terms, MAPs mean ensembles of stars whose abundances are within ≃0.15 dex in [Fe/H] and ≃0.08 dex in [α/Fe] (Bovy et al. 2012c), leading to about 50 different MAPs in Bovy et al. (2012d). Given the total sample size of ≃20,000 G-type dwarfs in SEGUE, typical MAP sample sizes in Bovy et al. (2012d) were a few hundred.

As laid out in Sect. 2, [Fe/H] and [α/Fe] abundances depend on both the degree of chemical enrichment and the speed with which it occurred. In general, less [α/Fe]-enhanced and more metal-rich stars probably have formed later (e.g., Schönrich and Binney 2009b). In particular for metallicity, the formation radius also plays an important role, as most galaxies show an outward decay in their mean metallicity (see Sect. 7). For language convenience, however, we will simply refer to [α/Fe]-enhanced stars as ‘α-old’, or ‘chemically old’.

6.2.1 The spatial structure of mono-abundance populations

As a main result from the Bovy et al. (2012d) analysis, the spatial structure of the Disk’s MAPs turned out to be remarkably simple over the observed range: fitting a number-density model that is a simple exponential in both the z and the R directions matches the data well. If the model complexity is enhanced to include two vertical scale-heights (a ‘thin’ and ‘thick’ component) the data do not point towards two scale heights of significant mass fractions and significantly different scale heights for any MAP. Therefore, each MAP can be characterized by its scale length R _d , scale height h _z and number-density normalization.

The complexity of the Disk and the power of MAPs comes in when considering the [Fe/H]–[α/Fe]-dependence of these structural parameters: R _d and h _z vary systematically with abundances, in a way that depends both on [Fe/H] and on [α/Fe], as shown in Fig. 10. Broadly speaking, there is a simple trend: chemically older MAPs form thicker disk components with shorter radial scale-lengths. Among the MAPs, the scale-heights range from ≃200 pc, the classical ‘thin-disk’ regime to ≥kpc, the classical ‘thick-disk’ regime. Note that components with h _z ≥200 pc should still be well sampled by SDSS/SEGUE (|z|≥300 pc), while very thin, young components with h _z ≃100 pc could be missed. Similarly, the radial scale lengths of these MAPs vary widely: from R _d ≤2 kpc for the chemically old MAPs, to an essentially flat radial profile, R _d ≥5 kpc for the chemically young MAPs (with solar [α/Fe]) of low [Fe/H]; note that for thin components and large R _d the SEGUE survey geometry is problematic (confined mostly to l>30^∘), as it samples only volumes will above the plane at R≠R ₀.

Fig. 10

Spatial structure of the ‘mono-abundance populations’ (MAPs) in the Disk from Bovy et al. (2012d). Each of the components, characterized by ([Fe/H],[α/Fe]), can be well-described by a simple exponential density profile in both the radial direction and vertical direction. The left two panels show the radial and vertical scales as a function of [Fe/H],[α/Fe]; the right two panels show R _d vs. h _z , as a function of [α/Fe] and [Fe/H], respectively. This figure illustrates that from the chemically old to chemically younger MAPs the structure changes systematical from ‘old, thick, radially concentrated’ to ‘younger, thin, radially extended’, but in a way that cannot be fully captured by [α/Fe] or [Fe/H] alone (cf. Bovy et al. 2012d)

This analysis shows empirically that the Disk contains a continuum of (MAP) stellar components that form a sequence from chemically old, metal-poor, thick, and radially concentrated to chemically young, metal-rich, thin, and radially extended. We compare these results with cosmological simulations in Sect. 7; but even at face value, these results point quite directly towards inside-out growth of the Disk.

On second look, the distribution of the MAPs’ structural parameters has some subtleties: e.g, for a given [α/Fe], the more metal-poor MAPs have longer scale lengths: there is an outward metallicity gradient in the disk. Finally, it is worth noting that R _d and h _z depend on abundances in a way that cannot be captured by any one-dimensional description of the abundances, i.e., by [Fe/H], [α/Fe], or any combination of them alone. This may not be surprising, as birth epoch and birth radius should be reflected in different ways in the two abundance coordinates.

This view of the Disk appears to be on first sight in stark contrast to purely geometric thin–thick Disk decompositions (e.g., Jurić et al. 2008). However, the Bovy et al. (2012d) analysis is the only case to date of a large-scale Disk structure analysis where the disk components have been selected solely by a structure-independent property: [Fe/H]–[α/Fe]. In all other analyses beyond the Solar neighborhood, the disk components have been defined by their geometry, leaving inevitably some level of circularity.

6.2.2 The kinematical structure of mono-abundance populations

Analogously, the kinematical structure of individual MAPs turns out to be simple, in some sense as simple as can be (Bovy et al. 2012c): for each MAP, the velocity dispersions σ _z and σ _R are vertically approximately isothermal: $\sigma_{z,R}(z|R,[\overrightarrow{\mathrm{X}/\mathrm{H}}])\simeq \mbox{const.}$ In particular for σ _z , which Bovy et al. (2012c) have investigated in detail, the degree of isothermallity is remarkable (see Fig. 11): the mean gradient is only |∂σ _z /∂z|=0.2±0.3 km s⁻¹ kpc⁻¹.

Fig. 11

Vertical kinematics of MAPs from Bovy et al. (2012c). The right panel shows the vertical dependence of the vertical velocity dispersion of MAPs: all MAPs exhibit an isothermal vertical profile at an individual level of a few km s⁻¹ kpc⁻¹; jointly they are consistent with being isothermal to 0.3 km s⁻¹ kpc⁻¹. The left panel shows that the vertical velocity dispersion increases when moving from metal-rich, solar [α/Fe] to more metal-poor and/or α-enhanced MAPs, similar to the h _z behavior in Fig. 10

As a function of Galactocentric radius, the dispersions show a slow decrease, $\sigma_{z,R}(R|z,[\overrightarrow{\mathrm{X}/\mathrm{H}}])\propto \exp{(-(R-R_{0})/7~\mathrm{kpc} )}$. This kinematics warrants careful dynamical modeling, but it seems qualitatively plausible that the redial dependence simply reflects the decrease in the restoring force to the disk plane (Bovy et al. 2012c).

Also analogous to the spatial structure, the characteristic velocity dispersion of the MAPs shows a distinct pattern as a function of [Fe/H] and [α/Fe] (Fig. 11): the chemically older and thicker components have higher dispersions, as anticipated from h _z and dynamics (Bovy et al. 2012c).

As mentioned already in Sect. 3.2.2, Bovy et al. (2012c) used the isothermality of MAPs to test the SEGUE abundance precision. This is possible, because the trends of thicker and kinematically hotter components for more metal-poor, [α/Fe]-enhanced MAPs would lead to an increase in vertical velocity dispersion as a function of height when substantial abundance errors lead to abundance mixing in MAPs. Bovy et al. (2012c) show that the degree of isothermality observed for MAPs requires an abundance precision of ≃0.15 dex in [Fe/H] and ≃0.07 dex in [α/Fe], close to the stated SEGUE-pipeline precision.

While the radial velocity dispersion seems to vary rather analogously to the vertical dispersion among the MAPs, there may be qualitative differences in the orbit structures of MAPs (especially at the extremes of [Fe/H]–[α/Fe] space), as pointed out by Liu and van de Ven (2012). Overall, the kinematics of all MAPs are dominated by orbits with relatively high angular momentum (Dierickx et al. 2010; Wilson et al. 2011; Liu and van de Ven 2012), making a denotation of disk, rather than halo sensible.

In summary, each MAP of the Disk has a very simple spatial and kinematical structure, their properties vary widely: the SDSS analysis yields components with σ _z from 15 to 50 km s⁻¹, h _z from 150 pc to 900 pc, and R _d from ≃1.5 kpc to an essentially flat radial profile at R ₀.

6.2.3 The overall structure of the Disk

Deconstructing the overall structure of the Disk into a large set of MAPs is a different approach from slicing the Disk as is commonly done. It behooves one then to explore what this implies for the overall structure of the Disk, when viewed as a superposition of MAPs.

This requires some additional considerations in order to put the different MAPs on the same footing. At first, such components in any survey such as SEGUE are defined at first in terms of the volume corrected number-densities of the sample members. However, any operative sample definition, such as SEGUE’s color cut 0.48<(g−r)<0.55, means that those stars stand in for differing fractions of the stellar mass of their underlying stellar population, depending on their [Fe/H] and t _age (see Sect. 4) By marginalizing over plausible age distributions, one can convert the z-integrated surface density of target stars into a surface mass density of stellar mass (Bovy et al. 2012b; Schlesinger et al. 2011).

Along these lines, Bovy et al. (2012b, Fig. 12) worked out what the surface-mass density distribution of each MAP is at the Solar radius, $\varSigma_{R_{0}} ([\mathrm{Fe}/\mathrm{H}], [\alpha/\mathrm {Fe}])$. As each MAP has a unique scale height h _z , or kinematical temperature σ _z,R , associated with it, one can then answer: How much of the total stellar surface mass density at R ₀ comes from stars with a scale-height h _z (or with a certain σ _z )? If there was a distinct ‘thin’ and ‘thick’ disk, one would expect a bimodal distribution in $\varSigma_{R_{0}} (h_{z})$, with ≃85 % of it in a thin disk peak (with scale heights covering he range h _z ≃100 to 250 pc) and ≃15 % in a thick disk (with h _z ≃700 pc) for a canonical disk decomposition (e.g., Jurić et al. 2008). However, Fig. 13 shows a different picture. There is a continuous distribution of $\varSigma_{R_{0}} (h_{z})$, with no sign of bimodality, a distribution that is quite well-approximated by $\varSigma_{R_{0}} (h_{z})\propto\exp{( -h_{z}/280~\mathrm{pc} )}$. The F distribution of $\varSigma_{R_{0}} (\sigma_{z})$ shows analogous behavior.

Fig. 12

Distribution of stellar element abundances ([α/Fe],[Fe/H]) from Bovy et al. (2012b): the top panel shows the number density distribution of stars as they occur within the SDSS/SEGUE sample; the bottom panel shows the stellar-mass-weighted, |z|-integrated distribution, which is quite dramatically different, illustrating the importance of incorporating the sample selection function and the stellar mass weighting

Fig. 13

The Milky Way has no distinct thick disk. This figure, from Bovy et al. (2012b), shows the stellar surface mass density contributions of individual MAPs (colored symbols), each of which has associated a unique vertical scale height. The black histogram shows the total stellar surface mass density contributions from MAPs with scale height h _z , which is exponentially decaying towards higher h _z , and shows no hint of thin–thick disk bimodality

This shows directly that while the Disk has a wide range of scale heights and temperatures, thinking of only two distinct thin and thick disk components is not consistent with the data: the Milky Way has no distinct thick disk (Bovy et al. 2012b). A few things are important to keep in mind: First, this result was able to emerge because selecting MAPs only by their abundances, and being able to associate a unique scale-height to each star, simply on the basis of its $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$, has enabled a very different look at the Disk. Second, the demonstrated $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ precision of SDSS/SEGUE argues strongly against the smoothly decreasing $\varSigma_{R_{0}} (h_{z})$ distribution as merely a consequence of poor abundance determinations (see also Bovy et al. 2012d). Third, this way of looking at the Disk, as made up from a continuum of components of many different scale heights (or temperatures), does not change the integrated disk properties (mass-weighted σ _z or h _z ), compared to the traditional thin–thick disk dichotomy; it just shows that there is no structural or kinematical dichotomy.⁵

To test for consistency of this picture with previous work, we can ‘re-assemble’ our decomposition of the disk into MAPs into the overall spatial, kinematical, and elemental-abundance structure of the Disk. Gilmore and Reid (1983) determined the overall vertical structure of the Disk in the solar neighborhood out to several kpc and found that it can be represented as the sum of two exponential distributions: a ‘thin disk’ with a scale height of 300 pc and a ‘thick disk’ with a scale height of 1350 pc. Later observations have confirmed this measurement (e.g., Jurić et al. 2008). We can compare the MAP measurements of the Disk’s structure to these studies by synthesizing the overall structure of the Disk—i.e., not split by elemental abundance—by summing the (mass-weighted) contributions from the MAPs. In Fig. 14, we show the overall (mass-weighted) vertical density profile in the Solar neighborhood implied by the MAP measurements. This figure shows that the overall density can be well described by the sum of two exponential distributions, a ‘thin disk’ at low heights and a ‘thick disk’ that starts dominating at heights >1 kpc, even though the distribution is made up of dozens of MAPs with the scale height distribution of Fig. 13. Thus, the MAP decomposition does not conflict with the measurement of Gilmore and Reid (1983), but the decomposition into MAPs based on elemental abundances has allowed a qualitatively somewhat different description of the overall Disk structure to be found; the description in terms of two exponentials can certainly be views as a convenient and well-working fitting function to the mass-weighted structure of the Disk.

Fig. 14

Overall vertical density profile in the Solar neighborhood implied by the MAP decomposition. The full line is the mass-weighted density profile obtained by summing the contributions from the various MAPs (Figs. 10 and 13). The points are a noisy sampling of this density and the straight dashed lines are exponential fits to the low- and high-height ‘data points’. This figure can be directly compared to Fig. 6 of Gilmore and Reid (1983). The sum of the two exponentials is the curved dashed line, which is barely distinguishable from the full line, showing that the Disk’s overall vertical density profile implied by MAPs can still be represented by a two-exponential fitting function

Analogously, in the MAP way of looking at the Disk, any vertical or radial gradients in abundances or kinematical properties arise foremost from the changing contributions of different MAPs at a given (R,z). Of course, given a set of MAPs, one can construct spatial gradients in the population mean of, e.g., metallicity or velocity dispersion. We illustrate for the concrete case of the SEGUE-derived MAPs and for z-gradients that this leads to predictions that are consistent with direct measurements. As an example, Fig. 15 shows that the predicted gradients from the Bovy et al. (2012b, 2012c, 2012d) MAPs and the direct abundance gradients from Schlesinger et al. (2011). Similarly, integrating over all abundances and deriving σ _z (z) leads to a nearly linear rise of the dispersion with height above the plane.

Fig. 15

Comparison of the metallicity gradients implied by the MAP way of looking at the Disk with a direct estimate from Schlesinger et al. (2011)

We can also use the MAP model for the Disk to predict the [Fe/H]–[α/Fe] distribution at |z|≈0. The MAP abundance distribution extrapolated to |z|<50 pc is shown as contours in Fig. 16, where it is compared to the observed distribution from Adibekyan et al. (2012). The [α/Fe] in this figure is the combination measured by SEGUE—$0.5[\mathrm{Mg/Fe}]+0.3[\mathrm{Ti/Fe}]+0.1[\mathrm {Ca/Fe}]+0.1[\mathrm{Si/Fe}]$—and we have subtracted 0.06 from the model’s [α/Fe] to put the [α/Fe] on approximately the same scale. The MAP model, constrained at |z|>300 pc, does a remarkably good job of producing the main features of the |z|<50 pc abundance distribution, except for appearing too metal-poor, which is probably due to an imperfect description of the more metal-rich, |z|<300 pc stellar content.

Fig. 16

Abundance distribution of stars within ≤100 pc based on high-dispersion spectroscopy (based on data form Adibekyan et al. 2012). This figure shows that the distribution of [α/Fe]-abundances appears to be bimodal, albeit not as two disjoint distribution as claimed by Fuhrmann (2011); see discussion in Sect. 6.3

The dissection and subsequent global synthesis of the Disk through MAPs is ultimately an empirical approach that is distinct from synthetic models such as the Besancon model (Robin et al. 2003), Trilegal (Girardi et al. 2005), or the model of Just and Jahreiß (2010), which we do not discuss in detail here. These models build a global Disk model using a mix of stellar populations of different spatial, kinematical, and chemical properties through the application of stellar-population synthesis models and observational relations and correlations between the model variables, such as the age–velocity relation and metallicity gradients. The strength of these synthetic Galaxy models lies in their ability to summarize our current understanding of the Disk into a consistent—if not always dynamically consistent—stellar-populations-based model that can be used to simulate the expected content of new surveys (e.g., Robin et al. 2012a), test Disk analyses on realistic mock data, and provide fiducial or background models for the interpretation of new data.

6.3 The abundance distribution of the Disk stars

Beyond a few 100 pc, the abundance distribution of the Disk has only been studied very recently with sizable samples (Boeche et al. 2011). However, in the immediate Solar neighborhood a number of studies, usually based on the Hipparcos catalog, have revealed quite striking abundance patterns in their samples (especially (Bensby et al. 2003, 2005; Nordström et al. 2004; Feltzing and Bensby 2008; Navarro et al. 2011; Fuhrmann 2011). To be explicit, we take the chemical abundance distribution to be the mass-weighted probability distribution of chemical abundances, $p_{\mathrm{mass}}([\overrightarrow{\mathrm{X}/\mathrm{H}}]|R,z)$ at (R,z). It is worthwhile stating this explicitly, because the published sample abundance distributions often differ (for good reasons) drastically from this p _mass distribution, making a direct comparison difficult if not impossible. In particular, many studies have explicitly included kinematical pre-selections of the target stars (e.g., Bensby et al. 2003, 2011; Feltzing and Bensby 2008); others, e.g. Navarro et al. (2011), are foremost literature compilations without quantitative accounting for the selection function.

Rightfully prominent among these abundance distribution studies are those of Fuhrmann (1998, 2004, 2008, 2011), which assembled an approximately volume-limited sample of about 300 stars within 25 pc of the Sun (i.e., a volume of 6×10⁻⁵ kpc³), with precise individual element abundances from high-resolution spectroscopy. Fuhrmann finds a distribution that is strikingly bimodal in the [Fe/H]–[α/Fe] plane. Recent studies, initially geared at exoplanet searches, have yielded similar information for stars at typical distances of ≃100 pc (Adibekyan et al. 2012): they, too, find a bimodal distribution in the [Fe/H]–[α/Fe] plane, though they do not confirm an actual ‘gap’ in the abundance plane, as Fig. 16 shows. So, detailed abundance studies based on high-resolution spectra show consistently that when nearby samples are split by their motions into those with kinematics typical ‘thin’ and of ‘thick’ disk stars, their abundance patterns are distinctly and clearly different (see also Bensby et al. 2003, 2005; Nordström et al. 2004; Feltzing and Bensby 2008).

The questions remains to which extent this abundance bimodality in itself argues that there is (at least chemically) a distinct thick disk component (cf. Fuhrmann’s work), attributable to an early (thick disk) star-formation epoch in the Galaxy, and a significantly later thin disk formation epoch, with a star-formation hiatus in between. Because in contrast to that view, Schönrich and Binney (2009b) have argued that ([α/Fe]-)abundance bimodality, though no gap, could arise from a perfectly ‘smooth’ star-formation and enrichment history. This is because the [α/Fe]-enhancement fades rather rapidly, once SN Ia enrichment becomes important.

At the moment, excellent abundance information over very small volumes tell a somewhat different story about an abundance dichotomy in the stellar Disk population than the less precise information on 1 kpc scales. The next years, providing accurate abundances for large samples over kpc-scales from APOGEE and Gaia-ESO should sort this out.

In summary, the authors’ view—certainly guided and perhaps tainted by their own work—points towards a structural description of the Disk in terms of an approximately continuous distribution of stellar scale-heights or velocity dispersions, which appears inconsistent with a structural thin–thick Disk dichotomy or clear bimodality. The recent, vastly larger data sets with abundances seem to imply that a thin–thick disk description is too simplistic, rather than being ‘wrong’. Yet, as of this writing, there is no universal acceptance in the community of this view, for understandable reasons: on the one hand, there is a large number of previous results that seem very well explained by a thin–thick disk dichotomy; while for some of these results, consistency with the continuously varying MAP picture has been demonstrated (see above and cf. Fig. 14, and Fig. 15), other previous results still await their comparison with the continuous MAP picture. On the other hand, the element abundance structure in the Solar neighborhood (<100 pc) does show clear evidence for abundance-bimodality, with some data sets pointing towards an actual dichotomy. These have yet to be fully confronted or reconciled with the continuous MAP picture.

A currently open question is whether this MAP view of the galactic disk provides useful and new constraints on the extensive body of chemical evolution models of the disk that has been developed over the last two decades (e.g., Matteucci and Francois 1989; Prantzos and Aubert 1995; Chiappini et al. 2001; Fraternali and Binney 2008; Marinacci et al. 2011). An exploration of this issues is beyond the scope of this review.

Taken together, viewing the Disk as a superposition of MAPs appears as a promising framework for studies ahead, irrespective of the question of a thin–thick dichotomy. In the final section of this review, we will sketch two aspects where MAPs are useful, which will bring us to the initial issues, the implications of Disk studies for dynamics and galaxy formation.

7 Whither Disk studies?

In the closing Section of this review, we now return to the two broad issues laid out in the introduction: First, what steps still need to be taken to understand the 3D gravitational potential near the Disk as well as we can, and to draw optimal inferences about the dark-matter distribution in the Galaxy. Second, how can the empirical description of the Disk be linked to galaxy formation mechanisms? We start by describing emerging approaches towards comprehensive dynamical modeling, followed by illustrative initial comparisons of the Disk structure to cosmological simulations in the framework of MAPs. We end with our best guess of what the conceptual and practical modeling and interpretation challenges are in the Gaia era.

7.1 Towards implementing comprehensive dynamical modeling

Approaches to stringent dynamical modeling of the Disk, which are going beyond the modeling frameworks described, have also greatly progressed foremost owing to J. Binney and P. McMillan. Yet, all the elements still have not yet quite come together to address: what are the best quantitative constraints on the Galactic potential and on the Disk’s distribution function one can derive from the available, or soon available, data? Neither is there a stringent tool for experiment forecasting to address what pieces of observational data are most informative on a given dynamical questions.

These questions require models that are both global, dynamically consistent, and can predict the likelihood of diverse data sets. The following section reflects not only the authors’ thoughts and attempts for a roadmap towards such a modeling machinery, but extensively draws on the work and plans laid out eloquently by Binney and McMillan (Binney 2010, 2012a; Binney and McMillan 2011; McMillan and Binney 2012):

• Given the complexity of the problem, fully dynamically self-consistent models should be implemented in the steady-state, axisymmetric regime first, before proceeding to non-axisymmetric, time-dependent Disk modeling. That alone would provide enormous progress over the status quo. The limitations of such modeling can be straightforwardly tested against mock-data from numerical disk simulations, which have now reached high-enough resolution (≥300 Million particles, e.g., D’Onghia et al. 2012).

• Given the vast number of discrete observational constraints, model predictions need to be continuous in x,v, to directly calculate the likelihood for (discrete) data. This argues for a ‘distribution function based’ approach, rather than a discrete particle or orbit-based representation of the distribution function.

• To make the joint optimization, or sampling, of Φ(x) and distribution function in light of large data sets practical, both Φ(x) and distribution function should be describable by a modest number of parameters. For the gravitational potential this leaves several options: one can describe the potential by a number of discrete, traditional components, such as the bulge, bar, halo, thin disk, thick disk and gaseous disk (e.g., McMillan 2011). Or, as the mono-abundance analysis of Bovy et al. (2012b, 2012c, 2012d) indicates that a sub-division into a few discrete Disk components is not sensible, one can describe Φ(x) in terms of only two parameterized ‘components’, a spheroidal (not spherical) one and a flat, disk-like component, with flexibility in their r, and R,z profiles.

• The family of distribution functions advocated by Binney and McMillan (2011), which is cast in terms of actions appears as a conceptually attractive and now also practical approach. Specifically, a distribution function cast in terms of the radial, azimuthal and vertical actions J≡(J _R ,J _ϕ ≡L _z ,J _z ) of the form

  

  (11)

  seems a sensible choice (Binney 2012a), where λ _J is a set of parameters to describe the distribution function. Elements of λ _J in this case are $\tilde{f}(L_{z})$, C _R (L _z ), and D _R (L _z ) (Ting et al. 2012b). Overall $\tilde{f}(L_{z})$ sets the radial profile of the disk, given Φ(x); C _R (L _z ) and D _R (L _z ) set the radius-dependent disk ‘temperature’ in the radial and vertical direction. Ting et al. (2012b) showed that these distribution function families can reproduce the radial and vertical properties of mono-abundance Disk populations well, demonstrating that suitable simply parameterized families of distribution functions are available.

  While action-based distribution functions are easy and elegant to write down, community acceptance seems to have been hampered by their reputation to be hard (or slow) to calculate, beyond the ‘azimuthal action’, J _ϕ ≡L _z , which is the angular momentum. Recent progress in calculating and testing the accuracy of approximate actions (Solway et al. 2012; Binney 2012b; Sanders 2012) should help overcome this issue.

• ‘Modeling’ requires efficient computation of (x,v)↔(J _R ,L _z ,J _z ), given Φ(x). Clearly, (x,v|Φ(x))→(J _R ,L _z ,J _z ) is easier to calculate, as this does not involve explicit treatment of the orbital angles that complement the actions; in steady-state modeling, the angles are assumed to be distributed uniformly. This argues for modeling approaches that only go computationally from configuration to action space.

• Yet, models need to be evaluated against data in the ‘configuration space’ of observable data, i.e., we have to determine $\mathcal{L}( \{ \mathrm{data}\}|\lambda_{\boldsymbol{J}}, \varPhi(\boldsymbol{x}|\lambda_{\varPhi}))$, with $\{ \mathrm{data}\}=\{p(\boldsymbol{x},\boldsymbol{v},[\overrightarrow{\mathrm {X/H}}],t_{\mathrm{age}})\}_{i}$. This will then inform us about the potential after marginalizing over the distribution function parameters, $\mathcal{L} ( \{ \mathrm{data}\}| \varPhi(\boldsymbol{x}|\lambda_{\varPhi}))$; or about the distribution function after marginalizing over Φ(x), $\mathcal{L}( \{ \mathrm {data}\}| \lambda_{\boldsymbol{J}})$.

• To calculate meaningful likelihoods of the data for different λ _J given Φ(x|λ _Φ ), it is necessary to interpret the distribution function as a probability distribution. This is where in this context the spatial sample selection functions come in (e.g., McMillan and Binney 2012). One approach to incorporating it (McMillan and Binney 2012; Ting et al. 2012b) is to ‘normalize’ the distribution function over the observable volume, f(λ _J )→c _selection⋅f(λ _J ), where

  $$ c_{\mathrm{selection}}^{-1}\equiv\int \mathrm{d}\boldsymbol{x}\,\mathrm{d}\boldsymbol{v} p_{\mathrm {selection}}(\boldsymbol{x}) \cdot f\bigl(\boldsymbol{J}( \boldsymbol{x}, \boldsymbol{v})| \lambda_{\boldsymbol{J}},\varPhi(\boldsymbol{x}|\lambda_\varPhi)\bigr). $$

  (12)

• Of course, the ‘data’, $\{p(\boldsymbol{x},\boldsymbol{v},[\overrightarrow {\mathrm{X}/\mathrm{H}}],t_{\mathrm{age}})\}_{i}$ are not precise points in (x,v), but have uncertainties, or may even be missing in some dimensions. In practice, this implies yet another marginalization over the data’s uncertainties, i.e., an integral over $\delta\boldsymbol{x},\delta\boldsymbol{v},\delta[\overrightarrow {\mathrm{X}/\mathrm{H}}],\delta t_{\mathrm{age}}$. How to do this computationally efficiently and well enough, is yet to be clarified.

• All of the observables of course depend on the Sun’s position and motion, where the aspects of the observed velocities that simply are the Sun’s reflex motion are a notorious source of uncertainty. As recent work has showed, the ‘local standard of rest’ is still under extensive debate: as Bovy et al. (2012a) showed, the Sun’s motion should also be an explicit model parameter.

• Any modeling should exploit the measured chemical abundances as ‘integrals of motion’ that separate sub-populations. In essence, the above procedure should hold for any MAP, with a distinct distribution function for each, but of course the same Φ(x) for all. By adding the log-likelihood contributions from all the MAPs, inferences about Φ(x) should be straightforward.

• Finally, the dynamics of the Disk does not care about the particulars of the various surveys described in Sect. 3.3, which offer observational constraints in different (ℓ,b,D) regimes. Hence models need to be fit simultaneously to data from different surveys. This has happened far too little to date. Again, this should be straightforward, as any given model (distribution function, Φ(x)) can predict the likelihoods for any survey, and data (log-) likelihoods simply have to be added. The practical difficulties lie in the tedious task of compiling the various sample selection functions.

As of now, only initial demonstrations of theses approaches exist, retrieving information from pseudo-data: McMillan and Binney (2012) showed how well the distribution functions of ensembles of 5000 stars could be retrieved, if a priori disjoint thin and thick disk components were presumed. Ting et al. (2012b) explored how well the parameters of a simplified 3D model for the Galactic potential could be retrieved, with mock-survey data that resemble SDSS/SEGUE G-dwarfs; they could show that the shape of the potential could be constrained, but that such constraints are much harder to get than constraints on, say, v _circ.

Overall, the above roadmap shows that basically all elements are in place to do such comprehensive modeling. This suggest that much more can and will be learned about the Galactic potential, drawing on existing data well before the first extensive Gaia releases, even if those stay on their 2012 schedule. This should provide us with a much firmer picture of Φ(x) for the Disk and with a solid base-line distribution function description of the Disk.

7.1.1 Chemo-dynamical substructure in the Disk

A distribution function description of the Disk and its MAPs will also provide a much more sensible basis to characterize deviations from it as “substructure”. Note that substructure can be both ‘clumps’ in action-space as well as in angle space, an aspect that has yet to be explored.

7.2 Mono-abundance populations in a galaxy formation context

A second avenue for the near future is to place the emerging empirical results about the Disk in the context of galaxy formation. Here we outline what we deem to be a promising approach, looking at MAPs in cosmological disk formation simulations. As laid out in Sect. 6, an empirical picture seems to emerge in which the Disk is ‘seen’ to exhibit an age-sequence from ‘thick’ (large h _z ) and centrally concentrated (small R _d ) MAPs to thin and radially extended ones, if [α/Fe] and [Fe/H] can indeed provide an approximate relative age ranking of MAPs in the Disk.

In two ways, this picture qualitatively resonates with well established concepts of galaxy formation. One the one hand, disk galaxy formation should proceed from the inside out (e.g., Mo et al. 1998). On the other hand, there are several reasons why older components of the Disk should be thicker (or have higher velocity dispersion): they may have been born with higher dispersion (Bournaud et al. 2009; Förster Schreiber et al. 2011), they may have been heated by subsequent tidal interactions or satellite infall (e.g., Quinn et al. 1993); outward radial migration appears to conserve approximately the vertical action (not the vertical energy, cf. Schönrich and Binney 2009b), which will slightly thicken the disk portions that have migrated outward and slightly decrease their vertical velocity (Solway et al. 2012; Minchev et al. 2012a).

To push a comparison with expectations in the cosmological context further, predictions of galaxy formation simulations for MAPs are needed. As described in Sect. 2, disk galaxy formation simulations have made enormous strides in producing outcomes that resemble Milky Way like galaxies (Guedes et al. 2012; Martig et al. 2012; Stinson et al. 2013), with dominant flat disks and only a modest fraction of the stars in a central bulge. Some of these simulations also treat the chemical enrichment self-consistently (e.g., Stinson et al. 2013) and these simulations provide an initial, at least qualitative, comparison of MAPs between cosmological simulations and direct Milky Way observations. Recently, Stinson et al. (2013) has carried out such a comparison with the patterns found by Bovy et al. (2012d). As illustrated in Fig. 17, they found remarkable agreement. This figure shows edge-on views of the present-day stellar density distribution in the simulations, sorted according to the $[\mathrm{O/Fe}]$ (as proxy for [α/Fe]). As observed in the Disk, there is a sequence of centrally compact and thick configurations at the $[\mathrm{O/Fe}]$-enhanced end to radially extended, thin distributions at Solar $[\mathrm{O/Fe}]$ values. Quantifying this picture by plotting h _z vs. R _d for MAPs in the simulations, confirms that this simulation shows the same behavior as the data. This agreement lends encouragement to query the simulations about the extent to which mono-abundance populations can serve as proxy for mono-age populations. Figure 18 shows the mean age and the age dispersion as a function of [Fe/H] and [α/Fe] in the simulations. Remarkably, in most mono-abundance bins of these simulations, the age dispersion is ≤1 Gyr, justifying the use of 2D-abundances as age proxies.

Fig. 17

Present-day structure of ‘mono-age populations’ in a cosmological formation simulation that led to a Milky-Way-like galaxy from Stinson et al. (2013), where each panel shows a present-day, edge-on of stellar subsets in the simulations, sorted by their age: there is a clear trend of ‘old, thick, centrally concentrated’ to ‘young, thin, extended’

Fig. 18

How well do MAPs reflect mono-age populations in simulations? This figure from Stinson et al. (2013), whose simulations track chemical enrichment, shows the age dispersion of stars within each (simulated) MAP bin. For most MAPs the age dispersion is less than 1 Gyr, implying that MAPs are reasonably good approximations to mono-age populations

Of course, at present the above is only an anecdotal comparison with one simulation; albeit a state-of-the-art simulation that was ‘tuned’ to match the stellar-mass / halo-mass relation of Moster et al. (2012) at redshift zero, and that produces a large, fairly massive disk and a small bulge, with the spatial and temporal abundance pattern only a consequence of it. Clearly, this kind of data model comparison warrants much further exploration, as we lay out in the final subsection.

Some readers may pine for ‘tests’ of galaxy evolution mechanism that do not depend on comparison with numerical simulations. But such tests may be far and few between, as the present-day dynamical structure mostly tells us about the present day. This can be illustrated by the quest to find tests for the efficacy of radial migration. The Hermes/GALAH experiment (Freeman et al. 2010) has set out to provide such a clean test: the ambition is to identify, through ‘abundance fingerprinting’, stars that were formed basically at the same time with the same orbital actions and phases. If we can look at their orbits (say angular momenta) now, and if we know their ages, then one gets a direct estimate of the importance of radial migration, though still no clear hint about the cause of that migration (bars, spiral arms, satellites, etc.).

7.3 Peripheral Disk issues

The Galactic stellar Disk, as defined here, does of course not live in isolation, but it interfaces with other Galactic ‘components’ at its extremes: with the bar and (pseudo-)bulge at small radii; with the slightly warped, complex, and almost messy outer reaches of the Disk (>12 kpc); and with the Galactic stellar halo, which the data suggest is truly a ‘distinct’ component from the bulk of the Disk (Majewski 1994; Ivezić et al. 2008). We review only briefly the status and prospects in these areas.

• The innermost Disk: Massive late-type galaxies like ours often have bars at the center (Barazza et al. 2008) and a thick central portion that is described as a pseudo-bulge (e.g., Kormendy and Kennicutt 2004); the Milky Way fits that pattern, as it has a large-scale stellar bar (Binney et al. 1991, 1997; Blitz and Spergel 1991; Weinberg 1992). This bar must have formed from stars that were part of the pre-existing Disk, and clear separation between the components is perhaps moot (e.g., Shen et al. 2010). In practice, the present end of the bar is a sensible dividing line, presumably at corotation 2.5±0.5 kpc (Binney et al. 1991). As the patterns speeds of bars change secularly (Debattista and Sellwood 2000), it is unclear—and should be clarified—whether this radius implies any changes in the abundance or age structure.

• The Outer Fringes of the Disk: The stellar disk of our neighbor galaxy, M31, is manifestly frayed in its very outer parts (Ferguson et al. 2002; Ibata et al. 2005), possibly because much of the material is tidally disrupted satellite debris or possibly because disk material has been grossly perturbed by such infall events. There is ample evidence that the outer parts of the Galactic Disk are just as messy: the structure variously known as the ‘anticenter ring’, ‘Monoceros ring’, ‘Canis Major feature’ (Yanny et al. 2003; Martin et al. 2004; de Jong et al. 2010) reflects the fact that there are far more stars at R _GC=15 to 20 kpc (Conn et al. 2012) with |z|>1 kpc than a simple double exponential disk model suggests. This ‘feature’ of the outer Disk has elicited extensive discussion, as two very different (and in the pure form probably simplistic) explanations have been advanced to explain it: either purely as deposited stellar debris from a satellite that had merged on a low-latitude, low-eccentricity prograde orbit (e.g., Peñarrubia et al. 2005), or simply as a combination of a disk warp and flare (e.g., Momany et al. 2006). Because the abundance distribution and kinematics of possible ‘Monoceros ring’ member stars are not grossly different from the expectations for an outer disk, it will take comprehensive area coverage (e.g., from PS1), good distances from Gaia, and extensive spectroscopy (1000’s of stars) yielding velocities and abundances to sort out to which extent these are stars that have been ‘dragged into’ the Disk vs. ‘kicked out of’ the Disk.

7.4 Some specific tasks for the next years

Having described the various elements of gathering, analyzing and (dynamically and cosmologically) modeling stellar Disk surveys, we now try to cast answering some of introductory questions in this review into possible projects that appear feasible and necessary for the next years:

7.4.1 What factors limit dynamical Disk modeling?

With the modeling machinery of Sect. 7.1 in place, at least in principle, all elements have come together to answer this question. The most straightforward approach to doing this is to create mock data sets from N-body simulations of disks that are self-consistent by construction, and feed them though the modeling machinery to see how well Φ(x) and distribution function can be recovered. Recently, non-cosmological simulations of disk galaxies have reached particle sizes of ≃300 Million particles (D’Onghia et al. 2012), where mock-data sets that match the current generation of survey data (RAVE, SDSS, APOGEE, etc.) can be drawn directly without supersampling. Then selection functions, distance estimates with either random or systematic errors, and (appropriate or inappropriate) de-reddening estimates can be applied, where the reddening model would be a version of the currently emerging 3D extinction maps for the Milky Way (cf. Sect. 3.2.4). Deriving probability distribution functions on Φ(x) in light of a suite of mock data sets, would reveal the factors that limit the accuracy of the potential inference. Similar, or even the same, mock-data sets can explore to which extent non-axisymmetry of disk galaxies such as the Milky Way, in particular spiral arms and a central bar, would affect the Φ(x) inferences made under axisymmetric assumptions. In turn, with such analyses one can explore what it would take to, e.g., measure the strength of the spiral arms dynamically. What the mock data, at least in the very high resolution, hence ‘non-cosmological’ simulations, do not easily supply is an ‘abundance tag’ that allows to define MAPs. Hence, the best way to test how much is gained in dynamical analyses by splitting the tracer samples into MAPs still needs to be devised. Current experiments along those lines (Ting et al. 2012b) indicate that the sheer sample size plays a sub-dominant role in constraining the potential in the current regime (≥10⁴–10⁵ stars). Such mock data sets will also be crucial in finding out whether vast numbers of stars with partial phase-space information (e.g., without v _los) have comparable information content than far smaller sets with complete phase-space information.

7.4.2 How to get to the best chemo-orbital distribution function?

In the context of comprehensive dynamical modeling (Sect. 7.1), an estimate of the distribution function of course results ‘automatically’. Yet, the issues of getting an optimal estimate for distribution function are different. On the one hand, slight systematic errors in Φ(x) probably lead to a (smooth) distribution function that looks very similar to the correct one; so to get a sense of whether the vertical action distribution of MAPs varies little with radius (as expected for asymptotically efficient radial migration), an approximate potential probably suffices. On the other hand, it is perhaps distribution function substructure or fine-scale structure that is most interesting. In the limit of a ‘cold stellar stream’, i.e., stars of the same actions that differ only in phase (e.g., Koposov et al. 2010), the most plausible potential may be the one that makes the distribution function of that stream most like a δ-function, even if that potential is not necessarily the most likely in light of the overall set of tracers. Further, sample size, precision of the individual (x,v) estimates, and chemical abundances matter far more than for merely estimating Φ(x). Sample size matters, because diagnostically precious sub-populations (e.g., streams) may only make up a very small fraction of the Disk mass; (x,v)-precision matters, because ‘cold’ substructures, those very compact in distribution function space, are of preeminent interest, and $[\overrightarrow{\mathrm{X}/\mathrm{H}}]$ matters, because the distribution function has to be strictly separable in chemical abundances, which resemble effective separating integrals of motion. Therefore, even with only an initial estimate of distribution function, a full exploration of MAP distribution functions, with the largest possible samples and the most precise phase-space coordinate estimates will be the next step. This is clearly also a direction where dramatic progress using Gaia data will be very straightforward.

7.4.3 The next steps mapping the gravitational potential

Initial attempts have been made to bring the diverse constraints on the Galactic gravitational potential on the same footing (Catena and Ullio 2010; McMillan 2011; Bovy and Tremaine 2012), the outer halo constraints, the rotation curve, and the local dark-matter estimates from K _z (z). But the step of measuring K _z (z) as a function of R _GC, which is feasible even with the existing data from 6 kpc to 12 kpc, is currently missing. Getting the dynamically measured disk mass scale length (presumably over 2 to 3 scale lengths, i.e., an order of magnitude in Σ(R)) will break the ‘disk–halo degeneracy’ and allow us to take strides towards better quantifying the amount of dark matter within R ₀. In constraining the rotation curve, the emerging stellar surveys will eventually allow for testing less constrained models, and the combination of stellar kinematics with good distances and the emerging results from the Galactic maser survey (Brunthaler et al. 2011) will be the most powerful constraints on global asymmetries of the Galactic potential, such a lopsidedness. This is because masers are the most feasible tracer of the rotation curve on the far side of the Galaxy. Untangling the disk and halo contributions to the potential at R≤10 kpc will then permit tighter constraints on the shape of the dark matter and—ultimately—a test for the existence of dark matter (as opposed to alternative gravity laws) on the bases of the shape of the acceleration/potential map alone; such analyses probably require Gaia data, foremost to get very good proper motions to D≃10 kpc.

7.4.4 Closing remarks

In summary, an enormous amount of practical work needs to be carried out and conceptual modeling issues need to be sorted out, even before Gaia data are available. It seems crucial to do this work, even if some aspects (but clearly not all—abundances, radial velocities of faint stars) will be dramatically superseded by Gaia. This is because the currently emerging data will be key in making sure we are asking the right questions of the Gaia data, and think through what the most critical ‘complementary data’ to ESA’s next flagship mission are. In return, the field promises an information revolution that is probably unmatched in the field of galaxy studies in this decade, ALMA and JWST notwithstanding.

But the attentive and persistent reader will have noticed that we have not fully closed the circle on using the Galactic Disk to test ‘mechanisms of disk galaxy formation’. While Sect. 7.2 has sketched some specific examples of how to test aspects of disk galaxy formation by comparing ab initio simulations to the data, it has not tackled head-on some of the broad initial questions (Sect. 2.2): To which extent were stars born (vertically) hot or subsequently heated? Is there testable evidence that the feedback implemented in the simulations actually took place? Can we recognize stellar satellite debris well enough to quantify the fraction of Disk stars with external origin?

That means that also much conceptual work needs to be done. It may serve as a useful compass to thoroughly think about the following scenario: if one had the perfectly ‘analyzed and modeled’ Gaia data (and those from all other surveys) at hand, what are the crispest inferences one could draw about how our Galaxy and other disk galaxies, have formed?