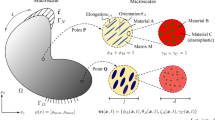
Abstract
In this work, we propose a novel method for predicting stress within a multiscale lattice optimization framework. On the microscale, a scalable stress is captured for each microstructure within a large, full factorial design of experiments. A multivariate polynomial response surface model is used to represent the microstructure material properties. Unlike the traditional solid isotropic material with a penalization-based stress approach or using the homogenized stress, we propose the use of real microscale stress components with macroscale strains through linear superposition. To examine the accuracy of the multiscale stress method, full-scale finite element simulations with non-periodic boundary conditions were performed. Using a range of microstructure gradings, it was determined that 6 layers of microstructures were required to achieve periodicity within the full-scale model. The effectiveness of the multiscale stress model was then examined. Using various graded structures and two load cases, our methodology was shown to replicate the von Mises stress in the center of the unit lattice cells to within 10% in the majority of the test cases. Finally, three stress-constrained optimization problems were solved to demonstrate the effectiveness of the method. Two stress-constrained weight minimization problems were demonstrated, alongside a stress-constrained target deformation problem. In all cases, the optimizer was able to sufficiently reduce the objective while respecting the imposed stress constraint.
Similar content being viewed by others
1 Introduction
In engineering design, maximizing the strength-to-weight ratio of components has always been a primary objective. Reducing the weight of a component under stress constraints can often lead to a significant reduction in costs and increase the performance of the entire assembly. The design methodologies employed in the past were often limited by the manufacturing processes available at the time. Until recently, subtractive manufacturing, where components are manufactured by removing material from a solid block, imposed severe constraints on the design of components, limiting the potential performance improvements that could be made. With the advent of additive manufacturing (AM) processes (Ngo et al. 2018), where components are built layer-by-layer, many of these constraints have been lifted. This has led researchers to reformulate old design methodologies to suit the advantages posed by AM better. Examples of this are multiscale optimization methods. Here, parameterized periodic microstructures are used to vary the material properties throughout a discretized domain. As shown by Ashby (1983), the material properties of periodic microstructures are functions of their relative densities and configuration. By varying the density and microstructure configurations throughout the domain, the extremum of a given objective function, such as compliance, is sought after. Multiscale optimization methods are commonly performed across two scales and can lead to the formation of metamaterials. Here, the macroscale properties are derived from the arrangement of the periodic microstructures, rather than the bulk material properties. Multiscale structures have been shown to exhibit extreme material properties. For example, Sigmund (2000) proposed a class of two- and three-dimensional composite microstructures with bulk moduli close to the theoretical limits, as defined by the Hashin-Shtrikman bounds (Liu 2010).
An ideal optimization framework would possess the ability to go from optimized design straight to manufacture and real-world application with minimal human intervention and limited, if any, post-processing. To enable this, stress is an important factor to consider during the optimization, rather than as an afterthought. Optimized structures without stress considerations are of limited practical use and so the inclusion of stress constraints has been studied extensively for classical topology optimization (TO) problems (Gebremedhen et al. 2019; Yang et al. 2018; de Troya and Tortorelli 2018; Holmberg et al. 2013a, b; Hyun et al. 2013; Bruggi and Duysinx 2012; Le et al. 2010; París et al. 2010). The inclusion of stress in optimization however can be problematic. In TO, the “singularity” problem describes a phenomenon where the optimum solution lies in a degenerate subspace, inaccessible by gradient-based optimization approaches (Sved and Ginos 1968; Cheng and Jiang 1992). Several solutions have been proposed to this, most notably the “qp” method, as introduced by Bruggi (2008), or the ε-relaxation technique proposed by Cheng and Guo (1997). Stress constraints are also problematic due to the local nature of stress. Ideally, stress constraints should be imposed locally, one for each cell, as implemented by Duysinx and Bendsøe (1998). However, this formulation can lead to thousands of constraints depending on the discretization. Due to the highly nonlinear response of stress, computing the gradients of large numbers of stress constraints is very inefficient. Duysinx and Sigmund (1998) proposed the use of a global constraint to overcome this. By aggregating the individual cell stresses throughout the domain into a single value, the computational expense can be greatly reduced. The reduction in effort however comes at a cost to accuracy. As the aggregation function essentially smears the stress distribution, the optimization loses local stress control. Clustered aggregation (París et al. 2010; Holmberg et al. 2013b; Le et al. 2010) approaches aim to provide greater control of the local stresses by splitting the domain into several clusters and computing aggregated stress values for each cluster.
Due to their importance, stress constraints have also been studied within multiscale optimization frameworks. Arabnejad and Pasini (2012) optimized hip implants using graded orthotropic microstructures. By using the homogenized stiffness tensor of the microstructures, the stress on the microstructure resulting from macroscale strains was computed, in order to predict yield. Using the inverse homogenization method, Collet et al. (2018) proposed the use of an energy-based stress method for avoiding stress concentrations in solid isotropic material with penalization (SIMP)-based two-scale TO. While the authors were able to optimize the microstructures to reduce stress concentrations, the macroscale was not considered, and the optimization was performed through the application of arbitrary strain fields. Coelho (2019) also performed optimization on the microscale to optimize microstructures under stress constraints. By using the qp method to avoid stress singularities, the authors performed TO to derive optimal microstructures for various load cases. Yu et al. (2019) developed a stress-constrained optimization for 2D shell-lattice infill structures. The authors proposed the use of two stress constraints, the von Mises yield criterion for the solid outer shell layer and the Tsai-Hill yield criterion, for the lattice infill. Cheng et al. (2019) applied a modified Hill’s yield criterion to optimize structures using a cubic graded lattice subject to stress constraints. Using polynomial functions to generate models of the elastic properties and the anisotropic yield criterion, the authors were able to experimentally validate their models.
In this work, we present a multiscale stress formulation to determine the stress within microstructures without the use of a homogenized stiffness tensor. By introducing a novel, scalable stress matrix, we can determine the stress within the microstructures directly using the macroscale strains. To our knowledge, this has not been achieved in literature to date. For example, in Cheng et al. (2019) and Arabnejad and Pasini (2012), the researchers use the homogenized stiffness tensor term to determine the homogenized stress. In Section 2, we present the microstructure homogenization process to obtain the elastic properties, followed by the introduction of a novel scalable stress measure. Section 3 outlines the numerical validation performed using FEA simulation to determine the accuracy of the multiscale stress model. Finally, in Sections 4 and 5, we apply our methodology to several multiscale optimization problems before drawing conclusions.
2 Homogenization of lattice material properties
In this work, a periodic lattice microstructure, as introduced by Imediegwu et al. (2019), is employed. The lattice is parameterized by the radii of seven cylindrical members within a periodic unit cell. As shown in Fig. 1, four diagonal members (numbered 1–4) connect each opposing vertex of the cell and three members (numbered 5–7) align to the principal axes. By varying the radius of each member individually, the material properties of the microstructure can be altered, which in many cases gives rise to anisotropic material properties.
To derive the material properties of the periodic microstructures, this work leverages the asymptotic homogenization (AH) method (Francu 1982; Bendsøe and Kikuchi 1988). The advantage of using the AH method is the large reduction in the computational expense associated with simulating the periodic structure. Representing the lattice unit cells as homogeneous solids eliminates the need for explicit, full-scale FEA of the multiscale structure during the optimization. The effectiveness of the AH method has been demonstrated widely in topology optimization (Groen and Sigmund 2018; Fan and Yan 2019; Pasini et al. 2018; Yi et al. 2016), composites (Bacigalupo et al. 2016), plate structures (Cai et al. 2014), and several other fields. Furthermore, Wang et al. (2018) were able to confirm the validity of the AH method through FEA and experiments.
The AH method links the macroscale and microscale through their respective characteristic dimensions, often referred to as the slow and fast variables. The slow variable, representing the macroscopic coordinate, is defined as x and the microscopic fast variable is defined as \(\boldsymbol {y} = \frac {\boldsymbol {x}}{\xi }\), where ξ (0 < ξ ≪ 1) indicates the ratio of the size of the periodic unit cell to the macroscale structure. With these variables, a two-scale displacement field can be represented through the asymptotic expansion
where u is the exact displacement field, composed of the macroscopic displacement u0 and the microscopic perturbations caused by the periodic nature of the microscale. Thus, it follows that the displacement field varies ξ− 1 times faster with the microscopic variable y compared with the macroscopic variable x. Provided there is a large scale of separation between the macroscopic and microscopic variables, terms higher than the first order may be neglected, enabling the effective material properties from a periodic microstructure to be imposed on the macroscale. The exact scale of separation required is further examined in Section 3. Due to the layout of the lattice microstructure with independently varying member radii, it is possible to achieve fully anisotropic material properties. The homogenized stiffness tensor EH, containing 21 independent terms can be used to describe the homogenized material properties of the periodic microstructure, defined as
By imposing periodic boundary conditions (PBC) on the microstructure, EH can be obtained by solving the equation (Hollister and Kikuchi 1992; Arabnejad and Pasini 2012)
where E is the stiffness tensor of the microstructure bulk material, Ω is the domain of the microstructure, M is the structural tensor relating the microscopic and macroscopic stress defined as
where \(\overline {\varepsilon }\) and ε are the macroscopic and microscopic strains respectively and δ is the Kronecker delta function. The term ε∗kl corresponds to the microscopic strain field resulting from the kl component of the macroscopic strain tensor. Using the virtual strain (\(\boldsymbol {\varepsilon }^{1}_{ij}(v)\)), the term ε∗kl is then obtained by solving the equation
As linear theory is assumed, \(\boldsymbol {\overline {\varepsilon }}_{kl}\) can be defined as the linear combination of 6 unit strains for three-dimensional problems. In this case, the 6 unit strains are defined using Voigt notation as
For a comprehensive derivation of the homogenization process, the reader is referred to Hollister and Kikuchi (1992).
2.1 Microscale stress
In standard SIMP-based TO, stress is penalized for intermediate design variables in a similar way to the penalisation applied to the stiffness tensor (Duysinx and Bendsøe 1998; Holmberg et al. 2013b; Yang et al. 2018). In stress-constrained lattice-based optimization, the stress has been derived using the homogenized stiffness tensor (Cheng et al. 2019; Arabnejad and Pasini 2012). In this work, we present a method for calculating the real stress within the microstructures using the macroscale strains. Due to the local nature of stress, the homogenized stress results in unreliable stress predictions of the microscale. To ensure more reliable predictions of the microscale stress, a multiscale stress methodology is proposed in this work.
Using the strain fields, ε∗kl, from (6), stress fields within the microstructure can be determined for each strain imposed. Using Hooke’s law, the stress can be obtained from the equation
The stress resulting from each unit strain defined in (7) can then be defined in vector form using Voigt notation as
where σn is the stress resulting from the nth unit strain imposed, as defined in (7). The 6 stress vectors can then be assembled into a stress matrix, Φ, defined as
where each row corresponds to the stress vector σn resulting from the n th strain vector εn. As linear theory is assumed throughout this work, the stress matrix, Φ can be used to calculate the stress within the microstructure as a result of any arbitrary strain imposed on the microstructure. For an imposed strain, \(\boldsymbol {\tilde {\varepsilon }}\), the scaled stresses, \(\overline {\boldsymbol {\Phi }}\), are defined as
where ⊙ indicates row-wise multiplication. It is important to note that the equation above represents scaling of the stresses using the real strains observed on the macroscale. We are able to achieve this as we are assuming linear theory and \(\overline {\varepsilon }\) are unit strains. Finally, to determine the stress vector resulting from the imposed strain, the scaled stresses are superimposed according to
where \(\boldsymbol {\tilde {\sigma }}\) is the stress resulting from an arbitrary strain \(\boldsymbol {\tilde {\varepsilon }}\) imposed on the microstructure. Equations (11) and 12 can be combined and written compactly as \(\boldsymbol {\tilde {\sigma }} = \boldsymbol {\Phi }^{T}\boldsymbol {\tilde {\varepsilon }}\). Due to the large number of microstructures simulated in this work, as discussed in Section 2.2, it is infeasible to store the entire Φ field within each microstructure. To reduce the computational expense, Φ is only stored at the center of the domain for each microstructure. Maximum stresses were also considered as an alternative to storing the stress in the center of the microstructures. However, it was found that a very fine mesh was required to achieve convergence for the maximum stress due to the presence of artificial stress concentrations. These stress concentrations arise from the rapid change in material properties across cell boundaries, combined with the sharp edges that are formed due to the hexahedral mesh used. Although nodal averaging, as shown in Imediegwu et al. (2019), was employed, a very fine adaptive mesh would be required to completely remove the artificial stress concentrations. Due to the vast array of microstructures being simulated as part of the DOE, it is impractical to mesh and simulate the microstructures using such fine meshes. Furthermore, a key criterion that was required from the chosen metric was obtaining smoothly varying gradients. The stress in the center of the domain can be expected to vary smoothly with the change in microstructure permutations. However, due to the local nature of stress, the maximum stress might not appear in the same location for every microstructure permutation, leading to potentially large discontinuous changes in the gradient. While the stress at the center of each microstructure may not predict the exact maximum stress, the main goal of this work is to show that it is possible to replicate the real stress within the microstructures resulting from macroscale strains, and apply these stresses to stress-constrained optimization problems. As the method proposed here relies on capturing the stress at the center of the unit cell, it is only applicable to lattice designs where the material passes through the center of the unit cell. In particular, it requires that all the design variables are defined through the center to ensure it is possible to obtain gradients. However, it may be possible to modify and extend this methodology for use with other unit cell designs, by choosing alternative locations for the stress capture. The accuracy of the stress measure is further examined in Section 3.
2.2 Response surface methodology
The material properties of various permutations of lattice microstructures were determined using FEA simulations. The individual permutations of the microstructures were generated using a full factorial design of experiments (DOE) using 7 levels of radii for each structural member, leading to 77 (823,543) permutations. The radii levels were selected evenly within the range 0.05 ≤ ri ≤ 0.38, allowing for fully dense structures. As shown by Imediegwu et al. (2019), due to the 3 planes of symmetry present within the microstructure, only 40,817 microstructures are unique, known as parent microstructures. The remaining 782,726 child microstructures can be derived using rotations and reflections of their respective parents. By obtaining the material properties for the parent microstructures, the child microstructures can easily be derived, greatly reducing the computational expense of the microstructure simulations. The FEA simulations were carried out using the open-source partial differential equation (PDE) solver FEniCS 2019.1.0 (Alnæs et al. 2015). To avoid remeshing for each microstructure, a fixed hexahedral mesh was used. Following a convergence study of the stiffness tensor and stress terms, the domain was discretized using 1 million equal-sized elements. Cells containing material were assigned a Young’s modulus E = 2 GPa and Poisson’s ratio ν = 0.3 using the material assignment algorithm outlined by Imediegwu et al. (2019). Any cells deemed to be void were assigned E = 100 Pa to avoid numerical instabilities.
The material properties of isotropic and anisotropic cellular solids are functions of their relative densities, known as the scaling law (Ashby 1983; Koudelka et al. 2011). Due to the anisotropic material properties of the microstructures employed in this work, the material properties are modelled as functions of radii rather than density, using multivariate polynomial functions. The general form of multivariate polynomials can be defined as
where \(\hat {y}\) is the dependent variable, m denotes the order of the polynomial, k = 7 is the number of independent variables, β are the coefficient terms, and j is the number of coefficient terms in the polynomial. Various degrees of polynomials were tested to fit the discrete DOE to ensure accurate approximations while limiting overfitting. A 6th-order polynomial was found to provide the best trade-off to create the response surfaces of EH, Φ and the volume v. By generating these response surface models to describe the lattice material properties, the discrete material property space is transformed into a continuous, differentiable property space, which enables the use of gradient-based optimization techniques. The number of coefficients can be calculated using \(j = \frac {(k+m)!}{k!m!} = 1716\). The polynomials were fitted by solving a series of least squares problems. The response surfaces generated can be defined as
where the hat variables are the continuous, 7-dimensional response surface models (RSMs) representing the respective microstructure properties. Due to the major symmetry in the stiffness tensor, 21 RSMs were created to assemble EH and 36 RSMs were generated to construct Φ. A response surface was also created to model the volume, v, of the microstructure permutations with respect to the member radii. The average R2 values obtained for response surfaces generated can be found in Table 1.
2.3 Macroscale yield criterion
To predict the yield of the microscale lattices, the von Mises yield criterion is used. The von Mises criterion has been used widely in literature, both in classical TO (Duysinx and Bendsøe 1998; Hyun et al. 2013; Liu et al. 2019) and in multiscale optimization (Yu et al. 2019; Collet et al. 2018; Coelho 2019), where yield is predicted to occur when the von Mises stress exceeds the yield strength of the material. The von Mises stress criterion can be defined as
where σy is the yield strength of the material and σi,i = 1,..,6 are the components of the stress vector obtained using
where \(\tilde {\epsilon }\) is the macroscale strain obtained by solving the PDE defining the macroscale system.
Since stress is a local measure, the simplest formulation of the stress constraints on the macroscale involves introducing a stress constraint for every cell in a discretized domain. The local stress constraints can be defined as
where N denotes the number of cells in the domain and sf is the chosen safety factor. However, due to the large computational cost associated with computing the gradient of a large number of nonlinear stress constraints, this problem setup is highly inefficient. While it is possible to re-define the constraint as \({\max \limits } (g) \leq 1\), this function is non-differentiable and so is incompatible with gradient-based optimization algorithms. To overcome this problem, constraint aggregation methods have been proposed in literature. The two most commonly used aggregation functions are the P-norm (Duysinx and Sigmund 1998; Liu et al. 2019) and Kreisselmeier–Steinhsauser (KS) (Kreisselmeier and Steinhauser 1979; Martins and Poon 2005) functions. The P-norm function was utilized in this work and can be defined as
where gpn is the aggregated “pseudo-maximum” value of stress and p is the aggregation parameter controlling the accuracy and non-linearity of the aggregation function. The P-norm function has the property
As the aggregation parameter is increased, the function provides more accurate predictions of the maximum stress within the domain. However, this also leads to the function becoming more non-linear and can cause numerical issues during the optimization. For finite values of p, the P-norm function leads to overly conservative estimates with \(g_{pn}(g,p) > \max \limits (g)\). To account for this property, an adaptive correction method, as proposed by Le et al. (2010), is employed. The corrected P-norm value can be defined as
where I ≥ 1 is the iteration number, \(g_{pn}^{\gamma }\) is the scaled P-norm value, and γI is the current adaptive correction factor defined as
where α is a continuity term controlling the level of contribution from the previous iteration to avoid large changes in the scaling. Initially, α is set to 0.5. As the optimization converges, the ratio \( \frac {\sigma ^{vm}_{max}}{g_{pn}}\) and by extension γ should converge to a single value. When the change in γ is less than 1%, α is set to 1, removing the influence of previous iterations.
3 Numerical validation
To validate the stress method introduced in the previous section, full-scale FEA was performed using ABAQUS v6.14 with non-periodic boundary conditions (BCs). As shown in Section 2, the multiscale methodology relies on a large scale of separation between the macro- and microscale structures, to ensure periodicity on the microscale is enforced. Due to computational, time, and manufacturing limits, the microstructures cannot be made infinitesimally small in comparison with the macroscale structure as assumed by the homogenization theory. In order to compare the von Mises stresses predicted from the multiscale method proposed in this work with the actual stress within a full-scale model, convergence studies were first performed to identify the minimum relative size of microstructures required to achieve periodicity within the microstructure. While there have been studies in literature examining this, the studies have been conducted using uniform microstructures where a single microstructure permutation is distributed throughout the macroscale domain. Recently, Cheng et al. (2019) examined the convergence properties of a uniform cubic microstructure and found that 6 microstructures along each edge of a cube were required to achieve convergence for displacement. To examine the impact of spatially varying microstructures on the convergence, full-scale FEA was performed using various graded distributions of microstructures. To reduce the computational expense of the FEA model, only the face to face members, r5, r6, and r7 in Fig. 1, were simulated. To ensure a fair comparison, additional response surfaces were generated using the 3-member lattice design, following the procedure outlined in Section 2. These face to face member response surfaces were used in the following sections to compare the accuracy of the multiscale stress method against full-scale model results. While the general behavior of the 7-member lattice shown in Fig. 1 and the 3-member lattice used in this section will differ, these differences are accounted for through the Φ matrix.
3.1 Homogenization convergence
A 1000 mm3 cube was used for all the convergence studies. A force of 80 N was distributed on the top surface (y = H) with fixed BCs (ux = uy = uz = 0) along the bottom (y = 0). The bulk material properties applied during the homogenization process in Section 2 were also used for the FEA model with E = 2 GPa and ν = 0.3. The convergence properties were examined by increasing the number of layers of microstructures within the cube, from two to ten layers, for a selection of graded microstructures. There were two types of grading applied, a linear grading and a sinusoidal grading. In both cases, the grading was applied in the x- and y-directions independently. The linear and sine grading function equations are shown in Table 2. The corresponding graded structures are shown in Fig. 2. These grading functions were chosen to simulate a variable lattice geometry. While the exact distribution of lattices observed during an optimization will be highly problem dependent, the grading functions were used to determine the robustness of the proposed methodology, when subject to a variable lattice geometry. The magnitudes of the functions were chosen to ensure that the lattice truss radii fall in radii range defined in Section 2.2.
Figure 3 shows the convergence of the normalized maximum displacement for a varying number of microstructure layers. In each case, the displacement converges to within 2% when using six layers compared with the ten-layer case. These results are in line with the results observed by Cheng et al. (2019) for a uniform microstructure and suggests that the distribution of microstructures within the macroscale structure has limited impact on the relative size of microstructure required to achieve periodicity on the microscale.
3.2 Multiscale stress vs. full-scale stress
To examine the accuracy of the multiscale stress method, the von Mises stress predicted using the multiscale method was compared with the stresses observed from full-scale FEA using various microstructure distributions. In total eight cases were tested, a compressive load and a shear load, individually applied to the four graded structures shown in the previous section. The geometry and BCs used for assessing the convergence of the microscale properties were replicated for these analyses. Using six layers of microstructures, the von Mises distribution through a single column of the microstructure was used to examine the accuracy of the multiscale model as shown in Fig. 4. Due to the large computational cost of including additional layers and based on the result from the convergence study shown in Fig. 3, six layers of microstructures were chosen to study the stress response of the full-scale model. The multiscale model was evaluated using the python library FEniCS 2019.1.0 (Alnæs et al. 2015). A mesh convergence study was conducted, and 27,000 hexahedral elements were required for the multiscale model and an average of 30 million tetrahedral elements were used for the full-scale models. A 2.7-GHz quad-core CPU with 16 GB of memory was used to run the multiscale model, with a total compute time of 1 min. The full-scale FEA models took on average 120 min, which includes the model generation, meshing, and the FE system solve. The full-scale model was solved using 32 Intel Xeon E5 cores with MPI and 64 GB of memory. This large disparity in mesh size and compute times highlights the significant advantage of using the AH method.
As shown in Figs. 5 and 6, the multiscale stress model is able to replicate the von Mises stress in the center of the microstructures from the full-scale FEA simulations to within 10% in six out of eight cases tested here. In both the load cases, periodic distributions of von Mises stress can be seen, with peaks and troughs in stress forming due to the interaction of the vertical and horizontal members. In the compressive case, the horizontal members provide additional load paths, reducing the stress in the center of the unit lattice. In the shear case, the stress peaks depend on the microstructure configuration. For example, the relatively thin horizontal members in the linear-y and sin-y graded structures lead to stress spikes in the lattice centers, and the large horizontal members in the linear-x and sin-x cases produce to troughs in von Mises stress. For a more thorough examination, the six individual stress components used to construct the von Mises have been plotted in Figs. 7 and 8. An important feature to note in these figures is the impact of edge effects. As there is a breakdown in periodicity at the domain boundaries, the multiscale method cannot make accurate predictions of the field variables in this region. Examples of this can be seen in the regions y = 10mm and y = 0mm within Fig. 7b and d, with the deviation of σyy, σxx in Fig. 8a or σxy in Fig. 8d. From Figs. 7 and 8, we observe that that the multiscale stress method is able to effectively predict the dominant stress components (σyy in compression and σxy in shear) and replicate their magnitude in the center of the unit cells for both load cases. The error (for the dominant terms) in the center of the unit cells in the middle of the structure is less than 10% for all the compressive cases and the shear load cases for the linear-x and sin-y graded structures, when compared with the full FEA results. In the linear-y and sin-x graded cases under a shear load, the multiscale method overpredicts the magnitude of stress by 20% and 40% respectively. Based on these plots and the contour plots shown in Figs. 5 and 6, it is clear that the peak stresses often occur in the structural members themselves or at their intersection. As the current methodology is restricted to capturing the stress in the center of the unit cell due to computational limitations, it cannot accurately represent these stresses. However, in future research, there is scope to include additional points of stress capture, allowing for better replication of the interaction of the structural members and thus the peak stresses that occur in the lattices. In this work, the focus is aimed at replicating the real stress at the center of the microstructures, and applying these stresses to optimization problems. As shown through the von Mises distributions in Figs. 5 and 6, as well as the individual components of stress shown in the Figs. 7 and 8, the multiscale stress method has been shown to be effective at predicting the stress in the center of periodic lattice microstructures and gives confidence in its use in optimization problems.
4 Macroscale optimization
A common approach in multiscale optimization is to map microstructures onto TO results using the microstructure densities. In this work, we directly optimize the domain using the response surface models generated to represent the microstructure properties (stiffness tensor and stress). The optimizer is able to independently vary the radii (density) of the 7 structural members shown in Fig. 1, within each cell in the domain. In this work, the design variables for the optimization are the N × 7 radii, defining each member of each microstructure that makes up the macroscale domain. The design variables used in the optimization can be defined as a matrix
where each row corresponds to the vector of microstructure radii within each cell and each column represents one of the 7 structural members shown in Fig. 1. The flowchart shown in Fig. 9 outlines the stress-constrained optimization methodology proposed in this work. From the flowchart, it can be seen that the approach taken in this work does not involve simultaneous optimization of the micro- and macroscale topologies. The optimization is performed by employing a predetermined microstructure design, shown in Fig. 1, for which a full factorial DOE is created prior to the macroscale optimization. The discrete DOE is converted into a continuous response surface model which allows for the use of gradient-based optimization techniques and avoids the need to simulate every microstructure encountered during an optimization. During the optimization, the optimizer is able to vary the radii of the microstructures in each macroscale cell, to generate a range of material properties which are defined by EH, v, and Φ. As this optimization approach selects microstructures to tailor the distribution of EH, it can in some ways be compared with free material optimization techniques (Zowe et al. 1997). In this work, we consider the problem of minimizing a volume subject to a global stress constraint, obtained using the P-norm formulation defined in Section 2.3. The optimization problem can be defined as
where K is the global stiffness matrix of the structure, U is the nodal displacement vector, F is the load vector, V is the total volume, v is the cell volume, and N is the total number of cells. The member radii are bound by rmin = 0.08 and rmax = 0.38, to ensure the response surface models outlined in Section 2.2 remain valid. The global stiffness matrix is assembled using the element stiffness matrices, ke, which are defined by
where B is the strain-displacement matrix, Ωe is the cell volume, and \(\hat {\boldsymbol {E}}^{H}\) is the stiffness tensor obtained from the response surface model generated from the microstructure simulations. The optimization is terminated once the change in objective function over three iterations is less than 0.001.
Zhu et al. (2017) were able to demonstrate the capability of multiscale structures to optimize target deformation problems. Here, we are additionally including stress constraints into target deformation problems to ensure the final geometries do not yield. The target deformation problem can be defined as
where U and Ut are the actual and target displacements, respectively; β is a function defining the subdomain over which the target deformation is required. The objective function, η, measures the error between the target and achieved displacements over the subdomain. Once again, the optimization is terminated when the change in the objective function is less than 0.001 over three successive iterations.
To solve the optimization problems outlined above, the open source interior point optimization package IPOPT 3.12.12 (Wächter and Biegler 2006) was utilized. The gradients of the objective function and constraint required for the interior point method are obtained using the algorithmic differentiation (AD) python library dolfin-adjoint 2019.1.0 (Farrell et al. 2012).
4.1 Helmholtz filtering
In TO, the problem of checkerboarding is well known (Sigmund and Petersson 1998). Poor numerical modelling leads to the formation of void and solid elements in a non-physical alternating checkerboard fashion. Additionally, Sigmund and Petersson (1998) discussed the mesh-dependent nature of optimized geometries. Regularization is often used to circumvent these issues with density (Bourdin 2001) and sensitivity filters (Sigmund and Petersson 1998) being most commonly used. Recently, Lazarov and Sigmund (2011) presented a filtering method based on the solution of Helmholtz equations. The filtered design variables \(\tilde {r}\) can be obtained by solving the Helmholtz-type PDE
where κ is defined as the filter radius. In this work, κ has been set to 2D where D is the cell width used in the mesh. Due to the inherent penalization of lattice microstructures, the multiscale formulation outlined in Section 2 does not guarantee smoothly changing design variables (member radii) through the design domain. For the purposes of manufacturing and stress concentrations, avoiding discontinuous changes in the design variables is crucial. While the Helmholtz filter used serves a purpose of producing checkerboard free geometries and avoids mesh dependency, in the context of multiscale lattice optimization it also ensures smooth continuous structures within this optimization framework.
5 Results and discussion
To test our formulation, we employ three problems. The first two test cases were defined to ensure a stress constraint violation at initialization, to force the optimizer to simultaneously reduce the objective function and stress constraint violation.
5.1 Box problem
The first example used to validate the multiscale stress method optimization is a box problem. The problem domain is a cube supported at the bottom four corners, as shown in Fig. 10a. A distributed load of 70 N is applied over a 4 mm2 area in the center of the top surface. The domain is discretized using 27,000 hexahedral elements. The safety factor, sf, is set to 1.5 and p is set to 16 to allow for better local control of the stress. The p value was chosen based on experience, with the higher values of p found to cause numerical instabilities and convergence issues and lower values leading to overly conservative designs. The convergence plots for the volume fraction and stress, shown in Fig. 10, show the volume fraction converging to 0.28, which represents a weight saving of over 70% compared with that of a solid structure, while respecting the stress constraint of 33.3 MPa. The maximum stress increases rapidly at the beginning of the optimization as the volume fraction is reduced, leading to the formation of large stress concentrations. From iteration 30 and onwards, material is added to reduce the stress constraint violation. The combination of employing an adaptive stress constraint, which constantly scales the p-Norm value and due to the highly non-linear stress function resulting from the p-Norm formulation, the optimizer requires over 180 iterations before the stress constraint is respected. A potential solution to improve the convergence may be to initialize the problem with a low p value and progressively increase the value over course of the optimization. Alternatively, the continuity term, α, could also be tuned to avoid large changes in the adaptive scaling factor. It should be noted that this objective function value and corresponding lattice distribution, discussed below, are dependent on the chosen safety factor and p value. Higher safety factors or lower p values will lead to more conservative designs and alter the optimum lattice distribution. However, a full-design study exploring the impact of these parameters is outside the scope of this paper. The optimized distribution of the lattice members is shown in Fig. 14. For further clarity, the thresholded distribution of the diagonal lattice members is shown in Fig. 11 and the volume fraction is shown in Fig. 12. It is interesting to note that the principal stresses are aligned to the direction of the structures formed by each of the diagonal members. The structures themselves are also seen to align to the microstructure member directions on the microscale. For example, member 1 is aligned along the same direction on the macroscale and the microscale as seen in Figs. 11a and 1 respectively. In Fig. 13, the principal stresses have been overlaid on the cross section of the high-density regions formed by member 1 to highlight the alignment of the members in the direction of the principal stresses. By aligning the members in such a way, the optimizer is able to create efficient load paths to reduce the stresses induced within the microstructures while minimizing the overall volume fraction. In Figs. 12 and 14, the four corners are shown to contain the highest volume fractions, with the member radii reaching rmax. Due to the fixed BCs in the four corners, these areas are prone to stress concentrations, which are alleviated by the highly dense lattices.
5.2 MBB beam problem
The second stress-constrained volume minimization example is a 3D Messerschmitt–Bölkow–Blohm (MBB) beam problem, as shown in Fig. 15a. A total load of 2000 N is applied along the top surface with 2 fixed supports at each end of the beam. The domain is discretized using 90 × 18 × 18 hexahedral elements. The safety factor sf is set to 1.5 and the P-norm aggregation parameter, p, is set to 16. The convergence history for the volume fraction and stress are shown in Fig. 15. The volume fraction is initialized at 0.95 and converges to 0.3, with the stress simultaneously being reduced from 55 to 33.3 MPa. The initial oscillations in the maximum stress arise from a large reduction in volume fraction, causing spikes in the maximum stress. As with the box problem, the optimizer begins to add material after 40 iterations to reduce the stress concentrations. The von Mises distribution and principal stress directions are shown in Fig. 16. The optimized lattice distribution is shown in Fig. 17. The symmetry of the microscale members is once again present on the macroscale, as highlighted by the diagonal members surrounding the supports in Fig. 17. Comparing the distribution of members in Fig. 17 and the principal stress directions shown in Fig. 16b, the propensity of the principal stress and members to align along the same direction is once again clear. For example, member 6, which is aligned in the y-direction, is dominant directly above the supports where the stress travels directly down. Another notable feature is the distribution of the diagonal members. Members 1 and 4 appear on the left above the supports with members 2 and 3 mirrored on the right. Here, the diagonal members are aligned to most efficiently transfer the load to the supports from the area of high density in the center of the upper surface. As the angle of the principal stresses reduces closer to the horizontal, member 5, which is aligned to the x-axis, begins to dominate. The optimizer is biased toward using the face to face member in this case, as it has a smaller contribution to the volume fraction of each unit cell. Therefore, despite the principal stress not being fully aligned to the horizontal, the horizontal member can be seen to dominate between the high-density regions of the diagonal members and upper surface. As with the box problem, the regions of highest volume fraction are found near the supports due to the stress concentrations that arise as a result of the fixed BCs, as shown in Fig. 16a. By pushing the member radii to their maximum in this region, the optimizer is able to reduce the stress induced on the microstructures and ensure the constraint is obeyed.
5.3 Target deformation
The final problem solved in this work is a target deformation optimization with stress constraints, with application to the design of morphing structures. To induce a load on the beam geometry shown in Fig. 18a, fixed Dirichlet BCs of ux = 0.3 mm are specified at each end. The target deformation is a sine wave in the y-direction, defined according to the function
where y is the displacement (in mm) of the beam in the y direction, L is the length of the beam, and x is the distance along the beam. The wave is defined to achieve a maximum displacement of 0.5 mm in the center of the beam. The target deformation is only specified along the top surface of the beam and sf is set to 1 for this problem. The aggregation parameter p is set to 16 and the beam is discretized using 60 × 15 × 15 hexahedral elements. The plots depicting the objective function and maximum von Mises stress through the optimization are shown in Fig. 18. As a comparison, an unconstrained problem was also set up with the same parameters. While there are no sudden spikes in the stress during the optimization of the stress-constrained case as seen in previous problems, the stress convergence is much more oscillatory. This is caused by a frequent change in α leading to jumps in the adaptive scaling. This problem may be alleviated by further reducing the threshold at which the continuity term changes, or by including intermediate values of α. As expected, the unconstrained case leads to a better objective function. While the unconstrained problem reaches a maximum displacement of 0.498 mm with an RMS surface error of 1.35 × 10− 6 mm, the distribution of member radii leads to stress concentrations with a maximum von Mises stress of 134 MPa. The target, constrained and unconstrained displacements can be seen in Fig. 19. As shown in Fig. 20, the inclusion of the stress constraint has the effect of smearing the geometry, removing the stress concentrations and resulting in a maximum von Mises stress of 44 MPa. Despite the reducing the maximum stress within the structure, the constrained solution reaches a maximum displacement of 0.51 mm with an RMS surface error of 2.01 × 10− 6mm, demonstrating the effectiveness of the novel multiscale stress model introduced in this work. The optimized distributions of lattice member radii for the constrained and unconstrained cases are shown in Fig. 20. In the unconstrained case, the optimization results in an intricate compliant mechanism which restricts the displacement at either end of the beam while allowing for the extension in the center. On the other hand, the constrained solution appears to be heavily “filtered” compared with the unconstrained case. The distribution of the members is more homogeneous and with a lack of detail. This effect prevents the stress concentrations that arise from thin members, as seen in the unconstrained case. In the constrained problem, the optimizer limits the variation in member thickness to reduce the stress induced on the microstructures while ensuring the structure deforms as required.
6 Conclusion
In this work, we propose the use of real microscale stress components to perform stress-constrained optimization using graded lattice structures. Stress matrices were captured using the six independent strains applied during the homogenization process of the lattice microstructures. It was shown that it is possible to replicate the stress within the microstructure resulting from large-scale strains, through the superposition of the strain-scaled stress matrix. To validate this methodology, full-scale FEA was performed using non-periodic BCs and a simplified microstructure model. First, the scale of separation (number of microstructure layers) required to achieve periodicity was studied. It was determined that a minimum of six layers of microstructures are needed to replicate the conditions specified by the AH theory. Using this result, various graded microstructures were individually subjected to a compressive and a shear load to compare the predictions made by the proposed methodology with those from full-scale FEA. In six out of the eight cases tested, the multiscale stress model was able to replicate the von Mises stress in the center of the unit cells to within 10% of the values predicted by the full-scale modelling. The predictions of individual stress components were also presented. It was observed that the multiscale stress method is able to replicate the dominant stress components with reasonable accuracy, at the center of the lattice cells. Three numerical examples were then tackled using the proposed stress methodology. The first two examples were weight minimization problems, subject to maximum stress constraints. In both cases, the optimizer was able to reduce the weight (volume fraction) by over 60%, while respecting the imposed stress constraints. Examining the optimized structures, it was found that the principal stresses were aligned in the direction of the individual microstructure members, to create efficient load paths, reducing the excess strains imposed on the microstructures. The macroscale distribution of the individual microstructure members was also found to replicate the direction of the members on the microscale. Lastly, a target deformation problem was solved with and without stress constraints. In both cases, the optimizer was able to achieve the required deformation, without violating the stress constraint in the stress-constrained case.
Future research should be directed toward extending the proposed methodology by including additional points of stress capture to better represent the stresses found in the lattice struts and their intersections, as these are often locations of stress maxima. It may also be possible to include additional models to represent the behavior of the lattices at boundaries of the macroscale domain where there is a breakdown in the assumption of periodicity.
References
Alnæs MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN (2015) The FEniCS Project Version 1.5. Archive of Numerical Software DOI10.11588/ans.2015.100.20553
Arabnejad S, Pasini D (2012) Multiscale design and multiobjective optimization of orthopedic hip implants with functionally graded cellular material (March 2014), https://doi.org/10.1115/1.4006115
Ashby MF (1983) Mechanical properties of cellular solids. Metallurgical Transactions A, Physical Metallurgy and Materials Science 14 A(9):1755–1769. https://doi.org/10.1007/BF02645546
Bacigalupo A, Morini L, Piccolroaz A (2016) Multiscale asymptotic homogenization analysis of thermo-diffusive composite materials. Int J Solids Struct 85-86:15–33. https://doi.org/10.1016/j.ijsolstr.2016.01.016
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224. https://doi.org/10.1016/0045-7825(88)90086-2
Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(9):2143–2158. https://doi.org/10.1002/nme.116
Bruggi M (2008) On an alternative approach to stress constraints relaxation in topology optimization. Struct Multidiscip Optim 36(2):125–141. https://doi.org/10.1007/s00158-007-0203-6
Bruggi M, Duysinx P (2012) Topology optimization for minimum weight with compliance and stress constraints. Struct Multidiscip Optim 46(3):369–384. https://doi.org/10.1007/s00158-012-0759-7
Cai Y, Xu L, Cheng G (2014) Novel numerical implementation of asymptotic homogenization method for periodic plate structures. Int J Solids Struct 51(1):284–292. https://doi.org/10.1016/j.ijsolstr.2013.10.003
Cheng G, Guo X (1997) E-Relaxed approach in topology optimization. Structural Optimization 13(1972):258–266. https://doi.org/10.1007/BF01197454
Cheng G, Jiang Z (1992) Study on topology optimization with stress constraints. Eng Optim 20(2):129–148. https://doi.org/10.1080/03052159208941276
Cheng L, Bai J, To AC (2019) Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput Methods Appl Mech Eng 344:334–359. https://doi.org/10.1016/j.cma.2018.10.010
Coelho PG (2019) Topology optimization of cellular materials with periodic microstructure under stress constraints. Struct Multidiscip Optim 59:633–645. https://doi.org/10.1007/s00158-018-2089-x
Collet M, Bruggi M, Duysinx P, No L (2018) Topology optimization for microstructural design under stress constraints. Struct Multidiscip Optim 58:2677–2695. https://doi.org/10.1007/s00158-018-2045-9
Duysinx P, Bendsøe MP (1998) Topology optimisation of continuum structures with local stress constraints. International Journal for Numerical Methods in Engineering 1478(March):1453–1478. https://doi.org/10.1002/(SICI)1097-0207(19981230)43:8<1453::AID-NME480>3.0.CO;2-2
Duysinx P, Sigmund O (1998) New developments in handling stress constraints in optimal material distribution. In: 7Th AIAA/USAF/NASA/ISSMO symposium on multidisciplinary analysis and optimization, American Institute of Aeronautics and Astronautics Inc, AIAA, pp 1501–1509. https://doi.org/10.2514/6.1998-4906
Fan Z, Yan J (2019) Multiscale eigenfrequency optimization of multimaterial lattice structures based on the asymptotic homogenization method. Struct Multidiscip Optim 61:983–998. https://doi.org/10.1007/s00158-019-02399-0
Farrell PE, Ham DA, Funke SW, Rognes ME (2012) Automated derivation of the adjoint of high-level transient finite element programs. arXiv:1204.5577
Francu J (1982) Homogenization of linear elasticity equations, vol 27. http://eudml.org/doc/15229
Gebremedhen HS, Woldemicahel DE, Hashim FM, Min V (2019) Three-dimensional stress-based topology optimization using SIMP method. Int J Simul Multidisci Des Optim 1:1–10. https://doi.org/10.1051/smdo/2019005
Groen JP, Sigmund O (2018) Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int J Numer Methods Eng 113(8):1148–1163. https://doi.org/10.1002/nme.5575
Hollister SJ, Kikuchi N (1992) A comparison of homogenization and standard mechanics analyses for periodic porous composites. Comput Mech 10(2):73–95. https://doi.org/10.1007/BF00369853
Holmberg E, Torstenfelt B, Klarbring A (2013a) Global and clustered approaches for stress constrained topology optimization and deactivation of design variables. 10th World Congress on Structural and Multidisciplinary Optimization, pp 1–10
Holmberg E, Torstenfelt B, Klarbring A (2013b) Stress constrained topology optimization. Struct Multidiscip Optim 48:33–47. https://doi.org/10.1007/s00158-012-0880-7
Hyun S, Ho S, Choi Dh, Ho G (2013) Toward a stress-based topology optimization procedure with indirect calculation of internal finite element information. Comput Math Appl 66(6):1065–1081. https://doi.org/10.1016/j.camwa.2013.07.008
Imediegwu C, Murphy R, Hewson R, Santer M (2019) Multiscale structural optimization towards three-dimensional printable structures. Structural and Multidisciplinary Optimization. https://doi.org/10.1007/s00158-019-02220-y
Koudelka P, Jiroušek O, Valach J (2011) Determination of mechanical properties of materials with complex inner structure using microstructural models. Mach Technol Mater 1:39–42
Kreisselmeier G, Steinhauser R (1979) Systematic control design by optimizing a vector performance index. IFAC Proceedings Volumes https://doi.org/10.1016/s1474-6670(17)65584-8
Lazarov BS, Sigmund O (2011) Filters in topology optimization based on Helmholtz-type differential equations (December 2010), pp 765–781. https://doi.org/10.1002/nme
Le C, Norato J, Bruns T, Ha C, Tortorelli D (2010) Stress-based topology optimization for continua. Struct Multidiscip Optim 41(4):605–620. https://doi.org/10.1007/s00158-009-0440-y
Liu B, Guo D, Jiang C, Li G, Huang X (2019) Stress optimization of smooth continuum structures based on the distortion strain energy density. Comput Methods Appl Mech Eng 343:276–296. https://doi.org/10.1016/j.cma.2018.08.031
Liu LP (2010) Hashin-Shtrikman bounds and their attainability for multi-phase composites. Proceedings of the Royal Society a: Mathematical Phys Eng Sci 466 (2124):3693–3713. https://doi.org/10.1098/rspa.2009.0554
Martins JRRA, Poon NMK (2005) On structural optimization using constraint aggregation. 6th World Congress on Structural and Multidisciplinary Optimization (June):1–10
Ngo TD, Kashani A, Imbalzano G, Nguyen KT, Hui D (2018) Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Composites Part B: Engineering 143(December 2017):172–196. https://doi.org/10.1016/j.compositesb.2018.02.012
París J, Navarrina F, Colominas I, Casteleiro M (2010) Block aggregation of stress constraints in topology optimization of structures. Adv Eng Softw 41(3):433–441. https://doi.org/10.1016/j.advengsoft.2009.03.006
Pasini D, Moussa A, Rahimizadeh A (2018) Stress-constrained topology optimization for lattice materials (October):0–19, https://doi.org/10.1007/978-3-662-53605-6
Sigmund O (2000) A new class of extremal composites. Journal of the Mechanics and Physics of Solids 48(2):397–428. https://doi.org/10.1016/S0022-5096(99)00034-4
Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Structural Optimization 16(1):68–75. https://doi.org/10.1007/BF01214002
Sved G, Ginos Z (1968) Structural optimization under multiple loading. Int J Mech Sci 10 (10):803–805. https://doi.org/10.1016/0020-7403(68)90021-0
de Troya MA, Tortorelli DA (2018) Adaptive mesh refinement in stress-constrained topology optimization. Struct Multidiscip Optim 58(6):2369–2386. https://doi.org/10.1007/s00158-018-2084-2
Wächter A, Biegler LT (2006) On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 106(1):25–57. https://doi.org/10.1007/s10107-004-0559-y
Wang X, Zhang P, Ludwick S, Belski E, To AC (2018) Natural frequency optimization of 3D printed variable-density honeycomb structure via a homogenization-based approach. Additive Manufacturing 20:189–198. https://doi.org/10.1016/j.addma.2017.10.001
Yang D, Liu H, Zhang W, Li S (2018) Stress-constrained topology optimization based on maximum stress measures. Comput Struct 198:23–39. https://doi.org/10.1016/j.compstruc.2018.01.008
Yi S, Cheng G, Xu L (2016) Stiffness design of heterogeneous periodic beam by topology optimization with integration of commercial software. Comput Struct 172:71–80. https://doi.org/10.1016/j.compstruc.2016.05.012
Yu H, Huang J, Zou B, Shao W, Liu J (2019) Stress-constrained shell-lattice infill structural optimisation for additive manufacturing. Virtual and Physical Prototyping 0(0):1–14. https://doi.org/10.1080/17452759.2019.1647488
Zhu B, Skouras M, Chen D, Matusik W (2017) Two-scale topology optimization with microstructures. SIGIR 2019 - Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval 34(4):1281–1284. https://doi.org/10.1145/nnnnnnn.nnnnnnn
Zowe J, Kočvara M, Bendsøe MP (1997) Free material optimization via mathematical programming. Mathematical Programming, Series B 79(1-3):445–466. https://doi.org/10.1007/BF02614328
Acknowledgments
The first author would like to gratefully acknowledge the financial support from the Aeronautics Department at Imperial College London.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
The authors wish to withhold the code for commercialization purposes. This includes the database of microscale simulations and a python code implementing the optimization.
Additional information
Responsible Editor: Seonho Cho
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thillaithevan, D., Bruce, P. & Santer, M. Stress-constrained optimization using graded lattice microstructures. Struct Multidisc Optim 63, 721–740 (2021). https://doi.org/10.1007/s00158-020-02723-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-020-02723-z