Skip to main content
SpringerLink
Log in

Exponentially slow motion of interface layers for the one-dimensional Allen–Cahn equation with nonlinear phase-dependent diffusivity

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

This paper considers a one-dimensional generalized Allen–Cahn equation of the form

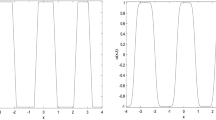
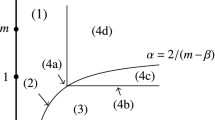
$$\begin{aligned} u_t = \varepsilon ^2 (D(u)u_x)_x - f(u), \end{aligned}$$

where \(\varepsilon > 0\) is constant, \(D = D(u)\) is a positive, uniformly bounded below, diffusivity coefficient that depends on the phase field u, and f(u) is a reaction function that can be derived from a double-well potential with minima at two pure phases \(u = \alpha \) and \(u = \beta \). It is shown that interface layers (namely, solutions that are equal to \(\alpha \) or \(\beta \) except at a finite number of thin transitions of width \(\varepsilon \)) persist for an exponentially long time proportional to \(\exp (C/\varepsilon )\), where \(C > 0\) is a constant. In other words, the emergence and persistence of metastable patterns for this class of equations is established. For that purpose, we prove energy bounds for a renormalized effective energy potential of Ginzburg–Landau type. Numerical simulations, which confirm the analytical results, are also provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27(6), 1085–1095 (1979)

    Google Scholar 

  2. Bethuel, F., Smets, D.: Slow motion for equal depth multiple-well gradient systems: the degenerate case. Discrete Contin. Dyn. Syst. 33(1), 67–87 (2013)

    MathSciNet  MATH  Google Scholar 

  3. Boltzmann, L.: Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Ann. Phys. 289(13), 959–964 (1894)

    MATH  Google Scholar 

  4. Braides, A.: \(\Gamma \)-convergence for beginners, vol. 22 of Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, Oxford (2002)

  5. Broadbridge, P.: Exact solvability of the Mullins nonlinear diffusion model of groove development. J. Math. Phys. 30(7), 1648–1651 (1989)

    MathSciNet  MATH  Google Scholar 

  6. Bronsard, L., Kohn, R.V.: On the slowness of phase boundary motion in one space dimension. Commun. Pure Appl. Math. 43(8), 983–997 (1990)

    MathSciNet  MATH  Google Scholar 

  7. Cahn, J .W.: Free energy of a nonuniform system. II. Thermodynamic basis. J. Chem. Phys 30(5), 1121–1124 (1959)

    Google Scholar 

  8. Cahn, J.W.: On spinodal decomposition. Acta Metall. 9(9), 795–801 (1961)

    Google Scholar 

  9. Cahn, J.W., Elliott, C.M., Novick-Cohen, A.: The Cahn–Hilliard equation with a concentration dependent mobility: motion by minus the Laplacian of the mean curvature. Eur. J. Appl. Math. 7(3), 287–301 (1996)

    MathSciNet  MATH  Google Scholar 

  10. Cahn, J .W., Hilliard, J .E.: Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys 28(2), 258–267 (1958)

    MATH  Google Scholar 

  11. Cahn, J.W., Hilliard, J.E.: Spinodal decomposition: a reprise. Acta Metall. 19(2), 151–161 (1971)

    Google Scholar 

  12. Carr, J., Pego, R.L.: Metastable patterns in solutions of \(u_t=\epsilon ^2u_{xx}-f(u)\). Commun. Pure Appl. Math. 42(5), 523–576 (1989)

    MATH  Google Scholar 

  13. Carr, J., Pego, R.L.: Invariant manifolds for metastable patterns in \(u_t=\epsilon ^2u_{xx}-f(u)\). Proc. R. Soc. Edinb. Sect. A 116(1–2), 133–160 (1990)

    MATH  Google Scholar 

  14. Chen, X.: Generation, propagation, and annihilation of metastable patterns. J. Differ. Equ. 206(2), 399–437 (2004)

    MathSciNet  MATH  Google Scholar 

  15. Cirillo, E.N.M., Ianiro, N., Sciarra, G.: Allen–Cahn and Cahn–Hilliard-like equations for dissipative dynamics of saturated porous media. J. Mech. Phys. Solids 61(2), 629–651 (2013)

    MathSciNet  MATH  Google Scholar 

  16. Cirillo, E.N.M., Ianiro, N., Sciarra, G.: Compacton formation under Allen–Cahn dynamics. Proc. R. Soc. A: Math. Phys. Eng. Sci. 472(2188), 20150852 (2016)

    MathSciNet  MATH  Google Scholar 

  17. Dai, S., Du, Q.: Computational studies of coarsening rates for the Cahn–Hilliard equation with phase-dependent diffusion mobility. J. Comput. Phys. 310, 85–108 (2016)

    MathSciNet  MATH  Google Scholar 

  18. Dai, S., Du, Q.: Weak solutions for the Cahn–Hilliard equation with degenerate mobility. Arch. Ration. Mech. Anal. 219(3), 1161–1184 (2016)

    MathSciNet  MATH  Google Scholar 

  19. Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence, vol. 8 of Progress in Nonlinear Differential Equations and their Applications, Birkhäuser Boston, Inc., Boston (1993)

  20. Dal Passo, R., Giacomelli, L., Novick-Cohen, A.: Existence for an Allen–Cahn/Cahn–Hilliard system with degenerate mobility. Interfaces Free Bound. 1(2), 199–226 (1999)

    MathSciNet  MATH  Google Scholar 

  21. De Giorgi, E., Franzoni, T.: Su un tipo di convergenza variazionale. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. (8) 58(6), 842–850 (1975)

    MathSciNet  MATH  Google Scholar 

  22. Elliott, C.M., Garcke, H.: On the Cahn–Hilliard equation with degenerate mobility. SIAM J. Math. Anal. 27(2), 404–423 (1996)

    MathSciNet  MATH  Google Scholar 

  23. Evans, L.C., Soner, H.M., Souganidis, P.E.: Phase transitions and generalized motion by mean curvature. Commun. Pure Appl. Math. 45(9), 1097–1123 (1992)

    MathSciNet  MATH  Google Scholar 

  24. Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band 153, Springer, New York Inc., New York (1969)

  25. Fife, P.C.: Pattern formation in gradient systems. In: Fiedler, B. (ed.) Handbook of Dynamical Systems, vol. 2, pp. 677–722. North-Holland, Amsterdam (2002)

    Google Scholar 

  26. Folino, R.: Slow motion for one-dimensional nonlinear damped hyperbolic Allen–Cahn systems. Electron. J. Differ. Equ. 2019(113), 1–21 (2019)

    MathSciNet  MATH  Google Scholar 

  27. Folino, R., Lattanzio, C., Mascia, C.: Slow dynamics for the hyperbolic Cahn–Hilliard equation in one-space dimension. Math. Methods Appl. Sci. 42(8), 2492–2512 (2019)

    MathSciNet  MATH  Google Scholar 

  28. Fusco, G., Hale, J.K.: Slow-motion manifolds, dormant instability, and singular perturbations. J. Dyn. Differ. Equ. 1(1), 75–94 (1989)

    MathSciNet  MATH  Google Scholar 

  29. Grant, C.P.: Slow motion in one-dimensional Cahn–Morral systems. SIAM J. Math. Anal. 26(1), 21–34 (1995)

    MathSciNet  MATH  Google Scholar 

  30. Green, H.S., Hurst, C.A.: Order-Disorder Phenomena, Monographs in Statistical Physics and Thermodynamics Vol. 5, Interscience Publishers, Wiley, London (1964)

  31. Hartley, G.S., Crank, J.: Some fundamental definitions and concepts in diffusion processes. Trans. Faraday Soc. 45(1), 801–818 (1949)

    Google Scholar 

  32. Ilmanen, T.: Convergence of the Allen–Cahn equation to Brakke’s motion by mean curvature. J. Differ. Geom. 38(2), 417–461 (1993)

    MathSciNet  MATH  Google Scholar 

  33. Kohn, R., Otto, F., Reznikoff, M.G., Vanden-Eijnden, E.: Action minimization and sharp-interface limits for the stochastic Allen–Cahn equation. Commun. Pure Appl. Math. 60(3), 393–438 (2007)

    MathSciNet  MATH  Google Scholar 

  34. Lee, C.F.: On the solution of concentration distributions in some binary alloy systems. Acta Metall. 19(5), 415–420 (1971)

    Google Scholar 

  35. Matano, C.: On the relation between the diffusion-coefficients and concentrations of solid metals. Jpn. J. Phys. 8(3), 109–113 (1933)

    Google Scholar 

  36. Modica, L., Mortola, S.: Il limite nella \(\Gamma \)-convergenza di una famiglia di funzionali ellittici. Boll. Un. Mat. Ital. A (5) 14(3), 526–529 (1977)

    MathSciNet  MATH  Google Scholar 

  37. Modica, L., Mortola, S.: Un esempio di \(\Gamma ^{-}\)-convergenza. Boll. Un. Mat. Ital. B (5) 14(1), 285–299 (1977)

    MathSciNet  MATH  Google Scholar 

  38. Mullins, W.W.: Theory of thermal grooving. J. Appl. Phys. 28(3), 333–339 (1957)

    Google Scholar 

  39. Otto, F., Reznikoff, M.G.: Slow motion of gradient flows. J. Differ. Equ. 237(2), 372–420 (2007)

    MathSciNet  MATH  Google Scholar 

  40. Owen, N.C., Sternberg, P.: Nonconvex variational problems with anisotropic perturbations. Nonlinear Anal. 16(7–8), 705–719 (1991)

    MathSciNet  MATH  Google Scholar 

  41. Rubinstein, J., Sternberg, P., Keller, J.B.: Fast reaction, slow diffusion, and curve shortening. SIAM J. Appl. Math. 49(1), 116–133 (1989)

    MathSciNet  MATH  Google Scholar 

  42. Sánchez-Garduño, F., Maini, P.K.: Travelling wave phenomena in non-linear diffusion degenerate Nagumo equations. J. Math. Biol. 35(6), 713–728 (1997)

    MathSciNet  MATH  Google Scholar 

  43. Schmid, A.: A time dependent Ginzburg–Landau equation and its application to the problem of resistivity in the mixed state. Phys. Konden. Mater. 5(4), 302–317 (1966)

    Google Scholar 

  44. Taylor, J.E., Cahn, J.W.: Linking anisotropic sharp and diffuse surface motion laws via gradient flows. J. Stat. Phys. 77(1–2), 183–197 (1994)

    MathSciNet  MATH  Google Scholar 

  45. Vázquez, J.L.: The Porous Medium Equation, Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, Oxford (2007). Mathematical theory

  46. Wagner, C.: On the solution of diffusion problems involving concentration-dependent diffusion coefficients. J. Met. 4(1), 91–96 (1952)

    Google Scholar 

Download references

Acknowledgements

We thank two anonymous referees whose comments greatly improved the quality of the paper. The work of R. G. Plaza was partially supported by DGAPA-UNAM, program PAPIIT, Grant IN-100318.

Author information

Authors and Affiliations

  1. Departamento de Matemáticas y Mecánica, Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas, Universidad Nacional Autónoma de México, Circuito Escolar s/n, Ciudad Universitaria, C.P. 04510, Cd. de México, Mexico

    Raffaele Folino, Luis Lopez Rios & Ramón G. Plaza

  2. Departamento de Matemática, Universidade Estadual de Maringá, Av. Colombo, 5790 Jd. Universitário, Maringá, PR, CEP 87020-900, Brazil

    César A. Hernández Melo

Authors
  1. Raffaele Folino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. César A. Hernández Melo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Luis Lopez Rios
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ramón G. Plaza
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raffaele Folino.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Folino, R., Hernández Melo, C.A., Lopez Rios, L. et al. Exponentially slow motion of interface layers for the one-dimensional Allen–Cahn equation with nonlinear phase-dependent diffusivity. Z. Angew. Math. Phys. 71, 132 (2020). https://doi.org/10.1007/s00033-020-01362-0

Download citation

  • Received:

  • Revised:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-020-01362-0

Keywords

Mathematics Subject Classification

Search

Navigation