Abstract
Measurements of anisotropic flow coefficients with two- and multi-particle cumulants for inclusive charged particles in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) and 2.76 TeV are reported in the pseudorapidity range |η| < 0.8 and transverse momentum 0.2 < pT < 50 GeV/c. The full data sample collected by the ALICE detector in 2015 (2010), corresponding to an integrated luminosity of 12.7 (2.0) μb−1 in the centrality range 0-80%, is analysed. Flow coefficients up to the sixth flow harmonic (v6) are reported and a detailed comparison among results at the two energies is carried out. The pT dependence of anisotropic flow coefficients and its evolution with respect to centrality and harmonic number n are investigated. An approximate power-law scaling of the form vn(pT) ∼ p n/3T is observed for all flow harmonics at low pT (0.2 < pT < 3 GeV/c). At the same time, the ratios vn/v n/ m m are observed to be essentially independent of pT for most centralities up to about pT = 10 GeV/c. Analysing the differences among higher-order cumulants of elliptic flow (v2), which have different sensitivities to flow fluctuations, a measurement of the standardised skewness of the event-by-event v2 distribution P(v2) is reported and constraints on its higher moments are provided. The Elliptic Power distribution is used to parametrise P(v2), extracting its parameters from fits to cumulants. The measurements are compared to different model predictions in order to discriminate among initial-state models and to constrain the temperature dependence of the shear viscosity to entropy-density ratio.

Article PDF
Download to read the full article text
Similar content being viewed by others

Fluctuations of anisotropic flow in Pb+Pb collisions at \( \sqrt{{\mathrm{s}}_{\mathrm{NN}}} \) = 5.02 TeV with the ATLAS detector
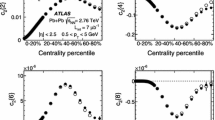
Measurement of flow harmonics with multi-particle cumulants in Pb+Pb collisions at \(\sqrt{s_{\mathrm {NN}}}=2.76\) TeV with the ATLAS detector
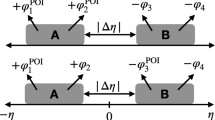
Transverse momentum decorrelation of the flow vector in Pb–Pb collisions at \(\sqrt{s_{_{\textrm{NN}}}}\) = 5.02 TeV
Avoid common mistakes on your manuscript.
References
J.-Y. Ollitrault, Anisotropy as a signature of transverse collective flow, Phys. Rev. D 46 (1992) 229 [INSPIRE].
S.A. Voloshin, A.M. Poskanzer and and R. Snellings, Collective phenomena in non-central nuclear collisions, Landolt-Bornstein 23 (2010) 293 [arXiv:0809.2949].
PHOBOS collaboration, B. Alver et al., System size, energy, pseudorapidity and centrality dependence of elliptic flow, Phys. Rev. Lett. 98 (2007) 242302 [nucl-ex/0610037] [INSPIRE].
PHOBOS collaboration, B. Alver et al., Importance of correlations and fluctuations on the initial source eccentricity in high-energy nucleus-nucleus collisions, Phys. Rev. C 77 (2008) 014906 [arXiv:0711.3724] [INSPIRE].
B. Alver and G. Roland, Collision geometry fluctuations and triangular flow in heavy-ion collisions, Phys. Rev. C 81 (2010) 054905 [Erratum ibid. C 82 (2010) 039903] [arXiv:1003.0194] [INSPIRE].
ALICE collaboration, Higher harmonic anisotropic flow measurements of charged particles in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV, Phys. Rev. Lett. 107 (2011) 032301 [arXiv:1105.3865] [INSPIRE].
ATLAS collaboration, Measurement of the azimuthal anisotropy for charged particle production in \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV lead-lead collisions with the ATLAS detector, Phys. Rev. C 86 (2012) 014907 [arXiv:1203.3087] [INSPIRE].
CMS collaboration, Measurement of higher-order harmonic azimuthal anisotropy in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV, Phys. Rev. C 89 (2014) 044906 [arXiv:1310.8651] [INSPIRE].
M. Luzum and P. Romatschke, Conformal relativistic viscous hydrodynamics: applications to RHIC results at \( \sqrt{s_{\mathrm{NN}}}=200 \) GeV, Phys. Rev. C 78 (2008) 034915 [Erratum ibid. C 79 (2009) 039903] [arXiv:0804.4015] [INSPIRE].
S. Voloshin and Y. Zhang, Flow study in relativistic nuclear collisions by Fourier expansion of Azimuthal particle distributions, Z. Phys. C 70 (1996) 665 [hep-ph/9407282] [INSPIRE].
T. Hirano et al., Hadronic dissipative effects on elliptic flow in ultrarelativistic heavy-ion collisions, Phys. Lett. B 636 (2006) 299 [nucl-th/0511046] [INSPIRE].
P. Romatschke, New developments in relativistic viscous hydrodynamics, Int. J. Mod. Phys. E 19 (2010) 1 [arXiv:0902.3663] [INSPIRE].
C. Shen, U. Heinz, P. Huovinen and H. Song, Systematic parameter study of hadron spectra and elliptic flow from viscous hydrodynamic simulations of Au+Au collisions at \( \sqrt{s_{\mathrm{NN}}}=200 \) GeV, Phys. Rev. C 82 (2010) 054904 [arXiv:1010.1856] [INSPIRE].
S. Ryu et al., Importance of the bulk viscosity of QCD in ultrarelativistic heavy-ion collisions, Phys. Rev. Lett. 115 (2015) 132301 [arXiv:1502.01675] [INSPIRE].
S. Pratt, E. Sangaline, P. Sorensen and H. Wang, Constraining the eq. of state of super-hadronic matter from heavy-ion collisions, Phys. Rev. Lett. 114 (2015) 202301 [arXiv:1501.04042] [INSPIRE].
J.E. Bernhard, J.S. Moreland, S.A. Bass, J. Liu and U. Heinz, Applying Bayesian parameter estimation to relativistic heavy-ion collisions: simultaneous characterization of the initial state and quark-gluon plasma medium, Phys. Rev. C 94 (2016) 024907 [arXiv:1605.03954] [INSPIRE].
J. Auvinen, J.E. Bernhard, S.A. Bass and I. Karpenko, Investigating the collision energy dependence of η/s in the beam energy scan at the BNL Relativistic Heavy Ion Collider using Bayesian statistics, Phys. Rev. C 97 (2018) 044905 [arXiv:1706.03666] [INSPIRE].
H. Niemi, K.J. Eskola, R. Paatelainen and K. Tuominen, Predictions for 5.023 TeV Pb+Pb collisions at the CERN Large Hadron Collider, Phys. Rev. C 93 (2016) 014912 [arXiv:1511.04296] [INSPIRE].
J. Noronha-Hostler, M. Luzum and J.-Y. Ollitrault, Hydrodynamic predictions for 5.02 TeV Pb-Pb collisions, Phys. Rev. C 93 (2016) 034912 [arXiv:1511.06289] [INSPIRE].
F.G. Gardim, F. Grassi, M. Luzum and J.-Y. Ollitrault, Mapping the hydrodynamic response to the initial geometry in heavy-ion collisions, Phys. Rev. C 85 (2012) 024908 [arXiv:1111.6538] [INSPIRE].
STAR collaboration, G. Agakishiev et al., Energy and system-size dependence of two- and four-particle v 2 measurements in heavy-ion collisions at RHIC and their implications on flow fluctuations and nonflow, Phys. Rev. C 86 (2012) 014904 [arXiv:1111.5637] [INSPIRE].
PHOBOS collaboration, B. Alver et al., Non-flow correlations and elliptic flow fluctuations in gold-gold collisions at \( \sqrt{s_{\mathrm{NN}}}=200 \) GeV, Phys. Rev. C 81 (2010) 034915 [arXiv:1002.0534] [INSPIRE].
PHOBOS collaboration, B. Alver et al., Event-by-event fluctuations of azimuthal particle anisotropy in Au+Au collisions at \( \sqrt{s_{NN}}=200 \) GeV, Phys. Rev. Lett. 104 (2010) 142301 [nucl-ex/0702036] [INSPIRE].
ALICE collaboration, Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV, Phys. Rev. Lett. 105 (2010) 252302 [arXiv:1011.3914] [INSPIRE].
S.A. Voloshin, A.M. Poskanzer, A. Tang and G. Wang, Elliptic flow in the Gaussian model of eccentricity fluctuations, Phys. Lett. B 659 (2008) 537 [arXiv:0708.0800] [INSPIRE].
L. Yan and J.-Y. Ollitrault, Universal fluctuation-driven eccentricities in proton-proton, proton-nucleus and nucleus-nucleus collisions, Phys. Rev. Lett. 112 (2014) 082301 [arXiv:1312.6555] [INSPIRE].
L. Yan, J.-Y. Ollitrault and A.M. Poskanzer, Eccentricity distributions in nucleus-nucleus collisions, Phys. Rev. C 90 (2014) 024903 [arXiv:1405.6595] [INSPIRE].
H. Grönqvist, J.-P. Blaizot and J.-Y. Ollitrault, Non-gaussian eccentricity fluctuations, Phys. Rev. C 94 (2016) 034905 [arXiv:1604.07230] [INSPIRE].
ATLAS collaboration, Measurement of flow harmonics with multi-particle cumulants in Pb+Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV with the ATLAS detector, Eur. Phys. J. C 74 (2014) 3157 [arXiv:1408.4342] [INSPIRE].
G. Giacalone, L. Yan, J. Noronha-Hostler and J.-Y. Ollitrault, Skewness of elliptic flow fluctuations, Phys. Rev. C 95 (2017) 014913 [arXiv:1608.01823] [INSPIRE].
ALICE collaboration, Multiparticle azimuthal correlations in p-Pb and Pb-Pb collisions at the CERN Large Hadron Collider, Phys. Rev. C 90 (2014) 054901 [arXiv:1406.2474] [INSPIRE].
L. Yan, J.-Y. Ollitrault and A.M. Poskanzer, Azimuthal anisotropy distributions in high-energy collisions, Phys. Lett. B 742 (2015) 290 [arXiv:1408.0921] [INSPIRE].
J. Jia and S. Radhakrishnan, Limitation of multiparticle correlations for studying the event-by-event distribution of harmonic flow in heavy-ion collisions, Phys. Rev. C 92 (2015) 024911 [arXiv:1412.4759] [INSPIRE].
M. Gyulassy, I. Vitev and X.N. Wang, High p T azimuthal asymmetry in noncentral A+A at RHIC, Phys. Rev. Lett. 86 (2001) 2537 [nucl-th/0012092] [INSPIRE].
X.-N. Wang, Jet quenching and azimuthal anisotropy of large pT spectra in noncentral high-energy heavy ion collisions, Phys. Rev. C 63 (2001) 054902 [nucl-th/0009019] [INSPIRE].
E.V. Shuryak, The azimuthal asymmetry at large p T seem to be too large for a ‘jet quenching’, Phys. Rev. C 66 (2002) 027902 [nucl-th/0112042] [INSPIRE].
ATLAS collaboration, Measurement of the azimuthal angle dependence of inclusive jet yields in Pb+Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV with the ATLAS detector, Phys. Rev. Lett. 111 (2013) 152301 [arXiv:1306.6469] [INSPIRE].
ALICE collaboration, Azimuthal anisotropy of charged jet production in \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV Pb-Pb collisions, Phys. Lett. B 753 (2016) 511 [arXiv:1509.07334] [INSPIRE].
CMS collaboration, Azimuthal anisotropy of charged particles with transverse momentum up to 100 GeV/c in PbPb collisions at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) TeV, Phys. Lett. B 776 (2018) 195 [arXiv:1702.00630] [INSPIRE].
CMS collaboration, Non-Gaussian elliptic-flow fluctuations in PbPb collisions at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) TeV, arXiv:1711.05594 [INSPIRE].
ALICE collaboration, Performance of the ALICE experiment at the CERN LHC, Int. J. Mod. Phys. A 29 (2014) 1430044 [arXiv:1402.4476] [INSPIRE].
ALICE collaboration, The ALICE experiment at the CERN LHC, 2008 JINST 3 S08002 [INSPIRE].
ALICE collaboration, Centrality determination of Pb-Pb collisions at \( \sqrt{s_{NN}}=2.76 \) TeV with ALICE, Phys. Rev. C 88 (2013) 044909 [arXiv:1301.4361] [INSPIRE].
A. Bilandzic, R. Snellings and S. Voloshin, Flow analysis with cumulants: direct calculations, Phys. Rev. C 83 (2011) 044913 [arXiv:1010.0233] [INSPIRE].
A. Bilandzic et al., Generic framework for anisotropic flow analyses with multiparticle azimuthal correlations, Phys. Rev. C 89 (2014) 064904 [arXiv:1312.3572] [INSPIRE].
STAR collaboration, C. Adler et al., Elliptic flow from two and four particle correlations in Au+Au collisions at \( \sqrt{s_{\mathrm{NN}}}=130 \) GeV, Phys. Rev. C 66 (2002) 034904 [nucl-ex/0206001] [INSPIRE].
M. Luzum and J.-Y. Ollitrault, Eliminating experimental bias in anisotropic-flow measurements of high-energy nuclear collisions, Phys. Rev. C 87 (2013) 044907 [arXiv:1209.2323] [INSPIRE].
R. Barlow, Systematic errors: Facts and fictions, in the proceedings of the Conference on Statistical Techniques in Particle Physics , March 18–22, Durhamm, U.K. (2002), hep-ex/0207026 [INSPIRE].
ALICE collaboration, Anisotropic flow of charged particles in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) TeV, Phys. Rev. Lett. 116 (2016) 132302 [arXiv:1602.01119] [INSPIRE].
STAR collaboration, K.H. Ackermann et al., Elliptic flow in Au + Au collisions at \( \sqrt{s_{\mathrm{NN}}}=130 \) GeV, Phys. Rev. Lett. 86 (2001) 402 [nucl-ex/0009011] [INSPIRE].
K.J. Eskola, K. Kajantie, P.V. Ruuskanen and K. Tuominen, Scaling of transverse energies and multiplicities with atomic number and energy in ultrarelativistic nuclear collisions, Nucl. Phys. B 570 (2000) 379 [hep-ph/9909456] [INSPIRE].
H. Niemi, K.J. Eskola and R. Paatelainen, Event-by-event fluctuations in a perturbative QCD + saturation + hydrodynamics model: Determining QCD matter shear viscosity in ultrarelativistic heavy-ion collisions, Phys. Rev. C 93 (2016) 024907 [arXiv:1505.02677] [INSPIRE].
N. Borghini and J.-Y. Ollitrault, Momentum spectra, anisotropic flow and ideal fluids, Phys. Lett. B 642 (2006) 227 [nucl-th/0506045] [INSPIRE].
B.H. Alver, C. Gombeaud, M. Luzum and J.-Y. Ollitrault, Triangular flow in hydrodynamics and transport theory, Phys. Rev. C 82 (2010) 034913 [arXiv:1007.5469] [INSPIRE].
D. Teaney, The effects of viscosity on spectra, elliptic flow and HBT radii, Phys. Rev. C 68 (2003) 034913 [nucl-th/0301099] [INSPIRE].
Z. Qiu and U.W. Heinz, Event-by-event shape and flow fluctuations of relativistic heavy-ion collision fireballs, Phys. Rev. C 84 (2011) 024911 [arXiv:1104.0650] [INSPIRE].
C. Andrés, M. Braun and C. Pajares, Energy loss as the origin of a universal scaling law of the elliptic flow, Eur. Phys. J. A 53 (2017) 41 [arXiv:1609.03927] [INSPIRE].
F.G. Gardim, F. Grassi, M. Luzum and J.-Y. Ollitrault, Breaking of factorization of two-particle correlations in hydrodynamics, Phys. Rev. C 87 (2013) 031901 [arXiv:1211.0989] [INSPIRE].
CMS collaboration, Evidence for transverse momentum and pseudorapidity dependent event plane fluctuations in PbPb and pPb collisions, Phys. Rev. C 92 (2015) 034911 [arXiv:1503.01692] [INSPIRE].
J. Bartels, K.J. Golec-Biernat and H. Kowalski, A modification of the saturation model: DGLAP evolution, Phys. Rev. D 66 (2002) 014001 [hep-ph/0203258] [INSPIRE].
S. McDonald et al., Phys. Rev. C 95 (2017) 064913 [arXiv:1609.02958] [INSPIRE].
W. Zhao, H.-j. Xu and H. Song, Collective flow in 2.76 A TeV and 5.02 A TeV Pb+Pb collisions, Eur. Phys. J. C 77 (2017) 645 [arXiv:1703.10792] [INSPIRE].
Z.-W. Lin et al., A Multi-phase transport model for relativistic heavy ion collisions, Phys. Rev. C 72 (2005) 064901 [nucl-th/0411110] [INSPIRE].
J.S. Moreland, J.E. Bernhard and S.A. Bass, Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions, Phys. Rev. C 92 (2015) 011901 [arXiv:1412.4708] [INSPIRE].
S.A. Bass et al., Microscopic models for ultrarelativistic heavy ion collisions, Prog. Part. Nucl. Phys. 41 (1998) 255 [nucl-th/9803035] [INSPIRE].
B. Betz et al., Cumulants and nonlinear response of high p T harmonic flow at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) TeV, Phys. Rev. C 95 (2017) 044901 [arXiv:1609.05171] [INSPIRE].
J. Noronha-Hostler et al., Bulk viscosity effects in event-by-event relativistic hydrodynamics, Phys. Rev. C 88 (2013) 044916 [arXiv:1305.1981] [INSPIRE].
B. Betz, M. Gyulassy and G. Torrieri, Fourier harmonics of high-p T particles probing the fluctuating intitial condition geometries in heavy-ion collisions, Phys. Rev. C 84 (2011) 024913 [arXiv:1102.5416] [INSPIRE].
R.J. Fries, V. Greco, and P. Sorensen, Coalescence models for hadron formation from quark gluon plasma, Ann. Rev. Nucl. Part. Sci. 58 (2008) 177 [arXiv:0807.4939].
ATLAS collaboration, Measurement of the distributions of event-by-event flow harmonics in lead-lead collisions at = 2.76 TeV with the ATLAS detector at the LHC, JHEP 11 (2013) 183 [arXiv:1305.2942] [INSPIRE].
ALICE collaboration, Event shape engineering for inclusive spectra and elliptic flow in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV, Phys. Rev. C 93 (2016) 034916 [arXiv:1507.06194] [INSPIRE].
J. Schukraft, A. Timmins and S.A. Voloshin, Ultra-relativistic nuclear collisions: event shape engineering, Phys. Lett. B 719 (2013) 394 [arXiv:1208.4563] [INSPIRE].
ALICE collaboration, Anisotropic flow of charged hadrons, pions and (anti-)protons measured at high transverse momentum in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=2.76 \) TeV, Phys. Lett. B 719 (2013) 18 [arXiv:1205.5761] [INSPIRE].
STAR collaboration, J. Adams et al., Azimuthal anisotropy at RHIC: the first and fourth harmonics, Phys. Rev. Lett. 92 (2004) 062301 [nucl-ex/0310029] [INSPIRE].
PHENIX collaboration, A. Adare et al., Elliptic and hexadecapole flow of charged hadrons in Au+Au collisions at \( \sqrt{s_{\mathrm{NN}}}=200 \) GeV, Phys. Rev. Lett. 105 (2010) 062301 [arXiv:1003.5586] [INSPIRE].
C. Gombeaud and J.-Y. Ollitrault, Effects of flow fluctuations and partial thermalization on v(4), Phys. Rev. C 81 (2010) 014901 [arXiv:0907.4664] [INSPIRE].
P.F. Kolb, L.-W. Chen, V. Greco and C.M. Ko, Momentum anisotropies in the quark coalescence model, Phys. Rev. C 69 (2004) 051901 [nucl-th/0402049] [INSPIRE].
P. Liu and R.A. Lacey, Acoustic scaling of linear and mode-coupled anisotropic flow; implications for precision extraction of the specific shear viscosity, arXiv:1802.06595 [INSPIRE].
R.A. Lacey, A. Taranenko, N.N. Ajitanand and J.M. Alexander, Scaling of the higher-order flow harmonics: implications for initial-eccentricity models and the ‘viscous horizon’, arXiv:1105.3782 [INSPIRE].
B. Alver, M. Baker, C. Loizides and P. Steinberg, The PHOBOS glauber Monte Carlo, arXiv:0805.4411 [INSPIRE].
J. Noronha-Hostler, L. Yan, F.G. Gardim and J.-Y. Ollitrault, Linear and cubic response to the initial eccentricity in heavy-ion collisions, Phys. Rev. C 93 (2016) 014909 [arXiv:1511.03896] [INSPIRE].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
A.I. Alikhanyan National Science Laboratory (Yerevan Physics Institute) Foundation, Yerevan, Armenia
A. Grigoryan & V. Papikyan
Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
H. Bello Martinez, R. S. Camacho, A. Fernández Téllez, P. González-Zamora, I. B. Guzman, E. G. Hernandez, M. I. Martínez, L. A. P. Moreno, S. R. Navarro, J. C. C. Noris, M. Rodríguez Cahuantzi, G. Tejeda Muñoz, A. Vargas, S. Vergara Limón & A. Villatoro Tello
Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine, Kiev, Ukraine
A. Alkin, V. Trubnikov, V. Yurchenko & G. Zinovjev
Bose Institute, Department of Physics and Centre for Astroparticle Physics and Space Science (CAPSS), Kolkata, India
R. Biswas, S. Biswas, S. Das, S. K. Ghosh, M. Mukherjee, S. K. Prasad & S. Raha
Budker Institute for Nuclear Physics, Novosibirsk, Russia
Y. Pestov
California Polytechnic State University, San Luis Obispo, California, United States
J. L. Klay
Central China Normal University, Wuhan, China
P. Bartalini, W. Chang, Y. Ding, S. Kar, X. L. Li, Y. Mao, P. Palni, H. Pei, X. Peng, X. Ren, Q. Shou, M. Wang, R. Xu, Z. Yin, X. Zhang, Y. Zhang, Z. Zhang, D. Zhou, H. Zhu, J. Zhu, Y. Zhu & S. Zou
Centre de Calcul de l’IN2P3, Villeurbanne, Lyon, France
R. Vernet
Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN), Havana, Cuba
C. Ceballos Sanchez, R. A. Diaz & E. López Torres
Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
G. Herrera Corral
Centro Fermi - Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi’, Rome, Italy
A. Alici, F. Carnesecchi, L. Cifarelli, D. De Gruttola, D. Hatzifotiadou, R. Nania, F. Noferini, J.-P. Revol & A. Zichichi
Chicago State University, Chicago, Illinois, United States
E. Garcia-Solis & A. Harton
China Institute of Atomic Energy, Beijing, China
X. Li
Chonbuk National University, Jeonju, Republic of Korea
E. J. Kim
Comenius University Bratislava, Faculty of Mathematics, Physics and Informatics, Bratislava, Slovakia
M. Meres, M. Pikna, B. Sitar, P. Strmen, A. Szabo & I. Szarka
COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
Y. Ali, J. B. Butt, M. U. Naru, M. Suleymanov, U. Tabassam & A. Zaman
Creighton University, Omaha, Nebraska, United States
C. Anson & J. E. Seger
Department of Physics, Aligarh Muslim University, Aligarh, India
M. D. Azmi, T. Hussain, S. Khan, A. Khatun, M. Mohisin Khan & M. Tariq
Department of Physics, Ohio State University, Columbus, Ohio, United States
J. T. Buxton, T. J. Humanic, A. M. Kubera & M. A. Lisa
Department of Physics, Pusan National University, Pusan, Republic of Korea
A. Borissov, S. U. Chung, J. Eum, B. Lim, J. Song & I.-K. Yoo
Department of Physics, Sejong University, Seoul, Republic of Korea
D. S. Hwang & S. Kim
Department of Physics, University of California, Berkeley, California, United States
F. T.-. Acosta
Department of Physics, University of Oslo, Oslo, Norway
I. C. Arsene, P. C. Batzing, O. Dordic, A. Lardeux, S. Lindal, S. M. Mahmood, M. Richter, K. Røed, T. B. Skaali, T. S. Tveter, J. Wikne & C. Zhao
Department of Physics and Technology, University of Bergen, Bergen, Norway
J. Alme, L. Altenkamper, Ø. Djuvsland, M. R. Ersdal, F. M. Fionda, J. Nystrand, A. Rehman, D. Röhrich, G. J. Tambave, K. Ullaland, A. Velure, B. Wagner & Z. Zhou
Dipartimento di Fisica dell’Università ‘La Sapienza’ and Sezione INFN, Rome, Italy
F. Meddi
Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
A. De Falco & G. L. Usai
Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
P. Camerini, R. Lea, G. V. Margagliotti, R. Rui & M. Suljic
Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
A. M. Barbano, L. Barioglio, S. Beole, A. Bianchi, E. Botta, S. Delsanto, A. Ferretti, G. G. Fronze, M. Gagliardi, M. Gallio, A. Lattuca, M. Masera, L. Micheletti, M. Puccio, K. Shtejer, S. Trogolo & E. Vercellin
Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
A. Alici, S. Arcelli, F. Bellini, F. Carnesecchi, L. Cifarelli, M. Colocci, B. Guerzoni, N. Jacazio, G. Scioli & A. Zichichi
Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Catania, Italy
R. Barbera, K. Garg, P. La Rocca, C. Petta & F. Riggi
Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padova, Italy
M. Faggin, A. Festanti, P. Giubilato, M. Lunardon, S. Moretto, A. Rossi, F. Scarlassara, F. Soramel & C. Terrevoli
Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
A. De Caro, D. De Gruttola, S. De Pasquale, M. Fusco Girard, E. Meninno & T. Virgili
Dipartimento DISAT del Politecnico and Sezione INFN, Turin, Italy
M. Agnello, S. Bufalino, F. Grosa & I. Ravasenga
Dipartimento di Scienze e Innovazione Tecnologica dell’Università del Piemonte Orientale and INFN Sezione di Torino, Alessandria, Italy
P. Cortese, L. Ramello & M. Sitta
Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
G. E. Bruno, D. Di Bari, M. Mazzilli, G. Trombetta & G. Volpe
European Organization for Nuclear Research (CERN), Geneva, Switzerland
G. Aglieri Rinella, D. Andreou, M. Angeletti, A. Augustinus, K. Barth, F. Bellini, D. Berzano, L. Betev, F. Bock, M. Bonora, G. E. Bruno, P. Buncic, F. Carena, W. Carena, S. Chapeland, V. Chibante Barroso, P. Chochula, D. Colella, F. Costa, A. Di Mauro, R. Divià, A. Dobrin, G. Eulisse, A. Festanti, M. Floris, A. Francescon, U. Fuchs, C. Gargiulo, C. Grigoras, J. F. Grosse-Oetringhaus, R. Haake, H. Hillemanns, P. Hristov, A. Kalweit, P. Karczmarczyk, M. Keil, J. Klein, A. Kluge, M. L. Knichel, I. Lakomov, E. Laudi, M. Lupi, M. Mager, P. Martinengo, M. Martinez Pedreira, N. Mohammadi, A. Morsch, L. Musa, R. A. Negrao De Oliveira, J. Niedziela, O. Pinazza, F. Reidt, P. Riedler, W. Riegler, D. Rohr, K. Šafařík, J. Schukraft, Y. Schutz, R. Shahoyan, K. M. Sielewicz, G. Simonetti, M. Suljic, A. Tauro, A. Telesca, J. W. Van Hoorne, P. Vande Vyvre, B. von Haller, D. Vranic, A. Wegrzynek, S. C. Wenzel, G. A. Willems, C. Zampolli & M. B. Zimmermann
Faculty of Engineering and Science, Western Norway University of Applied Sciences, Bergen, Norway
H. Helstrup, K. F. Hetland, B. Kileng, S. V. Nesbo & M. M. Storetvedt
Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
J. Bielčík, M. Broz, J. G. Contreras, D. Horak, R. Lavicka & V. Petráček
Faculty of Science, P.J. Šafárik University, Košice, Slovakia
M. Bombara, A. Kravčáková, M. Šefčík, L. Tropp & J. Vrláková
Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
J. de Cuveland, S. Gorbunov, D. Hutter, S. Kirsch, I. Kisel, M. Krzewicki, S. L. La Pointe, J. Lehrbach, V. Lindenstruth & G. Neskovic
Gangneung-Wonju National University, Gangneung, Republic of Korea
Y. W. Baek & J. S. Kim
Gauhati University, Department of Physics, Guwahati, India
B. Bhattacharjee, N. Hussain & P. Sarma
Helmholtz-Institut für Strahlen- und Kernphysik, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, Germany
M. Ball, B. Ketzer, K. Münning & V. Ratza
Helsinki Institute of Physics (HIP), Helsinki, Finland
E. J. Brucken, T. E. Hilden, V. Litichevskyi, M. M. Mieskolainen, R. Orava, S. S. Räsänen & S. Saarinen
Hiroshima University, Hiroshima, Japan
D. Sekihata, K. Shigaki, T. Sugitate, K. Yamakawa & S. Yano
Hochschule Worms, Zentrum für Technologietransfer und Telekommunikation (ZTT), Worms, Germany
R. Keidel
Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest, Romania
C. Andrei, A. Bercuci, A. Herghelegiu, M. Petrovici, A. Pop, C. Schiaua & M. G. Tarzila
Indian Institute of Technology Bombay (IIT), Mumbai, India
N. Agrawal, H. Bhatt, S. Dash, P. Dhankher, M. B. Jadhav, J. Kumar, S. Kumar, B. Naik, B. K. Nandi, A. Narayan, R. Nayak, A. K. Pandey, B. Sahoo, P. Sett & R. Varma
Indian Institute of Technology Indore, Indore, India
S. De, A. Khuntia, P. Pareek, P. Sahoo, R. Sahoo, D. Thakur & S. Tripathy
Indonesian Institute of Sciences, Jakarta, Indonesia
S. Sumowidagdo
INFN, Laboratori Nazionali di Frascati, Frascati, Italy
N. Bianchi, A. Fantoni, P. Gianotti, P. Larionov, V. Muccifora, S. Pisano, F. Ronchetti & M. Toppi
INFN, Sezione di Bari, Bari, Italy
F. Barile, F. Colamaria, D. Colella, G. de Cataldo, D. Elia, G. Fiorenza, V. Manzari, A. Mastroserio & E. Nappi
INFN, Sezione di Bologna, Bologna, Italy
A. Alici, P. Antonioli, F. Cindolo, D. Hatzifotiadou, A. Margotti, R. Nania, F. Noferini, O. Pinazza, R. Preghenella, E. Scapparone, J. Wilkinson & M. C. S. Williams
INFN, Sezione di Cagliari, Cagliari, Italy
E. A. R. Casula, C. Cicalo, A. Masoni & S. Siddhanta
INFN, Sezione di Catania, Catania, Italy
A. Badalà
INFN, Sezione di Padova, Padova, Italy
F. Antinori, A. Dainese, B. Di Ruzza, A. Rossi & R. Turrisi
INFN, Sezione di Roma, Rome, Italy
M. A. Mazzoni
INFN, Sezione di Torino, Turin, Italy
B. Alessandro, R. Arnaldi, S. Bagnasco, D. Berzano, E. Bruna, M. Concas, Y. Corrales Morales, N. De Marco, A. Feliciello, P. Giubellino, J. Klein, C. Oppedisano, B. Paul, F. Prino, E. Scomparin & V. Zaccolo
INFN, Sezione di Trieste, Trieste, Italy
E. Fragiacomo, G. Luparello & S. Piano
Inha University, Incheon, Republic of Korea
Y. W. Baek, N. K. Behera, S. Cho, M. Kim, V. Kučera, M. J. Kweon, J. Park & J. H. Yoon
Institut de Physique Nucléaire d’Orsay (IPNO), Institut National de Physique Nucléaire et de Physique des Particules (IN2P3/CNRS), Université de Paris-Sud, Université Paris-Saclay, Orsay, France
Z. Conesa del Valle, J. Crkovská, B. Espagnon, C. Hadjidakis, L. Massacrier, C. Suire & M. Tarhini
Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
D. Finogeev, A. Furs, O. Karavichev, T. Karavicheva, E. Karpechev, A. Konevskikh, A. Kurepin, A. B. Kurepin, A. Maevskaya, I. Pshenichnov, A. Reshetin, A. Shabanov, A. Tikhonov & N. Topilskaya
Institute for Subatomic Physics, Utrecht University/Nikhef, Utrecht, Netherlands
C. Bedda, L. V. R. Doremalen, A. Grelli, M. R. Haque, S. Jaelani, D. L. D. Keijdener, E. Leogrande, D. F. Lodato, J. Margutti, A. Mischke, N. Mohammadi, A. P. Mohanty, G. Nooren, T. Peitzmann, T. Richert, M. H. P. Sas, R. J. M. Snellings, B. A. Trzeciak, M. van Leeuwen, A. M. Veen, L. Vermunt & H. Wang
Institute for Theoretical and Experimental Physics, Moscow, Russia
A. Akindinov, S. Kiselev, D. Mal’Kevich, K. Mikhaylov, S. Shirinkin, R. Sultanov, K. Voloshin & N. Zhigareva
Institute of Experimental Physics, Slovak Academy of Sciences, Košice, Slovakia
D. Colella, P. Kalinak, I. Králik, M. Krivda & J. Musinsky
Institute of Physics, Bhubaneswar, India
S. Sahoo, P. K. Sahu & S. Swain
Institute of Physics of the Czech Academy of Sciences, Prague, Czech Republic
J. Mareš & P. Závada
Institute of Space Science (ISS), Bucharest, Romania
A. Danu, C. M. Mitu, C. Ristea, A. Sevcenco & I. Stan
Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
T. Alt, H. Appelshäuser, R. Bailhache, E. Bartsch, C. Blume, L. Bratrud, T. A. Broker, H. Buesching, P. Dillenseger, B. Dönigus, S. T. Heckel, E. Hellbär, P. Huhn, C. Klein, M. Krüger, P. Luettig, M. Marquard, R. H. Munzer, R. A. Negrao De Oliveira, E. Perez Lezama, V. Peskov, F. Pliquett, B. T. Rascanu, P. Reichelt, R. Renfordt, H. S. Scheid, N. V. Schmidt, A. Toia & J. Wiechula
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
E. Cuautle, S. A. Iga Buitron, A. N. Mishra, L. Nellen, A. Ortiz Velasquez, G. Paić, E. D. Rosas & O. V. Rueda
Instituto de Física, Universidade Federal do Rio Grande do Sul (UFRGS), Porto Alegre, Brazil
M. B. Gay Ducati, L. G. Pereira & R. P. Pezzi
Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
R. Alfaro Molina, D. M. Goméz Coral, V. Grabski, A. Menchaca-Rocha, A. Sandoval & E. Serradilla
iThemba LABS, National Research Foundation, Somerset West, South Africa
Z. Buthelezi, S. Foertsch, M. Marchisone, S. Murray, A. Sarkar & K. Senosi
Johann-Wolfgang-Goethe Universität Frankfurt Institut für Informatik, Fachbereich Informatik und Mathematik, Frankfurt, Germany
H. Engel, A. Gomez Ramirez, U. Kebschull & C. Lara
Joint Institute for Nuclear Research (JINR), Dubna, Russia
B. Batyunya, S. Grigoryan, L. Malinina, K. Mikhaylov, P. Nomokonov, V. Pozdniakov, E. Rogochaya, B. Rumyantsev & A. Vodopyanov
Korea Institute of Science and Technology Information, Daejeon, Republic of Korea
S. U. Ahn
KTO Karatay University, Konya, Turkey
A. Karasu Uysal & S. Yalcin
Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
G. Conesa Balbastre, J. Faivre, C. Furget, R. Guernane, H. Hassan, R. Hosokawa, J. Norman, A. Vauthier & H. Yokoyama
Lawrence Berkeley National Laboratory, Berkeley, California, United States
N. Apadula, A. Collu, L. Greiner, B. Jacak, P. M. Jacobs, Y. S. Lai, A. Liu, C. Loizides, M. I. A. Munoz & M. Ploskon
Lund University Department of Physics, Division of Particle Physics, Lund, Sweden
J. Adolfsson, P. Christiansen, H. M. Ljunggren, A. Oskarsson, T. Richert, D. Silvermyr, E. Stenlund & V. Vislavicius
Nagasaki Institute of Applied Science, Nagasaki, Japan
H. Hamagaki & K. Oyama
Nara Women’s University (NWU), Nara, Japan
M. Shimomura
National and Kapodistrian University of Athens, School of Science, Department of Physics, Athens, Greece
P. Ganoti, F. Roukoutakis & M. Vasileiou
National Centre for Nuclear Research, Warsaw, Poland
A. Deloff, O. Kovalenko, P. Kurashvili, R. Nair, K. Redlich, T. Siemiarczuk & G. Wilk
National Institute of Science Education and Research, HBNI, Jatni, India
R. C. Baral, A. Dash, M. Dukhishyam, C. Jena, S. Kundu, B. Mohanty, K. Nayak & R. Singh
National Nuclear Research Center, Baku, Azerbaijan
A. Rustamov
National Research Centre Kurchatov Institute, Moscow, Russia
D. Aleksandrov, D. Blau, S. Fokin, M. Ippolitov, V. Manko, S. Nikolaev, S. Nikulin, A. Nyanin, D. Peresunko, E. Ryabinkin, Y. Sibiriak, A. Vasiliev & A. Vinogradov
Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
I. G. Bearden, C. Bourjau, C. H. Christensen, J. J. Gaardhøje, K. Gajdosova, K. Gulbrandsen, B. S. Nielsen, V. Pacik, L. O. D. L. Pimentel, F. Thoresen & Y. Zhou
Nikhef, National institute for subatomic physics, Amsterdam, Netherlands
D. Caffarri, P. Christakoglou, C. Deplano, Z. Khabanova, P. G. Kuijer, F. Lehas & G. Simatovic
NRC ‘Kurchatov Institute’ IHEP, Protvino, Russia
S. Evdokimov, V. Izucheev, Y. Kharlov, E. Kondratyuk, B. Polichtchouk, R. Rogalev, S. Sadovsky & A. Shangaraev
NRNU Moscow Engineering Physics Institute, Moscow, Russia
V. Belyaev, A. Bogdanov, V. Grigoriev, V. Kaplin, N. Kondratyeva, V. Loginov, Y. Melikyan, V. Samsonov & I. Selyuzhenkov
Nuclear Physics Group, STFC Daresbury Laboratory, Daresbury, United Kingdom
L. S. Barnby & R. C. Lemmon
Nuclear Physics Institute of the Czech Academy of Sciences, Řež u Prahy, Czech Republic
D. Adamová, J. Bielč´ıková, F. Krizek, V. Kučera, S. Kushpil & M. Šumbera
Oak Ridge National Laboratory, Oak Ridge, Tennessee, United States
T. M. Cormier, L. Cunqueiro, M. Fasel, C. Loizides, M. G. Poghosyan, K. F. Read, B. Schaefer, N. V. Schmidt & P. Stankus
Petersburg Nuclear Physics Institute, Gatchina, Russia
Y. Berdnikov, V. Ivanov, A. Khanzadeev, E. Kryshen, M. Malaev, V. Nikulin, V. Riabov, Y. Ryabov, V. Samsonov & M. Zhalov
Physics department, Faculty of science, University of Zagreb, Zagreb, Croatia
F. Erhardt, M. Jercic, M. Planinic, N. Poljak & A. Utrobicic
Physics Department, Panjab University, Chandigarh, India
M. M. Aggarwal, S. Dudi, A. K. Duggal, L. Kumar, S. Parmar, A. Sharma & N. Sharma
Physics Department, University of Jammu, Jammu, India
R. Bala, A. Bhasin, I. R. Bhat, A. Gupta, R. Gupta, S. Rajput, S. Sambyal & A. Sharma
Physics Department, University of Rajasthan, Jaipur, India
R. Raniwala & S. Raniwala
Physikalisches Institut, Eberhard-Karls-Universität Tübingen, Tübingen, Germany
H. R. Schmidt, M. Schmidt & M. A. Völkl
Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
V. Anguelov, M. Arslandok, H. Beck, M. C. Danisch, A. Deisting, P. Glässel, J. Kim, M. Kim, S. Klewin, M. L. Knichel, M. K. Köhler, L. Leardini, J. Mercado Pérez, A. Ohlson, Y. Pachmayer, K. Reygers, R. Schicker, M. O. Schmidt, J. Stachel, D. F. Weiser & B. Windelband
Physik Department, Technische Universität München, Munich, Germany
O. W. Arnold, A. Bilandzic, A. Chauvin, T. Dahms, L. Fabbietti, P. Gasik, B. Hohlweger, A. M. Mathis, D. L. Mihaylov, G. Simonetti, O. Vázquez Doce & I. Vorobyev
Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung GmbH, Darmstadt, Germany
M. Al-Turany, A. Andronic, R. Averbeck, P. Braun-Munzinger, A. Caliva, A. Deisting, A. Dubla, P. Foka, U. Frankenfeld, C. Garabatos, P. Giubellino, V. Gonzalez, J. M. Gronefeld, R. Grosso, M. K. Habib, S. Hornung, M. Ivanov, R. T. Jimenez Bustamante, T. Kollegger, L. Kreis, C. Lippmann, P. Malzacher, A. Marín, N. A. Martin, S. Masciocchi, D. Miskowiec, M. Nicassio, J. Onderwaater, C. Schmidt, K. Schwarz, K. Schweda, I. Selyuzhenkov, F. Sozzi, D. Vranic & S. G. Weber
Rudjer Bošković Institute, Zagreb, Croatia
T. Antičić
Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
D. Budnikov, S. Filchagin, R. Ilkaev, A. Kuryakin, A. Mamonov, S. Nazarenko, V. Punin, A. Tumkin & N. Zaviyalov
Saha Institute of Nuclear Physics, Kolkata, India
S. Chattopadhyay, D. Das, I. Das, J. Ghosh, H. Hushnud, M. S. Islam, P. Roy, W. Shaikh & T. Sinha
School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
H. A. Andrews, D. Evans, K. L. Graham, P. G. Jones, A. Jusko, M. Krivda, R. Lietava, O. Villalobos Baillie, E. Willsher & N. Zardoshti
Sección Física, Departamento de Ciencias, Pontificia Universidad Católica del Perú, Lima, Peru
J. L. Bazo Alba, E. Calvo Villar, E. Endress, A. M. Gago & C. S. Meza
Shanghai Institute of Applied Physics, Shanghai, China
Q. Shou
Stefan Meyer Institut für Subatomare Physik (SMI), Vienna, Austria
P. Buhler, A. A. Capon, S. Lehner, K. Suzuki, M. Weber & J. Zmeskal
SUBATECH, IMT Atlantique, Université de Nantes, CNRS-IN2P3, Nantes, France
L. Aphecetche, B. Audurier, G. Batigne, B. Erazmus, A. Francisco, M. Germain, M. Guittiere, G. Martínez García, E. Masson, A. Morreale, P. Pillot, A. Shabetai, D. Stocco & M. Tarhini
Suranaree University of Technology, Nakhon Ratchasima, Thailand
C. Kobdaj & W. Poonsawat
Technical University of Košice, Košice, Slovakia
J. Cabala, S. Jadlovska, J. Jadlovsky, M. Oravec, M. Vala & D. Voscek
Technische Universität München, Excellence Cluster ‘Universe’, Munich, Germany
O. W. Arnold, A. Bilandzic, A. Chauvin, T. Dahms, L. Fabbietti, P. Gasik, C. Jahnke, A. M. Mathis, O. Vázquez Doce & I. Vorobyev
The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
J. Bhom, J. Figiel, L. Görlich, M. M. Kielbowicz, M. Kowalski, A. Matyja, C. Mayer, J. Otwinowski, A. Rybicki & I. Sputowska
The University of Texas at Austin, Austin, Texas, United States
J. T. Blair, E. F. Gauger, C. Markert & D. Thomas
Universidad Autónoma de Sinaloa, Culiacán, Mexico
L. G. E. Beltran, C. D. Galvan, I. León Monzón, P. L. M. Podesta-Lerma & S. R. Torres
Universidade de São Paulo (USP), São Paulo, Brazil
M. Bregant, C. de Conti, H. F. Degenhardt, D. Domenicis Gimenez, M. A. S. Figueredo, C. Jahnke, P. F. T. Matuoka, M. G. Munhoz, H. Natal da Luz, A. C. Oliveira Da Silva, A. A. P. Suaide & H. J. C. Zanoli
Universidade Estadual de Campinas (UNICAMP), Campinas, Brazil
D. S. D. Albuquerque, D. D. Chinellato, R. D. De Souza & J. Takahashi
Universidade Federal do ABC, Santo Andre, Brazil
M. R. Cosentino
University College of Southeast Norway, Tonsberg, Norway
R. Langoy & J. Lien
University of Cape Town, Cape Town, South Africa
J. Cleymans, T. Dietel, S. Mhlanga & A. M. Whitehead
University of Houston, Houston, Texas, United States
R. Anwar, R. Bellwied, L. Bianchi, M. Jin, A. G. Knospe, C. J. Myers, F. Ng, S. P. Pathak, L. Pinsky, D. B. Piyarathna, A. R. Timmins & E. N. Umaka
University of Jyväskylä, Jyväskylä, Finland
B. Chang, D. J. Kim, J. E. Parkkila, J. Rak, M. Slupecki, T. W. Snellman, W. H. Trzaska, M. Vargyas & J. Viinikainen
University of Liverpool, Department of Physics Oliver Lodge Laboratory, Liverpool, United Kingdom
M. Borri, M. Chartier, C. Hills, J. P. Iddon, S. W. Lindsay & J. Norman
University of Split, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Split, Croatia
S. Gotovac, P. Loncar, E. Mudnic & L. Vickovic
University of Tennessee, Knoxville, Tennessee, United States
R. A. Bertens, A. J. Castro, C. Hughes, A. Matyja, C. Nattrass, K. F. Read, S. Sorensen & W. E. Witt
University of the Witwatersrand, Johannesburg, South Africa
M. Marchisone & Z. Vilakazi
University of Tokyo, Tokyo, Japan
T. Gunji, S. Hayashi, H. Murakami, Y. Sekiguchi, T. Tsuji & Y. Watanabe
University of Tsukuba, Tsukuba, Japan
O. Busch, T. Chujo, R. Hosokawa, M. Inaba, B. Kim, Y. Miake, S. Sakai, N. Tanaka, Y. Watanabe & H. Yokoyama
Université Clermont Auvergne, CNRS/IN2P3, LPC, Clermont-Ferrand, France
V. Barret, N. Bastid, T. Chowdhury, P. Crochet, P. Dupieux, V. J. G. Feuillard, X. Lopez, F. Manso, S. Porteboeuf-Houssais, P. Rosnet & Z. Zhang
Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, Lyon, France
C. Cheshkov, B. Cheynis, L. Ducroux, M. Marchisone, B. Teyssier, R. Tieulent & A. Uras
Université de Strasbourg, CNRS, IPHC UMR 7178, F-67000 Strasbourg, France, Strasbourg, France
I. Belikov, J. C. Hamon, B. Hippolyte, C. Kuhn, A. Maire, F. Rami, C. Roy, Y. Schutz & S. Senyukov
Université Paris-Saclay Centre d’ Études de Saclay (CEA), IRFU, Department de Physique Nucléaire (DPhN), Saclay, France
A. Baldisseri, H. Borel, J. Castillo Castellanos, V. J. G. Feuillard, S. Panebianco, H. Pereira Da Costa & A. Rakotozafindrabe
Università degli Studi di Pavia, Pavia, Italy
G. Boca, S. Costanza & A. Rotondi
Università di Brescia, Brescia, Italy
G. Bonomi & D. Pagano
V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
I. Altsybeev, G. Feofilov, V. Kovalenko, V. Vechernin, A. Zarochentsev & V. Zherebchevskii
Variable Energy Cyclotron Centre, Kolkata, India
S. Acharya, Z. Ahammed, S. N. Alam, P. P. Bhaduri, S. Chandra, S. Chattopadhyay, A. K. Dubey, P. Ghosh, S. A. Khan, J. Mitra, S. Muhuri, T. K. Nayak, R. N. Patra, S. Sadhu, S. K. Saha, J. Saini, D. Sarkar, N. Sarkar, A. I. Sheikh, R. Singaraju, V. Singhal & S. Thakur
Warsaw University of Technology, Warsaw, Poland
L. K. Graczykowski, M. J. Jakubowska, M. A. Janik, A. Kisiel, J. W. Myrcha, J. Niedziela, J. Oleniacz, J. Pluta, P. S. Rokita, K. Roslon, T. P. Trzcinski & H. Zbroszczyk
Wayne State University, Detroit, Michigan, United States
S. Basu, M. Konyushikhin, W. J. Llope, J. Pan, C. A. Pruneau, J. Putschke, M. A. Saleh & S. A. Voloshin
Westfälische Wilhelms-Universität Münster, Institut für Kernphysik, Münster, Germany
A. Borissov, L. Cunqueiro, L. Feldkamp, F. Herrmann, C. Klein-Bösing, J. R. Luhder, D. A. Moreira De Godoy, D. Mühlheim, A. Passfeld, H. Poppenborg, J. P. Wessels, U. Westerhoff & G. A. Willems
Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
G. G. Barnaföldi, G. Bencedi, D. Berenyi, G. Biro, L. Boldizsár, G. Hamar, M. Kofarago, P. Lévai, A. Lowe, S. Pochybova, D. Varga & R. Vértesi
Yale University, New Haven, Connecticut, United States
S. Aiola, H. Caines, R. J. Ehlers, E. Epple, J. W. Harris, K. Lapidus, R. D. Majka, J. D. Mulligan, M. H. Oliver & N. Smirnov
Yonsei University, Seoul, Republic of Korea
J. H. Kang, D. Kim, H. Kim, T. Kim, T. Kim, Y. Kwon, S. Lee & H. Oh
Dipartimento DET del Politecnico di Torino, Turin, Italy
M. Concas
M.V. Lomonosov Moscow State University, D.V. Skobeltsyn Institute of Nuclear, Physics, Moscow, Russia
L. Malinina
Department of Applied Physics, Aligarh Muslim University, Aligarh, India
M. Mohisin Khan
Institute of Theoretical Physics, University of Wroclaw, Wroclaw, Poland
K. Redlich
- S. Acharya
You can also search for this author in PubMed Google Scholar
- F. T.-. Acosta
You can also search for this author in PubMed Google Scholar
- D. Adamová
You can also search for this author in PubMed Google Scholar
- J. Adolfsson
You can also search for this author in PubMed Google Scholar
- M. M. Aggarwal
You can also search for this author in PubMed Google Scholar
- G. Aglieri Rinella
You can also search for this author in PubMed Google Scholar
- M. Agnello
You can also search for this author in PubMed Google Scholar
- N. Agrawal
You can also search for this author in PubMed Google Scholar
- Z. Ahammed
You can also search for this author in PubMed Google Scholar
- S. U. Ahn
You can also search for this author in PubMed Google Scholar
- S. Aiola
You can also search for this author in PubMed Google Scholar
- A. Akindinov
You can also search for this author in PubMed Google Scholar
- M. Al-Turany
You can also search for this author in PubMed Google Scholar
- S. N. Alam
You can also search for this author in PubMed Google Scholar
- D. S. D. Albuquerque
You can also search for this author in PubMed Google Scholar
- D. Aleksandrov
You can also search for this author in PubMed Google Scholar
- B. Alessandro
You can also search for this author in PubMed Google Scholar
- R. Alfaro Molina
You can also search for this author in PubMed Google Scholar
- Y. Ali
You can also search for this author in PubMed Google Scholar
- A. Alici
You can also search for this author in PubMed Google Scholar
- A. Alkin
You can also search for this author in PubMed Google Scholar
- J. Alme
You can also search for this author in PubMed Google Scholar
- T. Alt
You can also search for this author in PubMed Google Scholar
- L. Altenkamper
You can also search for this author in PubMed Google Scholar
- I. Altsybeev
You can also search for this author in PubMed Google Scholar
- C. Andrei
You can also search for this author in PubMed Google Scholar
- D. Andreou
You can also search for this author in PubMed Google Scholar
- H. A. Andrews
You can also search for this author in PubMed Google Scholar
- A. Andronic
You can also search for this author in PubMed Google Scholar
- M. Angeletti
You can also search for this author in PubMed Google Scholar
- V. Anguelov
You can also search for this author in PubMed Google Scholar
- C. Anson
You can also search for this author in PubMed Google Scholar
- T. Antičić
You can also search for this author in PubMed Google Scholar
- F. Antinori
You can also search for this author in PubMed Google Scholar
- P. Antonioli
You can also search for this author in PubMed Google Scholar
- R. Anwar
You can also search for this author in PubMed Google Scholar
- N. Apadula
You can also search for this author in PubMed Google Scholar
- L. Aphecetche
You can also search for this author in PubMed Google Scholar
- H. Appelshäuser
You can also search for this author in PubMed Google Scholar
- S. Arcelli
You can also search for this author in PubMed Google Scholar
- R. Arnaldi
You can also search for this author in PubMed Google Scholar
- O. W. Arnold
You can also search for this author in PubMed Google Scholar
- I. C. Arsene
You can also search for this author in PubMed Google Scholar
- M. Arslandok
You can also search for this author in PubMed Google Scholar
- B. Audurier
You can also search for this author in PubMed Google Scholar
- A. Augustinus
You can also search for this author in PubMed Google Scholar
- R. Averbeck
You can also search for this author in PubMed Google Scholar
- M. D. Azmi
You can also search for this author in PubMed Google Scholar
- A. Badalà
You can also search for this author in PubMed Google Scholar
- Y. W. Baek
You can also search for this author in PubMed Google Scholar
- S. Bagnasco
You can also search for this author in PubMed Google Scholar
- R. Bailhache
You can also search for this author in PubMed Google Scholar
- R. Bala
You can also search for this author in PubMed Google Scholar
- A. Baldisseri
You can also search for this author in PubMed Google Scholar
- M. Ball
You can also search for this author in PubMed Google Scholar
- R. C. Baral
You can also search for this author in PubMed Google Scholar
- A. M. Barbano
You can also search for this author in PubMed Google Scholar
- R. Barbera
You can also search for this author in PubMed Google Scholar
- F. Barile
You can also search for this author in PubMed Google Scholar
- L. Barioglio
You can also search for this author in PubMed Google Scholar
- G. G. Barnaföldi
You can also search for this author in PubMed Google Scholar
- L. S. Barnby
You can also search for this author in PubMed Google Scholar
- V. Barret
You can also search for this author in PubMed Google Scholar
- P. Bartalini
You can also search for this author in PubMed Google Scholar
- K. Barth
You can also search for this author in PubMed Google Scholar
- E. Bartsch
You can also search for this author in PubMed Google Scholar
- N. Bastid
You can also search for this author in PubMed Google Scholar
- S. Basu
You can also search for this author in PubMed Google Scholar
- G. Batigne
You can also search for this author in PubMed Google Scholar
- B. Batyunya
You can also search for this author in PubMed Google Scholar
- P. C. Batzing
You can also search for this author in PubMed Google Scholar
- J. L. Bazo Alba
You can also search for this author in PubMed Google Scholar
- I. G. Bearden
You can also search for this author in PubMed Google Scholar
- H. Beck
You can also search for this author in PubMed Google Scholar
- C. Bedda
You can also search for this author in PubMed Google Scholar
- N. K. Behera
You can also search for this author in PubMed Google Scholar
- I. Belikov
You can also search for this author in PubMed Google Scholar
- F. Bellini
You can also search for this author in PubMed Google Scholar
- H. Bello Martinez
You can also search for this author in PubMed Google Scholar
- R. Bellwied
You can also search for this author in PubMed Google Scholar
- L. G. E. Beltran
You can also search for this author in PubMed Google Scholar
- V. Belyaev
You can also search for this author in PubMed Google Scholar
- G. Bencedi
You can also search for this author in PubMed Google Scholar
- S. Beole
You can also search for this author in PubMed Google Scholar
- A. Bercuci
You can also search for this author in PubMed Google Scholar
- Y. Berdnikov
You can also search for this author in PubMed Google Scholar
- D. Berenyi
You can also search for this author in PubMed Google Scholar
- R. A. Bertens
You can also search for this author in PubMed Google Scholar
- D. Berzano
You can also search for this author in PubMed Google Scholar
- L. Betev
You can also search for this author in PubMed Google Scholar
- P. P. Bhaduri
You can also search for this author in PubMed Google Scholar
- A. Bhasin
You can also search for this author in PubMed Google Scholar
- I. R. Bhat
You can also search for this author in PubMed Google Scholar
- H. Bhatt
You can also search for this author in PubMed Google Scholar
- B. Bhattacharjee
You can also search for this author in PubMed Google Scholar
- J. Bhom
You can also search for this author in PubMed Google Scholar
- A. Bianchi
You can also search for this author in PubMed Google Scholar
- L. Bianchi
You can also search for this author in PubMed Google Scholar
- N. Bianchi
You can also search for this author in PubMed Google Scholar
- J. Bielčík
You can also search for this author in PubMed Google Scholar
- J. Bielč´ıková
You can also search for this author in PubMed Google Scholar
- A. Bilandzic
You can also search for this author in PubMed Google Scholar
- G. Biro
You can also search for this author in PubMed Google Scholar
- R. Biswas
You can also search for this author in PubMed Google Scholar
- S. Biswas
You can also search for this author in PubMed Google Scholar
- J. T. Blair
You can also search for this author in PubMed Google Scholar
- D. Blau
You can also search for this author in PubMed Google Scholar
- C. Blume
You can also search for this author in PubMed Google Scholar
- G. Boca
You can also search for this author in PubMed Google Scholar
- F. Bock
You can also search for this author in PubMed Google Scholar
- A. Bogdanov
You can also search for this author in PubMed Google Scholar
- L. Boldizsár
You can also search for this author in PubMed Google Scholar
- M. Bombara
You can also search for this author in PubMed Google Scholar
- G. Bonomi
You can also search for this author in PubMed Google Scholar
- M. Bonora
You can also search for this author in PubMed Google Scholar
- H. Borel
You can also search for this author in PubMed Google Scholar
- A. Borissov
You can also search for this author in PubMed Google Scholar
- M. Borri
You can also search for this author in PubMed Google Scholar
- E. Botta
You can also search for this author in PubMed Google Scholar
- C. Bourjau
You can also search for this author in PubMed Google Scholar
- L. Bratrud
You can also search for this author in PubMed Google Scholar
- P. Braun-Munzinger
You can also search for this author in PubMed Google Scholar
- M. Bregant
You can also search for this author in PubMed Google Scholar
- T. A. Broker
You can also search for this author in PubMed Google Scholar
- M. Broz
You can also search for this author in PubMed Google Scholar
- E. J. Brucken
You can also search for this author in PubMed Google Scholar
- E. Bruna
You can also search for this author in PubMed Google Scholar
- G. E. Bruno
You can also search for this author in PubMed Google Scholar
- D. Budnikov
You can also search for this author in PubMed Google Scholar
- H. Buesching
You can also search for this author in PubMed Google Scholar
- S. Bufalino
You can also search for this author in PubMed Google Scholar
- P. Buhler
You can also search for this author in PubMed Google Scholar
- P. Buncic
You can also search for this author in PubMed Google Scholar
- O. Busch
You can also search for this author in PubMed Google Scholar
- Z. Buthelezi
You can also search for this author in PubMed Google Scholar
- J. B. Butt
You can also search for this author in PubMed Google Scholar
- J. T. Buxton
You can also search for this author in PubMed Google Scholar
- J. Cabala
You can also search for this author in PubMed Google Scholar
- D. Caffarri
You can also search for this author in PubMed Google Scholar
- H. Caines
You can also search for this author in PubMed Google Scholar
- A. Caliva
You can also search for this author in PubMed Google Scholar
- E. Calvo Villar
You can also search for this author in PubMed Google Scholar
- R. S. Camacho
You can also search for this author in PubMed Google Scholar
- P. Camerini
You can also search for this author in PubMed Google Scholar
- A. A. Capon
You can also search for this author in PubMed Google Scholar
- F. Carena
You can also search for this author in PubMed Google Scholar
- W. Carena
You can also search for this author in PubMed Google Scholar
- F. Carnesecchi
You can also search for this author in PubMed Google Scholar
- J. Castillo Castellanos
You can also search for this author in PubMed Google Scholar
- A. J. Castro
You can also search for this author in PubMed Google Scholar
- E. A. R. Casula
You can also search for this author in PubMed Google Scholar
- C. Ceballos Sanchez
You can also search for this author in PubMed Google Scholar
- S. Chandra
You can also search for this author in PubMed Google Scholar
- B. Chang
You can also search for this author in PubMed Google Scholar
- W. Chang
You can also search for this author in PubMed Google Scholar
- S. Chapeland
You can also search for this author in PubMed Google Scholar
- M. Chartier
You can also search for this author in PubMed Google Scholar
- S. Chattopadhyay
You can also search for this author in PubMed Google Scholar
- S. Chattopadhyay
You can also search for this author in PubMed Google Scholar
- A. Chauvin
You can also search for this author in PubMed Google Scholar
- C. Cheshkov
You can also search for this author in PubMed Google Scholar
- B. Cheynis
You can also search for this author in PubMed Google Scholar
- V. Chibante Barroso
You can also search for this author in PubMed Google Scholar
- D. D. Chinellato
You can also search for this author in PubMed Google Scholar
- S. Cho
You can also search for this author in PubMed Google Scholar
- P. Chochula
You can also search for this author in PubMed Google Scholar
- T. Chowdhury
You can also search for this author in PubMed Google Scholar
- P. Christakoglou
You can also search for this author in PubMed Google Scholar
- C. H. Christensen
You can also search for this author in PubMed Google Scholar
- P. Christiansen
You can also search for this author in PubMed Google Scholar
- T. Chujo
You can also search for this author in PubMed Google Scholar
- S. U. Chung
You can also search for this author in PubMed Google Scholar
- C. Cicalo
You can also search for this author in PubMed Google Scholar
- L. Cifarelli
You can also search for this author in PubMed Google Scholar
- F. Cindolo
You can also search for this author in PubMed Google Scholar
- J. Cleymans
You can also search for this author in PubMed Google Scholar
- F. Colamaria
You can also search for this author in PubMed Google Scholar
- D. Colella
You can also search for this author in PubMed Google Scholar
- A. Collu
You can also search for this author in PubMed Google Scholar
- M. Colocci
You can also search for this author in PubMed Google Scholar
- M. Concas
You can also search for this author in PubMed Google Scholar
- G. Conesa Balbastre
You can also search for this author in PubMed Google Scholar
- Z. Conesa del Valle
You can also search for this author in PubMed Google Scholar
- J. G. Contreras
You can also search for this author in PubMed Google Scholar
- T. M. Cormier
You can also search for this author in PubMed Google Scholar
- Y. Corrales Morales
You can also search for this author in PubMed Google Scholar
- P. Cortese
You can also search for this author in PubMed Google Scholar
- M. R. Cosentino
You can also search for this author in PubMed Google Scholar
- F. Costa
You can also search for this author in PubMed Google Scholar
- S. Costanza
You can also search for this author in PubMed Google Scholar
- J. Crkovská
You can also search for this author in PubMed Google Scholar
- P. Crochet
You can also search for this author in PubMed Google Scholar
- E. Cuautle
You can also search for this author in PubMed Google Scholar
- L. Cunqueiro
You can also search for this author in PubMed Google Scholar
- T. Dahms
You can also search for this author in PubMed Google Scholar
- A. Dainese
You can also search for this author in PubMed Google Scholar
- M. C. Danisch
You can also search for this author in PubMed Google Scholar
- A. Danu
You can also search for this author in PubMed Google Scholar
- D. Das
You can also search for this author in PubMed Google Scholar
- I. Das
You can also search for this author in PubMed Google Scholar
- S. Das
You can also search for this author in PubMed Google Scholar
- A. Dash
You can also search for this author in PubMed Google Scholar
- S. Dash
You can also search for this author in PubMed Google Scholar
- S. De
You can also search for this author in PubMed Google Scholar
- A. De Caro
You can also search for this author in PubMed Google Scholar
- G. de Cataldo
You can also search for this author in PubMed Google Scholar
- C. de Conti
You can also search for this author in PubMed Google Scholar
- J. de Cuveland
You can also search for this author in PubMed Google Scholar
- A. De Falco
You can also search for this author in PubMed Google Scholar
- D. De Gruttola
You can also search for this author in PubMed Google Scholar
- N. De Marco
You can also search for this author in PubMed Google Scholar
- S. De Pasquale
You can also search for this author in PubMed Google Scholar
- R. D. De Souza
You can also search for this author in PubMed Google Scholar
- H. F. Degenhardt
You can also search for this author in PubMed Google Scholar
- A. Deisting
You can also search for this author in PubMed Google Scholar
- A. Deloff
You can also search for this author in PubMed Google Scholar
- S. Delsanto
You can also search for this author in PubMed Google Scholar
- C. Deplano
You can also search for this author in PubMed Google Scholar
- P. Dhankher
You can also search for this author in PubMed Google Scholar
- D. Di Bari
You can also search for this author in PubMed Google Scholar
- A. Di Mauro
You can also search for this author in PubMed Google Scholar
- B. Di Ruzza
You can also search for this author in PubMed Google Scholar
- R. A. Diaz
You can also search for this author in PubMed Google Scholar
- T. Dietel
You can also search for this author in PubMed Google Scholar
- P. Dillenseger
You can also search for this author in PubMed Google Scholar
- Y. Ding
You can also search for this author in PubMed Google Scholar
- R. Divià
You can also search for this author in PubMed Google Scholar
- Ø. Djuvsland
You can also search for this author in PubMed Google Scholar
- A. Dobrin
You can also search for this author in PubMed Google Scholar
- D. Domenicis Gimenez
You can also search for this author in PubMed Google Scholar
- B. Dönigus
You can also search for this author in PubMed Google Scholar
- O. Dordic
You can also search for this author in PubMed Google Scholar
- L. V. R. Doremalen
You can also search for this author in PubMed Google Scholar
- A. K. Dubey
You can also search for this author in PubMed Google Scholar
- A. Dubla
You can also search for this author in PubMed Google Scholar
- L. Ducroux
You can also search for this author in PubMed Google Scholar
- S. Dudi
You can also search for this author in PubMed Google Scholar
- A. K. Duggal
You can also search for this author in PubMed Google Scholar
- M. Dukhishyam
You can also search for this author in PubMed Google Scholar
- P. Dupieux
You can also search for this author in PubMed Google Scholar
- R. J. Ehlers
You can also search for this author in PubMed Google Scholar
- D. Elia
You can also search for this author in PubMed Google Scholar
- E. Endress
You can also search for this author in PubMed Google Scholar
- H. Engel
You can also search for this author in PubMed Google Scholar
- E. Epple
You can also search for this author in PubMed Google Scholar
- B. Erazmus
You can also search for this author in PubMed Google Scholar
- F. Erhardt
You can also search for this author in PubMed Google Scholar
- M. R. Ersdal
You can also search for this author in PubMed Google Scholar
- B. Espagnon
You can also search for this author in PubMed Google Scholar
- G. Eulisse
You can also search for this author in PubMed Google Scholar
- J. Eum
You can also search for this author in PubMed Google Scholar
- D. Evans
You can also search for this author in PubMed Google Scholar
- S. Evdokimov
You can also search for this author in PubMed Google Scholar
- L. Fabbietti
You can also search for this author in PubMed Google Scholar
- M. Faggin
You can also search for this author in PubMed Google Scholar
- J. Faivre
You can also search for this author in PubMed Google Scholar
- A. Fantoni
You can also search for this author in PubMed Google Scholar
- M. Fasel
You can also search for this author in PubMed Google Scholar
- L. Feldkamp
You can also search for this author in PubMed Google Scholar
- A. Feliciello
You can also search for this author in PubMed Google Scholar
- G. Feofilov
You can also search for this author in PubMed Google Scholar
- A. Fernández Téllez
You can also search for this author in PubMed Google Scholar
- A. Ferretti
You can also search for this author in PubMed Google Scholar
- A. Festanti
You can also search for this author in PubMed Google Scholar
- V. J. G. Feuillard
You can also search for this author in PubMed Google Scholar
- J. Figiel
You can also search for this author in PubMed Google Scholar
- M. A. S. Figueredo
You can also search for this author in PubMed Google Scholar
- S. Filchagin
You can also search for this author in PubMed Google Scholar
- D. Finogeev
You can also search for this author in PubMed Google Scholar
- F. M. Fionda
You can also search for this author in PubMed Google Scholar
- G. Fiorenza
You can also search for this author in PubMed Google Scholar
- M. Floris
You can also search for this author in PubMed Google Scholar
- S. Foertsch
You can also search for this author in PubMed Google Scholar
- P. Foka
You can also search for this author in PubMed Google Scholar
- S. Fokin
You can also search for this author in PubMed Google Scholar
- E. Fragiacomo
You can also search for this author in PubMed Google Scholar
- A. Francescon
You can also search for this author in PubMed Google Scholar
- A. Francisco
You can also search for this author in PubMed Google Scholar
- U. Frankenfeld
You can also search for this author in PubMed Google Scholar
- G. G. Fronze
You can also search for this author in PubMed Google Scholar
- U. Fuchs
You can also search for this author in PubMed Google Scholar
- C. Furget
You can also search for this author in PubMed Google Scholar
- A. Furs
You can also search for this author in PubMed Google Scholar
- M. Fusco Girard
You can also search for this author in PubMed Google Scholar
- J. J. Gaardhøje
You can also search for this author in PubMed Google Scholar
- M. Gagliardi
You can also search for this author in PubMed Google Scholar
- A. M. Gago
You can also search for this author in PubMed Google Scholar
- K. Gajdosova
You can also search for this author in PubMed Google Scholar
- M. Gallio
You can also search for this author in PubMed Google Scholar
- C. D. Galvan
You can also search for this author in PubMed Google Scholar
- P. Ganoti
You can also search for this author in PubMed Google Scholar
- C. Garabatos
You can also search for this author in PubMed Google Scholar
- E. Garcia-Solis
You can also search for this author in PubMed Google Scholar
- K. Garg
You can also search for this author in PubMed Google Scholar
- C. Gargiulo
You can also search for this author in PubMed Google Scholar
- P. Gasik
You can also search for this author in PubMed Google Scholar
- E. F. Gauger
You can also search for this author in PubMed Google Scholar
- M. B. Gay Ducati
You can also search for this author in PubMed Google Scholar
- M. Germain
You can also search for this author in PubMed Google Scholar
- J. Ghosh
You can also search for this author in PubMed Google Scholar
- P. Ghosh
You can also search for this author in PubMed Google Scholar
- S. K. Ghosh
You can also search for this author in PubMed Google Scholar
- P. Gianotti
You can also search for this author in PubMed Google Scholar
- P. Giubellino
You can also search for this author in PubMed Google Scholar
- P. Giubilato
You can also search for this author in PubMed Google Scholar
- P. Glässel
You can also search for this author in PubMed Google Scholar
- D. M. Goméz Coral
You can also search for this author in PubMed Google Scholar
- A. Gomez Ramirez
You can also search for this author in PubMed Google Scholar
- V. Gonzalez
You can also search for this author in PubMed Google Scholar
- P. González-Zamora
You can also search for this author in PubMed Google Scholar
- S. Gorbunov
You can also search for this author in PubMed Google Scholar
- L. Görlich
You can also search for this author in PubMed Google Scholar
- S. Gotovac
You can also search for this author in PubMed Google Scholar
- V. Grabski
You can also search for this author in PubMed Google Scholar
- L. K. Graczykowski
You can also search for this author in PubMed Google Scholar
- K. L. Graham
You can also search for this author in PubMed Google Scholar
- L. Greiner
You can also search for this author in PubMed Google Scholar
- A. Grelli
You can also search for this author in PubMed Google Scholar
- C. Grigoras
You can also search for this author in PubMed Google Scholar
- V. Grigoriev
You can also search for this author in PubMed Google Scholar
- A. Grigoryan
You can also search for this author in PubMed Google Scholar
- S. Grigoryan
You can also search for this author in PubMed Google Scholar
- J. M. Gronefeld
You can also search for this author in PubMed Google Scholar
- F. Grosa
You can also search for this author in PubMed Google Scholar
- J. F. Grosse-Oetringhaus
You can also search for this author in PubMed Google Scholar
- R. Grosso
You can also search for this author in PubMed Google Scholar
- R. Guernane
You can also search for this author in PubMed Google Scholar
- B. Guerzoni
You can also search for this author in PubMed Google Scholar
- M. Guittiere
You can also search for this author in PubMed Google Scholar
- K. Gulbrandsen
You can also search for this author in PubMed Google Scholar
- T. Gunji
You can also search for this author in PubMed Google Scholar
- A. Gupta
You can also search for this author in PubMed Google Scholar
- R. Gupta
You can also search for this author in PubMed Google Scholar
- I. B. Guzman
You can also search for this author in PubMed Google Scholar
- R. Haake
You can also search for this author in PubMed Google Scholar
- M. K. Habib
You can also search for this author in PubMed Google Scholar
- C. Hadjidakis
You can also search for this author in PubMed Google Scholar
- H. Hamagaki
You can also search for this author in PubMed Google Scholar
- G. Hamar
You can also search for this author in PubMed Google Scholar
- J. C. Hamon
You can also search for this author in PubMed Google Scholar
- M. R. Haque
You can also search for this author in PubMed Google Scholar
- J. W. Harris
You can also search for this author in PubMed Google Scholar
- A. Harton
You can also search for this author in PubMed Google Scholar
- H. Hassan
You can also search for this author in PubMed Google Scholar
- D. Hatzifotiadou
You can also search for this author in PubMed Google Scholar
- S. Hayashi
You can also search for this author in PubMed Google Scholar
- S. T. Heckel
You can also search for this author in PubMed Google Scholar
- E. Hellbär
You can also search for this author in PubMed Google Scholar
- H. Helstrup
You can also search for this author in PubMed Google Scholar
- A. Herghelegiu
You can also search for this author in PubMed Google Scholar
- E. G. Hernandez
You can also search for this author in PubMed Google Scholar
- G. Herrera Corral
You can also search for this author in PubMed Google Scholar
- F. Herrmann
You can also search for this author in PubMed Google Scholar
- K. F. Hetland
You can also search for this author in PubMed Google Scholar
- T. E. Hilden
You can also search for this author in PubMed Google Scholar
- H. Hillemanns
You can also search for this author in PubMed Google Scholar
- C. Hills
You can also search for this author in PubMed Google Scholar
- B. Hippolyte
You can also search for this author in PubMed Google Scholar
- B. Hohlweger
You can also search for this author in PubMed Google Scholar
- D. Horak
You can also search for this author in PubMed Google Scholar
- S. Hornung
You can also search for this author in PubMed Google Scholar
- R. Hosokawa
You can also search for this author in PubMed Google Scholar
- P. Hristov
You can also search for this author in PubMed Google Scholar
- C. Hughes
You can also search for this author in PubMed Google Scholar
- P. Huhn
You can also search for this author in PubMed Google Scholar
- T. J. Humanic
You can also search for this author in PubMed Google Scholar
- H. Hushnud
You can also search for this author in PubMed Google Scholar
- N. Hussain
You can also search for this author in PubMed Google Scholar
- T. Hussain
You can also search for this author in PubMed Google Scholar
- D. Hutter
You can also search for this author in PubMed Google Scholar
- D. S. Hwang
You can also search for this author in PubMed Google Scholar
- J. P. Iddon
You can also search for this author in PubMed Google Scholar
- S. A. Iga Buitron
You can also search for this author in PubMed Google Scholar
- R. Ilkaev
You can also search for this author in PubMed Google Scholar
- M. Inaba
You can also search for this author in PubMed Google Scholar
- M. Ippolitov
You can also search for this author in PubMed Google Scholar
- M. S. Islam
You can also search for this author in PubMed Google Scholar
- M. Ivanov
You can also search for this author in PubMed Google Scholar
- V. Ivanov
You can also search for this author in PubMed Google Scholar
- V. Izucheev
You can also search for this author in PubMed Google Scholar
- B. Jacak
You can also search for this author in PubMed Google Scholar
- N. Jacazio
You can also search for this author in PubMed Google Scholar
- P. M. Jacobs
You can also search for this author in PubMed Google Scholar
- M. B. Jadhav
You can also search for this author in PubMed Google Scholar
- S. Jadlovska
You can also search for this author in PubMed Google Scholar
- J. Jadlovsky
You can also search for this author in PubMed Google Scholar
- S. Jaelani
You can also search for this author in PubMed Google Scholar
- C. Jahnke
You can also search for this author in PubMed Google Scholar
- M. J. Jakubowska
You can also search for this author in PubMed Google Scholar
- M. A. Janik
You can also search for this author in PubMed Google Scholar
- C. Jena
You can also search for this author in PubMed Google Scholar
- M. Jercic
You can also search for this author in PubMed Google Scholar
- R. T. Jimenez Bustamante
You can also search for this author in PubMed Google Scholar
- M. Jin
You can also search for this author in PubMed Google Scholar
- P. G. Jones
You can also search for this author in PubMed Google Scholar
- A. Jusko
You can also search for this author in PubMed Google Scholar
- P. Kalinak
You can also search for this author in PubMed Google Scholar
- A. Kalweit
You can also search for this author in PubMed Google Scholar
- J. H. Kang
You can also search for this author in PubMed Google Scholar
- V. Kaplin
You can also search for this author in PubMed Google Scholar
- S. Kar
You can also search for this author in PubMed Google Scholar
- A. Karasu Uysal
You can also search for this author in PubMed Google Scholar
- O. Karavichev
You can also search for this author in PubMed Google Scholar
- T. Karavicheva
You can also search for this author in PubMed Google Scholar
- P. Karczmarczyk
You can also search for this author in PubMed Google Scholar
- E. Karpechev
You can also search for this author in PubMed Google Scholar
- U. Kebschull
You can also search for this author in PubMed Google Scholar
- R. Keidel
You can also search for this author in PubMed Google Scholar
- D. L. D. Keijdener
You can also search for this author in PubMed Google Scholar
- M. Keil
You can also search for this author in PubMed Google Scholar
- B. Ketzer
You can also search for this author in PubMed Google Scholar
- Z. Khabanova
You can also search for this author in PubMed Google Scholar
- S. Khan
You can also search for this author in PubMed Google Scholar
- S. A. Khan
You can also search for this author in PubMed Google Scholar
- A. Khanzadeev
You can also search for this author in PubMed Google Scholar
- Y. Kharlov
You can also search for this author in PubMed Google Scholar
- A. Khatun
You can also search for this author in PubMed Google Scholar
- A. Khuntia
You can also search for this author in PubMed Google Scholar
- M. M. Kielbowicz
You can also search for this author in PubMed Google Scholar
- B. Kileng
You can also search for this author in PubMed Google Scholar
- B. Kim
You can also search for this author in PubMed Google Scholar
- D. Kim
You can also search for this author in PubMed Google Scholar
- D. J. Kim
You can also search for this author in PubMed Google Scholar
- E. J. Kim
You can also search for this author in PubMed Google Scholar
- H. Kim
You can also search for this author in PubMed Google Scholar
- J. S. Kim
You can also search for this author in PubMed Google Scholar
- J. Kim
You can also search for this author in PubMed Google Scholar
- M. Kim
You can also search for this author in PubMed Google Scholar
- S. Kim
You can also search for this author in PubMed Google Scholar
- T. Kim
You can also search for this author in PubMed Google Scholar
- T. Kim
You can also search for this author in PubMed Google Scholar
- S. Kirsch
You can also search for this author in PubMed Google Scholar
- I. Kisel
You can also search for this author in PubMed Google Scholar
- S. Kiselev
You can also search for this author in PubMed Google Scholar
- A. Kisiel
You can also search for this author in PubMed Google Scholar
- J. L. Klay
You can also search for this author in PubMed Google Scholar
- C. Klein
You can also search for this author in PubMed Google Scholar
- J. Klein
You can also search for this author in PubMed Google Scholar
- C. Klein-Bösing
You can also search for this author in PubMed Google Scholar
- S. Klewin
You can also search for this author in PubMed Google Scholar
- A. Kluge
You can also search for this author in PubMed Google Scholar
- M. L. Knichel
You can also search for this author in PubMed Google Scholar
- A. G. Knospe
You can also search for this author in PubMed Google Scholar
- C. Kobdaj
You can also search for this author in PubMed Google Scholar
- M. Kofarago
You can also search for this author in PubMed Google Scholar
- M. K. Köhler
You can also search for this author in PubMed Google Scholar
- T. Kollegger
You can also search for this author in PubMed Google Scholar
- N. Kondratyeva
You can also search for this author in PubMed Google Scholar
- E. Kondratyuk
You can also search for this author in PubMed Google Scholar
- A. Konevskikh
You can also search for this author in PubMed Google Scholar
- M. Konyushikhin
You can also search for this author in PubMed Google Scholar
- O. Kovalenko
You can also search for this author in PubMed Google Scholar
- V. Kovalenko
You can also search for this author in PubMed Google Scholar
- M. Kowalski
You can also search for this author in PubMed Google Scholar
- I. Králik
You can also search for this author in PubMed Google Scholar
- A. Kravčáková
You can also search for this author in PubMed Google Scholar
- L. Kreis
You can also search for this author in PubMed Google Scholar
- M. Krivda
You can also search for this author in PubMed Google Scholar
- F. Krizek
You can also search for this author in PubMed Google Scholar
- M. Krüger
You can also search for this author in PubMed Google Scholar
- E. Kryshen
You can also search for this author in PubMed Google Scholar
- M. Krzewicki
You can also search for this author in PubMed Google Scholar
- A. M. Kubera
You can also search for this author in PubMed Google Scholar
- V. Kučera
You can also search for this author in PubMed Google Scholar
- C. Kuhn
You can also search for this author in PubMed Google Scholar
- P. G. Kuijer
You can also search for this author in PubMed Google Scholar
- J. Kumar
You can also search for this author in PubMed Google Scholar
- L. Kumar
You can also search for this author in PubMed Google Scholar
- S. Kumar
You can also search for this author in PubMed Google Scholar
- S. Kundu
You can also search for this author in PubMed Google Scholar
- P. Kurashvili
You can also search for this author in PubMed Google Scholar
- A. Kurepin
You can also search for this author in PubMed Google Scholar
- A. B. Kurepin
You can also search for this author in PubMed Google Scholar
- A. Kuryakin
You can also search for this author in PubMed Google Scholar
- S. Kushpil
You can also search for this author in PubMed Google Scholar
- M. J. Kweon
You can also search for this author in PubMed Google Scholar
- Y. Kwon
You can also search for this author in PubMed Google Scholar
- S. L. La Pointe
You can also search for this author in PubMed Google Scholar
- P. La Rocca
You can also search for this author in PubMed Google Scholar
- Y. S. Lai
You can also search for this author in PubMed Google Scholar
- I. Lakomov
You can also search for this author in PubMed Google Scholar
- R. Langoy
You can also search for this author in PubMed Google Scholar
- K. Lapidus
You can also search for this author in PubMed Google Scholar
- C. Lara
You can also search for this author in PubMed Google Scholar
- A. Lardeux
You can also search for this author in PubMed Google Scholar
- P. Larionov
You can also search for this author in PubMed Google Scholar
- A. Lattuca
You can also search for this author in PubMed Google Scholar
- E. Laudi
You can also search for this author in PubMed Google Scholar
- R. Lavicka
You can also search for this author in PubMed Google Scholar
- R. Lea
You can also search for this author in PubMed Google Scholar
- L. Leardini
You can also search for this author in PubMed Google Scholar
- S. Lee
You can also search for this author in PubMed Google Scholar
- F. Lehas
You can also search for this author in PubMed Google Scholar
- S. Lehner
You can also search for this author in PubMed Google Scholar
- J. Lehrbach
You can also search for this author in PubMed Google Scholar
- R. C. Lemmon
You can also search for this author in PubMed Google Scholar
- E. Leogrande
You can also search for this author in PubMed Google Scholar
- I. León Monzón
You can also search for this author in PubMed Google Scholar
- P. Lévai
You can also search for this author in PubMed Google Scholar
- X. Li
You can also search for this author in PubMed Google Scholar
- X. L. Li
You can also search for this author in PubMed Google Scholar
- J. Lien
You can also search for this author in PubMed Google Scholar
- R. Lietava
You can also search for this author in PubMed Google Scholar
- B. Lim
You can also search for this author in PubMed Google Scholar
- S. Lindal
You can also search for this author in PubMed Google Scholar
- V. Lindenstruth
You can also search for this author in PubMed Google Scholar
- S. W. Lindsay
You can also search for this author in PubMed Google Scholar
- C. Lippmann
You can also search for this author in PubMed Google Scholar
- M. A. Lisa
You can also search for this author in PubMed Google Scholar
- V. Litichevskyi
You can also search for this author in PubMed Google Scholar
- A. Liu
You can also search for this author in PubMed Google Scholar
- H. M. Ljunggren
You can also search for this author in PubMed Google Scholar
- W. J. Llope
You can also search for this author in PubMed Google Scholar
- D. F. Lodato
You can also search for this author in PubMed Google Scholar
- V. Loginov
You can also search for this author in PubMed Google Scholar
- C. Loizides
You can also search for this author in PubMed Google Scholar
- P. Loncar
You can also search for this author in PubMed Google Scholar
- X. Lopez
You can also search for this author in PubMed Google Scholar
- E. López Torres
You can also search for this author in PubMed Google Scholar
- A. Lowe
You can also search for this author in PubMed Google Scholar
- P. Luettig
You can also search for this author in PubMed Google Scholar
- J. R. Luhder
You can also search for this author in PubMed Google Scholar
- M. Lunardon
You can also search for this author in PubMed Google Scholar
- G. Luparello
You can also search for this author in PubMed Google Scholar
- M. Lupi
You can also search for this author in PubMed Google Scholar
- A. Maevskaya
You can also search for this author in PubMed Google Scholar
- M. Mager
You can also search for this author in PubMed Google Scholar
- S. M. Mahmood
You can also search for this author in PubMed Google Scholar
- A. Maire
You can also search for this author in PubMed Google Scholar
- R. D. Majka
You can also search for this author in PubMed Google Scholar
- M. Malaev
You can also search for this author in PubMed Google Scholar
- L. Malinina
You can also search for this author in PubMed Google Scholar
- D. Mal’Kevich
You can also search for this author in PubMed Google Scholar
- P. Malzacher
You can also search for this author in PubMed Google Scholar
- A. Mamonov
You can also search for this author in PubMed Google Scholar
- V. Manko
You can also search for this author in PubMed Google Scholar
- F. Manso
You can also search for this author in PubMed Google Scholar
- V. Manzari
You can also search for this author in PubMed Google Scholar
- Y. Mao
You can also search for this author in PubMed Google Scholar
- M. Marchisone
You can also search for this author in PubMed Google Scholar
- J. Mareš
You can also search for this author in PubMed Google Scholar
- G. V. Margagliotti
You can also search for this author in PubMed Google Scholar
- A. Margotti
You can also search for this author in PubMed Google Scholar
- J. Margutti
You can also search for this author in PubMed Google Scholar
- A. Marín
You can also search for this author in PubMed Google Scholar
- C. Markert
You can also search for this author in PubMed Google Scholar
- M. Marquard
You can also search for this author in PubMed Google Scholar
- N. A. Martin
You can also search for this author in PubMed Google Scholar
- P. Martinengo
You can also search for this author in PubMed Google Scholar
- M. I. Martínez
You can also search for this author in PubMed Google Scholar
- G. Martínez García
You can also search for this author in PubMed Google Scholar
- M. Martinez Pedreira
You can also search for this author in PubMed Google Scholar
- S. Masciocchi
You can also search for this author in PubMed Google Scholar
- M. Masera
You can also search for this author in PubMed Google Scholar
- A. Masoni
You can also search for this author in PubMed Google Scholar
- L. Massacrier
You can also search for this author in PubMed Google Scholar
- E. Masson
You can also search for this author in PubMed Google Scholar
- A. Mastroserio
You can also search for this author in PubMed Google Scholar
- A. M. Mathis
You can also search for this author in PubMed Google Scholar
- P. F. T. Matuoka
You can also search for this author in PubMed Google Scholar
- A. Matyja
You can also search for this author in PubMed Google Scholar
- C. Mayer
You can also search for this author in PubMed Google Scholar
- M. Mazzilli
You can also search for this author in PubMed Google Scholar
- M. A. Mazzoni
You can also search for this author in PubMed Google Scholar
- F. Meddi
You can also search for this author in PubMed Google Scholar
- Y. Melikyan
You can also search for this author in PubMed Google Scholar
- A. Menchaca-Rocha
You can also search for this author in PubMed Google Scholar
- E. Meninno
You can also search for this author in PubMed Google Scholar
- J. Mercado Pérez
You can also search for this author in PubMed Google Scholar
- M. Meres
You can also search for this author in PubMed Google Scholar
- C. S. Meza
You can also search for this author in PubMed Google Scholar
- S. Mhlanga
You can also search for this author in PubMed Google Scholar
- Y. Miake
You can also search for this author in PubMed Google Scholar
- L. Micheletti
You can also search for this author in PubMed Google Scholar
- M. M. Mieskolainen
You can also search for this author in PubMed Google Scholar
- D. L. Mihaylov
You can also search for this author in PubMed Google Scholar
- K. Mikhaylov
You can also search for this author in PubMed Google Scholar
- A. Mischke
You can also search for this author in PubMed Google Scholar
- A. N. Mishra
You can also search for this author in PubMed Google Scholar
- D. Miskowiec
You can also search for this author in PubMed Google Scholar
- J. Mitra
You can also search for this author in PubMed Google Scholar
- C. M. Mitu
You can also search for this author in PubMed Google Scholar
- N. Mohammadi
You can also search for this author in PubMed Google Scholar
- A. P. Mohanty
You can also search for this author in PubMed Google Scholar
- B. Mohanty
You can also search for this author in PubMed Google Scholar
- M. Mohisin Khan
You can also search for this author in PubMed Google Scholar
- D. A. Moreira De Godoy
You can also search for this author in PubMed Google Scholar
- L. A. P. Moreno
You can also search for this author in PubMed Google Scholar
- S. Moretto
You can also search for this author in PubMed Google Scholar
- A. Morreale
You can also search for this author in PubMed Google Scholar
- A. Morsch
You can also search for this author in PubMed Google Scholar
- V. Muccifora
You can also search for this author in PubMed Google Scholar
- E. Mudnic
You can also search for this author in PubMed Google Scholar
- D. Mühlheim
You can also search for this author in PubMed Google Scholar
- S. Muhuri
You can also search for this author in PubMed Google Scholar
- M. Mukherjee
You can also search for this author in PubMed Google Scholar
- J. D. Mulligan
You can also search for this author in PubMed Google Scholar
- M. G. Munhoz
You can also search for this author in PubMed Google Scholar
- K. Münning
You can also search for this author in PubMed Google Scholar
- M. I. A. Munoz
You can also search for this author in PubMed Google Scholar
- R. H. Munzer
You can also search for this author in PubMed Google Scholar
- H. Murakami
You can also search for this author in PubMed Google Scholar
- S. Murray
You can also search for this author in PubMed Google Scholar
- L. Musa
You can also search for this author in PubMed Google Scholar
- J. Musinsky
You can also search for this author in PubMed Google Scholar
- C. J. Myers
You can also search for this author in PubMed Google Scholar
- J. W. Myrcha
You can also search for this author in PubMed Google Scholar
- B. Naik
You can also search for this author in PubMed Google Scholar
- R. Nair
You can also search for this author in PubMed Google Scholar
- B. K. Nandi
You can also search for this author in PubMed Google Scholar
- R. Nania
You can also search for this author in PubMed Google Scholar
- E. Nappi
You can also search for this author in PubMed Google Scholar
- A. Narayan
You can also search for this author in PubMed Google Scholar
- M. U. Naru
You can also search for this author in PubMed Google Scholar
- H. Natal da Luz
You can also search for this author in PubMed Google Scholar
- C. Nattrass
You can also search for this author in PubMed Google Scholar
- S. R. Navarro
You can also search for this author in PubMed Google Scholar
- K. Nayak
You can also search for this author in PubMed Google Scholar
- R. Nayak
You can also search for this author in PubMed Google Scholar
- T. K. Nayak
You can also search for this author in PubMed Google Scholar
- S. Nazarenko
You can also search for this author in PubMed Google Scholar
- R. A. Negrao De Oliveira
You can also search for this author in PubMed Google Scholar
- L. Nellen
You can also search for this author in PubMed Google Scholar
- S. V. Nesbo
You can also search for this author in PubMed Google Scholar
- G. Neskovic
You can also search for this author in PubMed Google Scholar
- F. Ng
You can also search for this author in PubMed Google Scholar
- M. Nicassio
You can also search for this author in PubMed Google Scholar
- J. Niedziela
You can also search for this author in PubMed Google Scholar
- B. S. Nielsen
You can also search for this author in PubMed Google Scholar
- S. Nikolaev
You can also search for this author in PubMed Google Scholar
- S. Nikulin
You can also search for this author in PubMed Google Scholar
- V. Nikulin
You can also search for this author in PubMed Google Scholar
- F. Noferini
You can also search for this author in PubMed Google Scholar
- P. Nomokonov
You can also search for this author in PubMed Google Scholar
- G. Nooren
You can also search for this author in PubMed Google Scholar
- J. C. C. Noris
You can also search for this author in PubMed Google Scholar
- J. Norman
You can also search for this author in PubMed Google Scholar
- A. Nyanin
You can also search for this author in PubMed Google Scholar
- J. Nystrand
You can also search for this author in PubMed Google Scholar
- H. Oh
You can also search for this author in PubMed Google Scholar
- A. Ohlson
You can also search for this author in PubMed Google Scholar
- J. Oleniacz
You can also search for this author in PubMed Google Scholar
- A. C. Oliveira Da Silva
You can also search for this author in PubMed Google Scholar
- M. H. Oliver
You can also search for this author in PubMed Google Scholar
- J. Onderwaater
You can also search for this author in PubMed Google Scholar
- C. Oppedisano
You can also search for this author in PubMed Google Scholar
- R. Orava
You can also search for this author in PubMed Google Scholar
- M. Oravec
You can also search for this author in PubMed Google Scholar
- A. Ortiz Velasquez
You can also search for this author in PubMed Google Scholar
- A. Oskarsson
You can also search for this author in PubMed Google Scholar
- J. Otwinowski
You can also search for this author in PubMed Google Scholar
- K. Oyama
You can also search for this author in PubMed Google Scholar
- Y. Pachmayer
You can also search for this author in PubMed Google Scholar
- V. Pacik
You can also search for this author in PubMed Google Scholar
- D. Pagano
You can also search for this author in PubMed Google Scholar
- G. Paić
You can also search for this author in PubMed Google Scholar
- P. Palni
You can also search for this author in PubMed Google Scholar
- J. Pan
You can also search for this author in PubMed Google Scholar
- A. K. Pandey
You can also search for this author in PubMed Google Scholar
- S. Panebianco
You can also search for this author in PubMed Google Scholar
- V. Papikyan
You can also search for this author in PubMed Google Scholar
- P. Pareek
You can also search for this author in PubMed Google Scholar
- J. Park
You can also search for this author in PubMed Google Scholar
- J. E. Parkkila
You can also search for this author in PubMed Google Scholar
- S. Parmar
You can also search for this author in PubMed Google Scholar
- A. Passfeld
You can also search for this author in PubMed Google Scholar
- S. P. Pathak
You can also search for this author in PubMed Google Scholar
- R. N. Patra
You can also search for this author in PubMed Google Scholar
- B. Paul
You can also search for this author in PubMed Google Scholar
- H. Pei
You can also search for this author in PubMed Google Scholar
- T. Peitzmann
You can also search for this author in PubMed Google Scholar
- X. Peng
You can also search for this author in PubMed Google Scholar
- L. G. Pereira
You can also search for this author in PubMed Google Scholar
- H. Pereira Da Costa
You can also search for this author in PubMed Google Scholar
- D. Peresunko
You can also search for this author in PubMed Google Scholar
- E. Perez Lezama
You can also search for this author in PubMed Google Scholar
- V. Peskov
You can also search for this author in PubMed Google Scholar
- Y. Pestov
You can also search for this author in PubMed Google Scholar
- V. Petráček
You can also search for this author in PubMed Google Scholar
- M. Petrovici
You can also search for this author in PubMed Google Scholar
- C. Petta
You can also search for this author in PubMed Google Scholar
- R. P. Pezzi
You can also search for this author in PubMed Google Scholar
- S. Piano
You can also search for this author in PubMed Google Scholar
- M. Pikna
You can also search for this author in PubMed Google Scholar
- P. Pillot
You can also search for this author in PubMed Google Scholar
- L. O. D. L. Pimentel
You can also search for this author in PubMed Google Scholar
- O. Pinazza
You can also search for this author in PubMed Google Scholar
- L. Pinsky
You can also search for this author in PubMed Google Scholar
- S. Pisano
You can also search for this author in PubMed Google Scholar
- D. B. Piyarathna
You can also search for this author in PubMed Google Scholar
- M. Ploskon
You can also search for this author in PubMed Google Scholar
- M. Planinic
You can also search for this author in PubMed Google Scholar
- F. Pliquett
You can also search for this author in PubMed Google Scholar
- J. Pluta
You can also search for this author in PubMed Google Scholar
- S. Pochybova
You can also search for this author in PubMed Google Scholar
- P. L. M. Podesta-Lerma
You can also search for this author in PubMed Google Scholar
- M. G. Poghosyan
You can also search for this author in PubMed Google Scholar
- B. Polichtchouk
You can also search for this author in PubMed Google Scholar
- N. Poljak
You can also search for this author in PubMed Google Scholar
- W. Poonsawat
You can also search for this author in PubMed Google Scholar
- A. Pop
You can also search for this author in PubMed Google Scholar
- H. Poppenborg
You can also search for this author in PubMed Google Scholar
- S. Porteboeuf-Houssais
You can also search for this author in PubMed Google Scholar
- V. Pozdniakov
You can also search for this author in PubMed Google Scholar
- S. K. Prasad
You can also search for this author in PubMed Google Scholar
- R. Preghenella
You can also search for this author in PubMed Google Scholar
- F. Prino
You can also search for this author in PubMed Google Scholar
- C. A. Pruneau
You can also search for this author in PubMed Google Scholar
- I. Pshenichnov
You can also search for this author in PubMed Google Scholar
- M. Puccio
You can also search for this author in PubMed Google Scholar
- V. Punin
You can also search for this author in PubMed Google Scholar
- J. Putschke
You can also search for this author in PubMed Google Scholar
- S. Raha
You can also search for this author in PubMed Google Scholar
- S. Rajput
You can also search for this author in PubMed Google Scholar
- J. Rak
You can also search for this author in PubMed Google Scholar
- A. Rakotozafindrabe
You can also search for this author in PubMed Google Scholar
- L. Ramello
You can also search for this author in PubMed Google Scholar
- F. Rami
You can also search for this author in PubMed Google Scholar
- R. Raniwala
You can also search for this author in PubMed Google Scholar
- S. Raniwala
You can also search for this author in PubMed Google Scholar
- S. S. Räsänen
You can also search for this author in PubMed Google Scholar
- B. T. Rascanu
You can also search for this author in PubMed Google Scholar
- V. Ratza
You can also search for this author in PubMed Google Scholar
- I. Ravasenga
You can also search for this author in PubMed Google Scholar
- K. F. Read
You can also search for this author in PubMed Google Scholar
- K. Redlich
You can also search for this author in PubMed Google Scholar
- A. Rehman
You can also search for this author in PubMed Google Scholar
- P. Reichelt
You can also search for this author in PubMed Google Scholar
- F. Reidt
You can also search for this author in PubMed Google Scholar
- X. Ren
You can also search for this author in PubMed Google Scholar
- R. Renfordt
You can also search for this author in PubMed Google Scholar
- A. Reshetin
You can also search for this author in PubMed Google Scholar
- J.-P. Revol
You can also search for this author in PubMed Google Scholar
- K. Reygers
You can also search for this author in PubMed Google Scholar
- V. Riabov
You can also search for this author in PubMed Google Scholar
- T. Richert
You can also search for this author in PubMed Google Scholar
- M. Richter
You can also search for this author in PubMed Google Scholar
- P. Riedler
You can also search for this author in PubMed Google Scholar
- W. Riegler
You can also search for this author in PubMed Google Scholar
- F. Riggi
You can also search for this author in PubMed Google Scholar
- C. Ristea
You can also search for this author in PubMed Google Scholar
- M. Rodríguez Cahuantzi
You can also search for this author in PubMed Google Scholar
- K. Røed
You can also search for this author in PubMed Google Scholar
- R. Rogalev
You can also search for this author in PubMed Google Scholar
- E. Rogochaya
You can also search for this author in PubMed Google Scholar
- D. Rohr
You can also search for this author in PubMed Google Scholar
- D. Röhrich
You can also search for this author in PubMed Google Scholar
- P. S. Rokita
You can also search for this author in PubMed Google Scholar
- F. Ronchetti
You can also search for this author in PubMed Google Scholar
- E. D. Rosas
You can also search for this author in PubMed Google Scholar
- K. Roslon
You can also search for this author in PubMed Google Scholar
- P. Rosnet
You can also search for this author in PubMed Google Scholar
- A. Rossi
You can also search for this author in PubMed Google Scholar
- A. Rotondi
You can also search for this author in PubMed Google Scholar
- F. Roukoutakis
You can also search for this author in PubMed Google Scholar
- C. Roy
You can also search for this author in PubMed Google Scholar
- P. Roy
You can also search for this author in PubMed Google Scholar
- O. V. Rueda
You can also search for this author in PubMed Google Scholar
- R. Rui
You can also search for this author in PubMed Google Scholar
- B. Rumyantsev
You can also search for this author in PubMed Google Scholar
- A. Rustamov
You can also search for this author in PubMed Google Scholar
- E. Ryabinkin
You can also search for this author in PubMed Google Scholar
- Y. Ryabov
You can also search for this author in PubMed Google Scholar
- A. Rybicki
You can also search for this author in PubMed Google Scholar
- S. Saarinen
You can also search for this author in PubMed Google Scholar
- S. Sadhu
You can also search for this author in PubMed Google Scholar
- S. Sadovsky
You can also search for this author in PubMed Google Scholar
- K. Šafařík
You can also search for this author in PubMed Google Scholar
- S. K. Saha
You can also search for this author in PubMed Google Scholar
- B. Sahoo
You can also search for this author in PubMed Google Scholar
- P. Sahoo
You can also search for this author in PubMed Google Scholar
- R. Sahoo
You can also search for this author in PubMed Google Scholar
- S. Sahoo
You can also search for this author in PubMed Google Scholar
- P. K. Sahu
You can also search for this author in PubMed Google Scholar
- J. Saini
You can also search for this author in PubMed Google Scholar
- S. Sakai
You can also search for this author in PubMed Google Scholar
- M. A. Saleh
You can also search for this author in PubMed Google Scholar
- S. Sambyal
You can also search for this author in PubMed Google Scholar
- V. Samsonov
You can also search for this author in PubMed Google Scholar
- A. Sandoval
You can also search for this author in PubMed Google Scholar
- A. Sarkar
You can also search for this author in PubMed Google Scholar
- D. Sarkar
You can also search for this author in PubMed Google Scholar
- N. Sarkar
You can also search for this author in PubMed Google Scholar
- P. Sarma
You can also search for this author in PubMed Google Scholar
- M. H. P. Sas
You can also search for this author in PubMed Google Scholar
- E. Scapparone
You can also search for this author in PubMed Google Scholar
- F. Scarlassara
You can also search for this author in PubMed Google Scholar
- B. Schaefer
You can also search for this author in PubMed Google Scholar
- H. S. Scheid
You can also search for this author in PubMed Google Scholar
- C. Schiaua
You can also search for this author in PubMed Google Scholar
- R. Schicker
You can also search for this author in PubMed Google Scholar
- C. Schmidt
You can also search for this author in PubMed Google Scholar
- H. R. Schmidt
You can also search for this author in PubMed Google Scholar
- M. O. Schmidt
You can also search for this author in PubMed Google Scholar
- M. Schmidt
You can also search for this author in PubMed Google Scholar
- N. V. Schmidt
You can also search for this author in PubMed Google Scholar
- J. Schukraft
You can also search for this author in PubMed Google Scholar
- Y. Schutz
You can also search for this author in PubMed Google Scholar
- K. Schwarz
You can also search for this author in PubMed Google Scholar
- K. Schweda
You can also search for this author in PubMed Google Scholar
- G. Scioli
You can also search for this author in PubMed Google Scholar
- E. Scomparin
You can also search for this author in PubMed Google Scholar
- M. Šefčík
You can also search for this author in PubMed Google Scholar
- J. E. Seger
You can also search for this author in PubMed Google Scholar
- Y. Sekiguchi
You can also search for this author in PubMed Google Scholar
- D. Sekihata
You can also search for this author in PubMed Google Scholar
- I. Selyuzhenkov
You can also search for this author in PubMed Google Scholar
- K. Senosi
You can also search for this author in PubMed Google Scholar
- S. Senyukov
You can also search for this author in PubMed Google Scholar
- E. Serradilla
You can also search for this author in PubMed Google Scholar
- P. Sett
You can also search for this author in PubMed Google Scholar
- A. Sevcenco
You can also search for this author in PubMed Google Scholar
- A. Shabanov
You can also search for this author in PubMed Google Scholar
- A. Shabetai
You can also search for this author in PubMed Google Scholar
- R. Shahoyan
You can also search for this author in PubMed Google Scholar
- W. Shaikh
You can also search for this author in PubMed Google Scholar
- A. Shangaraev
You can also search for this author in PubMed Google Scholar
- A. Sharma
You can also search for this author in PubMed Google Scholar
- A. Sharma
You can also search for this author in PubMed Google Scholar
- N. Sharma
You can also search for this author in PubMed Google Scholar
- A. I. Sheikh
You can also search for this author in PubMed Google Scholar
- K. Shigaki
You can also search for this author in PubMed Google Scholar
- M. Shimomura
You can also search for this author in PubMed Google Scholar
- S. Shirinkin
You can also search for this author in PubMed Google Scholar
- Q. Shou
You can also search for this author in PubMed Google Scholar
- K. Shtejer
You can also search for this author in PubMed Google Scholar
- Y. Sibiriak
You can also search for this author in PubMed Google Scholar
- S. Siddhanta
You can also search for this author in PubMed Google Scholar
- K. M. Sielewicz
You can also search for this author in PubMed Google Scholar
- T. Siemiarczuk
You can also search for this author in PubMed Google Scholar
- D. Silvermyr
You can also search for this author in PubMed Google Scholar
- G. Simatovic
You can also search for this author in PubMed Google Scholar
- G. Simonetti
You can also search for this author in PubMed Google Scholar
- R. Singaraju
You can also search for this author in PubMed Google Scholar
- R. Singh
You can also search for this author in PubMed Google Scholar
- V. Singhal
You can also search for this author in PubMed Google Scholar
- T. Sinha
You can also search for this author in PubMed Google Scholar
- B. Sitar
You can also search for this author in PubMed Google Scholar
- M. Sitta
You can also search for this author in PubMed Google Scholar
- T. B. Skaali
You can also search for this author in PubMed Google Scholar
- M. Slupecki
You can also search for this author in PubMed Google Scholar
- N. Smirnov
You can also search for this author in PubMed Google Scholar
- R. J. M. Snellings
You can also search for this author in PubMed Google Scholar
- T. W. Snellman
You can also search for this author in PubMed Google Scholar
- J. Song
You can also search for this author in PubMed Google Scholar
- F. Soramel
You can also search for this author in PubMed Google Scholar
- S. Sorensen
You can also search for this author in PubMed Google Scholar
- F. Sozzi
You can also search for this author in PubMed Google Scholar
- I. Sputowska
You can also search for this author in PubMed Google Scholar
- J. Stachel
You can also search for this author in PubMed Google Scholar
- I. Stan
You can also search for this author in PubMed Google Scholar
- P. Stankus
You can also search for this author in PubMed Google Scholar
- E. Stenlund
You can also search for this author in PubMed Google Scholar
- D. Stocco
You can also search for this author in PubMed Google Scholar
- M. M. Storetvedt
You can also search for this author in PubMed Google Scholar
- P. Strmen
You can also search for this author in PubMed Google Scholar
- A. A. P. Suaide
You can also search for this author in PubMed Google Scholar
- T. Sugitate
You can also search for this author in PubMed Google Scholar
- C. Suire
You can also search for this author in PubMed Google Scholar
- M. Suleymanov
You can also search for this author in PubMed Google Scholar
- M. Suljic
You can also search for this author in PubMed Google Scholar
- R. Sultanov
You can also search for this author in PubMed Google Scholar
- M. Šumbera
You can also search for this author in PubMed Google Scholar
- S. Sumowidagdo
You can also search for this author in PubMed Google Scholar
- K. Suzuki
You can also search for this author in PubMed Google Scholar
- S. Swain
You can also search for this author in PubMed Google Scholar
- A. Szabo
You can also search for this author in PubMed Google Scholar
- I. Szarka
You can also search for this author in PubMed Google Scholar
- U. Tabassam
You can also search for this author in PubMed Google Scholar
- J. Takahashi
You can also search for this author in PubMed Google Scholar
- G. J. Tambave
You can also search for this author in PubMed Google Scholar
- N. Tanaka
You can also search for this author in PubMed Google Scholar
- M. Tarhini
You can also search for this author in PubMed Google Scholar
- M. Tariq
You can also search for this author in PubMed Google Scholar
- M. G. Tarzila
You can also search for this author in PubMed Google Scholar
- A. Tauro
You can also search for this author in PubMed Google Scholar
- G. Tejeda Muñoz
You can also search for this author in PubMed Google Scholar
- A. Telesca
You can also search for this author in PubMed Google Scholar
- C. Terrevoli
You can also search for this author in PubMed Google Scholar
- B. Teyssier
You can also search for this author in PubMed Google Scholar
- D. Thakur
You can also search for this author in PubMed Google Scholar
- S. Thakur
You can also search for this author in PubMed Google Scholar
- D. Thomas
You can also search for this author in PubMed Google Scholar
- F. Thoresen
You can also search for this author in PubMed Google Scholar
- R. Tieulent
You can also search for this author in PubMed Google Scholar
- A. Tikhonov
You can also search for this author in PubMed Google Scholar
- A. R. Timmins
You can also search for this author in PubMed Google Scholar
- A. Toia
You can also search for this author in PubMed Google Scholar
- N. Topilskaya
You can also search for this author in PubMed Google Scholar
- M. Toppi
You can also search for this author in PubMed Google Scholar
- S. R. Torres
You can also search for this author in PubMed Google Scholar
- S. Tripathy
You can also search for this author in PubMed Google Scholar
- S. Trogolo
You can also search for this author in PubMed Google Scholar
- G. Trombetta
You can also search for this author in PubMed Google Scholar
- L. Tropp
You can also search for this author in PubMed Google Scholar
- V. Trubnikov
You can also search for this author in PubMed Google Scholar
- W. H. Trzaska
You can also search for this author in PubMed Google Scholar
- T. P. Trzcinski
You can also search for this author in PubMed Google Scholar
- B. A. Trzeciak
You can also search for this author in PubMed Google Scholar
- T. Tsuji
You can also search for this author in PubMed Google Scholar
- A. Tumkin
You can also search for this author in PubMed Google Scholar
- R. Turrisi
You can also search for this author in PubMed Google Scholar
- T. S. Tveter
You can also search for this author in PubMed Google Scholar
- K. Ullaland
You can also search for this author in PubMed Google Scholar
- E. N. Umaka
You can also search for this author in PubMed Google Scholar
- A. Uras
You can also search for this author in PubMed Google Scholar
- G. L. Usai
You can also search for this author in PubMed Google Scholar
- A. Utrobicic
You can also search for this author in PubMed Google Scholar
- M. Vala
You can also search for this author in PubMed Google Scholar
- J. W. Van Hoorne
You can also search for this author in PubMed Google Scholar
- M. van Leeuwen
You can also search for this author in PubMed Google Scholar
- P. Vande Vyvre
You can also search for this author in PubMed Google Scholar
- D. Varga
You can also search for this author in PubMed Google Scholar
- A. Vargas
You can also search for this author in PubMed Google Scholar
- M. Vargyas
You can also search for this author in PubMed Google Scholar
- R. Varma
You can also search for this author in PubMed Google Scholar
- M. Vasileiou
You can also search for this author in PubMed Google Scholar
- A. Vasiliev
You can also search for this author in PubMed Google Scholar
- A. Vauthier
You can also search for this author in PubMed Google Scholar
- O. Vázquez Doce
You can also search for this author in PubMed Google Scholar
- V. Vechernin
You can also search for this author in PubMed Google Scholar
- A. M. Veen
You can also search for this author in PubMed Google Scholar
- A. Velure
You can also search for this author in PubMed Google Scholar
- E. Vercellin
You can also search for this author in PubMed Google Scholar
- S. Vergara Limón
You can also search for this author in PubMed Google Scholar
- L. Vermunt
You can also search for this author in PubMed Google Scholar
- R. Vernet
You can also search for this author in PubMed Google Scholar
- R. Vértesi
You can also search for this author in PubMed Google Scholar
- L. Vickovic
You can also search for this author in PubMed Google Scholar
- J. Viinikainen
You can also search for this author in PubMed Google Scholar
- Z. Vilakazi
You can also search for this author in PubMed Google Scholar
- O. Villalobos Baillie
You can also search for this author in PubMed Google Scholar
- A. Villatoro Tello
You can also search for this author in PubMed Google Scholar
- A. Vinogradov
You can also search for this author in PubMed Google Scholar
- T. Virgili
You can also search for this author in PubMed Google Scholar
- V. Vislavicius
You can also search for this author in PubMed Google Scholar
- A. Vodopyanov
You can also search for this author in PubMed Google Scholar
- M. A. Völkl
You can also search for this author in PubMed Google Scholar
- K. Voloshin
You can also search for this author in PubMed Google Scholar
- S. A. Voloshin
You can also search for this author in PubMed Google Scholar
- G. Volpe
You can also search for this author in PubMed Google Scholar
- B. von Haller
You can also search for this author in PubMed Google Scholar
- I. Vorobyev
You can also search for this author in PubMed Google Scholar
- D. Voscek
You can also search for this author in PubMed Google Scholar
- D. Vranic
You can also search for this author in PubMed Google Scholar
- J. Vrláková
You can also search for this author in PubMed Google Scholar
- B. Wagner
You can also search for this author in PubMed Google Scholar
- H. Wang
You can also search for this author in PubMed Google Scholar
- M. Wang
You can also search for this author in PubMed Google Scholar
- Y. Watanabe
You can also search for this author in PubMed Google Scholar
- M. Weber
You can also search for this author in PubMed Google Scholar
- S. G. Weber
You can also search for this author in PubMed Google Scholar
- A. Wegrzynek
You can also search for this author in PubMed Google Scholar
- D. F. Weiser
You can also search for this author in PubMed Google Scholar
- S. C. Wenzel
You can also search for this author in PubMed Google Scholar
- J. P. Wessels
You can also search for this author in PubMed Google Scholar
- U. Westerhoff
You can also search for this author in PubMed Google Scholar
- A. M. Whitehead
You can also search for this author in PubMed Google Scholar
- J. Wiechula
You can also search for this author in PubMed Google Scholar
- J. Wikne
You can also search for this author in PubMed Google Scholar
- G. Wilk
You can also search for this author in PubMed Google Scholar
- J. Wilkinson
You can also search for this author in PubMed Google Scholar
- G. A. Willems
You can also search for this author in PubMed Google Scholar
- M. C. S. Williams
You can also search for this author in PubMed Google Scholar
- E. Willsher
You can also search for this author in PubMed Google Scholar
- B. Windelband
You can also search for this author in PubMed Google Scholar
- W. E. Witt
You can also search for this author in PubMed Google Scholar
- R. Xu
You can also search for this author in PubMed Google Scholar
- S. Yalcin
You can also search for this author in PubMed Google Scholar
- K. Yamakawa
You can also search for this author in PubMed Google Scholar
- S. Yano
You can also search for this author in PubMed Google Scholar
- Z. Yin
You can also search for this author in PubMed Google Scholar
- H. Yokoyama
You can also search for this author in PubMed Google Scholar
- I.-K. Yoo
You can also search for this author in PubMed Google Scholar
- J. H. Yoon
You can also search for this author in PubMed Google Scholar
- V. Yurchenko
You can also search for this author in PubMed Google Scholar
- V. Zaccolo
You can also search for this author in PubMed Google Scholar
- A. Zaman
You can also search for this author in PubMed Google Scholar
- C. Zampolli
You can also search for this author in PubMed Google Scholar
- H. J. C. Zanoli
You can also search for this author in PubMed Google Scholar
- N. Zardoshti
You can also search for this author in PubMed Google Scholar
- A. Zarochentsev
You can also search for this author in PubMed Google Scholar
- P. Závada
You can also search for this author in PubMed Google Scholar
- N. Zaviyalov
You can also search for this author in PubMed Google Scholar
- H. Zbroszczyk
You can also search for this author in PubMed Google Scholar
- M. Zhalov
You can also search for this author in PubMed Google Scholar
- X. Zhang
You can also search for this author in PubMed Google Scholar
- Y. Zhang
You can also search for this author in PubMed Google Scholar
- Z. Zhang
You can also search for this author in PubMed Google Scholar
- C. Zhao
You can also search for this author in PubMed Google Scholar
- V. Zherebchevskii
You can also search for this author in PubMed Google Scholar
- N. Zhigareva
You can also search for this author in PubMed Google Scholar
- D. Zhou
You can also search for this author in PubMed Google Scholar
- Y. Zhou
You can also search for this author in PubMed Google Scholar
- Z. Zhou
You can also search for this author in PubMed Google Scholar
- H. Zhu
You can also search for this author in PubMed Google Scholar
- J. Zhu
You can also search for this author in PubMed Google Scholar
- Y. Zhu
You can also search for this author in PubMed Google Scholar
- A. Zichichi
You can also search for this author in PubMed Google Scholar
- M. B. Zimmermann
You can also search for this author in PubMed Google Scholar
- G. Zinovjev
You can also search for this author in PubMed Google Scholar
- J. Zmeskal
You can also search for this author in PubMed Google Scholar
- S. Zou
You can also search for this author in PubMed Google Scholar
Consortia
The ALICE collaboration
Additional information
ArXiv ePrint: 1804.02944
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
The ALICE collaboration., Acharya, S., Acosta, F.T.. et al. Energy dependence and fluctuations of anisotropic flow in Pb-Pb collisions at \( \sqrt{s_{\mathrm{NN}}}=5.02 \) and 2.76 TeV. J. High Energ. Phys. 2018, 103 (2018). https://doi.org/10.1007/JHEP07(2018)103
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP07(2018)103
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative

