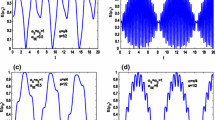
Abstract
We study chaos and scrambling in unitary channels by considering their entanglement properties as states. Using out-of-time-order correlation functions to diagnose chaos, we characterize the ability of a channel to process quantum information. We show that the generic decay of such correlators implies that any input subsystem must have near vanishing mutual information with almost all partitions of the output. Additionally, we propose the negativity of the tripartite information of the channel as a general diagnostic of scrambling. This measures the delocalization of information and is closely related to the decay of out-of-time-order correlators. We back up our results with numerics in two non-integrable models and analytic results in a perfect tensor network model of chaotic time evolution. These results show that the butterfly effect in quantum systems implies the information-theoretic definition of scrambling.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
P. Hayden and J. Preskill, Black holes as mirrors: Quantum information in random subsystems, JHEP 09 (2007) 120 [arXiv:0708.4025] [INSPIRE].
Y. Sekino and L. Susskind, Fast Scramblers, JHEP 10 (2008) 065 [arXiv:0808.2096] [INSPIRE].
N. Lashkari, D. Stanford, M. Hastings, T. Osborne and P. Hayden, Towards the Fast Scrambling Conjecture, JHEP 04 (2013) 022 [arXiv:1111.6580] [INSPIRE].
D.N. Page, Average entropy of a subsystem, Phys. Rev. Lett. 71 (1993) 1291 [gr-qc/9305007] [INSPIRE].
D.A. Roberts, D. Stanford and L. Susskind, Localized shocks, JHEP 03 (2015) 051 [arXiv:1409.8180] [INSPIRE].
S.H. Shenker and D. Stanford, Black holes and the butterfly effect, JHEP 03 (2014) 067 [arXiv:1306.0622] [INSPIRE].
S.H. Shenker and D. Stanford, Multiple Shocks, JHEP 12 (2014) 046 [arXiv:1312.3296] [INSPIRE].
D.A. Roberts and D. Stanford, Two-dimensional conformal field theory and the butterfly effect, Phys. Rev. Lett. 115 (2015) 131603 [arXiv:1412.5123] [INSPIRE].
S.H. Shenker and D. Stanford, Stringy effects in scrambling, JHEP 05 (2015) 132 [arXiv:1412.6087] [INSPIRE].
J. Maldacena, S.H. Shenker and D. Stanford, A bound on chaos, arXiv:1503.01409 [INSPIRE].
A. Kitaev, A simple model of quantum holography, talks given at The Kavli Institute for Theoretical Physics (KITP), University of California, Santa Barbara, U.S.A., 7 April 2015 and 27 May 2015.
T. Hartman and J. Maldacena, Time Evolution of Entanglement Entropy from Black Hole Interiors, JHEP 05 (2013) 014 [arXiv:1303.1080] [INSPIRE].
H. Liu and S.J. Suh, Entanglement Tsunami: Universal Scaling in Holographic Thermalization, Phys. Rev. Lett. 112 (2014) 011601 [arXiv:1305.7244] [INSPIRE].
H. Liu and S.J. Suh, Entanglement growth during thermalization in holographic systems, Phys. Rev. D 89 (2014) 066012 [arXiv:1311.1200] [INSPIRE].
F. Pastawski, B. Yoshida, D. Harlow and J. Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 [arXiv:1503.06237] [INSPIRE].
M.A. Nielsen and I.L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge (2000).
A. Kitaev and J. Preskill, Topological entanglement entropy, Phys. Rev. Lett. 96 (2006) 110404 [hep-th/0510092] [INSPIRE].
M. Levin and X.-G. Wen, Detecting Topological Order in a Ground State Wave Function, Phys. Rev. Lett. 96 (2006) 110405 [INSPIRE].
P. Hayden, M. Headrick and A. Maloney, Holographic Mutual Information is Monogamous, Phys. Rev. D 87 (2013) 046003 [arXiv:1107.2940] [INSPIRE].
H. Gharibyan and R.F. Penna, Are entangled particles connected by wormholes? Evidence for the ER=EPR conjecture from entropy inequalities, Phys. Rev. D 89 (2014) 066001 [arXiv:1308.0289] [INSPIRE].
M. Rangamani and M. Rota, Entanglement structures in qubit systems, J. Phys. A 48 (2015) 385301 [arXiv:1505.03696] [INSPIRE].
A. Almheiri, D. Marolf, J. Polchinski and J. Sully, Black Holes: Complementarity or Firewalls?, JHEP 02 (2013) 062 [arXiv:1207.3123] [INSPIRE].
S.L. Braunstein, S. Pirandola and K. Życzkowski, Better Late than Never: Information Retrieval from Black Holes, Phys. Rev. Lett. 110 (2013) 101301 [arXiv:0907.1190] [INSPIRE].
A. Almheiri, D. Marolf, J. Polchinski, D. Stanford and J. Sully, An Apologia for Firewalls, JHEP 09 (2013) 018 [arXiv:1304.6483] [INSPIRE].
J.M. Maldacena, Eternal black holes in anti-de Sitter, JHEP 04 (2003) 021 [hep-th/0106112] [INSPIRE].
A. Kitaev, Hidden correlations in the hawking radiation and thermal noise, talk given at The Fundamental Physics Prize Symposium, Stanford University, Standford, U.S.A., 10 November 2014.
S. Sachdev and J.-w. Ye, Gapless spin fluid ground state in a random, quantum Heisenberg magnet, Phys. Rev. Lett. 70 (1993) 3339 [cond-mat/9212030] [INSPIRE].
S. Sachdev, Bekenstein-Hawking Entropy and Strange Metals, Phys. Rev. X 5 (2015) 041025 [arXiv:1506.05111] [INSPIRE].
D.A. Roberts and B. Swingle, to appear.
E.H. Lieb and D.W. Robinson, The finite group velocity of quantum spin systems, Commun. Math. Phys. 28 (1972) 251 [INSPIRE].
M.B. Hastings and T. Koma, Spectral gap and exponential decay of correlations, Commun. Math. Phys. 265 (2006) 781 [math-ph/0507008] [INSPIRE].
M.B. Hastings, Locality in quantum systems, arXiv:1008.5137.
S. Leichenauer and M. Moosa, Entanglement Tsunami in (1+1)-Dimensions, Phys. Rev. D 92 (2015) 126004 [arXiv:1505.04225] [INSPIRE].
H. Casini, H. Liu and M. Mezei, Spread of entanglement and causality, arXiv:1509.05044 [INSPIRE].
D. Stanford, Scrambling and the entanglement wedge, unpublished.
M.C. Bañuls, J.I. Cirac and M.B. Hastings, Strong and weak thermalization of infinite nonintegrable quantum systems, Phys. Rev. Lett. 106 (2011) 050405 [arXiv:1007.3957].
F.G.S.L. Brandao, A.W. Harrow and M. Horodecki, Local random quantum circuits are approximate polynomial-designs, arXiv:1208.0692.
D. Stanford and L. Susskind, Complexity and Shock Wave Geometries, Phys. Rev. D 90 (2014) 126007 [arXiv:1406.2678] [INSPIRE].
B. Swingle, Entanglement Renormalization and Holography, Phys. Rev. D 86 (2012) 065007 [arXiv:0905.1317] [INSPIRE].
G. Vidal, Entanglement Renormalization, Phys. Rev. Lett. 99 (2007) 220405 [cond-mat/0512165] [INSPIRE].
Z. Yang, P. Hayden and X.-L. Qi, Bidirectional holographic codes and sub-AdS locality, arXiv:1510.03784 [INSPIRE].
A. Almheiri, X. Dong and D. Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 04 (2015) 163 [arXiv:1411.7041] [INSPIRE].
H. Kim and D.A. Huse, Ballistic spreading of entanglement in a diffusive nonintegrable system, Phys. Rev. Lett. 111 (2013) 127205 [arXiv:1306.4306].
S.G. Nezami, P. Hayden, X.L. Qi, N. Thomas, M. Walters and Z. Yang, Random tensor networks as models of holography, to appear.
M. Hastings, Random mera states and the tightness of the brandao-horodecki entropy bound, arXiv:1505.06468.
D. Marolf, H. Maxfield, A. Peach and S.F. Ross, Hot multiboundary wormholes from bipartite entanglement, Class. Quant. Grav. 32 (2015) 215006 [arXiv:1506.04128] [INSPIRE].
K. Dickman, On the frequency of numbers containing prime factors of a certain relative magnitude, Almqvist & Wiksell (1930).
L. Susskind, The Typical-State Paradox: Diagnosing Horizons with Complexity, Fortsch. Phys. 64 (2016) 84 [arXiv:1507.02287] [INSPIRE].
A.R. Brown, D.A. Roberts, L. Susskind, B. Swingle and Y. Zhao, Complexity Equals Action, arXiv:1509.07876 [INSPIRE].
A.R. Brown, D.A. Roberts, L. Susskind, B. Swingle and Y. Zhao, Complexity, Action and Black Holes, arXiv:1512.04993 [INSPIRE].
G. ’t Hooft, Dimensional reduction in quantum gravity, in Salamfest (1993) 0284 [gr-qc/9310026] [INSPIRE].
L. Susskind, The World as a hologram, J. Math. Phys. 36 (1995) 6377 [hep-th/9409089] [INSPIRE].
L. Susskind, Entanglement is not Enough, Fortsch. Phys. 64 (2016) 49 [arXiv:1411.0690] [INSPIRE].
M. Fannes, A continuity property of the entropy density for spin lattice systems, Commun. Math. Phys. 31 (1973) 291.
K.M.R. Audenaert, A sharp fannes-type inequality for the von neumann entropy, J. Phys. A 40 (2007) 8127 [quant-ph/0610146].
P. Calabrese and J.L. Cardy, Evolution of entanglement entropy in one-dimensional systems, J. Stat. Mech. 0504 (2005) P04010 [cond-mat/0503393] [INSPIRE].
P. Calabrese and J. Cardy, Quantum Quenches in Extended Systems, J. Stat. Mech. 0706 (2007) P06008 [arXiv:0704.1880] [INSPIRE].
P. Calabrese and J. Cardy, Entanglement entropy and conformal field theory, J. Phys. A 42 (2009) 504005 [arXiv:0905.4013] [INSPIRE].
C.T. Asplund, A. Bernamonti, F. Galli and T. Hartman, Holographic Entanglement Entropy from 2d CFT: Heavy States and Local Quenches, JHEP 02 (2015) 171 [arXiv:1410.1392] [INSPIRE].
V. Balasubramanian, A. Bernamonti, N. Copland, B. Craps and F. Galli, Thermalization of mutual and tripartite information in strongly coupled two dimensional conformal field theories, Phys. Rev. D 84 (2011) 105017 [arXiv:1110.0488] [INSPIRE].
A. Allais and E. Tonni, Holographic evolution of the mutual information, JHEP 01 (2012) 102 [arXiv:1110.1607] [INSPIRE].
C.T. Asplund, A. Bernamonti, F. Galli and T. Hartman, Entanglement Scrambling in 2d Conformal Field Theory, JHEP 09 (2015) 110 [arXiv:1506.03772] [INSPIRE].
D. Fattal, T.S. Cubitt, Y. Yamamoto, S. Bravyi and I.L. Chuang, Entanglement in the stabilizer formalism, quant-ph/0406168.
B. Yoshida and I.L. Chuang, Framework for classifying logical operators in stabilizer codes, Phys. Rev. A 81 (2010) 052302 [arXiv:1002.0085].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1511.04021
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hosur, P., Qi, XL., Roberts, D.A. et al. Chaos in quantum channels. J. High Energ. Phys. 2016, 4 (2016). https://doi.org/10.1007/JHEP02(2016)004
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP02(2016)004