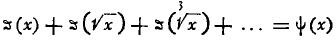Skip to main content
SpringerLink
Log in

Beiträge zur analytischen zahlentheorie

  • Published:
Rendiconti del Circolo Matematico di Palermo (1884-1940)

An Erratum to this article was published on 01 December 1909

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

References

  1. Sur la distribution des zéros de la fonction ζ (s)et ses conséquences arithmétiques [Bulletin de la Société Mathématique de France, Bd. XXIV (1896), S. 199–220], S. 200–202.

  2. Recherches analytiques sur la théorie des nombres premiers [Annales de la Société Scientifique de Bruxelles, Bd. XX, Teil II (1896), S. 183–256 und 281–397], S. 224–242 und 395–397.

  3. Über eine Eigenschaft der Riemann’schen ζ-Function [Sitzungsberichte der kaiserlichen Akademie der Wissenschaften in Wien, mathematisch-naturwissenschaftliche Classe, Bd. CVII (1898), Abt. IIa, S. 1431–1436].

  4. Zuerst in meiner Arbeit:Neuer Beweis des Primzahlsatzes und Beweis des Primidealsatzes [Mathematische Annalen, Bd. LVI (1903), S. 645–670] und später in einer Reihe anderer Abhandlungen.

  5. Sur une inégalité de M. Hadamard [Nouvelles Annales de Mathématiques, Ser. IV, Bd. VI (1906), S. 135–140].

  6. Vergl. meine ArbeitÜber den Picard’sehen Satz [Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich, Bd. LI (1906), S. 252–318], S. 275–277.

  7. Sur la fonction ζ (s)de Riemann et le nombre des nombres premiers inférieurs à une limite donnée [Mémoires couronnés et autres Mémoires publiés par l’Académie Royale de Belgique, Bd. LIX (1899), S. 1–74], S. 7–29.

  8. Vergl. S. 217–218 der in Anm. 1) zitierten Arbeit.

  9. Vergl. S. 251 der in Anm. 2) zitierten Arbeit.

  10. Vergl. S. 360–361 der in Anm. 2) zitierten Arbeit.

  11. On Arithmetical Series [The Messenger of Mathematics, Ser, II, Bd. XXI (1891), S. 1–19, 87–120], S. 9.

  12. Mémoire sur les nombres premiers [Journal de Mathématiques pures et appliquées, Ser. I, Bd. XVII (1852), S. 366–390; Mémoires présentés à l’Académie Impériale de St.-Pétersbourg par divers savants, Bd. VII (1854), S. 17–33;Œuvres, Bd. I (1899), S. 49–70], S. 379 bezw. S. 26 bezw. S, 61.

  13. Ein Beitrag zur analytischen Zahlentheorie [Journal für die reine und angewandte Mathematik, Bd. LXXVIII (1874), S. 46–62], S. 47–48. DerMertensrssche Beweis lautet kurz so: Wenn

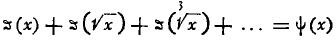
  14. Vergl. meine in Anm. 6) genannte Arbeit, S. 648–663.

  15. Es ist das wichtigste Ergebnis seiner in Anm. 12) genannten Arbeit; vergl. S. 5–6 derselben.

  16. Vergl. die in Anm. 12) genannte Arbeit, S. 63.

  17. Vergl. S. 6 seiner in Anm. 12) genannten Arbeit oder S. 664 meiner in Anm. 6) erwähnten Arbeit.

  18. Was Herrde la Vallée Poussin mit seiner Methode zu tun gezwungen ist.

  19. Sur la fonction ξ (t)de Riemann et son application à l’arithmétique [Vierteljahrsschrift der Naturforschenden Gesellschaft in Zürich, Bd. XLI (1896), S. 7–19].

  20. Sur la distribution des nombres premiers [Acta Mathematica, Bd. XXIV (1901), S. 159–182].

  21. Om primtalens fördelning [Öfversigt af Kongl. Svenska Vetenskaps-Akademiens Förhandlingar, Bd. LIX (1902), S. 221–225].

  22. Über die Multiplikation Dirichlet’scher Reihen [Rendiconti del Circolo Matematico di Palermo, Bd. XXIV (2. Semester 1907), S. 81–160], S. 123–125.

  23. Sur la fonction ζ (s)de Riemann et sur des fonctions analogues [Annales Scientifiques de l’École Normale supérieure, Ser. III, Bd. XI (1894), S. 75–164], S. 100.

  24. Théorème sur les séries entières [Acta Mathematica, Bd. XXII (1899), S. 55–63], S. 60–63.

  25. Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse [Monatsbericht der Königlichen Akademie der Wissenschaften zu Berlin, 1859, S. 671–680;Werke, 2. Aufl. (1892), S. 145–155], S. 672 bezw. 146.

  26. Über die Achse des Imaginären brauche ich zunächst nicht hinauszugehen.

  27. Vergl. die in Anm. 35) zitierten Stellen.

  28. Démonstration simplifiée du théorème de Dirichlet sur la progression arithmétique [Mémoires couronnés et autres Mémoires publiés par l’Académie Royale de Belgique, Bd. LUI (1896), S. 1–32], S. 6–8.

  29. Ich schliesse mich dem zweiten vonRiemann gegebenen Beweise an; vergl. die in Anm. 35) zitierte Arbeit, S. 673 bezw. S. 147.

  30. Vergl. z.B. Bachmann,Die analytische Zahlentheorie [Leipzig, 1894], S. 169–170 und S. 187, Fussnote.

  31. Étude sur les propriétés des fonctions entières et en particulier d’une fonction considérée pur Riemann [Journal de Mathématiques pures et appliquées, Ser. IV, Bd. IX (1893), S. 171–215], S. 210–215.

  32. Bei dieser Darstellung benutze ich Vereinfachungen des ursprünglichenHadamard’ schen Beweises, welche von anderen Autoren angebracht worden sind. Literaturangaben vergl. z.B. beiVivanti-Gutzmer,Theorie der eindeutigen analytischen Funktionen [Leipzig, 1906], S. 228.

  33. Dieselbe ist schon von HerrnHadamard in der Primzahltheorie verwendet worden; vergl. S. 211 seiner in Anm. 1) zitierten Arbeit.

  34. Vergl. S. 29–30 der in Anm. 12) zitierten Arbeit von Herrnde la Vallée Poussin.

  35. Vergl. S. 36 seiner Arbeit.

  36. I. c, S. 73–74.

  37. I. c, S. 23.

  38. Über die zahlentheoretische Funktion μ (k) [Sitzungsberichte der kaiserlichen Akademie der Wissenschaften in Wien, mathematisch-naturwissenschaftliche Klasse, Bd. CXII (1903), Abt. IIa, S. 537–570], S. 548.

  39. Sur un problème du calcul des fonctions asymptotiques [Journal für die reine und angewandte Mathematik, Bd. CXXVI (1903), S. 241–282].

  40. Vergl. S. 124 der in Anm. 32) zitierten Abhandlung.

  41. l. c, S. 62–63.

  42. Note sur la multiplication de deux séries [Nouvelles Annales de Mathématiques, Ser. III, Bd. VI (1887), S. 210–215], S. 214.

  43. Satz (XI) ist natürlich von derRiemann’ schen Vermutung unabhängig und steht auf festem Boden.

  44. Vergl. S. 62 der in Anm. 34) zitierten Arbeit.

  45. Vergl. S. 567 der in Anm. 69) genannten Arbeit.

  46. Vergl. seine in Anm. 38) erwähnte Abhandlung, S. 24–29.

  47. Über das Nichtverschwinden einer Dirichlet’sehen Reihe [Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 1906, S. 314–320], S. 319–320.

  48. Ueber Multiplication und Nichtverschwinden Dirichlet’scher Reihen [Journal fur die reine und angewandte Mathematik, Bd. CXVII (1897), S. 169–184], S. 181–184.

  49. Eine asymptotische Aufgabe [Sitzungsberichte der kaiserlichen Akademie der Wissenschaften in Wien, mathematisch-naturwissenschaftliche Classe, Bd. CVIII (1899), Abt. IIa, S. 32–37].

  50. Vergl. S. 315–319 meiner in Anm. 94) genannten Arbeit.

Download references

Author information

Authors and Affiliations

  1. Berlin

    Edmund Landau

Authors
  1. Edmund Landau
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Ein Erratum zu diesem Beitrag ist unter http://dx.doi.org/10.1007/BF03019659 zu finden.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Landau, E. Beiträge zur analytischen zahlentheorie. Rend. Circ. Matem. Palermo 26, 169–302 (1908). https://doi.org/10.1007/BF03018192

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03018192

Search

Navigation