Abstract
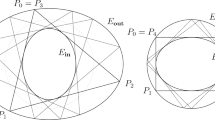
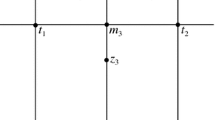
By means ofParallel Coordinates planar “graphs” of multivariate relations are obtained. Certain properties of the relationship correspond tothe geometrical properties of its graph. On the plane a point ←→ line duality with several interesting properties is induced. A new duality betweenbounded and unbounded convex sets and hstars (a generalization of hyperbolas) and between Convex Unions and Intersections is found. This motivates some efficient Convexity algorithms and other results inComputational Geometry. There is also a suprising “cusp” ←→ “inflection point” duality. The narrative ends with a preview of the corresponding results inR N.
Similar content being viewed by others
References
Ayres F (1967) Projective geometry. Schaum's Outline Series In Mathematics, McGraw-Hill, New York
Banchoff TF, Strauss CM (1979) Real time computer graphics analysis of figures in four-space in [5] pp. 159–167
Barnett V. Edit. (1981) Interpreting multivariate data. Wiley, New York
Bentley JL, Shamos MI (1978) Divide & conquer for linear expected time, Infor Proc Letters 7:87–97
Brissom D (ed.) (1979) Hypergraphics: visualizing complex relationships in art, science and technology. Am Assoc Adv Sci. Westview Press, Boulder
Brodetsky OS (1949) A first course in nomography. G. Bell & Sons, London (First Published 1920).
Burton RP, Smith DR (1982) A hidden-line algorithm for hyperspace. SIAM J. Comput 11:71–80
Busemann H, Kelly PJ (1953) Projective geometry and projective metrics. Academic Press, N.Y.
Cohan S (1984) Mobility analysis using parallel coordinate (to appear) in J Inter Fed Theory Mach Mech Available as IBM Los Angeles Scientific Center Report # G320-2754
Coxeter HSM (1974) Projective geometry. Univ. of Toronto Press, Toronto
Dimsdale B (1981) Conic transformations. IBM Los Angeles Scientific Center Report #G320-2713, October
Dimsdale B (1984) Conic transformations & projectivities. IBM Los Angeles Scientific Center Report #G320-2753
Hilbert D, Cohn-Vossen S (1952) Geometry and the imagination. Chelsea, New York
Grunbaum B (1967) Convex polytopes. Wiley, New York
Inselberg A (1981) N-dimensional graphics. Part I: Lines & hyperplanes. IBM Los Angeles Scientific Center Report G320-2711
Inselberg A, Reif M (1984) Convexity in parallel coordinates, submitted for publication. Presently available as IBM Los Angeles Scientific Center Report #G320-2738
Inselberg A, Reif M, Chomut T (1985) Convexity algorithms in parallel coordinates (to be submitted for publication)
Isaacson PL, Burton RP, Douglas DM (1984) Presentation of hypothesized 4-D phenomena. Comput Graph World 48–63
Osgood WF (1925) Advanced calculus. Macmillan, New York, pp. 186–194
Mersereau MR, Oppenheim AV (1974) Digital reconstruction of multidimensional signals from their projections. Proc IEEE 62:1319–1337
Rivero J, Inselberg A (1984) Extension al analisis del Espacio De Fase de Systemas Dinamicos por las Coordenadas Paralelas. Proc VII Systems Engr Workshop. Santiago Chile July 1984
Rockafellar RT (1970) Convex analysis Princeton University Press, Princeton
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Inselberg, A. The plane with parallel coordinates. The Visual Computer 1, 69–91 (1985). https://doi.org/10.1007/BF01898350
Issue Date:
DOI: https://doi.org/10.1007/BF01898350