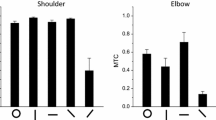
Abstract
Movement of multiple segment limbs requires generation of appropriate joint torques which include terms arising from dynamic interactions among the moving segments as well as from such external forces as gravity. The interaction torques, arising from inertial, centripetal, and Coriolis forces, are not present for single joint movements. The significance of the individual interaction forces during reaching movements in a horizontal plane involving only the shoulder and elbow joints has been assessed for different movement paths and movement speeds. Trajectory formation strategies which simplify the dynamics computation are presented.
Similar content being viewed by others
References
Abend, W., Bizzi, E., Morasso, P.: Human arm trajectory formation. Brain (1982) (in press)
Albus, J.S.: A new approach to manipulator control: the cerebellar model articulation controller (CMAC). J. Dyn. Syst. Meas. Control 97, 270–277 (1975)
Armstrong, W.W.: Recursive solution to the equations of motion of an n-link manipulator. Proc. 5th World Congress on Theory of Machines and Mechanisms, 1343–1346 (1979)
Bizzi, E., Dev, P., Morasso, P., Polit, A.: Effect of load disturbances during centrally initiated movements. J. Neurophys. 41, 524–555 (1978)
Bizzi, E., Polit, A., Morasso, P.: Mechanisms underlying achievement of final head position. J. Neurophysiol. 39, 435–444 (1976)
Feldman, A.G.: Change of muscle length due to shift of the equilibrium point of the muscle-load system. Biofizika 19, 534–538 (1974)
Golla, D.F., Garg, S.C., Hughes P.C.: Linear state feedback control of manipulators. J. Mech. Mach. Theor. 16, 93–103 (1981)
Hatze, H.: A model for the computational determination of parameter values of anthropomorphic segments. C.S.I.R. Tech. Rept., TWISK 79, Pretoria, 1979
Hogan, N.: Control of mechanical impedance of prosthetic joints. Proc. Joint Automatic Control Conference, San Francisco, aug. 13–15, 1980
Hollerbach, J.M.: A recursive formulation of lagrangian manipulator dynamics. IEEE Trans. Syst. Man Cybern. 10, 730–736 (1980)
Horn, B.K.P., Raibert, M.H.: Configuration space control. The Industrial Robot, 69–73 (June 1978)
Luh, J., Walker, M., Paul, R.: On-line computational scheme for mechanical manipulators. J. Dyn. Syst. Meas. Control 102, 69–76 (1980)
Morasso, P.: Spatial control of arm movements. Exp. Brain Res. 42, 223–227 (1981)
Orin, D.E., McGhee, R.B., Vukobratovic, M., Hartoch, G.: Kinematic and kinetic analysis of open-chain linkages utilizing Newton-Euler methods. Math. Biosci. 43, 107–130 (1979)
Raibert, M.H.: A model for sensorimotor control and learning. Biol. Cybern. 29, 29–36 (1978)
Sakitt, B.: A Spring Model and Equivalent Neural Network for Arm Posture Control. Biol. Cybern. 37, 227–234 (1980)
Silver, W.: On the equivalence of Lagrangian and Newton-Euler dynamics for manipulators. Proc. Joint Automatic Control Conference, Charlottesvill, Va., June 17–19, 1981
Soechting, J.F., Lacquaniti, E.: Invariant characteristics of a pointing movement in man. J. Neurosco. 1, 710–720 (1981)
Walker, M.W., Orin, D.E.: Efficient dynamic computer simulation of robot mechanisms. Proc. Joint Automatic Control Conference, Charlottesville, Va., June 17–19, 1981
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Hollerbach, J.M., Flash, T. Dynamic interactions between limb segments during planar arm movement. Biol. Cybern. 44, 67–77 (1982). https://doi.org/10.1007/BF00353957
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00353957