Skip to main content
SpringerLink
Log in

An experimental investigation of initial oscillations in a radial Hele-Shaw cell

  • Originals
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

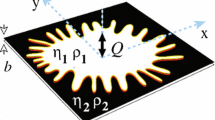
Hele-Shaw cell is a laboratory device consisting of two parallel plates of glass separated by a thin gap. In this cell, in the flow of two immiscible fluids, when a fluid of higher viscosity is displaced by a fluid of lower viscosity, the less viscous fluid is observed to form “fingers” into the more viscous one due to the unstable interface. The Saffman-Taylor or viscous finger instability has been examined and modeled for over forty years for the rectilinear Hele-Shaw cell and about half as long for the radial Hele-Shaw cell. In this paper, we study, in detail, the early development of viscous instabilities in a radial Hele-Shaw cell. This source flow configuration has been chosen so that the instability can be monitored precisely. The objective of this study is to examine the onset of fingering, i.e. initial number of fingers that form, and the evolution of interface instability. Our experiments suggest that there may be some order in this formation process and one can model this aspect by considering the unsteady velocity components and predicting temporal changes in wavenumber responsible for the initial number of fingers and may be later accounting for the fingertip oscillations and splitting.

We injected a water-based fluid into an oil in a radial Hele-Shaw cell at constant flow rate and recorded the movement of the less viscous droplet as it evolved. The relative curvature changes on the expanding droplet boundary was plotted with the angular positions about the interface and subtracting out the average radius, resulting in a plot of the change in amplitude with respect to time for the interface configuration. Three unstable configured tests at kinematic viscosity contrast (v O) of 0.34, 0.68, and 0.94 were run at approximately the same flow rate (2π cm2/s). The droplet exhibited oscillatory movement for these unstable configuration. The amplitude and the rate of oscillations were measured from digitized data. The smaller the viscosity difference, the smaller was the amplitude growth rate and resulted in a longer time to form visible finger initiation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Arneodo A; Couder Y; Grasseau G; Hakim V; Rabaud M (1990) Nonlinear evolution of spatio-temporal structures in dissipative continuous systems, pp. 481–488. New York: Plenum Press

    Google Scholar 

  • Beer F Pl; Johnston ER (1984) Vector mechanics for engineers: dynamics. New York: McGraw Hill

    Google Scholar 

  • Bird RB; Stewart WE; Lightfoot EN (1960) Transport phenomena. New York: Wiley

    Google Scholar 

  • Bouissou Ph; Perrin B; Tabeling P (1990) Nonlinear evolution of spatio-temporal structures in dissipative continuous systems, pp. 475–479. New York: Plenum Press

    Google Scholar 

  • Casademunt J; Jasnow David (1992) Interface equation and viscosity contrast in Hele-Shaw flow. J Mod Phy 6: 1647–1656

    Google Scholar 

  • Chandrasekhar S (1961) Hydrodynamic and hydromagnetic stability. London: Oxford University Press

    Google Scholar 

  • Chen JG (1989) Growth of radial viscous fingers in a Hele-Shaw cell. J Fluid Mech 201: 223–242

    Google Scholar 

  • Chen JG (1987) Radial viscous fingering patterns in Hele-Shaw cells. Exp Fluids 5: 363–371

    Article  Google Scholar 

  • Chikhliwala ED; Huang AB; Yortsos YC (1988) Numerical study of the linear stability of immiscible displacement in porous media. Transport in Porous Media 3: 257–276

    Article  Google Scholar 

  • Couder Y; Gerard N; Rabaud M (1986) Narrow fingers in the Saffman-Taylor instability. Phys Rev 34: 5175–5178

    Google Scholar 

  • Couder Y; Michalland S; Rabaud M; Thome H (1990) Nonlinear evolution of spatio-temporal structures in dissipative continuous systems, pp. 487–497. New York: Plenum Press

    Google Scholar 

  • Cowen R (1994) A fresh look at a familiar supernova. Science News 146: 81–96

    Google Scholar 

  • Degregoria AJ; Schwartz LW (1986) A boundary-integral method for two-phase displacement in Hele-Shaw cells. J Fluid Mech 164: 283–400

    MathSciNet  Google Scholar 

  • DiFrancesco MW; Rauseo SN; Maher JV (1987) Viscous fingering as a first step toward understanding dendrites. Superlattices and Microstructures 3: 617–623

    Article  Google Scholar 

  • Dougherty A; Kaplan PD; Gollub JP (1987) Development of side branching in dendritic crystal growth. Phys Rev Lett 58: 1652–1655

    Article  Google Scholar 

  • Gollub JP (1994) Instabilities of film flows. 8 August 1994 Seminar at University of Delaware, Department of Mechanical Engineering

  • Greenberg MD (1988) Advanced engineering mathematics. New Jersey: Prentice-Hall

    Google Scholar 

  • Hill S (1952) Channelling in packed columns. Chem Eng Sci 1: 247–253

    Google Scholar 

  • Harris CJ; Miles JF (1980) Stability of linear systems: some aspects of kinematic similarity. London: Academic Press

    Google Scholar 

  • Hoffmann FM; Wolf GH (1974) Excitation of parametric instabilities in statically stable and unstable fluid interfaces. J Appl Phys 45: 3859–3863

    Article  Google Scholar 

  • Homsy GM (1987) Viscous fingering in porous media. Ann Rev Fluid Mech 19: 271–311

    Article  Google Scholar 

  • Howison SD (1986) Fingering in Hele-Shaw cells. J Fluid Mech 167: 439–453

    MATH  MathSciNet  Google Scholar 

  • Kertesz J (1990) Statistical models for the fracture of disordered media, pp. 261–290. North-Holland: Elsevier Science Publishers

    Google Scholar 

  • Kessler DA; Koplik J; Levine H (1988) Pattern selection in fingered growth phenomena. Adv Phys 37: 255–339

    Article  Google Scholar 

  • Khabeev NS; Shagapov V Sh (1986) Oscillations of a gas-vapor bubble in an acoustic field. Izv Akad Nauk USSR Mekh Zhidk Gaza 3: 79–83

    Google Scholar 

  • Kopf-Sill AR; Homsy GM (1987) Narrow fingers in a Hele-Shaw cell. Phys Fluids 30: 2607–2609

    Article  Google Scholar 

  • Marion JB (1970) Classical dynamics of particles and systems, pp. 314–315. New York: Academic Press

    Google Scholar 

  • Matsushita M; Yamada H (1990) Dendritic growth of single viscous finger under the influence of linear anisotropy. J Crystal Growth 99: 161–164

    Google Scholar 

  • Maxworthy T (1987) The nonlinear growth of a gravitationally unstable interface in a Hele-Shaw cell. J Fluid Mech 177: 207–232

    Google Scholar 

  • Mclean JW; Saffman PG (1981) The effect of surface tension on the shape of fingers in a Hele-Shaw cell. J Fluid Mech 102: 455–469

    Google Scholar 

  • Meakin P; Family F; Vicsek T (1987) Viscous fingering simulated by off-lattice aggregation. J Colloid Interface Sci 117: 394–399

    Google Scholar 

  • Meiburg E; Homsy GM (1988) Nonlinear unstable viscous fingers in Hele-Shaw flows. Phys Fluids 31: 429–439

    Article  Google Scholar 

  • Miller CA; Scriven LE (1968) The oscillations of a fluid droplet immersed in another fluid. J Fluid Mech 32: 417–435

    Google Scholar 

  • Olabisi O (1982) Mechanisms of the structural web process. Pol Eng Rev 2: 29–70

    Google Scholar 

  • Paterson L (1981) Radial fingering in a Hele-Shaw cell. J Fluid Mech 113: 513–529

    Google Scholar 

  • Prigogine I; Stengers I (1984) Order out of chaos: man's new dialog with nature. NY: Bantam Books

    Google Scholar 

  • Prosperetti A (1980) Free oscillations of drops and bubbles: the initial-value problem. J Fluid Mech 100: 333–347

    MATH  Google Scholar 

  • Properetti A (1987) The linear stability of general two-phase flow models — II. J Multiphase Flow 13:] 161–171

    Google Scholar 

  • Rabaud M; Couder Y; Gerard N (1988) Dynamics and stability of anomalous Saffman-Taylor fingers. Phys Rev A 37: 935–947

    Article  Google Scholar 

  • Rauseo SN; Barnes Jr PD; Maher JV (1987) Development of radial fingering patterns. Phys Rev A 35: 1245–1251

    Google Scholar 

  • Reinelt DA (1987) The effect of thin film variations and transverse curvature on the shape of fingers in a Hele-Shaw cell. Phys Fluids 30: 2617–2623

    Article  MATH  Google Scholar 

  • Saffman PG (1959) Exact solutions for the growth of fingers from a flat interface between two fluids in a porous medium or Hele-Shaw cell. Quart J Mech Appl Math 12: 146–151

    MATH  MathSciNet  Google Scholar 

  • Saffman PG; Taylor GI (1958) The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc Roy Soc A 245: 312–329

    MathSciNet  Google Scholar 

  • Saffman PG (1986) Viscous fingering in Hele-Shaw cells. J Fluid Mech 173: 73–94

    MATH  MathSciNet  Google Scholar 

  • Saffman PG (1991) Selection mechanisms and stability of fingers and bubbles in Hele-Shaw cells. IMA J Appl Math 46: 137–145

    MATH  MathSciNet  Google Scholar 

  • Sarkar SK (1987) The effect of velocity-dependent boundary conditions on pattern formation. Superlattices and Microstructures 3: 589–594

    Article  Google Scholar 

  • Sarkar SK (1990) Scaling dynamics of immiscible radial viscous fingering. Phys Rev Lett 65: 2680–2683

    Article  Google Scholar 

  • Sarkar S; Jasnow D (1987) Quantitative test of solvability theory for the Saffman-Taylor problem. Phys Rev A 35: 4900–4903

    Google Scholar 

  • Schwartz LW; Degregoria J (1988) Two-phase flow in Hele-Shaw cells: numerical studies of sweep efficiency in a five-spot pattern. J Austral Math Soc Ser B 29: 375–400

    MathSciNet  Google Scholar 

  • Schwartz L (1986) Stability of Hele-Shaw flows: the wetting layer effect. Phys Fluids 29: 3086–3088

    Article  Google Scholar 

  • Streeter VL; Wylie EB (1975) Fluid mechanics. Tokyo: McGraw-Hill Kogakusha

    Google Scholar 

  • Tryggvason G; Aref H (1983) Numerical experiments on Hele-Shaw flow with a sharp interface. J Fluid Mech 136: 1–30

    Google Scholar 

  • Vanden-Broeck JM (1983) Fingers in a Hele-Shaw cell with surface tension. Phys Fluids 26: 2033–2034

    MathSciNet  Google Scholar 

  • Wilson SDR (1975) A note on the measurement of dynamic contact angles. J Colloid Interface Sci 51: 532–534

    Article  Google Scholar 

  • Weinstein SJ; Dussan VEB; Ungar LH (1990) A theoretical study of two-phase flow through a narrow gap with a moving contact line: viscous fingering in a Hele-Shaw cell. J Fluid Mech 221: 53–76

    Google Scholar 

  • Wei-Shen Dai; Kadanoff LP; Su-Min Zhou (1991) Singularities in complex interface dynamics. Growth and form. New York: Plenum Press

    Google Scholar 

  • Chia-Shun Yih (1977) Fluid mechanics: a concise introduction to the theory. Michigan: West River Press

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Delaware, 19716, Newark, DE, USA

    S. B. K. Burns & S. G. Advani

Authors
  1. S. B. K. Burns
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. G. Advani
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was supported by National Science Foundation, grant number EID-9017555. We also like to thank Dr. Len Schwartz, Professor of Mechanical Engineering at the University of Delware for his insight and helpful suggestions.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Burns, S.B.K., Advani, S.G. An experimental investigation of initial oscillations in a radial Hele-Shaw cell. Experiments in Fluids 21, 187–200 (1996). https://doi.org/10.1007/BF00191691

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00191691

Keywords

Search

Navigation