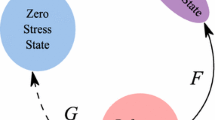Skip to main content
SpringerLink
Log in

A mathematical model for fibroblast and collagen orientation

  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

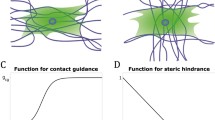
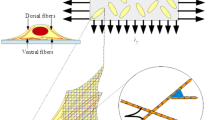
Due to the increasing importance of the extracellular matrix in many biological problems, in this paper we develop a model for fibroblast and collagen orientation with the ultimate objective of understanding how fibroblasts form and remodel the extracellular matrix, in particular its collagen component. The model uses integrodifferential equations to describe the interaction between the cells and fibers at a point in space with various orientations. The equations are studied both analytically and numerically to discover different types of solutions and their behavior. In particular we examine solutions where all the fibroblasts and collagen have discrete orientations, a localized continuum of orientations and a continuous distribution of orientations with several maxima. The effect of altering the parameters in the system is explored, including the angular diffusion coefficient for the fibroblasts, as well as the strength and range of the interaction between fibroblasts and collagen. We find the initial conditions and the range of influence between the collagen and the fibroblasts are the two factors which determine the behavior of the solutions. The implications of this for wound healing and cancer are discussed including the conclusion that the major factor in determining the degree of scarring is the initial deposition of collagen.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  • Alberts, B., B. Dennis, J. Lewis, M. Raff, K. Roberts and J. D. Watson (1994). Cell junctions, cell adhesion, and the extracellular matrix, in Molecular Biology of the Cell. 3 edn, pp. 978–986, Garland Publishing.

  • Besseau, L. and M. M. Giraud-Guille (1995). Stabilization of fluid cholesteric phases of collagen to ordered gelated matrices. J. Mol. Bio. 251, 197–202.

    Article  Google Scholar 

  • Birk, D. E. and R. L. Trelstad (1986). Extracellular compartments in tendon morphogenesis: Collagen fibril, bundle, and macroaggregate formation. J. Cell Bio. 103, 231–240.

    Article  Google Scholar 

  • Bray, D. (1992). Cell Movements. Garland Publishing.

  • Brown, P. N. and Y. Saad (1987). Hybrid Krylov Methods for Nonlinear Systems of Equations. Technical Report, Lawrence Livermore National Laboratory.

  • Byrne, H. M. and M. A. J. Chaplain (1996). Modelling the role of cell-cell adhesion in the growth and development of a carcinoma. Math. Comp. Modelling 24, 1–17.

    Article  MATH  Google Scholar 

  • Civelekoglu, G. and L. Edelstein-Keshet (1994). Modelling the dynamics of F-actin in the cell. Bull. Math. Bio. 56, 587–616.

    Article  MATH  Google Scholar 

  • Clark, R. A. F. (Ed.) (1996a). The Molecular and Cellular Biology of Wound Repair, 2 edn, New York: Plenum Press.

    Google Scholar 

  • Clark, R. A. F. (1996b). Wound repair overview and general considerations, in The Molecular and Cellular Biology of Wound Repair, (Ed.) R. A. F. Clark 2 edn, pp. 3–50, New York: Plenum Press.

    Google Scholar 

  • Clark, R. A. F., L. D. Nielsen, M. P. Welch and J. M. McPherson (1995). Collagen matrices attenuate the collagen-synthetic response of cultured fibroblasts to TGF-β. J. Cell Sci. 108, 1251–1261.

    Google Scholar 

  • Cook, J. (1995). Waves of alignment in populations of interacting, oriented individuals. Forma 10, 171–203.

    MATH  MathSciNet  Google Scholar 

  • Dale, P. D., J. A. Sherratt and P. K. Maini (1996). A mathematical model for collagen fibre formation during foetal and adult dermal wound healing. Proc. R. Soc. Lond. B263, 653–660.

    Google Scholar 

  • Deutsch, A. (1995). Towards analysing complex swarming patterns in biological systems with the help of lattice-gas cellular automata. J. Biol. Systems 3, 947–956.

    Article  Google Scholar 

  • Edelstein-Keshet, L. and B. G. Ermentrout (1990). Models for contact-mediated pattern formation: cells that form parallel arrays. J. Math. Bio. 29, 33–58.

    MathSciNet  MATH  Google Scholar 

  • Elsdale, T. (1973). The generation and maintenance of parallel arrays in cultures of diploid fibroblasts, in Biology of Fibroblast, E. Kulonen and J. Pikkarainen (Eds), New York: Academic Press.

    Google Scholar 

  • Geigant, E., K. Ladizhandsky and A. Mogilner (1998). An integro-differential model for orientational distributions of F-actin in cells. SIAM J. Appl. Math. to appear.

  • Grunbaum, D. (1994). Swarming behaviour as an aide to chemotaxis, in 3D Animal Aggregations, J. Parrish and W. Hammner (Eds), Cambridge: Cambridge University Press.

    Google Scholar 

  • Grunbaum, D. (1998). Advection-diffusion equations for generalised tactic searching behaviors. J. Math. Bio. in press.

  • Guido, S. and R. T. Tranquillo (1993). A methodology for the systematic and quantitative study of cell contact guidance in oriented collagen gels. J. Cell Sci 105, 317–331.

    Google Scholar 

  • Harmon, C. B., B. D. Zelickson, R. K. Roenigk, E. A. Wayner, B. Hoffstrom, M. R. Pittelkow and D. G. Brdoland (1995). Dermabrasive scar revision—immunochemical and ultrastructural evaluation. Dermatol. Surg. 21, 503–508.

    Article  Google Scholar 

  • Jiang, W. G. and R. E. Mansel (1996). Progress in anti-invasion and anti-metastasis research and treatment. Int. J. Oncology 9, 1013–1028.

    Google Scholar 

  • Maini, P. K. (1990). Superposition of modes in a caricature of a model for morphogenesis. J. Math. Bio. 28, 307–315.

    Article  MathSciNet  Google Scholar 

  • Mast, B. A. (1992). The skin, in Wound Healing Biochemical and Clinical Aspects, I. K. Cohen, R. F. Diegelmann and W. J. Lindblad (Eds), pp. 344–355, Philadelphia: Saunders.

    Google Scholar 

  • McCallion, R. L. and M. W. J. Ferguson (1996). Fetal wound healing and the development of antiscarring therapies for adult wound healing, in The Molecular and Cellular Biology of Wound Repair, 2 edn, R. A. F. Clark (Ed.), pp. 561–600, New York: Plenum Press.

    Google Scholar 

  • Mogilner, A. and L. Edelstein-Keshet (1995). Selecting a common direction. I. How orientational order can arise from simple contact responses between interacting cells J. Math. Bio. 33, 619–660.

    Article  MathSciNet  MATH  Google Scholar 

  • Mogilner, A. and L. Edelstein-Keshet (1996). Spatio-angular order in populations of self-aligning objects: formation of oriented patches. Physica D 89, 346–367.

    Article  MathSciNet  MATH  Google Scholar 

  • Mogilner, A., L. Edelstein-Keshet and B. G. Ermentrout (1996). Selecting a common direction. II. Peak-like solutions representing total alignment of cell clusters. J. Math. Bio. 34, 811–842.

    MathSciNet  MATH  Google Scholar 

  • Murray, J. D. (1993). Mathematical Biology, 2 edn, pp. 241–244, New York: Springer.

    MATH  Google Scholar 

  • Neubert, M. G., M. Kot and M. A. Lewis (1995). Dispersal and pattern formation in a discrete-time predator-prey model. Theoret. Pop. Bio. 48, 7–43.

    Article  MATH  Google Scholar 

  • Okuba, A. (1986). Dynamical aspects of animal grouping: swarms, schools flocks, and herds. Adv. Biophys. 22, 1–94.

    Article  Google Scholar 

  • Olsen, L., J. A. Sherratt and P. K. Maini (1995). A mechanochemical model for adult dermal wound contraction and the permanence of the contracted tissue displacement profile. J. Theor. Bio. 177, 113–128.

    Article  Google Scholar 

  • Osher, S. and S. R. Chakravarthy (1984). High resolution schemes and the entropy condition. SIAM J. Numer. Anal. 21, 955–984.

    Article  MathSciNet  MATH  Google Scholar 

  • Perumpanai, A. J., J. A. Sherratt, J. Norbury and H. M. Byrne (1996). Biological inferences from a mathematical model for malignant invasion. Invasion and Metastasis 16, 209–221.

    Google Scholar 

  • Pollard, T. D. and J. A. Cooper (1986). Actin and actin-binding proteins. A critical evaluation of mechanisms and function. Ann. Rev. Biochem. 55, 987–1035.

    Article  Google Scholar 

  • Shah, M., D. M. Foreman and M. W. J. Ferguson (1992). Control of scarring in adult wounds by neutralising antibody to transforming growth factor β. Lancet 339, 213–214.

    Article  Google Scholar 

  • Shah, M., D. M. Foreman and M. W. J. Ferguson (1994). Neutralising antibody to TGF-β 1,2 reduces cutaneous scarring in adult rodents. J. Cell Sci. 107, 1137–1157.

    Google Scholar 

  • Sherratt, J. A. and J. Lewis (1993). Stress-induced alignment of actin filaments and the mechanics of cytogel. Bull. Math. Bio. 55, 637–654.

    Article  MATH  Google Scholar 

  • Stevens, A. (1995). Trail following and aggregation of myxobacteria. J. Bio. Systems 3, 1059–1068.

    Article  Google Scholar 

  • Stopak, D. and A. K. Harris (1982). Connective tissue morphogenesis by fibroblast traction. Devel. Bio. 90, 383–398.

    Article  Google Scholar 

  • Sweby, P. (1984). High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 21, 995–1011.

    Article  MATH  MathSciNet  Google Scholar 

  • Thurburn, J. (1996). Multidimensional flux-limited advection schemes. J. Comp. Phys. 123, 74–83.

    Article  Google Scholar 

  • Welch, M. P., G. F. Odland and R. A. F. Clark (1990). Temporal relationships of F-actin bundle formation, collagen and fibronectin matrix assembly, and fibronectin receptor expression to wound contraction. J. Cell Bio. 110, 133–145.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematics Institute, University of Warwick, Coventry, CV4 7AL, UK

    John C. Dallon & Jonathan A. Sherratt

Authors
  1. John C. Dallon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jonathan A. Sherratt
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dallon, J.C., Sherratt, J.A. A mathematical model for fibroblast and collagen orientation. Bull. Math. Biol. 60, 101–129 (1998). https://doi.org/10.1006/bulm.1997.0027

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1006/bulm.1997.0027

Keywords

Search

Navigation