Skip to main content
SpringerLink
Log in

Kinematics and dynamics of deployable structures with scissor-like-elements based on screw theory

  • Published:
Chinese Journal of Mechanical Engineering Submit manuscript

Abstract

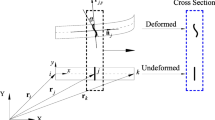
Because the deployable structures are complex multi-loop structures and methods of derivation which lead to simpler kinematic and dynamic equations of motion are the subject of research effort, the kinematics and dynamics of deployable structures with scissor-like-elements are presented based on screw theory and the principle of virtual work respectively. According to the geometric characteristic of the deployable structure examined, the basic structural unit is the common scissor-like-element(SLE). First, a spatial deployable structure, comprised of three SLEs, is defined, and the constraint topology graph is obtained. The equations of motion are then derived based on screw theory and the geometric nature of scissor elements. Second, to develop the dynamics of the whole deployable structure, the local coordinates of the SLEs and the Jacobian matrices of the center of mass of the deployable structure are derived. Then, the equivalent forces are assembled and added in the equations of motion based on the principle of virtual work. Finally, dynamic behavior and unfolded process of the deployable structure are simulated. Its figures of velocity, acceleration and input torque are obtained based on the simulate results. Screw theory not only provides an efficient solution formulation and theory guidance for complex multi-closed loop deployable structures, but also extends the method to solve dynamics of deployable structures. As an efficient mathematical tool, the simper equations of motion are derived based on screw theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. BALL R S. A treatise on the theory of screw[M]. Cambridge: Cambridge University Press, 1900.

    Google Scholar 

  2. HUNT K H. Kinematic geometry of mechanisms[M]. London: Oxford University Press, 1978.

    MATH  Google Scholar 

  3. MARTÍNEZ J M R, DUFFY J. An application of screw algebra to the acceleration analysis of serial chains[J]. Mechanism and Machine Theory, 1996, 31(4): 445–457.

    Article  Google Scholar 

  4. RICO J M, GALLARDO J, DUFFY J. Screw theory and higher order kinematic analysis of open serial and closed chains[J]. Mechanism and Machine Theory, 1999, (34): 559–586.

    Google Scholar 

  5. GALLARDO J, RICO-MARTINEZ J M, ALICI G. Kinematics and singularity analyses of a 4-DOF parallel manipulator using screw theory[J]. Mechanism and Machine Theory, 2006, 41(9): 1048–1061.

    Article  MathSciNet  MATH  Google Scholar 

  6. GALLARDO J, OROZCO-MENDOZA H, RODRÍGUEZ R C, et al. Kinematics of a class of parallel manipulators which generates structures with three[J]. Multibody Syst Dynamics, 2007, 17: 27–46.

    Article  MathSciNet  MATH  Google Scholar 

  7. GALLARDO J, AGUILAR C R, CASIQUE L, et al. Kinematics and dynamics of 2(3-RPS) manipulators by means of screw theory and the principle of virtual work[J]. Mechanism and Machine Theory, 2008, 43(10): 1281–1294.

    Article  MATH  Google Scholar 

  8. RICO J M, CERVANTES J J, GALLARDO J, et al. Velocity and acceleration analysis of lower mobility platforms via screw theory[C]//32nd Annual Mechanisms and Robotics Conference, Volume 2, Parts A & B. Brooklyn, New York, USA, August 3–6, 2008: 1313–1324.

    Google Scholar 

  9. JOSHI S A, TSAI L W. Jacobian analysis of limited-DOF parallel manipulators[J]. Journal of Mechanical Design, 2002, 124(2): 254–258.

    Article  Google Scholar 

  10. ZHU S J, HUANG Z, GUO X J. Forward/reverse velocity and acceleration analyses for a class of lower-mobility parallel mechanisms[C]//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 7, Parts A and B. Long Beach, California, USA, September 24–28, 2005: 949–955.

    Google Scholar 

  11. ZHU S J, HUANG Z, DING H F. Forward/reverse velocity and acceleration analysis for a class of lower-mobility parallel mechanisms[J]. Journal of Mechanical Design, 2007, 129(4): 390–396.

    Article  Google Scholar 

  12. LIU H T, HUANG T, CHETWYND D G. An approach for acceleration analysis of lower mobility parallel manipulators[J]. Journal of Mechanisms and Robotics-Transactions of the ASME, 2011, 3(0110131).

    Google Scholar 

  13. HUANG Z, ZHU S J. Kinematic analyses of 5-DOF 3-RCRR parallel mechanism[C]//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 7, Parts A and B. Long Beach, California, USA, September 24–28, 2005: 993–999.

    Google Scholar 

  14. TSAI L W. Robot analysis: the mechanics of serial and parallel manipulators[M]. John Wiley & Sons, Inc., 1999.

    Google Scholar 

  15. TIAN Z X, WU H T. Spatial operator algebra for free-floating space robot modeling and simulation[J]. Chinese Journal of Mechanical Engineering, 2010, 23(5): 635–640.

    Article  Google Scholar 

  16. MURRAY R M, LI Z, SASTRY S S. A mathematical introduction to robotic manipulation[M]. CRC Press, 1994.

    MATH  Google Scholar 

  17. SANG H Q, HE C, LI J M, et al. Dynamic modeling and trajectory tracking control for a 3-DOF instrument in minimally invasive surgery[C]//IEEE International Conference on Robotics and Biomimetics, Volume 1–4. Guilin, China, December 19–23, 2009: 331–336.

    Google Scholar 

  18. TSAI L W. Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work[J]. Journal of Mechanical Design. 2000, 122(1): 3–9.

    Article  Google Scholar 

  19. HUANG Y, LIAO Q, WEI S, LEI G. Research on dynamics of a bicycle robot with front-wheel drive by using Kane equations based on screw theory[C]//2010 International Conference on Artificial Intelligence and Computational Intelligence. Sanya, China, Oct 23–24, 2010: 546–551.

    Chapter  Google Scholar 

  20. CHEN W J, FU G Y, GONG J H, et al. Dynamic deployment simulation for pantographic deployable masts[J]. Mechanics of Structures and Machines, 2002, 30(2): 249–277.

    Article  Google Scholar 

  21. HU M, CHEN C, PAN J, et al. Dynamics analysis on deployment for the multi-deployment lock solar array[C]//2010 International Conference on E-Product E-Service and E-Entertainment(ICEEE). Henan, China: IEEE Computer Society, Nov 7–9. 2010: 1–5.

    Google Scholar 

  22. ZHAO J S, DAI J S. WANG J Y, et al. Mechanism synthesis of a foldable stair[J]. Journal of Mechanisms and Robotics-Transactions of the ASME, 2012, 4(0145021).

    Google Scholar 

  23. SUN Y T, WANG S M, LI J F, et al. Mobility analysis of the deployable structure of SLE based on screw theory[J]. Chinese Journal of Mechanical Engineering, 2013(4): 793–800.

    Google Scholar 

  24. HUANG Z, ZHAO Y, ZHAO T. Advanced spatial mechanism[M]. Beijing: Higher Education Press, 2006. (in Chinese)

    Google Scholar 

  25. LIU J, LI Y, HUANG Z. Mobility analysis of altman over-constrained linkages by modified Grübler-Kutzbach criterion[J]. Chinese Journal of Mechanical Engineering, 2011, 24(4): 638–646.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, 710072, PR China

    Yuantao Sun, Sanmin Wang & Changjian Zhi

  2. Department of Mechanical and Industrial Engineering, University of Toronto, 5 King’s College Rd., Toronto, Ontario, Canada

    James K. Mills

Authors
  1. Yuantao Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sanmin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. James K. Mills
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Changjian Zhi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuantao Sun.

Additional information

Supported by National Natural Science Foundation of China(Grant No. 51175422)

SUN Yuantao, born in 1985, is currently a PhD candidate at School of Mechanical Engineering, Northwestern Polytechnical University, China. His main research internets include space deployable structure and multi-bodies systems dynamics.

WANG Sanmin, born in 1961, is a professor at School of Mechanical Engineering, Northwestern Polytechnical University, China. His research interests include mechanism, mechanical vibration and control and mechanical dynamics.

MILLS James K, is a professor at Mechanical & Industrial Engineering, University of Toronto. His research interests include robot control, control of multi-robots, design of actuators, localization, development of fixtureless assembly technology, design and control of high speed machines.

ZHI Changjian, born in 1984, is a PhD candidate at School of Mechanical Engineering, Northwestern Polytechnical University, China.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, Y., Wang, S., Mills, J.K. et al. Kinematics and dynamics of deployable structures with scissor-like-elements based on screw theory. Chin. J. Mech. Eng. 27, 655–662 (2014). https://doi.org/10.3901/CJME.2014.0519.098

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3901/CJME.2014.0519.098

Keywords

Search

Navigation