Behavioral scientists have long sought to explore and understand causal relationships between variables. Knowing that one variable causes another provides valuable theoretical and practical information to the scientific community and users of its findings. For instance, if a self-compassion training program causes well-being to improve, it can become central to behavioral or therapeutic interventions that aim to improve an individual's mental health. But knowing that one variable causally influences another is only part of the story scientists seek to tell. Also important to the narrative is how that effect operates. For example, perhaps self-compassion increases well-being because greater self-compassion first causes greater optimism, which, in turn, causes well-being to improve. That is, perhaps self-compassion is acting indirectly, through optimism, to enhance one’s well-being.

Mediation analysis is frequently used to understand how some presumed causal antecedent variable (hereinafter, X) influences an outcome of interest (hereinafter, Y) by affecting one or more mediator(s) (hereinafter, M) that, in turn, influence the outcome. Mediation models—which focus primarily on the estimation of indirect effects of X on Y—are abundant in behavioral science research. For instance, in one study, Schönfeld et al. (2016) found that daily stress had a significant and negative effect on a person’s mental health. The researchers posited that more stress would reduce a person’s level of self-efficacy, and this reduction in self-efficacy is what causes poorer mental health. In other words, more stress would indirectly influence mental health through self-efficacy. A mediation analysis produced results consistent with this explanation. This is merely one of many examples of mediation analysis conducted in research. Mediation models have been applied in a number of fields, including communication (Hoffman & Young, 2011), public health (Ho et al., 2013), education (Jin et al., 2018), nursing (Van der Heijden et al., 2019), and business (Wieder & Ossimitz, 2015), among many other disciplines.

But real-world causal processes are typically complex, and it is unlikely that just one mechanism is transmitting X’s effect on Y. Rather, it is more plausible that X has effects on several mediating variables causally downstream, each of which then influences Y. For instance, self-compassion training (X) could cause both greater optimism (M1) and reduced rumination (M2), both of which then influence mental health (Y). Simultaneously estimating multiple mechanisms by which X affects Y (i.e., multiple indirect effects) can be beneficial to researchers for a variety of reasons, chief among them being that researchers can test competing theories against each other by comparing indirect effects through different mediators. For example, if both optimism and rumination were measured in the same study and included in a single mediation model, it would be possible to test if there is a difference between the effects of self-compassion training on mental health through optimism and through rumination to see whether one is larger, dominant, or "more important" in some sense in explaining the effect of X on Y.

A few techniques for comparing indirect effects have been discussed in the mediation analysis literature (e.g., MacKinnon, 2000; Preacher & Hayes, 2008; Raykov et al., 2008). However, the methods most widely used suffer from the limitation that they aren’t always appropriate when a researcher’s question focuses on whether the indirect effects are equal in magnitude rather than value. After reviewing the mechanics of the estimation of indirect effects in a mediation analysis, this paper contributes to the literature by first making the case for the need to compare indirect effects operating through different mediators. We then talk about the most common (albeit, regrettably rare) practice for comparing indirect effects, highlighting its shortcomings in situations in which two mechanisms are working in competition to each other. We then describe several alternative methods for comparing indirect effects that can be used to answer questions about magnitude and talk about the results of a simulation study examining their relative performance in situations where the indirect effects are consistent or opposing in direction. We also provide a concrete substantive example of the application of these methods while illustrating their implementation in statistical software.

Indirect effects in mediation models

Mediation models are typically estimated in one of two ways: structural equation modeling (SEM) or through a series of ordinary least squares (OLS) regression analyses. Although some researchers have taken a stance about which approach should be used to estimate mediation models (Iacobucci et al., 2007; Pek & Hoyle, 2016), observed-variable SEM and OLS regression produce largely identical results (Hayes et al., 2017; Rijnhart et al., 2017). There certainly are pros and cons to conducting mediation analysis through simultaneous estimation using maximum likelihood in SEM as opposed to a set of OLS regression analyses, but which is used is inconsequential to the difference(s) between indirect effects and the methods we discuss here can be used in either computational arena.

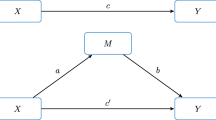
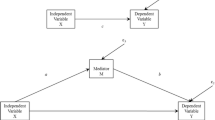
In a mediation model of X’s effect on Y through a single mediator M, assuming M and Y are continuous variables and X is either dichotomous or continuous, the effect of X operating directly and indirectly through M can be estimated using two linear equations, one for M and one for Y:

$$M={d}_M+ aX+{\varepsilon}_M$$
(1)
$$Y={d}_Y+{c}^{\prime }X+ bM+{\varepsilon}_Y$$
(2)

Figure 1A shows a statistical diagram of this model. In Eq. (1), a represents the estimated difference in M between two observations that differ by one unit on X. In Eq. (2), b represents the difference in Y between two observations that differ by one unit on M but who have the same X value and c′ represents the difference in Y between two observations that differ by one unit on X but have the same M value. Assuming proper model specification and the assumptions of valid causal inference are met, these regression weights are typically interpreted as representing causal effects (of X on M, M on Y controlling for X, and X and Y controlling for M, respectively). The indirect effect of X on Y, the effect of most interest in mediation analysis (the effect of X on Y through M), is obtained by multiplying a and b together (i.e., ab). The product ab represents the estimated difference in Y attributable to a one-unit difference in X that operates through the joint causal effect of X on M which in turn affects Y. The weight for X in Eq. (2), c′, is the direct effect of X on Y, meaning the effect of X on Y that does not operate through the mechanism represented by the mediator, M.

Fig. 1
figure 1

A simple (A) and a parallel multiple mediator model (B)

Full size image

Statistical evidence consistent with mediation is found in an inference that the indirect effect is different from zero by some kind of statistical test, such as rejection of the null that the indirect effect is zero, or a confidence interval that does not overlap zero. Inference about a single indirect effect is not the purpose of this paper. Suffice it to say that the approach most widely recommended and used of the many that have been proposed is the bootstrap confidence interval in one of several forms (see, e.g., Hayes & Scharkow, 2013; MacKinnon et al., 2004; Shrout & Bolger, 2002), a method that will be emphasized in this paper as a means of comparing indirect effects in models with more than one mediator. The mechanics of bootstrapping and confidence interval construction are described later.

Although the simple mediation model (i.e., a model with a single X, M, and Y) is the most popularly estimated mediation model in the research literature, it is unlikely that something as complex as our thoughts, feelings, and actions can be adequately described by such a simple three-variable causal system. A multiple mediation model is likely a more realistic (albeit still probably oversimplified) model that allows X’s effect on Y to be transmitted through more than one mediator simultaneously. An example of a two-mediator parallel multiple mediator model is depicted in Fig. 1B, called a “parallel” model because neither mediator is allowed to affect the other. More complex multiple mediator models are possible, including parallel models with more than two mediators, serial multiple mediators that allow for causal influence between mediators, and blended models with properties of parallel and serial models. For now, we restrict our discussion to the simplest two-mediator parallel case. We address more complex models later.

In the model depicted in Fig. 1B, the direct and two indirect effects of X on Y can be estimated with three equations, one for each of the mediators and one for Y:

$${M}_1={d}_{M_1}+{a}_1X+{\varepsilon}_{M_1}$$
(3)
$${M}_2={d}_{M_2}+{a}_2X+{\varepsilon}_{M_2}$$
(4)
$$Y={d}_Y+{c}^{\prime }X+{b}_1{M}_1+{b}_2{M}_2+{\varepsilon}_Y$$
(5)

The indirect effect of X on Y through mediator j is constructed by multiplying aj and bj. In this model, there are two indirect effects of X, a1b1 and a2b2, each called a specific indirect effect. A specific indirect effect is the indirect effect of X on Y through Mj controlling for the other mediator(s). As such, it quantifies something different than if only mediator j is used in a simple mediation model estimated with Eqs. (1) and (2). That is, the two specific indirect effects in a parallel multiple mediator model such as this are likely to be different than the indirect effects estimated in two simple mediation models, each using only one mediator. For simplicity, throughout the rest of this paper, in the context of multiple mediator models, specific indirect effects will simply be referred to as “indirect effects.”

Parallel multiple mediation models are commonly estimated by substantive researchers. For example, Wiedow et al. (2013) found that learning as a team significantly improved team outcomes. This relationship was mediated by both increased task knowledge and trust in other teammates. Another study by Copple et al. (2020) explored the relationship between science communication training and scientists’ public engagements. They found that a scientist’s communication efficacy and attitudes toward the audience mediated this relationship. Rudy et al. (2012) explored whether general self-efficacy and social self-efficacy mediated the relationship between negative self-talk and social anxiety in children. Their analyses only found support for general self-efficacy as a mediator of this relationship. Other examples are abundant in the literature (e.g., Brosowski et al., 2021; Gurmen & Rohner, 2014; Kurti & Dallery, 2014; Singla et al., 2021).

Comparing indirect effects: Value vs. magnitude

Hayes (2022) discusses some of the reasons to estimate a parallel multiple mediator model rather than several simple mediation models each with a single mediator. Most relevant to our discussion going forward is that estimating a multiple mediator model allows for a statistical comparison of indirect effects operating through different mediators. This is possible because any two indirect effects that share X and Y are scaled equivalently (in terms of the metrics of X and Y) even if the mediators are on different scales, allowing them to be formally compared with a statistical test (MacKinnon, 2000; Preacher & Hayes, 2008).

Such statistical comparisons between indirect effects can be useful. For example, an investigator might propose two (or more) processes by which X may affect Y, with the goal of the study to examine not only which mediators are at work but also whether one mechanism is more dominant, stronger, or otherwise different in size than others. Answering this question can be both theoretically and practically important. Consider the case of substance abuse and intervention research. Mediation analysis is common in these areas of study because it helps identify the mechanisms that lead to behavior change after an intervention (MacKinnon, 2000). If certain mechanisms lead to a greater change in a target behavior than others, then these intervention programs can focus on the more effective pathways and eliminate the ineffective (or less effective) ones, thus improving the quality of treatment and likelihood of behavior change.

Or one theory might predict that X’s effect on Y is transmitted through mediator A whereas another theory predicts that X’s effect on Y is carried through mediator B. The goal of the analysis may be to determine which theory has greater support. Perhaps one theory posits that optimism leads to resilience, and this increased resilience is what causes a person to be happy. A different theory might argue that optimism leads to increased self-trust, and this greater self-trust is what causes happiness to increase. If a comparison of the indirect effects suggested that the effect through resilience was larger than the effect through self-trust, the resilience theory about happiness now has more support than the self-trust theory.

Unfortunately, investigators estimating models with more than one mediator often conduct an inferential test for each indirect effect and then fall victim to the fallacy that a difference in significance between effects means they are significantly different (Gelman & Stern, 2006) or that equivalence of significance equals absence of difference. In the former case, if indirect effect A is deemed different from zero but indirect effect B is not, the researcher then concludes that indirect effect A is larger or more important in explaining the relationship than indirect effect B. But knowing that one indirect effect is statistically different from zero while another is not does not mean they are different from each other. In the latter case, knowing that two indirect effects are both different from zero doesn’t mean they are equal in value. A variant of this scenario is to conclude when neither indirect effect is different from zero that both mediators are equally uninformative about mechanisms at work transmitting X’s effect on Y. But it is possible that two effects that are both deemed not different from zero by a formal inferential test could still be different from each other when compared with an inferential test. In short, conducting an inference about the size of two indirect effects doesn’t provide an inference about the size of the difference between them. A formal statistical comparison of two indirect effects is required to claim they are the same or different.

Fortunately, some investigators do take the additional and, in our opinion, required step of comparing indirect effects to each other before making claims about their relative sizes. This is typically done by calculating what we will henceforth call the raw difference between the two indirect effects,

$${a}_1{b}_1-{a}_2{b}_2$$
(6)

and then conducting an inference about this difference. For instance, in the example of optimism and happiness above, one could compare the indirect effects through resilience (a1b1) and self-trust (a2b2) by calculating their raw difference and using one of the inferential tests discussed in the next section to determine whether this difference is significantly different from zero. In a real-world example, Scogin et al. (2015) reported the results of a multiple mediator model showing that even though the indirect effect of emotional distress on quality of life through hopelessness was over three times larger than the indirect effect through engagement in pleasant events (a1b1 =  − 0.13, a2b2 =  − 0.04, leading to a difference of −0.09 using the expression in (6)), a comparison of the two indirect effects using the raw difference revealed they were not significantly different from each other and, consequently, neither could be deemed a stronger mediator than the other. Other examples of the application of the raw difference to compare indirect effects include: Grund and Fries (2014), Romero-Moreno et al. (2016), Schotanus-Dijkstra et al. (2019), and Yıldız (2016).

Conducting inference for the difference

MacKinnon (2000) discussed inference for the raw difference between two indirect effects using the multivariate delta method. This method assumes the sampling distribution of the difference is normal in form. With this assumption, the estimate of the difference can be divided by an estimate of its standard error, producing a test statistic whose p-value for testing the null hypothesis of no difference can be derived using the standard normal distribution. Alternatively, a normal-theory confidence interval can be constructed as the point estimate ± 1.96 standard errors. The formula for the standard error of a difference between indirect effects is quite complex and its accuracy as an estimator requires meeting many assumptions.

However, assumptions don’t need to be made about the sampling distribution of the difference to compare two indirect effects. A bootstrap confidence interval can be used instead (Preacher & Hayes, 2008). To bootstrap the distribution of the raw difference, draw B random samples (where B is preferably at least 5000) of size n from the data with replacement, where n is the original sample size. In each of these B bootstrap samples, estimate the model and calculate a1b1 − a2b2. To construct a percentile bootstrap confidence interval for inference, the lower and upper bounds of a c% confidence interval using the percentile method are the [(100 – c)/2]th and [(c/2) + 50]th percentiles of the sorted distribution of B bootstrap estimates, respectively. Evidence of a difference between the indirect effects is found in a confidence interval that does not include zero.Footnote 1 This method makes no assumptions about the shape of the sampling distribution of the difference, and because it does not require an estimate of the standard error of the difference, it is easy to implement without making the assumptions typically required for unbiased estimation of the standard errors of estimates.

Comparing opposing indirect effects

Using the raw difference as an estimator of the difference between two indirect effects leads to an inference about whether the two indirect effects are equal in value—meaning whether the indirect effects are the same number or different numbers. This is not necessarily the same as an inference about whether the indirect effects are equal in magnitude. The magnitude of an indirect effect is its distance from zero and is what many people would think of as the size of the indirect effect or its strength. Two indirect effects could be different in value but equal in magnitude (or strength). Two things that are different in magnitude are, necessarily, different in value. But two things that are different in value are not necessarily different in magnitude. That means that an inference that two indirect effects are different in value using the raw difference approach described above does not necessarily lead to the inference that the indirect effects are different in magnitude or strength. The raw difference approach quantifies difference in magnitude only for indirect effects that are the same sign.

To illustrate this distinction between value and magnitude, consider an intervention to reduce alcohol consumption among alcoholics. Various mechanisms to reduce alcohol use might be targeted by such an intervention, including increasing self-efficacy and reducing depression (O’Rourke & MacKinnon, 2018). However, intervention programs can have unintended effects on behavior that work in opposition to the targeted mechanisms of the invention. For example, a physical activity intervention might have certain beneficial effects on mental health but could also increase body mass because of higher caloric intake (Cerin & MacKinnon, 2009). And drug-prevention programs could (unintentionally) inform participants of more reasons to use a drug (MacKinnon, 2000). Such cases of opposing indirect effects are an example of inconsistent mediation in the context of multiple mediator models (Davis, 1985).Footnote 2

Assume self-efficacy and reasons to drink were measured as part of an evaluation of an intervention to reduce alcohol use. When looking at the effect through self-efficacy, the indirect effect (a1b1) could be negative as expected, with the intervention increasing self-efficacy (a1 > 0) which in turn decreases drinking behavior (b1 < 0), and so a1b1 < 0. But the intervention might also remind participants of additional reasons to drink (a2 > 0) which in turn increases alcohol use (b2 > 0), resulting in a positive indirect effect through reasons to drink (a2b2 > 0). Both mechanisms could be at work transmitting the effect of the intervention, but they operate in different directions.

Now further suppose that the indirect effect through self-efficacy, a1b1, was –0.60 and the effect through reasons to drink, a2b2, was 0.60. The raw difference between them is not zero (a1b1 − a2b2 = –1.20), and an inference that relies on the raw difference could very well lead to the correct inference that the indirect effects are not the same value. But it is not as if one of these is necessarily more important than the other in explaining drinking behavior following the intervention. They are equal in magnitude or strength because they are equidistant from zero—they are merely operating in different directions. Put simply, the mechanism through self-efficacy reduces drinking by the same amount that the mechanism through reasons to drink increases drinking.

Perhaps this example is far-fetched even if it does make the point. But findings like these do exist in the literature. For instance, Chen et al. (2017) found that employee mentoring (X) may reduce work–family conflict (Y) by increasing access to job-related resources (M1) which in turn can lower work–family conflict (a1b1 < 0). At the same time, that mentoring can increase feelings of workload (M2), which results in more work–family conflict (a2b2 > 0). Some other examples of opposing indirect effects in parallel multiple mediation models include Levant and Wimer (2014); Pitts et al. (2018); Romano and Balliet, 2017; and Ter Hoeven et al. (2016).

So, if one wants to test whether two indirect effects are different in magnitude when they are of different signs, a different method must be used. We offer some approaches below that can be used to test whether two indirect effects differ in magnitude that also, by definition, double as tests of difference in value. All but one of these can be used regardless of the whether the signs of the indirect effects are the same or different.

The difference in the absolute values

One possibility is using the difference between the absolute values of the indirect effects,

$$\left|{a}_1{b}_1\right|-\left|{a}_2{b}_2\right|$$
(7)

This difference would be zero in a scenario like described above (i.e., when the two opposing indirect effects are equal in magnitude but opposite in sign). Bootstrap confidence intervals can be constructed for inference about this difference as described above. If the confidence interval for the difference does not contain zero, then the two indirect effects are deemed different in magnitude (and value), regardless of whether they are of the same or different sign.

The sum

Ter Hoeven et al. (2016) had the insight that two opposing indirect effects can be compared by using their sum

$${a}_1{b}_1+{a}_2{b}_2$$
(8)

In a parallel multiple mediator model with two mediators, this sum is equivalent to the total indirect effect (which is not usually interpreted as a quantification of the difference in magnitude of the two indirect effects). However, when indirect effects are of opposing signs and equal magnitude, the expected value of the sum is equal to zero. The standard error of the sum is available and easy to calculate, though derivation of a p value or confidence interval using the standard error requires assuming the sum is normally distributed. Inference through bootstrapping doesn’t require this assumption. If a bootstrap confidence interval doesn’t contain zero, then the indirect effects are deemed different in magnitude (and value). It is worth emphasizing that if the two indirect effects have the same sign, this approach provides no information about difference in magnitude or value.

The ratio

A comparison of indirect effects does not require the use of a difference or sum. The ratio of the indirect effects can also be used, though specific indirect effects that are zero or near zero can produce problems with ratio-based measures, as we discuss below. To test whether two indirect effects are different using the simplest ratio approach, we calculate

$$\frac{a_1{b}_1}{a_2{b}_2}$$
(9)

Like the difference between absolute values, a bootstrap confidence interval for this ratio can be used for inference about both magnitude and value regardless of the signs of the two indirect effects. When the two indirect effects are the same in value (both positive or both negative), this ratio is one, whereas when they are equal in magnitude but opposite in sign, the ratio is negative one. A bootstrap confidence interval that doesn’t include one or negative one supports the claim that the two indirect effects are different in magnitude (and value).

A concern with this and some related approaches discussed next is the presence of a zero in the denominator, which produces an indeterminate statistic. In (9), if a2b2 is zero, then the result is indeterminate and impossible to interpret. And if a1b1 is zero and a2b2 is nonzero, the ratio is 0. But it is arbitrary which indirect effect goes in the numerator and which in the denominator. Whether the ratio is zero or indeterminant in these cases is determined by an arbitrary computational decision. Although this is true, it is extremely rare to observe or compute a value that is exactly zero. Even still, if one of the indirect effects (the point estimate or in a bootstrap sample) is close to zero, the ratio can be very small or very large. Bootstrap distributions that are very unusual in form and untrustworthy for construction of confidence intervals could result whenever one of the indirect effects is very small.

The ratio of absolute values

The point estimate that results from the ratio of the indirect effects can range from (–∞, ∞). A modification is the ratio of the absolute values of the indirect effects:

$$\frac{\mid {a}_1{b}_1\mid }{\mid {a}_2{b}_2\mid }$$
(10)

This ratio is bounded from [0, ∞). A bootstrap confidence interval that does not contain one results in the inference that the indirect effects are different in magnitude (and value) regardless of their signs. But the presence of a zero or near-zero value in the numerator or denominator may pose the same problems as it did with the simple ratio of the indirect effects.

The proportional absolute value

It is possible to further bound the ratio of indirect effects. The ratio of the absolute value of one indirect effect to the sum of the absolute values of the two indirect effects, which we will call the proportional absolute value,

$$\frac{\mid {a}_1{b}_1\mid }{\left|{a}_1{b}_1\right|+\mid {a}_2{b}_2\mid }$$
(11)

is bound between [0, 1]. It would be equal to 0.5 if the two indirect effects are equal in magnitude (and value). Thus, a bootstrap confidence interval that does not contain 0.5 provides evidence that the two indirect effects are different in magnitude (and value) regardless of their signs. But as with the other ratios, the meaningfulness of this statistic is contingent on neither the numerator nor denominator equaling zero.

Note that inference using the ratio of absolute values (10) should generally produce an identical inference as the use of the proportional absolute value (11), as these are just monotonic transformations of each other. To demonstrate why this is, say ∣a1b1∣ is 8 and ∣a2b2∣ is 2. Plugging these values into (10) produces a value of 4 whereas (11) produces a value of .8. However, if we take \(\frac{.8}{\left(1-.8\right)}\) we get back to the value from Eq. (10) (i.e., 4). This is true for any two values you plug into the equations except when a2b2 is zero, which is indeterminate for (10) but 1 for (11). We argue the proportional absolute value produces a more elegant estimate than the ratio of absolute values that is easier to interpret (the values approach zero and one instead of zero and infinity), and since they provide the same information about relative size of the two indirect effects, we recommend Eq. (11) over Eq. (10) if one of these is to be used.

Example application

We next illustrate the use of these approaches in comparing indirect effects. The health of veterans returning from war has been of keen interest to researchers, citizens, and of course, veterans and active military personnel. It is well understood that combat experiences are a cause of posttraumatic stress in veterans. Understanding the process(es) by which combat experiences lead to posttraumatic stress and other negative outcomes like alcohol abuse and suicide is of the utmost importance for those wishing to better the lives of veterans who have given a part of theirs to help protect the country.

In a retrospective study, Pitts et al. (2018) explored a few mechanisms by which veterans' combat experiences (X) could cause posttraumatic stress (PTS) symptoms (Y) once they returned home from war. They hypothesized that army medics who experienced combat during their most recent deployment would perceive more threats to their life during the deployment (M1), and this greater level of perceived threat would lead to more PTS symptoms upon returning home. They also hypothesized that combat experience would lead to greater perceived benefits of deployment (M2), which would in turn lead to fewer PTS symptoms. They fit a parallel multiple mediator model as in Fig. 1B, with socially desirable response tendencies used as a covariate by adding it to the equations for both mediators and the outcome, Y.

The data from the original study come from a questionnaire administered to 324 Army combat medics. As the data are only correlational in nature, causality cannot be unequivocally established, but it is still possible to estimate the indirect effects of interest assuming causality. Without access to their data—and only for the purpose of illustration—we used their published matrix of correlations between variables as well as their means and standard deviations to produce a simulated data set that exactly reproduced these statistics (and it is this simulated dataset that we analyzed). The point estimates of effects we report in our example as well as the substantive interpretation of our analysis reproduce theirs—except they did not conduct the comparisons between indirect effects using the methods we employ in this example. Had they done so, their results using their data might be different even if the substantive conclusions are the same. (Due to the random nature of bootstrapping, the distribution of effects using different data sets would likely produce somewhat different results even if the models, means, standard deviations, and correlations between variables in the model are the same.) The analysis was conducted using the PROCESS macro for SPSS, SAS, and R (Hayes, 2022).Footnote 3 In the Appendix, we provide PROCESS code and output and follow-up SPSS, SAS, and R code for processing the bootstrap estimates from PROCESS, as well as code for conducting the analysis using the lavaan package in R.

Estimating Eqs. (3–5) (adding socially desirable responding to each equation as Pitts et al., 2018, did) yields the following results (also summarized in Table 1). More combat experiences were associated with greater perceived threat to life (a1 = 0.691) and greater perceived benefits of deployment (a2 = 0.190). As expected, controlling for other variables in the model of PTS symptoms, perceiving more threats to life was associated with more PTS symptoms (b1 = 0.235), and the more benefits one perceived from deployment, the fewer PTS symptoms they reported (b2 = –0.378). The specific indirect effects of combat experience on PTS symptoms are constructed by multiplying the a and b paths, and inference for each indirect effect was conducted using a percentile bootstrap confidence interval based on 10,000 bootstrap samples. The (specific) indirect effect of combat experiences through perceived threat is a1b1 = 0.162, 95% CI = [0.057, 0.277]. Assuming causality, a one-unit increase in combat experience seems to increase PTS symptoms indirectly (because a1b1 is positive) by 0.162 units by increasing feelings of threat to life (because a1 is positive) which in turn increases PTS symptoms (because b1 is positive). The specific indirect effect through perceived benefits of deployment is a2b2 = −0.072, 95% CI = [−0.147, −0.018]. Again, assuming causality, a one-unit increase in combat experience seems to decrease PTS symptoms indirectly (because a2b2 is negative) by 0.072 units by first increasing perceived benefits of deployment (because a2 is positive) which in turn decreases PTS symptoms (because b2 is negative). As both confidence intervals for the indirect effects exclude zero, we can say that the effect of combat experiences on PTS symptoms operates through both mechanisms simultaneously to cause a decrease (and increase) in PTS symptoms. These mechanisms are working in opposition to each other.

Table 1 Unstandardized model coefficients, indirect effects, and comparisons between indirect effects from the analysis of the simulated Pitts et al. (2018) data
Full size table

But are these indirect effects the same or different in value? In magnitude? We used all methods discussed above to compare a1b1 and a2b2. The confidence intervals and standard deviations of the bootstrap distributions can be found in Table 1, and Fig. 2 visualizes the bootstrap distributions for these metrices of difference. The confidence interval for the raw difference leads to the conclusion that the indirect effects are different in value (a1b1 − a2b2= 0.234; 95% CI = [0.118, 0.359]). But because the indirect effects are opposite in sign, we cannot conclude with this result that they are different in magnitude or strength. Using the difference in absolute values—which requires the confidence interval not include zero to claim differences in magnitude—does not support a claim of difference in magnitude, |a1b1| − |a2b2| = 0.090, 95% CI = [−0.046 to 0.226]. Nor does a confidence interval based on the sum of the indirect effects support such a claim, a1b1 + a2b2 = 0.090, 95% CI = [−0.046, 0.226]. The other three methods for comparing magnitude that involve division produce the same conclusion: No difference in the magnitude of the two indirect effects. The bootstrap confidence interval for the ratio of indirect effects included −1, a1b1/a2b2 = −2.250, 95% CI = [−9.969, −0.590], and the interval for the ratio of absolute values included 1, ∣a1b1 ∣ / ∣ a2b2∣ = 2.250, 95% CI = [0.602, 10.092]. A claim of difference in magnitude using the proportional absolute value requires the confidence interval exclude 0.50. That criterion was not met: ∣a1b1 ∣ /(|a1b1|+| a2b2| ) = 0.692, 95% CI = [0.376, 0.910].

Fig. 2
figure 2

Bootstrap distributions of the difference between indirect effects from the analysis of the Pitts et al. (2018) simulated data, with 95% bootstrap confidence interval endpoints next to dashed lines. The solid arrow points at the test value that confidence interval should exclude to conclude two indirect effects are different. The hollow arrow points at the point estimate of the difference

Full size image

Notice that, in this example, the point estimates and confidence intervals for the difference in absolute values and sum approaches are identical. This would tend to occur in larger sample sizes when the point estimates of the indirect effects are sufficiently distant from zero such that rarely (if ever) are any of the bootstrap estimates of the indirect effects different in sign than the point estimates. In such a case, the sum and the difference in absolute values will have essentially the same bootstrap distribution. This is not a general phenomenon but, rather, specific to this example.

It is also important to point out the existence of many extreme bootstrap estimates of the ratio and ratio of absolute value bootstrap distributions noted in two of the panels in Fig. 2. As mentioned earlier, these two statistics can explode in value toward positive or negative infinity as the denominator approaches zero. A few dozen estimates of these two quantities in our analysis do not show up in the histograms because scaling the horizontal axis to include them obscures the appearance of the distribution where most of the bootstrap estimates reside. The consequence of these extremes is a standard error for the statistic that is huge relative to the point estimates, as can be seen in Table 1. This would tend to occur frequently when one or more of the indirect effects is close to zero. Although standard errors are not used in the derivation of the percentile bootstrap confidence interval, many extremes in the bootstrap distribution (a few bootstrap estimates were greater than 400 or less than −400) can influence the width of confidence intervals and this no doubt can affect performance of these approaches in some circumstances. Indeed, notice the very wide width of the confidence intervals (from Table 1) for these two metrics of difference.

This analysis is consistent with the claim that both mechanisms by which combat experience can influence posttraumatic stress appear to be operating, but they do so in different directions. Furthermore, the indirect effect of combat experience on posttraumatic stress through perceived benefits is indeed different in value from the indirect effect through perceived threats to life. However, it would be inappropriate and incorrect to say that one of the indirect effects is stronger or weaker than the other. Using the metrics of difference in magnitude we discuss here, the proper conclusion is that neither mechanism is stronger or larger in magnitude than the other.

Although the raw difference is the predominant method of comparing indirect effects (especially indirect effects of consistent signs), no formal study has evaluated its efficacy. Additionally, as shown in the previous example, the raw difference does not function as a test of equality of magnitude when the indirect effects have opposing signs. Most of the methods we proposed above serve as a test of equality of magnitude regardless of the consistency of the signs of the indirect effects. Thus, we aimed to evaluate the performance of the raw difference (the current standard) relative to the methods we proposed when the indirect effects have the same sign and evaluate the performance of the proposed methods when the current standard is inappropriate as a test of equality of magnitude—that is, when the indirect effects are of different signs.

Relative performance: Simulation findings and recommendations

With several plausible metrics of difference that can be used to compare two indirect effects, it is important to answer the question: Does one perform better than another or is the choice of which to use largely inconsequential? To help answer this question, we conducted a Monte Carlo simulation, the results of which we only briefly summarize here with an eye toward practical recommendations. The simulation examined the performance of these methods for comparing the magnitude of two indirect effects in a parallel multiple mediator model with two mediators. The simulation used a variety of sample sizes (20, 50, 100, 200, 500) and combinations of the values of the a and b paths (−0.59, −0.39, −0.14, 0, .14, .39, .59), with normal population distributions of X and standard normal errors in estimation of M and Y, as is typical in simulations examining the performance of tests of mediation (e.g., Fritz & MacKinnon, 2007; Hayes & Scharkow, 2013). We tested the null hypothesis of equality of magnitude using 95% bootstrap confidence intervals, rejecting the null when the confidence interval excluded the pertinent test value (e.g., 0 for the raw difference). We also quantified confidence interval coverage, meaning how frequently the confidence interval included the true difference in magnitude. We summarize the simulation findings in terms of type I error, power, and confidence interval coverage before offering recommendations about which method to prefer depending on whether the indirect effects are the same or different in sign. For all the details of the simulation and a more comprehensive discussion of the results, see Coutts (2020).

Type I error and power

All methods performed reasonably well across most conditions. Although all methods were conservative (excessively low type I error rates) in smaller samples, false positives converged upward to the nominal rate of 0.05 as the sample and effect size increased. The metrics based on absolute values (i.e., difference and ratio of absolute values, proportional absolute value) were usually more conservative than the raw difference or sum approaches. Therefore, (and not surprisingly) these absolute-value based measures were correspondingly lower in power than the raw or sum metrics. However, in some conditions, the absolute value-based metrics had excessively high type I error rates—as high as 10–14%. This generally occurred when both indirect effects were zero, either because all paths were zero or one of the paths was nonzero and large but the other paths were zero. Put simply, the raw difference had slightly closer-to-nominal type I error (and higher power) when the indirect effects were of the same sign, and the sum had similarly better performance when the indirect effects were of different signs.

Coverage of the true difference

Although type I error rate and power (1 – type II error rate) are important to consider when choosing a test, coverage of the true value is also an important indicator of the quality of confidence interval-based methods. Looking at the frequency of coverage of the true value, performance mirrored the type I error and power rate results discussed above, with the raw difference and sum approaches performing better than the other methods (for indirect effects of the same and different signs, respectively).

A seemingly anomalous finding was that coverage of the true contrast value was zero for the ratio of absolute values and proportional absolute value methods when one of the indirect effects was zero. To understand why this happens, consider the case where the population values of a1b1 and a2b2 are different but one is zero (e.g., a1b1= 0, a2b2 = −0.3). In this scenario, the population ratio is zero for these metrics. But the only way a bootstrap estimate of this ratio could be as small as zero (and remember that neither of these metrics can be less than zero) is if a1b1 in a bootstrap sample is exactly zero, which for all intents and purposes won’t ever happen. Consequently, a bootstrap confidence interval would never contain the population value in this scenario.Footnote 4 Because the population contrast value is unlikely to be covered by the confidence intervals for the division-based absolute value methods when one of the population indirect effects is zero, we recommend avoiding these methods (since other methods perform as well as or better without this problem).

Summary and recommendations

Due to the slightly superior coverage, these results lead us to recommend the use of the raw difference or sum when the interest is in testing the equality of magnitude of two indirect effects (see Table 2 for a summary of our recommendations). But because the raw difference is sensitive to difference in magnitude only when the indirect effects are like-signed, and the sum only when the indirect effects are opposite in sign, we suggest that an a priori hypothesis should guide the choice. When theory or other reasoned arguments predict indirect effects of opposing signs, use the sum of the indirect effects to compare their magnitude, whereas the raw difference should be used when the indirect effects are predicted to be of the same sign.

Table 2 A summary of the recommendations from the simulation study when the question is of equality of magnitude
Full size table

But there may be circumstances in which there are no a priori expectations for the signs of indirect effects, or an investigator is merely exploring differences between indirect effects without a guiding theoretical framework. In that case, we recommend using the difference in absolute values as the metric, as it is sensitive to difference in magnitude irrespective of the signs of the indirect effects. Although it is slightly conservative in smaller samples and has excessive type I error rates in some situations, many would find this worth the price for a more general test. Although the other absolute-value based measures are mathematically equivalent and will lead to the same decision in many circumstances, we have trouble recommending a confidence interval-based inferential tool when coverage is necessarily zero in certain situations or when the population value of the statistic can be indeterminant (as for the ratio and ratio of absolute value metrics).

Discussion

Indirect effects provide information relevant to understanding the mechanism(s) by which some causal effect of X on Y operates. Given that most effects probably operate through multiple mechanisms simultaneously, it makes empirical sense for a mediation model to capture those mechanisms at once in a multiple mediator model. Doing so affords the ability not only to estimate different mechanisms at work but also to determine and test hypotheses about the relative magnitude or strength of those mechanisms in driving the effect. This is accomplished by comparing, descriptively and inferentially, two indirect effects operating through different mediators.

Though still relatively rare in the literature, researchers do sometimes formally compare two indirect effects, typically using the raw difference. When the indirect effects are of the same sign, this seems to be a reasonable approach. However, when the indirect effects being compared differ in sign, which occurs when two mechanisms compete against each other in the direction they “move” Y as a function of X, the raw difference between indirect effects only tests whether those effects differ in value. Thus, one would need to use a different contrast metric to test equality of strength. From our simulation results, we recommend using either the sum of the indirect effects or the difference in their absolute values as the metric for comparing two opposing indirect effects.

Our focus in this paper has been on comparing two specific indirect effects in a mediation model with multiple mediators. For simplicity, we have couched our discussion in the context of the most basic of such models with two mediators operating in parallel with all variables observed rather than latent. In such a model, only one comparison between indirect effects is possible. But our argument for the need to compare indirect effects and the methods we describe for doing so generalize to models with any number of mediators working in parallel or serial as well as latent variable models. In a parallel multiple mediator model with k mediators, there are 0.5(k2 − k) possible comparisons between specific indirect effects, and in a serial model that includes all possible indirect effects, there are k2 − k − 1 possible comparisons. For some of these comparisons, the raw difference approach might be appropriate, but for others, a method that is sensitive to questions about difference in magnitude for indirect effects that differ in sign may be required to test the hypothesis of interest. A tool like PROCESS could not be used for latent variable models, but SEM programs are built for this and are widely available and relatively easy to use with a bit of training (for a discussion of latent variable mediation analysis, see Cheung & Lau, 2008; Lau & Cheung, 2012; MacKinnon, 2008).Footnote 5 The methods discussed here translate without modification to the comparison of indirect effects defined from the structural part of a latent variable structural equation model.

Our discussion and recommendations from our simulation have been based on the comparison of indirect effects in their unstandardized form. In this form, an indirect effect scales differences in Y due to a one-unit difference in X resulting from X’s effect on Y which in turn affects M. The differences in X and Y in the prior sentence are quantified in the original unit of measurement of X and Y. Investigators may prefer to instead scale indirect effects in standard deviations of differences rather than the original metric. Examples of such rescaling, often discussed in the content of measures of “effect size” in mediation analysis, include the partially and completely standardized indirect effects discussed by Preacher and Kelly (2011) and Hayes (2022).

The difference metrics in Eqs. (6–11) can be used for comparing the value or magnitude of partially and completely standardized indirect effects. For the difference between completely standardized indirect effects, multiply each indirect effect by sX/sY prior to the computation of the difference metric, where sX and sY are the standard deviations of X and Y, respectively. For the difference between partially standardized indirect effects, first multiply each indirect effect by 1/sY . For the raw difference (6), difference in absolute values (7) and sum metrics (8), the result is equivalent to multiplying this metric by this same ratio. But when using the ratio (9), absolute value of ratios (10), and proportional absolute value (11) metrics, these rescaling computations are unnecessary, as this rescaling of the specific indirect effects appears in both the numerator and denominator of the difference metric and cancels out. This means that these three metrics of difference can be used unmodified to quantify the difference between unstandardized, partially standardized, or completely standardized indirect effects. And the performance of these methods documented in Coutts (2020) and summarized in this paper generalize exactly.

We believe our recommendations also generalize to the comparison of partially and completely standardized indirect effects when using the raw difference, difference in absolute values, and sum metrics, but we must acknowledge a caveat. Bootstrap estimates of the difference in standardized indirect effects rely on bootstrap estimates of variation in X and Y in each bootstrap sample rather than variation observed in the original sample (cf., Cheung, 2009). This introduces a new source of random variation in bootstrap estimates not present when comparing unstandardized indirect effects. The consequence of this additional source of variation is that the rank order correlation of the bootstrap estimates or distributions of difference using unstandardized, partially standardized, and completely standardized indirect effects may not be one. So when using any of these three metrics of difference, it would be possible for a bootstrap confidence interval for the difference between unstandardized indirect effects to result in a different conclusion than when using standardized indirect effects. However, this would tend to be fairly rare in practice, especially in larger samples. Although this extra source of variation might produce greater conservativism in comparisons based on standardized indirect effects (i.e., reduced power and type I error), we see no basis for believing that any such differences in conclusion would change the relative performance of these metrics to such a degree that our recommendations would change.

Our treatment of the mathematics of mediation analysis has been based on the traditional regression or SEM approach that has dominated the behavioral sciences. The counterfactual or potential outcomes approach is becoming increasingly popular (see e.g., Imai et al., 2010; Pearl, 2012; Vanderweele, 2015; Vanderweele & Vansteelandt, 2014). One of the major differences between the counterfactual approach and the traditional approach is its flexibility in the definition of the indirect effect for different types of models for outcomes (variables on the left-hand sides of the equations) that are dichotomous, ordinal, count, time to event, and so forth that are not as appropriately analyzed using Eqs. (1–5). This counterfactual approach also need not assume the absence of interaction between X and the mediator(s) in the model of Y, as we have in our discussion and mathematical definition of indirect effects. This paper also did not cover more complicated models such as generalized linear models, survival models, or nonlinear models. However, these differences in mathematics and assumptions do not change the generalizability of the methods we discuss for comparing indirect effects (though the simulation results may not generalize beyond what we examined). They merely change the mathematics of the estimation of those indirect effects. Researchers who prefer the counterfactual approach or a different modeling framework to mediation analysis can still use the methods we describe here when their question focuses on whether two indirect effects in a multiple mediator model differ from each other, whether in value or magnitude. Although we suspect our recommendations summarized in Table 2 would not change, it is unknown the extent to which our simulation results would generalize to different modeling frameworks.

Regardless of the scaling of indirect effects or modeling preference, we encourage researchers to move their thinking away from the descriptive and qualitative mindset to comparing indirect effects (e.g., “this effect is significant, that one is not, so these effects differ”) in favor of a more rigorous, quantitative orientation that considers the difference between two indirect effects and a hypothesis about that difference as things that can be quantified, estimated, and tested.