Single-case experimental designs (SCEDs) are a form of interrupted time-series design where observations on a single subject (i.e. a single child, patient, or sampling unit) are measured repeatedly during a baseline phase and at least one intervention or treatment phase. They are widely used in education (e.g. Lambert, Cartledge, Hewrad, & Lo, 2006), psychology (e.g. Shih, Chang, Wang, & Tseng, 2014), and medicine (as n-of-1 designs, Gabler, Duan, Vohra, & Kravitz, 2011). President Obama’s 2015 State of the Union 2015 address emphasized personalized (precision) medicine initiatives. Subsequently, the National Institutes of Health established the Precision Medicine Initiative Cohort Program. Based on credibility of evidence, the Oxford Centre for Evidence-based Medicine ranked randomized n-of-1 trial evidence as level-1 evidence for treatment decision purposes (Howick et al., 2011). Given the increased interest in SCEDs, several agencies are setting methodological standards for SCEDs to ensure high-quality causal inferences (e.g. American Speech-Language-Hearing Association, 2004; Cook et al., 2014; Kratochwill et al., 2013). The goal of most analyses in SCEDs is to show that the observations in the treatment phase are only a function of the treatment and that no alternate explanations exist.

In SCEDs, no treatment is administered during the baseline phase, and a treatment is administered during the treatment phase. The baseline and treatment phases are referred to as phases A and B, respectively. Visual analysis of a plot of observations over time is the most common SCED data analysis technique (Kratochwill et al., 2013). In SCEDs, evidence of treatment effect is demonstrated by establishing (1) a stable pattern among the observations within each phase, (2) a difference in patterns of observations across phases, and (3) a change in the patterns of observations immediately following the introduction or removal of treatment, which is called immediacy. Establishing treatment effect in SCEDs also requires that three demonstrations of treatment effect are shown, along with absence of non-effects. Absence of non-effects is established by (1) documenting the consistency of level, trend, and variability within phases; (2) documenting immediacy, proportion of overlap of observations across phases, and difference in the observed and predicted patterns of the observations; and (3) examining anomalies and external factors. Although establishing treatment effect using visual analysis alone may be easy for some data, this is not always the case. Difficulties may arise when (1) immediacy is not possible due to the nature of the treatment, (2) errors are auto-correlated, and (3) the experimental effect size is not striking.

Immediacy is one of the criteria for demonstrating strong evidence of treatment effect (Kratochwill et al., 2013). A rapid change in the observations across phases indicates an immediate effect. An immediate effect provides convincing evidence that change in the outcome measure was due to manipulation of the independent variable. When the treatment lacks immediacy, the researcher may not know whether the observations were solely a function of the treatment. Even though one knows when the administration of the treatment started or ended, one does not know when the treatment effect started or ended. Effect sizes computed while ignoring the lack of immediacy underestimate the treatment effect. Lack of immediacy in treatments that are expected to have immediacy compromises the internal validity of the design. However, no clear guidelines exist about decisively concluding the presence of immediacy.

Improvement over the existing approach

With the exception of Natesan and Hedges’ Bayesian unknown change point model (BUCP; Natesan & Hedges, 2017), immediacy is usually established by computing the change in the mean or median levels between the last three to five observations in a phase and the first three to five observations in the subsequent phase. In contrast, BUCP uses all data points to establish immediacy. Change points are the time points in the SCED where there is a change that is discerned by functionally different relationships between time and the outcome variable in the difference phases. In this confirmatory approach, BUCP is used to investigate and quantify immediacy in two-phase designs. This model confirms whether a change has taken place where it is designed to happen. In the presence of immediacy and a clear treatment effect, the change point posterior mode would be accurately estimated and the posterior standard deviation would be very small. Natesan and Hedges showed how analyzing the posterior of the change point could be used to investigate and quantify immediacy in AB and multiple-baseline designs (MBDs).

However, AB designs cannot provide strong evidence of causality, because they cannot be used to show three demonstrations of treatment effect unless they are extended to multiple subjects as MBDs or replicated within a subject as multiple-phase-change designs. Two-phase designs with only one participant have poor control of threats to internal validity because they do not account for other possible confounding effects that may explain treatment effect. A commonly used SCED is a multiple-phase-change design (e.g. the ABAB design). Multiple-phase-change designs contain at least two change points. However, estimating multiple unknown change points with small sample data with autocorrelation quickly becomes complicated. As a result, the popular Gibbs sampling algorithm will not compute efficiently for multiple-phase-change designs. This is because the change points in a multiple-change-point model are simulated one at a time from full conditional distributions rather than from the joint distribution (for more details about issues with this approach, refer to Chib, 1998). Because the draws from the posterior are not independent and identically distributed (iid), the uncertainty in estimating a previous change point affects the uncertainty in estimating subsequent change points. As a result, wide credibility intervals will be obtained for change points. With this approach, the logic of confirming the presence of immediacy by investigating the standard errors of change points is rendered unusable. Therefore, an alternate method is needed to extend Natesan and Hedges’ confirmatory approach of quantifying immediacy to multiple-phase-change designs such as the ABAB, ABA’B, and ABCD designs.

The ABAB design is a commonly used multiple-phase-change reversal/withdrawal design. Assume that the target variable is problem behavior of a child with autism. Effective demonstration of an experimental effect would be indicated by a clear difference in the functional relationships between the scores across the phases. Specifically, the child’s scores within the baseline phase (A1) would be larger than his scores in the treatment phase (B1). In an ABAB design, the treatment is withdrawn (A2) after B1 and then reintroduced (B2). A clear increase in problem behavior from B1 to A2 and a subsequent decrease in problem behavior from A2 to B2 are two additional distinct demonstrations of experimental effect. ABAB-type designs are referred to as withdrawal designs. In some designs, the treatment may not be completely withdrawn but replaced by another treatment, or serve as baseline for the next target behavior (changing criterion design).

However, not all treatments are aimed at reverting to baseline behavior following withdrawal. Some treatments, especially in health, may aim for an improvement in the second baseline phase rather than reversal to the original baseline’s range of values. That is, studies may aim for a treatment effect that lasts even after the treatment phase is complete (Tate et al., 2013). Examples include improving communication skills, anger management techniques, and remediating gait dysfunction. Such a design would be an ABA’B design. Similarly, there are ABCD designs where the four phases may differ in their treatments.

Purpose

The purpose of the present study is to examine the performance of a variational Bayesian unknown change point model in investigating and quantifying immediacy in multiple-phase-change SCEDs. The first part of the study uses simulation to investigate the performance of the model for various data conditions. To this end, a variational Bayesian (VB) method is used to estimate the parameters of an unknown change point model with auto correlated errors and four phases for commonly occurring data conditions in SCED research. The number of time points per phase, autocorrelations, and standardized mean difference effect sizes are varied to simulate different data conditions that would mimic real-life SCED data (Shadish & Sullivan, 2011). The goal of the present study is twofold: (1) to test the feasibility of variational Bayesian in estimating the parameters of the four-phase unknown change point model with autocorrelations, and (2) to identify the conditions that would be required to estimate the parameters of said model so that SCED researchers could use the model to investigate experimental effects in SCEDs.

In the second part, the feasibility of applying these models to real data is tested by fitting the model to 13 data sets from six ABAB studies published within the past 5 years. These allow researchers and practitioners to understand the efficiency of the algorithm under various data conditions and illustrate how the method can be applied to real data. We use VB estimation to overcome the challenges of the Gibbs sampler. The proposed method extends and differs from the one presented by Natesan and Hedges (2017) in three ways: (1) it estimates multiple change points instead of one change point, (2) it evaluates the accuracy of the change points using probabilities rather than width of credibility intervals, and (3) it uses VB instead of MCMC to estimate the parameters. Although the width of credibility intervals can be obtained from the probabilities, we chose to use probabilities of obtaining the correct combination of change points as a diagnostic for our study. This is because we are interested in the correct estimate of the combination of change points, not a single change point alone. To our knowledge, this is the first inferential statistical method that can confirm immediacy in multiple-phase-change designs. This study is also the first of its kind to apply VB to SCEDs.

Quantitative challenges in SCEDS

SCED data are often auto correlated and have only a few observations per case. For instance, 45.3% of the studies reviewed by Shadish and Sullivan (2011) had five or fewer points per phase. The presence of autocorrelation in SCEDs (1) is impossible to detect through visual analysis (Kazdin, 2011), (2) increases type I errors (Matyas & Greenwood, 1990), and (3) is associated with low interrater reliability (Brossart, Parker, Olson, & Mahadevan, 2006). Therefore, quantitative methods for SCEDs have been gaining momentum in recent years (e.g. Hedges, Pustejovsky, & Shadish, 2012, 2013; Moeyaert, Ferron, Beretvas, & Van den Noortgate, 2013; Shadish et al., 2014). However, auto correlated errors violate the independence of observations assumption of most parametric and nonparametric statistics and result in biased estimates. Frequentist estimates of autocorrelation are negatively biased and have larger sampling errors for samples with fewer than 50 observations (Shadish, Rindskopf, Hedges, & Sullivan, 2013). Therefore, the researcher has to depend on large sample methods such as maximum likelihood (ML). However, SCED sample sizes are too small to work well with ML.

With the exception of Natesan and Hedges (2017), all quantitative developments in SCEDs assume that the observed variable truly belongs to the phase it is designed to belong to. However, this may not always be the case, especially when latency is expected. Latency happens when a treatment takes time to take effect when administered or to stop taking effect when removed. Although latency is not desirable in SCEDs, it may be expected in some cases due to the nature of the treatment and the outcome variable. For instance, a child diagnosed with autism may not respond immediately to a certain therapy, or a drug may take some time to be completely excreted from of the human body. In such cases, one must ascertain gradual and/or delayed effects or account for these with appropriate analytical strategies to untangle them from long-term treatment effects (Duan, Kravitz, & Schmid, 2013). Our method can be used to evaluate immediacy, which is one aspect of quantifying SCED findings via transparent, objective, and replicable procedures.

Need for the present study

Several types of SCEDs are used in practice. Maggin et al. (2011) reported that withdrawal designs such as ABAB are the most commonly used designs in SCEDs. The Institute of Education Sciences (IES) What Works Clearinghouse (WWC) pilot standards for single-case designs (Kratochwill et al., 2013) recommended showing three different demonstrations of the experimental effect at three different points in time within a single case or across different cases for successful demonstration of an experimental effect. The Single-Case Reporting Guideline in Behavioural Interventions (SCRIBE) SCED reporting guidelines (Tate et al., 2016) reiterated the advantages of multiple-phase over two-phase designs. We can therefore expect to see an increase in the use of multiple-phase-change designs, which creates a pressing need for an inferential tool that can be used to investigate and quantify immediacy within this framework.

The proposed method can be applied in all cases of four-phase designs, because it assumes that the four phases are not related to each other. Subsequently, the parameters of the four phases (e.g. intercepts, slopes) are estimated independently of each other in the proposed algorithm. Therefore, the model in the present study can be applied to any SCED with four phases.

Establishing immediacy is an important criterion for demonstrating strong evidence of treatment effect in SCEDs (Kratochwill et al., 2013). This is because the researcher has more evidence to make a case that a change in the dependent variable is initiated by a change in the treatment condition. In addition to confirming immediacy, there is a need to quantify the evidence that confirms immediacy. According to American Educational Research Association (AERA) guidelines, the presence of an effect must be accompanied by an index of uncertainty of that effect (AERA, 2006). The proposed method can be a valuable addition to the SCED researchers’ toolkit because it both identifies and quantifies immediacy. Additionally, this quantification of immediacy sheds light on how reliable the slope and intercept estimates of the phases are. For instance, when there is lack of clear immediacy, slopes and intercepts will have wider credible intervals.

The unknown change point model

In an SCED with clear treatment effect, the dependent variable is expected to be a function of the phase to which it belongs (Natesan & Hedges, 2017). Therefore, in the presence of immediacy and treatment effect, a change in phase is reflected by the change in the function that maps the observation to its corresponding phase. In the present study, an intercept-only model is fitted to each phase where the boundary between the phases is assumed unknown a priori. The data define the change points between the phases. Treatment effect is indicated based on the proximity between the estimated and true values of the change points. By allowing the data to speak for themselves, this confirmatory approach investigates and quantifies the presence of immediacy or delayed effects in SCEDs.

Several approaches to change point models have been proposed in the past few decades. A least-squares estimation approach (Bai, 1994, 1997), Bayesian analysis of Poisson-distributed data (Raftery & Akman, 1986), Bayesian online change point detection (Adams & MacKay, 2007), and extensions of BUCP to multiple unknown change points using hidden Markov models, genetic algorithms, and annealing stochastic approximation by Chib (1998), Jann (2000), Jeong and Kim (2013), and Kim and Cheon (2011), respectively, are some examples. BUCPs have been applied in ecology (Thomson et al., 2010), marine biology (Durban & Pitman, 2011), hydrometeorology (Perreault, Bernier, Bobée, & Parent, 2000), signal processing (Punskaya et al., 2002), and stock data (Lin, Chen, & Li, 2012). Recently, Kim and Jeong (2016) developed an approach to change-point modeling in auto-correlated time series where the number of change points is unknown. Barry and Hartigan (1993), and Carlin, Gelfand, and Smith (1992) provide good background materials for Bayesian change-point problems.

Bayesian estimation

Bayesian methods often outperform classical methods in particularly small samples, allow more probabilistic interpretation of statistics than classical methods, and can more easily accommodate model complexities such as using distributions that reflect the scale of the observed variable, modeling autocorrelations, and representing hierarchical data structure. Bayesian estimation works well with small sample data because it does not depend on asymptotic or large sample theory (Ansari & Jedidi, 2000; Gelman, Carlin, Stern, & Rubin, 2004). This makes Bayesian particularly advantageous for SCEDs. Bayesian estimates a probability distribution for each parameter. This posterior distribution can be used to compute any summary statistic for the parameter of interest, and its 95% highest density interval (HDI) can be directly interpreted as having 95% probability of containing the true value (Lynch, 2007). Posteriors of change points with high probability mass at several time points indicate weak evidence of treatment effect. Bayesian estimates of autocorrelation have the advantage of being more accurate than frequentist estimates. Frequentist confidence intervals of autocorrelation have undercoverage (Shadish et al., 2013). Gelman, Carlin, Stern, Dunson, Vehtari, and Rubin (2013) provide a comprehensive discussion of Bayesian methods.

Variational Bayesian

Variational Bayesian (VB) is a type of Bayesian inference that is computationally more efficient than MCMC (e.g. Natesan, Nandakumar, Minka, & Rubright, 2016). For models having smooth and unimodal posterior distributions, the cost of Bayesian inference can be reduced significantly by making analytical approximations. VB (Beal & Ghahramani, 2003) inference is one such approach that consists of fitting a simple approximating family (such as Gaussian or gamma) to the posterior distribution by minimizing Kullback-Leibler (KL) divergence. KL divergence is a nonsymmetrical measure of the difference between the distributions (Kullback & Leibler, 1951). Computationally, the VB procedure visits each random variable in the model and incrementally improves its posterior approximation, repeating this for several iterations. Each step is similar in complexity to Gibbs sampling, but instead of drawing thousands of samples, variational inference typically sweeps through the model a few dozen times before convergence. Beal and Ghahramani (2003) and Bishop (2006) are some good background materials in VB. The Infer.NET software program (Minka, Winn, Guiver, & Knowles, 2012) provides several options for performing KL divergence minimization. When compared with MCMC, which provides a technique for approximating the exact posterior using a set of samples, VB provides a locally optimal, exact analytical solution to the posterior.

Model and notation

A continuous, normally distributed dependent variable with no trend (slope) is considered in the simulation study. This can be extended to models with trend by estimating the slopes as shown in the “Study 2” section, which illustrates the algorithm with real data. This framework can be adapted for different variable and distribution types by modifying Eqs. 1, 7, and 8. Consider the observed value at time yt, which follows a normal distribution with the mean of μt, which is the expected value of the target behavior at time t and standard deviation of σε as shown in Eq. 1.

$$ {y}_t\sim \mathit{\operatorname{norm}}\left({\mu}_t,{\sigma}_{\varepsilon}^2\right). $$
(1)

In SCEDs, the errors of the data are typically considered to be lag-1 auto-correlated (Huitema, 1985; Huitema & McKean, 1998, 2000). It is of interest to note that although autocorrelations of errors are modeled in SCED data, they are never interpreted and are considered only as a nuisance parameter. Consider an ABAB design with four phases, that is, three phase changes at times i1, i2, and i3, and a total of T time points. The predicted value \( {\hat{y}}_t \)at time point t can be modeled as

$$ {\hat{y}}_t=\rho {r}_{t-1}+{\beta}_{0p}, $$
(2)

where ρ is the autocorrelation, rt − 1is the residual at time t − 1, and β0p is the intercept of the linear regression model for phase p that time-point t belongs to. If phct represents the phase change at a given time-point t, that is, it equals 1 if t denotes the start of a new phase and 0 otherwise, the residual is modeled for P phases as

$$ {r}_{t-1}=\left\{\begin{array}{c}{g}_p, if\ {phc}_t=1\\ {}{y}_{t-1}-{\hat{y}}_{t-1}, if\ {phc}_t=0\ \end{array}\right., where $$
(3)
$$ {g}_p\sim \mathit{\operatorname{norm}}\left(0,\frac{\sigma_{\varepsilon}^2}{\left(1-{\rho}^2\right)}\right);p=1,\dots, P. $$
(4)

Equation 4 gives the relationship between autocorrelation, the variance of the random error (\( {\sigma}_{\varepsilon}^2 \)), and the white noise created by the combination of autocorrelation and random error (e.g. Natesan & Hedges, 2017). The intercepts β0p at time t are modeled as

$$ {\beta}_{0p}=\left\{\begin{array}{c}{\beta}_{01}, if\ t\le {i}_1\kern3.25em \\ {}{\beta}_{0\left(j+1\right)}, if\ {i}_j<t\le {i}_{j+1}\\ {}{\beta}_{0P}, otherwise\kern2.5em \end{array}\right.;j=1,2 $$
(5)

The following priors were used:

$$ {\sigma}_{\varepsilon}\sim gamma\left(1,1\right) $$
(6)
$$ \rho \sim \mathit{\operatorname{norm}}\left(0,100\right); bounded\ by\ \left(-1,1\right) $$
(7)
$$ {\beta}_{0p}\sim \mathit{\operatorname{norm}}\left(0,100\right);p=1,\dots, P $$
(8)

The priors are weakly informative. All change points were specified to be sampled from discrete uniform distributions ranging from time-point 1 to T and then ordered. In Eq. 9, cat stands for categorical distribution. The term ip would indicate one of the P-1 change points based on the probabilities given in Eq. 10. In this case, there is equal probability of the time point being any of the change points.

$$ {i}_p\sim cat(pi);p=1,\dots, P-1 $$
(9)
$$ pi=\left(\frac{1}{T},\frac{1}{T},\dots, \frac{1}{T}\right); length(pi)=T $$
(10)
$$ {i}_1<{i}_2<{i}_3 $$
(11)

The ordered constraints in Eq. 11 are modeled as loops in Infer.NET. When the estimated values of i1, i2, and i3 are the same as the true value, that is, when the correct combination of these parameters has the highest probability in the marginal posterior, we can say that we have some evidence of immediacy. Note that immediacy can only be indicated and not confirmed.

Method

To perform Bayesian inference in this model, the method starts by enumerating all possible combinations of change point locations. The number of change points is assumed known. For each combination, variational inference was run to obtain approximate posteriors for the parameters (\( \rho, {\sigma}_{\varepsilon}^2,{\beta}_{0p} \)) as well as an approximate value for the marginal likelihood. The Infer.NET software library (Minka et al., 2014) was used to perform these computations. VB implementation in Infer.NET is similar to the implementation of syntax in popular Bayesian software programs such as JAGS. Because the prior is uniform, the marginal likelihood is proportional to the marginal probability of the change-point locations. Therefore, we take the set of marginal likelihoods just computed and normalize them to obtain the marginal posterior over the change-point locations. These probabilities of the combinations of change points obtained and the marginal posteriors can be used to make inferences about immediacy. If the correct combination of change points is estimated as having the maximum probability, evidence for immediacy can be deemed sufficient.

Study 1: Simulation

Three phase lengths (l = 5, 8, and 10 time points per phase), four standardized mean difference values (d = 1, 2, 3, 5), and four autocorrelation values (ρ = 0, 0.2, 0.5, 0.8) were simulated based on commonly occurring values in single case studies (Maggin, O’Keefe, & Johnson, 2011; Shadish & Sullivan, 2011). Although some autocorrelation is always present in SCED data, an autocorrelation value of 0 was added as a reference point to see how the presence of autocorrelation affects the accuracy of estimates. One hundred data sets were generated for each combination of conditions, resulting in 4800 data sets in a fully crossed 3 × 4 × 4 design. The intercepts of the baseline phases were set to 0 and the treatment phases computed as σd, where the standard deviation within each phase σ = 0.2.

Diagnostics and interpretation

The accuracy of the algorithm was examined using average probability-weighted norm (APWN), average probability of obtaining the accurate combination (\( \overline{p} \)), and the combinations with highest average probabilities. If in the rth replication pr is the vector of true values of change points and qr is the vector of change-point estimates, and Pr(qr) is the probability of qr where within a given replication \( \sum \limits_{q_r}\Pr \left({\boldsymbol{q}}_{\boldsymbol{r}}\right)=1 \), then the APWN over R replications is given by

$$ APWN=\frac{1}{R}\sum \limits_{r=1}^R\sum \limits_{{\boldsymbol{q}}_{\boldsymbol{r}}}\Pr \left({\boldsymbol{q}}_{\boldsymbol{r}}\right)\left\Vert {\boldsymbol{q}}_{\boldsymbol{r}}-{\boldsymbol{p}}_{\boldsymbol{r}}\right\Vert $$
(12)

In Eq. 12, ‖qr− pr‖ refers to the norm or the positive length between the two vectors. APWN weights the distance between the estimated and true values with the probability of obtaining them, while \( \overline{p} \) (pbar) considers only the probability of correctly estimating the true values. APWN is an unbounded statistic, a combination of distance and probability, and depends on the phase length in addition to the other quantities in Eq. 12. Both the probability of the estimates and the distance between the true and estimated values are important in determining the accuracy of the estimate, which is the reason for using APWN. If the probability of a combination is high and the discrepancy between the combination of estimates and true values (‖qr − pr‖) is high, APWN will be large, indicating poor estimates. If either the probability or the discrepancy is low, APWN will be smaller, indicating better estimates. Thus, smaller values of APWN are more desirable, indicating more accurate estimates. The fraction of data sets in a given condition where the true values of the change points were estimated was also computed as a diagnostic. Root-mean-square errors and average standard errors were also computed for the autocorrelations and intercept estimates. Thirteen analysis of variance (ANOVAs) were conducted with APWN, \( \overline{p} \), and fraction correct, and root mean squared error (RMSEs) and average standard errors of intercepts and autocorrelations as the dependent variables, respectively. The independent variables in the ANOVAs were d, l, and ρ. The eta-squared effect sizes from the ANOVAs were used to understand the pattern of the accuracy of the estimates with change in the data conditions. Coverage rates could not be computed because VB estimates standard errors and not the credible intervals.

Results

The results of the simulation and the eta-squared effect sizes from independent ANOVAs for the change-point diagnostics are reported in Tables 1 and 2, respectively. The correct estimates of change points had the maximum average probability for all conditions, except when the standardized mean difference d = 1 for autocorrelations less than 0.8. Even in cases where an incorrect combination was estimated with maximum average probability, the probability of the correct combination was very close to the maximum average probability (difference < .005). In all other cases, the correct change-point combinations had the highest average probability of being estimated. APWN decreased very slightly with ρ and l, but decreased substantially with an increase in d. The average probability \( \overline{p} \) and fraction of data sets with correct change-point estimates both increased with an increase in d (i.e. standardized mean difference) but decreased with ρ (i.e. autocorrelation). Although phase length did not have a high effect size on APWN, \( \overline{p} \), and fraction correct, there seems to be an interaction between phase length and d. For phase lengths of 8 or more, \( \overline{p} \) and fraction correct increased drastically when d increased from 3 to 5, while APWN decreased with an increase in d. Standardized mean difference explained the maximum variation in APWN, \( \overline{p} \), and fraction correct, as seen in Table 2. Variation in autocorrelation explained the medium variance in APWN, while all other main and two-way interaction effects were low-medium on APWN and almost negligible on \( \overline{p} \) and fraction correct. These trends are clear from the interaction plots in Fig. 1. Although the model seems to require a large effect size, the correct change-point combination was identified for most data conditions, indicating that immediacy can be identified even for data sets with effect sizes as small as 2 standard deviations apart.

Table 1 Diagnostics of change points from the simulation
Full size table
Table 2 Eta-squared of change-point diagnostics in percentages from the ANOVAs
Full size table
Fig. 1
figure 1

Interaction plots of APWN, fraction correct, \( \overline{p}\Big( \)avg_prob), and rho RMSE with d, l, and

Full size image

RMSEs and average standard errors of the autocorrelation and intercept estimates by condition are shown in Table 3. The corresponding effect sizes from the ANOVAs are shown in Table 4. Variance in RMSE of autocorrelations was explained the most by the true value of autocorrelation, phase length, and their interaction as shown in Fig. 1. Autocorrelation RMSE decreased with the increase in phase length and decrease in true autocorrelation value. Average standard error of autocorrelation and of all intercept estimates decreased with an increase in phase length, as expected. Although RMSEs of the intercepts were explained by most of the data conditions, all these RMSEs varied only to the second decimal place. Therefore, they are not interpreted.

Table 3 RMSE and average SE of parameter estimates from simulation
Full size table
Table 4 Eta-squared values in percentages from ANOVAs of RMSEs and average SEs
Full size table

Study 2: Real data applications

We analyzed 13 data sets from six ABAB design studies published between 2012 and 2015 (Allen, Baker, Nuernberger, & Vargo, 2013; Lin & Chang, 2014; Neely, Rispoli, Camargo, Davis, & Boles, 2013; Shih et al., 2014; Shih, Chiang, & Shih, 2015; Shih, Wang, Chang, & Kung, 2012). The dependent variables in these studies included challenging behavior, percentage of intervals of academic engagement, number of occurrences of correct moves, rate of collaborative walking, number of correct responses per session, and rate of collaborative pointing for children with autism, and problem behavior for a woman with dual diagnosis of moderate intellectual disability and schizoaffective disorder. The number of time points per phase ranged from 3 to 21 across these studies. Of the 13 data sets analyzed, 11 sets of change-point estimates had 98–100% probability of being estimated accurately. The estimation took less than 3 seconds for each data set. The set of change-point estimates from one data set (Shih et al., 2012) had 92.98% accuracy, while a different set of change points was estimated to be 99.4% accurate for another data set (Neely et al., 2013). We discuss these probabilities, their interpretation, and the reasons for the inaccurate estimates. We fit the same unknown change-point model with intercepts for all data sets considering the dependent variable to be interval-scaled. Upon visual inspection, we decided that this was a reasonable model to be fit for all data for illustration purposes.

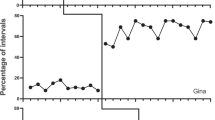
Consider the data for subject 1 from Shih et al. (2012) as shown in Fig. 2. The true values of change points are at 8, 26, and 33. The corresponding estimates for all parameters are shown in Table 5. The only probable values for change points were estimated to be at 8, 26, and 33. The pattern is also clear from the data. The standard error of the intercepts ranges from 0.289 to 0.498. The posterior densities of the change points had only a single probable value. Both change-point estimates and their accuracy (probability) show support for immediacy.

Fig. 2
figure 2

Data for subject 1 from Shih et al. (2012)

Full size image
Table 5 Estimates from Shih et al. (2012) and Neely et al. (2013)
Full size table

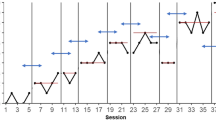
Consider the estimates of subject 2 from the same study, whose plot and posteriors are shown in the top and the bottom panels of Fig. 3, respectively. Although the probability value for the change-point estimates and the individual probability for 8 being the first change point is only 0.93, the probability of every other change-point estimate being the first change point is less than 2%. Similarly, the probability of 26 and 33 being the second and third change points is greater than 99.5%, as seen in Table 5. This shows strong evidence of immediacy and that the changes indeed occurred at the time points where they were designed to take place. The standard error of intercepts ranges from 0.22 to 0.37 and that of autocorrelation is 0.11.

Fig. 3
figure 3

Data for subjects and Posteriors of change points for subject 2

Full size image

Let us consider the change-point estimates that were inaccurate (Table 5). The data and the posterior plots are given in the top and bottom panels of Fig. 4, respectively. The probability of the set of change points and each change point is greater than 99%. The first and the third change points were accurately estimated, but the second data point was estimated to be 13 instead of 12. Closer inspection of the data plot sheds light on why this is the case. The observed values at time-points 12 and 13 are much closer (3% difference) than the values at 13 and 14 (15% difference). There is a possible washout effect from the treatment in this case and therefore indication of lack of immediacy. That is, the treatment effect possibly lingered on even after the treatment was stopped.

Fig. 4
figure 4

Data for Dan’s challenging behavior from Neely et al. (2013) and the corresponding posteriors of change points

Full size image

Discussion

The present study demonstrates how the variational Bayesian unknown change point model could be used to investigate and quantify immediacy in SCED data for multiple-phase-change designs. VB estimates in the present study were better than the MCMC estimates in Natesan and Hedges, because unlike in the latter study, phase length had a very small effect on the accuracy of the estimates in our study. This means that, even conservatively, researchers need only five data points per phase to estimate the change points with accuracy, as long as the standardized mean difference effect size is at least 2. However, accuracy does improve with increased effect size. This is a major improvement over the Natesan and Hedges (2017) study, which required eight data points per phase but for a simpler model with only two phases (AB model). There are several advantages to the method we presented: (1) It is an inferential statistical tool that can be used to investigate and quantify immediacy in multiple-phase-change designs, which are commonly used SCEDs. (2) Bayesian methods allow the user to examine the shape of the posterior distribution of the change points. These help provide a clearer evaluation of the quality of the estimates, because the researcher has more information about the probability of each value the change point can take. (3) By treating the change points as unknown, the researcher can remain objective, allow the data to speak for themselves, and confirm the presence of treatment effect. This is also useful for identifying the presence and length of delayed effects. (4) The model can be modified to accommodate other distribution types, data types, functional relationships between time and the dependent variable, and additional explanatory variables. (5) By using VB, the amount of time taken for estimation is reduced to a fraction of what would be taken by commonly used Bayesian software programs such as BUGS (Lunn, Spiegelhalter, Thomas, & Best, 2009) and JAGS (Plummer, 2003). (6) The model is a one-stop shop for simultaneously estimating all the associated parameters in the model, such as the intercepts and slopes of the phases, effect sizes, and autocorrelations.

Although the simulation results show high accuracy when the data have a standardized difference between the phases of 5 or higher, we believe this model shows promise in terms of still estimating the correct combination of change points even for an effect size of 2 with a phase length of 5. We acknowledge that an effect size of 5 places a heavy demand on the data. However, requiring only five data points per phase for a complex model such as this is still a significant advantage.

A strong treatment effect is indicated when the change-point posterior mode is accurately estimated and the distribution is narrow and clearly unimodal. Inaccurate estimates, as in Dan’s case, may indicate possible washout or lag effect. This can be a valuable tool for treatments and interventions that are effective but do not have immediacy. A posterior distribution with large variance but surrounding the true value indicates a weak treatment effect and possible lack of immediacy. A posterior distribution with large variance but with most of the probability mass concentrated around the true value indicates a moderate to strong treatment effect depending on the shape of the posterior.

To our knowledge, the present study is the first of its kind to apply VB estimation to SCEDs. VB generally trades accuracy for speed. However, the approximation by VB was negligible. For two-phase models, Natesan and Hedges (2017) recommended a standardized mean difference of at least 3 to detect immediacy. For practical purposes, the correct combination is still chosen even with a standardized mean difference as small as 2. This means that practitioners will still be able to show some evidence of immediacy for smaller effect sizes. However, given the complexity of the model, larger effect sizes do improve accuracy. The multiple-phase-change model considered in the present study has three latent change-point variables and is therefore more complicated than the biphasic model, which has one latent change-point variable. The biphasic Bayesian model took about 3 minutes to run, whereas the VB model took up to 3 seconds to run. These data indicate that VB is a viable and efficient method to be used in SCEDs.

However, we do not declare that the model presented in this study is the ideal solution for SCED data analysis. First, the model places heavy demand on the data, such as requiring an effect size of at least 5 for high accuracy of estimation. Second, it is unclear how the priors have affected the estimates. Although we used weakly informative priors, the estimates might be improved by using more informative priors, especially in small sample cases such as these. This is an avenue for further research. Third, we were unable to compare these estimates with MCMC because of convergence issues in the latter. Therefore, we are unable to declare these estimates as superior to MCMC, although we can note that this model is more feasible than its exact MCMC counterpart. Finally, there is a learning curve associated with implementing VB for estimating the parameters of an unknown change-point model. Still, readers can access the program by downloading the zip folder in the supplemental material (https://github.com/prathiba-stat/Multiple-Unknown-Changepoints-Model). The program is currently set to run four-phase models for continuous data. Extensions of the script to accommodate these other models will be released pending investigation of the corresponding algorithms.