Signal-detection theory, and the analysis of receiver operating characteristic (ROC) curves in particular, plays an important role in understanding the processes supporting performance in different cognitive domains, such as perception (e.g., Aly & Yonelinas, 2012), working memory (e.g., Rouder et al., 2008), and episodic memory (Egan, 1958; Green & Swets, 1988; Yonelinas, 1999; for review, see Yonelinas & Parks, 2007). Moreover, ROC analysis has been used to shed light on the cognitive process affected in numerous clinical populations, such as individuals with medial temporal lobe damage (Bowles et al., 2007, 2010; Yonelinas et al., 2002), Alzheimer’s disease (Ally, Gold, & Budson, 2009; for review, see Koen & Yonelinas, 2014), and schizophrenia (Libby, Yonelinas, Ranganath, & Ragland, 2013). Indeed, the use of ROC analysis is very popular in many different areas of cognitive psychology. However, there is no standard analysis package to fit different signal detection models to ROC data. This paper introduces the ROC Toolbox, which was developed to address this gap in the field and provide a standardized framework for the analysis of ROC data.

The ROC Toolbox is an open source code designed to fit different models to ROCs derived from confidence ratings. The current release of the toolbox can downloaded at https://github.com/jdkoen/roc_toolbox/releases. The ROC toolbox was written in the Matlab programming language because of the widespread use of the Matlab in both behavioral and neuroscience research. Importantly, Matlab is a user-friendly programming language that does not require extensive computer programming expertise to use. There were three primary goals in the development of this toolbox. The first, and most important, goal was to develop code that can flexibly define ROC models across numerous experimental designs. The second goal was to develop a toolbox that uses widely accepted methods, such as maximum likelihood estimation (Myung, 2003), for fitting models to ROC data that are transparent to researchers and controllable by the end-user. The third goal was to develop the toolbox so that it can be expanded in the future to include new models, goodness-of-fit measures, and other advancements related to ROC analysis.

The remainder of this paper will outline the features of the ROC Toolbox in more detail. First, a brief overview of constructing ROCs is presented. Second, the signal-detection models that are currently included in the ROC Toolbox will be outlined. Third, an example that outlines how to format data for use with the ROC Toolbox, and how to define and fit a model to observed data is provided. Some additional features of the ROC toolbox are then discussed, with attention given to how the toolbox might be expanded in the future. Given that some of the models that will be described below were primarily developed to account for various recognition memory phenomena (Yonelinas & Parks, 2007), much of the descriptions and discussion are couched in the context of a simple recognition memory study.

Constructing ROCs from confidence data: A brief overview

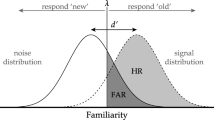
In a simple recognition memory experiment, participants are presented with a list of items (e.g., words or pictures) to remember for a subsequent recognition test. At test, the studied items are re-presented and intermixed with new items that have not been studied, and participants are tasked with classifying studied items as old (i.e., targets) and items not from the study list as new (i.e., lures.). Although there are numerous ways for obtaining data tailored to ROC analysis, the most commonly used method is to ask participants to rate how confident they are in their memory decisions (for examples of alternative approaches, see Koen & Yonelinas, 2011; Snodgrass & Corwin, 1988). The most common method is to have participants make their old/new decisions using a 6-point confidence scale (e.g., 6 – sure old, 5 – maybe old, 4 – guess old, 3 – guess new, 2 – maybe new, 1 – sure new). The idea is that the different levels of confidence reflect different levels of response bias, or a tendency to classify a test item as old. An ROC is constructed by plotting the cumulative hit rate (i.e., correctly calling an old item “old”) against the cumulative false alarm rate (i.e., incorrectly calling a new item “old”) for the different confidence ratings beginning with the “6– Sure Old” response (i.e., the most conservative response bias; see Fig. 1). Specifically, from left to right, the first point on the ROC plots represents the hit and false alarm rates for the most confident old response (e.g., six responses), the second point represents the hit and false alarm rates for the two highest confidence old responses (e.g., six and five responses), and so on. Typically, the highest confidence new (lure) response is not plotted on ROCs because it is constrained to have hit and false alarm rates equal to 1.0.

Fig. 1
figure 1

An example receiver-operating characteristic (ROC) curve derived from standard a 6-point confidence scale where a 6 and 1 response correspond to Sure Target and Sure Lure judgments, respectively. Successive points on the ROC are, starting with the highest confidence decision for targets, the cumulative hit rate plotted against the cumulative false alarm rate

Full size image

There are many issues to consider when designing a study for ROC analysis, including the number of target and lure trials, the number of bins in the confidence scale, and the model one wishes to fit to the data. These issues are beyond the scope of the present paper. We refer readers to Yonelinas and Parks (2007) in which these issues are discussed.

Signal-detection models

It is generally accepted that the shape of an observed ROC curve provides information about the cognitive processes that support performance on a particular task. To this end, many different models have been put forth to account for data from various paradigms in cognitive psychology (e.g., recognition memory). These models range from simple threshold and continuous models to more complex models in which multiple distributions are mixed together (for a detailed description of many different models, see Yonelinas & Parks, 2007). The initial release of the ROC Toolbox includes three of the most commonly used signal detection models: the unequal-variance signal detection (UVSD) model (Egan, 1958; Mickes, Wixted, & Wais, 2007), the dual-process signal detection (DPSD) model (Yonelinas, 1994, 1999), and the mixture signal detection (MSD) model (DeCarlo, 2002, 2003; Onyper, Zhang, & Howard, 2010).

Before outlining the parameterization of each model, there are several issues that bear mention. First, for consistency, the parameter notation utilized in this report and in the ROC Toolbox is consistent with the notation that has been used in the extant literature. In some cases, the notation used to describe the parameters of a model are theoretically loaded. For example, two of the parameters of the DPSD model have been dubbed the recollection and familiarity parameters, which implies that the parameters directly measure the theoretical constructs of recollection and familiarity. However, the parameters of a given signal-detection model are purely a mathematical description of the shape of the (best-fitting) ROC to the data. The value of the best-fitting parameters does not provide confirmation that a particular psychological process does or does not contribute to performance on a given task. Whether a given parameter actually reflects a given theoretical process can at best only be inferred by measuring how the parameter behaves across different experimental conditions (DeCarlo, 2002; e.g., DeCarlo, 2003; Harlow & Donaldson, 2013; for a detailed discussion of this issue, see Koen, Aly, Wang, & Yonelinas, 2013).

Second, the ROC Toolbox defines the UVSD, DPSD, and MSD in their most general form. This provides the greatest flexibility with respect to the models a researcher might want to fit to their data. By defining models in the most general form, this greatly increases the number of models that are available to researchers because any model nested within a more complex model can be fit to a given data set with the application of simple parameter constraints.

The following sections present the mathematical functions of the the UVSD, DPSD, and MSD models. Moreover, the sections below focus on the parameters that are specific to a given model. The parameters for the response criteria – the rate at which individuals classify items as belonging to a target category – are always included in any signal detection model that is fit to ROC data. In a typical model with N different rating bins, there are N-1 criteria parameters for each pair of target and lure trials. The parameters for the response criteria are designated as c i , where i represents the i th rating bin.

The UVSD model

The unequal-variance signal-detection (UVSD) model proposes that the memory strength of target and lure items falls on a continuum with the target distribution having a higher average strength compared to the lure distribution. The lure distribution is represented by a standard normal distribution with a mean of 0 and a unit standard deviation. The free parameters in this model are the mean (d ') and standard deviation (σ) of the target distribution. Specifically, the UVSD model predicts the cumulative proportion of target and lure trials in each rating bin (B i ) using the following formulas:

$$ \begin{array}{c}\hfill p\left( Target|{B}_i\right) = \Phi \left[\frac{d\hbox{'}-{c}_i}{\sigma}\right]\hfill \\ {}\hfill p\left( Lure|{B}_i\right) = \Phi \left[-{c}_i\right]\hfill \end{array} $$

The Ф denotes a cumulative normal distribution. The left side of the equations represents the predicted cumulative proportion of target and lure items, respectively, that received a rating greater than or equal to the i th rating bin. This notation is also used in the models reported below. Moreover, the cumulative proportion of trials for both targets and lures in the last rating bin (which corresponds to the highest confidence lure response) is always 1. The UVSD model can be reduced to a simpler equal-variance signal-detection (EVSD) model by constraining σ to unity.

The DPSD model

The dual-process signal detection (DPSD) model is derived from dual-process theories of recognition memory that propose recognition memory is supported by two qualitatively distinct processes – recollection and familiarity (for reviews, see Yonelinas, 2002; Yonelinas, Aly, Wang, & Koen, 2010). The DPSD model in its most complex form is characterized as a mixture of a two-high threshold model and a UVSD model. The two-high threshold component of the DPSD model defines a target threshold parameter being labeled recollection of “oldness” (Ro) and the lure threshold parameter being labeled recollection of “newness” (Rn). The UVSD component of the model – typically labeled the familiarity component of the DPSD model – comprises a parameters for the mean (d ' F ) and standard deviation (σ F ) of the familiarity distribution. The DPSD model predicts the cumulative proportion of target and lure trials in each rating bin (B i ) using the following formulas:

$$ \begin{array}{c}\hfill p\left( Target|{B}_i\right)={R}_o+\left(1-{R}_o\right)\Phi \left[\frac{d_F^{\hbox{'}}-{c}_i}{\sigma_F}\right]\hfill \\ {}\hfill p\left( Lure|{B}_i\right)=\left(1-{R}_n\right)\Phi \left[-{c}_i\right]\hfill \end{array} $$

For target items, the idea is that an item with a strength above the R o threshold will always be classified as a target, whereas classification of a target item falling below the R o threshold is determined by the familiarity component of the model. Lure items that have a strength above the R n threshold are always classified as new. When a lure item’s strength falls below the R n threshold, classification of new items is governed by a standard normal distribution. The free parameters in the full model are R o , R n , d ' F , and σ F . Although the σ F parameter is allowed to vary in the ROC Toolbox, in the most common formulation of the DPSD model the σ F parameter is constrained to equal 1 (equivalent to an equal-variance signal detection, or EVSD, model).

The MSD model

The mixture signal-detection (MSD) model proposes that classification of target and lure items on a recognition test are best modeled as a mixture of different Gaussian distributions. There are numerous theoretical proposals for why targets and lures could be modeled with a mixture of two distributions, but an in depth discussion is beyond the scope of this paper (for discussion, see DeCarlo, 2002, 2003; Harlow & Donaldson, 2013; Koen et al., 2013; Onyper et al., 2010). The ROC toolbox incorporates an expanded version of the models outlined by DeCarlo (2003) and Onyper and colleagues (2010). The MSD predicts the cumulative proportion of target and lure trials in each rating bin (B i ) using the following formulas:

$$ \begin{array}{c}\hfill p\left( Target|{B}_i\right)={\lambda}_T\Phi \left[\frac{\left({d}_{\lambda_T}^{\hbox{'}}+{d}_{\left(1-{\lambda}_T\right)}^{\hbox{'}}\right)-{c}_i}{\sigma_{\lambda_T}}\right]+\left(1-{\lambda}_T\right)\Phi \left[\frac{d_{\left(1-{\lambda}_T\right)}^{\hbox{'}}-{c}_i}{\sigma_{\left(1-{\lambda}_T\right)}}\right]\hfill \\ {}\hfill p\left( Lure|{B}_i\right)={\lambda}_L\Phi \left[\frac{-{d}_{\lambda_L}^{\hbox{'}}-{c}_i}{\sigma_{\lambda_L}}\right]+\left(1-{\lambda}_L\right)\Phi \left[-{c}_i\right]\hfill \end{array} $$

Note that the subscript for the d ' and σ parameters correspond to whether the distribution falls above (i.e., λ T ) or below (i.e., 1 − λ T ) a threshold. Additionally, a T subscript indicates a parameter specific to the distribution for target items whereas a L subscript indicates a parameter specific to the distribution for lure items.

In the above model, the distribution representing target items is modeled as a mixture of two Gaussian distributions with (potentially) different means and standard deviations. Specifically, target items that fall above the threshold for the target distribution (λ T ) are sampled from a Gaussian distribution with a mean that is \( {d}_{\lambda_T}^{\hbox{'}} \) units larger than the mean of the Gaussian distribution that falls below the target threshold (\( {d}_{\left(1-{\lambda}_T\right)}^{\hbox{'}} \)). The variances of the two distributions are \( {\sigma}_{\lambda_T} \) and \( {\sigma}_{\left(1-{\lambda}_T\right)} \) for the distribution falling above and below λ T , respectively.

Similarly, lure items are modeled as a mixture of two distributions. The distribution falling below the lure item threshold λ L (i.e., 1 − λ L ) is a standard normal distribution. The distribution above the lure item threshold λ L has a mean and standard deviation of \( {d}_{\lambda_L}^{\hbox{'}} \) and \( {\sigma}_{\lambda_L} \), respectively. Note that the mean for the above mentioned lure item distribution is negative, which simply reflects the fact that this distribution is measuring the average strength that an item is a lure (i.e., not a target). The potential free parameters of the MSD model defined above are λ T , \( {d}_{\lambda_T}^{\hbox{'}} \), \( {\sigma}_{\lambda_T} \), \( {d}_{\left(1-{\lambda}_T\right)}^{{\textstyle \hbox{'}}} \), \( {\sigma}_{\left(1-{\lambda}_T\right)} \), λ L , and \( {d}_{\lambda_L}^{\hbox{'}} \). Typically, only a subset of these parameters will be relevant to a given experimental question. For example, the standard model fit to data from the simple item recognition we outlined previously only estimates λ T and \( {d}_{\lambda_T}^{\hbox{'}} \), and the remaining parameters are set to fixed values (which are outlined in the manual).

Fitting models to data

This section briefly illustrates how to format data for use with the ROC Toolbox and how to define and fit models to observed data. The example response frequency data used in the example outlined below is in Table 1. This data is from a single participant in an unplublished study conducted by Koen and Yonelinas. Participants in this experiment studied an intermixed list of low and high frequency words for a subsequent recognition memory test. At test, participants discriminated studied words (targets) from new words (lures) using a 20-point confidence scale with the following anchor points: 20 – Sure Old, 11 – Guess Old, 10 – Guess New, 1 – Sure New.

Table 1 Example response frequencies from a single participant in an unplublished study by Koen and Yonelinas
Full size table

In this example, the most commonly applied form of DPSD model is fit to the example data set with two conditions: high versus low frequency targets and lures. For each condition, separate R o and d ' F parameters, but not the R n and σ F , are estimated.Footnote 1 The R o was allowed to take any value between 0 and 1. There were no bound constraints on the d ' F . The raw data and Matlab code for this example are include as a Supplemental Material and as a file in the ROC Toolbox (https://github.com/jdkoen/roc_toolbox/blob/master/examples/BRM_paper_supp_material.m).Footnote 2 Any reference to variables or functions used in the example code appear in Courier New.

Step 1: Formatting data

The ROC Toolbox requires as data the response frequencies in each rating (i.e., confidence) bin separately for target and lure items in each condition. Specifically, two separate matrices – one for the response frequencies to the target items and another lure items – are required for the ROC Toolbox. Each matrix must comprise C columns and R rows. The columns of each matrix represent the different rating bins. The bins must be ordered in a descending fashion such that the rating bin associated with the highest confidence decision for a target item (e.g., 20 – Sure Old) is in the first column and the rating bin associated with the highest confidence lure response is in the last column (e.g., 1 – Sure New). The rows of each matrix represents different within-participant experimental conditions. Before continuing the discussion of the response frequency matrices, we first define the data shown in Table 1 in the appropriate format. The matrix for the response frequencies of each rating bin to target items (the targf variable in the Supplemental Material) is:

$$ \left[\begin{array}{c}\hfill 77\hfill \\ {}\hfill 57\hfill \end{array}\ \begin{array}{c}\hfill 18\hfill \\ {}\hfill 25\hfill \end{array}\ \begin{array}{c}\hfill 13\hfill \\ {}\hfill 13\hfill \end{array}\ \begin{array}{c}\hfill 8\hfill \\ {}\hfill 9\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 9\hfill \end{array}\ \begin{array}{c}\hfill 3\hfill \\ {}\hfill 3\hfill \end{array}\ \begin{array}{c}\hfill 5\hfill \\ {}\hfill 7\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 8\hfill \end{array}\ \begin{array}{c}\hfill 8\hfill \\ {}\hfill 13\hfill \end{array}\ \begin{array}{c}\hfill 7\hfill \\ {}\hfill 11\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 8\hfill \end{array}\ \begin{array}{c}\hfill 5\hfill \\ {}\hfill 11\hfill \end{array}\ \begin{array}{c}\hfill 3\hfill \\ {}\hfill 5\hfill \end{array}\ \begin{array}{c}\hfill 7\hfill \\ {}\hfill 2\hfill \end{array}\ \begin{array}{c}\hfill 1\hfill \\ {}\hfill 4\hfill \end{array}\ \begin{array}{c}\hfill 5\hfill \\ {}\hfill 3\hfill \end{array}\ \begin{array}{c}\hfill 5\hfill \\ {}\hfill 5\hfill \end{array}\ \begin{array}{c}\hfill 7\hfill \\ {}\hfill 6\hfill \end{array}\ \begin{array}{c}\hfill 11\hfill \\ {}\hfill 0\hfill \end{array}\ \begin{array}{c}\hfill 5\hfill \\ {}\hfill 1\hfill \end{array}\right] $$

The corresponding matrix for lure items (the luref variable in the Supplemental Material) is:

$$ \left[\begin{array}{c}\hfill 3\hfill \\ {}\hfill 5\hfill \end{array}\ \begin{array}{c}\hfill 2\hfill \\ {}\hfill 9\hfill \end{array}\ \begin{array}{c}\hfill 8\hfill \\ {}\hfill 6\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 8\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 4\hfill \end{array}\ \begin{array}{c}\hfill 3\hfill \\ {}\hfill 5\hfill \end{array}\ \begin{array}{c}\hfill 1\hfill \\ {}\hfill 7\hfill \end{array}\ \begin{array}{c}\hfill 4\hfill \\ {}\hfill 4\hfill \end{array}\ \begin{array}{c}\hfill 11\hfill \\ {}\hfill 11\hfill \end{array}\ \begin{array}{c}\hfill 8\hfill \\ {}\hfill 12\hfill \end{array}\ \begin{array}{c}\hfill 15\hfill \\ {}\hfill 20\hfill \end{array}\ \begin{array}{c}\hfill 15\hfill \\ {}\hfill 13\hfill \end{array}\ \begin{array}{c}\hfill 6\hfill \\ {}\hfill 10\hfill \end{array}\ \begin{array}{c}\hfill 7\hfill \\ {}\hfill 7\hfill \end{array}\ \begin{array}{c}\hfill 6\hfill \\ {}\hfill 8\hfill \end{array}\ \begin{array}{c}\hfill 11\hfill \\ {}\hfill 5\hfill \end{array}\ \begin{array}{c}\hfill 14\hfill \\ {}\hfill 15\hfill \end{array}\ \begin{array}{c}\hfill 28\hfill \\ {}\hfill 17\hfill \end{array}\ \begin{array}{c}\hfill 33\hfill \\ {}\hfill 28\hfill \end{array}\ \begin{array}{c}\hfill 17\hfill \\ {}\hfill 6\hfill \end{array}\right] $$

There are some important issues to consider when formatting data for the ROC Toolbox. First, great care must be taken to format the data correctly as the ROC Toolbox makes assumptions about how the data are organized, but will still provide output, albeit incorrect output, if these assumptions are violated. In addition to the assumption that the data are formatted such that the columns are ordered in the fashion described above, the ROC Toolbox also assumes that the response frequencies for the target and lure trials from the same condition are in the same row in the target and lure matrices. In the example above, the response frequencies for the low frequency targets and lures are in the first row of the respective target and lure matrices, whereas the high frequency targets and lures are in the second row. Second, the matrices for target and lure items must be the same size else the functions will return an error. Thus, rating bins that are not used for one trial type (e.g., targets) cannot be omitted from the response frequency matrix for targets. Additionally, the target and lure matrices must be the same size even in experimental designs with multiple conditions for target trials relative to a single condition for lure items (e.g., deep vs. shallow processing at encoding).Footnote 3 To help ensure the data are correctly formatted, the ROC Toolbox includes a function to import data from CSV or text files (roc_import_data).

Step 2: Defining the model

The ROC Toolbox requires four pieces of information to define a model to fit to the data: the number of rating bins, the number of different conditions, the type of model to fit to the data (i.e., UVSD, DPSD, MSD), and the model-specific parameters that are allowed to freely vary. This information is passed to the a function called gen_pars, which is the primary function used to define the model to fit to the data. The input for number of rating bins and conditions is simply the number of columns and rows of the matrix for target (or lure) items (e.g., the targf or luref variables in the example script; see Supplemental Material). The number of rating bins define the number of criteria parameters to estimate. In experiments collecting confidence ratings, this should always be one less than the total number of confidence bins for each within-participant condition. In this example there are a total of 38 response criteria parameters (19 for each condition). The model specific parameters that are allowed to vary are specified as a cell array of strings corresponding to the labels for the parameters, which in this example are 'Ro' and 'F' for the R o and d ' F parameters of the DPSD model. Importantly, parameters that are not specified as free parameters are constrained to equal a pre-determined value. The pre-determined values are documented in the manual, and can also be changed by the user.

The gen_pars function outputs three matrices: (1) a matrix for the starting values of the optimization routine (x0), (2) a matrix for the lower bound each parameter can take (LB), and (3) a matrix for the upper bound of each parameter (UB). The latter two matrices are the ones that define which parameters are free, and which parameters are constrained to equal a set value.Footnote 4 Specifically, parameters are constrained (not estimated) when the lower and upper bounds of parameter have the same value. Note that if not estimated, the parameter takes the value of that is in the matrix defining the upper (and lower) bounds of the parameters. For example, to constrain the R n parameter to equal 0, the lower and upper bounds should both equal 0.

Step 3: Fitting the model to the data

The roc_solver function fits the model defined by the x0, LB, and UB matrices to the data defined in targf and luref using either maximum likelihood estimation (Myung, 2003) or by minimizing the sum-of-squared errors. The latter approach minimizes the squared differences between the observed and predicted (non-cumulative) proportion of trials in each rating bin. Optimization is carried out using the interior point algorithm (Byrd, Gilbert, & Nocedal, 2000; Byrd, Hribar, & Nocedal, 1999; Byrd, Schnabel, & Shultz, 1988) implemented in the fmincon function of Matlab’s Optimization Toolbox (http://www.mathworks.com/help/optim/ug/fmincon.html). The roc_solver function stores data in a structure variable that contains the best fitting parameter values, transformations of the observed frequencies (e.g., cumulative proportions), goodness-of-fit measures, and standard signal detection measures of accuracy and response bias, and also generates a summary plot. The summary plot from the analysis of the example data, which can be reproduced with the example code in the Supplemental Material, is shown in Fig. 2. As can be seen in Fig. 2a-c, the roc_solver function outputs numerous accuracy, response bias, and goodness-of-fit measures (see below). Figure 2d lists the best fitting parameter estimates as well as the standard error of each parameter estimate (see below). Figure 2e plots the observed and model predicted ROC and z-transformed ROC (zROC), respectively.

Fig. 2
figure 2

Example of the summary information output by the roc_solver function from fitting the DPSD model to the example data set described in the text (see also Supplemental Material). The output includes information about the participant, model, and exit status of the optimization routine (a), measures of accuracy/discrimination and response bias (b), goodness-of-fit and model selection measures (c), the best-fitting parameter estimates and the standard error of the parameter estimates (d), and the observed and model-predicted ROCs and zROCs (e). The standard errors were estimated from 1,000 iterations of the non-parametric bootstrap procedure described in the main text. The NaN values are given for parameters that were not estimated in the model

Full size image

The standard errors are estimated with a non-parametric bootstrap procedure whereby individual target and lure trials are randomly sampled with replacement from the observed data to create a new sample of target and lure trials. The model fit to the observed data is also fit to each of the randomly sampled sets of target and lure trials. The standard error values in Fig. 2 were estimated from 1,000 iterations of the non-parameteric bootstrap sampling procedure.Footnote 5 The number of iterations used to estimate the standard error of the parameter estimates can be controlled by the end-user.

An important feature of the ROC Toolbox is that numerous different models that are fit to the same data can be stored in a single data structure (output by the roc_solver function). Morever, there are many additional options for the roc_solver function, some of which are used in the example code in the Supplemental Material, that are detailed in the documentation of the ROC Toolbox.

Accuracy, response, goodness-of-fit and model selection measures

The ROC Toolbox outputs numerous measures that index accuracy/discrimination and response bias provided by Macmillan and Creelman (2005), as well as numerous goodness-of-fit measures to evaluate model fit and perform model selection. The measures of accuracy and discrimination include the hit and false alarm rates, the hit minus false alarm measure, d’, A’, d a, A z, and area under the curve (AUC). Additionally, we include the d r measure described in Mickes et al. (2007), which is similar to the d a measure. The response bias measures include c and β. The fit and model selection measures included are the log-likelihood value, regular and adjusted R 2, χ2, G (Sokal & Rohlf, 1994), the Akaike Information Criterion (AIC; Akaike, 1974), AICc (Burnham & Anderson, 2004), and Bayesian Information Criterion (Schwarz, 1978).

Concluding remarks and future directions

The ROC Toolbox provides a large set of tools that analyze ROC data. Importantly, the ROC Toolbox can flexibly define statistical models to fit to ROC data derived from many different types of experimental designs. Individual models and goodness-of-fit measures are defined as separate functions within the ROC Toolbox, and these are utilized by generic model-fitting wrappers (e.g., gen_pars, roc_solver). Thus, the ROC toolbox can easily be expanded with new models and goodness-of-fit measures. Additional future directions for the ROC Toolbox include adding functionality to fit ROCs derived from non-ratings based methods, such as manipulation of response bias with reward (e.g., Fortin, Wright, & Eichenbaum, 2004; Koen & Yonelinas, 2011), and incorporating Bayesian estimation of the models with the ability to flexibly define different priors for each parameter. Our hope is that researchers both with and without experience in ROC analysis will find this toolbox useful in the their own research endeavors.