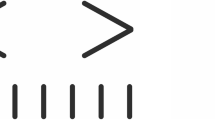
Numerous studies have shown that the visual perception of the length of different parts of the stimulus can be significantly distorted (the so-called geometric illusions of extent) due to the presence of neighboring contextual objects (distractors). A considerable number of experimental results indicate also that the length misjudgments can largely be caused by local positional shifts of elements specifying the ends of the spatial intervals of stimuli (terminators), and this fact generally contradicts the popular “perspective” theory (Gillam, 1998; Gregory, 1968; Nanay, 2009; Redding & Vinson, 2010), which implies uniform resizing of the entire stimulus. For example, it was shown in experiments with subdividing in equal-appearing segments of the shaft of figures of the Müller–Lyer type (widely known stimuli with flanking arrowhead wings; see Fig. 1a) that illusion effects occur only for segments in the immediate vicinity of the wings-shaft intersections (Morgan, Hole, & Glennerster, 1990; Post, Welch, & Caufield, 1998; Predebon, 2001). The use of auxiliary nontarget dots with the Müller–Lyer figures demonstrated that the illusion magnitude could be substantially altered only if these additional dots are presented within relatively small regions surrounding the wings vertices (Searleman, Porac, Dafoe, & Hetzel, 2005).

Fig. 1
figure 1

Examples of stimuli that induce different geometric illusions of extent. a The Brentano version of the Müller–Lyer figures. b The conventional Oppel–Kundt figure with equally spaced distracting dots. c The three-dot figure with continuous filling (line segment) of the reference part

Full size image

Some psychophysical studies’ findings revealed that the perception of the spatial separation of visual objects is strongly affected by neural processes of localization of the centroids of their luminance profiles (Baud-Bovy & Soechting, 2001; Hirsch & Mjolsness, 1992; McGraw, Whitaker, Badcock, & Skillen, 2003; Watt & Morgan, 1985; Whitaker, McGraw, Pacey, & Barrett, 1996; Wright, Morris, & Krekelberg, 2011). The implementation of the concept of “centroid biases” (Morgan et al., 1990) in modeling the Müller–Lyer illusion (Bulatov, Bertulis, Bulatova, & Loginovich, 2009; Bulatov, Bertulis, Gutauskas, Mickienė, & Kadzienė, 2010) quantitatively confirmed that length misjudgments can be associated with errors in the perceptual localization of stimuli terminators. According to the model, the illusion occurs because of local processes of automatic centroid extraction (one of the options for spatial-frequency filtering through spatial convolution), which causes metric distortions of the profile of neural activity (i.e., physically change the distance between the profile peaks). Nevertheless, even with the success achieved in fitting the model functions to various experimental data, an important issue remains unresolved, because the “centroid” explanation implicitly assumes the existence of a certain higher level neural mechanism responsible for the perceptual coding and assessment of metric changes in the excitation profile.

Another well-known example of geometric illusions of extent is the so-called illusion of interrupted spatial extent (or the Oppel–Kundt illusion; see Fig. 1b): The spatial interval subdivided in parts by some visual elements appears to be larger than an empty, undivided interval of the same length. Because of the long history of investigations, a number of different properties of this visual phenomenon have been established and well documented (cf. Wackermann, 2017). For example, one of the most remarkable features of the Oppel–Kundt illusion is its nonmonotonic dependence on the number of regularly distributed filling elements: With an increase in the number of fillers to a certain value, the magnitude of the illusion increases to a relatively flat maximum, and gradually decreases thereafter (Bulatov, Bertulis, & Mickienė, 1997; Coren, Girgus, Ehrlichman, & Hakistan, 1976; Noguchi, Hilz, & Rentshler, 1990; Obonai, 1933; Piaget & Osterrieth, 1953; Spiegel, 1937; Wackermann & Kastner, 2010). The illusion’s magnitude varies with the luminance (Bulatov & Bertulis, 2005; Dworkin & Bross, 1998; Long & Murtagh, 1984; Wackermann, 2012) or color contrast (Surkys, 2007) between the stimuli elements and depends noticeably on the temporal duration (Bailes, 1995; Bertulis, Surkys, Bulatov, & Bielevičius, 2014; Dworkin & Bross, 1998) and the way (Coren & Hoenig, 1972; Piaget & Bang, 1961) of illusory figures observation.

At the same time, it should be recognized that the current understanding (and the number of known explanations) of the Oppel–Kundt (and related) illusion is still very limited, even compared with the Müller–Lyer illusion (cf. Wackermann, 2017). Perhaps this is largely because stimuli with evenly distributed clearly distinguishable fillers (the conventional Oppel–Kundt patterns that cause relatively stronger illusory effects) have traditionally attracted much more attention from researchers, while the illusion characteristics in the case of high-density (or even continuous) filling were undeservedly ignored. Recently, we performed psychophysical experiments (Bulatov, Bulatova, Surkys, & Mickienė, 2017) with figures containing contextual distractors (shaft-line segments; see Fig. 1c) that continuously fill the reference part of the three-dot stimulus, and proposed a preliminary quantitative interpretation of the data obtained. After the subsequent development (Bulatov, Marma, Bulatova, & Mickienė, 2019), the model equations turned out to be suitable to account for data obtained with stimuli containing both continuous and discrete fillers. However, it is important to note that in order to avoid confusion with historically established definitions, we did not directly identify the effects caused by stimuli containing continuous distractors with the effects of the conventional Oppel–Kundt illusion, and have named the studied visual phenomenon as the continuously filled-space illusion (cFSI). It was demonstrated that the cFSI can be associated mainly with local integration of distractor-evoked effects in regions surrounding the terminators of stimulus spatial intervals (i.e., akin to the Müller–Lyer illusion). However, contrary to the “centroid” explanation, which implies some specific changes in the excitation profile (peaks displacement caused by spatial-frequency filtering), the model of the cFSI suggests a context-induced increase in the overall neural response (i.e., regardless of metric changes in the profile) of some hypothetical subsystem of coding of retinal coordinates of stimulus terminators. That is, a certain relationship was supposed between the terminator’s visual eccentricity and the magnitude of the response of some region of distractor influence (or area of weighted spatial summation; AWS) centered at the terminator: The response increases with eccentricity due to the wider aggregated profile of overlapping receptive fields (and, thus, a larger relevant AWS) affected by this terminator, and, vice versa, a greater response denotes a perceptually greater eccentricity. Assuming, for simplicity, circular Gaussian profiles (with the same dimensions that linearly scale with retinal eccentricity; see Fig. 2) of neural excitation (I) and AWS (A), the magnitude (Sρ) of the response evoked by a single dot (e.g., stimulus terminator) presented at eccentricity (ρ) can be evaluated by the integration of the product of two Gaussians, which leads to a certain quadratic relationship (Bulatov et al., 2019):

$$ {S}_{\rho }=\underset{\infty }{\iint }A\left(x,y,\sigma \left(\rho \right)\right)I\left(x,y,\sigma \left(\rho \right)\right) dxdy=\underset{\infty }{\iint }{e}^{-\kern0.33em \frac{x^2+{y}^2}{{\left( k\rho +{\sigma}_0\right)}^2}} dxdy=\pi {\left( k\rho +{\sigma}_0\right)}^2=\pi \sigma {\left(\rho \right)}^2, $$
(1)
Fig. 2
figure 2

Diagrams illustrating the modeling. a Two-dimensional view of the weighting profile, A(x,y,σ(ρ)), of the AWS represented by the circular Gaussian function. b Ωl and Ωr represent (for illustrative purpose, shown as the Gaussian distribution of the grey-level intensity) regions of distractors’ influence (AWSs) centered at stimulus terminators (dots) located at eccentricities ρl and ρr, respectively; Χ represents the position of gaze fixation

Full size image

where k and σ0 represent the slope and the intercept of the linear regression of the standard deviation σ(ρ), respectively. Conversely, the target eccentricity is encoded by the response as:

$$ \rho =\frac{\sqrt{S_{\rho }}}{k\sqrt{\pi }}-\frac{\sigma_0}{k}=\frac{\sqrt{S_{\rho }}-\sqrt{S_0}}{k\sqrt{\pi }}, $$
(2)

where S0 represents some constant value (i.e., the response of the foveal AWS). Then, the presence of a contextual distractor near the stimulus terminator should increase the cumulative response of the AWS (due to the distractor-evoked additional excitation sadd), and this response increment can be interpreted by the visual system as a bias (δ) in the perceived localization of the terminator, Sρ+δ = Sρ+sadd, thereby causing the illusion:

$$ \delta =\frac{\sqrt{S_{\rho }+{s}_{add}}-\sqrt{S_{\rho }}}{k\sqrt{\pi }} $$
(3)

Thus, according to the model, the cFSI magnitude (as well as the perceptual estimation of eccentricity) depends on the integral response of the relevant AWS and, consequently, on the parameters of spatial summation within this region of distractor’ influence surrounding the stimulus terminator. Because of the circular symmetry of the region’s profile, it also immediately follows that the perceptual positional biases should emerge approximately equally for stimuli with distractors located (within the limits of the AWS) at any place around the stimulus terminator (i.e., not only inside the reference interval), and this prediction was generally confirmed in our previous study (Bulatov et al., 2019). However, in Formula 1, the most elementary circular Gaussian profile of the AWS was simply postulated (i.e., without sufficient experimental evidence), so the issue regarding its actual two-dimensional spatial structure remains largely unclear. To overcome this drawback, in the present study, we performed psychophysical experiments with three-dot stimuli that contain distracting line segments whose position can be shifted (relative to the lateral terminator) either along or perpendicular to the stimulus axis (see Fig. 3a–b), thus allowing a certain “scan” of the profile of the AWS in two orthogonal directions. For additional examination of the profile, we used stimuli with the rotation of distractors around the lateral terminator (see Fig. 3c). In all cases, we arranged the distractors symmetrically with respect to the stimulus terminator in order to exclude the possible manifestation of the illusion of the Müller–Lyer type (which is supposedly caused by the bias of the terminator centroid). The use of stimuli with simple homogeneous elements (dots and line segments) made it possible to reduce significantly the influence of poorly identifiable irrelevant parameters in the experiments.

Fig. 3
figure 3

Examples of stimuli used in the study. The three-dot (tR, tC, and tT) stimuli with two distracting line segments oriented orthogonally (a) or parallel (b) to the main stimulus axis. c Stimulus with tilted (angle, ϕ) distractor. R and T, the length of the reference and test interval, respectively; s, the offset of distractors. The length of distracting line segments equal to R. In experiments, white stimuli (luminance of all the dots and lines, 20 cd/m2) were presented against a dark, round-shaped background (8° in diameter and 0.4 cd/m2 in luminance); two stimulus orientations (horizontal and vertical) were used

Full size image

The proposed model of the cFSI, even in its simplified initial form, provided a successful interpretation of experimental results with various stimuli modifications (Bulatov et al., 2017; Bulatov et al., 2019). Moreover, preliminary numerical estimates indicate that the model can be considered as a potential candidate for the aforementioned higher level neural mechanism (i.e., which is implicitly assumed in the “centroid” explanation of the Müller–Lyer illusion) for assessment of filtering-caused distortions within the profile of neural activity (by specifying retinal coordinates of different loci). Evidently, the illusions of extent are directly associated with the perceptual estimation of the visual objects’ dimensions or their mutual localization. The very fact of the illusions occurrence indicates that the corresponding neural mechanisms are built in such a way as to ensure optimal adaptive behavior in the relevant visual environment and fail to perform correctly the required tasks for some unusual (relative to the capacity of these mechanisms) stimulus conditions (Morgan et al., 1990). Therefore, a comprehensive study of the conditions (i.e., factors determining the illusory effects evoked by stimuli with various contextual distractors) can substantially narrow the range of theoretical interpretations regarding the possible organization of the underlying neural machinery and thereby contribute to a better understanding of the general principles of visual perception of spatial relationships. In this regard, we also think that a quantitative computational approach in the illusions study seems to be most preferable since it offers the most rigorous description of the illusion behavior for different variations of stimulus parameters, thus providing an immediate and purposeful experimental verification of the theoretical predictions.

Method

Apparatus

All experiments were carried out in a dark room (the surrounding illumination < 0.2 cd/m2). A Sony SDM-HS95P 19-inch LCD monitor (spatial resolution 1280 × 1024 pixels, frame refresh rate 60 Hz) was used for the stimuli presentations. A Cambridge Research Systems OptiCAL photometer was applied as a means of the monitor luminance range calibration and gamma correction. A chin and forehead rest was used to maintain a constant viewing distance of 200 cm (at this distance each pixel subtended about 0.5 arcmin); an artificial pupil (an aperture with a 3-mm diameter of a diaphragm placed in front of the eye) was applied to reduce optical aberrations.

We presented stimuli in the center of a round-shaped background of about 8° in diameter and 0.4 cd/m2 in luminance (the monitor screen was covered with a black mask with a circular aperture to prevent observers from being able to use the edges of the monitor as a vertical/horizontal reference). For all the stimuli drawings, the Microsoft GDI+ antialiasing technique was applied to avoid jagged-edge effects.

Stimuli

The stimuli used in the experiments comprised three base dots (dot size, 3 arcmin; luminance, 20 cd/m2), which were considered as terminators (tR, tC, and tT; see Fig. 3) specifying the ends of the reference and test stimulus intervals. The study used two different orientations (horizontal and vertical arrangement of terminators) and two sizes of stimuli (the length, R of the reference interval equal to 30 and 60 arcmin).

In experiments with displacement of the distractors, we presented the two line segments (line width, 1 arcmin; luminance, 20 cd/m2) symmetrically with respect to the lateral stimulus terminator (tR) and oriented orthogonally (see Fig. 3a, Type I stimulus) or parallel (Fig. 3b, Type II stimulus) to the main stimulus axis (i.e., along which the length judgments were performed). The offset (s) of the line segments relative to the terminator was randomly changed in a range from 0 to 0.5 R. In experiments with the rotation of the distractor (Type III stimulus), orientation (ϕ, relative to the main stimulus axis) of a single line segment (centered at the lateral terminator tR) was randomly varied in a range from 0° to 180° (see Fig. 3c). In all experiments, the length of distracting line segments was equal to R.

Procedure

The method of adjustment was used in the study: During the experimental run, we asked the subjects to manipulate the keyboard buttons “←” and “→” to move the lateral terminator tT of the test interval into a position that makes both stimulus parts perceptually equal in length (see Fig. 3). The physical difference between the lengths of the test and reference intervals, I = T − R, was considered as the illusion magnitude; the values of the relative overestimation of the reference interval length,\( rI=\frac{I}{R}100\% \), were also used. A single button push varied the position of the terminator by one pixel corresponding approximately to 0.5 arcmin. The initial length differences between the stimulus intervals were randomized and distributed evenly within a range of ±10 arcmin.

Were instructed the subjects to maintain their gaze on the central stimulus terminator; however, observation time was not limited, and subjects’ eye movements were not registered. A combination of two types of stimulus presentation conditions (for different conditions, the stimulus orientation differed by 180°; i.e., the reference and test stimulus parts were swapped) was used in each experimental run. Trials from different conditions were randomly interleaved in order to minimize (by averaging subjects’ responses) effects of the left/right or up/down visual field anisotropy and reduce stimulus persistence. An experimental run comprised 124 stimulus presentations—that is, 31 different values of the independent variable for each stimulus condition were taken (in a pseudorandom order) twice. For each type of stimulus, each subject carried out at least five experimental runs on different days (i.e., performed at least 124 × 5 × 3 × 2 × 2 = 7,440 stimuli observations throughout the study).

Subjects

Were collected data from four human observers (19–31-year-olds, three males and one female), which were naïve with respect to the purpose of the study, and all had normal or corrected-to-normal vision. With an aim to provide more strict viewing conditions and eliminate potential effects related to binocularity, the right eye was always tested, irrespective of whether it was the leading eye or not. All subjects gave their informed consent before taking part in the experiments performed in accordance with the ethical standards of the Declaration of Helsinki.

Experimental results

Experiment 1: displacement of distractors oriented orthogonally to the stimulus axis

The aim of these series of experiments was to quantify the dependence of the illusion magnitude on the distance between the lateral terminator and distracting line segments oriented orthogonally to the main axis of the stimulus (see Fig. 3a). In the first (horizontal stimulus) and the second (vertical stimulus) series, the length of the stimulus reference interval was fixed at 30 arcmin, and the offset of distractors was randomly changed from 0 to 15 arcmin. In the next two series of experiments (i.e., with either horizontal or vertical stimuli), the length of the reference interval was increased to 60 arcmin, and the displacement of distractors varied from 0 to 30 arcmin.

As can be seen from the graphs in Fig. 4, the experimental results from all subjects yielded curves of similar shape for stimuli of different sizes and orientations. The illusion magnitude rapidly increases from about zero to maximum value (on average, rI ≈ 15% and rI ≈ 13% for stimulus reference interval length equal to 30 and 60 arcmin, respectively) with an increase in the offset of distracting line segments to about one-sixth of the length of the reference interval (the position of maximum and its value varies slightly for different subjects and stimulus orientations). Afterward, the magnitude decreases smoothly to about zero for contextual distractors positioned at the maximum distance from the lateral terminator. Comparison of data (averaged over all subjects) for stimuli with different orientations showed a substantially random character of their differences—the paired t test, df = 30, α = 0.05: t(30) = 0.886, p = .383, and t(60) = 1.584, p = .124, with the preliminary Shapiro–Wilk test for the normality of residuals: W(30) = 0.946, p = .13, and W(60) = 0.968, p = 0.475, for stimulus reference interval length equal to 30 and 60 arcmin, respectively.

Fig. 4
figure 4

The illusion magnitude as a function of the offset of distractors oriented orthogonally to the stimulus axis (see Fig. 3a). In the graphs, closed and open symbols represent the data for horizontal and vertical orientation of the stimulus, respectively; the length of the stimulus reference interval (and that of distracting line segments) equal to 30 (left column), and 60 (right column) arcmin. Data for subjects S1–S4

Full size image

We think that the most interesting and unexpected result (given the assumption of the cFSI model regarding a simple circular Gaussian profile of the AWS) is related to the fact that the distractor with zero offset (i.e., when two distracting line segments merge into one, which position coincides with that of the terminator) practically does not affect the length judgments.

Experiment 2: Displacement of distractors oriented parallel to the stimulus axis

The results of experiments with the Type II stimuli (see Fig. 3b) containing distracting line segments oriented parallel to the stimulus axis are presented in Fig. 5; as in Experiment 1, we used stimuli of two different sizes and orientations. As can be seen from the graphs, fairly simple experimental curves were obtained for all subjects: The magnitude of length misjudgments gradually decreases to about zero with increase in the distance between the lateral terminator and distractors. In contrast to the results obtained with a Type I stimulus, in the case in which two distracting line segments merge into one, which position coincides with the position of the terminator (i.e., for zero offsets), the experimental data show the maximum magnitude of the illusion (on average, rI ≈ 17% and rI ≈ 18% for stimulus reference interval length equal to 30 and 60 arcmin, respectively). We think that, as well as in previous series of experiments, differences between the data for horizontal and vertical stimuli are largely observer specific: Comparison of data averaged over all subjects for stimuli with different orientations demonstrated the absence of statistically significant difference—the paired t test, df = 30, α = 0.05: t(30) = 1.906, p = .066, and t(60) = 0.986, p = .332, with the preliminary Shapiro–Wilk test for the normality of residuals: W(30) = 0.972, p = .581, and W(60) = 0.98, p = .802, for stimulus reference interval length equal to 30 and 60 arcmin, respectively.

Fig. 5
figure 5

The illusion magnitude as a function of the offset of distractors oriented parallel to the stimulus axis (see Fig. 3b). In the graphs, closed and open symbols represent the data for horizontal and vertical orientation of the stimulus, respectively; the length of the stimulus reference interval (and that of distracting line segments) equal to 30 (left column), and 60 (right column) arcmin. Data for subjects S1–S4

Full size image

Experiment 3: Rotation of the distractor

For additional assessment of properties of the two-dimensional profile of AWS for a wider range of distractor orientations (relative to the stimulus axis), we used the Type III stimuli with the rotation of a single line segment around the lateral terminator (see Fig. 3c); again, the illusion magnitude was established for two different sizes and orientations of the stimuli. As can be seen from the graphs in Fig. 6, the results of all subjects are largely consistent with the data obtained in experiments with displacements of distractors. The greatest illusion magnitude (on average, rI ≈ 17% and rI ≈ 16% for stimulus reference interval length equal to 30 and 60 arcmin, respectively) refers to the distracting line segment lying on the stimulus axis (distractor orientations 0° and 180°), and decreases to the minimum value (about zero) for distractor orientations near to 90°. As well as in previous series of experiments, the residuals of data (averaged over all subjects) for stimuli with two different orientations demonstrated significant randomness of their differences—the paired t test, df = 30, α = 0.05: t(30) = 1.656, p = .108, and t(60) = 1.917, p = .065, with the preliminary Shapiro–Wilk test for the normality of residuals: W(30) = 0.984, p = .908, and W(60) = 0.952, p = .175, for stimulus reference interval length equal to 30 and 60 arcmin, respectively. We think that the effects related to an observer-specific way of stimuli viewing (e.g., different patterns of gaze fixation) may also be responsible for some asymmetry of the experimental curves (particularly in the case of the subject S4) with respect to the orthogonal (90°) orientation of the distractor. In turn, comparable values of the illusion magnitude obtained for the same set of stimuli parameters in different series of experiments (i.e., distractors zero offset for stimuli of Type II, and 0° [180°] distractor orientation for stimuli of Type III) provide an additional argument in favor of a good precision of experimental measurements—the paired t test, df = 7, α = 0.05: t(30) = 0.896, p = .40, and t(60) = 1.306, p = .233, with the preliminary Shapiro–Wilk test for the normality of residuals: W(30) = 0.9, p = .292, and W(60) = 0.902, p = .303, for stimulus reference interval length equal to 30 and 60 arcmin, respectively.

Fig. 6
figure 6

The illusion magnitude as a function of the distractor tilting (see Fig. 3c). In the graphs, closed and open symbols represent the data for horizontal and vertical orientation of the stimulus, respectively; the length of the stimulus reference interval (and that of distracting line segments) equal to 30 (left column), and 60 (right column) arcmin. Data for subjects S1–S4

Full size image

Data analysis and discussion

Perceptual assessment of the stimulus spatial parameters is associated with a considerable number of factors that essentially affect the experimental results. Most of these factors may be attributed to inherent inaccuracy of the method of adjustment used in the present study—for example, errors due to the inability to control the individual pattern of gaze fixations and distribution of attention during stimulus observations (Krauzlis, Goffart, & Hafed, 2017), or cognitive bias (observers may establish individual criteria for determining whether parts of the stimulus differ in length) in judgments and decision-making (Morgan, Melmoth, & Solomon, 2013). As follows from the experimental results (see Figs. 4, 5, and 6), the differences between the data obtained for the horizontal and vertical stimulus orientations are to a large extent observer specific. Therefore, in order to reduce the manifestation of these irrelevant factors and emphasize the most common regularities in the body of data gathered in the study, it seems reasonable to average data for both stimulus orientations and consider the grand means calculated for the entire group of observers (see Fig. 7). We think that small values of SEM (not exceeding 0.88% overestimation of the reference interval length for smaller stimuli, and 0.69% for larger stimuli) for the grand means indirectly confirm our assumption regarding the similarity of the individual curves shape.

Fig. 7
figure 7

Grand means of the individual data for all four subjects who participated in the study. In the left column, closed and open symbols represent the grand-mean data for Type I and Type II stimulus, respectively; in the right column, open symbols represent the grand-mean data for Type III stimulus. The length of the stimulus reference interval (and that of distracting line segments) equal to 30 (upper row), and 60 (lower row) arcmin. Solid curves represent the least squares fitting of the Functions 5–7 to relevant experimental data; dash-dot curves represent confidence intervals of the fitting. Error bars depict ±1 standard error of the mean (SEM)

Full size image

As can be seen from the graphs in Fig. 7, the grand-mean data demonstrate a similar shape of the curves (and reasonably close values of the relative illusion magnitude, rI) for the same type of stimulus of two different sizes. This similarity may indicate a linear relationship between the illusion magnitude and the size of the stimulus (and therefore the retinal eccentricity of its elements). Besides, of interest is the lack of a noticeable decrease in the illusion magnitude when two distracting line segments oriented parallel to the stimulus axis merge into a single one (Type II stimulus, zero offsets of distractors). We believe that this fact may testify in favor of another important principle underlying the cFSI explanation (Bulatov et al., 2019)—namely, the assumption of normalization to a certain constant range of input neural excitation. The use of normalization procedure agrees with numerous reports in the literature (Carandini & Heeger, 2012; Olsen, Bhandawat, & Wilson, 2010; Reynolds & Heeger, 2009; Vokoun, Huang, Jackson, & Basso, 2014), and is necessary in the cFSI model to ensure amplitude-independent conditions for unambiguous coding of retinal coordinates of visual objects.

In turn, the shape and quantitative parameters of the obtained experimental curves allow us to make some suggestions regarding the weighting profile of the proposed region of distractor influence. We suppose that the simplest suitable two-dimensional profile of the AWS can be described as the product of two functions: the absolute value of the first derivate of a Gaussian along the main stimulus x-axis (i.e., along which the length judgments are performed) and the Gaussian function along the orthogonal y-axis (see Fig. 8a):

$$ W\left(x,y,\sigma \right)=\kern0.5em \left(\frac{\left|x\right|}{\sigma^2}{e}^{-\frac{x^2}{2{\sigma}^2}}\right){e}^{-\frac{y^2}{2{\sigma}^2}}=\frac{\left|x\right|}{\sigma^2}{e}^{-\frac{x^2+{y}^2}{2{\sigma}^2}}, or\ in\ polar\ coordinates,W\left(r,\phi, \sigma \right)=\kern0.5em \frac{\left|r\cos \left(\phi \right)\right|}{\sigma^2}{e}^{-\frac{r^2}{2{\sigma}^2}}, $$
(4)

where σ represents the standard deviation.

Fig. 8
figure 8

Diagrams illustrating the calculations. a Two-dimensional view of the weighting profile, W(x,y,σ(ρ)), of the AWS represented by the absolute value of the first derivative of Gaussian and the Gaussian functions in mutually orthogonal stimulus axes x and y. b, c, and d Diagrams illustrating the calculations by Formulas 5, 6, and 7, respectively

Full size image

Then, given the assumption of the cFSI model that the illusion is determined by the integration of distractor-induced additional neural excitation, the dependence of the illusion magnitude on the distractor offset (s) along the stimulus x-axis (see Fig. 8b) can be evaluated as follows (i.e., by the integration along the line segment oriented collinearly with the stimulus y-axis):

$$ {F}_x\left(s,\sigma, R\right)={C}_x+{\mu}_x{\int}_{-0.5R}^{0.5R}W\left(s,y,\sigma \right) dy={C}_x+{\mu}_x\sqrt{\frac{\pi }{2}}\mathit{\operatorname{erf}}\left(\frac{R}{2\sqrt{2}\sigma}\right)\frac{s}{\sigma }{e}^{-\frac{s^2}{2{\sigma}^2}}, $$
(5)

where C, μ, and R represent a constant component, a certain coefficient of proportionality, and the length of the distracting line segment, respectively. Obviously, Formula 5 allows only an approximate assessment of the cFSI magnitude changes, since the spatial distribution of neural excitation caused by distracting segments was not taken into account, for simplicity. The numerical examination of Function 5 using in calculations reasonably wide profile of neural excitation showed that the illusion, although greatly reduced, does not completely disappear (due to some residual overlap of the excitation and AWS profiles) in the case of zero offsets of distractors.

Similarly, the dependence of the illusion magnitude on the distractor offset along the orthogonal y-axis (see Fig. 8c) can be described by Formula 6:

$$ {F}_y\left(s,\sigma, R\right)=\kern0.5em {C}_y+{\mu}_y{\int}_{-0.5R}^{0.5R}W\left(x,s,\sigma \right) dx=\kern0.5em {C}_y+{\mu}_y\left(1-{e}^{-\frac{R^2}{8{\sigma}^2}}\right){e}^{-\frac{s^2}{2{\sigma}^2}} $$
(6)

In turn, the distractor rotation (see Fig. 8d) should cause the illusion magnitude changes, which can be calculated as follows:

$$ {F}_{\phi}\left(\phi, \sigma, R\right)=\kern0.5em {C}_{\phi }+\kern0.5em {\mu}_{\phi }{\int}_{-0.5R}^{0.5R}W\left(r,\phi, \sigma \right) dr=\kern0.5em {C}_{\phi }+{\mu}_{\phi}\left(1-{e}^{-\frac{R^2}{8{\sigma}^2}}\right)\left|\cos \left(\phi \right)\right| $$
(7)

where ϕ represents the distractor tilt angle (relative to the stimulus x-axis).

To quantitatively examine the validity of our assumptions regarding the two-dimensional weighting profile of the region of distractor influence, we fitted Functions 5–7 to the corresponding grand-mean data (the method of least squares, LeastSquaresFit function, Mathcad, Parametric Technology Corporation). First, we approximated (using Function 5 with three free parameters: C, μ, and σ) the data collected in Experiment 1 with distractor shifts along the stimulus x-axis (Type I stimulus), since these curves with a single well-expressed maximum are most reliable in terms of stability of the results of the least-squares procedure. Thereafter, the established values for σ (see Table 1) were used in Formulas 6 and 7 (with two free parameters: C and μ) to fit the data from experiments with displacements along the y-axis and the rotation of the distractors, respectively. The fitting demonstrated a good correspondence between the computational and experimental results (see Fig. 7, solid curves); the values of the coefficient of determination in all the cases were higher than 0.9 (see Table 1). With the aim of a more thorough examination of the goodness of fit, we performed statistical analysis of the data with the Shapiro–Wilk test (assessment of normality of residuals; see Table 1); we also calculated confidence intervals for the predicted values at each point over the range of the independent variable (see Fig. 7, dash-dot curves).

Table 1. The resulting parameters of fitting functions 5 – 7 to experimental data
Full size table

We think that the success in fitting of Functions 5–7 to the grand-mean curves supports our suggestions regarding the shape of the two-dimensional profile of the region of distractor influence and indicates that the obtained experimental data are consistent with the cFSI explanation based on the assumption of integration of context-evoked neural activity. As an additional argument in favor of the validity of the suggestions regarding the profile of the region, we can consider the ratio of the maximum illusion magnitudes obtained in experiments with stimuli of Types II and I. According to Formulas 5 and 6 (assuming Cx = Cy = 0, and μx = μy), this ratio can be calculated as follows:

$$ \eta \left(\sigma, R\right)=\frac{F_y\left(0,\sigma, R\right)}{F_x\left(\sigma, \sigma, R\right)}=\kern0.5em \sqrt{\frac{2e}{\pi }}\frac{\left(1-{e}^{-\frac{R^2}{8{\sigma}^2}}\right)}{\mathit{\operatorname{erf}}\left(\frac{R}{2\sqrt{2}\sigma}\right)}, $$
(8)

and is equal to η(4.56,30) = 1.311 and η(9.87,60) = 1.306 for the distractor length, R equal to 30 and 60 arcmin, respectively. For comparison, the corresponding ratios calculated (taking into account the values of the constant components, C, and the differences between the coefficients of proportionality, μ; see Table 1) from grand-mean data shown in Fig. 7 are equal to 1.319 ± 0.005 and 1.308 ± 0.007. In turn, such a good correspondence may also serve as an argument against an explanation of the results of the present study by simple summation of the Müller–Lyer effects of the opposite sign within an asymmetric (along the x-axis of the stimulus) Gaussian profile.

The obtained two-dimensional profile of the AWS (Function W, Formula 4) differs significantly from the circular Gaussian (Function A, Formula 1) that was used in our previous modeling of the cFSI (Bulatov et al., 2019). Consequently, an important question is how this difference can affect the computational procedures of the model. Adhering to the basic assumptions underlying the explanation of the cFSI, in the case of the AWS profile established in the present study, the cumulative response, Sρ evoked by a dot-target can be evaluated as follows—that is, by substituting A(x,y,σ(ρ)) with W(x,y,σ(ρ)) in Formula 1:

$$ {S}_{\rho }=\underset{\infty }{\iint }W\left(x,y,\sigma \left(\rho \right)\right)I\left(x,y,\sigma \left(\rho \right)\right) dxdy=\underset{\infty }{\iint}\frac{\left|x\right|}{\sigma {\left(\rho \right)}^2}{e}^{-\frac{x^2+{y}^2}{\sigma {\left(\rho \right)}^2}} dxdy=\sqrt{\pi}\sigma \left(\rho \right)=\sqrt{\pi}\left( k\rho +{\sigma}_0\right), $$
(9)

and, therefore, the retinal eccentricity of the target can be encoded by the response of the relevant AWS through a simple linear relationship:

$$ \rho =\frac{S_{\rho }}{k\sqrt{\pi }}-\frac{\sigma_0}{k}=\frac{S_{\rho }-{S}_0}{k\sqrt{\pi }}. $$
(10)

That is, the use of the AWS profile comprising the first derivative of the Gaussian avoids the use of the nonlinear square root extraction procedure (Formula 2) for coding retinal coordinates, which implementation is complicated in terms of neural processing (and, therefore, less biologically plausible). Of note, we are fully aware that the proposed quantitative description, because of its extreme simplicity, does not pretend to identify any specific neural mechanism that underlies the illusion occurrence and in its current state offers only directions for further research. At the same time, derivatives of the Gaussian function, as the weighting profiles are common and widely used to describe the properties of neural structures at different levels of the visual system—for example, receptive fields for motion (Young, Lesperance, & Meyer, 2001) and edge detection (Elder & Sachs, 2004; McIlhagga & Mullen, 2018) or for automatic centroid extraction (Bulatov, Bulatova, Loginovich, & Surkys, 2015). Assuming that during the stimulus observations, gaze fixation is generally tied to the stimulus x-axis (i.e., this axis is located on the visual meridian), the two-dimensional profiles of AWSs can be considered as oriented with their derivative of the Gaussian function along the radial direction in the visual field (and therefore with the Gaussian function located along the tangential direction). Along with this, it should be recognized that the absence of direct experimental data on the actual distribution of gaze fixation during stimulus observations can be considered as one of the important shortcomings of the present study, which should be resolved in future research (by modification of experimental methods).

As noted above, we applied several essential simplifications (e.g., ignoring the spatial structure of the profile of neural excitation), which can cause certain inaccuracies in the calculations, in the quantitative interpretation of the results of the present study. In addition, because of the limitations of the experimental methods used (i.e., the need for symmetrical positioning of two distractors), it is impossible to evaluate a potential skewness of the AWS profile (Ottes, Gisbergen, & Eggermont, 1986); among other things, this asymmetry of the profile may cause some residual effects of the Müller–Lyer illusion. Another potential drawback of the present study is associated with the possible manifestation of attentional bias caused by relatively more salient distracting lines. However, we think that the general consistency of experimental data collected with different naïve subjects during experimental runs performed on different days confirms the reliability of the obtained results. Besides, we believe that a successful approximation by the relevant theoretical functions of the data obtained in experiments with different stimuli can be considered as an additional argument in favor of the validity of the suggestions made in the present study. Nevertheless, in future studies of the cFSI, in order to compensate for possible attentional bias, it seems reasonable to use stimuli with a completely filled test spatial interval.

The basic assumptions underlying the proposed mechanism of coding of a target retinal eccentricity through the magnitude of the response of relevant AWS mainly follow from the analysis of the cFSI characteristics established in our previous experiments (Bulatov et al., 2017; Bulatov et al., 2019). However, these speculations are also indirectly supported by human fMRI data (Dumoulin & Wandell, 2008; Silva et al., 2018; Welbourne, Morland, & Wade, 2018) on eccentricity-dependent changes in the size of the neuronal population receptive fields, as well as by the results of extracellular recordings from the lateral intraparietal area (LIP) of macaque monkeys (Bremmer, Kaminiarz, Klingenhoefer, & Churan, 2016; Graf & Andersen, 2014; Sereno & Lehky, 2011). It has been shown that the size of the neuronal population receptive fields increases linearly with their eccentricity, and that the changes in LIP population activity strongly correlate with the target eccentricity and with the size of an upcoming saccade. Unfortunately, at present, at least in the literature known to us, there are no other sufficiently developed quantitative (i.e., those making predictions that can be unambiguously tested in experiments) explanations of the cFSI (or conventional illusions of interrupted spatial extent, such as the Oppel–Kundt illusion); therefore, a comprehensive comparison of the current results with others on this topic seems complicated. It also remains probable that the studied effects of distractors’ influence on the length judgments, despite their successful interpretation in terms of the cFSI model, represent the phenomenon that is more specific for the perception of stimuli made up of separate visual elements (such as the three-dot stimuli used in the present study). Nevertheless, we think that even in this case, the effects under consideration should not be ignored when trying to explain the results of experiments with various geometric illusions of extent.

At present, it is still difficult to specify any particular neural mechanisms responsible for the emergence of the cFSI and related illusions of extent. However, given the basic principles of our modeling and a good agreement between the theoretical and experimental data from current and previous research (Bulatov et al., 2017; Bulatov et al., 2019), it can be hypothesized that the superficial layers of the superior colliculus (as well as cortical areas such as the frontal eye fields and functional equivalents of macaque area LIP in human parietal cortex) are actively involved in the visual information processing related to the phenomenon under study. It is widely known (Bremmer et al., 2016; Hafed, Lee, Lovejoy, & Krauzlis, 2013; Krauzlis et al., 2017; Krauzlis, Lovejoy, & Zènon, 2013; Vokoun et al., 2014) that these brain regions are associated with the control of spatial attention and gaze fixations and are directly engaged in neural coding of information on the retinal localization of visual objects.

According to the main assumption of our model of the cFSI (Bulatov et al., 2019), the magnitude of the illusory displacement of stimulus terminator strongly depends on the size of the corresponding AWS, which linearly increases with retinal eccentricity (i.e., depends on the actual position of gaze fixation). In this regard, for a better understanding of the underlying neural mechanisms, it is of interest to study in more detail the relationship between the properties of the cFSI and the parameters of another visual phenomenon—namely, saccadic eye movements. Earlier, the “centroid” effect with respect to amplitudes of saccades was demonstrated by Gilster and Kuhtz-Buschbeck (2010) when compared with the perceptual (adjustment of lengths) and action (amplitude of saccades) effects of the Müller–Lyer illusion. It was shown that the perceived length of the wings-out figure was overestimated (which correlates with overshoots of saccades in eye-movement experiments), and the length of the wings-in figure was underestimated (with corresponding undershoots of saccades) compared with some neutral figure. Because both the Müller–Lyer illusion and the cFSI are presumably caused by perceptual spatial shifts of stimuli terminators, some similar correspondence can be expected between the perceptual and action effects in the case of the cFSI. However, we found no literature data on the interrelation between the cFSI (or the Oppel–Kundt illusion) and saccades parameters; therefore, the experimental examination of this relationship can be considered as one of the interesting challenges for future illusion studies.

Conclusions

The aim of the present study was to investigate the spatial structure of the two-dimensional weighting profile of the region of distractor’ influence (i.e., AWS) on the magnitude of length misjudgments. It was shown in psychophysical experiments with three different types of stimuli that for distracting line segments oriented perpendicularly to the stimulus axis, the magnitude of the illusion increases to the maximum value and smoothly decreases to zero with the increase of distractor offset. For distractors oriented parallel to the stimulus axis, the illusion magnitude monotonically decreases with the increase of distractor offset. For stimuli with distractor rotation, the greatest illusion magnitude refers to orientations of the distracting line segment along the stimulus axis, and decreases to the minimum value for the orthogonal orientation. Based on the analysis of established functional dependencies, we proposed a simple quantitative interpretation of the experimental data obtained in the present study. A good correspondence between the experimental and theoretical results supports the suggestion that the two-dimensional profile of the AWS can be described as the absolute value function of the first derivate of a Gaussian along the radial direction in the visual field and the Gaussian function along the tangential direction.