Introduction

Many everyday actions occur in the context of other activities, including those that are relevant to accomplishing a task and those that are irrelevant to that task, actions that might demand attention and cognitive resources and constrain perception or motor performance. In experimental psychology, dual-task methodology,Footnote 1 which requires participants to perform two or more concurrent activities, has been extensively used in various paradigms. A subset of these studies examines the attentional demands of motor tasks. For example, Kerr, Condon, and McDonald (1985) found that a concurrent standing balance task disrupted recall on a spatial memory task. The authors attributed this finding to a reliance of postural control and cognitive spatial processing on common central neural mechanisms. Lajoie, Teasdale, Bard, and Fleury (1993) demonstrated longer reaction times to auditory stimuli when participants stand and walk than when they sit. Also, Pellecchia (2005) found that postural sway increased when a cognitive task was performed concurrently with a postural task.

In the study of gait control, in particular, there are also studies related to the dual-task application. Most existing dual-task applications to the study of gait, however, have been to demonstrate the increased attentional resources needed for gait control (in the elderly, e.g., Brown, Shumway-Cook, & Woollacott, 1999; Lajoie, Teasdale, Bard, & Fleury, 1996; Marsh & Geel, 2000, or in patient populations such as those with Parkinson’s and Alzheimer’s disease, e.g., Morris, Iansek, Smithson, & Huxham, 2000; Morris, Iansek, Summers, & Matyas, 1995; Camicioli, Howieson, Lehman, & Kaye, 1997; see also Abernethy, Hanna, & Plooy, 2002). Ebersbach, Dimitrijevic, and Poewe (1995) suggested that although walking is a highly practiced task, gait parameters related to control of balance are subject to modifications according to the attentional demand of concurrent tasks. Daniels and Newell (2003) examined walk-to-run transitions when participants walked on an accelerating treadmill. They found that walk-to-run transition speeds increased when the participants solved mental arithmetic at two levels of difficulty.

The present study was aimed at studying the effect of concurrent cognitive activity on the dynamics of human adults’ walk-to-run (WR) and run-to-walk (RW) transitions on a treadmill and in particular the phenomenon known as hysteresis. Hysteresis is one of the characteristics of nonlinear phase transitions. Hysteresis has a long history in inanimate systems and has, in recent years, been variously reported in different animate systems. In particular it has been reported in a number of human perception-action experiments (e.g., Fitzpatrick, Carello, Schmidt, & Corey, 1994; Lopresti-Goodman, Richardson, Baron, Carello, & Marsh, 2009; Richardson, Marsh, & Baron, 2007; Tuller, Case, Ding, & Kelso, 1994; Van der Kamp, Savelsbergh, & Davis, 1998). Diedrich and Warren (1995) provided a dynamical systems account for human gait transition (with walking and running as two attractive states of the system) and demonstrated that gait transitions satisfy the criteria of nonlinear phase transitions – specifically, they exhibit hysteresis, that is, higher transition speed for WR in a sequence of increasing treadmill speeds than for RW in a sequence of decreasing treadmill speeds.Footnote 2

It has been suggested that concurrent cognitive activity affects hysteresis. For example, Lopresti-Goodman et al. (2009) discovered exaggerated hysteresis with increased cognitive task difficulty in perception of the affordance of graspability. For instance, when participants performed the concurrent cognitive task of counting backward from a three-digit number by sevens more hysteresis was observed than when they performed the simultaneous arithmetic task of counting backward by ones. Figure 1 shows a hypothetical schema of such an exaggeration of the hysteresis in the context of human gait transitions.

Fig. 1
figure 1

Schematic representation of exaggeration in hysteresis in gait transition by concurrent cognitive activity. The darkest loop corresponds to no concurrent cognitive activity; the solid line represents an ascending sequence or increasing the speed, while the dashed line represents a descending sequence or decreasing the speed. With the addition of concurrent cognitive activity of increasing difficulty, the area inside the hysteresis loop increases. Lighter lines represent the “easier” mental arithmetic task (counting backward by ones), the lightest lines correspond to the “harder” mental arithmetic task (counting backward by sevens). The larger area between the lighter trajectories corresponds to the more exaggerated hysteresis

Full size image

There are enough hints (summarized above) to suggest that imposing cognitive constraints upon walking or running suffices to change their dynamics. For example, Getchell and Whitall (2004) showed that intentional switching between gaits from different symmetry classes (e.g., walk vs. gallop) resulted in changes in dynamical hysteresis.Footnote 3 In the present experiment, extending the findings of Daniels and Newell (2003), the effect of conducting a simple cognitive activity in parallel with walking and running has been studied. Specifically, it has been hypothesized that concurrent cognitive activity may affect the WR or RW transition speeds and consequently the degree of hysteresis in ordinary bipedal locomotion.

Method

Participants

Six women and nine men (mean age = 23.1 ± 3 years; mean leg length = 89 cm) from the University of Connecticut participated in this experiment. Participants were paid at a rate of US$10 per hour for their participation. The university’s Institutional Review Board approved all procedures.

Materials

A Trackmaster TMX-425 treadmill (180-kg capacity, running surface of 76 × 160 cm, speed range 0.22–5.36 m/s) with a manual controller and safety siderails was used.

Procedure

Each participant completed two repetitions of walk-to-run with increasing treadmill speed and two repetitions of run-to-walk with decreasing treadmill speed for each of three cognitive conditions (no concurrent cognitive activity, counting backwards by ones and counting backwards by sevens). Prior to the experiment, each participant completed a practice trial for each of the two sequence conditions (ascending or descending). The participants were asked to avoid holding safety siderails unless necessary.

In the case of counting backwards, the participants did the task verbally and loudly. The performance sequence (walk-to-run preceding run-to-walk or vice versa) and the different task conditions were counterbalanced across participants. The participant’s leg length was defined by adding the measures of hip-to-knee and knee-to-ankle. The participants were tested on the treadmill with constantly increasing or decreasing speed at constant increments of 0.045 m/s (0.1 mph) every 2 s (yielding a constant acceleration or deceleration of approximately 0.02 m/s2). The final results were based on averaging across repetitions.

Design and analysis

The experiment employed a 2 (sequence: walk-to-run, run-to-walk) × 3 (condition: no counting, counting backwards by ones, counting backwards by sevens) within-subjects design. There were two repetitions for each trial. Hence, participants performed 12 trials in sum. The transition speeds were averaged across repetitions. The critical Froude numbersFootnote 4 (Fr) were computed for each participant by dividing transition speed squared (v 2) by the participant’s leg length and gravitational acceleration (Fr = v 2/ lg; g = 9.81 m/s2).

Results

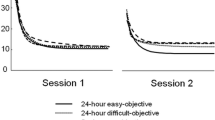
The experimental results showed that participants switched from walking to running at larger Froude numbers in the ascending sequences (0.46 ± 0.08) than in the descending sequences (0.33 ± 0.06). A 3 (Task) × 2 (Sequence) within-subjects ANOVA on the mean Froude numbers revealed significant effects for Cognitive Task, F(2, 28) = 7.2, p < 0.01, Sequence (Ascending vs. Descending), F(1, 14) = 81.8, p < 0.001, and Sequence × Cognitive Task, F(2, 28) = 13.8, p < 0.001. Hysteresis was least in the absence of a concurrent cognitive task (ΔFr mean = 0.07), intermediate when counting backward by ones (ΔFr mean = 0.13), and most when counting backward by sevens (ΔFr mean = 0.20). Figure 2 shows the percentage transition versus Froude numbers for the three conditions and the two sequences for each, ascending and descending. It is evident in Fig. 2 that the area between the two curves (for Ascending and Descending sequences) increases with the increasing cognitive task difficulty indicating an exaggerated hysteresis across the conditions.

Fig. 2
figure 2

Exaggeration in hysteresis with increase in the difficulty of concurrent cognitive task. Top panel: no concurrent cognitive activity. Middle panel: counting backward by ones. Bottom panel: counting backward by sevens

Full size image

Figure 3 depicts the mean critical Fr numbers for different conditions. As shown, mean critical Fr for ascending sequences increased from 0.45 for no concurrent cognitive task condition to 0.47 for both “easy” and “hard” task conditions. However, post-hoc paired mean comparisons of ascending sequences across task conditions did not reveal significant results. For descending sequences, mean critical Fr decreased from 0.37 for no concurrent task condition to 0.34 and 0.27 for “easy” and “hard” task conditions, respectively. Post-hoc paired mean comparisons of descending sequences showed significant results (p < 0.01) across all task conditions.

Fig. 3
figure 3

Mean values of critical Froude numbers for task conditions (error bars represent standard error of the means)

Full size image

Discussion

The results of the experiment confirmed expectations about the dynamics of gait transition when participants are engaged in a concurrent cognitive task. The predictions followed from prior empiric observations of hysteresis in behavioral transitions (e.g., Lopresti-Goodman et al., 2009). The question of the present study was how concurrent cognitive activity might function as a constraint on bipedal dynamics, specifically, the hysteresis in transiting from walk to run and vice versa. It was predicted that increases in task difficulty would result in increases in the degree of hysteresis exhibited (ΔFr).

The results of the experiment were compatible, in part, with those reported in Daniels and Newell (2003). In their study, they examined the hypothesis that cognitive perceptual processes are involved in determining the WR transition in human locomotion. They recorded WR transition speeds and peripheral rating of perceived exertion of healthy participant walking on a treadmill with increasing speed while solving mental arithmetic at two levels of difficulty (easy and hard). Daniels and Newell observed that the transition speeds increased during both levels of mental arithmetic. They concluded that cognitive load distracts attentional focus from physiologic cues that contribute to triggering human gait transitions. In the present study, although only a mild increase in the WR transition values was observed, the cognitive load showed significant impact on the RW transition values. The overall results were also reported in terms of hysteresis. It was observed that hysteresis was significantly affected by concurrent cognitive activity.

Cognitive constraint can alter the intrinsic dynamics of the perceiver with regard to the environment. In dynamical systems theory, this alteration is in the form of relocation of attractors. The results of the present experiment are also comparable with the predictions with regard to impact of concurrent cognitive activity on the attractor dynamics (Pellecchia & Turvey, 2001; Pellecchia, Shockley, & Turvey, 2005). For instance, Pellecchia and Turvey (2001) inquired how the attractors of bimanual rhythmic coordination, given as the solutions of a motion equation in relative phase, were affected by cognitive activity. In their experiments, participants were required to swing two pendulums with their two hands in an in-phase or anti-phase manner while performing an information reduction task (Posner, 1964). They observed that cognitive activity amplified deviation from both in-phase (0°) and anti-phase (180°) to the same degree with amplification (in degrees), a linear increasing function of magnitude of information reduction (in bits). In the present study, even though the detuning was manifest in the critical Fr for RW transitions, the post-hoc analysis did not reveal symmetric changes for WR transitions. One can explain this observed phenomenon through the interplay between the attentional resources and biomechanical constraints. In WR transitions, in the presence of a concurrent counting task, participants tend to delay the transition from walk to run until the biomechanical limits are reached and transition to run is inevitable. In contrast, in RW transitions in the absence of biomechanic constraints, cognitive resources taken by the counting task, lead participants to delay transitioning from run to walk until the speed is so low that continuing running is more demanding than dealing with the transition and the associated attentional resources. Additionally, since the transitions are performed on a treadmill and the post-transition gait needs to be stabilized to reduce the risk of losing balance, participants delay the transition until the speed is low enough to comfortably stabilize post-transition gait. This interpretation is compatible with the prediction that the transition speeds are amplified by the difficulty of concurrent cognitive task.