Suboptimal decision criteria are predicted by subjectively weighted probabilities and rewards

Abstract

Subjects performed a visual detection task in which the probability of target occurrence at each of the two possible locations, and the rewards for correct responses for each, were varied across conditions. To maximize monetary gain, observers should bias their responses, choosing one location more often than the other in line with the varied probabilities and rewards. Typically, and in our task, observers do not bias their responses to the extent they should, and instead distribute their responses more evenly across locations, a phenomenon referred to as ‘conservatism.’ We investigated several hypotheses regarding the source of the conservatism. We measured utility and probability weighting functions under Prospect Theory for each subject in an independent economic choice task and used the weighting-function parameters to calculate each subject’s subjective utility (SU(c)) as a function of the criterion c, and the corresponding weighted optimal criteria (wc _opt ). Subjects’ criteria were not close to optimal relative to wc _opt . The slope of SU(c) and of expected gain EG(c) at the neutral criterion corresponding to β = 1 were both predictive of the subjects’ criteria. The slope of SU(c) was a better predictor of observers’ decision criteria overall. Thus, rather than behaving optimally, subjects move their criterion away from the neutral criterion by estimating how much they stand to gain by such a change based on the slope of subjective gain as a function of criterion, using inherently distorted probabilities and values.

Appendix

Experiment 1 - Contrast Threshold Measurement

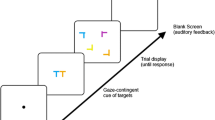
Experiment 1 was completed in a single session. We used a 2AFC detection task to determine the Gabor contrasts corresponding to d′ = .5 and 1 for each subject for use in Experiment 3. The trial sequence is shown in Fig. 13. Each block began with a nine-point calibration of the eyetracker. On each trial, the subject fixated a central cross-flanked at 10 deg of eccentricity by 3 deg diameter disks containing noise patches. They initiated the trial by key press. Following a random ISI of 300–700 ms, the target stimulus appeared on the left or right side, chosen at random, and remained visible for 200 ms. The target stimulus disappeared leaving only the noise image (the same noise image was used throughout the trial). Trials in which the subject broke fixation between initiation of the trial and offset of the target were discontinued and rerun later on a randomly selected trial. If fixation was maintained, a small question mark appeared in place of the fixation cross instructing the observer to indicate the side on which the target stimulus appeared by key press. Subjects received auditory feedback on each trial in the form of a high tone for a correct and a low tone for an incorrect response.

Fig. 13

Trial sequence for Experiment 1

Stimulus contrast on each trial was determined by one of two staircases (1-up/3-down, 1-up/2-down) selected at random independently of the side on which the target appeared. Contrasts were sampled from 25 logarithmically spaced values ranging from .01−.95. The initial stepsize for each staircase was three. The step size was decreased by one after the first and second reversals. Each subject completed two blocks of 200 trials each in a single session. The staircases were initiated at the beginning of each block. The first block served to stabilize the subjects’ performance in the task. Only the 200 trials of the second block (100 per staircase) were analyzed. Each subject’s data were pooled across the two staircases. Probability correct as a function of contrast was modeled using a Weibull function fit to the data by maximum likelihood. Peak contrasts corresponding to d′ = .5 and 1 were estimated from the fit curve. These contrast values ranged from .04 to .08 (d′ = .5), and .06 to .09 (d′ = 1).

Experiment 2 - Weighting Function Parameter Measurement

As mentioned above, observers’ preferences for a reward, V, given the probability of receiving it, p, deviate from those predicted by assuming the observer maximizes expected gain. They are well predicted by a model that assumes non-linear weighting of probabilities, w(p), and rewards, u(V). Here we assume standard functional forms for w and u (Tversky & Kahneman, 1992; Fox & Poldrack, 2009):

$$ w(p) = \frac{p^{\gamma}}{\left(p^{\gamma}+(1-p)^{\gamma}\right)^{\frac{1}{\gamma}}} $$

$$ u(V) = V^{\alpha}, $$

and estimate the values of the parameters, γ and α, by modeling observers’ preferences for particular probability/reward pairs, i.e., prospects.

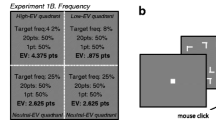
On each trial, observers were presented with a choice between a pair of prospects of the form (Fig. 14):

$$(p_{i},X;(1-p_{i}),0)\quad\quad\quad \text{or}\quad\quad\quad ((1-p_{i})V_{i,j};p_{i},0), $$

where X is a value that is held constant across trials, and V is a value that changes on each trial. They were instructed to choose which ‘gamble’ they would prefer. It was explained to the subjects that the dollar values, X and V, were amounts they could actually win and that the probabilities represented the chance of “blindly reaching into a box containing a huge number of lottery tickets, some with the dollar value on them, some with $0 on them, and selecting a winning ticket.” All subjects indicated that they understood the task. Upon completion, a prospect was selected at random from all those chosen by the subject and the outcome of the gamble was generated pseudo-randomly by computer. The subject received the payoff, which ranged from $0-$50 across subjects.

Fig. 14

Sample display from Experiment 2. See text for description

On each trial, the value of p _i was selected at random from: {.1, .18, .28, .4}. The value of X was fixed at $50. For each value of p _i , five values of V _{i, j} were employed corresponding to five values of the psychometric function, {.2,.35,.5,.65,.8}, that gives probability, P(choose V), of choosing the prospect containing V _{i, j} (as a function of only V _{i, j} ) given the current estimates of the parameters γ and α.

An additional parameter, δ, was added to account for patterns of choice observed in piloting Experiment 2. In piloting the experiment, we found that subjects’ choices were consistent with an additional weighting of the changing value, δV _{i, j} (for δ > 1), such that increases in its value are subjectively exaggerated. Experiment 2 results in data to which four psychometric functions (each corresponding to one of the four values of p _i ), giving P(choose V) as a function of V _{i, j} , are fit. The parameters γ and α determine the relative spacing of the four psychometric functions. Increasing values of δ shift the four functions uniformly toward lower values of V _{i, j} . The addition of δ led to a substantial reduction in the error of the fits. The method for selecting the values of V _{i, j} is explained below.

Under prospect theory, as modified by the additional δ parameter, the subject will choose the lottery containing V _{i, j} when:

$$w(1-p_{i})u(\delta V_{i,j})>w(p_{i})u(X). $$

Putting this in terms of the unweighted value of V _{i, j} and rearranging the terms, we obtain:

$$ \text{choose \textit{V} when: } V_{i,j}>\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}}\frac{X}{\delta} $$

and equivalently:

$$ \text{choose \textit{V} when: }\frac{V_{i,j}}{\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}}\frac{X}{\delta}}>1 $$

and taking the log of each side:

$$\text{choose \textit{V} when: } \ln(V_{i,j})-\ln\left(\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}}\frac{X}{\delta}\right)>0. $$

We assume that the subject’s internal representation of the difference on the left of the inequality is corrupted by noise drawn as a random sample from a normal distribution with mean=0. Furthermore, we assume under Weber’s law that the SD of the distribution for each value of i is equal in log value. The probability of choosing the lottery containing V _{i, j} is thus given by:

$$P_{i}(\text{choose }\textit{V}) = {\Phi}\left(\frac{\ln(V_{i,j})-\ln\left(\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}}\frac{X}{\delta}\right)}{\sigma}\right). $$

Initial values for V _{i, j} were derived by choosing five values for P _i (choose V) that span the psychometric function: {.2, .35, .5, .65, .8}, and then solving:

$$V_{i,j}=\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}} \frac{X}{\delta} \exp{\left(\sigma{\Phi}^{-1}\left(P_{i}(\text{choose }V)\right)\right)} $$

with parameter values: α = .65, γ = .5, and σ = .2 chosen to represent reasonable parameter estimates given a survey of estimates across many studies (Fox & Poldrack, 2009), and the initial value of δ set to 1. The maximum value of V _{i, j} never exceeded $50 so that the prospect containing V _{i, j} was never stochastically dominant.

Prospects were presented using the method of constant stimuli. Values of p _i and their corresponding V _{i, j} were chosen at random from each of the four probability and five value levels with equal numbers of trials from each level (i.e., five trials per probability/value pair) within each block. To avoid stereotyped responses, displayed values of V _{i, j} were randomly jittered by an amount no more than ±1/4 of the minimum difference between any two values of V for the given block. To avoid response-side bias, the side with the lottery containing V was selected at random on each trial. Subjects indicated their preferred prospect on each trial by key press.

Subjects completed four 100-trial blocks in a single session. At the end of each block, estimated α, γ, σ, and δ were fit to the binned data from all preceding blocks by maximum likelihood where the estimated probability of choosing the prospect containing V _{i, j} is given by:

$$\hat P_{i}(V_{i,j}) = {\Phi}\left(\frac{ln(V_{i,j})-ln\left(\left(\frac{p_{i}}{1-p_{i}}\right)^{\frac{\gamma}{\alpha}}\frac{X}{\delta}\right)}{\sigma}\right). $$

The resulting estimates of α, γ, σ, and δ were used to select new values of V _{i, j} for use in the subsequent block. The fit parameters and weighting functions for each subject are shown in Fig. 2.

All subjects were debriefed following the task as to any strategy they may have employed. One subject indicated that they had merely calculated the expected gain of the prospects. Their data were excluded from the analyses and they did not continue with Experiment 3. In addition, five subjects employed ad hoc strategies for which the model above cannot account. Two subjects chose the lottery containing the higher probability and lower value, V, on more than 90 % of trials, a strategy which effectively ignores values. Three subjects chose the lottery containing the constant value X on the majority of trials when the probabilities associated with V and X were nearly equal, i.e., when p = .4, but seemed to employ more typical weightings of probabilities and values for other probability levels. These subjects’ data were also excluded and their participation was discontinued since the model above cannot account for these strategies nor can we make valid estimates of decision criteria in the subsequent experiment if such strategies are being employed. Note that these subjects were excluded not because they used strategies that are alternative to calculating the subjective utility of the prospects. Rather, we assume that all subjects, under general circumstances, subjectively weight probabilities and values in the way described by prospect theory. The ad hoc strategies employed simply make it impossible to measure their weighting functions without increasing the complexity of the model to account for idiosyncratic strategies.