Perceptual matching and sorites: experimental study of an ancient Greek paradox

Abstract

Loosely derived from the sorites “paradox” attributed to the 4th century BCE Greek philosopher Eubulides, comparative soritical sequence of stimuli is defined as an enumeration of several stimuli, x ₁, x ₂, …, x _n , such that, when these stimuli are presented pairwise, any two of them with consecutive numbers appear “identical, ” whereas the first and the last ones do not. There is a widespread belief that stimuli of virtually any kind can be arranged in soritical sequences. This belief, often presented as a “well-known” empirical fact, is in fact based on the following piece of persuasive reasoning: an observer “obviously” should not be able to distinguish physically very similar stimuli, whereas sufficient number of very small differences eventually add up to an arbitrarily large and clearly discernible one. However, this view overlooks the well-known empirical fact that discrimination judgments are fundamentally probabilistic. One and the same pair of stimuli, including two physically identical ones, will sometimes be judged the same and sometimes different. Therefore, in order for the truth or falsity of the relation “stimulus x is perceptually matched by stimulus y” to be uniquely determined by x and y, this relation should be computed from probability distributions rather than directly observed. We show that if one uses conventional psychophysical computations of matching stimuli, soritical sequences need not exist, and that in fact there is no empirical evidence they do. In particular, we develop a mathematical theory for a procedure in which stimuli are repeatedly adjusted to match each other, and we present negative results of an experimental investigation aimed at detecting soritical sequences.

Introduction

It is a widespread belief among philosophers dealing with perceptual phenomenology, but also among psychologists, that the relation “x is perceptually matched by y” is reflexive, symmetric, but not transitive (Armstrong, 1968; Dummett, 1975; Goodman, 1951; Wright, 1975). The lack of transitivity is taken to mean that if x is matched by y in appearance, and y is matched by z, it is possible that x is not matched by z. Reflexivity (x is always matched by x) and symmetry (if x is matched by y, then y is matched by x) are considered “obvious” both by the many who argue against transitivity and by the few (Graff, 2001; Jackson & Pinkerton, 1973) who argue for it.

In psychology, the belief that perceptual matching is intransitive led to the powerful algebraic notion of semiorders. In the article introducing this notion Luce (1956) presents the following example:

Find a subject who prefers a cup of coffee with one cube of sugar to one with five cubes (this should not be difficult). Now prepare 401 cups of coffee with $(1+\frac {i}{100})x$ grams of sugar, i = 0, 1, …, 400, where x is the weight of one cube of sugar. It is evident (our emphasis, E.D. & L.P.) that he will be indifferent between cup i and cup i + 1, for any i, but by choice he is not indifferent between i = 0 and i = 400 (p. 179).

This example may be interpreted in two different ways.

Interpretation 1: Classificatory sorites

Assume the cups of coffee are being tasted one at a time and judged to be either “too sweet” or “not too sweet.” The “indifference” mentioned in the example then means that if a cup of coffee with v amount of sugar was assigned the category “not too sweet, ” then the same category will have to assigned to the cup of coffee with v + Δv amount of sugar, provided Δv is small enough; and if v was assigned the category “too sweet, ” then so will have to be v − Δv.

The truth of these statements may seem entirely “evident” (if not, many can be induced to accept them if one makes Δv even smaller than mentioned by Luce, say, a single molecule of sugar), as will probably seem the truth of the following generalization:

Classificatory Tolerance: when choosing between two categories, two stimuli that are sufficiently close physically are assigned the same category.

The terms “sorites” and “soritical” derive from the piece of reasoning attributed to a Greek philosopher Eubulides of Miletus who lived in the 4th century BCE. “Soros” in Greek means “heap.” Eubulides argued that if N grains of sand form a heap, then the same should be true for N − 1 grains of sand; but by removing from a heap one grain at a time one will necessarily end up with too few grains to form a heap — a contradiction. (There is another popular form of the paradox, known by the Greek name “falakros” (bald), in which “heap” is replaced with “full head of hair” and grains with hairs.) Sorites, including its comparative version discussed below, has been and remains one of the hotly debated issues in philosophy (see, e.g., the book of chapters edited by Beall, 2003)).

Interpretation 2: Comparative sorites

Assume now the cups of coffee are being presented in pairs, Luce’s subject sips first from one of them, then from another, and judges them to be “same” or “different” (in sweetness). In this scenario the “indifference” means the assignment of the category “same”: if Δv is sufficiently small (think again of a single molecule of sugar), the coffee cups with v and v + Δv sugar are “evidently” to be judged to be the same.

The generalization of this is the following proposition:

Comparative Tolerance: when presented pairwise, two stimuli that are sufficiently close physically are judged to match (to appear the same).

This category of sorites (sometimes also referred to as “phenomenological sorites”) may appear to be just a minor modification of the classificatory one, but they are easily shown to be fundamentally different.

Consider a sequence of coffee cups containing v ₁, v ₂, …, v _n amounts of sugar, with the following properties:

• (CL1) for each i = 1, 2, ..., n − 1, v _i and v _{i + 1} are so close physically that they have to be assigned the same category in accordance with Classificatory Tolerance;

• (CL2) the categories assigned to v ₁ and v _n are different.

This so-called classificatory soritical sequence (Dzhafarov & Dzhafarov, 2010a) is clearly a logical impossibility. As with any other logical contradiction, this indicates that some false or mutually incompatible assumptions are involved.

Consider now a similarly enumerated sequence of coffee cups but with the following properties:

• (CO1) for each i = 1, 2, ..., n − 1, v _i and v _{i + 1} are so close physically that the pair (v _i , v _{i + 1}) has to be assigned the category “they match” (or “they appear the same”), in accordance with Comparative Tolerance;

• (CO2) the category assigned to the pair (v ₁, v _n ) is “they do not match” (“they appear different”).

This is called a comparative soritical sequence (Dzhafarov & Dzhafarov, 2010b), and such a sequence is easily seen to entail no contradiction. Thus, for a computer program that prints out “they match” when two numbers differ by less than 0.01 and “they do not match” otherwise, 1, 1.004, 1.008, 1.012 is a comparative soritical sequence.

Why are CL1-CL2 so different from CO1-CO2? Because whatever the meaning of the categories used in the classificatory sorites (such as “too sweet” and “not too sweet”) their coincidence or difference is an objective relation: “too sweet”=“too sweet” and “too sweet” ≠”not too sweet.” By contrast, the category “match” can be given different meanings, and some of them (e.g., “match” means “approximately equal”) can create comparative soritical sequences. It is a theoretical question what meaning of “matching” pertains to human comparative judgments, and an empirical problem to find out whether it is of the variety that can produce soritical sequences.

The incompatible assumptions underlying classificatory sorites have been analyzed on a very high level of generality in Dzhafarov & Dzhafarov (2010a, 2012). The present paper focuses on comparative sorites. Dzhafarov & Dzhafarov (2010b, 2012) argued that although comparative soritical sequences are logically possible, it is far from being evident that human judgments of perceptual matching can lead to such sequences, provided one uses the conventional psychophysical ways of determining what is matched by what. In fact, it is far from being obvious how the transitivity is to be defined in the context of perceptual matching, and the same applies to symmetry and reflexivity.

In this paper, following a brief logical analysis of the issues involved, we present empirical evidence supporting the view that the relation “is matched by” is transitive in the context of matching by adjustment, when the participant is presented a pair of stimuli and asked to adjust one of them until she judges the two stimuli to appear the same. The experimental procedure used and its theoretical treatment extend those described in Dzhafarov and Perry (2010).

To prevent confusion, although we chose to make Luce’s example with coffee cups our departure point, we are not dealing with preferences in the sense of comparative attractiveness of perceptually distinct stimuli (gambles, purchases, election candidates, meeting locations, etc.). One may be indifferent between two cups of coffee because they taste the same to her (which is the meaning we focus on) or because she does not think one of them tastes any better than the other, even if they taste clearly different. Or she can indicate that it does not matter to her whether she gets x cents or x + 1 cents, even though she clearly understands the difference and would abandon her indifference if the purchasing power of 1 cent increased. In the analysis of preference and attractiveness the issues related to various forms of transitivity are numerous and complex (see, e.g., Regenwetter et al., 2011); Regenwetter & Davis-Stober, 2012), but they have little to do with the soritical issues. One can, as usual, find boundary cases, but we need not consider them. The belief in the ubiquitous soritical sequences that we are concerned with here is based on if not confined to clear-cut perceptual attributes, such as color, loudness, shape, or sweetness.

Comparative sorites under psychophysical scrutiny

Observation areas

One aspect of soritical situations that escapes all philosophers and most psychologists is that when x and y are compared, overall or in some property, they must clearly differ in some properties that define them as two distinct stimuli. In perceptual tasks these properties necessarily include temporal order and/or spatial locations. If one compares the shape of a drawing x to that of a drawing y, one of them may be on the left and the other on the right, or one may be presented first and the other second.

In the terminology proposed in Dzhafarov (2002, 2006) and Dzhafarov and Colonius (2006), x and y in such examples belong to two distinct observation areas (OAs). Thus, a line segment of length a presented on the left, x = a ^(left), is different from a line segment of the same length a presented on the right, y = a ^(right), so that no stimulus is ever compared with “itself.” The pair

$$x=a^{\left(left\right)}, x=a^{\left(left\right)}$$

is a single stimulus, and no question can be formulated as to whether “they” match or not. The question can only be formulated and answered with respect to

$$x=a^{\left(left\right)}, y=b^{\left(right\right)},$$

including the case when a (which can be referred to as the value of the stimulus in OA “left”) is the same as b (the value of the stimulus in OA “right”).

This view of stimulus identity (OA+value) immediately rules out, paradoxical as it may look at first, the reflexivity property of matches: however the relation “x is matched by y” is defined, x and y should belong to different OAs, whence it cannot be the case that x is matched by x. Of course, one can ask whether it is always true that

$$x=a^{\left(left\right)}\textnormal{ is matched by y=\ensuremath{a^{\left(right\right)}}, }$$

but this is a different question (to which the answer is negative — this is not always true), on a par with asking whether the shape of a drawing is preserved if one turns it upside down or colors it differently.

The symmetry property is well-defined, but it requires caution not to be misidentified. If

$$x=a^{\left(left\right)}\textnormal{ is matched by }y=b^{\left(right\right)},$$

but

$$x^{\prime}=b^{\left(left\right)}\textnormal{ is matched by }y^{\prime}=a^{\left(right\right)},$$

this is not a violation of symmetry: the stimulus pair (x, y) has no obvious relation to the stimulus pair (x′, y′). To speak about the same two stimuli but taken in another order, one should ask whether it is true that

$$y=b^{\left(right\right)}\textnormal{ is matched by }x=a^{\left(left\right)}$$

provided that we know that

$$x=a^{\left(left\right)}\textnormal{ is matched by }y=b^{\left(right\right)}.$$

The answer will depend on our definition of the matching relation and our matching procedure.

Suppose, e.g., that a robot is instructed, given a segment in one OA, to draw a 10% larger segment in the other OA. Suppose we (or the robot) decided to call the segment drawn in response to a given one a “matching segment.” Then a segment a ^(left) is matched by the segment (1.1a)^(right), but the segment (1.1a)^(right) is matched by (1.21a)^(left) rather than by a ^(left). This is an example of a non-symmetric (even antisymmetric) matching. However, if the robot is instructed, given a segment in one OA, to draw a “matching” segment in another OA so that the right segment is 1.1 times the left one, then the relation of matching is symmetric: a ^(left) is matched by b ^(right) if and only if b ^(right) is matched by a ^(left): both statements are equivalent to b = 1.1a. Note that in this last example, if a ^(left) is matched by b ^(right), then b ^(left) is not matched by a ^(right).

Transitivity requires an even greater caution not to be misidentified. In Luce’s example with cups of coffee, let $x=v_{1}^{\left (1st\right )}$ be the cup of coffee that contains v ₁ amount of sugar and is tasted first, and let $y=v_{2}^{\left (2nd\right )}$ be defined analogously. Suppose that $x=v_{1}^{\left (1st\right )}$ is matched by $y=v_{2}^{\left (2nd\right )}$. If the later is matched by some z, then z must belong to the OA “first, ” $z=v_{3}^{\left (1st\right )}$, as we cannot compare a second cup of coffee to a second cup of coffee. But then $x=v_{1}^{\left (1st\right )}$ cannot be compared to $z=v_{3}^{\left (1st\right )}$, by the same logic.

Thus, the usual “triadic” form of transitivity is not applicable if one deals with only two OAs. One can meaningfully ask, however, whether

$$x=v_{1}^{\left(1st\right)}\textnormal{ is matched by \ensuremath{y^{\prime}=v_{4}^{\left(2nd\right)}}}$$

if

$$\begin{array}{c} x=v_{1}^{\left(1st\right)}\textnormal{ is matched by }y=v_{2}^{\left(2nd\right)}, \\ y=v_{2}^{\left(2nd\right)}\textnormal{ is matched by }x^{\prime}=v_{3}^{\left(1st\right)}, \\ x^{\prime}=v_{3}^{\left(1st\right)}\textnormal{ is matched by }y^{\prime}=v_{4}^{\left(2nd\right)} \end{array}$$

(a tetradic form of transitivity). See Dzhafarov and Colonius (2006) for a detailed discussion of the notion of OAs, and numerous examples of OAs defined by properties other than spatial locations and temporal order.

With all this in mind, let us consider a comparative soritical sequence of coffee cups, x ₁, x ₂, …, x _n , with the respective amounts of sugar v ₁, v ₂, …, v _n . In the logic of comparative sorites, (x _i , x _{i + 1}) and (x _{i + 1}, x _{i + 2}) should share one and the same x _{i + 1}, because of which the OAs “first” and “second” in the sequence must alternate:

$$x_{1}=v_{1}^{\left(1st\right)}, x_{2}=v_{2}^{\left(2nd\right)}, x_{3}=v_{3}^{(1st)}, \ldots, x_{n}=v_{n}^{(2nd)},$$

the first and the last elements necessarily belonging to different OAs in order to be comparable.

We can easily see now a scenario under which a soritical sequence would not be possible. Suppose that any coffee cup x has a single, unique match y, and the matching relation is symmetric. Then, even if v ₁ < v ₂ we never get anything like v ₂ < v ₃ < … < v _n . Rather, since the matches are unique and symmetric, $x_{2}=v_{2}^{\left (2nd\right )}$ can match both $x_{1}=v_{1}^{\left (1st\right )}$ and $x_{3}=v_{3}^{(1st)}$ only if v ₁ = v ₃. Continuing in this fashion we get

$$v_{1}=v_{3}=\ldots=v_{n-1}\textnormal{ and }v_{2}=v_{4}=\ldots=v_{n}.$$

As a result

$$x=v_{1}^{\left(1st\right)}\textnormal{ is matched by \ensuremath{x_{n}=v_{n}^{(2nd)}.}}$$

Of course, Luce in his 1956 example clearly excluded the possibility that the matches are unique: he considered it evident (and encoded this in the notion of semiorders) that there is a whole range of stimulus values that are indistinguishable from a given one. But is one justified to say this is really the case? We suggest below one is not. (As we discuss in Conclusion, Luce too came to this view in later publications.)

Probabilistic judgments

The second aspect of soritical situations that escapes most philosophers (see Hardin, 1988, for an exception) is that when it comes to discrimination judgments among very similar stimuli, the judgments are not assigned to stimulus pairs deterministically. For a psychologist, of course, this is one of the basic facts about discrimination judgments: they are fundamentally probabilistic, so the relations like “x is matched by y” should be computed from probability distributions rather than directly observed in a trial.

With Luce’s coffee cups, the “evident” departure point is that if v and w (sugar amounts) are very close, the pair x = v ^(1st), y = w ^(2nd) should be assigned the category “same.” But this statement is false if this pair is sometimes judged to be “same” and sometimes “different.” This has nothing to do with how small |w − v| is, because the response “different” will be given with some nonzero probability even if w = v (as any textbook account of signal detection theory would tell us).

With responses being probabilistic, one cannot even begin formulating the soritical “paradox” in the way it is usually done. In a sequence of coffee cups x ₁, x ₂, …, x _n , if the respective amounts of sugar form an increasing sequence v ₁ < v ₂ < … < v _n , every two stimuli (x _i , x _j ) will be judged to be different with some probability. Is there anything noteworthy here when the probabilities for consecutive pairs (x _i , x _{i + 1}) are compared to that for the first-last pair (x ₁, x _n )? Not much, until one uses these probabilities to define the notion of “indifference, ” or matching, and asks whether this notion applies to (x ₁, x _n ) whenever it applies to all (x _i , x _{i + 1}).

One finds such definitions in standard psychophysical theory ((Luce & Galanter, 1963); Dzhafarov, 2002, 2006; Dzhafarov & Colonius, 2006). In the most wide-spread discrimination paradigm the response “they appear the same” is not even allowed, and the computation of what matches what is based on the choice between responses

“ v ⁽¹⁾ (in OA ₁) is greater than w ⁽²⁾ (in OA ₂)”

and

“ w ⁽²⁾ (in OA ₂) is greater than v ⁽¹⁾ (in OA ₁)”(in some respect, such as brightness, or sweetness). Assuming that the probability

$$ \gamma\left(v, w\right)=\Pr\left[y=w^{(2)}\textnormal{ is greater than }x=v^{(1)}\right]$$

(1)

is known for all v, w, let us choose some $x_{0}=v_{0}^{(1)}$ and pair it with all possible y = w ⁽²⁾. The value of y that matches x ₀ is referred to as the Point of Subjective Equality (PSE) for x ₀, and it is traditionally defined as a value of $y_{0}=w_{0}^{(2)}$ at which γ(v ₀, w ₀) = 1/2 (Fig. 1, left). Assuming that γ(v ₀, w) is increasing in w, the matching y ₀ for x ₀ is determined uniquely.

Fig. 1

Definition of matches (or Points of Subjective Equality, PSEs) for a stimulus x in two discrimination paradigms: (left) when the observer has to designate which of the two OAs contains a greater stimulus (in a specified respect), and (right) when the observer judges whether the two stimuli are the same or different (overall or in a specified respect). In the former case the PSE is the median of the psychometric function, in the latter case it is the argmin of the psychometric function. The PSEs for y are defined analogously.

This definition is not logically inevitable (no definition is), but it seems to be the only one not entirely arbitrary. One could consider as matches for x ₀ all y’s within an “uncertainty interval, ” defined, e.g., by 1/4≤γ(v ₀, w) ≤ 3/4. But it should be clear with such a definition that the endpoints are chosen arbitrarily, and that the declared matches for x ₀ will be all different, some less and some more discriminable from x ₀.

In another paradigm the pairs of stimuli are judged by choosing between the categories “same” and “different.” The probability function (1) is replaced then with

$$ \psi\left(v, w\right)=\Pr\left[y=w^{(2)}\textnormal{ is different from }x=v^{(1)}\right].$$

(2)

A matching stimulus for any chosen and fixed $x_{0}=v_{0}^{(1)}$ then is defined as $y_{0}=w_{0}^{(2)}$ for which ψ(v ₀, w ₀) is smaller than ψ(v ₀, w) for any w ≠ w ₀. Assuming that this minimum is achieved at a single point w ₀ the matching y ₀ for x ₀ is determined uniquely (Fig. 1, right).

Although no counterexamples to the uniqueness of the minimum are known, one might find it unrealistic that a function begins increasing as soon as we move away from w ₀, however small the change. (This would be an example of one’s soritical intuition, the reason soritical arguments are so compelling.) One should consider, however, that the only alternative to this “unrealisitic” view is that the function ψ(v, w) is flat on some interval of (w ₁, w ₂) including w ₀, and that then the endpoints w ₁, w ₂ would exhibit the same property one finds unrealistic for w ₀: the function begins increasing as soon as we move to the right from w ₂ or to the left from w ₁.

The paradigm we are primarily concerned with in this paper is that of matching by adjustment: a stimulus in one OA is held fixed, and the observer, by means of a controlling device, changes the stimulus in another OA until it appears to match the fixed one. The standard definition of the PSE for a fixed $x_{0}=v_{0}^{(1)}$ in this paradigm is a measure of central tendency of the distribution formed by the values of y judged to match x ₀ in individual trials (Fig. 2). The choice of this measure depends on the parameterization of the stimuli (see Dzhafarov & Perry, 2010). The assumption is that a parameterization exists under which the distribution has symmetry properties allowing one to uniquely define its center (as shown in Fig. 2).

Fig. 2

Definition of the match (PSE) for a fixed stimulus x in the matching by adjustment paradigm: a measure of central tendency for the distribution of individual adjustments of y. The stimuli are shown to have two-dimensional values, as in our experiments. The PSE for a fixed y is defined analogously.

No Sorites property

Our main contention is that with PSEs defined in accordance with standard psychophysical prescriptions, the relation “is matched by” allows for no soritical sequences: given any sequence of OAs α ₁, α ₂, …, α _n , not necessarily pairwise distinct, there are no stimuli

$$x_{1}=v_{1}^{\left(\alpha_{1}\right)}, x_{2}=v_{2}^{\left(\alpha_{2}\right)}, \ldots, x_{n}=v_{n}^{\left(\alpha_{n}\right)},$$

such that x _i is matched by x _{i + 1} for all i = 1, 2, …, n − 1, but x ₁ is not matched by x _n . We call this the No-Sorites property.

It would be a difficult task if this statement had to be separately tested for different arrangements of OAs. Fortunately, the following theorem reduces the investigation of the (im)possibility of soritical sequences to two simple special cases.

Theorem 1 (Dzhafarov & Dzhafarov, 2010b)

Any soritical sequence either contains a tetradic soritical subsequence involving two distinct OAs,

$$ x=a^{(1)}, y=b^{(2)}, x^{\prime}=c^{(1)}, y^{\prime}=d^{(2)}$$

(3)

(upper panel in Fig. 3 ), or it contains a triadic soritical subsequence involving three distinct OAs,

$$ x=a^{(1)}, y=b^{(2)}, z=c^{(3)}$$

(4)

Fig. 3

Soritical sequences whose exclusion guarantees the No-sorites property. The top panel: a bi-areal tetradic soritical sequence in which a in OA ₁ is matched by b in OA ₂ that is matched by c in OA ₁ that is matched by d in OA ₂, but a is not matched by d. The bottom panel: a tri-areal triadic soritical sequence in which a in OA ₁ is matched by b in OA ₂ that is matched by c in OA ₃, but a is not matched by c.

(lower panel in Fig. 3 ).

It follows that experimental work can be confined to demonstrating that using standard psychophysical definitions of PSEs one cannot obtain soritical sequences of the form (3) or of the form (4).

Matching by adjustment

Notation

From here on we only consider stimulus sequences involving either two or three OAs, and this allows us to simplify notation. We will use letters x, y, and z to designate stimuli in OA ₁, OA ₂, OA ₃, respectively, and we will conveniently confuse stimuli and stimulus values. Thus, x is a stimulus in OA ₁ whose value is also denoted by x; and analogously for y and z. We will tacitly assume that the values of x, y, z are real numbers or vectors of real numbers (in the experiments reported below x, y, z are two-component vectors).

We denote by F _yx (x) the y-PSE function for x, i.e., the y stimulus that matches x. In the matching by adjustment procedure, F _yx (x) is an appropriately defined center of the distribution of individual adjustments of y to match x. The PSE functions F _yz (z), F _xy (y), F _xz (z), etc. are defined and interpreted analogously.

Bi-areal “ping-pong” matching

We need now to translate the investigation of the soritical sequences depicted in Fig. 3 into experimental procedures using matching by adjustment.

Consider first bi-areal tetradic sequences. The No-Sorites property means that if one forms a chain-matched tetradic sequence

$$ \begin{array}{c} x\\ \downarrow\\ y=F_{yx}\left(x\right)\\ \downarrow\\ x^{\prime}=F_{xy}\left(F_{yx}\left(x\right)\right)\\ \downarrow\\ y^{\prime}=F_{yx}\left(F_{xy}\left(F_{yx}\left(x\right)\right)\right) \end{array}$$

(5)

then x is matched by y′, that is,

$$ F_{yx}\left(F_{xy}\left(F_{yx}\left(x\right)\right)\right)=F_{yx}\left(x\right) $$

(6)

One can, with the same two OAs, begin the tetradic sequence with y, and then the No-Sorites property implies

$$ F_{xy}\left(F_{yx}\left(F_{xy}\left(y\right)\right)\right)=F_{xy}\left(y\right) $$

(7)

If, with no loss of generality, one confines one’s attention to only those x-stimuli that can match some y-stimuli, and vice versa, i.e., if one excludes the stimuli that cannot be presented in the form F _xy (y) or F _yx (x), the No-Sorites conditions (6) and (7) are reduced to the symmetry statements: x is matched by y if and only if y is matched by x. In terms of the PSE functions,

$$ \begin{array}{c} F_{yx}\left(F_{xy}\left(y\right)\right)=y, \\ F_{xy}\left(F_{yx}\left(x\right)\right)=x. \end{array}$$

(8)

An ideal use of matching by adjustment to study bi-areal tetradic sequences would therefore have been

• 1. to obtain multiple adjustments of y to some x ₀ (about which we know that it can match some y), compute the center F _yx (x ₀) of the distribution of all these y’s, and declare F _yx (x ₀) the match for x ₀; and then

• 2. to obtain multiple adjustments of x to F _yx (x ₀), to compute the center F _xy (F _yx (x ₀)) of the distribution of all these x’s and declare it the match for (F _yx (x ₀).

The analysis then would consist in determining whether x ₀ is the same stimulus as F _xy (F _yx (x ₀)): if they are not, we have a soritical sequence (and a violation of symmetry), if they are, we do not.

This procedure, however, is not feasible: the computation of the matching stimuli F _yx (x ₀) and F _xy (F _yx (x ₀)) in it would have to be separated by considerable intervals to collect the adjustments needed to compute them. Any difference between x ₀ and F _xy (F _yx (x ₀)) obtained in such an experiment could then be attributed to the participant’s changing perceptual state.

A realistic procedure was proposed in Dzhafarov (2006) and dubbed “ping-pong” matching. In essence, it replaces a tetradic sequence (5) with a long sequence

$$x_{0}, y_{1}, x_{1}, y_{2}, x_{2}, \ldots, y_{m}, x_{m}, y_{m+1}, x_{m+1}, \ldots$$

in which each element is a single adjustment made in the corresponding trial to match the previous element. Thus, y ₁ is the true but unknown to us match for x ₀ plus some adjustment error,

$$y_{1}=\underset{true\: match\: for\: x_{0}}{\underbrace{F_{yx}\left(x_{0}\right)}}+\underset{adjustment\: error}{\underbrace{\delta y_{1}}}.$$

Similarly,

$$x_{1}=\underset{=F_{xy}\left(y_{1}\right), \: true\: match\: for\: y_{1}}{\underbrace{F_{xy}\left(F_{yx}\left(x_{0}\right)+\delta y_{1}\right)}}+\underset{adjustment\: error}{\underbrace{\delta x_{1}}},$$

$$y_{2}=\underset{=F_{yx}\left(x_{1}\right), \: true\: match\: for\: x_{1}}{\underbrace{F_{yx}\left(F_{xy}\left(F_{yx}\left(x_{0}\right)+\delta y_{1}\right)+\delta x_{1}\right)}}+\underset{adjustment\: error}{\underbrace{\delta y_{2}}},$$

and so on.

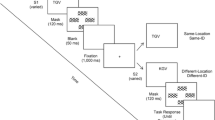
To prevent the participant from simply leaving the values of stimuli from some trial on untouched (because they already “all match each other”), in the beginning of each trial the stimulus to be adjusted is abruptly offset from its current value to some randomly chosen value, as shown in Fig. 4.

Fig. 4

A temporal profile of the adjustment paradigm for two OAs. Filled circles represent stimulus values, schematically shown as if they were unidimensional (they need not). A series of adjustments consists of several consecutive trials. In trials 1, 3, 5, … stimulus y remains fixed (at its previously established value, which, in trial 1, is the initial value), while x at the beginning of the trial is randomly offset from its previous position, as shown by the vertical dotted line, and at the end of the trial, is adjusted by the participant to a position where x appears to match y. In trials 2, 4, 6, … the procedure repeats with the x and y exchanging their roles

Typically, the values of x _i , y _{i + 1}, x _{i + 1}, y _{i + 2} would occupy a relatively small region around the initial matches (x ₁, y ₁), and within this region it is reasonable to assume that the PSE functions F _yx and F _xy can be effectively linearized (i.e., they are differentiable and the higher-order terms are negligibly small). The adjustment errors are assumed to be symmetric about zero (or, if they are multicomponent vectors, this is assumed about each component). With these assumptions in mind, we compute first-order differences

$${\Delta} x_{i}=x_{i}-x_{i-1}, {\Delta} y_{i}=y_{i}-y_{i-1}$$

for i = 2, 3, ….

It can be shown now that if (8) holds, then the first order differences Δx ₁, Δx ₂, … are stochastically independent random variables (or vectors) identically distributed about zero (componentwise); the same holds for the first order differences Δy ₁, Δy ₂, …. For details and proofs see Dzhafarov (2006) and Dzhafarov and Perry (2010). We do not recapitulate them here because they are essentially the same as in the detailed analysis presented below for the tri-areal matching.

Typical results of one experiment conducted using the procedure just described are presented in Fig. 5. This experiment is a bi-areal version of the tri-areal matching experiment described below. Under the hypothesis of No-Sorites, represented by the symmetry statement (8), the distributions of the Δx and Δy (each of which is a two-component vector) should be componentwise symmetric about zero. We see this prediction to be well corroborated by the three statistical tests reported.

Fig. 5

Histograms of the first-order differences (Δ’s) for a participant in the bi-areal ping-pong matching experiment. The stimulus values x and y here are the adjustable (by means of moving a trackball) positions of the non-central dots in the two circles (left). The positions are represented by horizontal and vertical Cartesian coordinates (measured in screen pixels, 1 px ≈ 62 sec arc) with respect to fixed central dots. Each panel shows the mean and median of the corresponding Δ (in sec arc), with the p-values for the hypotheses that the population mean and median equal zero, as well as the x ² test and the p-value for the hypothesis that the histogram is symmetric about zero. The procedural and statistical details are the same as in the experiments reported below. From Dzhafarov and Perry (2010), with permission

In another experiment from Dzhafarov and Perry (2010), the participants were asked to move a trackball to adjust certain parameters of a floral shape on the left or on the right until it matched a fixed floral shape shown on the right or on the left, respectively (Fig. 6, left panel). Typical results are shown in the right panel of Fig. 6, in a very good agreement with the No-Sorites property.

Fig. 6

Histograms of the first-order differences (Δ’s) for a participant in the bi-areal ping-pong matching of floral shapes, examples of which are shown in the left panel. A ₃ and A ₅ are amplitudes in the formula for the floral shapes in polar coordinates (r, 𝜃): r = R + A ₃ cos3𝜃 + A ₅ cos5𝜃, with |A ₃|+|A ₅|≤R = const. The rest is as in the previous figure. From Dzhafarov and Perry (2010), with permission

In yet another experiment, described in Dzhafarov (2006), the participants adjusted the length of one line segment until it matched the length of a fixed line segment. Typical results are shown in Fig. 7. Again, there is no doubt that the distributions are almost perfectly symmetrical, as they should be in accordance with the No-Sorites property.

Fig. 7

Histograms of the Δ’s for bi-areal ping-pong matching of line segments’ lengths. The upper panel shows the result of an experiment with two horizontal lines, on the left and on the right; in the lower panel the results are for a horizontal line on the left and a vertical line on the right. The abscissae are calibrated in screen pixels (1 px ≈ 55 sec arc). The p-values for the population mean and median being zero are very large, and the symmetry is obvious. From Dzhafarov (2006), with permission

Tri-areal “ping-pong” matching

Consider now the matching experiment whose temporal profile is depicted in Fig. 8,

$$ z_{0}, x_{1}, y_{1}, z_{1}, x_{2}, y_{2}, z_{2}, \ldots, x_{m}, y_{m}, z_{m}, \ldots$$

(9)

Although the stimuli are shown as unidimensional, in our experiments x, y, z are two-component vectors, and this will be assumed throughout,

$$x=\left(x^{1}, x^{2}\right), y=\left(y^{1}, y^{2}\right), z=\left(z^{1}, z^{2}\right),$$

so that x _m means $\left ({x_{m}^{1}}, {x_{m}^{2}}\right )$, etc. (To prevent notational confusion: OAs in the previous sections were designated by superscripts in parentheses, as in x = v ⁽¹⁾, whereas now the three OAs are indicated by use of x, y, and z, and their coordinates are designated by superscripts without parentheses, as in x ¹.)

Fig. 8

A temporal profile of the adjustment paradigm for three OAs. In trials 1, 4, 7, … stimuli y and z remain fixed (at their previously established values, which, in trial 1, is the initial value), while x at the beginning of the trial is randomly offset from its previous position, as shown by the vertical dotted line, and at the end of the trial, is adjusted by the participant to a position where x appears to match z. This position is referred to as “balance point.” In trials 2, 5, 8, …x and z remains fixed (at their initial or previously established values), and y is first randomly offset from its previous position (dotted vertical line) and then adjusted to the position (balance point) that appears to match x. In trials 3, 6, 9, …x and y remains fixed, and z is adjusted to match y. The balance points are numbered x ₁, x ₂, … in OA ₁, y ₁, y ₂, … in OA ₂, and z ₁, z ₂, … in OA ₃. Note the scheme: each stimulus, x, y, or z, is adjusted to match a particular stimulus (in our example, z, x, and y, respectively), and the next adjustment is made in the remaining stimulus (here, y, z, or x, respectively).

The No-Sorites property means here that, for any x, y, z,

$$ \begin{array}{c} F_{yx}\left(F_{xz}\left(z\right)\right)=F_{yz}\left(z\right), \\ F_{xz}\left(F_{zy}\left(y\right)\right)=F_{xy}\left(y\right), \\ F_{zy}\left(F_{yx}\left(x\right)\right)=F_{zx}\left(x\right). \end{array}$$

(10)

In view of the symmetry property that we consider to be empirically corroborated in the bi-areal matching experiments (see Section “Bi-areal “ping-pong” matching”), this is equivalent to

$$ \begin{array}{c} F_{zy}\left(F_{yx}\left(F_{xz}\left(z\right)\right)\right)=z, \\ F_{yx}\left(F_{xz}\left(F_{zy}\left(y\right)\right)\right)=y, \\ F_{xz}\left(F_{zy}\left(F_{yx}\left(x\right)\right)\right)=x. \end{array}$$

(11)

Our task is to test this hypothesis against a suitably chosen alternative. This cannot be a generic rejection of (11), which would be the statement that, for some z, F _zy (F _yx (F _xz (z)))≠z, allowing for an arbitrary deviation pattern from the equality. We need a more specific alternative: assuming that all the matches occur in a relatively small region V of (x, y, z), our alternative model states that

$$ \begin{array}{c} F_{zy}\left(F_{yx}\left(F_{xz}\left(z\right)\right)\right)=z+s_{z}\left(z\right), \\ F_{yx}\left(F_{xz}\left(F_{zy}\left(y\right)\right)\right)=y+s_{y}\left(y\right), \\ F_{xz}\left(F_{zy}\left(F_{yx}\left(x\right)\right)\right)=x+s_{x}\left(x\right), \end{array}$$

(12)

where in $s_{z}\left (z\right )=\left ({s_{z}^{1}}\left (z\right ), {s_{z}^{2}}\left (z\right )\right )$, $s_{y}\left (y\right )=\left ({s_{y}^{1}}\left (y\right ), {s_{y}^{2}}\left (y\right )\right )$, and $s_{x}\left (x\right )=\left ({s_{x}^{1}}\left (x\right ), {s_{x}^{2}}\left (x\right )\right )$ each of the components either exceeds some positive value or is below some negative value (i.e., within the region in question it preserves its sign and does not get arbitrarily small in absolute value) .

What follows is a simplified (in a non-essential way, merely to avoid cumbersome calculus) version of the mathematical analysis presented in Dzhafarov and Perry (2010) for two observation areas. The simplification consists in assuming that in the small region V just mentioned the PSE functions can be linearized. That is, we can put

$$ \begin{array}{c} F_{xz}\left(z\right)=a_{xz}z+\epsilon_{xz}, \\ F_{yx}\left(x\right)=a_{yx}x+\epsilon_{yx}, \\ F_{zy}\left(y\right)=a_{zy}y+\epsilon_{zy}, \end{array}$$

(13)

with all higher-order terms dropped. Note that a _xz , a _yx , a _zy here are 2×2 matrices, and all other terms are two-component vectors (columns). By simple algebra, (11) then transforms into

$$ \begin{array}{c} a_{xz}a_{zy}a_{yx}=I=\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right], \\ a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}=O=\left[\begin{array}{c} 0\\ 0 \end{array}\right]. \end{array}$$

(14)

We will call this the null-model, later to be translated into statistical null-hypotheses. The alternative model (12) states that, within the region V,

$$\begin{array}{@{}rcl@{}} \begin{array}{c} \left(a_{zy}a_{yx}a_{xz}\right)z+\left(a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}\right)-z=\left[\begin{array}{c} {s_{z}^{1}}\left(z\right)\\ {s_{z}^{2}}\left(z\right) \end{array}\right], \\ \\ \left(a_{yx}a_{xz}a_{zy}\right)y+\left(a_{yx}a_{xz}\epsilon_{zy}+a_{yx}\epsilon_{xz}+\epsilon_{yx}\right)-y=\left[\begin{array}{c} {s_{y}^{1}}\left(y\right)\\ {s_{y}^{2}}\left(y\right) \end{array}\right], \\ \\ \left(a_{xz}a_{zy}a_{yx}\right)x+\left(a_{xz}a_{zy}\epsilon_{yx}+a_{xz}\epsilon_{zy}+\epsilon_{xz}\right)-x=\left[\begin{array}{c} {s_{x}^{1}}\left(x\right)\\ {s_{x}^{2}}\left(x\right) \end{array}\right], \end{array} \end{array}$$

(15)

with each of the components on the right-hand side falling either above a positive value or below a negative one.

Our next assumption is that adjustments in the region V are made with errors normally distributed about zero. With reference to Fig. 8, when x (or y, or z) is adjusted to match z (respectively, x or y) the results are

$$ \begin{array}{c} x=\left(a_{xz}z+\epsilon_{xz}\right)+\delta x, \\ y=\left(a_{yx}x+\epsilon_{yx}\right)+\delta y, \\ z=\left(a_{zy}z+\epsilon_{zy}\right)+\delta z, \end{array}$$

(16)

where δx = (δx ¹, δx ²) and δx ¹ and δx ² are random variables (generally stochastically interdependent) normally distributed about zero; analogously for δy = (δy ¹, δy ²) and δz = (δz ¹, δz ²). The three random vectors δx, δy, δz are assumed to be stochastically independent, with distributions that, at least within the small region V, can be viewed as fixed (i.e., not changing with, respectively, x, y, and z).

It is convenient to group the trials into triples, as shown in Fig. 8, denoting the matching adjustments (balance points) achieved in trials 1, 2, 3 by x ₁, y ₁, z ₁, those achieved in trials 4, 5, 6 by x ₂, y ₂, z ₂, etc., so that x _m , y _m , z _m are the matching adjustments achieved in trials 3m − 2, 3m − 1, 3m, respectively (m = 1, 2, …). With no loss of generality, put the initial value z ₀ in OA ₃ equal to zero (in both components).

Since x ₁ in Fig. 8 is a match for z ₀ = 0, we have

$$x_{1}=\underset{constant}{\underbrace{\epsilon_{xz}}}+\underset{error}{\underbrace{\delta x_{1}}}.$$

Next, y ₁ is chosen as a match for x ₁,

$$y_{1}=a_{yx}x_{1}+\epsilon_{yx}+\delta y_{1}=\underset{constant}{\underbrace{a_{yx}\epsilon_{xz}+\epsilon_{yx}}}+\underset{error}{\underbrace{a_{yx}\delta x_{1}+\delta y_{1}}},$$

and then z ₁is chosen as a match for y ₁,

$$\begin{array}{l} z_{1}=a_{zy}y_{1}+\epsilon_{zy}+\delta z_{1}\\ =\underset{constant}{\underbrace{a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}}}+\underset{error}{\underbrace{a_{zy}a_{yx}\delta x_{1}+a_{zy}\delta y_{1}+\delta z_{1}}}. \end{array}$$

Continuing in this fashion we get (as can be formally established by induction),

$$ \begin{array}{l} x_{m}=a_{xz}\left({\sum}_{i=0}^{m-2}\left(a_{xz}a_{zy}a_{yx}\right)^{i}\right)\\ \times\left(a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}\right)+\epsilon_{xz}\\ +{\sum}_{i=1}^{m-1}\left(\begin{array}{l} \left(a_{xz}a_{zy}a_{yx}\right)^{m-i}\delta x_{i}\\ +a_{xz}a_{zy}\left(a_{yx}a_{xz}a_{zy}\right)^{m-i-1}\delta y_{i}\\ +a_{xz}\left(a_{zy}a_{yx}a_{xz}\right)^{m-i-1}\delta z_{i} \end{array}\right)+\delta x_{m}, \\ \\ y_{m}=a_{yx}a_{xz}\left({\sum}_{i=0}^{m-2}\left(a_{zy}a_{yx}a_{xz}\right)^{i}\right)\\ \times\left(a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}\right)+a_{yx}\epsilon_{xz}+\epsilon_{yx}\\ +{\sum}_{i=1}^{m-1}\left(\begin{array}{l} a_{yx}\left(a_{xz}a_{zy}a_{yx}\right)^{m-i}\delta x_{i}\\ +\left(a_{yx}a_{xz}a_{zy}\right)^{m-i}\delta y_{i}\\ +a_{yx}a_{xz}\left(a_{zy}a_{yx}a_{xz}\right)^{m-i-1}\delta z_{i} \end{array}\right)\\ +a_{yx}\delta x_{m}+\delta y_{m}, \\ \\ z_{m}=\left({\sum}_{i=0}^{m-1}\left(a_{zy}a_{yx}a_{xz}\right)^{i}\right)\left(a_{zy}a_{yx}\epsilon_{xz}+a_{zy}\epsilon_{yx}+\epsilon_{zy}\right)\\ \quad+{\sum}_{i=1}^{m}\left(\begin{array}{l} a_{zy}a_{yx}\left(a_{xz}a_{zy}a_{yx}\right)^{m-i}\delta x_{i}\\ +a_{zy}\left(a_{yx}a_{xz}a_{zy}\right)^{m-i}\delta y_{i}\\ +\left(a_{zy}a_{yx}a_{xz}\right)^{m-i}\delta z_{i} \end{array}\right). \end{array}$$

(17)

Now, in the null model (14), this transforms into

$$ \begin{array}{l} x_{m}=\epsilon_{xz}+\delta x_{m}\\ +{\sum}_{i=1}^{m-1}\left(\delta x_{i}+a_{xz}a_{zy}\delta y_{i}+a_{xz}\delta z_{i}\right), \\ \\ y_{m}=\left(a_{yx}\epsilon_{xz}+\epsilon_{yx}\right)+\left(a_{yx}\delta x_{m}+\delta y_{m}\right)\\ +{\sum}_{i=1}^{m-1}\left(a_{yx}\delta x_{i}+\delta y_{i}+a_{yx}a_{xz}\delta z_{i}\right), \\ \\ z_{m}={\sum}_{i=1}^{m}\left(a_{zy}a_{yx}\delta x_{i}+a_{zy}\delta y_{i}+\delta z_{i}\right). \end{array}$$

(18)

We are interested in the first-order differences, or “deltas, ” beginning with m = 2:

$${\Delta} x_{m}=x_{m}-x_{m-1}, \;{\Delta} y_{m}=y_{m}-y_{m-1}, \;{\Delta} z_{m}=z_{m}-z_{m-1}.$$

(Δz _m is also defined for m = 1, but we do not consider this for uniformity.) In the null model, it follows from (18) that

$$ \begin{array}{l} {\Delta} x_{m}=a_{xz}a_{zy}\delta y_{m-1}+a_{xz}\delta z_{m-1}+\delta x_{m}, \\ \\ {\Delta} y_{m}=a_{yx}a_{xz}\delta z_{m-1}+a_{yx}\delta x_{m}+\delta y_{m}, \\ \\ {\Delta} z_{m}=a_{zy}a_{yx}\delta x_{m}+a_{zy}\delta y_{m}+\delta z_{m}. \end{array}$$

(19)

It is clear that in the null model Δx ₂, Δx ₃, Δx ₄, … are independent random variables identically normally distributed about zero, and that so are Δy ₂, Δy ₃, Δy ₄, … and Δz ₂, Δz ₃, Δz ₄, …. For any m, however, the six random variables

$${\Delta} {x_{m}^{1}}, {\Delta} {x_{m}^{2}}, {\Delta} {y_{m}^{1}}, {\Delta} {y_{m}^{2}}, {\Delta} {z_{m}^{1}}, {\Delta} {z_{m}^{2}}$$

are generally interdependent stochastically.

In the alternative model, it follows from (17) and (15) that

$$ \begin{array}{l} {\Delta} x_{m}=\left[\begin{array}{c} {s_{x}^{1}}\left(x_{m-1}\right)\\ {s_{x}^{2}}\left(x_{m-1}\right) \end{array}\right]+\delta x_{m}^{*}, \\ \\ {\Delta} y_{m}=\left[\begin{array}{c} {s_{y}^{1}}\left(y_{m-1}\right)\\ {s_{y}^{2}}\left(y_{m-1}\right) \end{array}\right]+\delta y_{m}^{*}, \\ \\ {\Delta} z_{m}=\left[\begin{array}{c} {s_{z}^{1}}\left(z_{m-1}\right)\\ {s_{z}^{2}}\left(z_{m-1}\right) \end{array}\right]+\delta z_{m}^{*, } \end{array}$$

(20)

where

$$\begin{array}{c} \delta x_{m}^{*}=\textnormal{LC}_{1}\left(\begin{array}{c} \delta x_{1}, \delta y_{1}, \delta z_{1}, \\ \ldots, \\ \delta x_{m-1}, \delta y_{m-1}, \delta z_{m-1}, \\ \delta x_{m} \end{array}\right), \\ \\ \delta y_{m}^{*}=\textnormal{\ensuremath{\textnormal{LC}_{2}}}\left(\begin{array}{c} \delta x_{1}, \delta y_{1}, \delta z_{1}, \\ \ldots, \\ \delta x_{m-1}, \delta y_{m-1}, \delta z_{m-1}, \\ \delta x_{m}, \delta y_{m} \end{array}\right), \\ \\ \delta z_{m}^{*}=\textnormal{LC}_{3}\left(\begin{array}{c} \delta x_{1}, \delta y_{1}, \delta z_{1}, \\ \ldots, \\ \delta x_{m}, \delta y_{m}, \delta z_{m} \end{array}\right), \end{array}$$

with LC standing for a linear combination. The cumbersome explicit expressions need not be presented, as the only relevant property is that $\delta x_{m}^{*}, \delta y_{m}^{*}, \delta z_{m}^{*}$ are random vectors with components normally distributed about zero. That is, each component of each of the Δx _m , Δy _m , Δz _m is a random variable normally distributed about a center above some positive value or below some negative value.

Unlike in the null model, the random variables Δx ₂, Δx ₃, Δx ₄, … in the alternative model generally are not stochastically independent, and the same is true for Δy ₂, Δy ₃, Δy ₄, … and Δz ₂, Δz ₃, Δz ₄, ….

In Section Statistical hypotheses we show how the null and the alternative hypotheses translate into statistically testable propositions.

Experimental evidence

Participants

The participants were three Purdue university students, two females and one male, around 24 years of age, right-handed, with normal or corrected to normal vision. One of the female participants was a coauthor of this study (LP).

Stimuli and procedure

The stimuli were three adjacent circles whose centers contained dots forming an equilateral triangle (Fig. 9). Each circle also contained an additional, non-central dot whose position was manipulated as described below. Taking the position of the fixed central dot in each of the circles 1, 2, and 3 for (0, 0), denote the positions of the non-central dots in them (x ¹, x ²), (y ¹, y ²), and (z ¹, z ²), respectively. In each trial the participant adjusted the coordinates of the non-central dot within one of the circles by moving a trackball with her/his dominant (right) hand. The horizontal and vertical movements of the trackball controlled the horizontal (x ¹, y ¹, or z ¹) and vertical (x ², y ², or z ²) coordinates of the dots, respectively.

Fig. 9

Stimuli used in the tri-areal experiment. The stimuli were presented on a flat-screen monitor, at a distance of 90 cm from a chin rest supporting the participant’s head. At this distance 1 pixel (px) subtends 62 sec arc. The stimuli were low luminance, grayish-white circles and dots on a black background, viewed in darkness. The thickness of the circles’ circumference and the diameters of the dots were 5 px, the circles’ radii measured 70 px, and the distance between the centers of any two circles was 150 px. In each trial we recorded the adjustable position (i.e., the horizontal and vertical Cartesian coordinates) of the non-central dot in one of the circles with respect to the fixed central dot. The position of the dot in the first trial for all three circles was (27 px

Prior to trial 1, all three non-central dots were at the initial position (27 px, 16 px). There were two possible orders of adjustments, clockwise and counterclockwise, used in separate sessions. In the counterclockwise sessions, the position of the non-central dot was first adjusted in Circle 1 to match that in Circle 3, then in Circle 2 to match Circle 1, then in Circle 3 to match Circle 2, then again in Circle 1 to match Circle 3, and so on. In the clockwise sessions the position of the non-central dot was first adjusted in Circle 1 to match that in Circle 2, then in Circle 3 to match Circle 1, then in Circle 2 to match Circle 3, and then this cycle repeated many times.

In each trial where the position of the non-central dot in Circle i was adjusted to match that in Circle j, the trial began by the dot position in Circle i randomly changing in accordance with Fig. 10. The participant then adjusted this position and indicated that a match was achieved by clicking a button on the trackball device. This position was recorded and referred to as a “balance point.” It remained fixed for the next two trials. The participants were given unrestricted time to achieve a match in each trial, the successive trials being separated by 500 ms intervals.

Fig. 10

A detail of the adjustment procedure. The picture shows the first quadrant of the circle during a trial in which the position of the non-central dot in this circle was adjusted to match the constant position in another circle. Denoting the position of the dot prior to the trial by (r, ϕ), in polar coordinates, the trial began by abruptly changing this position to one randomly chosen according to the uniform distribution over the rectangle [𝜃 − π/18, 𝜃 + π/18] × [r − 0.1⋅r, r + 0.1⋅r] (the shaded box around the dot)

All experimental sessions started with 21 practice trials (7 matching adjustments in each circle), which were not recorded. After the practice trials, a recorded counterclockwise or clockwise session was conducted, consisting of 219 trials (73 match adjustments in each circle). Midway through the main session the participant was instructed to take a short break before completing the second half of the trials. After this break, the experiment resumed with the dot in the position established in the trial previous to the break.

In total, ten sessions were completed for each of the clockwise and counterclockwise orders of matching, with the orders alternating. This resulted in 730 balance points, and 720 first-order differences for each of the two orders.

Statistical hypotheses

The two models of Section “Matching by adjustment”, the null and the alternative ones, were translated into three pairs of opposing statistical hypotheses. The range of possible values for each of the deltas

$${\Delta} {x_{m}^{1}}, {\Delta} {x_{m}^{2}}, {\Delta} {y_{m}^{1}}, {\Delta} {y_{m}^{2}}, {\Delta} {z_{m}^{1}}, {\Delta} {z_{m}^{2}}$$

were subdivided into the following intervals:

$$\begin{array}{ll} \textnormal{interval }-9: & {\Delta}<-8\textnormal{ px}\\ \textnormal{interval }-8: & {\Delta}=-8\textnormal{ px}\\ {\ldots} & \ldots\\ \textnormal{interval }-1: & {\Delta}=-1\textnormal{ px}\\ \textnormal{interval }\quad0: & {\Delta}=0\textnormal{ px}\\ \textnormal{interval }+1: & {\Delta}=1\textnormal{ px}\\ {\ldots} & \ldots\\ \textnormal{interval }+8: & {\Delta}=8\textnormal{ px}\\ \textnormal{interval }+9: & {\Delta}>8\textnormal{ px}. \end{array}$$

The non-marginal intervals are all of 1 pixel width, with 1 px ≈1 min arc. The range of ±8 pixels was chosen as a reasonable idea of a small range, as well as for the comparability with the results in Dzhafarov and Perry (2010). The occurrences above and below this range were infrequent and sparsely distributed.

The hypotheses are as follows.

(H1₀): The histogram of Δ’s is symmetric around zero, versus the alternate hypothesis, H1 _A , that this is not so. We used the x ² test statistic

$$ {\sum}_{i=1}^{9}\frac{\left[\#({\Delta}\in interval\: i)-\#({\Delta}\in interval-i)\right]{}^{2}}{\#({\Delta}\in interval\: i)+\#({\Delta}\in interval\:-i)},$$

(21)

where # designates number of occurrences. With the assumptions we made about adjustment errors, and given that this statistic is computed from 720 data points per condition, one can easily check that under the null hypothesis H1₀ the test statistic has the x ²-distribution with df = 9. The distribution under H1 _A is not known due to the lack of independence in successive realizations of the Δ’s, but for approximate power computations one might assume the noncentral x ²-distribution with df = 9.

(H2₀): The population median of Δ is zero, i.e.

$$\text{Pr}[{\Delta}>0]+\frac{\text{Pr}[{\Delta}=0]}{2}=1/2,$$

versus the alternate hypothesis, H2 _A , that this probability is not 1/2. We used the x ² test statistic

$$ \frac{\left[(\#({\Delta}>0)-\#({\Delta}<0)\right]{}^{2}}{\#(\textnormal{all }{\Delta})}.$$

(22)

The distributions of this test statistic under H2₀ and H2 _A are the same as above, but with df = 1.

(H3₀): The expected value of Δ is zero, versus the alternate hypothesis, H3 _A , that it is not zero. We used the standard t-statistic

$$ \frac{\textnormal{Mean }{\Delta}}{\textnormal{Standard Error of }{\Delta}}.$$

(23)

Given that this statistic is based on 720 data points in each condition, under H3₀ it is standard normally distributed, and under H3 _A (assuming the unknown stochastic interdependence in successive realizations of the Δ’s can be ignored), it is normally distributed with some nonzero mean and unit variance.

Results

The findings are presented in Figs. 11-22.

Fig. 11

Histograms of the first-order differences (Δ’s) for the clockwise order of matching, horizontal coordinate, participant LP. The insets show the time series of the matching adjustments from which the Δ’s were computed. Each panel shows the mean and median of the corresponding Δ (in sec arc), with the p-values for the hypotheses that the population mean and median equal zero, as well as the x ²(df = 9) value and the p-value for the symmetry test

Fig. 12

Histograms of Δ’s for the counterclockwise order of matching, horizontal coordinate, participant LP. The rest is same as in Fig. 11

Fig. 13

Histograms of Δ’s for the clockwise order of matching, vertical coordinate, participant LP. The rest is same as in Fig. 11

Fig. 14

Histograms of Δ’s for the counterclockwise order of matching, vertical coordinate, participant LP. The rest is same as in Fig. 11

Fig. 15

Histograms of Δ’s for the clockwise order of matching, horizontal coordinate, participant P1. The rest is same as in Fig. 11

Fig. 16

Histograms of Δ’s for the counterclockwise order of matching, horizontal coordinate, participant P1. The rest is same as in Fig. 11

Fig. 17

Histograms of Δ’s for the clockwise order of matching, vertical coordinate, participant P1. The rest is same as in Fig. 11

Fig. 18

Histograms of Δ’s for the counterclockwise order of matching, vertical coordinate, participant P1. The rest is same as in Fig. 11

Fig. 19

Histograms of Δ’s for the clockwise order of matching, horizontal coordinate, participant P2. The rest is same as in Fig. 11

Fig. 20

Histograms of Δ’s for the counterclockwise order of matching, horizontal coordinate, participant P2. The rest is same as in Fig. 11

Fig. 21

Histograms of Δ’s for the clockwise order of matching, vertical coordinate participant P2. The rest is same as in Fig. 11

Fig. 22

Histograms of Δ’s for the counterclockwise order of matching, vertical coordinate, participant P2. The rest is same as in Fig. 11

Each figure presents the histograms of first-order differences (Δ’s) for the three circles. The bins of the histograms are one pixel wide throughout (≈1 min arc). The insets show the time series of the matching adjustments from which the Δ’s are computed. The abscissa of the inset shows successive trials in which adjustments are made. For Circle 1 these are trials 1, 4, 7, …. For Circle 2 and Circle 3 it depends on the adjustment order: in the clockwise condition, for Circle 2 the trials are 3, 6, 9, …, and for Circle 3 they are 2, 5, 8, …; in the counterclockwise condition it is the other way around. The ordinate axis of the inset corresponds to the abscissa of the histogram.

With three circles, two adjustment orders (clockwise and counterclockwise), and two Cartesian coordinates, there are twelve conditions for each participant. Each panel presents the observed mean, median and the results of the three tests described in Section “Statistical hypotheses” performed on the data for the corresponding condition.

Discussion

Let us first inspect individual tests. The observed means in all cases are very small: most of them are just a few sec arc. For comparison, one pixel on the screen subtends about 1 min arc, which is an average value for minimum separabile in normal vision. So the values well below 1 min arc may be difficult to interpret. No mean is statistically significant at α = 0.05.

The hypothesis that the Δ ’s are symmetrically distributed about zero is also retained in all cases at α = 0.05.

All observed medians are zero, but in two cases (Circle 3 in Figs. 15 and 16) the hypothesis that the population median is zero produces 0.01 < p≤0.05. These small p-values, however, should be expected by pure chance under multiple testing (the p-values are uniformly distributed under a correct null hypothesis). Equivalently, the rejection of the null hypothesis at α = 0.05 in these two cases can be safely atttributed to the high overall Type I error rate.

The Type I error rate is based on multiple statistical tests whose test statistics are not all stochastically independent. In fact, all 18 statistical tests performed on a given participant for a given matching order (3 tests × 3 OAs × 2 coordinates) should be considered interdependent in some unknown way. The test results for six applications of these 18 tests to different participants × matching orders are treated as stochastically independent.

This leads us to the following formula for the overall Type I error at any chosen alpha level per test (in our case, 0.01 or 0.05):

$$ 1-(1-\alpha)^{6}\leq\Pr\left[\textnormal{Type I error}\right]\leq1-(1-\alpha\times18)^{6}.$$

(24)

The computations are summarized in Table 1.

At the significance level 0.05 the overall Type I error is between 0.26 – 1.00, and there are only two observed rejections out of 108 tests. The probability of two or more rejections at the given range of Type I errors is almost 1. At the α = 0.01 there are no observed rejections out of 108 tests (the overall p-value therefore is precisely 1).

The alternative model tells us that the Δ’s in (20) are normally distributed about the corresponding s-components, but we do not know their standard deviation values or stochastic interdependence pattern. To crudely evaluate the power of our tests, we assume that successive realizations of the Δ’s can be treated as if they were independent (see Section “Statistical hypotheses”), and that the population standard deviations are close to those empirically observed. The distributions of the test statistics under our alternative hypotheses H1 _A , H2 _A , H3 _A then can be approximated by noncentral counterparts of the two χ ²-distributions and t-distribution, with the same degrees of freedom as in the null hypotheses.

The computations are presented in Fig. 23. As the observed standard deviations all were well between 1 and 4 min arc values, the power was computed for population sigmas in the same range. We see that in all cases the effect size values approaching minimum separabile (in our case, 1 px) would be detected with almost 100% percent assurance. For smaller effect sizes, assuming they can be given plausible interpretation, the power of the t-test is the highest and the power of the χ ²-test for symmetry is the lowest; but even at one-half of a pixel size, the detection probability by the least powerful of the three tests is more than 50%.

Fig. 23

Power curves for the three tests reported in Figs. 11-22. Effect size is one of the $s_{\cdot }^{i}\left (\cdot \right )$ in (20), chosen in accordance with the OA and matching order, and σ is population standard deviaiton

Conclusion

It is not possible to definitively prove that soritical sequences do not exist. One can always entertain the possibility that s _z (z), s _y (y), s _x (x) in (12) and (15) are nonzero, but they are so small or change sign so often that we cannot detect them even with sample sizes as large as in our experiments. Our claim, however, is not that soritical sequences cannot exist in principle, but rather that we do not have any empirical evidence that they exist.

The widespread belief in the existence and even ubiquity of soritical sequences, so often declared to be “well-known” and “evident, ” is not grounded in empirical knowledge. Rather it is a metaphysical belief of enormous psychological persuasiveness: big and clumsy systems like ourselves should not be able to detect microscopic differences, while, of course, microscopic changes can be accumulated into arbitrarily large and hence perfectly detectable ones.

This metaphysical belief crumbles under psychophysical scrutiny. Any pair of similar stimuli, including identical ones, leads to judgements “same” and “different” with some probabilities. One cannot therefore simply observe that a stimulus on the right matches the stimulus on the left. One has to compute this matching relation from the probability distributions of judgments or adjustments. When these computations are done properly (which prominently includes not overlooking that stimuli being compared have to belong to distinct OAs, such as left and right, constituting part of their identity), soritical arguments lose their persuasiveness. Then it comes as no surprise if we in fact find no soritical sequences empirically.

Although this paper is about matching by adjustment, the other two main psychophysical paradigms mentioned in Section “Probabilistic judgments” (Fig. 1) provide additional support. In the pairwise comparison paradigm with “greater than” versus“less than” judgments, the computations of matches is based on the probabilities (1). With two fixed OAs, in our simplified notation,

$$\gamma\left(x, y\right)=\Pr\left[y\textnormal{ is greater than }x\right].$$

It is assumed, in agreement with all available experiments, that the psychometric function y↦γ(x ₀, y), for a fixed x ₀, continuously increases with y from a value below 1/2 to a value above 1/2. Then the match y ₀ for x ₀ is uniquely defined by the condition γ(x ₀, y ₀) = 1/2. By the same argument, for the continuously decreasing function x↦γ(x, y ₀), the match $x^{\prime }_{0}$ for y ₀ is uniquely defined by the same condition $\gamma \left (x^{\prime }_{0}, y_{0}\right )=1/2$. From this we conclude that the relation “is matched by” here is symmetric: $x^{\prime }_{0}=x_{0}$. Dzhafarov (2003) called this symmetry Regular Mediality. In the bi-areal comparisons, as we know from section “Bi-areal “ping-pong” matching”, this symmetry is all one needs to ensure that no soritical sequences are possible: refer to (8) in relation to (6) and (7). In the pairwise comparison paradigm with “same” versus “different” judgments, the computations of matches is based on the probabilities (2), or, in the simplified notation,

$$\psi\left(x, y\right)=\Pr\left[x\textnormal{ and \ensuremath{y}are different}\right].$$

It is assumed, in agreement with all available observations, that the psychometric function y↦ψ(x ₀, y) achieves its global minimum at some point y ₀, and this point is taken to be the match for x ₀. The value $x^{\prime }_{0}$ at which the psychometric function y↦ψ(x, y ₀) achieves its minimum is analogously taken to match y ₀. If $x_{0}^{\prime }$ and x ₀ coincide, then we again have symmetry with the ensuing No-Sorites property. The equality $x^{\prime }_{0}=x_{0}$ (called Regular Minimality in Dzhafarov, 2002) is not guaranteed mathematically, but there is no empirical evidence that it is violated (see Section “Empirical Evidence” in Dzhafarov & Colonius, 2006, for a review).

Since we have made a prominent use of the example with coffee cups taken from Luce (1956), it should be mentioned that in later publications Luce abandoned the interpretation of semiorders in terms of intervals of stimuli that are pairwise indistinguishable. In Luce and Galanter (1963) semiorders are treated as intervals of stimuli between two fixed levels of the psychometric functions γ(x, y): for an arbitrarily chosen probability π between 1/2 and 1, x and y are “ π-indifferent” (or perhaps an observer is “ π-indifferent” to their difference) if 1−π≤γ(x, y)≤π. If now two “ π-indifferent” stimuli were to be declared matching each other, soritical sequences would indeed be easily constructed, both of the tetradic bi-areal variety and the triadic tri-areal one. To present this construction as evidence for soritical sequences, however, would be analogous to declaring numerical equality intransitive because one can also define approximate numerical equality.

Summarizing, all available empirical evidence is in a good agreement with the matching relation being irreflexive (because the stimuli being compared must belong to different OAs), symmetric, and transitive, provided these properties are understood as discussed in Section “Observation areas”.

In fact, to prevent possible misformulations of these properties, it is more convenient to replace them with a more clearly defined notion of a well-matched regular stimulus space (Dzhafarov & Dzhafarov, 2010b). This definition deals with an arbitrary set of OAs, not necessarily just two or three of them. Imagine, e.g., an experiment in which point-size flashes can appear pairwise in any two distinct locations on a screen, and the task is to compare or match their brightness: the set of the OAs in this case is infinite (or very large if physical constraints, such as pixelation, are considered).

The well-matched regular spaces of stimuli are defined by the following two properties: (Well-Matchedness) For any three OAs, not necessarily distinct, and any stimulus a ⁽¹⁾ (in OA ₁), one can choose b ⁽²⁾ and c ⁽³⁾ (in the remaining two OAs) such that any two of these stimuli match each other. (Regularity) If two stimuli a ⁽¹⁾ and b ⁽¹⁾ (in the same OA) are matched by a third stimulus, c ⁽²⁾ (in another OA), then a = b.An obvious consequence of regular well-matchedness is the No-Sorites property.

In more general conceptual settings, the equality a = b in the Regularity condition is to be replaced with the equivalence of a ⁽¹⁾ and b ⁽²⁾. Equivalence of two stimuli in the same OA is defined by their matching or mismatching any other stimulus together. This notion, as distinct from that of matching, was proposed by Goodman (1951). The equivalence of stimuli is an important notion in some applications, e.g., color comparisons, where each color can be represented by an infinity of metamorphic spectra. However, in tasks like the ones discussed in this paper (comparison of dot locations, or segments, or shapes), the equivalence under the conventional parameterizations simply means identity. Moreover, stimuli in well-matched regular space can always be transformed to make equivalent stimuli identically labeled. See Dzhafarov and Colonius (2006) for discussion and examples.

Table 1 Summary of the results presented in Fig. 11-22. Overall Type I error is calculated by (24)

The correct way to view the definition of regular well-matchedness is to consider it a desideratum for a well-constructed notion of matching relation in a specific experimental paradigm. Our claim definitely is not that any definition of matching relation should comply with the two conditions above: one can always construct a definition that will not (e.g., Luce and Galanter’s 1963“π-indifference”). The claim is rather that (a) these conditions are applicable to the conventional psychophysical computations of Points of Subjective Equality; and therefore (b) they can serve as guiding principle for constructing new definitions.