Skip to main content
SpringerLink
Log in

Analysis of dynamic behavior of vehicle shimmy system with stochastic clearance

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract—

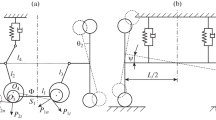
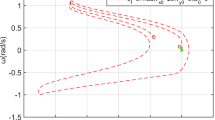
Based on a 6 degrees-of-freedom dynamic model of vehicle shimmy system with consideration of stochastic clearance, the influence of clearance joints on the dynamic characteristic of the vehicle shimmy system is analyzed. The global analysis is also carried out to discuss the influence of vehicle speeds and clearance parameters on the dynamic behavior of the vehicle shimmy system. Moreover, the influence of stochastic clearance on the shimmy amplitude is investigated by means of the Monte Carlo method. According to the analysis of the amplitude distribution of the vehicle shimmy system, a reliability index is introduced to evaluate the system stability. The results show that with the increase of contact stiffness, the large amplitude domain can be reduced even with a relatively large mean value of stochastic clearance, which is an economical and effective way to attenuate vehicle shimmy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.

Similar content being viewed by others

REFERENCES

  1. S. Beregi, D. Takacs, and G. Stepan, “Bifurcation analysis of wheel shimmy with non-smooth effects and time delay in the tyre-ground contact,” Nonlin. Dyn. 98 (1), 841–858 (2019). https://doi.org/10.1007/s11071-019-05123-1

    Article  Google Scholar 

  2. S. H. Ran, I. J. M. Besselink, and H. Nijmeijer, “Application of nonlinear tyre models to analyse shimmy,” Veh. Syst. Dyn. 52 (Sup1), 387–404 (2014). https://doi.org/10.1080/00423114.2014.901542

  3. J. W. Lu, J. Y. Xin, A. F. Vakakis, and L. A. Bergman, “Influences of system parameters on dynamic behavior of the vehicle shimmy system with clearance in steering linkage,” J. Vib. Control. 21 (2), 359–370 (2015). https://doi.org/10.1177/1077546313483786

    Article  Google Scholar 

  4. H. B. Pacejka, Tire and Vehicle Dynamics, 2nd Edition (Butterworth and Heinemann, Oxford, 2006).

    Google Scholar 

  5. V. Ph. Zhuravlev, “On plane self-excited vibrations of a cantilever suspended wheel,” Mech. Solids. 47 (2), 155–159 (2012). https://doi.org/10.3103/S002565441202001X

    Article  ADS  Google Scholar 

  6. D. G. Wei, Y. J. Zhu, T. Jiang, et al., “Multiple limit cycles shimmy of the dual-front axle steering heavy truck based on bisectional road,” J. Comput. Nonlin. Dyn. 14 (5), 051005 (2019). https://doi.org/10.1115/1.4042294

    Article  Google Scholar 

  7. P. Flores and H. M. Lankarani, “Dynamic response of multibody systems with multiple clearance joints,” J. Comput. Nonlin. Dyn. 7 (3), 13–18 (2012). https://doi.org/https://doi.org/10.1115/1.4005927

    Article  Google Scholar 

  8. B. Zhou, N. Zhang, and L. Sun, “Study on steering wheel shimmy with clearance of kingpin,” Int. J. Veh. Noise Vib. 9 (3), 234–247 (2013). https://doi.org/10.1504/IJVNV.2013.055808

    Article  Google Scholar 

  9. P. Eret, J. Kennedy, and G. J. Bennett, “Effect of noise reducing components on nose landing gear stability for a mid-size aircraft coupled with vortex shedding and freeplay,” J. Sound Vib. 354, 91–103 (2015). https://doi.org/10.1016/j.jsv.2015.06.022

    Article  ADS  Google Scholar 

  10. C. Howcroft, M. Lowenberg, S. Neild, et al., “Shimmy of an aircraft main landing gear with geometric coupling and mechanical freeplay,” J. Comput. Nonlin. Dyn. 10 (5), 05–011 (2015). https://doi.org/10.1115/1.4028852

  11. D. M. Zhao, Q. C. Zhang, and Y. Tan, “Random flutter of a 2-DOF nonlinear airfoil in pitchand plunge with freeplay in pitch,” Nonlin. Dyn. 58, 643–654 (2009). https://doi.org/10.1007/s11071-009-9507-y

    Article  MATH  Google Scholar 

  12. J. Sinou, J. Didier, and B. Faverjon, “Stochastic nonlinear response of a flexible rotor with local nonlinearities,” Int. J. Nonlin. Mech. 74, 92–99 (2015). https://doi.org/10.1016/j.ijnonlinmec.2015.03.012

    Article  Google Scholar 

  13. A. Hajiloo and W. F. Xie, “The stochastic robust model predictive control of shimmy vibration in aircraft landing gears,” Asian J. Control. 17 (2), 476–485 (2015). https://doi.org/10.1002/asjc.1048

    Article  MathSciNet  MATH  Google Scholar 

  14. T. Li, J. B. Chen, and J. Li, “Point group identification algorithm in dynamic response analysis of nonlinear stochastic systems,” J. Sound Vib. 366, 248–263 (2016). https://doi.org/10.1016/j.jsv.2015.12.007

    Article  ADS  Google Scholar 

  15. J. Z. Jiang, J. W. Lu, and H. Zhang, “Dynamic behavior analysis of vehicle shimmy system with consideration of dynamics coupling between movement pairs with clearance,” J. Vib. Shock. 35 (1), 66–69 (2016).

    Google Scholar 

  16. M. Sebèsa, H. Cholleta, J. B. Ayassea, and L. Chevalier, “A multi-Hertzian contact model considering plasticity,” Wear 314 (1–2), 118–124 (2014). https://doi.org/10.1016/j.wear.2013.11.036

  17. F. Luchi and R. A. Krohling, “Differential evolution and Nelder-Mead for constrained non-linear integer optimization problems,” Procedia Comput. Sci. 55, 668–677 (2015). https://doi.org/10.1016/j.procs.2015.07.071

    Article  Google Scholar 

  18. J. Rang, “Improved traditional Rosenbrock-Wanner methods for stiff ODEs and DAEs,” J. Comput. Appl. Math. 286, 128–144 (2015). https://doi.org/10.1016/j.cam.2015.03.010

    Article  MathSciNet  MATH  Google Scholar 

  19. S. Golchi and D. A. Campbell, “Sequentially constrained Monte Carlo,” Comput. Stat. Data Anal. 97, 98–113 (2016). https://doi.org/10.1016/j.csda.2015.11.013

    Article  MathSciNet  MATH  Google Scholar 

  20. P. Massimiliano, L. Bruno, and B. Antonio, “Experimental contact pattern analysis for a gear-rack system,” Meccanica 47 (1), 51–61 (2012). https://doi.org/10.1007/s11012-010-9415-8

    Article  MATH  Google Scholar 

  21. J. R. Babu and A. Asha, “Modeling in selective assembly with symmetrical interval-based Taguchi loss function for minimizing assembly loss and clearance variation,” Int. J. Manuf. Technol. Manag. 29 (5–6), 288–308 (2015). https://doi.org/10.1504/IJMTM.2015.071223

Download references

Funding

This research was supported by Program for New Century Excellent Talents in University under grant no. NCET-10-0358, the National Natural Science Foundation of China under Grant Agreement No [51875150] and Innovation Project of New Energy Vehicle and Intelligent Connected Vehicle of Anhui Province.

Author information

Authors and Affiliations

  1. School of Automotive and Transportation Engineering, Hefei University of Technology, 230009, Hefei, China

    Heng Wei, Jianwei Lu & Junzhao Jiang

Authors
  1. Heng Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianwei Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junzhao Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junzhao Jiang.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, H., Lu, J. & Jiang, J. Analysis of dynamic behavior of vehicle shimmy system with stochastic clearance. Mech. Solids 57, 139–148 (2022). https://doi.org/10.3103/S0025654422010058

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654422010058

Keywords:

Search

Navigation