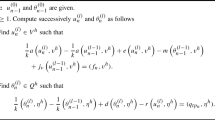Abstract
A quasi-static coupled contact problem of thermoelasticity that deals with a sliding frictional contact with taking into account the frictional heating is considered. Exact solutions of the problem are constructed in the form of Laplace convolutions, after calculating which the solution has been written in form of infinite series over eigenvalues of problem. The study of these eigenvalues in relation to three dimensionless parameters of the problem is carried out. Based on the analysis of the solutions obtained, it is possible to distinguish the domains of stable and unstable solutions in the space of dimensionless parameters. The properties of the obtained solutions are studied in relation to the dimensional and dimensionless parameters of the problem. Within the framework of the main research problem, partial problems of monitoring the sliding parameters as well as problems of controlling contact parameters in order to avoid thermoelastic instability are formulated and solved.
Similar content being viewed by others
References
M. A. Biot, “Thermoelasticity and Irreversible Thermodynamics,” J. Appl. Phys. 27 (3), 240–253 (1956).
H. Deresiewicz, “Solution of the Equations of Thermoelasticity,” in Proc. 3rd Nat. Congr. Appl. Mech. ASME (Providence: Brown University, 1958), pp. 287–291.
P. Chadwick, “Thermoelasticity. The dynamical theory,” in Progress in Solid Mechanics, Ed. by I. N. Sneddon and R. Hill (North-Holland Publishing Company, Amsterdam, 1960), pp. 263–328.
B. A. Boley and J. H. Weiner, Theory of Thermal Stresses (Wiley, N.Y., London, 1960; Mir, Moscow, 1964).
W. Nowacki, Dynamic Problems of Thermoelasticity (PWN, Warszawa, 1966; Mir, Moscow, 1970).
R. E. Nickell and J. L. Sackman, “Approximate Solutions in Linear, Coupled Thermoelasticity,” J. Appl. Mech. 35 (2), 255–266 (1968).
J. T. Oden, “Finite Element Analysis of Nonlinear Problems in the Dynamical Theory of Coupled Thermoelasticity,” Nucl. Eng. Des. 10 (4), 465–475 (1969).
J. H. Prevost and D. Tao, “Finite Element Analysis of Dynamic Coupled Thermoelasticity Problems with Relaxation Times,” J. Appl. Mech. 50 (4a), 817–822 (1983).
J.P. Carter and J. R. Booker, “Finite Element Analysis of Coupled Thermoelasticity,” Comp. Struct. 31 (1), 73–80 (1989).
A. Hacquin, P. Montmitonnet, and J.P. Guillerault, “A Steady State Thermo–Elastoviscoplastic Finite Element Model Of Rolling With Coupled Thermo–Elastic Roll Deformation,” J. Mat. Proc. Tech. 60 (1), 109–116 (1996).
M. Repka and A. Lion, “Simulation of the Coupled Thermo-Elastic Behavior of Constrained Films in Differential Scanning Calorimetry Using the Finite Element Method,” Thermochim. Acta. 581, 62–69 (2014).
V. F. Gribanov and N. G. Panichkin, Coupled and Dinamic Problems of the Thermal Elasticity (Mashinostroenie, Moscow, 1984) [in Russian].
N.V. Slonovskii, “On Thermoelastic Stability with Sliding Friction,” Zh. Prik. Math. Mekh. 33 (1), 124–127 (1969) [J. Appl. Math. Mech. (Engl. Trans) 33 (1), 124–127 (1969)].
T. A. Dow and R. A. Burton, “Thermoelastic Instabilities of Sliding Contact in the Absence of Wear,” Wear 19 (3), 315–328 (1972).
T. A. Dow and R. A. Burton, “The Role of Wear in the Initiation of Thermoelastic Instabilities of Rubbing Contact,” J. Lubr. Technol. 95 (1), 71–75 (1973).
T. A. Dow, “Thermoelastic Effects in a Thin Sliding Seal—a Review,” Wear 59, 31–52 (1980).
R. A. Burton, V. Nerlikar, and S. R. Kilaparti, “Thermoelastic Instability in a Eeal-Like Configuration,” Wear 24 (2), 177–188 (1973).
C.P. Chen and R. A. Burton, “Thermoelastic Effects in Brushes with High Current and High Sliding Speeds,” Wear. 5 (1) 277–288 (1979).
R. A. Burton and M. D. Bryant, “Transient Thermal Deformation in Electrical Brushes,” J. Therm. Stress. 4 (2), 223–235 (1981).
L. Afferrante and M. Ciavarella, “A Note on Thermoelastodynamic Instability (TEDI) for a 1D Elastic Layer: Force Control,” Int. J. Sol. Struct. 44 (5), 1380–1390 (2007).
L. Afferrante and M. Ciavarella, “Thermo-Elastic Dynamic Instability (TEDI) in Frictional Sliding of Two Elastic Half-Spaces,” J. Mech. Phys. Solids. 55 (4), 744–764 (2007).
V. B. Zelentsov, B. I. Mitrin, A. S. Vasiliev, and S. S. Volkov, “Thermoelastodynamic Instability of Contact Problem Solution for Coating Considering Frictional Heat Generation,” Vestn. Donsk. Gos. Tekh. Univ., 14 (4), 17–29 (2014).
V. B. Zelentsov, B. I. Mitrin, and S. M. Aizikovich, “Dynamic and Quasi-Static Instability of Sliding Thermoelastic Frictional Contact,” Trenie Iznos 37 (3), 280–289 (2016) J. Frict.Wear. 37 (3), 213–220 (2016)
A. D. Kovalenko, Thermoelasticity (Vyshcha Shkola, Kiev, 1975) [in Russian].
V. A. Ditkin and A.P. Prudnikov, Operational Calculus (Vysshaya Shkola, Moscow, 1975) [in Russian].
Yu.A. Brychkov and A.P. Prudnikov, Intergral Transforms of Generalized Functions (Nauka, Moscow, 1977) [in Russian].
E. C. Titchmarsh, The Theory of Functions (Oxford University Press, 1932; Nauka, Moscow, 1980).
P.P. Zabreiko, A. I. Koshelev, M.A. Kransnosel’skii, et al., Integral Equations (Nauka, Moscow, 1968) [in Russian].
Acknowledgments
This study was financially supported by the Ministry of Science and Higher Education of the Russian Federation (governmental assignment 9.1481.2017/4.6) and Russian Foundation for Basic Research (grants 16-07-00929-a, 17-07-01376-a).
Author information
Authors and Affiliations
Corresponding author
Additional information
Russian Text © The Author(s), 2019, published in Izvestiya Akademii Nauk, Mekhanika Tverdogo Tela, 2019, No. 1, pp. 72–87.
About this article
Cite this article
Zelentsov, V.B., Mitrin, B.I. Thermoelastic Instability in the Quasi-Static Coupled Thermoelasticity Problem Dealt with the Sliding Contact with Frictional Heating. Mech. Solids 54, 58–69 (2019). https://doi.org/10.3103/S0025654419010059
Received:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0025654419010059