Skip to main content
SpringerLink
Log in

On the local convergence of Kung-Traub’s two-point method and its dynamics

  • Published:
Applications of Mathematics Aims and scope Submit manuscript

Abstract

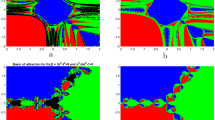
In this paper, the local convergence analysis of the family of Kung-Traub’s two-point method and the convergence ball for this family are obtained and the dynamical behavior on quadratic and cubic polynomials of the resulting family is studied. We use complex dynamic tools to analyze their stability and show that the region of stable members of this family is vast. Numerical examples are also presented in this study. This method is compared with several widely used solution methods by solving test problems from different chemical engineering application areas, e.g. Planck’s radiation law problem, natch distillation at infinite reflux, van der Waal’s equation, air gap between two parallel plates and flow in a smooth pipe, in order to check the applicability and effectiveness of our proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. Ahmad, F. Soleymani, F. Khaksar Haghani, S. Serra-Capizzano: Higher order derivative-free iterative methods with and without memory for systems of nonlinear equations. Appl. Math. Comput. 314 (2017), 199–211.

    MathSciNet  MATH  Google Scholar 

  2. F. Ahmad, E. Tohidi, M. Z. Ullah, J. A. Carrasco: Higher order multi-step Jarratt-like method for solving systems of nonlinear equations: Application to PDEs and ODEs. Comput. Math. Appl. 70 (2015), 624–636.

    MathSciNet  Google Scholar 

  3. S. Amat, S. Busquier, S. Plaza: Review of some iterative root-finding methods from a dynamical point of view. Sci., Ser. A, Math. Sci. (N.S.) 10 (2004), 3–35.

    MathSciNet  MATH  Google Scholar 

  4. S. Amat, S. Busquier, S. Plaza: A construction of attracting periodic orbits for some classical third-order iterative methods. J. Comput. Appl. Math. 189 (2006), 22–33.

    MathSciNet  MATH  Google Scholar 

  5. I. K. Argyros: A unifying local-semilocal convergence analysis and applications for two-point Newton-like methods in Banach space. J. Math. Anal. Appl. 298 (2004), 374–397.

    MathSciNet  MATH  Google Scholar 

  6. I. K. Argyros: Computational Theory of Iterative Methods. Studies in Computational Mathematics 15. Elservier, Amsterdam, 2007.

    Google Scholar 

  7. I. K. Argyros: Convergence and Applications of Newton-Type Iterations. Springer, New York, 2008.

    MATH  Google Scholar 

  8. I. K. Argyros, A. Cordero, Á. A. Magreñán, J. R. Torregrosa: Third-degree anomalies of Traub’s method. J. Comput. Appl. Math. 309 (2017), 511–521.

    MathSciNet  MATH  Google Scholar 

  9. I. K. Argyros, S. Hilout: An improved local convergence analysis for a two-step Steffensen-type method. J. Comput. Appl. Math. 30 (2009), 237–245.

    MathSciNet  MATH  Google Scholar 

  10. I. K. Argyros, S. Hilout: Computational Methods in Nonlinear Analysis: Efficient Algorithms, Fixed Point Theory and Applications. World Scientific, Hackensack, 2013.

    MATH  Google Scholar 

  11. I. K. Argyros, M. Kansal, V. Kanwar: Ball convergence for two optimal eighth-order methods using only the first derivative. Int. J. Appl. Comput. Math. 3 (2017), 2291–2301.

    MathSciNet  MATH  Google Scholar 

  12. I. K. Argyros, M. Kansal, V. Kanwar, S. Bajaj: Higher-order derivative-free families of Chebyshev-Halley type methods with or without memory for solving nonlinear equations. Appl. Math. Comput. 315 (2017), 224–245.

    MathSciNet  MATH  Google Scholar 

  13. I. K. Argyros, Á. A. Magrenán, L. Orcos: Local convergence and a chemical application of derivative free root finding methods with one parameter based on interpolation. J. Math. Chem. 54 (2016), 1404–1416.

    MathSciNet  MATH  Google Scholar 

  14. I. K. Argyros, H. Ren: On an improved local convergence analysis for the Secant method. Numer. Algorithms 52 (2009), 257–271.

    MathSciNet  MATH  Google Scholar 

  15. A. F. Beardon: Iteration of Rational Functions: Complex Analytic Dynamical Systems. Graduate Texts in Mathematics 132. Springer, New York, 1991.

    Google Scholar 

  16. R. Behl, A. Cordero, S. S. Motsa, J. R. Torregrosa: An eighth-order family of optimal multiple root finders and its dynamics. Numer. Algorithms 77 (2018), 1249–1272.

    MathSciNet  MATH  Google Scholar 

  17. F. I. Chicharro, A. Cordero, J. R. Torregrosa: Drawing dynamical and parameters planes of iterative families and methods. Sci. World J. 2013 (2013), Article ID 780153, 11 pages.

  18. C. Chun: Some variants of King’s fourth-order family of methods for nonlinear equations. Appl. Math. Comput. 290 (2007), 57–62.

    MathSciNet  MATH  Google Scholar 

  19. C. Chun, M. Y. Lee, B. Neta, J. Dzunic: On optimal fourth-order iterative methods free from second derivative and their dynamics. Appl. Math. Comput. 218 (2012), 6427–6438.

    MathSciNet  MATH  Google Scholar 

  20. A. Cordero, L. Feng, Á. A. Magreñán, J. R. Torregrosa: A new fourth-order family for solving nonlinear problems and its dynamics. J. Math. Chem. 53 (2015), 893–910.

    MathSciNet  MATH  Google Scholar 

  21. A. Cordero, J. García-Maimó, J. R. Torregrosa, M. P. Vassileva, P. Vindel: Chaos in King’s iterative family. Appl. Math. Lett. 26 (2013), 842–848.

    MathSciNet  MATH  Google Scholar 

  22. A. Cordero, L. Guasp, J. R. Torregrosa: CMMSE 2017: On two classes of fourth- and seventh-order vectorial methods with stable behavior. J. Math. Chem. 56 (2018), 1902–1923.

    MathSciNet  MATH  Google Scholar 

  23. A. Cordero, T. Lotfi, K. Mahdiani, J. R. Torregrosa: Two optimal general classes of iterative methods with eighth-order. Acta Appl. Math. 134 (2014), 61–74.

    MathSciNet  MATH  Google Scholar 

  24. A. Cordero, T. Lotfi, K. Mahdiani, J. R. Torregrosa: A stable family with high order of convergence for solving nonlinear equations. Appl. Math. Comput. 254 (2015), 240–251.

    MathSciNet  MATH  Google Scholar 

  25. A. Cordero, T. Lotfi, J. R. Torregrosa, P. Assari, K. Mahdiani: Some new bi-accelerator two-point methods for solving nonlinear equations. Comput. Appl. Math. 35 (2016), 251–267.

    MathSciNet  MATH  Google Scholar 

  26. A. Cordero, F. Soleymani, J. R. Torregrosa, F. Khaksar Haghani: A family of Kurchatovtype methods and its stability. Appl. Math. Comput. 294 (2017), 264–279.

    MathSciNet  MATH  Google Scholar 

  27. P. Fatou: Sur les équations fonctionelles. Bull. Soc. Math. Fr. 47 (1919), 161–271. (In French.)

    MathSciNet  MATH  Google Scholar 

  28. P. Fatou: Sur les équations fonctionelles. Bull. Soc. Math. Fr. 48 (1920), 208–314. (In French.)

    MathSciNet  Google Scholar 

  29. J. M. Gutiérrez, M. A. Hernández, N. Romero: Dynamics of a new family of iterative processes for quadratic polynomials. J. Comput. Appl. Math. 233 (2010), 2688–2695.

    MathSciNet  MATH  Google Scholar 

  30. P. Jarratt: Some fourth order multipoint iterative methods for solving equations. Math. Comput. 20 (1966), 434–437.

    MATH  Google Scholar 

  31. L. O. Jay: A note on Q-order of convergence. BIT 41 (2001), 422–429.

    MathSciNet  MATH  Google Scholar 

  32. G. Julia: Mémoire sur l’itération des fonctions rationnelles. Journ. de Math. 8 (1918), 47–245. (In French.)

    MATH  Google Scholar 

  33. R. F. King: A family of fourth order methods for nonlinear equations. SIAM J. Numer. Anal. 10 (1973), 876–879.

    MathSciNet  MATH  Google Scholar 

  34. H. T. Kung, J. F. Traub: Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 21 (1974), 643–651.

    MathSciNet  MATH  Google Scholar 

  35. D. Li, P. Liu, J. Kou: An improvement of Chebyshev-Halley methods free from second derivative. Appl. Math. Comput. 235 (2014), 221–225.

    MathSciNet  MATH  Google Scholar 

  36. T. Lotfi, Á. A. Magreñán, K. Mahdiani, J. Javier Rainer: A variant of Steffensen-King’s type family with accelerated sixth-order convergence and high efficiency index: Dynamic study and approach. Appl. Math. Comput. 252 (2015), 347–353.

    MathSciNet  MATH  Google Scholar 

  37. T. Lotfi, F. Soleymani, M. Ghorbanzadeh, P. Assari: On the construction of some tri-parametric iterative methods with memory. Numer. Algorithms 70 (2015), 835–845.

    MathSciNet  MATH  Google Scholar 

  38. Á. A. Magreñán: Different anomalies in a Jarratt family of iterative root-finding methods. Appl. Math. Comput. 233 (2014), 29–38.

    MathSciNet  MATH  Google Scholar 

  39. A. K. Maheshwari: A fourth order iterative method for solving nonlinear equations. Appl. Math. Comput. 211 (2009), 383–391.

    MathSciNet  MATH  Google Scholar 

  40. B. Neta, C. Chun, M. Scott: Basins of attraction for optimal eighth order methods to find simple roots of nonlinear equations. Appl. Math. Comput. 227 (2014), 567–592.

    MathSciNet  MATH  Google Scholar 

  41. A. M. Ostrowski: Solutions of Equations and System of Equations. Pure and Applied Mathematics 9. Academic Press, New York, 1966.

    Google Scholar 

  42. M. S. Petković, B. Neta, L. D. Petković, J. Džunić: Multipoint Methods for Solving Nonlinear Equations. Elsevier, Amsterdam, 2013.

    MATH  Google Scholar 

  43. S. Qasim, Z. Ali, F. Ahmad, S. Serra-Capizzano, M. Z. Ullah, A. Mahmood: Solving systems of nonlinear equations when the nonlinearity is expensive. Comput. Math. Appl. 71 (2016), 1464–1478.

    MathSciNet  Google Scholar 

  44. W. C. Rheinboldt: An adaptive continuation process for solving systems of nonlinear equations. Mathematical Models and Numerical Methods. Banach Center Publications 3. Banach Center, Warsaw, 1978, pp. 129–142.

    Google Scholar 

  45. G. E. Roberts, J. Horgan-Kobelski: Newton’s versus Halley’s method: A dynamical systems approach. Int. J. Bifurcation Chaos Appl. Sci. Eng. 14 (2004), 3459–3475.

    MathSciNet  MATH  Google Scholar 

  46. M. Scott, B. Neta, C. Chun: Basin attractors for various methods. Appl. Math. Comput. 218 (2011), 2584–2599.

    MathSciNet  MATH  Google Scholar 

  47. M. Shacham: An improved memory method for the solution of a nonlinear equation. Chem. Eng. Sci. 44 (1989), 1495–1501.

    Google Scholar 

  48. F. Soleymani, S. Karimi Vanani: Optimal Steffensen-type methods with eighth order of convergence. Comput. Math. Appl. 62 (2011), 4619–4626.

    MathSciNet  MATH  Google Scholar 

  49. F. Soleymani, T. Lotfi, E. Tavakoli, F. Khaksar Haghani: Several iterative methods with memory using self-accelerators. Appl. Math. Comput. 254 (2015), 452–458.

    MathSciNet  MATH  Google Scholar 

  50. J. F. Traub: Iterative Methods for the Solution of Equations. Series in Automatic Computation. Prentice-Hall, Englewood Cliffs, 1964.

    MATH  Google Scholar 

  51. H. Veiseh, T. Lotfi, T. Allahviranloo: A study on the local convergence and dynamics of the two-step and derivative-free Kung-Traub’s method. Comput. Appl. Math. 37 (2018), 2428–2444.

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors would like to express their deep gratitude to the editors and referees for their valuable suggestions which led us to a better presentation of this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, College of Basic Sciences, Hamedan Branch, Islamic Azad University, Imam Khomeini Bldv, 6518115743, Hamedan, Iran

    Parandoosh Ataei Delshad & Taher Lotfi

Authors
  1. Parandoosh Ataei Delshad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Taher Lotfi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Taher Lotfi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ataei Delshad, P., Lotfi, T. On the local convergence of Kung-Traub’s two-point method and its dynamics. Appl Math 65, 379–406 (2020). https://doi.org/10.21136/AM.2020.0322-18

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.21136/AM.2020.0322-18

Keywords

MSC 2020

Search

Navigation