Skip to main content
SpringerLink
Log in

Role of the pore-size distribution function on water flow in unsaturated soil

孔径分布函数对水分在非饱和土体中迁移的作用

  • Published:
Journal of Zhejiang University SCIENCE A Aims and scope Submit manuscript

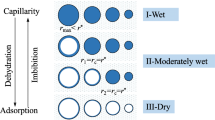
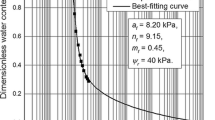
Abstract

The hydraulic properties of soil (i.e. soil-water characteristic curve (SWCC) and coefficient of permeability) govern the moisture flow in it. Previous research has indicated that the hydraulic properties of soil are dependent on its pore-size distribution. An improved capillary model is now proposed to explain the concept of the pore-size distribution in soil and its relationship to SWCC. A new model, the “valve model”, is also proposed as the explanation for water flow in unsaturated soil. The pore-size distribution function is incorporated in the “valve model” and is used to calculate the relative coefficient of permeability for unsaturated soil. In this paper, the role of the pore-size distribution function in the estimation of SWCC and the permeability function are explained. Equations are proposed for estimating the pore-size distribution function from the experimental data of relative coefficient of permeability. The results from the proposed equations agree with the experimental data from laboratory measurement and published data.

中文概要

目的

了解孔径分布函数对水分在非饱和土体中迁移的 影响,并提出相关数学模型,量化非饱和土体在 不同吸力作用下的渗透系数。

创新点

从孔径分布函数出发探讨土体的工程性质,以日 常生活中所用的阀门模型解释非饱和土体在不 同吸力作用下的渗透系数。提出采用非饱和土渗 透系数的实验数据,间接估算土体的孔径分布函 数。

方法

从物理模型推导相关数学公式,并用实验结果对 数学公式进行验证。

结论

孔径分布函数主导非饱和土的渗透系数;孔径分 布函数是连接土体两大水力特性(包括水土特征 曲线和渗流方程)的桥梁。孔径分布函数对水分 在土体中迁移的作用可以用日常生活中使用的 阀门模型简单描述。基于阀门模型,土体的孔径 分布函数也可以由土体的非饱和渗透系数的相 关实验数据间接估算得到。

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Brooks RH, Corey AT 1964. Hydraulic Properties of Porous Media. Colorado State University, Fort Collins, CO, USA.

    Google Scholar 

  • Childs EC, Collis-George N, 1950. The permeability of porous materials. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 201(1066): 392–405. https://doi.org/10.1098/rspa.1950.0068

    Google Scholar 

  • Fredlund DG, Rahardjo H, 1993. Soil Mechanics for Unsaturated Soils. Wiley, New York, USA.

    Google Scholar 

  • Fredlund DG, Xing AQ, 1994. Equations for the soil–water characteristic curve. Canadian Geotechnical Journal, 31(3): 521–532. https://doi.org/10.1139/t94–061

    Google Scholar 

  • Fredlund DG, Xing AQ, Huang SY, 1994. Predicting the permeability function for unsaturated soils using the soilwater characteristic curve. Canadian Geotechnical Journal, 31(4): 533–546. https://doi.org/10.1139/t94–062

    Google Scholar 

  • Fredlund DG, Rahardjo H, Fredlund MD, 2012. Unsaturated Soil Mechanics in Engineering Practice. Wiley, New York, USA.

    Google Scholar 

  • Gardner WR, 1958. Mathematics of isothermal water conduction in unsaturated soils. Proceedings of the 37th Annual Meeting of the Highway Research Board.

    Google Scholar 

  • Goh SG, 2012. Hysteresis Effects on Mechanical Behavior of Unsaturated Soil. PhD Thesis, Nanyang Technological University, Singapore.

    Google Scholar 

  • Goh SG, Rahardjo H, Leong EC, 2015. Modification of triaxial apparatus for permeability measurement of unsaturated soils. Soils and Foundations, 55(1): 63–73. https://doi.org/10.1016/j.sandf.2014.12.005

    Google Scholar 

  • Kosugi K, 1994. Three–parameter lognormal distribution model for soil water retention. Water Resources Research, 30(4): 891–901. https://doi.org/10.1029/93WR02931

    Google Scholar 

  • Kunze RJ, Uehara G, Graham K, 1968. Factors important in the calculation of hydraulic conductivity. Soil Science Society of America Journal, 32(6): 760–765. https://doi.org/10.2136/sssaj1968.03615995003200060020x

    Google Scholar 

  • Lambe TW, 1955. The permeability of compacted fine–grained soils. Symposium on Permeability of Soils, ASTM.

    Google Scholar 

  • Leong EC, Rahardjo H, 1997. Review of soil–water characteristic curve equations. Journal of Geotechnical and Geoenvironmental Engineering, 123(12): 1106–1117. https://doi.org/10.1061/(asce)1090–0241(1997)123:12(1106)

    Google Scholar 

  • Marshall TJ, 1958. A relation between permeability and size distribution of pores. Journal of Soil Science, 9(1): 1–8. https://doi.org/10.1111/j.1365–2389.1958.tb01892.x

    Google Scholar 

  • Millington RJ, Quirk JP, 1961. Permeability of porous media. Nature, 183(4658): 387–388. https://doi.org/10.1038/183387a0

    Google Scholar 

  • Mualem Y, 1976. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12(3): 513–522. https://doi.org/10.1029/WR012i003p00513

    Google Scholar 

  • Pedroso DM, Sheng DC, Zhao JD, 2009. The concept of reference curves for constitutive modelling in soil mechanics. Computers and Geotechnics, 36(1–2): 149–165. https://doi.org/10.1016/j.compgeo.2008.01.009

    Google Scholar 

  • Prion, 2016. Anisotropy in Hydraulic Properties of Unsaturated Soils. PhD Thesis, Nanyang Technological University, Singapore.

    Google Scholar 

  • Rahimi A, Rahardjo H, 2016. New approach to improve soil–water characteristic curve to reduce variation in estimation of unsaturated permeability function. Canadian Geotechnical Journal, 53(4): 717–725. https://doi.org/10.1139/cgj–2015–0199

    Google Scholar 

  • Reinson JR, Fredlund DG, Wilson GW, et al., 2005. Unsaturated flow in coarse porous media. Canadian Geotechnical Journal, 42(1): 252–262. https://doi.org/10.1139/t04–070

    Google Scholar 

  • Richards LA, 1952. Water conducting and retaining properties of soils in relation to irrigation. Proceedings of International Symposium on Desert Research, p.523–546.

    Google Scholar 

  • Tuli A, Hopmans JW, 2004. Effect of degree of fluid saturation on transport coefficients in disturbed soils. European Journal of Soil Science, 55(1): 147–164. https://doi.org/10.1046/j.1365–2389.2002.00493.x–i1

    Google Scholar 

  • Tuli A, Hopmans JW, Rolston DE, et al., 2005. Comparison of air and water permeability between disturbed and undisturbed soils. Soil Science Society of America Journal, 69(5): 1361–1371. https://doi.org/10.2136/sssaj2004.0332

    Google Scholar 

  • van Genuchten MT, 1980. A closed–form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5): 892–898. https://doi.org/10.2136/sssaj1980.03615995004400050002x

    Google Scholar 

  • Vogel HJ, 1997. Morphological determination of pore connectivity as a function of pore size using serial sections. European Journal of Soil Science, 48(3): 365–377. https://doi.org/10.1111/j.1365–2389.1997.tb00203.x

    Google Scholar 

  • Wildenschild D, Hopmans JW, Rivers ML, et al., 2005. Quantitative analysis of flow processes in a sand using synchrotron–based X–ray microtomography. Vadose Zone Journal, 4(1): 112–126. https://doi.org/10.2136/vzj2005.0112

    Google Scholar 

  • Zapata CE, 1999. Uncertainty in Soil–water Characteristic Curve and Impacts on Unsaturated Shear Strength Predictions. PhD Thesis, Arizona State University, Tempe, USA.

    Google Scholar 

  • Zhai Q, Rahardjo H, 2012a. Determination of soil–water characteristic curve variables. Computers and Geotechnics, 42:37–43. https://doi.org/10.1016/j.compgeo.2011.11.010

    Google Scholar 

  • Zhai Q, Rahardjo H, 2012b. Reply to the discussion by Bellia et al. on “Determination of soil–water characteristic curve variables”. Computers and Geotechnics, 45:151–152. https://doi.org/10.1016/j.compgeo.2012.03.008

    Google Scholar 

  • Zhai Q, Rahardjo H, 2015. Estimation of permeability function from the soil–water characteristic curve. Engineering Geology, 199:148–156. https://doi.org/10.1016/j.enggeo.2015.11.001

    Google Scholar 

  • Zhai Q, Rahardjo H, Satyanaga A, et al., 2017a. Effect of bimodal soil–water characteristic curve on the estimation of permeability function. Engineering Geology, 230:142–151. https://doi.org/10.1016/j.enggeo.2017.09.025

    Google Scholar 

  • Zhai Q, Rahardjo H, Satyanaga A, 2017b. Effects of residual suction and residual water content on the estimation of permeability function. Geoderma, 303:165–177. https://doi.org/10.1016/j.geoderma.2017.05.019

    Google Scholar 

  • Zhai Q, Rahardjo H, Satyanaga A, 2017c. Uncertainty in the estimation of hysteresis of soil–water characteristic curve. Environmental Geotechnics, in press. https://doi.org/10.1680/jenge.17.00008

    Google Scholar 

  • Zhai Q, Rahardjo H, Satyanaga A, 2018a. Estimation of the air permeability function from the soil–water characteristic curve. Canadian Geotechnical Journal, in press. https://doi.org/10.1139/cgj–2017–0579

    Google Scholar 

  • Zhai Q, Rahardjo H, Satyanaga A, 2018b. A pore–size distribution function based method for estimation of hydraulic properties of sandy soils. Engineering Geology, 246: 288–292. https://doi.org/10.1016/j.enggeo.2018.09.031

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. The State Key Laboratory for Reinforcement Concrete and Prestress Reinforcement Concrete Structures of the Ministry of Education, Southeast University, Nanjing, 210096, China

    Qian Zhai & Guo-liang Dai

  2. School of Civil and Environmental Engineering, Nanyang Technological University, Singapore, 639798, Singapore

    Qian Zhai, Harianto Rahardjo, Alfrendo Satyanaga &  Priono

Authors
  1. Qian Zhai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Harianto Rahardjo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alfrendo Satyanaga
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Priono
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guo-liang Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Harianto Rahardjo.

Additional information

Project supported by the National Natural Science Foundation of China (No. 51878160), the National Key Research and Development Program of China (No. 2017YFC00703408), and the Fundamental Research Funds for the Central Universities (No. 2242018K41046), China

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhai, Q., Rahardjo, H., Satyanaga, A. et al. Role of the pore-size distribution function on water flow in unsaturated soil. J. Zhejiang Univ. - Sci. A 20, 10–20 (2019). https://doi.org/10.1631/jzus.A1800347

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1631/jzus.A1800347

Key words

CLC number

关键词

Search

Navigation