Introduction

The name-giving mineral cheralite (CaTh(PO4)2, formerly known as brabantite) is a naturally occurring mineral that has first been described by Rose [1]. It belongs to the monazite group and is formed by complete substitution of the rare-earth elements in LnPO4 (Ln = La-Gd) with Ca2+ and Th4+ via the substitution mechanism:

$$2[{\text{Ln}}^{{3 + }} {\text{PO}}_{4} ] + {\text{Ca}}^{{2 + }} + {\text{Th}}^{{4 + }} \rightleftarrows [{\text{Ca}}^{{2 + }} {\text{Th}}^{{4 + }} \left( {{\text{PO}}_{4} } \right)_{2} ] + 2{\text{Ln}}^{{3 + }} .$$

Cheralite-type materials with other divalent cations, e.g. CdTh(PO4)2, SrTh(PO4)2 and PbTh(PO4)2 have been reported [2]. Phosphates with the monazite structure have been proposed as suitable waste forms for the conditioning of actinide-rich waste streams based on a number of advantageous characteristics including high chemical flexibility, low critical temperatures, high leaching stability, and favourable sintering properties (e.g. Schlenz et al. [3]). Natural cheralite minerals that have been able to withstand self-irradiation for millions of years, demonstrating their exceptional radiation tolerance [4].

The monazite structure is composed of alternating edge-sharing LnO9 polyhedra and PO4 tetrahedra forming infinite chains along the [001] direction. The polyhedra can be described as an equatorial pentagon formed by five oxygen atoms, interpenetrated by a tetrahedron constituted by four oxygen atoms which are part of the PO4 tetrahedra [5]. Monazite crystallises in the monoclinic space group P21/n.

Several authors have described the synthesis of monazite-cheralite solid solutions. While a few studies have been published about different hydrothermal syntheses of monazite-cheralite solid solutions [6, 7] the most widely used method in literature is a solid state reaction (e.g. [8,9,10,11]). To our knowledge, only Montel et al. [2] have made use of a precipitation method for the synthesis of cheralite so far.

In this study, two monazite-cheralite solid solutions were prepared via a co-precipitation route involving a rhabdophane precursor, which is especially suited for aqueous, actinide-rich waste streams. In contrast to solid state methods, this synthesis route mostly avoids the use of solids thus reducing possibilities for dust formation. Additionally, the temperatures required for the conversion of rhabdophane to monazite (500–800 °C, according to Jonasson et al. [12]) have been reported to be considerably lower than those needed for solid state synthesis (≥ 1200 °C) [8, 9] hence improving the feasibility for large-scale application. Working at ambient pressure also facilitates future upscaling and reduces hazards connected to pressurized vessels.

Single crystals of cheralite were grown using a high temperature flux method. They were analysed with X-ray diffraction to investigate the structural distortion of cheralite with respect to monazite as described by Raison et al. [9]. Deviations from the ideal behaviour can have significant impact on the physicochemical properties of a solid solution and should therefore be studied in detail.

Materials and methods

Powder synthesis

Both monazite-cheralite solid solutions La1-xCax/2Thx/2PO4 and Gd1-xCax/2Thx/2PO4 were produced via a co-precipitation route following the literature protocol by Heuser et al. [13]. The respective metal nitrates were mixed with phosphoric acid and citric acid, which was used as a complexing agent. Commercial La(NO3)3⋅6H2O (Merck, 99%), Gd(NO3)3⋅6H2O (Sigma-Aldrich, 99.9%), Ca(NO3)2 (Alfa Aesar, 97%), Th(NO3)4 (Th-232), citric acid (Merck, 99%) and phosphoric acid (Sigma-Aldrich, 99,8%) were used in the synthesis. All nitrates were dried overnight at 90 °C. Precipitation of rhabdophane was induced by increasing the pH with 12.5 % ammonia solution. The precipitate was washed six times with ultrapure water. After a drying step, the powders were pre-calcined at 550 °C for 3 h and calcined at 1200 °C for 4 h under Ar atmosphere to remove crystal water and obtain monazite. The applied temperature is well below the decomposition temperature of cheralite, which was reported to be 1400 °C [8] and high enough to ensure complete and rapid phase conversion. All synthesis steps were performed in a glovebox.

Single crystal synthesis

Cheralite single crystals were synthesized by a high-temperature solution (flux) method as described by Cherniak et al. [14]. The molar ratio of the flux components was 75:25:2 ≡ MoO3:Li2CO3:Ca0.5Th0.5PO4 or La0.5Ca0.25Th0.25PO4 assuming the full conversion of CaO, La2O3, ThO2 and NH4H2PO4 to cheralite during single crystal growth. Commercial MoO3 (Acros, 99.5%), Li2CO3 (Merck, 99%), CaO (Thermo Scientific, 99.95%), La2O3 (Alfa Aesar, 99.9%) and NH4H2PO4 (Bernd Kraft, 99%) were used in the synthesis while ThO2 was obtained by precipitation from the Th(NO3)4 (Th-232) stock solution using 12.5% ammonia solution. The precipitate was washed with Milli-Q water and calcined at 600 °C for 4 h. The homogeneity of the flux solution was ensured by holding it at 1350 °C for more than 12 h for complete dissolution of the metal oxides. Subsequent cooling to 870 °C with a cooling rate of 2 °C/h enabled single crystal growth. Afterwards, the solutions were removed from the furnace and cooled in air. The grown single crystals were extracted by dissolving the flux in water in an ultrasonic bath. All experiments were carried out in closed platinum crucibles.

XRD

Powder X-ray diffraction patterns were obtained with a Rigaku MiniFlex 600 diffractometer equipped with a one-dimensional Rigaku D/teX Ultra Si strip detector, using a Cu-tube and a Ni-filter at a tube voltage of 40 kV and a current of 15 mA. The measurements were performed at ambient temperatures in the 2θ-range of 5°–90°. Structure refinements were performed using the Rietveld-method [15] within the Topas Academic software (Version 7.20) [16]. During the refinements, a ten coefficient Chebyshev-polynomial was used to describe the background. Crystallite size, lattice parameters, and fractional coordinates of all sites were allowed to vary. To account for the lower scattering power of oxygen and phosphorous compared to lanthanides, soft distance restraints for the P – O bonds were implemented at a value of 1.52 Å. The LaPO4 structure published by Hirsch et al. [17] was used as starting model for the structural refinement. It should be noted that the estimated standard deviations of refined parameters are systematically underestimated in Rietveld refinements due to local correlations [18].

Single crystals were placed in mineral oil, cut, mounted on a 100 µm MiTeGen Dual Thickness MicroMount and located in the temperature-controlled N2 gas flow at 100 K from Oxford instruments. The data was collected on a Bruker D8 VENTURE diffractometer equipped with a Photon II 7 array detector and micro focus Mo Kα radiation (λ = 0.71073 Å) with mirror optics monochromator. The computer programs SMART [19] and SAINT [20] were used for data collection in ϕ- and ω-scan modes and data processing, respectively. Absorption correction was performed using SADABS [21]. All structures were solved using ShelXT [22] and all atoms were refined with a Gauss-Newton model in Olex2 v1.3-ac4 [23]. Due to the close spatial proximity, the thermal displacement parameters of lanthanum, calcium and thorium atoms were refined isotropically to reduce correlation effects.

Results and discussion

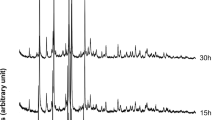
The synthesis of both solid solutions La1-xCax/2Thx/2PO4 and Gd1-xCax/2Thx/2PO4 was successful over the complete range of substitutions as shown in Figure 1. Rietveld analysis confirmed the monazite structure in all samples. Powders with a substitution level of x ≥ 0.5 of both solid solutions were found to contain minute amounts of thorium phosphate-diphosphate Th4(PO4)4P2O7 (β-TPD), which itself has been proposed as a waste matrix due to its resistance to aqueous corrosion [24].

Fig. 1
figure 1

Powder diffractograms of the solid solutions of Ca0.5Th0.5PO4 with LaPO4 (left) and GdPO4 (right). Reflections originating from β-TPD are marked in the cheralite diffractogram

Full size image

The evolution of the lattice parameters within the solid solutions is displayed in Fig. 2a for La1-xCax/2Thx/2PO4 and Fig. 2b for Gd1-xCax/2Thx/2PO4. The unit cell parameters of both solid solutions vary almost linearly according to Vegard’s law resulting in a small excess volume (VE/VVegard < 0.3 %, compare Table I in the SI). The excess volume is an indicator for non-ideal mixing of the cations due to different oxidation states and ionic radii. Excess volumes of similar magnitude have been reported by Konings et al. [10] for the solid solutions LnPO4-Ca0.5Th0.5PO4 with Ln = La and Ce.

Fig. 2
figure 2

Evolution of the lattice parameters of the solid solutions of Ca0.5Th0.5PO4 with a LaPO4 and b GdPO4. Unit cell parameters change almost linearly and agree well with data published from different synthesis routes. Error bars are smaller than the symbols used

Full size image

No significant differences can be observed between the evolution of lattice parameters in this study and other studies using hydrothermal [6] and solid state methods [10] apart from somewhat larger values for the monoclinic angle β. This highlights the equivalence of the synthesis procedures with respect to the product quality.

In available literature, it has been established that the lattice parameters of monazite compounds containing any two Ln(III) cations (La-Gd) change linearly with the average effective ionic radius [25]. This behaviour is not reproduced by the two newly synthesised solid solutions, as shown in Fig. 3. A deviation of the unit cell volume of cheralite from this linear relationship has first been described by Raison et al. [9], who attributed this observation to distortions in the PO4 tetrahedra, despite the general finding that the tetrahedra are intrinsically more rigid in the monazite structure than the LnO9 polyhedra [26]. In a subsequent publication, Raison et al. [27] revoked this conclusion based on neutron diffraction measurements. These indicated a small displacement of the calcium and thorium atoms from the central position of the LnO9 polyhedron, thus imitating a cation with a radius of 1.29 Å rather than the average effective ionic radius of 1.135 Å calculated from the ionic radii given in Shannon [28].

Fig. 3
figure 3

Evolution of the unit cell parameters of monazite solid solutions as a function of their effective ionic radius according to Shannon [28]. The cheralite solid solutions deviate from the linear behaviour of the solid solutions containing only trivalent Ln

Full size image

Single crystal structure refinements on crystals of the compositions Ca0.5Th0.5PO4 and La0.5Ca0.25Th0.25PO4 confirm the observations made by Raison et al. [27] (see Table II in the SI for refinement parameters). The distances between the cation positions were found to be dTh-Ca = 0.204(7) Å in Ca0.5Th0.5PO4 and dTh-Ca = 0.160(14) Å, dLa-Ca = 0.198(14) Å and dLa-Th = 0.127(5) Å in La0.5Ca0.25Th0.25PO4. As described by Raison et al. [27], the thorium ions occupy a position closer to the centre of the polyhedron compared to calcium as evidenced by the more homogeneous bond length distribution (2.337(8)-2.863(8) Å for Th-O vs 2.412(10)-3.065(10) Å for Ca-O, see Table 1). In the case of La0.5Ca0.25Th0.25PO4, the La-O-bonds show the smallest spread (2.339(5)-2.830(5) Å) followed by Th-O (2.374(5)-2.943(6) Å) and Ca-O (2.384(10)-3.003(14) Å). It is interesting to note that the La-O bond distance distribution is still significantly larger than that in the LaPO4 structure (2.459(8)-2.827(8) Å, [17]). This, however, is biased by the spatial averaging of the environment of Th, La, and Ca, respectively: In the final refinement, for each oxygen position one set of fractional coordinates (x, y, z) was refined, which is probably not an adequate description of the local, disordered situation. However, no significant distortion of the PO4 tetrahedra was observed in any of the refinements. A tilt of the tetrahedra with respect to the polyhedra in dependence of the central cation was checked for in corresponding refinements allowing for 2 (or 3, respectively) sets of fractional coordinates for each oxygen position, but could not be confirmed by the results. Hence, some of the local features of the La/Th/Ca-environment most likely were lost in the spatially averaging diffraction experiment.

Table 1 Atomic distances and angles in Ca0.5Th0.5PO4 and La0.5Ca0.25Th0.25PO4
Full size table

One major difference between the structural models obtained from powder samples and single crystals is the evolution of the lattice parameters. Both single crystal refinements result in larger unit cell volumes than observed in powder samples, including powders synthesised in this study and literature data [6, 10, 27] (see Fig. 3). This is counterintuitive, since the single crystals were measured at a lower temperature (100 K) compared to powder X-ray diffraction (ambient). Moreover, the surface to volume ratio is generally higher in powder samples, rather giving rise to the expectation of slightly larger unit cells for powder over single crystal data. A notable difference, however, was the sample preparation: The single crystals were obtained at high temperature (up to 1350 °C; powder: 1200 °C) over longer periods of time (18 days; powder: 7 h). Thus, a higher entropic contribution due to less statistically ordered occupation at the Ca/Th position in the single crystals over the powder sample is conceivable [30]. Furthermore, it cannot be ruled out that the deviation originates in part from the fact that the determination of lattice parameters from single crystals is less precise than from powders. As no chemical analysis of the single crystals was undertaken, we cannot exclude an influence of a hypothetical incorporation of the flux material, e.g. Mo6+O4 tetrahedra. This, however, has never been reported for flux-grown monazite single crystals containing trivalent lanthanides or actinides. Hence, the discrepancy in the lattice parameters needs to be resolved in a future study.

Conclusion

The present study demonstrates the chemical flexibility of the La1-xCax/2Thx/2PO4 and Gd1-xCax/2Thx/2PO4 monazite-cheralite system, achieving full solid solutions with both LaPO4 and GdPO4 endmembers, representing the largest and smallest lanthanides to form thermodynamically stable monazite. A previously reported structural deviation between cheralite and monazite evolves linearly with increasing substitution levels. The successful synthesis through a co-precipitation route presents a promising path for a scalable high-level waste conditioning process that reduces hazards arising from dust formation or pressurised reactions. To our knowledge, cheralite single crystals have been grown for the first time using a high temperature flux method, enabling us to study the atomic positions in the cheralite structure more precisely. We were able to confirm the conclusions drawn by Raison et al. [27] regarding the displacement of thorium and calcium ions from the central position in the LnO9 polyhedron using standard laboratory XRD measurements.