Introduction

Modeling fracture is an important frontier in materials research [1,2,3,4] and a challenging problem for modeling and simulation. In typical fracture problems a specimen with defect(s) is exposed to mechanical loading [2, 5], and the response to such boundary conditions are examined to predict stress and strain field, overall fracture toughness, or statistics of specific features of the resulting mechanical fields (Fig. 1) [6,7,8].

Figure 1
figure 1

Summary of the fracture mechanics field problem considered here, focused specifically on atomic-level stress data. (A) summary of the boundary condition and elliptical crack-like voids used in the training set. We use a fixed boundary indicated by the dashed line to constrain movement at the outside, in order to apply strain-controlled loading. (B) Molecular dynamics (MD) simulation setup, including a close-up view of the atomistically resolved stress field and an indication of the four fixed boundary strips used in LAMMPS [9]. The simulation domain of all mobile atoms is indicated in red color. (C) Two examples of input and output data pairs produced by MD simulation. As shown in the zoomed-in view on the right, the resolution of the output images is sufficiently high to resolve individual atoms and detailed stress variations—at the atomic level—near the edges. The region shown in magnified view is indicated by the dashed grey box. The hexagonal lattice structure is clearly visible, with the spacing of atomic distances marked in panel C to provide a reference for the key scales in the problem. As marked with the scale bar in panel A, the system size is approximately 32 nm (assuming that σ = 1 Å).

Full size image

Whereas molecular-level models (e.g., molecular dynamics, MD) provide accurate predictive results (especially using accurate force fields) [10], such simulations can be computationally expensive and quickly challenge the capabilities of computational resources. On the other hand, deep learning has emerged as a potential approach to help address the multiscale problem, as it could both serve as a proxy model for MD or finite element methods (FE) or as a way to bridge scales [11,12,13,14,15]. In scale-bridging applications, such methods should ideally have a generalization capacity that allows them to make predictions beyond the scope of the training data.

This question about the predictive power of physics-based deep learning has been a subject of various investigations [16, 17], and is an important frontier in the field. In this paper we particularly focus on the use of deep learning for fracture applications, and explore the application of a small dataset and the generalization capacity towards a broader use of a deep learning method in a multiscale scheme. This assessment will provide us with insights on potential uses of such methods as a scale-bridging tool to effective capture how building blocks of materials (atoms, molecules, amino acids, etc.) interact to create specific sets of functions. A particular novelty of this study is the use of a physics-inspired diffusion machine learning approach, and an assessment of whether or not such a model is capable of adequately learning complex singular field data near cracks.

Language-based models for physical sciences

We propose the use of language models, specifically using the self-attention architecture seen for instance in transformer neural networks [18,19,20], which offers a building block approach that is native to many materials science problems—linking structure, process and properties at a building block perspective, in a natural way, similar to language [21,22,23,24,25]. Earlier work in this field has demonstrated the suitability of convolutional and transformer architecture for solid mechanics problems including elasticity and fracture applications [26,27,28,29], as well as materials design based on human language input [23, 24]. More broadly, the use of transformer architectures has emerged as a broadly applicable approach for many data modalities including state-of-the-art text-to-image generation (e.g., VQGAN-CLIP [20, 30], GLIDE [31], DALL-E 2 [32, 33], or Imagen [34]).

Here we build on this body of knowledge and recent developments of state-of-the-art image generation methods [34] and explore the use of a new class of progressive diffusion models [34, 35]. We specifically focus on the following materials science questions:

  1. 1.

    Can progressive diffusion models be an effective approach to predict physical field solution from prompts that delineate the input microstructure?

  2. 2.

    Can we successfully train a complex progressive diffusion transformer model with relatively small datasets of only a thousand image-to-image pairs?

  3. 3.

    Can such a model be used to predict solutions for input microstructures that are distinct from the types of data seen during training, so that the model can be used to generalize solutions?

While we use a similar architecture as in state-of-the-art text-to-image generation methods [34] including a successive denoising strategy that transforms noise to conditioned field solutions, our conditioning prompt is not text here; rather, the input prompt is an encoding of the input microstructure representation from which the model then learns to construct the field solution. In the cases discussed in this paper we predict the Von Mises stress field from the prompt; however, other fields or properties can be predicted as well and the model can be easily adapted (either training from scratch, or more efficiently, using transfer learning). The primary objective in this work is to develop a framework that can predict high-resolution field predictions that features exquisite detail of the resulting physical variables, at reasonable computational cost. The successive upscaling of the resulting field prediction from smaller to larger and larger resolution becomes tractable through the use of a cascading series of deep neural networks, as illustrated in Fig. 2. While limited to a 2D model material in this study, we anticipate that the general framework can be useful for a variety of scenarios and many other field data classes.

Figure 2
figure 2

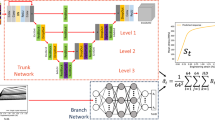
Summary of the neural network architecture of a diffusion-based generative model, consisting of three U-Net architectures (Unet 1, Unet 2 and Unet 3) that are used to translate the input microstructure into the final field output, over three successive stages of translation and upscaling, ultimately reaching a resolution of 1024 × 1024.

Full size image

Paper outline

We begin the discussion with a brief review of the dataset, the neural network architecture, and then proceed to a presentation of the results. We review training and testing performance, as well as the exploration of using the model in scenarios far from the original dataset used in training, to explore generalization capacity. A discussion with domain knowledge in fracture mechanics is included, to further understand the model’s predictive power. Finally we discuss opportunities for future work that include experimental studies, integration with other types of field data, as well as transfer learning modalities.

Results and discussion

Neural network architecture

Diffusion models, sometimes referred to as denoising diffusion models, have emerged as state-of-the-art tools in image generation especially when combined with transformer architectures, realized in methods such as DALL-E 2 or Imagen, and often exceed the performance of generative adversarial neural nets (GANs) [33, 35,36,37]. The key task in such models is that they learn a reverse process to perform denoising in order generate data, such as images or field data, from noise [37]. While these models have been widely used in the image synthesis literature, their exploration in the physical sciences, and specifically mechanics applications for materials science, has not yet been investigated.

Here we use a progressive neural network architecture that progressively upscales the prediction from the input prompt, to realize very high-resolution images with exquisite detail and quality. Figure 2 shows a summary of the neural network architecture of a diffusion-based generative model, consisting of a series of three U-Net architectures (Unet 1, Unet 2 and Unet 3) that are used to translate the input microstructure into the final field output, over three successive stages of translation and upscaling, ultimately reaching a resolution of 1024 × 1024. Each U-net consists of a combination of ResNet blocks and self-attention layers, as described in [34]. Further details are provided in the Materials and Methods section.

Model training and testing

The model is trained successively whereby each of the U-Nets is trained individually (first Unet 1, then Unet 2, and then Unet 3). As a training set, we deliberate limit the scope to a very small set of 1,000 image pairs, as shown in Fig. S1 for a few sample geometries (full dataset see link in Materials and Methods). Training performances are shown in Figs. S3 and S4. Figure S4 specifically shows images during training, revealing training performance for test and validation set, for the first U-net (Unet1) to give the readers a sense for how the model learns and performs during this process. As can be seen, during training epochs (top to bottom), the prediction accuracy increases successively. Similar behaviors are seen for the other U-Nets in the model.

Validation and extrapolation

We now use the trained model and apply it to examine how well it can predict stress fields for a variety of vases. All predictions presented here are for the fully trained model, whereby images of size 1024 × 1024 are generated.

Figure 3 shows predictions based on a test microstructure [Fig. 3(A)], for the three different stages in the neural network. Figure 3(B) shows results for three different resolutions, corresponding to the three stages described in Fig. 2. The figure also shows a zoomed-in view of the area marked in panel B, left. Figure 3(D) shows a close-up view of the final result, as marked up in the right panel of B. The individual atoms and associated stress fields can be clearly seen. The detailed view of the input microstructure shows that individuals atoms are not provided, and rather, solely the overall shape of the crack/material distribution. The model is still able to predict not only the stress field but also the position of atoms within the domain. A detailed visual inspection confirms that the predicted fields are similar in nature from the original data as shown in Fig. 1(C). These results indicate that the model has adequately learned how to predict stress fields from input microstructures, for data similar to the training set.

Figure 3
figure 3

Predictions based on a test microstructure (A), for the three different stages in the neural network (B). Panel B shows the results for three different resolutions (see stages in Fig. 2), and panel D shows a zoomed-in view of the area marked in panel B, left. Panel D depicts a close-up view of the final result, as marked up in the right panel of B. The individual atoms and associated stress fields can be clearly seen (top: input, bottom: prediction). Visual inspection confirms that the predicted fields are similar in nature from the original data as shown in Fig. 1(C). Detailed, small-scale variations of atomic stresses (marked by the two arrows) can be predicted well using the model, due to the high resolution in this model. The small rectangles show even finer zoomed-in views of the input/output, to show more details.

Full size image

Next, we examine how the model performs for cases that are distinct from the type of data provided in the training set. To test this we next present additional validation cases predicted using the trained model, as shown in Fig. 4. Here we compare microstructures distinct from the ones included in the training set. Figure 4(A–D) show results for a single crack, respectively, and Fig. 4(E–H) depict results for a microstructure that features multiple cracks. We emphasize that the training set does not include cases of single cracks. However, as the results show, the model is able to accurately predict the stress field including long-range order. This suggests that the model has learned key physical insights about fracture mechanics in solids, and is able to generalize from the training set.

Figure 4
figure 4

Validation cases predicted using the trained model, where we compare microstructures distinct from the ones included in the training set. (A–D) show results for a single crack, respectively, and (E–H) show results for a system with multiple cracks. The training set does not include cases of single cracks. However, the model is able to accurately predict the stress field including long-range order. This confirms that the model has learned key physical insights about fracture mechanics in solids, and is able to generalize from the training set.

Full size image

Figure 5 depicts more comparisons of validation cases of single cracks (top two) and multiple crack cases (bottom two). The left column of the figure shows a histogram of the Von Mises stress field, comparing ground truth and predictions. The results show that the model can accurately predict not only the specific stress distributions (see also Fig. 4) but also overall statistics of stress fields. This is possible even for cases that are quite distinct from the training data.

Figure 5
figure 5

Additional comparisons of validation cases of single cracks (top 2) and multiple crack cases (bottom 2). The left column of the figure shows a histogram of the Von Mises stress field, comparing ground truth and predictions. The results show that the model can accurately predict not only the specific stress distributions (see also Fig. 4) but also overall statistics of stress fields. This is possible even for cases that are quite distinct from the training data.

Full size image

For a deeper and quantitative analysis of how the model performs for generalization cases outside of the training set, Fig. 6 shows a correlation plots between statistical properties of the stress fields, for ground truth and model prediction, for standard deviation of the Von Mises stress field [Fig. 6(A)], and the variance [Fig. 6(B)]. The R2 values for the correlations are 0.97 for the standard deviation and 0.98 for the variance. The colors indicate different types of microstructures considered (red = single cracks, blue = multiple cracks). Overall, we find that the correlation is excellent for all cases. The data further shows that single cracks, and the type of multiple-crack geometries used in this validation set, are not included in the training set, thus serving as a means to test generalizability.

Figure 6
figure 6

Correlation plots between statistical properties of the stress fields, for ground truth and model prediction, for standard deviation of the Von Mises stress field (A), and the variance (B). R2 values are 0.97 for the standard deviation (A) and 0.98 for the variance (B). The colors indicate different types of microstructures considered (red = single cracks, blue = multiple cracks). The correlation is excellent for all cases. Single cracks, and the type of multiple-crack geometries used in this validation set, are not included in the training set, thus serving as a means to test generalizability.

Full size image

Figure 7 shows an application of the model to distinct geometries very different from the data seen during training, including a crack defined by the MIT logo (A-B) and a star-shaped crack (C-D). Close inspection of the results confirms that the model makes accurate predictions in all cases, including the stress fields and the overall statistics as seen in the histogram. The field predictions include an accurate representation of complex relationships between crack/defect shape and resulting stress field. The model is also capable of discerning key fracture mechanics theoretical predictions [8], such as showing higher stress concentration at cracks perpendicular to the loading condition, and much smaller stress concentrations at cracks oriented towards the loading condition [Fig. 7(C), for instance]. This general behavior is predicted in Inglis’ solution [38] [see Fig. 8(A) for geometry] tnat predicts the local stress at the tip of an elliptical defect:

Figure 7
figure 7

Application of the model to distinct geometries very different from the data seen during training, including a crack defined by the MIT logo (A, B) and a star-shaped crack (C, D). The model makes accurate predictions in all cases, including the stress fields and the overall statistics as seen in the histogram.

Full size image
Figure 8
figure 8

Detailed analysis of stress field for microstructure with a larger number of cracks (25 randomly placed defects of varied size). A close analysis of the resulting stress fields reveals that the model captures several important fracture mechanics concepts. (A) Large defects yield high stress concentrations, and asymptotic stress fields across multiple large defects connect to form a stress path. (B) Large defects but orientated in the loading direction tend to yield smaller stress concentrations (see two “tips” marked with B that each do not generate a significant stress concentration). C Shows a small crack that generates a relatively small stress concentration. The area marked with D depicts an example for crack tip shielding, whereas the larger neighboring defects play a role to protect the smaller defect marked with D.

Full size image
$${\sigma }_{\mathrm{max}}={\sigma }_{\infty }\left(1+2\frac{a}{b}\right),$$
(1)

where \({\sigma }_{\infty }\) is the remotely applied stress, and \(a\) and \(b\) describe the geometry of an elliptical crack. When \(a\gg b\), the crack is oriented perpendicar to the loading and yieds high stresses at the crack tip, and vice versa.

Analyzing all these validation results, there are specific details that the model has learned, including the fact that horizontally oriented cracks show a smaller or vanishing stress concentration, as opposed to largely vertically oriented cracks that lead to a more significant stress concentration. Similar arguments can be made with respect to the size of the crack; where larger defects tend to yield stronger stress concentrations. These results agree well with what is known from fracture mechanics theories [38].

To provide further analysis of the results and a comparison with fracture theories, Fig. 8(B) shows a detailed analysis of stress field for microstructure with a larger number of cracks than what was seen during training. As can be seen in the figure, the model captures several important fracture mechanics concepts. The area marked by A shows that large defects yield high stress concentrations, and asymptotic stress fields across multiple large defects connect to form a stress path. As seen in the two areas marked with B, large defects but orientated in the loading direction tend to yield smaller stress concentrations. The area highlighted with C shows a small crack that generates a relatively small stress concetration. As another example, the point hightlighted with D shows an example for crack tip shielding, whereas the larger neighboring defects play a role to protect the smaller defect.

Can the model also predict initiation of cracks? Fig. 9 shows initial explorations of the model to address this question. Indeed, we identify a potential to not only predict static, elastic stress fields near cracks but also a learned capacity to predict whether or not cracks will propagate. The two examples shown here where crack propagation occurs, compared with the results shown in Figs. 3, 4, 5 where cracks do not propagate, seems to suggest that the model has already learned certain aspects of this general problem. In fact, close inspection of the training dataset does include a few cases where cracks nucleate. The model is capable to generalize this knowledge and predict, for large cracks and cracks oriented orthogonal to the loading direction, that nucleation occurs. This also agrees with fracture mechanics theories [38]. Further, the results shown in Fig. 7(C) where crack initiation is predicted at the very top/bottom of the star-shaped defect, but not at the other edges. A more detailed exploration of this and related aspects is left to future work.

Figure 9
figure 9

In initial explorations of the model we identify a potential to not only predict static, elastic stress fields near cracks but also a learned capacity to predict whether or not cracks will propagate. The two examples shown here where crack propagation occurs, compared with the results shown in Figs. 3, 4, 5 where cracks do not propagate, seems to suggest that the model has already learned certain aspects of this general problem. In fact, close inspection of the training dataset does include a few cases where cracks nucleate. The model seems to be able to generalize this knowledge and predict, for large cracks and cracks oriented orthogonal to the loading direction, that nucleation occurs. Due to the stochastic nature of cracking, the model shows some more pronounced differences between the prediction and ground truth near the crack tips where cracking occurs.

Full size image

Conclusion

This paper reported a comprehensive workflow to translate input microstructures into complex field predictions. As the results depicted in Figs. 3, 4, 5, 6, 7 reveal, not only does the model accurate predict results for input microstructures close to the original type of structures considered, but generalizes well for distinct cases such as single cracks (Figs. 4, 5, 6, 8) and very different shapes (Fig. 7). Our study was based on a simplistic interatomic potential, used here for proof-of-concept for a model material using an existing dataset [27] as a test case, within the scope of a model material [8, 39, 40]. This limitation can be easily addressed by training the model with a dataset derived from more accurate interatomic potentials, [41,42,43,44]and hence more realistic material data [15, 45]. We leave these explorations to future work but do not anticipate that this is an intrinsic limitation of the model architecture proposed here, and that it hence offers many immediate research opportunities. The input data does not have to originate from molecular modeling, it can also be based on mesoscale or continuum models, or experimental data.

At the outset of this paper we posed three materials science questions. Based on the results reported here, we conclude:

  1. 1.

    Progressive diffusion models can be an effective approach to predict physical field solution from prompts that delineate the input microstructure; based on a deep-learning implementation of a conditioned denoising process.

  2. 2.

    A progressive diffusion transformer model can be trained with a relatively small datasets of only a thousand image-to-image pairs.

  3. 3.

    Such a model can be used to predict solutions for input microstructures that are distinct from the types of data seen during training. Importantly, we find that the model can be used to generalize solutions.

The ability to predict very high-resolution data from simple input prompts [see, specifically Fig. 3(D), left panels for a detailed view] offers many opportunities, both for image/field-based models as done here but also when treating data explicitly where each “pixel” could represent an individual atom or molecule, or other data. In the way the model was used here, the resolution of the output images is sufficiently high to resolve individual atoms and detailed stress variations—at the atomic level—near the edges, as is shown for instance in Fig. 3. Moreover, since transformer models provide a high level of flexibility when it comes to data modalities, the model can likely be used for a variety of translational problems in the physical sciences, including text-to-field, or graph-to-property or field translation, or others. The use of image data, or by extension, time-series of images or videos, provides a direct linkage with many common datasets obtainable in materials research applications, such as high-resolution transmission electron microscopy, or others [46,47,48]. It is further noted that while the dataset used for training the model in this paper was based on one particular boundary condition (see Fig. 1), this can be generalized to either train multiple models for varied boundary conditions, or to train one model whereby different boundary conditions are encoded in the prompt.

Another exciting direction is the exploration of the model to predict crack initiation, or even multiple frames of cracking. The initial observation shown in Fig. 9 suggests that this is indeed in the realm of possibility. Other future directions can be a direct implementation of various boundary conditions, which can be realized easily as additional input in the transformer architecture. Similar to a text prompt, the ability to provide a variety of modalities and descriptors to drive the generation of the final prediction, the formulation based on a language model provides innate advantages.

In regards to the size of the training set, we deliberately designed this computational experiment to use a very small dataset of only 1000 pairs of input microstructures and fields. We showed that even with this limitation, the model has learned to generalize predictions and learned physical insights. This offers exciting possibilities for extensions of this work by using larger datasets or transfer learning that have already been shown to perform well for attention-based models both in language applications and in language model based physics applications [26, 49].

Along those lines, we expect that adding more data to the training set—and using larger sets of pairs of images, would help to improve the model. Albeit the computational experiments reported here were designed to focus on a very small dataset and specifically on atomic-level stress data derived from molecular simulations, this would likely expand the transferability and prediction capacity of the model even further.

In terms of computational expense, a model trained on relatively small datasets can provide rapid predictions. Whereas the generation of the dataset may take significant computational resources, along with the training cost, a trained model offers unprecedented access to a vast design space of solutions. A key element is the use of advanced diffusion algorithms [35] that allows us to obtain excellent results with only 96 total diffusion steps (as opposed to 1000 s in the original approach [34]). This offers a substantial computational advantage during generation and validation.

While the methods developed and reported in the paper is believed to be generally applicable to any kind of field data, the specific training set used to train the deep learning model is developed from atomistic-level simulations. As such, the predictions only hold for atomic-level stresses near cracks. Additional training data would be needed, e.g., developed from experimental measurements [e.g., digital image correlation, DIC [50]] or continuum models, to expand the applicability including via the use of multiscale modeling schemes [51,52,53]. This is beyond the scope of the paper, however, but opens exciting opportunities for future work in particular in conjuction with transfer learning strategies. More broadly, some studies have provided evidence for the validity of continuum theories at the atomistic scale [8, 54,55,56], including recent experimental-computational studies that compared atomic-level deformations from simulations with high-resolution in situ TEM [57]. Going beyond the current scope of the model that did not include plasticity, future work may include a range of other dissipative effects near cracks (including plasticity, dislocation nucleation, etc.) and damage spreading, and more generally a full analysis of the dynamics of failure.

Materials and methods

Molecular dynamics (MD) simulations and dataset generation

A simple setup of a fracture model of is used to generate the dataset, which consists of input microstructures and corresponding stress fields [8, 41, 58], as originally reported in [27]. Here we provide only a short review of that dataset for completeness of the presentation. We consider the geometry shown in Fig. 1(A, B), depicting a simple triangular lattice with a 12:6 Lennard–Jones (LJ) interatomic interactions [59, 60] under uniaxial loading.

The LJ interatomic potential used here takes the form

$$\phi ({r}_{ij} )=4 \varepsilon \left[{\left(\frac{\sigma }{{r}_{ij}}\right)}^{12}-{\left(\frac{\sigma }{{r}_{ij}}\right)}^{6}\right]$$
(2)

While the LJ potential is a simplistic representation of materials, its use in a 2D hexagonal geometry yields a brittle material [8, 60], which serves the purpose of the study reported here as a simple material model (hence, mechanisms around cracks, once failure is initiatied, are largely bond rupture events in accordance with what is seen in brittle materials). The input geometry features a series of randomly located and oriented cracks of different sizes and aspect ratios, as shown in Fig. 1(B), showing also the fixed boundaries in which forces and velocities of atoms are set to zero to allow for application of strain for mechanical loading. The system is confined to 2D atomic motions in the x- and y-directions. The LJ interatomic potential parameters used in the generation of the dataset, as defined in Eq. (2) (see [27] for further details) are \(\varepsilon =1\) and \(\sigma =1\) with a cutoff radius of \({r}_{\mathrm{cut}}=1.2\) (all simulations carried out in non-dimensional units). For instance, lengths are expressed as x*=x/σ and pressures/stresses are expressed as \({p}^{*}=p\frac{{\sigma }^{3}}{\varepsilon }\). As marked with the scale bar, the system size is approximately 32 nm (assuming that σ = 1 Å).

It is emphasized that the training set used to train the model includes only cases with a larger number of randomly situated cracks (see Supplementary Information). Validation cases include both very small/single crack cases or scenarios with a much larger number of defects and with a different crack geometry than what was used in training.

The MD simulations are carried out using the LAMMPS simulation package. All samples are exposed to homogeneous uniaxial tensile strain of 1% in the x-direction. As described in [27] we compute atomic von Mises stress \({\sigma }_{\mathrm{von Mises}}\) [61] in LAMMPS [9]. The fields are then visualized using matplotlib and we save images of both the input microstructure and the resulting stress fields to generate the data sets (see Fig. 1(C) for examples of the image pairs including a zoomed-in view). Input and output images are stored in CSV files and then used by the data reader for processing in the machine learning code.

For the discussions in this paper we limit the exploration to the Von Mises stress as a simple stress measure that allows us to plot field data; whereas the von Mises stress is calculated from the stress tensor \({\sigma }_{ij}\) as:

$$\sigma_{{\text{von Mises}}} = \sqrt {\frac{1}{2} \left( {\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + \left( {\sigma_{22} - \sigma_{33} } \right)^{2} + \left( {\sigma_{33} - \sigma_{11} } \right)^{2} + 6\left( {\sigma_{23}^{2} + \sigma_{31}^{2} + \sigma_{12}^{2} } \right)} \right)}$$
(3)

We generate field plots by using the matplotlib scatter function; where blue corresponds to p* = 0.00053 and red to p* = 2.84 (stress values smaller or larger than these limits are plotted in blue or red, respectively). It is noted that the work reported here focus on pre-cracking stress fields where we primarily observe stretching of bonds (and hence generating particular stress fields based on the interatomic forces). That being said, some incipient failure mechanisms are observed, as shown in Fig. 9 and the surrounding discussion.

The stress contour plots along slices of the simulation domain are obtained by converting the field data with 3 color channels into a grayscale image, by multiplying the three channels with [0.299, 0.5870, 0.114] and then adding them, yielding a scalar field data of the van Mises stress and microstructure, respectively, that measures pixel-level intensity. All stress values are normalized such that the smallest value overall is 0, and the largest 1, for simpler comparison in the field plots and the histogram analysis.

The final training set used for the neural network training is based on 1000 images total for the computational experiments, 90% of which is used for training and the rest for testing. The dataset can be accessed at https://www.dropbox.com/s/3i22igvfeeb3iac/DataSet_large_mosaic.zip?dl=0.

Additional validation examples are created consisting of single cracks and a series of cases with multiple cracks but different crack geometries and number of cracks than in the training set. Further, we generate a validation set that includes distinct geometries of cracks such as the MIT logo and a star-shaped void.

Machine learning model

Our model is based on the Imagen architecture [34], but instead of conditioning the input on text prompts we condition the predictions on microstructure embeddings (which define the material’s microstructure), as shown schematically in Fig. 2. The model consists of three U-Net architectures: Unet 1 (constructed based on [36]), Unet 2 and Unet 3 (both constructed as Efficient U-Nets as proposed in [37]) that are used to translate the input microstructure into the final field output, over three successive stages of translation and upscaling, ultimately reaching a resolution of 1024 × 1024.

As proposed in [35, 62] we use the improved sampling and training processes, which yield computationally more efficient and better predictions. Table 1 provides details about the model architecture and Fig. S2 a detailed PyTorch model readout to reveal the entire architecture. The implementation is based on the code published at [63].

TABLE 1 Parameters used in the progressive transformer diffusion model (parameters for the three U-Nets, the integrated architecture, and additional parameters are provided). See also Fig. S2.
Full size table

The microstructure encoder scales the 8-bit pixel values to be between 0 and 1 and feeds each of the three-color channels to the neural networks in the embedding dimension. Since the input microstructures solely consist of white (no material) and black (material) building blocks, the input embeddings consist solely of (1,1,1) and (0,0,0) tensors for each building block that makes up the material microstructure. In some sense, this can be seen as a language prompt that provides a series of letters—“W” for void, “B” for material, to the model. Future work can expand on this easily and provide either more material choices or gradations, or text prompts that describe certain types of boundary conditions.

The total number of parameters in the model is 987,891,378. Unet 1 features 107,837,860 trainable parameters, Unet 2 735,122,066 trainable parameters and Unet 3 144,931,452 trainable parameters: 144,931,452.

The model is trained successfully, whereby each of the U-Nets is trained individually (first Unet 1, then Unet 2, and then Unet 3). Training performances are shown in Figs. S3 and S4. Unet 1 is trained for 18 K steps, and Unet 2/Unet 3 are trained for 27 K steps each.