Skip to main content
SpringerLink
Log in

Error Estimates of High-Order Numerical Methods for Solving Time Fractional Partial Differential Equations

  • Research Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

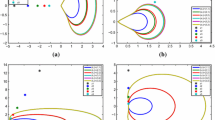
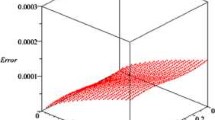
Error estimates of some high-order numerical methods for solving time fractional partial differential equations are studied in this paper. We first provide the detailed error estimate of a high-order numerical method proposed recently by Li et al. [21] for solving time fractional partial differential equation. We prove that this method has the convergence order O(τ3−α) for all α ∈ (0, 1) when the first and second derivatives of the solution are vanish at t = 0, where τ is the time step size and α is the fractional order in the Caputo sense. We then introduce a new time discretization method for solving time fractional partial differential equations, which has no requirements for the initial values as imposed in Li et al. [21]. We show that this new method also has the convergence order O(τ3−α) for all α ∈ (0, 1). The proofs of the error estimates are based on the energy method developed recently by Lv and Xu [26]. We also consider the space discretization by using the finite element method. Error estimates with convergence order O(τ3−α + h2) are proved in the fully discrete case, where h is the space step size. Numerical examples in both one- and two-dimensional cases are given to show that the numerical results are consistent with the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E.E. Adams, L.W. Gelhar, Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis. Water Resources Res. 28 (1992), 3293–3307.

    Article  Google Scholar 

  2. J. Cao, C. Li,and Y. Chen, High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (II). Fract. Calc. Appl. Anal. 18, No 3 (2015), 735–761; 10.1515/fca-2015-0045; https://www.degruyter.com/view/j/fca.2015.18.issue-3/issue-files/fca.2015.18.issue-3.xml.

    Article  MathSciNet  Google Scholar 

  3. F. Chen, Q. Xu, and J.S. Hesthaven, A multi-domain spectral method for time-fractional differential equations. J. Comput. Phys. 293 (2015), 157–172.

    Article  MathSciNet  Google Scholar 

  4. S. Chen, J. Shen, and L.-L. Wang, Generalized Jacobi functions and their applications to fractional differential equations. Math. Comp. 85 (2016), 1603–1638.

    Article  MathSciNet  Google Scholar 

  5. N.J. Ford, M.L. Morgado, and M. Rebelo, Nonpolynomial collocation approximation of solutions to fractional differential equations. Fract. Calc. Appl. Anal. 16, No 4 (2013), 874–891; 10.2478/s13540-013-0054-3; https://www.degruyter.com/view/j/fca.2013.16.issue-4/issue-files/fca.2013.16.issue-4.xml.

    Article  MathSciNet  Google Scholar 

  6. N.J. Ford, K. Pal, and Y. Yan, An algorithm for the numerical solution of two-sided spacefractional partial differential equations. Comput. Methods Appl. Math. 15 (2015), 497–514.

    Article  MathSciNet  Google Scholar 

  7. N.J. Ford, M.M. Rodrigues, J. Xiao, and Y. Yan, Numerical analysis of a two-parameter fractional telegraph equation. J. Comput. Appl. Math. 249 (2013), 95–106.

    Article  MathSciNet  Google Scholar 

  8. N.J. Ford, J. Xiao, and Y. Yan, Stability of a numerical method for a space-time-fractional telegraph equation. Comput. Methods Appl. Math. 12 (2012), 1–16.

    Article  MathSciNet  Google Scholar 

  9. N.J. Ford, J. Xiao, and Y. Yan, A finite element method for time-fractional partial differential equations. Fract. Calc. Appl. Anal. 14, No 3 (2011), 454–474; 10.2478/s13540-011-0028-2; https://www.degruyter.com/view/j/fca.2011.14.issue-3/issue-files/fca.2011.14.issue-3.xml.

    Article  MathSciNet  Google Scholar 

  10. N.J. Ford, Y. Yan, An approach to construct higher order time discretisation schemes for time fractional partial differential equations with nonsmooth data. Fract. Calc. Appl. Anal. 20, No 5 (2017), 1076–1105; 10.1515/fca-2017-0058; https://www.degruyter.com/view/j/fca.2017.20.issue-5/issue-files/fca.2017.20.issue-5.xml.

    Article  MathSciNet  Google Scholar 

  11. G.-H. Gao, Z.-Z. Sun, and H.-W. Zhang, A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259 (2014), 33–50.

    Article  MathSciNet  Google Scholar 

  12. R. Gorenflo, F. Mainardi, Random walk models for space fractional diffusion processes. Fract. Calc. Appl. Anal. 1, No 2 (1998), 167–191.

    MathSciNet  MATH  Google Scholar 

  13. Y. Hatano, N. Hatano, Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resources Res. 34 (1998), 1027–1033.

    Article  Google Scholar 

  14. B. Jin, R. Lazarov, D. Sheen, and Z. Zhou, Error estimates for approximations of distributed order time fractional diffusion with nonsmooth data. Fract. Calc. Appl. Anal. 19, No 1 (2016), 69–93; 10.1515/fca-2016-0005; https://www.degruyter.com/view/j/fca.2016.19.issue-1/issue-files/fca.2016.19.issue-1.xml.

    Article  MathSciNet  Google Scholar 

  15. B. Jin, R. Lazarov, and Z. Zhou, Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM J. Sci. Comput. 38 (2016), A146–A170.

    Article  MathSciNet  Google Scholar 

  16. B. Jin, R. Lazarov, and Z. Zhou, An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. of Numer. Anal. 36 (2016), 197–221.

    MathSciNet  MATH  Google Scholar 

  17. T.A.M. Langlands, B.I. Henry, The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 205 (2005), 719–736.

    Article  MathSciNet  Google Scholar 

  18. H. Li, J. Cao, and C. Li, Higher-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (III). J. Comput. Appl. Math. 299 (2016), 159–175.

    Article  MathSciNet  Google Scholar 

  19. C. Li, H. Ding, Higher order finite difference method for the reaction and anomalous-diffusion equation. Appl. Math. Model. 38 (2014), 3802–3821.

    Article  MathSciNet  Google Scholar 

  20. Z. Li, Z. Liang, and Y. Yan, High-order numerical methods for solving time fractional partial differential equations. J. Sci. Comput. 71 (2017), 785–803.

    Article  MathSciNet  Google Scholar 

  21. C. Li, R. Wu, and H. Ding, High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations. Commun. Appl. Ind. Math. 6 (2014), e–536.

    MathSciNet  MATH  Google Scholar 

  22. X. Li, C. Xu, Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 8 (2010), 1016–1051.

    Article  MathSciNet  Google Scholar 

  23. Z. Li, Y. Yan, and N.J. Ford, Error estimates of a high order numerical method for solving linear fractional differential equation. Appl. Numer. Math. 114 (2017), 201–220.

    Article  MathSciNet  Google Scholar 

  24. H. Liao, D. Li, and J. Zhang, Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 56 (2018), 1112–1133.

    Article  MathSciNet  Google Scholar 

  25. Y. Lin, C. Xu, Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225 (2007), 1533–1552.

    Article  MathSciNet  Google Scholar 

  26. C. Lv, C. Xu, Error analysis of a high order method for time-fractional diffusion equations. SIAM J. Sci. Comput. 38 (2016), A2699–A2724.

    Article  MathSciNet  Google Scholar 

  27. W. McLean, K. Mustapha, Time-stepping error bounds for fractional diffusion problems with non-smooth initial data. J. Comput. Phys. 293 (2015), 201–217.

    Article  MathSciNet  Google Scholar 

  28. R. Metzler, J. Klafter, The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen. 37 (2004), 161–208.

    Article  MathSciNet  Google Scholar 

  29. R.R. Nigmatulin, The realization of the generalized transfer equation in a medium with fractal geometry. Phys. Stat. Sol. B 133 (1986), 425–430.

    Article  Google Scholar 

  30. K. Pal, Y. Yan, and G. Roberts, Numerical Solutions of Fractional Differential Equations by Extrapolation. In: Finite Difference Methods, Theory and Applications. FDM 2014 (I. Dimov, I. Faragó, L. Vulkov, Eds.) Lecture Notes in Computer Science # 9045 (2015), 291–299.

    Google Scholar 

  31. E. Sousa, A second order explicit finite difference method for the fractional advection diffusion equation. Comput. Math. Appl. 64 (2012), 3143–3152.

    Article  MathSciNet  Google Scholar 

  32. Y. Yan, K. Pal, and N.J. Ford, Higher order numerical methods for solving fractional differential equations. BIT Numer. Math. 54 (2014), 555–584.

    Article  MathSciNet  Google Scholar 

  33. S. B. Yuste, Weighted average finite difference methods for fractional diffusion equations. J. Comput. Phys. 216 (2006), 264–274.

    Article  MathSciNet  Google Scholar 

  34. S. B. Yuste, L. Acedo, An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations. SIAM J. Numer. Anal. 42 (2005), 1862–1874.

    Article  MathSciNet  Google Scholar 

  35. F. Zeng, C. Li, F. Liu, and I. Turner, The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 35 (2013), A2976–A3000.

    Article  MathSciNet  Google Scholar 

  36. F. Zeng, Z. Zhang, and G.E. Karniadakis, Fast difference schemes for solving high-dimensional time-fractional subdiffusion equations. J. Comput. Phys. 307 (2016), 15–33.

    Article  MathSciNet  Google Scholar 

  37. Y.-N. Zhang, Z.-Z. Sun, and H.-L. Liao, Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J. Comput. Phys. 265 (2014), 195–210.

    Article  MathSciNet  Google Scholar 

  38. M. Zheng, F. Liu, V. Anh, and I. Turner, A high order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 40 (2016), 4970–4985.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Luliang University, Lishi, 033000, P. R. China

    Zhiqiang Li

  2. Department of Mathematics, Shanghai University, Shanghai, 200444, P. R. China

    Zhiqiang Li

  3. Department of Mathematics, University of Chester, Parkgate Road, Chester, CH1 4BJ, UK

    Yubin Yan

Authors
  1. Zhiqiang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yubin Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhiqiang Li.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Yan, Y. Error Estimates of High-Order Numerical Methods for Solving Time Fractional Partial Differential Equations. FCAA 21, 746–774 (2018). https://doi.org/10.1515/fca-2018-0039

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1515/fca-2018-0039

MSC 2010

Key Words and Phrases

Search

Navigation