Introduction

The impact of hepatic or renal impairment on the exposure of an investigational drug is a key clinical pharmacology endpoint in drug development (1, 2). Conventionally, this impact is assessed in a small clinical trial with 6–12 healthy participants (HPs) as reference and one or more levels of renal or hepatic impairment, with rich sampling following clinically relevant dosing to aid assessment of individual non-compartmental analysis (NCA) pharmacokinetic (PK) metrics. The HPs enrolled in these studies are usually matched to organ impaired participants with respect to factors that can impact exposure of the drug being evaluated such as age, race, weight, and sex. These studies are not powered to support significance testing, but regulatory agencies still advise the use of confidence intervals in assessing the exposure ratios between groups (3, 4).

The use of HPs, a group that never derives medical benefit from exposure to the investigational drug, and application of inadequate inferential statistics introduce ethical and methodological problems to the conventional approach. There are alternative methods that have been supported, including a population PK (PopPK) model method fitting the PK data of impaired clearance patients organically recruited to efficacy and safety trials (5); this approach is usually only supported if there is not a major effect expected, and would necessarily be inferring differences from sparse data. Other model-based methods can be applied, including a largely in silico assessment using physiologically-based PK (PBPK) models, but there are many situations where this would not be sufficient (6).

Recently, an approach was proposed and assessed in the development of ritlecitinib, where a PopPK model was used to simulate many arms of matched HP PK data, which was compared to observed renal impairment data in lieu of an observed HP arm (5). The approach in that case considered the distribution of geometric mean ratios for NCA exposure metrics generated from the comparison of simulated HP arms to observed impaired clearance arms as a surrogate to the inferred distribution from a conventional, all-observed study design. In the report on that method, the approach was tested with another ritlecitinib study for hepatic impairment, finding that the results of the simulation compared well to the conventional results. To test the feasibility and limits of generalizability for this approach, it was retrospectively applied to a sample of internal organ impairment studies and library of models for the respective study drugs.

Methods

Selection of Studies and Models

Internal clinical study reports featuring the words “renal,” “hepatic,” “healthy” or “normal” in the titles for Phase 1 studies with last subject last visit in 2005 or later were queried in an internal database. Of those, RI and HI studies involving HPs were selected if the pharmacokinetics of the unmodified parent drug was the primary endpoint of interest. Finally, studies could only be included in the analysis if PopPK modeling work that had been completed for the associated programs was accessible and could be feasibly reproduced with current software. No PopPK model updates were conducted, and the respective available models were used without alteration except for the minor changes noted below, as part of this assessment.

For each program, models were sought that were either in draft or published state at the time selected studies were being conducted (ATT = “at the time”), or were considered the current best model for the drug (Final). In the case where a Final model was fitted using data from the RI or HI study under assessment (the “index” study), the model was refit without index study data. The rationale for including both ATT and Final models was that if the proposed approach were used when the studies were being run, only the ATT model would be available, but the Final model provides an example of a robust, well-informed model which may be expected to have better predictive capacity than the earlier model.

Simulation and Analytical Approach

For each study for the respective drug, basic matching based on age, weight and sex demographics for impaired subjects were used to generate N = 1000 virtual HP study cohorts. Exact dosing and sampling schedules were generated by using the observed HP data which was utilized in the original study. The methodology employed for generating the HP cohorts was identical to the Clinical Trial Simulation approach described by Purohit et al. (5). Briefly, this approach uses the PopPK model (ATT or Final) to simulate the PK data for a large number (N = 1000, in the present case) of HP arms/cohorts (having a matching number of participants, each), using the demographic, dosing and sampling information for the observed RI/HI participants. Each simulated arm is considered to arise from the distribution of PK exposures expected for HPs that would have been included in the RI/HI study. Purohit et. al. also performed sensitivity analyses where historical data were used in place of simulated data, which was not reproduced in the present work. Simulations were performed using the package mrgsolve (version 0.10.4) (7) in R version 4.0.3 (8). For all simulated and observed subject data, NCA exposure metrics were computed using the package PKNCA (version 0.9.4) (9); for simulated subjects the concentration used in NCA incorporated residual unexplained variability, it was not the individual predicted values. Numerical predictive checks (NPCs) of the models for the exposure metrics of interest were assessed.

The NCA metrics used in this analysis were the area under the concentration–time curve (AUC) and the maximum concentration (CMAX). Because there was a mix of single- and multiple-dose studies analyzed, all AUC metrics were referred to as “AUCtau,” but the default for single-dose studies was AUClast. For each model version and study for the respective drugs, the geometric mean of the exposure metrics of all simulated cohorts (N = 1000) and observed study arm was estimated. To compare the simulation-based analytical approach to the conventional one, analysis of variance (ANOVA) was performed for the observed NCA metrics in the trial, giving the conventional geometric mean ratio (GMR) and 90% confidence intervals (CIs). The simulation-based analysis determined the distributions of GMRs using the NCA metrics observed in the impaired arms and the 1000 simulated HP arms; median GMR and 90% CIs were pulled from the distribution. A schematic for the complete simulation based methodology is provided in Fig. 1.

Fig. 1
figure 1

Diagram of the analytical approach. For each study, healthy participant (HP) cohort pharmacokinetic (PK) data are simulated from the current final model for the drug or the model available at-the-time (ATT). The exposure metrics area under the concentration–time curve (AUC) and maximum concentration (Cmax) were calculated for each simulated subject and observed renal or hepatic impairment (RI/HI) participants. From the large number of simulated HP cohorts and the observed RI/HI cohort(s), distributions of geometric mean ratios (GMRs) for each comparison could be generated

Full size image

Whether a dose-adjustment for HI or RI was included in the label or recommended in the study report was not considered in this analysis. Since the decision to adjust dose in these circumstances is based mainly on the balance of exposure and safety (at least in the set of studies included in the analysis) and this approach is only suitable for exposure, it was considered outside the scope of the present work.

Ethics Statement

All study protocols were reviewed and approved by each clinical research site’s institutional review board or ethics committee and conducted in accordance with the Declaration of Helsinki and in compliance with all International Council for Harmonisation Good Clinical Practice Guidelines. All participants provided written, informed consent.

Results

Included Organ Impairment Studies and PopPK Models

The study characteristics, demographics of study participants, and demographics of model-fitting datasets are shown in Table I. The majority of sampled studies were in the setting of HI, but there was representation from all levels of RI and HI. For most studies, the model-fitting datasets represented a broader range of demographic input and in all cases a larger sample than the HP recruited to the study. In one case (Study 9, Drug H) the final model population did not include any HP data. While not shown, there was a wide variety of molecular characteristics, clearance pathways and lead indications for the included compounds.

Table I Study Descriptions and Demographics. Some demographic variables were not collected from the central database (NC) for several of the historical datasets used to generate this table. All hepatically impaired or renally impaired (HI/RI) participants for each study are pooled for brevity. For at-the-time (ATT) and final models, when demographic variables were missing, the sample size (N) is not applicable (NA). Continuous variables are summarized by median and range. Number of healthy participants used to fit ATT and final models are shown; demographic data are for the complete model-fitting population and not only the healthy subset
Full size table

Most impairment studies were associated with programs having both ATT and Final models, with the exceptions of Drugs C, D and H, which only had Final models. The NPC results for all models are presented in Fig. 2 and Table S1. There were two ATT models and one Final model that did not adequately predict the HP exposure metrics. The NPC results for Study 9 were comparable to other final model NPCs despite the final model not including HP data.

Fig. 2
figure 2

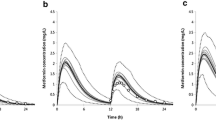
Numeric predictive check of models with healthy participant data. Geometric mean (points) and 90% confidence intervals (lineranges) for AUCtau and Cmax for healthy participants in the included trials, normalized to the observed geometric mean to account for different scales. For each study, the 90% confidence interval of the observed data are also shown with a gray box to emphasize overlap with simulation results. Simulation central tendency and confidence intervals are generated from the median, 5th and 95th quantiles of geometric means for the exposure metrics for 1000 simulations. Numeric estimates not normalized to the observed values are available in Table S1

Full size image

Clinical Trial Simulation Approach Results and Comparison

Numerical differences were observed between the simulation-based distribution of GMRs and the distribution inferred from ANOVA of the observed data (Fig. 3, Tables S2 and S3). As seen in Fig. 3, the concordance between simulation and ANOVA results is generally predictable by the NPC results. Most trials did not have simulation-based median GMR and CIs having the same central tendency and widths as the ANOVA-based GMR and CIs.

Fig. 3
figure 3

Comparison of simulated ratio distribution and observed ANOVA results. Geometric mean ratio (central) and 90% confidence intervals (upper and lower) for ratios of AUCtau and Cmax for each trial, with the median of 90% confidence intervals for the corresponding geometric mean ratios from simulated trials. ANOVA results with 90% confidence intervals are emphasized with vertical lines and gray boxes to facilitate comparison to simulated results. Arms for each study are labeled based on severity (e.g., RI2, RI3 and RI4 are moderate, severe and end-stage/hemodialysis renal impairment, respectively). Ranges are colored by model stage, and numeric predictive check (NPC) results indicate the position of the observed healthy participant geometric mean metric with respect to the 90% confidence interval for that mean (Fig. 2). Numbers for this plot are listed in Tables S2 and S3

Full size image

Discussion

The retrospective analysis revealed that, while the simulation approach does not perfectly reproduce the results of ANOVA from observed data, it does arrive at a similar distribution of likely results that would likely support identical conclusions and dosing recommendations as made with the original study. Where differences exist, they could be driven by both the (in)adequacy of the PopPK model to describe HP data or limitations in the observed data itself. During review of this manuscript, another retrospective analysis of this approach was published which found many of the same conclusions as described in in this report (10).

Small studies designed to determine the effects of organ impairment on drug exposure are not powered to support significance testing and thus confidence intervals are typically very wide. This is acceptable as a standard practice since it is expected that any large enough increases in exposure (e.g., greater than 25%), will be captured in the point estimate; this approach is also practical since recruitment of many stable renal/hepatic function patients with the disease state of interest who are otherwise uncomplicated is rarely feasible. Recruitment of HPs for these trials is often challenging. As the HPs are usually matched to organ-impaired participants with respect to age, race, weight, and sex, they are not typical HPs and therefore have a high screen failure rate. As a result, additional time is needed to recruit the HP group leading to prolonged study timelines. This simulation approach addresses not only the concern related to the recruitment of HP, but also the concern that given modest variability the central estimate for NCA metrics in the small HP arm may significantly differ from the central estimate of the population of HPs exposed to the study drug. That concern is compounded by same issues being present in the impaired clearance arm data, so each pairwise comparison to HP is doubly uncertain. The strength of the present approach over the conventional parallel design is that, by leveraging the wealth of PK data already collected from the clinical development program, the uncertainty within the small sample of HPs is not so influential or is minimized, and instead the central estimate of NCA exposure estimates in the population of HPs is used as a reference. The proposed approach is also amenable to prespecification of model and population as part of the protocol and can enable decision making when reduced study designs (2, 3) or sequential study designs where cohorts of varying degrees of impairment are recruited in sequence.

There are other methods that are similar to the HP in silico cohort approach in that they provide alternative analytical or study conduct approaches (11). Linear mixed effects (LME) models of NCA parameters could be performed in a conventional study design to minimize the effects of variability, or could also be used to incorporate historical data (especially if those data were derived from different doses provided linear PK) (12). PBPK models could be used if the expected effects of organ impairment on the drug PK properties are consistent with the mechanisms described by available models, and that the acceptance criteria for PBPK are not too lenient (13, 14). Combining the benefits of LME and theory of PBPK, conventional PopPK where a covariate on bioavailability and/or systemic clearance are fitted could also be used (15), but if additional model-building is needed it would be difficult to claim the analysis was fully a priori. The present approach is not proposed as being more valid or accurate than these other options, but it does offer some conveniences. Simulations from a documented model already assessed for its predictive performance in the population of interest, without making assumptions (valid or not) about the effects of organ impairment on PK parameters provides an advantage over a conventional PopPK approach or a PBPK approach. The hybrid approach of simulation and observed data means that the observed data from organ impairment (or Test) cohorts are not being stretched beyond their limits to define properly-adjusted point estimates, as may occur with the mixed effects approaches of LME or conventional PopPK.

Matching was used in the current analysis because it was intended to compare with the observed studies where matching was used. However, because the simulation approach would be valid for any control arm adequately predictable by the selected model, matched HPs could be one of many comparisons made. The model could be used to predict the PK in difficult-to-recruit, normal organ function patients with disorders that affect renal or hepatic function. It could also be used to simulate unmatched HPs, who would be expected to support a more conservative estimate of the impact of impaired clearance on PK. There is nothing inherent to this approach that would prevent the generation of control arms of varying characteristics, provided the model’s capacity to predict the target PK in that arm has been demonstrated. Furthermore, one can envisage the application of this approach to any parallel group study which requires a reference PK cohort for which an adequate PopPK model is available.

There were several models that did not include matching demographic factors as covariates, so even though matching was simulated it would not have an impact on subsequent exposure. It is expected that this would not change conclusions from the analysis. An assumption in this approach is that any demographics that would typically be included for matching have been assessed as PopPK covariates. If a model does not have weight, age or sex as covariates, it is because it is either a base model (which is not appropriate for this approach) or more often because these very common covariates were tested and there was no difference when taking them into account. As such, if there is no difference, matching is not necessary but can still be simulated for the sake of convention even if it does not influence the results. A key rationale for matching demographics in the conventional approach is to isolate impact of organ impairment on the exposure of the drug. In practice, matching of demographic characteristics is achieved using weight, sex and age due to study conduct considerations and may not include other factors that impact PK. Hence, even in the conventional approach, matching demographics may not be achieving its objective due to the somewhat empiric nature by which matching is achieved.

There are several limitations to the proposed approach which are associated with the statistical methodology. The ability of a model to predict a valid HP arm for a study is a situation that must be judged on a model-by-model basis, and a single set of tests to demonstrate a model’s validity will not be proposed here. As noted in the presented analysis 2 ATT and 1 Final model did not concur with the trial results, which would suggest that they were not suitable for this analysis. There are various potential causes, including formulation changes, dose non-linearity or concerns about minimizing doses for HPs; these pharmacological and methodological issues would render the simulation outside the scope of the model, and therefore may be attributed to the potentially flawed assumptions of extrapolation. We have not provided the details around each drug for simplicity, and also because this approach is independent of the ADME properties of the drug. If there is an adequate PopPK model that describes the HP data, except for the complexities described, this approach should be applicable.

It is possible that the assumption of the observed HPs having PK within the variability expected from the model may be incorrect, even when there is no apparent extrapolation or model misspecification. There are no major trends in prediction errors across all models, but there may be systematic issues that led to overprediction or underprediction. One unmeasured confounder (in the case of this analysis) that could explain overprediction would be that the inclusion criteria selects for HPs with augmented renal or hepatic function (eg, higher eGFR > 120 mL/min, fast metabolizers, etc.) that goes beyond that which was captured in the model, and thus the model would tend to underestimate HP clearance and overpredict HP AUC. The available data (see Table I) show HPs had typical renal and hepatic function, so this may not explain most issues. However, augmented hepatic function (not demonstrated by serum albumin shown in Table I) could explain major overprediction in Study 4 or the overprediction in Study 3, both of which used final models. A possible cause of underprediction would be renal or hepatic near-insufficiency in the observed HPs, in which functioning would be enough to consider them HPs but reduced enough from model-based HPs to show an exposure difference. This would lead to a greater overlap in exposures between minimally impaired HPs (ie, numerically unimpaired but near a threshold) and RI or HI arms, which would not be reproduced by simulations assuming unimpaired HPs. If it was the case that typical, unimpaired HPs have markedly different exposure from minimally impaired HPs, the dependence of PK on RI and HI would have to be substantial, and therefore the more conservative result returned by the approach (which assumes typical unimpaired HPs) should be supported. Covariate effects on renal or hepatic function measurements were intentionally not included in the models, since they were usually informed by the studies under investigation, but could be considered as post hoc sensitivity if possible..

Another limitation of the proposed approach is the different treatment of data from impaired clearance arms and healthy participants; only the point estimates (geometric means) of the impaired clearance arms are used and there was no attempt to adjust for several levels of variability. This could be resolved in part by performing a bootstrap resampling of the observed data for each GMR estimation used to determine the distribution, which would add rigor to address this limitation but given the small sample sizes for these studies is unlikely to change any resulting decisions. Similarly, the uncertainty of (PopPK model) parameter estimates was not considered in the present analysis, which is expected to have resulted in a narrower distribution of exposure metrics. In a small sensitivity analysis (not shown), the effect of parameter uncertainty (diagonal variance only, not considering covariance) was tested, and although some distributions were widened only a few were impacted; the effect was also predictable by the parameters observed to have very high uncertainty. The question of incorporating parameter uncertainty is another one that should be answered case-by-case and includes the complexities of which type of uncertainty to consider (asymptotic from standard error, variance–covariance sampling, bootstrap-based or sampling importance respampling-based). If this approach were used a priori outside of a retrospective analysis, it would be reasonable to consider parameter uncertainties. Given these few limitations, a risk-based approach to utilizing this methodology may be implemented guided by information on the therapeutic index of the drug and potential impact on dosing recommendations.

An assumption in the PopPK approach used here is that the trends observed in patient data reflect predicted trends in HP data. Meaning, for example, if a model was built using HP data with ages ranging 18–30, and patient data with ages ranging 12–72, this approach assumes PK in HPs up to age 72 could be predicted provided the model accounts for HP/patient differences. The appropriateness of this assumption cannot be generally determined, and the crux of the issue returns to the discussion on extrapolation. Demonstrated by the adequate performance of the approach for Study 9, which used a model that was albeit mature, but was not based on any HP data, it is clear there are circumstances where the interaction between HP and other covariate effects is negligible. If this approach were to be used in a situation where extrapolation is inevitable, efforts should be made to demonstrate the acceptability of the extrapolation with appropriate sensitivity analyses and qualify the results in appropriate context.

Conclusion

Simulation of HPs in impaired clearance studies is a convenient, efficient, and robust alternative to the conventional approach of recruiting HPs and will support similar conclusions and dosing recommendations. This approach could shorten timelines for understanding the impact of organ impairment on drug PK and thus facilitate earlier enrollment of patients with organ impairment in Phase 2 and Phase 3 trials The methodology should be considered to supplement or replace other parallel study designs where one or more groups have well-characterized (by a PopPK model) exposure.