Introduction

For the past few decades, cardiovascular diseases have become the third largest cause of mortality across the globe, where stenoses are of special concern [1, 2]. An abnormal reduction of the cross-sectional area of the artery by deposition of fats and other lipid substances in the beneath of the artery is known as arterial stenosis. Arterial stenosis leads to a significant variation in blood flow parameters, i.e., changes in the velocity gradients and flow structure. In most of the cases, blood flows are considered as laminar [3]. However, it may turn out to turbulent as the intensity of the perturbation of the blood flow created by stenosis. Due to high blood flow velocity at the throat of the stenosis, there may arise high shear stress that causes serious damage to the arterial walls. This affects the behaviors of blood flow [4].

The disease caused by arterial stenosis is known as atherosclerosis [5] which is one of the most widespread diseases of the cardiovascular system globally. The leading causes of death in the world are due to heart diseases such as atherosclerosis [6]. Blood vessels carry a higher level of cholesterols in the form of low-density lipoprotein (LDL) molecules for a longer period of time [7]. This tends to settle in the innermost layer of the blood vessel which is generally unable to remove sufficient fats from microphage by high-density lipoprotein (HDL). These LDL molecules are generally absorbed by the epithelial cells and form a very thin layer between the tunica interna and tunica muscularis, and this is known as plaque. For a longer period, this plaque spreads along the artery and creates constriction inside the blood vessels which result in a slowdown of the blood flow. These epithelial cells may rapture due to various reasons for example high blood pressure and high wall shear stress (WSS) and expose the fatty core which activates the platelets [8]. This eventually forms a clot inside the vessel [9]. However, sometime this clotting block the entire artery and people may face some physiological disturbance like heart attack and brain strokes which might be the cause of sudden death of a human. Thus, the study on arterial stenosis bears significant importance to understand the details on the behavior of blood flow which causes cardiovascular disease.

Currently, in the era of the vast availability of computational fluid dynamics (CFD) tools and machines with high computational efficiency [10], there is a possibility to perform numerical simulations of the complex physical phenomena occurring inside the human organism, e.g., blood flow in the cardiovascular system [4]. Along with the other fields in fluid dynamics, CFD is already proven to be a prevailing and reliable tool in biomedical applications for the virtual analysis of blood flow patterns [11]. This technique is applied in real-life applications to ensure better product quality and a more robust design. The use of CFD, however, is not only limited to these. In recent times, the application of CFD has grown rapidly in the cardiovascular system studies [12]. For example, CFD is widely used across the spectrum of coronary, valvular, congenital, myocardial, peripheral vascular diseases, risk prediction, and virtual treatment planning [11]. Here in this study to avoid redundant radiation of invasive procedure (i.e., angiography), different non-invasive tools to enhance the understanding of physiological parameters of blood flow were used. Moreover, technological advances in the ultra-sound imaging, the magnetic resonance image, computed tomography, and the computational fluid dynamics are widely used to analyze the effect of the initiation and the progression of the cardiovascular diseases. These are associated with heart failure and brain strokes.

Disturbance of blood flow occurs significantly at low Reynolds number. However, for the comparative of higher severity of constrictions, the flow becomes turbulence which intensifies the viscous and pressure head losses. In the blood flow simulation, a significant number of computational as well as experimental methods are found from the literature which are related to the arterial stenosis [13]. Accuracy of the simulation largely depends on a suitable numerical approach, realistic model geometry, and boundary conditions. Early of the seventieth decay, Lee and Fung [12] carried out a numerical simulation on a locally constricted circular tube to understand atherosclerosis. The flow was considered as steady, homogeneous, and Newtonian viscous. Simulations were restricted for low Reynolds number ranging from 0-25 to avoid instabilities in the numerical procedure that is in for higher Reynolds number in their study. Ahmed and Giddens [7] used Lasser Doppler measurements and flow visualization techniques in a rigid transparent tube with different severity of axisymmetric constrictions of steady. In addition, pulsatile flow was taken into consideration to investigate the various effects on flow at the post stenotic zone. This study found that at the early stages of stenosis development, the flow disturbance of discrete oscillation frequency is more important than turbulence. Young and Tsai [14] discussed the detailed description of pressure loss at constraint and separation of flow. The nature of the flow away from occlusion was also explored, i.e., laminar flow, transitional, or turbulent flow. Blood flow due to pumping action of the heart is considered as pulsatile in nature. Ku et al. [9] carried out their experimental study for pulsatile flow. Their study showed correspondence between plaque locations and wall shear stress. The correspondence was shown in such a way that higher shear stress regions are athero-protective and low and oscillating wall shear can lead to various types of plaque formations. Zhang, Bhatti [15] and Mekheimer, Zaher [16] studied entropy analysis on the blood flow through anisotropically tapered arteries filled with magnetic zinc-oxide (ZnO) nanoparticles. Ryval et al. [17] used Wilcox’s standard k-ω model and studied sinusoidal pulsatile flow for the severity of stenosis 75% and 90%, respectively at Reynolds number 500 and 1000. In their study, they found that the transitional version of the standard k-ω model gives a better agreement with the experimental data that of Ahmed and Giddens [7]. Sherwin and Blackburn [13] used both linear stability analyses as well as direct numerical simulation techniques. They considered an axisymmetric pipe with 75% smooth constrictions and a spectral-element approach with around 20, 00,000 nodes to investigate the transition to turbulence of steady and pulsatile flow. Transition to turbulence under pulsatile conditions at a Reynolds number 535 and under steady inlet conditions at Reynolds number 722 were reported in their study.

The blood flow through the artery is spiral. This is due to the heart twisting on its own axis. It is evident from the findings of Stonebridge and Brophy [18] and Stonebridge et al. [19] and Paul et al. [20]. A number of theoretical advantages can be gained when the spiral flow of blood is treated as laminar. For example, reduced turbulence in the artery due to the rotation induced stability and induced lateral force shows a positive effect on arterial damage [19]. A large number of studies conducted to understand the spiral flow of blood in a model of arterial stenosis. However, a complete understanding is still lacking. Many studies found on the effect of both spiral and non-spiral flow in stenosis [21]. Studies on the effect of spiral flow at the different magnitude of spiral speeds are also available in literature. Paul and Lamran [20] showed the spiral flow effect in stenosis at different Reynolds numbers and in their study; they used only two different Reynolds numbers (i.e., 500 and 1000). Kabir et al. [22] used different Reynolds numbers to get an insight into the sensitivity of spiral flow in relation to the Reynolds number. However, blood flow with double stenosis with different area reduction is not well studied yet. Basic knowledge of local hemodynamic parameters in blood flow in the human artery is essential in the diagnosis and treatment of patients with cardiovascular disease [23].

Therefore, the prime objective of this study is to enhance the understanding of pulsatile blood flow along with spiral components by conducting numerical simulations of blood flow with different area reduction. This is done with multiple symmetric arterial stenoses using computational fluid dynamic techniques. Here, the changes of fluid properties in an artery with single stenosis at different area reduction and changes of fluid properties in an artery with double stenosis at different area reduction were studied. Finally, a comparison was performed on blood flow at different stenosis.

Methods

Geometry formulation of arteries

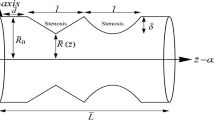
This study aimed to understand the change in velocity distribution, pressure drop, and wall shear stress in the stenosed artery, artery with single and double stenosis at different area reduction. To do this, first, the geometry of three different types of arteries, i.e., normal artery without stenosis, artery with single stenosis and artery with double stenosis (Fig. 1) was made. Later geometry for different area reduction at the stenosis region was made.

Fig. 1
figure 1

Model artery without stenosis, with single stenosis (a) and double stenosis (b) with different area reductions for simulations

Full size image

The artificial geometrical model of the blood vessel with stenosis was created by using the following formula of cosine curve [7],

$$ \frac{r(Z)}{R}=1-{\delta}_c\left[1+\cos \left(\frac{Z\pi}{D}\right)\right],\kern0.75em -D\le Z\le D $$
(1)

This equation was modified for double stenosis as follows:

$$ \frac{r(Z)}{R}=\Big\{1-{\delta}_c\left[1+\cos \left(\frac{Z\pi}{D}\right)\right],{\kern0.75em }_{5D\le Z\le 7D}^{-D\le Z\le D} $$
(2)

In eq.1, r and Z are the radial and axial coordinates respectively; R and D are the radius and diameter of the un-stenosed vessel respectively. The percentage of the stenosis was controlled by the parameter δc. The constrictions of the artery followed in the cosine curve with the reduction of the area. For single stenosis, the area was reduced as 60% and 75%. For double stenosis, the area of first and second stenosis was reduced as 60% and 60%, 60% and 75%, 75% and 60%, and 75% and 75%. This smooth reduction of the cross-sectional area produced the inside of the vessel by using eq. 1. This provides a fairly accurate representation of the biological form of arterial stenosis. This was employed previously in theoretical calculations by Deshpande et al. [24] and Din et al. [25]. The entire span of the biological form of the model was taken as 540 mm (27D) [24], where diameter D = 20 mm and the length of the upstream, downstream, and stenosed zone are taken as 4D, 21D, and 2D, respectively for single stenosis. 4D, 2D, 4D, 2D, and 15D are the length of upstream, first stenosis, first downstream, second stenosis, and second downstream respectively. In most of the cases, blood flow through different models was considered as incompressible and Newtonian-homogeneous fluid [23] with a density (ρ) of j1060 kg/m3. The constant dynamic viscosity (μ) was taken as of 3.71 × 10−3 Pa s whereas in this study non-Newtonian model has been used.

The Reynolds averaged Navier–Stokes equations (RANS equations) were considered as the governing equations for blood flow motion. The RANS equations are time-averaged equations of motion for fluid flow. The equations are generally used to describe the turbulent flows and the idea is to Reynolds decomposition where an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities [26]. RANS models employ an empirical closure hypothesis to compute the components of the Reynolds stress tensor [27]. Classification of RANS models is based on the number of additional differential transport equations required to determine turbulence quantities [28]. After applying the Reynolds time-averaging techniques, the Reynolds averaged Navier–Stokes (RANS) are obtained as tensor form [29] as:

$$ \frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{i}}}=0 $$
(3)
$$ \frac{\partial }{\partial t}\left(\rho {u}_i\right)+\frac{\partial }{\partial {x}_j}\left(\rho {u}_i{u}_j\right)=-\frac{\partial p}{\partial {x}_i}+\frac{\partial }{\partial {x}_j}\left[\mu \left(\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial {u}_j}{\partial {x}_i}\right)\right]+\frac{\partial {\tau}_{ij}}{\partial {x}_j} $$
(4)

In eqs. 2 and 3, xi = (x, y, z) are the Cartesian coordinate systems, ui is the mean velocity components, ρ is the density, p is the pressure, and τij are the Reynolds stress (wall shear stress). The Boussinesq hypothesis is employed to model the Reynolds stress τij for our current simulations. The Reynolds stress is the component of the total stress tensor in a fluid obtained from the averaging operation over the Navier–Stokes equations to account for turbulent fluctuations in fluid momentum [30]. Reynolds stress model can successfully capture the turbulence characteristics [31]. Recently, a theoretical basis for determination of the Reynolds stress in canonical flows has been presented [32]. It is based on the turbulence momentum balance for a control volume moving at the local mean flow speed [33]. Therefore, it constitutes a Lagrangian analysis for the momentum transport, which happens to contain the Reynolds stress term [33].

This is given as follows:

$$ {\tau}_{ij}=-\rho \left\langle u{\hbox{'}}_iu{\hbox{'}}_j\right\rangle ={\mu}_t\left(\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial {u}_j}{\partial {x}_i}\right)-\frac{2}{3}\rho k{\delta}_{ij} $$
(5)

In eq. 4, u'i are the fluctuating velocity components and \( k=\frac{1}{2}\left\langle u{\hbox{'}}_iu{\hbox{'}}_j\right\rangle \) is the turbulent kinetic energy. The turbulent eddy viscosity is denoted as μt which is obtained by employing the standard k-ω model of Wilcox. The eddy viscosity is modeled as:

$$ {\mu}_t=\frac{\rho k}{\omega } $$
(6)

where ω is the specific dissipation rate.

The following equation of Wilcox [18] is solved to obtain k and ω:

$$ \frac{\partial k}{\partial t}+\frac{\partial k\left\langle {u}_j\right\rangle }{\partial {x}_j}=-\frac{1}{\rho}\left\langle \rho u{\hbox{'}}_iu{\hbox{'}}_j\right\rangle \frac{\partial \left\langle {u}_i\right\rangle }{\partial {x}_j}-{\beta}^{\ast } k\omega +\frac{\partial }{\partial {x}_j}\left[\frac{1}{\rho}\left(\mu +{\sigma}^{\ast }{\mu}_t\right)\frac{\partial k}{\partial {x}_j}\right] $$
(7)
$$ \frac{\partial \omega }{\partial t}+\frac{\partial \omega \left\langle {u}_j\right\rangle }{\partial {x}_j}=-{\alpha}_1\frac{\omega }{\rho k}\left\langle \rho u{\hbox{'}}_iu{\hbox{'}}_j\right\rangle \frac{\partial \left\langle {u}_i\right\rangle }{\partial {x}_j}-{\beta \omega}^2+\frac{\partial }{\partial {x}_j}\left[\frac{1}{\rho}\left(\mu +{\sigma \mu}_t\right)\frac{\partial \omega }{\partial {x}_j}\right] $$
(8)

where σ* = 0.5, ß* = 0.072, σ = 0.5, α1= 1.0, ß = 0.072

In computational fluid dynamics, the k–omega (k–ω) turbulence model is a common two-equation turbulence model, that is used as an approximation for the Reynolds-averaged Navier–Stokes equations. The model attempts to predict turbulence by two partial differential equations for two variables, k and ω, with the first variable being the turbulence kinetic energy (k) while the second (ω) is the specific rate of dissipation. Details of the derivation of the model (eqs. 7 and 8) are given in Wilcox [34] and Wilcox [35]. The detailed descriptions of these turbulent models are explained in Varghese et al. [36].

When blood is treated as non-Newtonian fluid and then the viscosity of blood can be calculated from different models such as the Power-law model, Cross model, and Carreau model. In this study, the well-known Carreau model was used with parameters verified by previous studies [20]. The Carreau model is defined as:

$$ \mu \left(\left|\overset{\bullet }{\gamma}\right|\right)={\mu}_{\infty }+\left({\mu}_0-{\mu}_{\infty}\right){\left[1+{\left(\lambda \overset{\bullet }{\gamma}\right)}^2\right]}^{\left(n-1\right)/2} $$
(9)

where μ∞ (0.00345 Pa) is the infinite shear viscosity, μ0 (0.056 Pa) is the blood viscosity at zero shear rate, γ is the instantaneous shear rate, λ (3.313) is the time constant which is associated with the viscosity that changes with shear rate and n is the power-law index.

A total of seven inflexible and solid circular model arteries were used as the model artery with different symmetric stenosis. Firstly, the geometry of an inflexible and solid circular model artery without stenosis was developed. Secondly, the geometry of two arteries with single stenosis (i.e., 60% and 75% area reduction) was developed. Thirdly, the geometry of four arteries with double stenosis (i.e., 60% and 60%, 60% and 75%, 75% and 75%, and 75% and 60% area reduction) was developed.

Boundary conditions and computational procedure

No-slip boundary condition with zero velocity (ui = 0) relative to the boundary along with a pulsatile velocity profile has been imposed at the inlet of the model. The pulsatile velocity profile is computed with the following equation:

$$ {\displaystyle \begin{array}{l}{V}_{inlet}(t)=\left\{\begin{array}{l}0.5\sin \left[4\pi \left(1+0.0160236\right)\right]:0.5n<t\le 0.5n+0.218\\ {}0.1:0.5n+0.218<t\le 0.5\left(n+1\right)\end{array}\right.\\ {}n=0,1,2,.\dots \dots \dots \end{array}} $$
(10)

where V (0.5) Vis the bulk stream-wise velocity related to the Reynolds number, Re = ρVD/μRe = ρVD/μ of the blood flow. Inside the blood-vessel, a proportion of the forward spiral velocity (Ω) was calculated by using the following equation:

$$ \Omega =\frac{V}{R}C $$
(11)

A constant C= 1/6 was used to limit the magnitude of the spiral speed.

The outlet of the model has been treated as a pressure outlet and setting for the gauge pressure to become 13332 Pa as the systolic and diastolic pressure of a healthy human is around 15999 Pa (i.e., 120 mmHg) and 10666 Pa (i.e., 80 mmHg), respectively. Thus, the average pressure of the two phases, we use 100 mmHg (around 13332 Pascal). All simulations were performed with the commercially available computational fluid dynamics (CFD) software Fluent [37]. This software uses finite volume method for the discretization of the flow governing equations. The finite volume method evaluates partial differential equations in the form of algebraic equations. Pressure based solver was used to solve the flow equations with the implicit formulation method. Besides, the semi-implicit method for pressure-linked equation scheme for pressure-velocity coupling was used. In the spatial discretization process, the least squares based cell scheme was used for the gradient and bounded central differencing scheme was used for momentum. Bounded second-order implicit scheme was used for transient formulation, while the second-order accurate scheme was used for the Poisson-like pressure equation. The minimum time-step size used for the simulation was 1 × 10−2 s with 10000 numbers of total time-steps. The maximum iterations were 20 per each time step to collect the statistical data. The inlet boundary conditions for the stream-wise velocity was written in C-language using the interface of user defined function of Fluent and linked with the solver. The solution process was initiated using arbitrary values of the velocity components and k-ω, and their residuals are monitored at every iteration. The magnitude of the residuals dropped gradually, which is a strong indicator of stable and accurate solutions. The iteration process was stopped when the residuals are leveled off at 10−4 and the final converged solutions are achieved.

Results and discussion

To check the sensitivity of the numerical solutions that are independent of the choice of the grid arrangements, a grid-independent test was carried out. Grid independence test is a mesh convergence test meaning that computing the solution on successively finer grids. The difference between the two refinements is usually taken as a measure of the accuracy of the coarser of the two. It will never show independence unless the difference is of the order of machine zero. We used three different mesh grids points (grids 1, 2, and 3) to perform the grid independence tests. The grids are developed automatically using a regular interval using the CFD software. Firstly, the computational domain for grid 1 was discretized into a total number of 77520 control volumes. For grid 2, the total number of control volumes was increased to 32% of grid 1 (i.e., 102570 control volumes). Finally, for grid 3, total of 127,540 control volumes were used which is approximately 64% increase of total control volumes of grid 1. Grid independence test suggested that the axial velocity profiles at two different positions (at 0D and 1D positions of the model artery with 75% and 60% area reduction, respectively) remain similar for the arteries with different control volumes of grids 1, 2, and 3 (Fig. 2a and b). Similar results were found for the centerline axial velocity (Fig. 2c) and the centerline pressure along the flow (Fig. 2d). This suggests that simulations of this study are independent of the grid.

Fig. 2
figure 2

Grid dependency test for the simulations. a velocity at 0D position, b velocity at 1D position, c centerline axial velocity, and d pressure

Full size image

Figure 3 shows the change in axial velocity in normal artery, and artery with single and double stenosis at different area reduction. The axial velocity was almost similar (0.2 m/s) throughout the artery while no stenosis was considered. However, when stenosis was considered in the artery, the values drastically change and axial velocity peaks at the stenosis. For single stenosis, one peak in the velocity and for double stenosis two major peaks in the axial velocity was observed. It is notable that axial velocity differs significantly between normal artery and stenosed artery. From the contour plots (Fig. 4a and b), the axial velocity distribution can be observed quite easily. Although the magnitude of axial velocity depends on the percentage of area reduction, for multiple stenoses, the magnitude of the maximum velocity was found almost similar (0.57 m/s). Distinctive velocities with rapid change in magnitudes are also found at the throat of the stenosed arteries as well. For both cases, i.e., single and double stenosis, at the stenosis region axial velocity increased with the increase of area reduction. The velocity eventually creates a three dimensional twisting effect on the blood flow. The intensity of the twisting effect increases in the downstream, which can also be explained by the streamlines velocity. Similar results are also reflected in the plot of velocity vectors at different positions (Fig. 5a and b). Our findings of axial velocity are consistent with the study of Mishra and Panda [38], and Young and Tsai [14].

Fig. 3
figure 3

Changes in axial velocity in normal artery and arteries with single and multiple stenosis

Full size image
Fig. 4
figure 4

a Velocity contour for single stenosis along XY plane, and b velocity contour for multiple stenoses along XY plane

Full size image
Fig. 5
figure 5

Velocity at different surfaces along stream-wise direction

Full size image

The effect on total pressure in the modeled arteries is shown in Figs. 6 and 7. The pressure distribution in the blood vessel wall is irregular and segmental. In addition, the pressure at the inlet is overall larger than the outlet. Pressure variation is observed with the change in stenosis areas and the larger the stenosis the larger the pressure drop. A maximum pressure drop of 70 Pa was found in the case of the 75-75% stenosed artery. While one pressure drop occurred for single stenosis, multiple pressure drops occurred for the same number of stenosis.

Fig. 6
figure 6

Variation of pressure in the normal arter and arteries with single and double stenosis

Full size image
Fig. 7
figure 7

a Pressure contour for single stenosis and b pressure contour for multiple stenoses

Full size image

In the artery with single stenosis, pressure peaks before the stenosis and pressure drops largely at the stenosis and remain constant to the rest of the artery. In the artery with single stenosis, pressure peaks before the first stenosis and pressure drops largely after the first stenosis. After this drop, pressure increases again until the start of the second stenosis. Similar to the first stenosis, pressure drops at the second stenosis. The intensity of the pressure increases with the increase in the area reduction on the artery, i.e., the higher reduction in area causes a higher level of drops in pressure. The change in pressure after and before the stenosis is also reflected in the pressure contour plot (not shown here). A similar result for the pressure drop at the stenosis was found by Manchester et al. [39] and Abdelsalam, Mekheimer [40]. Venkateswarlu and Rao [41] found that pressure increases with the increase in the area reduction on the artery which is similar to our findings.

The effect on radial velocity in the modeled arteries is shown in Fig. 8. The radial velocity is stable (magnitude is almost zero) throughout the artery without stenosis. However, in the artery with single stenosis, there is a slight peak in the radial velocity at the stenosis. However, this peak is negligible. The radial velocity in the arteries with the double stenosis shows different patterns compared to normal and artery with single stenosis. Radial velocity peaks twice at the artery with double stenosis, i.e., two peaks at the two stenosis regions. It is important to note that the radial velocity is positively related to the area reduction of the artery, and, in the case of multiple stenoses, maximum velocity increase is observed at the first stenosis. Mustapha et al. [42] found two peaks in radial velocity at the two stenosis regions. A positive relation of radial velocity with the area reduction of the artery was found by Kanai et al. [43]. These findings are in line with the output of the simulations from our model.

Fig. 8
figure 8

Effect on radial velocity (× 10−2, left) and tangential velocity (× 10−2, right)

Full size image

The tangential velocity in the modeled arteries (Fig. 8) shows a similar pattern of radial velocity. The tangential velocity is nearly zero throughout the artery without stenosis, i.e., tangential velocity is stable in the normal artery. In the artery with the single stenosis, there is a slight peak in the tangential velocity at the stenosis and this peak is not significantly high. On the other hand, for multiple stenosed arteries, multiple peaks in the velocity have been observed.

The influence of flow on the wall shear stress (WSS) at different arteries is shown in Fig. 9. WSS plays a very crucial role in the analysis of atherosclerosis in arteries [44]. Even the rupture of plaque can occur due to higher values of WSS. Moreover, low and oscillating wall shear stress is known to be responsible for the formation of plaque [45]. For each artery, the wall shear stress is studied at two perpendicular planes of the artery. The wall shear stress is similar throughout the artery without stenosis. Maximum wall shear stress occurs at upstream to the throat, so this can lead to the possibility of rupture of plaque at this location. This is consistent with the model outputs of Lovett and Rothwell [46] and Sweed and Mekheimer [47]. An increase in severity increases the WSS as flow accelerates more due to an increase in occlusion level to maintain flow rate. The severity of the stenosis increases from 60 to 75%, WSS increases by almost 117%. Besides, the maximum WSS was found to be 19.07 Pa for 75-60% stenosis combination. From this value, we can conclude that WSS becomes maximum when the first stenosis has more area reduction than the following stenosis. For double stenosis, the value of WSS increased slightly compared to the single stenosis although the length between the stenosis has been kept constant throughout the experiment. The artery with single stenosis shows one peak while the artery with double stenosis shows double peaks. From our study, it is clear that the WSS increase with the increase in the area of reduction at the stenosis.

Fig. 9
figure 9

Effect on wall sheer stress for single and multiple stenoses

Full size image

The eddy viscosity shows that before the stenosis the eddy viscosity is high. However, after the stenosis, the eddy viscosity drops and remains constant throughout the artery. The turbulence kinetic energy (TKE) also shows that before the stenosis the TKE is higher. However, after the stenosis, the TKE drops and remains constant throughout the artery. In the normal artery (i.e., without any stenosis).

Conclusions

Arterial stenosis with double stenosis with different area reduction is poorly defined. However, data from existing studies indicate that the arterial stenosis for patients with different area reduction is sufficiently defined. Due to the lack of information on the change in fluid parameters in an artery with double stenosis and different area reduction had created many problems to understand the heart disease problem associated with plaque deposition. This study depicted the changes in velocity distribution, pressure drop, and wall shear stress in the stenosed artery, artery with single and double stenosis at different area reduction. This investigation can play a vital role in the determination of axial velocity, shear stress, and fluid acceleration in particular situations. Since this study has been carried out for a situation, it bears the promise of significant application in cardiovascular disease treatment, which has gained enough popularity. After simulations, we found a significant difference in stated fluid properties among the three types of arteries (i.e., stenosed artery, artery with single and double stenosis at different area reduction). The fluid properties showed a peak in an occurrence at the stenosis for both in the artery with single and double stenosis. Besides, we also found that the magnitudes of stated fluid properties increase with the increase of the area reduction. Our findings may enable risk assessment of patients with cardiovascular diseases and can play a significant role to find a solution to such types of diseases.