1 Background

When waves advance into the region of shallow water, they tend to be affected by the ocean bottom. This leads to the disruption of free water in orbital motion, and the water molecules in the orbital motion can no longer return to their initial position. In turn, environmental hazards such as coastal erosion and the tsunami wave described in [19] are caused by this phenomenon, which often leads to loss of land and damage to the properties of people living in coastal regions [43]. Sailors do simulate the consequences of shallow water waves as it increases the realism of the virtual ocean scene and also supplies accurate parameters to the ship maneuvering model [3]. The intensity of a water wave can be measured by its dispersion. This dispersion is either caused by the interaction of the wave with the transmitting medium or by the geometry and physical constraints [32]. Different mathematical models have been developed to study the impact, significance, and ways of controlling water waves. Among these models are the Boussinesq wave model and the shallow water wave model in [37] and [41], respectively.

Of interest is the dispersive partial differential equation named the Korteweg–de Vries (KDV) equation [26]. It governs weakly and nonlinearly interacting radio waves above 1 km in wavelength with a frequency of 300 kHz traveling in canals of shallow water [28]. The general form of this equation can be found in [8, 31]. The homogenous Korteweg–de Vries equation [7, 36], which described the mathematical model of solitary water waves in a shallow water domain, was coined by Kruskal and Zabusky [2, 9, 17]. Unlike the shallow water equation (which does not take into account the frequency of wave dispersion) and the Boussinesq wave equation (where the use of wave reflections is limited), the Korteweg–de Vries equation can be applied to waves propagating in a single direction that have both frequency and amplitude of dispersion. A recent study in [14] discussed the behavior of different types of traveling waves in the solution of relativistic wave equations associated with the notable Schrödinger equation.

Although the analytic solution of this problem is often not feasible to obtain, an analytic study on the solution of a third-order dispersive partial differential equation was conducted in [13]. The Laplace–Adomian decomposition method (LADM) was applied in [27] to obtain the analytical solutions of third-order dispersive fractional partial differential equations. The fractional derivatives are in Caputo sense, and the approximate solution obtained converges directly to the exact solutions. Some semi-analytic techniques have also been employed to solve this well-known equation, one of which is in [39], where the Laplace–Adomian decomposition method (LADM), differential transform method (DTM), homotopy perturbation method (HPM), and homotopy perturbation transform method (HPTM) were applied to obtain the solution of linearized dispersive KDV equations. Other numerical techniques, such as the variational iteration method (VIM) proposed by [33], were applied in [6] to solve the higher-order nonlinear KDV equation, and its modification was applied in [7] to obtain the analytical solution of this equation.

Lately, fractional calculus has been an area of interest for modern researchers. This is due to the higher degree of freedom and more realistic behavior exhibited by physical problems governed by it. There exists a diverse set of fractional operators; these consist of the Riemann–Liouville [44], Caputo [11], Caputo–Fabrizio [42], and Antagana–Baleanu [12] operators. These operators are often used as generalized tools for investigating diverse phenomena with a non-local kernel, such as fractal and chaotic phenomena with long-range memory. The strength and limitations of these concepts can be found in [44]. Several authors have proposed potent mathematical models capable of simulating chaotic and fractal systems. An example is a study presented in [29] where the numerical solutions and synchronization of a variable-order fractional chaotic system were conducted. A research study on the robust study of listeriosis disease was carried out in [38]. Their study implemented the use of fractal fractional operators to conduct their analysis. Their results show that these operators are productive for the purpose of their study.

Water waves are one of the many non-localized physical phenomena described by natural processes found around us. The sequencing pattern of the motion caused by water waves is often associated with fractals [16]. Research presented in [25] shows that modeling of these patterns cannot be carried out with ordinary classical derivatives that are localized. They claimed that the long-established differentiation technique (integer-order derivatives) is local and that using it to describe physical phenomena with unbounded disparities would be inappropriate because the impact of a larger neighborhood could not be ignored. They discussed that a fractional derivative is a global operator, whose properties thrive on examining the impacts of a larger neighborhood ignored by the local operator as it creates the likelihood of several possibilities for backward and forward motion of waves. They concluded that a non-localized derivative such as the Caputo fractional-order derivative should be employed in the modeling of water waves. The properties and application of these non-localized derivatives were applied in [15], where hybrid Caputo fractional modeling for thermostats with hybrid boundary value conditions was carried out. Investigation of a new version of HIV mathematical model using a new approach to fractional derivatives (Caputo–Fabrizio) was applied in [45]. This Caputo–Fabrizio fractional derivative was also applied in [1] to a mathematical theoretical study for the Rubella disease model, as they stated that fractional derivatives, such as Caputo and Riemann derivatives, have their own limitations because their kernel is singular and they cannot be applied to describe the memory effect of the physical system applicable to their problem.

To obtain the solutions of the fractional-order Korteweg–de Vries equation, researchers in [18] successfully applied the fractional differential transform method (FDTM) and modified differential transform method (MDTM) to obtain the solution of the third-order dispersive partial differential equation. In [20], the Laplace–Adomian decomposition method was applied to obtain the solution of the fractional-order model of measles, and in [21], this same method was applied to obtain the numerical solution of the fractional-order smoking model.

In this paper, an initial guess technique applied in [4, 5, 40] is modified to be of arbitrary order in a Caputo sense. We coupled it with the homotopy perturbation method introduced in [22, 23, 34, 35] to suit the computation of an approximate solution of the fractional-order Korteweg–de Vries equation of the form:

$$u_{t}^{\alpha } (x,t) + \xi u(x,t)u_{x} (x,t) + \gamma u_{xxx} (x,t) = 0,\quad 0 < \alpha \le 1$$
(1)

subject to the initial condition:

$$u(x,0) = \phi (x).$$
(2)

\(u(x,t)\) is a function of real variables which denotes the wave elongation at space \(x\) and time \(t,\) respectively. \(u(x,t)u_{x} (x,t)\) is the nonlinear term, \(u_{xxx} (x,t)\) represents the direction of the wave dispersion, and \(\xi ,\gamma\) are arbitrary constants put in place to obtain a uniformly propagating wave solution.

2 Methods

2.1 Preliminaries

Here, we state some fundamental properties of fractional calculus applicable in this paper.

Definition 1

A real function \(\phi (t),\,\,t > 0,\,\,\) is said to be in the space \(C_{\mu \,} ,\,\,\mu \in R\,\) if there exist a real number \(m > \mu\) such that \(\phi (t) = t^{m} \phi_{1} (t).\,\) where \(\phi_{1} (t) \in C(0,\infty ),\) and it is said to be in the space \(C^{n}_{\mu \,}\) if and only if \(\phi^{(n)} \in C_{\mu } ,\,n \in N.\)

Definition 2

The Riemann–Liouville fractional integration of order \(\eta \ge 0\) for a real positive function \(\phi (t) \in C_{\mu \,} ,\,\,\mu \ge - 1\,\,\,t > 0\) is defined as:

$$I^{\eta } \phi (t) = \frac{1}{\Gamma (\eta )}\int\limits_{0}^{t} {(t - x)^{\eta - 1} \phi (x)dx} .$$

The following properties hold for fractional integral operator \(I^{\eta }\) for \(\phi (t) \in C_{\mu \,} ,\,\,\mu \ge - 1\,\,\,\eta ,\alpha \ge 0\,\) and \(\,\beta \ge - 1\):

  1. 1.

    \(I^{\eta } I^{\alpha } \phi (t) = I^{\eta + \alpha } \phi (t),\)

  2. 2.

    \(I^{\eta } I^{\alpha } \phi (t) = I^{\alpha } I^{\beta } \phi (t),\)

  3. 3.

    \(I^{\eta } t^{\beta } = \frac{\Gamma (\beta + 1)}{{\Gamma (\eta + \beta + 1)}}t^{\eta + \beta } .\)

Definition 3

The Caputo fractional derivative of a positive real function \(\phi (t) \in C_{\mu }\) is mathematically expressed as

$$D^{\eta } \phi (t) = \frac{1}{\Gamma (n - \eta )}\int\limits_{0}^{t} {(t - x)^{n - \eta - 1} \phi^{(n)} (x)dx} ,\quad n - 1 < \eta \le n,n \in N.$$

The fractional integration of Caputo derivative for \(n - 1 < \eta \le n,\,\,n \in N,\,\,\phi \in \mathop c\nolimits_{ - 1}^{n} ,\,\mu \ge - 1\) is:

$$I^{\eta } D^{\eta } \phi (t) = \phi (t) - \sum\limits_{k = 0}^{n - 1} {\phi^{(k)} (0)\frac{{t^{k} }}{k!}} .$$

2.2 Homotopy perturbation method

The fundamental scheme of He’s homotopy perturbation method can be illustrated by considering the general nonlinear differential equation of the form:

$$D(u) - f(\omega ) = 0,\quad \omega \varepsilon \Omega .$$
(3)

subject to the boundary condition:

$$\beta (u,u_{n} ) = 0,\quad \omega \varepsilon \Gamma .$$
(4)

The general differential operator is denoted by \(D\) and the boundary operator by \(\beta\). \(f(\omega )\) is an analytic function, and \(\Gamma\) is the boundary operator in the domain \(\Omega\). The operator \(D\) is separable into two parts:

$$D^{\alpha } (u) = \ell (u) + \eta (u).$$
(5)

The functions \(\ell \,and\,\,\eta\) represent the linear and nonlinear operator, respectively. Substituting Eq. (5) into Eq. (3) yields

$$\ell (u) + \eta (u) - f(\omega ) = 0.$$
(6)

A homotopy can be constructed for Eq. (6):

$$H(v,p) = (1 - p)\left[ {\ell (v) - \ell (u_{0} )} \right] + p\left[ {D(v) - f(\omega )} \right] = 0;$$
(7)

simplifying Eq. (7) yields

$$H(v,p) = \ell (v) - \ell (u_{0} ) + p\ell \left[ {v_{0} } \right] + p\left[ {\eta (v) - f(\omega )} \right] = 0.$$
(8)

where \(p\) is an embedded parameter which undergoes deformation process of changing from 0 to 1: When \(p = 0,\)

$$H(v,0) = \ell (v) - \ell (u_{0} ) = 0,$$
(9)

and at \(p = 1,\)

$$H(v,1) = D(v) - f(\omega ) = 0.$$
(10)

A power series solution can be assumed for Eqs. (9) and (10):

$$v(x,t) = v_{0} (x,t) + pv_{1} (x,t) + p^{2} v_{2} (x,t) + \cdots p^{n} v_{n} (x,t),$$
(11)

and the approximate solution of Eq. (3) is:

$$\mathop {Lim}\limits_{p \to 1} v(x,t) = v_{0} (x,t) + v_{1} (x,t) + v_{2} (x,t) + \cdots v_{n} (x,t).$$
(12)

The convergence of this series has been proven in [34]. Substituting Eq. (11) into Eq. (8) and equating coefficients of equal powers of p,

$$\left. {\begin{array}{*{20}c} {p^{0} :v_{0} - f(\omega ) = 0,} \\ {p^{1} :v_{1} - H\left( {v_{0} } \right) = 0,} \\ \vdots \\ {p^{n} :v_{n} - H\left( {v_{0} ,v_{1} ,v_{2} ,v_{3} , \ldots ,v_{n - 1} } \right) = 0.} \\ \end{array} } \right\}$$
(13)

The approximate result of each iteration is obtained by solving Eq. (13).

2.3 Modified initial guess homotopy perturbation method (MIGHPM)

In view of the proposed modified initial guess homotopy perturbation method, a power series correctional functional of arbitrary order can be constructed for Eq. (1):

$$u(x,t) = u(x,0) + \sum\limits_{n = 1}^{\infty } {\lambda_{n} t^{n\alpha } } ,\quad 0 < \alpha \le 1.$$
(14)

Substituting the initial condition \(u(x,0) = \phi (x)\) into Eq. (14),

$$u(x,t) = \phi (x) + \lambda_{1} t^{\alpha } + \lambda_{2} t^{2\alpha } + \cdots .$$
(15)

From Eq. (15), \(\lambda_{1} t^{\alpha } = u_{1} (x,t),\,\,\lambda_{2} t^{2\alpha } = u_{2} (x,t),\) and so on.

As an assumed solution of Eq. (1), Eq. (15) must satisfy Eq. (1) with unique values of \(\lambda_{1} ,\,\,\lambda_{2} ,\,\lambda_{3} , \cdots \lambda_{n} .\) Thus to evaluate these values, the following derivatives are obtained:

$$u_{t} (x,t) = \lambda_{1} \Gamma (\alpha + 1) + \lambda_{2} \frac{\Gamma (2\alpha + 1)}{{\Gamma (\alpha + 1)}}t^{\alpha } + \cdots ,\;u_{x} (x,t) = \phi \prime (x),\;{\text{and}}\;u_{xxx} (x,t) = \phi \prime \prime \prime (x),$$
(16)

such that evaluation of Eq. (1) using Eq. (16) yields:

$$\left( {\lambda_{1} \Gamma (\alpha + 1) + \lambda_{2} \frac{\Gamma (2\alpha + 1)}{{\Gamma (\alpha + 1)}}t^{\alpha } + \cdots } \right) + \xi \left( {\phi (x) + \lambda_{1} t^{\alpha } + \lambda_{2} t^{2\alpha } + \cdots } \right)\phi \prime (x) + \gamma \phi \prime \prime \prime (x) = 0.$$
(17)

At \(t = 0\), Eq. (17) becomes,

$$\lambda_{1} \Gamma (\alpha + 1) + \xi \phi (x)\phi \prime (x) + \gamma \phi \prime \prime \prime (x) = 0.$$
(18)

And solving for \(\lambda_{1}\) yields:

$$\lambda_{1} = \frac{{ - \left( {\xi \phi (x)\phi ^{\prime}(x) + \gamma \phi \prime \prime \prime (x)} \right)}}{\Gamma (\alpha + 1)}.$$
(19)

Since \(u_{1} (x,t) = \lambda_{1} t^{\alpha }\), the first approximation is:

$$u_{1} (x,t) = \frac{{ - \left( {\xi \phi (x)\phi \prime (x) + \gamma \phi \prime \prime \prime (x)} \right)}}{\Gamma (\alpha + 1)}t^{\alpha } .$$
(20)

Subsequent approximations can be obtained by constructing a homotopy for Eq. (1):

$$(1 - p)\left[ {u_{t}^{\alpha } (x,t)} \right] + p\left[ {u_{t}^{\alpha } (x,t) + \xi u(x,t)u_{x} (x,t) + \gamma u_{xxx} (x,t)} \right] = 0,\quad 0 < \alpha \le 1.$$
(21)

Simplifying Eq. (21) yields:

$$u_{t}^{\alpha } (x,t) + p\left[ {\xi u(x,t)u_{x} (x,t) + \gamma u_{xxx} (x,t)} \right] = 0.$$
(22)

Substituting Eq. (11) into Eq. (22) and equating coefficients of equal powers of \(p^{n} ,\,\,n \ge 2\),

$$\left. {\begin{array}{*{20}c} {p^{2} :} & {\frac{{\partial^{\alpha } u_{2} (x,t)}}{{\partial t^{\alpha } }}} & + & {\xi \left( {u_{0} (x,t)\frac{{\partial u_{1} (x,t)}}{\partial x} + u_{1} (x,t)\frac{{\partial u_{0} (x,t)}}{\partial x}} \right)} & + & {\gamma \frac{{\partial^{3} u_{0} (x,t)}}{{\partial x^{3} }}} & = & {0,} \\ {p^{3} } & {\frac{{\partial^{\alpha } u_{3} (x,t)}}{{\partial t^{\alpha } }}} & + & {\xi \left( {u_{0} (x,t)\frac{{\partial u_{2} (x,t)}}{\partial x} + u_{1} (x,t)\frac{{\partial u_{1} (x,t)}}{\partial x} + u_{2} (x,t)\frac{{\partial u_{0} (x,t)}}{\partial x}} \right)} & + & {\gamma \frac{{\partial^{3} u_{1} (x,t)}}{{\partial x^{3} }}} & = & {0.} \\ \vdots & \vdots & {} & \cdots & {} & \vdots & {} & \vdots \\ \end{array} } \right\}$$
(23)

The coefficient of \(p^{2}\) is evaluated using Eq. (20), and the Riemann–Liouville fractional integral operator \(I^{\alpha }\) is applied to obtain the second approximation \(u_{2} (x,t)\). Subsequent approximations \(u_{3} (x,t),u_{4} (x,t), \ldots\) are likewise computed.

Theorem 1

Let there be a contractive nonlinear mapping \(\tau :\aleph \to Y\) defined on two Banach spaces \(\aleph\), \(Y\;\forall \;m,n \in \aleph\) then \(\left\| {\tau (m) - \tau (n)} \right\|_{Y} \le \varepsilon \left\| {m - n} \right\|_{\aleph }\), \(0 < \varepsilon < 1\) such that the sequence \(m_{s + 1} = \tau^{n} (m_{0} ) = \tau (m_{0} )\) for some \(m_{0} \in \aleph\) which converges to a unique fixed point \(\tau\) [30].

Proof

Consider the Picard sequence \(m_{s + 1} = \tau (m_{s} ) \subseteq Y\) we want to show that \(m_{s}\) is convergent in \(Y\) for all \(r \ge s\) \(\left\| {m_{s} - m_{r} } \right\| \le \left\| {m_{s} - m_{s + 1} } \right\| + \left\| {m_{s + 1} - m_{s + 2} } \right\| + \left\| {m_{s + 2} - m_{s + 3} } \right\| + \cdots + \left\| {m_{s - 1} - m_{r} } \right\|\).

We define the proof by applying mathematical induction on the contractive property of (C):

\(\left\| {m_{s} - m_{s + 1} } \right\| \le \varepsilon^{s} \left\| {m_{0} - m_{1} } \right\|\). By implication, \(\mathop {\lim }\limits_{r \to \infty } \left\| {m_{s} - m_{r} } \right\| \le \frac{{\varepsilon^{s} }}{1 + \varepsilon }\left\| {m_{0} - m_{1} } \right\| = 0\,\,as\,\,s \to \infty\).

This proves that \((m_{s} )\) is convergent in \(Y\) and through completeness of \(Y\), we can find \(\omega \in Y\): \(\mathop {\lim }\limits_{s \to \infty } (m_{s} ) = \omega \in Y\). Clearly, the continuity of \(\tau\) is ensured by the contraction (C). Thus, \(\omega = \mathop {\lim }\limits_{s \to \infty } m_{s + 1} = m_{r}\).

3 Application and results

3.1 Example 1

Consider the dispersive KDV equation

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} - 6\mu (x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = 0,$$
(24)

subject to the initial condition:

$$\mu (x,0) = \frac{x - 2}{{12}}.$$
(25)

By modified initial guess homotopy perturbation method,

$$\mu (x,t) = \mu (x,0) + \lambda_{1} t^{\alpha } + \cdots .$$
(26)

Equation (24) is evaluated using the following derivatives in Eq. (27)

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} = \lambda_{1} \Gamma (\alpha + 1),\;\frac{\partial \mu (x,t)}{{\partial x}} = \frac{1}{12},\;\frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = 0,$$
(27)

such that at \(t = 0,\)

$$\lambda_{1} = \frac{(x - 2)}{{24\Gamma (\alpha + 1)}}.$$
(28)

Therefore,

$$\mu_{1} (x,t) = \frac{(x - 2)}{{24\Gamma (\alpha + 1)}}t^{\alpha } .$$
(29)

Constructing a homotopy for Eq. (24),

$$\left( {1 - p} \right)\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + p\left( {\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} - \mu (x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }}} \right) = 0;$$
(30)

simplifying Eq. (30),

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + p\left( { - 6\mu (x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }}} \right) = 0.$$
(31)

We can assume a series solution of the form:

$$\mu (x,t) = \mu_{0} (x,t) + p\mu_{1} (x,t) + p^{2} \mu_{2} (x,t) + \cdots p^{n} \mu_{n} (x,t).$$
(32)

Substituting Eq. (32) into Eq. (31) and equating coefficients of equal powers of \(p^{n} ,\,\,n \ge 2\);

$$p^{2} :\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} - 6\left( {\mu_{0} (x,t)\frac{{\partial \mu_{1} (x,t)}}{\partial x} + \mu_{1} (x,t)\frac{{\partial \mu_{0} (x,t)}}{\partial x}} \right) + \frac{{\partial^{3} \mu_{0} (x,t)}}{{\partial x^{3} }} = 0,$$
(33)
$$p^{3} :\frac{{\partial^{\alpha } \mu_{3} (x,t)}}{{\partial t^{\alpha } }} - 6\left( {\mu_{0} (x,t)\frac{{\partial \mu_{2} (x,t)}}{\partial x} + \mu_{1} (x,t)\frac{{\partial \mu_{1} (x,t)}}{\partial x} + \mu_{2} (x,t)\frac{{\partial \mu_{0} (x,t)}}{\partial x}} \right) + \frac{{\partial^{3} \mu_{1} (x,t)}}{{\partial x^{3} }} = 0.$$
(34)

Evaluating Eq. (33) using \(\mu_{0} (x,t)\,\,\& \mu_{1} (x,t)\),

$$\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} - \frac{(x - 2)}{{24\Gamma (\alpha + 1)}}t^{\alpha } = 0 \Rightarrow \frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} = \frac{(x - 2)}{{24\Gamma (\alpha + 1)}}t^{\alpha } .$$
(35)

Applying operator \(I^{\alpha }\) to both sides of Eq. (35),

$$\mu_{2} (x,t) = \frac{(x - 2)}{{24\Gamma (2\alpha + 1)}}t^{2\alpha } .$$
(36)

Repeating the iterative process,

$$\mu_{3} (x,t) = \left( {\frac{{(x - 2)4\left( {\Gamma (1 + \alpha )} \right)^{2} + \Gamma (1 + 2\alpha )}}{{96\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 3\alpha )}}t^{3\alpha } } \right),$$
(37)
$$\mu_{4} (x,t) = \left( {\frac{{(x - 2)4\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 2\alpha ) + \left( {\Gamma (1 + 2\alpha )} \right)^{2} + 2\Gamma (1 + \alpha )\Gamma (1 + 3\alpha )}}{{96\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 2\alpha )\Gamma (1 + 4\alpha )}}t^{4\alpha } } \right),$$
(38)

and so on. The subsequent terms can be evaluated using MATHEMATICA 12 software package.

The approximate solution of Eq. (24) is therefore obtained as:

$$\mu_{n} (x,t) = \left. \begin{gathered} \frac{x - 2}{{12}} + \frac{(x - 2)}{{24\Gamma (\alpha + 1)}}t^{\alpha } + \frac{(x - 2)}{{24\Gamma (2\alpha + 1)}}t^{2\alpha } + \frac{{(x - 2)4\left( {\Gamma (1 + \alpha )} \right)^{2} + \Gamma (1 + 2\alpha )}}{{96\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 3\alpha )}}t^{3\alpha } \hfill \\ \frac{{(x - 2)4\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 2\alpha ) + \left( {\Gamma (1 + 2\alpha )} \right)^{2} + 2\Gamma (1 + \alpha )\Gamma (1 + 3\alpha )}}{{96\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 2\alpha )\Gamma (1 + 4\alpha )}}t^{4\alpha } \hfill \\ \end{gathered} \right\}.$$
(39)

When \(\alpha = 1\),

$$\mu_{n} (x,t) = \frac{(x - 2)}{{12}} + \frac{(x - 2)t}{{24}} + \frac{{(x - 2)t^{2} }}{48} + \frac{{(x - 2)t^{3} }}{96} + \frac{{(x - 2)t^{4} }}{192} + \cdots .$$

And the closed form of the solution is

$$\mathop {\lim }\limits_{n \to \infty } \mu_{n} (x,t) = \frac{x - 2}{{12 - 6t}}$$

(Fig. 1, Table 1).

Fig. 1
figure 1

A traveling solitary translatory wave, which preserves its form by not interacting with any local disturbances. The directions of wave propagation in space and time coordinate \((x,t)\) at different degrees of freedom on the interval \(0 \le \alpha \le 1\) were presented in A–E. E particularly reflects that the translatory wave tends to converge to the exact direction of the wave propagation presented in F at an integer order

Full size image
Table 1 Numerical results of problem one at an exact value \(\alpha = 1\)
Full size table

3.2 Convergence of Solution

Following the theorem of nonlinear mapping \(X\), the convergence of modified initial guess homotopy perturbation method strictly relies on contraction \(X\).

Thus, \(\left\| {\mu_{0} - \mu_{e} } \right\| = \left\| {\frac{x - 2}{{12}} - \frac{x - 2}{{12 - 6t}}} \right\| = \frac{1}{12}\left\| {\frac{(x - 2)t}{{(t - 2)}}} \right\|\). For \(\frac{1}{2} < \kappa ,\,0 < \kappa < 1,\)

$$\left\| {\mu_{1} - \mu_{e} } \right\| = \left\| {\mu_{0} + \mu_{1} - \mu_{e} } \right\| = \left\| {\frac{1}{24}\frac{{(x - 2)t^{2} }}{(t - 2)}} \right\| \le \kappa \left\| {\mu_{0} - \mu_{e} } \right\|,$$
$$\left\| {\mu_{2} - \mu_{e} } \right\| = \left\| {\mu_{0} + \mu_{1} + \mu_{2} - \mu_{e} } \right\| = \left\| {\frac{1}{48}\frac{{(x - 2)t^{3} }}{(t - 2)}} \right\| \le \kappa^{2} \left\| {\mu_{0} - \mu_{e} } \right\|,$$
$$\left\| {\mu_{3} - \mu_{e} } \right\| = \left\| {\mu_{0} + \mu_{1} + \mu_{2} + \mu_{3} - \mu_{e} } \right\| = \left\| {\frac{1}{96}\frac{{(x - 2)t^{4} }}{(t - 2)}} \right\| \le \kappa^{3} \left\| {\mu_{0} - \mu_{e} } \right\|,$$
$$\left\| {\mu_{n} - \mu_{e} } \right\| = \left\| {(\mu_{0} + \mu_{1} + \mu_{2} + \cdots \mu_{2} ) - \mu_{e} } \right\| = \left\| {\frac{1}{{12 \cdot 2^{n} }}\frac{{(x - 2)t^{4} }}{(t - 2)}} \right\| \le \kappa^{n} \left\| {\mu_{0} - \mu_{e} } \right\|.$$

Clearly,\(\mathop {\lim }\limits_{n \to \infty } \kappa^{n} = 0\); therefore, \(\mathop {\lim }\limits_{n \to \infty } \left\| {\mu_{n} - \mu_{e} } \right\| \le \kappa^{n} \left\| {\mu_{0} - \mu_{e} } \right\| = 0\,\). Thus, modified initial guess homotopy perturbation method agrees that \(\mu_{e} = \mathop {\lim }\limits_{n \to \infty } \mu_{n} (x,t) = \frac{x - 2}{{12 - 6t}}\) which is the exact solution of the problem.

3.3 Problem 2

Consider the following linear homogenous KDV equation

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + 7\frac{\partial \mu (x,t)}{{\partial x}} + 6\frac{\partial \mu (x,t)}{{\partial x^{3} }} = 0,$$
(40)

subject to the condition:

$$\mu (x,0) = \cos (x).$$
(41)

By modified initial guess homotopy perturbation method, we can construct

$$\mu (x,t) = \mu_{0} (x,0) + \lambda_{1} t^{\alpha } + \cdots;$$
(42)

substituting Eq. (41) into Eq. (42),

$$\mu (x,t) = \cos (x) + \lambda_{1} t^{\alpha } + \cdots .$$
(43)

Equation (40) is evaluated using the following derivatives in Eq. (44),

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} = \lambda_{1} \Gamma (\alpha + 1),\quad \frac{\partial \mu (x,t)}{{\partial x}} = - \sin (x),\quad \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = \sin (x),$$
(44)

such that

$$\lambda_{1} \Gamma (\alpha + 1) + 7( - \sin x) + 6(\sin x) = 0.$$
(45)

Solving for \(\lambda_{1}\) in Eq. (45),

$$\lambda_{1} = \frac{\sin (x)}{{\Gamma (\alpha + 1)}}.$$
(46)

Since \(\mu_{1} (x,t) = \lambda_{1} t^{\alpha }\), therefore

$$\mu_{1} (x,t) = \frac{\sin (x)}{{\Gamma (\alpha + 1)}}t^{\alpha } .$$
(47)

To obtain further approximations, we construct a homotopy for Eq. (40):

$$(1 - p)\left[ {\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }}} \right] + p\left[ {\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + 7\frac{\partial \mu (x,t)}{{\partial x}} + 6\frac{\partial \mu (x,t)}{{\partial x^{3} }}} \right] = 0;$$
(48)

simplifying Eq. (48),

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} = p\left[ { - 7\frac{\partial \mu (x,t)}{{\partial x}} + 6\frac{\partial \mu (x,t)}{{\partial x^{3} }}} \right].$$
(49)

We assume a series solution of the form:

$$\mu (x,t) = \mu_{0} (x,t) + p\mu_{1} (x,t) + p^{2} \mu_{2} (x,t) + \cdots p^{n} \mu_{n} (x,t).$$
(50)

Substituting Eq. (50) into Eq. (49) and comparing coefficients of equal powers of \(p^{n} ,\,\,n \ge 2\),

$$\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} = - 7\frac{{\partial \mu_{1} (x,t)}}{\partial x} + 6\frac{{\partial \mu_{1} (x,t)}}{{\partial x^{3} }},$$
(51)
$$\frac{{\partial^{\alpha } \mu_{3} (x,t)}}{{\partial t^{\alpha } }} = - 7\frac{{\partial \mu_{2} (x,t)}}{\partial x} + 6\frac{{\partial \mu_{2} (x,t)}}{{\partial x^{3} }},$$
(52)
$$\begin{array}{*{20}c} {\frac{{\partial^{\alpha } \mu_{4} (x,t)}}{{\partial t^{\alpha } }}} & = & { - 7\frac{{\partial \mu_{3} (x,t)}}{\partial x}} & + & {6\frac{{\partial \mu_{3} (x,t)}}{{\partial x^{3} }},} \\ \vdots & {} & \vdots & {} & \vdots \\ \end{array}$$
(53)
$$\frac{{\partial^{\alpha } \mu_{n} (x,t)}}{{\partial t^{\alpha } }} = - 7\frac{{\partial \mu_{n - 1} (x,t)}}{\partial x} + 6\frac{{\partial \mu_{n - 1} (x,t)}}{{\partial x^{3} }}.$$
(54)

Evaluating Eq. (51) using \(\mu_{0} (x,t)\,\,\& \mu_{1} (x,t)\) and applying \(I^{\alpha }\) to both sides,

$$\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} = - \frac{\cos x}{{\Gamma (\alpha + 1)}}t^{\alpha } ,$$
(55)

and

$$I^{\alpha } \left( {\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }}} \right) = I^{\alpha } \left( { - \frac{\cos x}{{\Gamma (\alpha + 1)}}t^{\alpha } } \right),$$
(56)

such that

$$\mu_{2} (x,t) = - \frac{\cos x}{{\Gamma (2\alpha + 1)}}t^{2\alpha } .$$
(57)

Evaluating Eq. (53) using \(\mu_{0} (x,t)\,\,,\mu_{1} (x,t)\,\& \mu_{2} (x,t)\) yields

$$\frac{{\partial^{\alpha } \mu_{3} (x,t)}}{{\partial t^{\alpha } }} = - \frac{\sin x\,}{{\Gamma (2\alpha + 1)}}t^{2\alpha };$$
(58)

applying operator \(I^{\alpha }\),

$$\mu_{3} (x,t) = - \frac{\sin x}{{\Gamma (3\alpha + 1)}}t^{3\alpha } .$$
(59)

Subsequently the proceeding iterations are:

$$\left. {\begin{array}{*{20}c} {\mu_{4} (x,t) = \frac{\cos x}{{\Gamma (4\alpha + 1)}}t^{4\alpha } ,} & {\mu_{5} (x,t) = \frac{\sin x}{{\Gamma (5\alpha + 1)}}t^{5\alpha } ,} & {\mu_{6} (x,t) = - \frac{\cos x}{{\Gamma (6\alpha + 1)}}t^{6\alpha } ,} \\ {\mu_{7} (x,t) = - \frac{\sin }{{\Gamma (7\alpha + 1)}}t^{7\alpha } ,} & {\mu_{8} (x,t) = \frac{\cos x}{{\Gamma (8\alpha + 1)}}t^{8\alpha } ,} & {\mu_{9} (x,t) = \frac{\sin x}{{\Gamma (9\alpha + 1)}}t^{9\alpha } .} \\ \end{array} \cdots } \right\}$$
(60)

And the approximate result is

$$\mu_{n} (x,t) = \left. \begin{gathered} \cos x + \frac{\sin x}{{\Gamma (\alpha + 1)}}t^{\alpha } - \frac{\cos x}{{\Gamma (2\alpha + 1)}}t^{2\alpha } - \frac{\sin x}{{\Gamma (3\alpha + 1)}}t^{3\alpha } + \frac{\cos x}{{\Gamma (4\alpha + 1)}}t^{4\alpha } \hfill \\ \quad + \frac{\sin x}{{\Gamma (5\alpha + 1)}}t^{5\alpha } - \frac{\cos x}{{\Gamma (6\alpha + 1)}}t^{6\alpha } + \frac{\cos x}{{\Gamma (8\alpha + 1)}}t^{8\alpha } + \frac{\sin x}{{\Gamma (7\alpha + 1)}}t^{7\alpha } - \frac{\sin x}{{\Gamma (9\alpha + 1)}}t^{9\alpha } + \cdots . \hfill \\ \end{gathered} \right\}$$
(61)

such that

$$\mu_{n} (x,t) = \left. {\begin{array}{*{20}c} {\cos x\left( {1 - \frac{{t^{2\alpha } }}{\Gamma (2\alpha + 1)} + \frac{{\,t^{4\alpha } }}{\Gamma (4\alpha + 1)} - \frac{{t^{6\alpha } }}{\Gamma (6\alpha + 1)} + \frac{{t^{8\alpha } }}{\Gamma (8\alpha + 1)} + \cdots } \right)} \\ {\quad + \sin x\left( {\frac{{t^{\alpha } }}{\Gamma (\alpha + 1)} - \frac{{t^{3\alpha } }}{\Gamma (3\alpha + 1)} + \frac{{t^{5\alpha } }}{\Gamma (5\alpha + 1)} - \frac{{\sin t^{7\alpha } }}{\Gamma (7\alpha + 1)} + \cdots } \right)} \\ \end{array} } \right\}$$
(62)

When \(\alpha = 1\),

$$\mu_{n} (x,t) = \cos x\left( {1 - \frac{{t^{2} }}{2} + \frac{{\,t^{4} }}{4!} - \frac{{t^{6} }}{6!} + \frac{{t^{8} }}{8!} + \cdots } \right) + \sin x\left( {t - \frac{{t^{3} }}{3!} + \frac{{t^{5} }}{5!} - \frac{{t^{7} }}{7!} + \cdots } \right)$$
(63)

The modified method agrees that

$$\mathop {\lim }\limits_{n \to \infty n} \mu (x,t) = \mu (x,t).$$
(64)

By convergence, the exact solution is

$$\mu (x,t) = \cos x\cos t + \sin x\sin t.$$

In closed form (Fig. 2, Table 2),

$$\mu (x,t) = \cos (x - t).$$
Fig. 2
figure 2

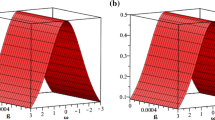
A traveling transverse wave which occurrence can be in the form of surface ripples on water. A–H show the different types of disturbance caused by the wave as \(0 \le \alpha \le 1\). In E, it could be observed that proper crests are formed as \(\alpha \to 1\). This means that the frequency of the disturbance will peak at an integer order. Figure G shows the behavioral pattern of the wave amplitude at different levels of \(\alpha\). The amplitude is periodically accelerated as \(\alpha\) increases, and the highest amplitude is recorded as a unit for the wavelength considered. In H, the efficiency of the modified initial guess technique is proved as it produces an approximate result that converges to the exact solution

Full size image
Table 2 Numerical results of problem two at an exact value \(\alpha = 1\)
Full size table

3.4 Problem 3

Consider the following nonlinear homogenous KDV equation

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + \xi u(x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = 0,$$
(65)

subject to the initial condition

$$\mu (x,0) = x.$$
(66)

By modified initial guess homotopy perturbation method,

$$\mu (x,t) = \mu (x,0) + \lambda_{1} t^{\alpha } + \cdots ,$$
(67)
$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} = \lambda_{1} \Gamma (\alpha + 1),\quad \frac{\partial \mu (x,t)}{{\partial x}} = 1,\quad \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = 0.$$
(68)

Evaluating Eq. (65) using Eq. (68),

$$\lambda_{1} \Gamma (\alpha + 1) + \xi \left( {x + \lambda t^{\alpha } } \right) = 0.$$
(69)
$${\text{At}}\;t = 0,\;\lambda_{1} = \frac{ - \xi x}{{\Gamma (\alpha + 1)}}.$$
(70)

Thus,

$$\mu_{1} (x,t) = \frac{ - \xi x}{{\Gamma (\alpha + 1)}}t^{\alpha }$$
(71)

Constructing a homotopy for Eq. (65),

$$\left( {1 - p} \right)\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + p\left( {\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} + \xi \mu (x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }}} \right) = 0.$$
(72)

Simplifying Eq. (72),

$$\frac{{\partial^{\alpha } u(x,t)}}{{\partial t^{\alpha } }} + p\left( {\xi u(x,t)\frac{\partial u(x,t)}{{\partial x}} + \frac{{\partial^{3} u(x,t)}}{{\partial x^{3} }}} \right) = 0.$$
(73)

Substituting Eq. (50) into Eq. (73) and comparing coefficients of equal powers of \(p^{n} ,\,\,n \ge 2\).

$$p^{2} :\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} + \xi \left( {\mu_{0} (x,t)\frac{{\partial \mu_{1} (x,t)}}{\partial x} + \mu_{1} (x,t)\frac{{\partial \mu_{0} (x,t)}}{\partial x}} \right) + \frac{{\partial^{3} \mu_{0} (x,t)}}{{\partial x^{3} }} = 0,$$
(74)
$$p^{3} :\frac{{\partial^{\alpha } \mu_{3} (x,t)}}{{\partial t^{\alpha } }} + \xi \left( {\mu_{0} (x,t)\frac{{\partial \mu_{2} (x,t)}}{\partial x} + \mu_{1} (x,t)\frac{{\partial \mu_{1} (x,t)}}{\partial x} + \mu_{2} (x,t)\frac{{\partial \mu_{0} (x,t)}}{\partial x}} \right) + \frac{{\partial^{3} \mu_{1} (x,t)}}{{\partial x^{3} }} = 0,$$
(75)

Evaluating Eq. (74) using \(\mu_{0} (x,t)\,\& \,\mu_{1} (x,t)\),

$$\frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} - \frac{{2\xi^{2} x}}{\Gamma (\alpha + 1)}t^{\alpha } = 0 \Rightarrow \frac{{\partial^{\alpha } \mu_{2} (x,t)}}{{\partial t^{\alpha } }} = \frac{{2\xi^{2} x}}{\Gamma (\alpha + 1)}t^{\alpha } .$$
(76)

Applying operator \(I^{\alpha }\) to Eq. (76),

$$\mu_{2} (x,t) = \frac{{2\xi^{2} x}}{\Gamma (\alpha + 2)}t^{\alpha + 1} .$$
(77)

Subsequently,

$$\mu_{3} (x,t) = - \left( {\frac{{\xi^{3} x\Gamma (1 + 2\alpha )}}{{\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 3\alpha )}}t^{3\alpha } + \frac{{4\xi^{3} x}}{\Gamma (2 + 2\alpha )}t^{1 + 2\alpha } } \right)$$
(78)

and so on. The approximate solution is:

$$\mu_{n} (x,t) = x - \frac{ - \xi x}{{\Gamma (\alpha + 1)}}t^{\alpha } + \frac{{2\xi^{2} x}}{\Gamma (\alpha + 2)}t^{\alpha + 1} - \left( {\frac{{\xi^{3} x\Gamma (1 + 2\alpha )}}{{\left( {\Gamma (1 + \alpha )} \right)^{2} \Gamma (1 + 3\alpha )}}t^{3\alpha } + \frac{{4\xi^{3} x}}{\Gamma (2 + 2\alpha )}t^{1 + 2\alpha } } \right) + \cdots$$
(79)

When \(\alpha = 1\), the integer solution is:

$$\mu_{n} (x,t) = x - tx\xi + t^{2} \xi^{2} x - t^{3} \xi^{3} x + \cdots .$$
(80)

The modified method agrees that

$$\mu (x,t) = \mathop {\lim }\limits_{n \to \infty } \mu_{n} (x,t);$$

therefore, the closed form of Eq. (64) is obtained as:

$$\mu (x,t) = \frac{x}{1 + \xi t},$$
(81)

which is the exact solution.

3.5 Application to oceanography

The mathematical model of shallow water waves in dimensional form described in [24] to clarify the disturbance caused by waves in the ocean bottom is:

$$\frac{{h^{2} }}{6}\partial R_{\theta }^{3} + \frac{3}{{2\sqrt {gh} }}R\partial R_{\theta } + \partial R_{\varphi } = 0.$$
(82)

They applied the transformation \(R(\theta ,\varphi ) = - \frac{{\sqrt {16g} h^{\frac{7}{6}} }}{{\sqrt[3]{6}}}\mu (x,t)\) to reduce Eq. (82) to canonical KDV equation presented as:

$$\frac{{\partial^{\alpha } \mu (x,t)}}{{\partial t^{\alpha } }} - 6\mu (x,t)\frac{\partial \mu (x,t)}{{\partial x}} + \frac{{\partial^{3} \mu (x,t)}}{{\partial x^{3} }} = 0.$$
(83)

Let the initial condition be:

$$\mu (x,0) = x.$$
(84)

Then, Eq. (83) becomes a particular case of Eq. (65) when \(\xi = - 6\),

such that

$$\mu_{n} (x,t) = x + 6tx + 36t^{2} x + 216t^{3} x + \cdots ,$$
(85)

and

$$\mu (x,t) = \frac{x}{1 - 6t}.$$
(86)

3.6 Numerical simulation

Here, we conduct a numerical simulation of the disturbance caused by water waves in the domain of shallow water described by \(R(x,t) = \left\{ {(x,t)\left| { - 0.05 \le x \le 0.05} \right.,\,\,\,0 < t < 0.42} \right\}\). Equation (86) is substituted into the transformation \(R(\theta ,\varphi ) = - \frac{{\sqrt {16g} h^{\frac{7}{6}} }}{{\sqrt[3]{6}}}\mu (x,t)\) to obtain the theoretical solution of Eq. (82).

$$R(\theta ,\varphi ) = - \frac{{\sqrt {16g} h^{\frac{7}{6}} }}{{\sqrt[3]{6}}}\left( {\frac{x}{1 - 6t}} \right)$$
(87)

Also, Eq. (85) is substituted into \(R(\theta ,\varphi )\) such that the following numerical solution is obtained (Fig. 3, Table 3)

$$- \frac{{\sqrt {16g} h^{\frac{7}{6}} }}{{\sqrt[3]{6}}}(x + 6tx + 36t^{2} x + 216t^{3} x + \cdots )$$
(88)
Fig. 3
figure 3

A comprehensive clarification of the interference caused by wave propagation in the given domain of shallow water with a depth of 7 m and a width of 0.1 m. B–H depict the swirling direction of the wave as the degree of freedom increases. It was observed that the fluid tends to undergo less turbulence when hit by the wave at a lower level of \(\alpha\). G interprets the convergence of fractional order to integer order, and H is employed to show the accuracy of the method applied. To a great extent, it was observed that the approximate solution agrees with the exact solution

Full size image
Table 3 Numerical results of problem three at an exact value \(\alpha = 1\)
Full size table

3.7 Theoretical perspective

Physical problems are well modeled with the aid of the Caputo derivative concept. This study reveals that its differentials are powerful tools for modeling linear and nonlinear systems where the order affects the output of functional parameters they contain. The impact of wave interference on nature is determined by the amount of wave crest that forms, which is referred to as “Frequency.” The analysis conducted with the aid of the Caputo derivative employed in this research reveals that the crests formed by water waves are always maximum at an integer-order derivative. This integer order represents a situation in which a water wave is directly propagating in a region with no feasible obstructions. This direct propagation can result in ocean floor landslides and the redistribution of sand and sediment in coastal areas. This can potentially lead to environmental hazards such as flooding and erosion, and the end results are often the loss of life and damage to the properties of people living in coastal regions. To avoid wind-generated waves, direct propagation of winds into the water should be kept to a minimum, which can be accomplished by embracing environmental aiding techniques such as tree planting (which acts as a windbreaker). Other options for controlling water waves include the construction of groins along the shoreline, jetties along coastal lines, and breakwater barriers along the shoreline.

4 Discussion

Unlike previous numerical methods, which required several iterations and tedious computational work to achieve convergence, the proposed method is effective and faster and requires less computation time to obtain the approximate solitons of the fractional-order KDV equation. In a similar but different study presented in [14], the effectiveness of Caputo differentials was seen. It was applied as one of their operators to provide a computational approach for solving shallow water KDV equations. They achieved this by blending the Caputo derivative with a numerical technique that combines the q-homotopy analysis transform technique and the Laplace transform method, although the objectives of their research extend to hiring two other fractional derivatives named “Caputo–Fabrizio” and “Atangana–Baleanu” to show their impact in generalizing mathematical models associated with power law, non-locality, singularity, and non-singularity kernels. In this study, this same Caputo operator proved that it cannot be overridden when it comes to modeling non-localized phenomena. It shares an accurate insight into wave properties and behavior through numerical simulation. A major limitation of computing fractional-order derivatives is its restriction to a few symbolic software packages such as the Mathematica software package; hence, it is recommended that laptops with the minimum specifications: Disk Space: 19 GB; System Memory (RAM): 4 GB+, are applied to ensure high computation speed [10].

5 Conclusion

In this research, we proposed an analytical way of solving the fractional-order Korteweg–de Vries equation. The method was derived by coupling an initial guess technique with He’s homotopy perturbation method. The new method was applied to different KDV equations with Caputo fractional derivatives. The approximate solution obtained gives a series solution in fractional order, which accelerates rapidly to the exact solution at an integer order. A conceptual study of the fractional-order derivative in wave dispersion was carried out by simulating the approximate traveling wave solution and investigating the disturbance caused by waves in the shallow water domain using the MAPLE 18 software. The outcome, which was extensively discussed, reveals the significant impact of Caputo’s fractional-order derivative in wave dispersion and propagation, and it also gives insight on ways of controlling wave-associated hazards.