Introduction

Structured light, characterized by desired amplitude, phase, and polarization in spatial, temporal, or spatial-temporal domains, has proven to be a potent tool in various applications [1, 2]. Notably, structured light with multiple degrees of freedom offers extensive capabilities for multi-dimensional information encoding, transfer, storage, and communication [3,4,5,6,7,8,9,10,11]. Optical encryption has gained prominence for enhancing information security in these applications, with various strategies employing structured light beams [12,13,14,15]. Techniques involving holograms, metasurfaces, and integrated optical platforms have been proposed for multi-dimensional optical encryption [16,17,18,19,20]. However, these methods, relying on the modulation of fully coherent light, often encounter issues such as unwanted speckles, beam wanders, and intensity scintillations [21, 22].

Conversely, partially coherent light has been shown to effectively suppress speckle noise and reduce beam wanders and scintillations during light-matter interactions due to its low coherence feature [23,24,25,26]. The rapid development of theory and experiment in optical coherence structure engineering has extended the application of partially coherent light to optical encryption [27, 28]. Unlike conventional methods that control the deterministic qualities of fully coherent light, optical coherence structure engineering involves the modulation of second-order statistical properties of random light [29]. By tailoring the spatial coherence structure, it has been demonstrated that a partially coherent beam can exhibit extraordinary propagation features, including self-shaping, self-focusing, self-splitting, and self-reconstruction in free space [30]. The optical coherence structure is now considered an efficient and unique degree of freedom for partially coherent light, finding applications in sub-Rayleigh optical imaging [31, 32], robust information transmission [33, 34], particle trapping [35], beam shaping [36], and optical measurement and sensing [37,38,39].

Recently, an optical encryption protocol leveraging coherence structure engineering of a scalar partially coherent light beam was proposed [28]. In the protocol, the second-order spatial coherence structure of the beam serves as the information carrier for optical encryption, in contrast to deterministic characteristics like amplitude, phase, and polarization of fully coherent optical fields. It was demonstrated that coherence-based optical encryption holds an advantage over encryption methods based on fully coherent light modulation in terms of security. Additionally, the encoded information in the spatial coherence structure is more robust against complex environmental disturbances, such as optical turbulence. However, this method relies on engineering a scalar spatial coherence structure, allowing only single-channel optical encryption. Thus, it faces challenges in achieving multi-channel optical information encoding and encryption. Furthermore, the encryption of color information, crucial in applications such as vision and target recognition, remains unaddressed by coherence-based technology.

In this study, we present a protocol for multi-channel optical information encoding and encryption using vectorial spatial coherence engineering of a partially coherent vector beam. The vectorial spatial coherence structure for a beam is characterized by a \(2 \times 2\) coherence matrix. We demonstrate that, although the elements in the coherence matrix are correlated, all three components in the three-dimensional coherence Stokes vector [40], derived from the coherence matrix, are uncorrelated and can be independently controlled. Thus, the coherence Stokes vector for a partially coherent light beam can be regarded as the information carrier, allowing for three-channel optical information encoding and encryption. Associating the three independent components of the coherence Stokes vector with three primary color channels—red, green, and blue—we illustrate that the coherence Stokes vector can be flexibly utilized for color image encoding and encryption. It is noteworthy that, unlike the polarization Stokes vector obtained from the polarization matrix, the coherence Stokes vector is a two-point dependent quantity, describing the second-order statistical properties of the partially coherent vector beam. Through our experiments, we demonstrate that this two-point dependent coherence Stokes vector, and consequently the encoded three-channel information, remains robust even when the partially coherent beam is subjected to random noise of varying strength. Our results pave the way for higher-dimensional optical encoding and encryption in complex environments with partially coherent light.

Principle

Coherence Stokes vector and three-channel optical encryption

The second-order statistical properties of a partially coherent vector beam can be characterized by a \(2 \times 2\) coherence matrix [41]. In the space-frequency domain, the coherence matrix for a partially coherent vector beam, propagating along z axis, is specified by a cross-spectral density matrix, i.e.,

$$\begin{aligned} \textbf{W} (\textbf{r}_1, \textbf{r}_2) = \left[ \begin{array}{ll} W_{xx}(\textbf{r}_1, \textbf{r}_2) &{} W_{xy}(\textbf{r}_1, \textbf{r}_2) \\ W_{yx}(\textbf{r}_1, \textbf{r}_2) &{} W_{yy}(\textbf{r}_1, \textbf{r}_2) \end{array}\right] , \end{aligned}$$
(1)

in which the elements are expressed as

$$\begin{aligned} W_{\alpha \beta }(\textbf{r}_1, \textbf{r}_2) = \langle E_\alpha ^*(\textbf{r}_1) E_\beta (\textbf{r}_2) \rangle , \end{aligned}$$
(2)

with \((\alpha , \beta ) \in (x,y)\). Above, \(\textbf{r}_1\) and \(\textbf{r}_2\) are two arbitrary position vectors in the transverse plane, \(E_x(\textbf{r})\) and \(E_y(\textbf{r})\) are the x and y components for the random field realizations, the asterisk denotes the complex conjugate, and the angle brackets denote the ensemble average over the field realizations.

According to the generalized van Cittert–Zernike theorem, a partially coherent beam source can be generated by propagating a spatially incoherent source. Therefore, the coherence matrix for a partially coherent beam can be expanded as [42, 43]

$$\begin{aligned} W_{\alpha \beta }(\textbf{r}_1, \textbf{r}_2) = \int \!\!\!\int p_{\alpha \beta }(\textbf{v}) H^*_{\alpha }(\textbf{r}_1, \textbf{v})H_{\beta }(\textbf{r}_2, \textbf{v}) \textrm{d}^2 \textbf{v}, \end{aligned}$$
(3)

where

$$\begin{aligned} p_{\alpha \beta }(\textbf{v}) = \langle E_\alpha ^*(\textbf{v}) E_\beta (\textbf{v}) \rangle , \end{aligned}$$
(4)

is the polarization matrix of the spatially incoherent source with \(E_x (\textbf{v})\) and \(E_y (\textbf{v})\) being the x and y components of its field realization (\(\textbf{v}\) being the position vector in the incoherent beam source plane), and \(H_x(\textbf{r}, \textbf{v})\) and \(H_y(\textbf{r}, \textbf{v})\) are the response functions, for the x and y field components, of the optical system between the incoherent source and the partially coherent beam source. In principle, the response functions can be any well-behaving functions, while \(p_{\alpha \beta }(\textbf{v})\) must satisfy the nonnegative condition, i.e., \(p_{xx}(\textbf{v})\ge 0\), \(p_{yy}(\textbf{v})\ge 0\), and \(p_{xx}(\textbf{v}) p_{yy}(\textbf{v})-p_{xy}(\textbf{v}) p_{yx}(\textbf{v}) \ge 0\) for any \(\textbf{v}\).

From Eq. (3), it is found that by the generalized van Cittert–Zernike theorem, the polarization matrix of an incoherent source can be encoded into the coherence matrix, which is also named as vectorial spatial coherence structure of a partially coherent beam source. This finding has been used in synthesizing the partially coherent vector beams with nonconventional spatial coherence structures [44,45,46,47]. In this work, we use this relation to realize the multi-channel optical information encoding and encryption. The diagonal elements \(p_{xx}(\textbf{v})\) and \(p_{yy}(\textbf{v})\) in the polarization matrix , and thus \(W_{xx}(\textbf{r}_1, \textbf{r}_2)\) and \(W_{yy}(\textbf{r}_1, \textbf{r}_2)\) in the coherence matrix, can be controlled independently. However, the anti-diagonal elements \(p_{xy}(\textbf{v})\) and \(p_{yx}(\textbf{v})\) [\(W_{xy}(\textbf{r}_1, \textbf{r}_2)\) and \(W_{yx}(\textbf{r}_1, \textbf{r}_2)\)] are connected tightly to the diagonal elements \(p_{xx}(\textbf{v})\) and \(p_{yy}(\textbf{v})\) [\(W_{xx}(\textbf{r}_1, \textbf{r}_2)\) and \(W_{yy}(\textbf{r}_1, \textbf{r}_2)\)]. Therefore, the anti-diagonal elements in the polarization and coherence matrices cannot be used to encode additional independent information as the diagonal elements.

To separate all the independent degrees of freedom in this encoding, we adopt the famous polarization Poincare sphere, in which the three orthogonal coordinates, \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), and \(S_3(\textbf{v})\) can be controlled independently [48]. These three orthogonal coordinates form the polarization Stokes vector

$$\begin{aligned} \textbf{S}(\textbf{v}) = [S_1(\textbf{v}), S_2(\textbf{v}), S_3(\textbf{v})], \end{aligned}$$
(5)

with its elements being determined totally by the polarization matrix \(\textbf{p}(\textbf{v})\), i.e.,

$$\begin{aligned} S_j(\textbf{v})=\textrm{tr}[\textbf{p}(\textbf{v}) \varvec{\sigma }_j],~~~ j \in (1,2,3). \end{aligned}$$
(6)

Above

$$\begin{aligned} \varvec{\sigma }_1 = \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array}\right) , \varvec{\sigma }_2 = \left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \end{array}\right) , \varvec{\sigma }_3 = \left( \begin{array}{cc} 0 &{} -i \\ i &{} 0 \end{array}\right) , \end{aligned}$$
(7)

are three Pauli spin matrices and \(\textrm{tr}\) denotes the matrix trace. As the polarization matrix is Hermitian, the elements in the polarization Stokes vector are real quantities. Consequently, the polarization Stokes vector can be employed to encode spatial information with real values across three distinct channels.

Akin to the polarization Stokes vector, the coherence Stokes vector for the partially coherent vector beam can be defined as [40]

$$\begin{aligned} \textbf{S}(\textbf{r}_1, \textbf{r}_2) = [S_1(\textbf{r}_1, \textbf{r}_2), S_2(\textbf{r}_1, \textbf{r}_2), S_3(\textbf{r}_1, \textbf{r}_2)], \end{aligned}$$
(8)

where the three elements are obtained from the coherence matrix, i.e.,

$$\begin{aligned} S_j(\textbf{r}_1, \textbf{r}_2)=\textrm{tr} [\textbf{W}(\textbf{r}_1, \textbf{r}_2) \varvec{\sigma }_j],~~~ j \in (1,2,3). \end{aligned}$$
(9)

The coherence Stokes vector is a two-position dependent vector that describes the second-order statistical properties of the partially coherent vector beam [49, 50]. The three elements in the coherence Stokes vector have clear physical interpretations [51] such that \(S_1(\textbf{r}_1, \textbf{r}_2)\), \(S_2(\textbf{r}_1, \textbf{r}_2)\), and \(S_3(\textbf{r}_1, \textbf{r}_2)\) describe the differences of the electric-field x- and y-component, \(+\pi /4\)- and \(-\pi /4\)-linearly polarized component, and right- and left-circularly polarized component correlations at points \(\textbf{r}_1\) and \(\textbf{r}_2\), respectively.

Taking Eq. (6) into Eq. (3) and letting the response functions \(H_x(\textbf{r}, \textbf{v}) = H_y(\textbf{r}, \textbf{v}) = H(\textbf{r}, \textbf{v})\), we obtain a generalized van Cittert–Zernike theorem for the Stokes vectors, i.e., [52]

$$\begin{aligned} S_{j}(\textbf{r}_1, \textbf{r}_2) = \int \!\!\!\int S_{j}(\textbf{v}) H^*(\textbf{r}_1, \textbf{v})H(\textbf{r}_2, \textbf{v}) \textrm{d}^2 \textbf{v}. \end{aligned}$$
(10)

Based on the above relation, we find that the polarization Stokes vector, carrying three-channel optical information such as three independent optical images, can be encoded into the coherence Stokes vector of a partially coherent beam. Furthermore, the response function \(H(\textbf{r}, \textbf{v})\) can contribute additional encryption keys during the encoding process. Consequently, the initially described three-channel optical encoding system transforms into a more comprehensive three-channel optical encryption protocol.

Fig. 1
figure 1

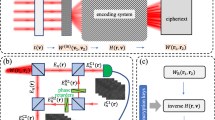
Principle of three-channel optical information encoding and encryption based on engineering the coherence Stokes vector of a partially coherent beam. a Schematic of encoding three-channel information \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), and \(S_3(\textbf{v})\) into the coherence Stokes vector \(\textbf{S}(\textbf{r}_1, \textbf{r}_2) = [S_1(\textbf{r}_1, \textbf{r}_2), S_2(\textbf{r}_1, \textbf{r}_2), S_3(\textbf{r}_1, \textbf{r}_2)]\) of a partially coherent beam via the encoding system H. The three-channel information is decoded by the decoding system \(H^{-1}\). b Three-channel images encoding and decoding. c Color image encoding and decoding

Full size image

Figure 1 shows the schematic of our three-channel optical information encoding and encryption protocol based on the vectorial spatial coherence structure engineering of a partially coherent light beam. The proposed protocol consists of three stages. At the first stage, three-channel optical information (plaintext) \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), \(S_3(\textbf{v})\), modulated in a fully coherent structured light beam, is encoded into the three two-point coherence Stokes vector elements \(S_{1}(\textbf{r}_1, \textbf{r}_2)\), \(S_{2}(\textbf{r}_1, \textbf{r}_2)\), and \(S_{3}(\textbf{r}_1, \textbf{r}_2)\) of a partially coherent random light beam via a generalized van Cittert–Zernike theorem [c.f., Eq. (10)]. In Fig. 1a, the dynamic diffuser is used to transform a fully coherent light beam into a spatially incoherent beam, while the encoding system H is used to transform the spatially incoherent beam into the partially coherent random beam. At the second stage, the coherence Stokes vector (ciphertext) of the partially coherent beam is measured through a generalized Hanbury Brown and Twiss experiment [53, 54]. The elements in the coherence Stokes vector are complex in general, since the coherence matrix only follows the quasi-Hermitian property, i.e., \(\textbf{W} ^{\dagger} (\textbf{r}_1, \textbf{r}_2) = \textbf{W} (\textbf{r}_2, \textbf{r}_1)\), where the dagger denotes the Hermitian adjoint. Finally, the three-channel optical information is decoded by using the measured complex coherence Stokes vector and the inverse response function \(H^{-1}\) embedded with the correct decryption keys.

As a specific example, we demonstrate in Fig. 1b the theoretical simulation for encoding and decoding three different images with engineering and measuring the polarization and coherence Stokes vectors of optical beams. In the simulation, the amplitude images (letters ‘A’, ‘B’, and ‘C’) is firstly loaded by the three elements of the polarization Stokes vector of a fully coherent structured beam by controlling the amplitude and phase of its two orthogonal field components \(E_x(\textbf{v})\) and \(E_y(\textbf{v})\). Through adding random phase into the electric field, \(E_x(\textbf{v})\) and \(E_y(\textbf{v})\) become the components of the random field realization for an spatially incoherent source. We then let the incoherent beam propagates through an optical system with its response function having Fourier transform form, i.e., \(H(\textbf{r}, \textbf{v}) = A_0 \exp \left[ \frac{\textrm{i}\pi }{\lambda f} ( \textbf{v}^2 - 2\textbf{v} \cdot \textbf{r} \right]\), where \(A_0\) is an constant, \(f = 250\) mm is the focal distance of the Fourier transform thin lens, and \(\lambda = 532\) nm is the wavelength. In the output plane, the spatially incoherent beam becomes a partially coherent beam. We collect the field realizations \(E_x(\textbf{r})\) and \(E_y(\textbf{r})\) of the partially coherent beam in the output plane. The coherence Stokes vector \([S_1(\textbf{r}_1, \textbf{r}_2), S_2(\textbf{r}_1, \textbf{r}_2), S_3(\textbf{r}_1, \textbf{r}_2)]\) can be calculated by Eqs. (2) and (9). The simulated real and imaginary parts of the coherence Stokes vector elements are shown in Fig. 1b. Finally, we find the encoded three optical images are well recovered by inversely Fourier transform of the measured coherence Stokes vector elements.

One remarkable application of our three-channel optical encoding protocol is to realize the color image encoding and encryption. In optics, all colorful image can be decomposed into three primary-color-channels, i.e., red (R), green (G), and blue (B) channels. Therefore, as shown in Fig. 1c, in our protocol, we let \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), and \(S_3(\textbf{v})\) carry information of our lab logo in R, G, B channels, respectively. By the generalized van Cittert–Zernike theorem, the colorful image can be encoded into the coherence Stokes vector of a partially coherent light beam. As shown in Fig. 1c, through measuring the coherence Stokes vector and using the inverse Fourier transform, the lab logo can be well recovered with correct colors.

It is notable that different from the traditional encryption protocols, the three-channel plaintext information in our optical-coherence-based one is encoded into the second-order field correlations rather than into the deterministic characteristics of a fully coherent light beam. Since it requires an entire statistical ensemble of a large number of field realizations to reconstruct the second-order field correlations, the multi-channel information concealed in the ciphertext of the optical-coherence-based protocol is more difficult to compromise, compared to the protocols based on fully coherent light modulation. In addition, it has been proved that the second-order field correlations are much more robust than the deterministic characteristics when the beam suffers disturbances or noisy environments, leading to a robust multi-channel optical encryption.

Synthesis of partially coherent vector beam for three-channel optical encoding

We now turn to discuss how to synthesize the partially coherent vector beam in experiment to realize the three-channel information encoding. In our experiment, the partially coherent vector beam is synthesized with the help of the complex-random-mode representation (RMR), with which the coherence matrix is expanded as the summation of N vector modes [55, 56]

$$\begin{aligned} \textbf{W} (\textbf{r}_1, \textbf{r}_2) = \sum \limits _{n=1}^{N} \lambda _n \textbf{E}^*_n (\textbf{r}_1) \textbf{E}^{\text {T}}_n (\textbf{r}_2) , \end{aligned}$$
(11)

where \(\textbf{E}_n (\textbf{r})\) and \(\lambda _n\) are the vectorial complex random mode and the corresponding modal weight. According to the expression in Eq. (11), the partially coherent vector beam can be synthesized by superposing a set of vectorial complex random modes. In the RMR method, the modal weights for all random modes are equal to 1/N and the electric field of the random mode can be written as

$$\begin{aligned} \textbf{E}_n(\textbf{r}) = \tau _x(\textbf{r})T_{x,n}(\textbf{r})\hat{\textbf{e}}_x + \tau _y(\textbf{r})T_{y,n}(\textbf{r})\hat{\textbf{e}}_y, \end{aligned}$$
(12)

where \(\tau _x(\textbf{r})\) and \(\tau _y(\textbf{r})\) are the common amplitudes for all random modes, \(T_{x,n}(\textbf{r})\) and \(T_{y,n}(\textbf{r})\) are the complex random functions imposed on the deterministic common amplitudes, and \(\hat{\textbf{e}}_x\) and \(\hat{\textbf{e}}_y\) are two Cartesian unit vectors along the x and y directions. Through Eqs. (2), (11), and (12), it is found that the auto-correlations of the complex random functions \(T_{x,n}(\textbf{r})\) and \(T_{y,n}(\textbf{r})\) give rise to the diagonal elements \(W_{xx}(\textbf{r}_1, \textbf{r}_2)\) and \(W_{yy}(\textbf{r}_1, \textbf{r}_2)\) of the coherence matrix, while the cross-correlations between \(T_{x,n}(\textbf{r})\) and \(T_{y,n}(\textbf{r})\) introduce the anti-diagonal elements \(W_{xy}(\textbf{r}_1, \textbf{r}_2)\) and \(W_{yx}(\textbf{r}_1, \textbf{r}_2)\).

We now focus on how to encode the auto- and cross-correlations, i.e., all the information of the coherence matrix, into two complex random functions. We first obtain the polarization matrix \(\textbf{p}(\textbf{v})\) for the fully coherent beam by using the three-channel plaintext information \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), and \(S_3(\textbf{v})\). Two complex random functions for the partially coherent beam are then obtained by introducing random functions into the electric field of the fully coherent beam and letting the resulting spatially incoherent beam propagates through the optical system with response function \(H(\textbf{r}, \textbf{v})\), i.e.,

$$\begin{aligned} T_{x,n}(\textbf{r}){} & {} = \int \!\!\!\int R_{x,n}(\textbf{v}) \sqrt{p_{xx}(\textbf{v})} H(\textbf{r}, \textbf{v}) \textrm{d}^2 \textbf{v}, \end{aligned}$$
(13)
$$\begin{aligned} T_{y,n}(\textbf{r}){} & {} = \int \!\!\!\int R_{y,n}(\textbf{v}) \sqrt{p_{yy}(\textbf{v})} H(\textbf{r}, \textbf{v}) \textrm{d}^2 \textbf{v}, \end{aligned}$$
(14)

where

$$\begin{aligned} R_{x,n}(\textbf{v}){} & {} = [r_{1,n}(\textbf{v}) + i r_{2,n}(\textbf{v})]/\sqrt{2}, \end{aligned}$$
(15)
$$\begin{aligned} R_{y,n}(\textbf{v}){} & {} = C^*(\textbf{v})[r_{1,n}(\textbf{v}) + i r_{2,n}(\textbf{v})]/\sqrt{2} + \sqrt{1-|C(\textbf{v})|^2} [r_{3,n}(\textbf{v}) + i r_{4,n}(\textbf{v})]/\sqrt{2}. \end{aligned}$$
(16)

Above, \(r_{1,n}(\textbf{v})\), \(r_{2,n}(\textbf{v})\), \(r_{3,n}(\textbf{v})\), and \(r_{4,n}(\textbf{v})\) are four independent random functions obeying Gaussian statistics with zero-mean and unit-variance, \(C(\textbf{v}) = p_{xy}(\textbf{v})/\sqrt{p_{xx}(\textbf{v}) p_{yy}(\textbf{v}) }\) is a complex function that controls the anti-diagonal elements in the coherence matrix of the synthesized partially coherent beam [57, 58].

By adding all the complex random modes with Eq. (11), the partially coherent beam, with three-channel plaintext information encoded in its vectorial coherence structure, can be synthesized. The RMR method used in our work is quite similar to the protocol that using the rotating ground-glass disk. Nevertheless, our method is more compact and flexible since the complex random modes \(\textbf{E}_n(\textbf{r})\) can be generated and modulated flexibly by a single spatial light modulator (SLM).

Fig. 2
figure 2

a Experimental setup for realizing the three-channel optical information encoding and decoding. b The target three-channel optical images. c A realization of the corresponding computer-generated holograms (CGH) loaded in the spatial light modulator (SLM) for generating the components of the field realization. d and e The experimentally measured instantaneous intensities for the x and y field components. f The experimental results of the coherence Stokes vector by spatial average over the instantaneous intensities. g The corresponding simulation results

Full size image

Experimental demonstration of three-channel optical encoding and encryption

We next discuss how to experimental realize the three-channel optical encoding and encryption. Figure 2a shows our experimental setup. A fully coherent laser beam with wavelength \(\lambda =532\) nm is emitted from a single-longitudinal-mode laser and is converted into a y-linearly polarized beam by a half-wave plate (HWP). After expanded by a beam splitter (BE\(_{1}\)), the beam splits into two parts by a beam-splitter (BS) and then they go into two different arms. The purpose of the Arm 1 in Fig. 2a is to encode the three-channel information into the coherence Stokes vector of a partially coherent light beam, while the purpose of Arm 2 is to create the reference beams for measuring the coherence properties of the synthesized partially coherent beam.

In Arm 1, the incident beam is first modulated by a phase-only SLM. The screen of the SLM is split into two halves that are used to realize the independent modulation of the x and y components for the complex random modes \(\textbf{E}_n(\textbf{r})\). The computer-generated hologram (CGH) on the SLM is displayed dynamically to ensure the synthesis of partially coherent light beam. Figure 2b and c show an example for encoding the three-channel target images “1”, “2”, and “3” (for short, “123”) into the partially coherent beam. Figure 2c displays a realization of the corresponding dynamic CGHs loaded in the SLM. The details for creating the CGHs can be found in Supplementary material 1. After modulated by the SLM, the reflected light beam goes into a 4f common-path interferometric arrangement composed by thin lenses L\(_{1}\) and L\(_{2}\) with the same focal distance \(f = 250\) mm. We note the distances between the SLM and L\(_{1}\), between L\(_{2}\) and the Ronchi grating (RG) are both f, and the distance between the L\(_{1}\) and L\(_{2}\) is 2f. The SLM is located in the input plane (i.e., front focal plane of L\(_{1}\)) of the 4f system, while a two-pinhole filter is placed in the spatial-frequency plane (rear focal plane of L\(_{1}\)) of the system to select out two \(+1\) diffraction orders from the SLM. The beams from two diffraction orders are converted into x and y polarization states, respectively, by two different HWPs. In the output plane (rear focal plane of L\(_{2}\)), two beam modes \(E_{x,n}(\textbf{r}) \hat{\textbf{e}}_x\) and \(E_{y,n}(\textbf{r}) \hat{\textbf{e}}_y\) are synthesized by a RG. By dynamically playing the CGHs on the SLM, the partially coherent beam, with three-channel target images encoded in its coherence Stokes vector, is synthesized.

We employ the Arm 2 in the Fig. 2a to generate coherent reference light beams. The y-polarization light beam incidents onto a neutral density filter (NDF), linear polarizer (LP), and a quarter-wave plate (QWP). The axis of the LP is set to be \(\pi /4\) with respect to the x axis, while the fast axis of the QWP is set to be parallel or perpendicular to the polarization direction of the beam transmitted from LP. Thus, two \(\pi /4\) linearly polarized beams with a \(\pi /2\) phase difference can be generated, respectively. The reference beams are then expanded by a BE\(_{2}\) to produce the collimated beams of virtually uniform intensity distribution. Two reference beams are interfered with the synthesized partially coherent beam, respectively, by a polarization beam splitter (PBS). The thin lens L\(_{3}\), positioned after the RG, is used to create a 4f imaging system for imaging the synthesized partially coherent source into the CCD1 and CCD2. The distances between the RG and L\(_{3}\), as well as between L\(_{3}\) and CCD\(_{1(2)}\), are both 2f, where \(f=250\) mm is the focal distance of L\(_{3}\). We then record the instantaneous intensities for the x and y field components. The CCD\(_{1}\) and CCD\(_{2}\) are controlled by a direct-digital-synthesis (DDS) signal generator, used to simultaneously capture the intensities of the x and y components of the composite random field. With the principle of the generalized Hanbury Brown and Twiss experiment, the real and imaginary parts of the coherence matrix can be obtained by [54]

$$\begin{aligned} W^\prime _{\alpha \beta } (\textbf{r}_1, \textbf{r}_2){} & {} = \frac{\left\langle I^{\text {C1}}_\alpha (\textbf{r}_1) I^{\text {C1}}_\beta (\textbf{r}_2)\right\rangle -\left\langle \left[I_\alpha (\textbf{r}_1)+I^{\text {R1}}_\alpha (\textbf{r}_1)\right] \left[I_\beta (\textbf{r}_2)+I^{\text {R1}}_\beta (\textbf{r}_2)\right]\right\rangle }{2\sqrt{I^{\text {R1}}_\alpha (\textbf{r}_1) I^{\text {R1}}_\beta (\textbf{r}_2)}}, \end{aligned}$$
(17)
$$\begin{aligned} W^{\prime \prime }_{\alpha \beta } (\textbf{r}_1, \textbf{r}_2){} & {} = -\frac{\left\langle I^{\text {C1}}_\alpha (\textbf{r}_1) I^{\text {C2}}_\beta (\textbf{r}_2)\right\rangle -\left\langle \Big[I_\alpha (\textbf{r}_1)+I^{\text {R1}}_\alpha (\textbf{r}_1)\Big] \left[I_\beta (\textbf{r}_2)+I^{\text {R2}}_\beta (\textbf{r}_2)\right]\right\rangle }{2\sqrt{I^{\text {R1}}_\alpha (\textbf{r}_1) I^{\text {R2}}_\beta (\textbf{r}_2)}}, \end{aligned}$$
(18)

where the prime and double-prime denote the real and imaginary parts, respectively, \(I^{\text {C1}}_\alpha (\textbf{r})\) and \(I^{\text {C2}}_\alpha (\textbf{r})\) denote the \(\alpha\) component intensities for the fields composed by the partially coherent beam and two reference beams, respectively, \(I_\alpha (\textbf{r})\) is the \(\alpha\) component intensity for the partially coherent field, while \(I^{\text {R1}}_\alpha (\textbf{r})\) and \(I^{\text {R2}}_\alpha (\textbf{r})\) are the \(\alpha\) component intensities for the first and the second reference beams. The angle brackets in Eqs. (17) and (18) denote the ensemble average. We note that in the experiment, the ensemble average can be replaced with the spatial average over a single field realization if the partially coherent light beam is synthesized by a Fourier or a fractional Fourier transform system [28, 59, 60], i.e., the response function \(H(\textbf{r}, \textbf{v})\) obeys Fourier or fractional Fourier transform form. The details for the generalized Hanbury Brown and Twiss experiment are shown in Supplementary material 1. After the complex coherence matrix is measured, the coherence Stokes vector can be obtained by using Eq. (9).

Figure 2d and e show the measured instantaneous intensities in the case when the target images “123” are encoded in the partially coherent beam, while Fig. 2f shows the three elements of the coherence Stokes vector by the spatial average over these instantaneous intensities. The corresponding simulation results for the coherence Stokes vector are shown in Fig. 2g. It is found that the measured coherence Stokes vector is consistent well with the simulation. We will show in the next section that by the inverse transform of the measured coherence Stokes vector, the encoded three-channel images can be well reconstructed.

Fig. 3
figure 3

Experimental results of the recovered three-channel optical images from the measured coherence Stokes vectors. a, h, and l are the target images. b–g The recovered images “123” and their enlarged images. i–k The recovered images “ABC”. m–o The recovered images of “circle, square, and triangle” shapes. The corresponding simulation results for the recovered three-channel images are shown in the inset (within the yellow dashed circle)

Full size image

Results and discussion

Three-channel optical images encoding

According to the relation in Eq. (10), once the elements of the coherence Stokes vector \(S_j(\textbf{r}_1, \textbf{r}_2)\) are determined, all the information (including the shapes and positions) on the encoded three-channel target images can be recovered by using the inverse transform system whose response function is \(H^{-1}(\textbf{r}, \textbf{v})\). We first study three-channel optical images encoding with a Fourier transform system. Therefore, by evaluating an inverse Fourier transform of the measured coherence Stokes vector, the three-channel optical images \(S_1(\textbf{v})\), \(S_2(\textbf{v})\), and \(S_3(\textbf{v})\) can be reconstructed. In Fig. 3b–d, we show the recovered three-channel images “123” by the inverse Fourier transform of the measured coherence Stokes vector shown in Fig. 2f. The original target images are shown in Fig. 3a. The enlarged images are shown in Fig. 3e–g. We find that, indeed, both the shape and the position of the target images are well recovered from the measured coherence Stokes vector. To verify the flexibility of our method, we change the three-channel target images to the capital letters “ABC” [see in Fig. 3h] and to the “circle, square, and triangle” shapes [see in Fig. 3l], respectively. The experimentally reconstructed images are shown in Fig. 3i–k and m–o. The corresponding simulation results are shown in each inset of the figures. The experimental and simulation results verify that the three-dimensional coherence Stokes vector, indeed, can be viewed as an effective information carrier for realizing three-channel optical encoding.

Color image encoding

Next, we demonstrate the color image encoding with partially coherent vector beam. The information of three primary-color-channels for a color image is first encoded into three elements of the coherence Stokes vector, respectively, by engineering the dynamic CGHs in the SLM. We then measure the complex coherence Stokes vector by the generalized Hanbury Brown and Twiss experiment. Through the inverse Fourier transform, the three primary-color-channels and therefore the color image can be recovered. In Fig. 4 we display the recovered results of four different target color images. The left panels of Fig. 4 show the target images, i.e., the colorful letters “RGB”, a color windmill, a color peking opera mask, and our lab logo. The corresponding recovered images including the separate primary-color-channels are shown in four right panels of Fig. 4. The numerical simulation results are displayed in the inset of each figures. We find the color images is recovered, however with disturbance in the recovered color images. We note the disturbance is due to that in our experiment only a single realization of the measured intensities is used to calculate the complex coherence Stokes vector, i.e., in Eqs. (17) and (18) the ensemble average is replaced with the spatial average over a single realization.

Fig. 4
figure 4

Experimental results of the recovered color images from the measured coherence Stokes vectors. a, f, k, and p are the target images. b–e The recovered colorful letters “RGB” and its the separate primary-color-channels. g–j The recovered color windmill. l–o The recovered color peking opera mask. q–t The recovered lab logo. The corresponding simulation results for the recovered color images are shown in the inset (within the yellow dashed circle)

Full size image
Fig. 5
figure 5

Experimental results of the recovered color images with variable number N of intensities realizations. a–j The recovered color windmill. k–t The recovered color peking opera mask

Full size image

By increasing the number of the realizations in calculating the coherence Stokes vector, the recovered image quality can be further improved. In Fig. 5a–j and k–t, we show the recovered windmill and peking opera mask with different number N of intensities realizations. We can find that the recovered image quality can be improved gradually with the increase of N. The quality of the recovered color images is nearly perfect comparing to the target color images when \(N=10\). We remark here that by further increase of the number of realizations used in calculating the coherence Stokes vector, the quality of the recovered image can be further improved. The quality of the recovered image depends also on the complexity of the image itself, i.e., more complex structure of the image, more number of the realizations is required to recover well the encoded image (for example, see in Supplementary Fig. S1 for the recovery of our lab logo).

Robust property

The advantage of our three-channel optical information encoding based on the coherence Stoke vector engineering is that the system is effectively resistant to the disturbances induced by the complex environments, such that when the partially coherent vector beam, with three-channel information encoded in its coherence Stokes vector, suffers random noise, the encoded information can still be well recovered. Here, we demonstrate such robustness by introducing white noise in the partially coherent beam. In our experiment, the white noise with different strengths are added into the \(E_{x,n}(\textbf{r})\) and \(E_{y,n}(\textbf{r})\) components of the complex random modes \(\textbf{E}_{n} (\textbf{r})\). We note the complex random modes \(\textbf{E}_{n} (\textbf{r})\) are used to synthesize the partially coherent beam by the RMR method. Figure 6 shows the experimental results for the reconstructed three-channel optical images “123” and color “windmill” from the partially coherent vector beams with different signal-to-noise ratios (SNRs). The SNR is defined as [61]

$$\begin{aligned} \textrm{SNR} =10 \textrm{log}_{10} \frac{\int I^{\text {signal}} \textrm{d}^2\textbf{r}}{\int I^{\mathrm{total}} \mathrm{d}^2\textbf{r}}, \end{aligned}$$
(19)

where \(I^{\text {signal}}\) and \(I^{\text {total}}\) denote the intensity of the complex random mode \(\textbf{E}_{n} (\textbf{r})\) with and without introducing the white noise, respectively. The measured instantaneous intensities of \(\textbf{E}_{n} (\textbf{r})\) with \(\textrm{SNR} = -0.77\) dB, \(-6.53\) dB, and \(-13.47\) dB for the partially coherent vector beams with three-channel images “123” encoded inside are displayed in Fig. 6a, e, and i, respectively. The respective ratios of signal power to total power are 45.60 %, 18.20 %, and 4.30 %, respectively. Figure 6b–d, f–h, and g–l show the experimental results of the recovered three-channel images under the three different SNRs. It can be found that the three-channel images “123” can be reconstructed well in all three cases. The color “windmill” and its three primary-color-channels are recovered in the noisy environments with \(\textrm{SNR} = -0.17\) dB, \(-6.92\) dB, and \(-13.68\) dB, respectively. The corresponding signal power ratios to the total power are 49.03 %, 16.89 %, and 4.11 %, respectively. The experimental recovered results are shown in Fig. 6m–x. The experimental results are consistent well with our predictions (see in simulation results in Supplementary Fig. S2) that the color images can also be recovered with high quality in the noisy environments. Our experimental and simulation results verified that our protocol is quite insensitive to the environmental noise. Thus, the two-point coherence Stokes vector of a partially coherent light beam can be regarded as a robust information carrier for three-dimensional optical encoding.

Fig. 6
figure 6

Robustness of the recovered images in noisy environments. a, e, and i The measured instantaneous intensities of \(\textbf{E}_{n} (\textbf{r})\) with \(\textrm{SNR} = -0.77\) dB, \(-6.53\) dB, and \(-13.47\) dB for the partially coherent vector beams with three-channel images “123” encoded inside. b–d, f–h, and g–l The corresponding recovered three-channel images in the noisy environments. m–p, q–t, and u–x The recovered color images in the noise environments with \(\textrm{SNR} = -0.17\) dB, \(-6.92\) dB, and \(-13.68\) dB, respective

Full size image

Three-channel optical encryption

Finally, our protocol can significantly enhance information security for optical information encoding, specifically enabling three-channel optical encryption by customizing the encoding rules of the response function \(H(\textbf{r}, \textbf{v})\). We would like to emphasize here that our protocol is adaptable to any encoding system, similar to those utilized in previous optical encryption protocols with fully coherent light. This flexibility arises from the fact that the response function \(H(\textbf{r}, \textbf{v})\) can be designed arbitrarily. To illustrate the feasibility of our three-channel optical encryption, we present an example in which the optical encryption system performs a fractional Fourier transform with a controllable fractional order. The corresponding transfer function is expressed as [13, 28]:

$$\begin{aligned} H(\textbf{r}, \textbf{v}) = A_0 \exp \left[ \frac{\textrm{i}\pi }{\lambda f} (\textrm{cot}\varphi _{\text {E}} \textbf{v}^2 - 2\textrm{csc} \varphi _{\text {E}} \textbf{v} \cdot \textbf{r} + \textrm{cot} \varphi _{\text {E}} \textbf{r}^2) \right] , \end{aligned}$$
(20)

where \(A_0 = - {\textrm{i csc}} \varphi _{\text {E}} / \lambda f\) and \(\varphi _{\text {E}} = p_{\text {E}} \pi /2\) with \(p_\text {E}\) being the fractional order of the fractional Fourier transform. The value of \(p_\text {E}\) serves as an encryption key for the protocol, with \(p_\text {E} \in (0,1]\); setting \(p_\text {E} = 1\) reduces it to the ordinary Fourier transform. Following from Eq. (10), the ciphertext can be expressed as:

$$\begin{aligned} S_{j}(\textbf{r}_1,\textbf{r}_2) = A^2_0 \int S_{j}(\textbf{v}) \exp \left[ \frac{\textrm{i}\pi }{\lambda f}\left(2 \textrm{csc} \varphi _{\text {E}}\textbf{v}\cdot \Delta \textbf{r} - \textrm{cot} \varphi _{\text {E}} \textbf{r}_1^2 + \textrm{cot} \varphi _{\text {E}} \textbf{r}_2^2\right) \right] \textrm{d}^2 \textbf{v}, \end{aligned}$$
(21)

where \(S_{j}(\textbf{v})\) with \(j\in (1,2,3)\) denote the three-channel plaintext information and \(\Delta \textbf{r} = \textbf{r}_1 - \textbf{r}_2\). The three-channel plaintext information is now encoded into the coherence Stokes vector of the partially coherent beam via the fractional Fourier transform system. In the experiment, such the partially coherent beam can still be synthesized with the RMR method. We only require to modulate the dynamic CGHs in the SLM by following Eqs. (13) and (14). After the coherence Stokes vector being measured, the encoded three-channel information can be recovered by the inverse fractional Fourier transform, i.e.,

$$\begin{aligned} S^{\text {R}}_{j}(\textbf{v}) = \int \!\!\!\int S^{\text {R}}_{j}(\textbf{r}_1,\textbf{r}_2) \exp \left[ -\frac{\textrm{i}\pi }{\lambda f}(2 \textrm{csc} \varphi _{\text {R}} \Delta \textbf{r}\cdot \textbf{v} - \textrm{cot} \varphi _{\text {R}} \textbf{r}_1^2 + \textrm{cot} \varphi _{\text {R}} \textbf{r}_2^2 ) \right] \textrm{d}^2 \textbf{r}_1\textrm{d}^2 \textbf{r}_2. \end{aligned}$$
(22)

Above, \(S^{\text {R}}_{j}(\textbf{v})\) denotes the recovered three-channel information, \(S^{\text {R}}_{j}(\textbf{r}_1,\textbf{r}_2)\) denotes the measured coherence Stokes vector, and \(\varphi _{\text {R}} = p_{\text {R}} \pi /2\) with \(p_{\text {R}}\) serving as a decoding key. It is noted that only when the measured \(S^{\text {R}}_{j}(\textbf{r}_1,\textbf{r}_2)\) matches the ciphertext \(S_{j}(\textbf{r}_1,\textbf{r}_2)\), and the decoding key \(p_{\text {R}} = p_{\text {E}}\), the encoded information can be correctly recovered.

Fig. 7
figure 7

Three-channel optical encryption with coherence Stokes vector. a–c and j–m show the recovered three-channel images and color image with correct decryption key, i.e., \(p_{\text {R}}=0.80\). d–f and n–q show the recovered three-channel images and color image with incorrect decryption key, \(p_\text {R}=1.00\). g–i and r–u show the recovered images in the noise environments with \(\textrm{SNR} = -13.40\) dB and \(\textrm{SNR} = -13.61\) dB, respectively

Full size image

As a proof-of-principle experiment, the encryption key, i.e., the fractional order of the transform system is set to be \(p_\text {E}=0.80\). Figure 7 depicts our experimental decryption results for the three-channel images “123” and the color “windmill”. Figure 7a–c and j–m show the recovered results with correct decryption key, i.e., \(p_\text {R}=0.80\), while Fig. 7d–f and n–q show the recovered results with incorrect decryption key, i.e., \(p_\text {R}=1.00\). It can be inferred from the recovered results that the target images can be well recovered only when the encryption and decoding keys match well. Otherwise, the recovered images cannot be recognized. It is emphasized that our decryption results are quite sensitive to the value of \(p_\text {R}\) (see in Supplementary Fig. S3). We also carry out the experiment by introducing the white noise in the partially coherent beams. For the noisy beams, the \(\textrm{SNR} = -13.40\) dB and \(\textrm{SNR} = -13.61\) dB, respectively. The recovered images are shown in Fig. 7g–i and r–u. It is noted that the recovered images are nearly unaffected by the noisy environment, indicating the robustness of the three-channel optical encryption with partially coherent vector light.

Conclusions

In summary, we have introduced a novel approach for three-channel optical encoding and encryption by engineering a single partially coherent vector light beam. The three-channel information carried by the polarization Stokes vector of a fully coherent light beam is initially encoded into the three components of the two-point coherence Stokes vector of a partially coherent beam via the generalized van Cittert–Zernike theorem. Subsequently, the encoded three-channel information is recovered by measuring the coherence Stokes vector through the recently introduced generalized Hanbury Brown–Twiss experiment. The advanced protocol exhibits several key advantages, including increased resilience to disturbances induced by complex environments and enhanced security for the encoding information through the introduction of additional quantities as encryption keys in the encoding system. In addition, we have shown that by associating the three independent components of the coherence Stokes vector with three primary color channels, the coherence Stokes vector can be flexibly utilized for color image encoding and encryption. The feasibility of our protocol has been demonstrated through a proof-of-principle experiment and numerical simulation. Both results affirmed that the encoded three-channel optical images and color images can be successfully decoded or decrypted even in the presence of high levels of random noise during the recovery process. Our findings suggest that partially coherent light engineering may find applications in multi-target image encryption and high-security, multi-channel optical communication in complex environments.