Abstract
The present study scrutinizes slip effects and stagnation point flows of upper-convected Maxwell fluid past a stretching sheet. The non-linear ordinary differential equations are obtained from the governing partial differential equations and solved using implicit finite difference method. The impacts of non-dimensional governing parameters such as Brownian motion parameter, velocity ratio, velocity slip parameter, suction/injection parameter, Lewis numbers, upper-convected Maxwell parameter, magnetic field, thermophoresis parameter, chemical reactions parameter, thermal slip parameter, solutal slip parameter, and heat source parameter on the velocity field, heat and mass transfer characteristics are discussed and presented through graphs. The values of local Sherwood number, local Nusselt number, and skin friction coefficient are discussed and presented through tables. The results indicate that when the magnetic field is intensified, it reduces velocity profiles and raises temperature and concentration profiles. Moreover, with an upsurge in velocity slip parameter, the local Nusselt number and local Sherwood number diminish.
Similar content being viewed by others
Introduction
Nanofluid is a colloidal postponement containing nanoparticles in a base fluid. Nanofluids have enhanced physical properties such as mass diffusivity, thermal diffusivity and conductivity, viscosity, and convective heat transfer coefficients compared to those of base fluids. Nanofluids can be rummage-sale in a plethora of engineering applications extending from the use in the automotive industry to the medical field to use in power plant cooling systems, as well as computers viz. heat transfer applications (in industrial cooling applications as smart fluids, in nuclear reactors, in extraction of geothermal energy sources), automotive applications (as nanofluid coolant and nanofluid in fuel, brake, and other vehicular nanofluids), electronic applications (cooling of microchips, micro scale fluid applications), and biomedical applications (nano drug delivery, cancer therapeutics, cryopreservation, nano cryosurgery), etc. Because of these original properties, nanofluids are important to study. Therefore, more precise researches are presented in this topic in the references [1,2,3,4,5,6].
Because of its comprehensive applications in biomechanics, industry, and engineering, the research on boundary layer flows of non-Newtonian fluids past a stretching surface is very important. Accordingly, Jayachandra and Sandeep [7], Reddy et al. [8], Vijayalakshmi et al. [9], and Tian et al. [10] examined with different parameters on the non-Newtonian fluid flow past various stretching surfaces. The effect of thermal radiations on MHD three-dimensional flow over a stretching sheet was studied by Nasir et al. [11]. In the presence of graphene nanoparticles, Khan et al. [12] investigated the Eyring-Powell slip flow of a nano liquid film.
The upper-convected Maxwell fluid is a type of a viscoelastic or rate type fluid. This model is very important since it predicts the relaxation time effect and it excludes complicated effects of shear-dependent viscosity. Commonly, many researchers have studied upper-convected Maxwell fluid flow. Yu Bai et al. [13], Imran et al. [14], Elsayed Mohamed Abdel Rahman Elbashbeshy et al. [15], Vajravelu et al. [16], Omowaye and Animasaun [17], Alireza Rahbari et al. [18], Gireesha et al. [19], and Meysam Mohamadali [20] scrutinized non-Newtonian Maxwell fluid with different physical conditions such as viscous dissipation, Newtonian heating, homogeneous-heterogeneous chemical reactions, and thermal stratification past different stretching surfaces. Their result shows that as Prandtl number increases, temperature, as well as rate of heat transfer, dwindled.
The research on stagnation point flow of nanofluid over stretching surface has different applications in industries and technology. As a result, Sajid et al. [21], Sirinivasulu et al. [22], and Wubshet [23] investigated MHD stagnation point flow in different non-Newtonian fluids such as Oldroyd-B fluid Casson and upper-convected Maxwell fluid on a stretching sheet with various physical parameters. Similarly, Mageswari and Nirmala [24] scrutinized stagnation point flow on stretching sheet with Newtonian heating. Moreover, Abuzar et al. [25] have examined the effect of radiation and convective boundary condition on oblique stagnation point of non-Newtonian nanofluids over the stretching surface. Furthermore, stagnation point flow of nanofluid due to inclined stretching sheet was studied numerically by Yasin Abdela et al. [26]. The numerical result shows that when velocity ratio parameter, Grashof number, solutal expansion parameter, and angle of inclination velocity increased, the boundary layer thickness increases.
The studies of chemical reaction and slip boundary condition with heat transfer have important application in technology and industry. Accordingly, the slip effect on MHD flow with different model of non-Newtonian nanofluids such as Casson fluid and Jeffrey nanofluid past a stretching sheet with various physical conditions are investigated by Sathies Kumar [27], Raghawendra Mishra [28], Manjula and Jayalakshmi [29], and Mohamed Abd El-Aziz and Ahmed Afify [30]. Their study displays that if velocity ratio, momentum slip, and magnetic parameters increase, then the velocity boundary layer thickness become reduced. Krishnamurthy et al. [31], Mabood et.al [32], and Ibrahim et.al [33] probed the effect of chemical reaction on mass and heat transfer MHD boundary layer flow with viscous dissipation, thermal radiation, mixed convection, etc., past stretching sheet and observed that with an increasing magnetic field, the Nusselt number, skin friction coefficient, and Sherwood number are increased. Madasi krishnaiah et al. [34] studied the effect of slip conditions, viscous dissipation, and chemical reaction on MHD stagnation point flow of nanofluid. They observed that as the values of suction parameter rise, the velocity upsurges, also the temperature and concentration profiles are reduced. Moreover, the reference covering slip effects and chemical reaction are described in references [35,36,37,38,39,40,41,42,43,44,45,46,47].
All the above investigators disregard the effects of nanoparticles with slip effects in the analysis of the problem of MHD stagnation point flow of upper-convected Maxwell fluid with chemical reaction. So, the objective of the present paper is to inspect the effect of nanoparticle and chemical reaction on MHD slip stagnation point flow, the boundary layer flow, and heat and mass transfer of upper-convected Maxwell fluid above a stretching sheet via implicit finite difference method. Therefore, the inclusion of the effect of nanoparticles with chemical reaction and slip effect in upper-convected Maxwell fluids makes this study a novel one.
Mathematical formulation
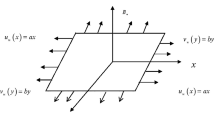
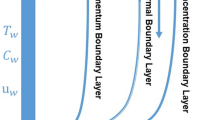
Let us contemplate time-independent and incompressible MHD slip flow of upper-convected Maxwell (UCM) fluid with chemical reaction along a stretching sheet. It is expected that the free stream velocity Ue(x) and the stretching velocity Uw(x) are of the forms Ue(x) = dx and Uw(x) = cx where c and d are constants. For this, study x-axis is along the sheet and normal to the sheet y-axis is chosen. Over the stretching sheet, the concentration is represented by Cw and temperature is represented by Tw. Moreover, the ambient temperature and the ambient concentration are represented by T∞ and C∞. Under these assumptions, the governing equations of time-independent and incompressible boundary layer flow nanofluid over stretching sheet are given by:
The appropriate boundary conditions are:
where u and v are the velocity components along the x and y directions, respectively, ρf is the density of the base fluid, \( {\alpha}_m=\frac{k}{\rho {c}_f} \) is the thermal diffusivity, ξ is the relaxation time parameter of the fluid, B0 is the strength of the magnetic field, ν is the kinematic viscosity of the fluid, k is the thermal conductivity of the fluid, DB is the Brownian diffusion coefficient, Dτ is the thermophoretic diffusion coefficient, \( \tau =\frac{{\left(\rho c\right)}_p}{{\left(\rho c\right)}_f} \) is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid, c is the volumetric volume expansion coefficient, and ρ is the density of the particles Fig. 1.
We can write for the radiation using Rosseland approximation
where σ∗ is the Stefan-Boltzman constant and k∗ is the absorption coefficient; assuming the temperature difference within the flow in such that T4 may be expanded in a Taylor series about T∞ and neglecting higher orders we get \( {T}^4=4T{T}_{\infty}^3-3{T}_{\infty}^4 \).
Hence,
Introducing similarity transformations
We choose the stream function ψ(x, y) such that
Using the similarity transformation defined by (9), Eqs. 1–4 are transformed into the non-dimensional ordinary differential equation form as follows:
The transformed boundary conditions are
where f is dimensionless velocity, θ is dimensionless temperature, ϕ is dimensionless concentration, and η is the similarity variable. The prime denotes differentiation with respect to η.
The overall governing parameters are defined as the following:
\( S=-{v}_w(x)\sqrt{\frac{2x}{\nu {u}_{\infty }}} \) is the suction-injection parameter, \( E=\frac{d}{c} \) is velocity ratio, β = ξc is Deborah number, \( M=\frac{\sigma {B}_0^2x}{\rho {u}_{\infty }} \)is magnetic field parameter, \( \lambda =\mathrm{A}\sqrt{\frac{c}{\nu }} \)is velocity slip parameter, \( \delta =\mathrm{B}\sqrt{\frac{c}{\nu }} \)is thermal slip parameter, \( \gamma =\mathrm{K}\sqrt{\frac{c}{\nu }} \)is solutal slip parameter, \( \mathrm{R}=\frac{k{k}^{\ast }}{4{\sigma}^{\ast }{T}_{\infty}^3} \)is thermal radiation parameter, k = (ρcp)f, \( \mathit{\Pr}=\frac{\nu }{\alpha } \) is Prandtl number, \( Nb=\frac{{\left(\rho c\right)}_p{D}_B\left({C}_w-{C}_{\infty}\right)}{{\left(\rho c\right)}_f\nu } \) is Brownian motion parameter, \( Nb=\frac{{\left(\rho c\right)}_p{D}_{\tau}\left({T}_w-{T}_{\infty}\right)}{{\left(\rho c\right)}_f\nu {T}_{\infty }} \)is thermophoresis parameter, \( Le=\frac{\nu }{D_B} \)is Lewis number, \( h=\frac{h_r}{c} \)is chemical reaction parameter, and \( Q=\frac{Q_0}{a{\left(\rho {c}_p\right)}_f} \) is heat source parameter.
The skin friction Cf, local Nusselt number Nux, and the Sherwood number Shx are the important physical quantities of interest in this problem which are defined as
Here \( {\tau}_w=\mu \left(1+\beta \right)\frac{\partial u}{\partial y} \) is the surface shear stress, \( {q}_w=-k{\left(\frac{\partial T}{\partial y}\right)}_{\left(y=0\right)}+{q}_r \) is the surface heat flux, and\( {q}_m=-{D}_B{\left(\frac{\partial C}{\partial y}\right)}_{\left(y=0\right)} \)
Using the similarity transformation in (9) we have the following relations:
\( {C}_f{\mathit{\operatorname{Re}}}_x^{\frac{1}{2}}=f^{\prime\prime }(0), \) \( {Nu}_x{\mathit{\operatorname{Re}}}_x^{-\frac{1}{2}}=-\left(1+\frac{4}{3R}\right)\theta^{\prime }(0), \) \( {Sh}_x{\mathit{\operatorname{Re}}}_x^{-\frac{1}{2}}=-\phi^{\prime }(0) \), where Rex is the local Reynolds number.
Numerical solution
-
a.
The Keller-box method
The transfigured ordinary differential Eqs. (11), (12), and (13) subject to the boundary conditions (14) and (15) are solved numerically using an implicit finite difference method (Keller-box) in combination with Newton’s linearization techniques. The key topographies of this method are:
- i)
Unconditionally stable and has a second-order accuracy with arbitrary spacing and attractive extrapolation features.
- ii)
The most reliable and powerful numerical methods for nonlinear boundary layer flows that are generally parabolic in nature.
- iii)
Tolerates very speedy x variations.
The Keller-box scheme comprises four steps:
- 1)
Reducing the order ordinary differential equations into a system of fist order equations.
- 2)
Using central differences write difference equations.
- 3)
Linearizing the resulting algebraic equations by using Newton’s method and writing in matrix-vector form.
- 4)
By using block-tridiagonal elimination method solving the linearized system of equations.
- b.
The finite difference scheme
- b.
We write the governing third-order momentum Eq. (11) and second-order energy and concentration Eqs. (12) and (13) in terms of a first-order equations. For this purpose, we introduce new dependent variables u, v, t, θ = s(x, η), ϕ(η) = g(x, η) such that f′ = u, u′ = v, s′ = t, and g′ = z
Thus Eqs. (11), (12), and (13) can be written as
The boundary conditions are
where prime denotes the differentiation with respect to η.
We now consider the net rectangle in the x − η plane shown in Fig. 2 and the net points defined as below
where ki is the ∆x-spacing and hj is the ∆η-spacing. Here, i and j are the sequence of numbers that indicate the coordinate location, not tensor indices or exponents.
Since only first derivatives appear in the governing equations, centered differences and two-point averages can be constructed involving only the four corner nodal values of the “box.” For example, if g represents any of the dependent variables u, v, s, and t then
Now write the finite difference approximations for first-order ordinary differential equation for the mid-point \( \left({x}^i,{\eta}_{j-\frac{1}{2}}\right) \) of the segment P1P2using centered difference derivatives. This process is called centering about \( \left({x}^i,{\eta}_{j-\frac{1}{2}}\right) \). We get
where \( {P}_{1-\frac{1}{2}}=-\left({\mathrm{v}}_j-{\mathrm{v}}_{j-1}\right)-{h}_j{\left(f\mathrm{v}\right)}_{j-\frac{1}{2}}+{h}_j{\left({u}^2\right)}_{j-\frac{1}{2}}-2{h}_j{\left( fu\mathrm{v}\right)}_{j-\frac{1}{2}}+\frac{\beta }{4}{\left({f}^2\right)}_{j-\frac{1}{2}}\left({\mathrm{v}}_j-{\mathrm{v}}_{j-1}\right)-M{h}_j\left(E-{(u)}_{j-\frac{1}{2}}\right)-{h}_j{E}^2 \)and
We note that \( \kern0.5em {P}_{1-\frac{1}{2}} \), \( {Q}_{j-\frac{1}{2}} \), and \( {S}_{j-\frac{1}{2}} \) involve only known quantities if we assume that the solution is known on
x = xi − 1. In terms of the new dependent variables, the boundary conditions become
Equations in Eq. (21) are imposed for j = 1, 2, 3, …, J and the transformed boundary layer thickness ηJ is sufficiently large so that it is beyond the edge of the boundary layer Cebeci and Bradshaw [48]. The boundary condition yields at x = xi are
Newton’s method
Equations in Eq. (21) are nonlinear algebraic equations and therefore have to be linearized before the factorization scheme can be used. Let us write the Newton iterates as follows: For (k + 1)th iterates, we write
Equation (21) can be written as
By dropping the quadratic and higher-order terms in \( \delta {f}_j^{(i)},\delta {u}_j^{(i)},\delta {\mathrm{v}}_j^{(i)},\delta {s}_j^{(i)},\delta {g}_j^{(i)},\delta {t}_j^{(i)}, and\ \delta {z}_j^{(i)} \), a linear tridiagonal system of equations will be obtained as follows:
where
Where
To complete the system (28) we recall the boundary conditions (23) which can be satisfied exactly with no iteration. Therefore, in order to maintain these correct values in all the iterates, we take δf0 = 0, δu0 = 0, δs0 = 0, δg0 = 0 δuJ = 0, δsJ = 0, and δgJ = 0.
In a general case, Eq. (31) in vector matrix forms:
where
In Eq. (31), the elements are defined by
To solve Eq. (34), we assume that A is nonsingular and can be factored into
where
and
where [I] is the identity matrix of order 7 and [αi] and [Γi] are 7 × 7 matrices, in which elements are determined by the following equations:
Equation (30) can now be substituted into Eq. (34) and we get
If we define
Equation (37) becomes
where
and the [ Wj] are 7 × 1 column matrices. The element W can be solved from Eq. (39):
The step in which Γj, αj, and Wj are calculated is usually referred to as the forward sweep. Once the element of W is found, Eq. (38) then gives the solution in the so-called backward sweep, in which the elements are obtained by the following relations:
These calculations are repeated until some convergence criterion is satisfied and calculations are stopped when
where ε1is a small arranged value.
Its exactness and heftiness have been confirmed by different investigators. We have compared our results with investigators Shravani Ittedi et al. [49] to further check on the exactness of our numerical computations and have found to be in an admirable agreement.
Results and discussions
This paper analyzed the effects of slip and chemical reaction on upper-convected Maxwell fluid flow over a stretching sheet. Transfigured governing Eqs. (11–13) with the boundary conditions (14) and (15) are coupled non-linear differential equations. Thus, it is impossible to solve directly with the analytical method. Therefore, to solve this coupled non-linear differential equations, we use implicit finite difference (Keller-box) method by MatLabR2013a software. For various values of effective governing parameters such as velocity ratio S, the suction-injection parameter, E velocity ratio, Deborah number β, magnetic field parameter M, velocity slip parameter λ, thermal slip parameter δ, solutal slip parameter γ, thermal radiation parameter M, Prandtl number Pr, Brownian motion parameter Nb, thermophoresis parameter Nt, Lewis number Le, chemical reaction parameter h, and heat source parameter Q, the numerical solutions of velocity, temperature, and concentration are obtained with step size ∆η = 0.1. Unless otherwise the parameters are specified, the value parameters are M = 1.0, β = 0.1, λ = 0.1, δ = 0.1, γ = 0.1, Pr = 2.0, Le = 2.0, Nb = 0.1, S = 0.1, Nt = 0.1, R = 0.1, h = 0.1, Q = 0.0, E = 0.1. For this study, the range of parameters is 1 ≤ M ≤ 4, 0 ≤ β ≤ 1, 0 ≤ S ≤ 1.5, 0 ≤ h ≤ 1, 0.1 ≤ E ≤ 1.0, 0.1 ≤ Nb ≤ 1.5, 0.1 ≤ Nt ≤ 1.0, −1.5 ≤ Q ≤ 0.0, 2 ≤ Le ≤ 15, 0 ≤ R ≤ 1.0, 0.0 ≤ λ ≤ 1.5, 0 ≤ δ ≤ 1.5, 0 ≤ γ ≤ 1.0
The comparison of the variation of the skin coefficient f ′ ′ (0) for different values of magnetic field parameter M with respect to another study is presented in Table 1. The values show that our result is in admirable agreement with the results given by researchers Shravani Ittedi et al. [49] in limiting conditions. Moreover, a comparison of heat and mass transfer rate for different values of δ and λ is made in Table 2 to check the accuracy of the numerical solution with Shravani Ittedi et al. [49] and we have found an admirable agreement with him. Therefore, we are assured that for the analysis of our problem, the numerical method is appropriate.
For different values of S, E, λ , and β , the variation of f ′ ′ (0), −θ ′ (0), and −ϕ ′ (0) is given in Table 3. From the table, when the suction-injection parameter S and Deborah number β increases, we see that skin friction coefficient increases but decreases with an increase of velocity ratio E and velocity slip parameter λ. Moreover, the table shows that the local Nusselt number −θ ′ (0) and the local Sherwood number −ϕ ′ (0) of the flow field increases as the values of S and E and decreases with an upsurge of Deborah number β and velocity slip parameter λ.
The sways of magnetic field parameter on flow velocity, temperature, and concentration are displayed through Figs. 3, 4, and 5. From the figures, we have perceived that as magnetic field increased, the velocity of the fluid decreased; in contrast, the temperature and concentration profiles demonstrated the behavior of increasing. These are because of the magnetic field offerings a retarding body force known as Lorentz force performs transverse to the direction of the practical magnetic field. The boundary layer flow and the thickness of the momentum boundary layer are abridged by this body force. Similarly, because of Lorentz force, a fractional resistive force which opposes the fluid motion, it produces heat. Due to this fact the stronger the magnetic field, the thicker the thermal boundary layer and concentration boundary layer. Figures 6, 7, and 8 reveal the characteristic of velocity, temperature, and concentration profiles with respect to the variation in suction parameter S. As the values of S increase the temperature, velocity and concentration profile results diminish. The variations of chemical reaction parameter on concentration profile are executed in Fig. 9. These figures afford a clear insight that increasing the value of chemical reaction, the concentration in the boundary layer falls. This is due to the fact that negative chemical reaction reduces the concentration boundary layer thickness and raises the mass transfer.
The influences of velocity ratio parameter on flow velocity and temperature profiles are revealed through Figs. 10 and 11. As the values of velocity ratio upsurge, the boundary layer thickness rises and the flow has boundary layer structure. The graph of velocity is possible when the free steam velocity is less than or equal to the velocity of stretching sheet. That is when velocity ratio is less than or equal to one. But as the value of velocity ratio parameter increases, thermal boundary layer thickness decreases.
The influence of Brownian motion parameter on concentration and temperature profiles is depicted through Figs. 12 and 13. From the figures, it can be seen that as the values of Brownian motion parameter rises, the thermal boundary layer thickness increases and at the surface, the temperature gradient demises. But we witnessed an opposite result on the concentration profiles and concentration boundary layer thickness as Brownian motion parameter upsurges. Figures 14 and 15 are devoted to demonstrate the impact of thermophoresis parameter on temperature and concentration profiles. From the figures, it is perceived that when thermophoresis parameter rises, there is an improvement of the thermal and concentration boundary layer thickness. Figure 16 is plotted to examine the effect of heat generation/absorption parameter on temperature profiles. From the figure, it can be seen that the temperature profiles increases as heat generation/absorption parameter upsurges. This is because the thermal state of the fluid rises with increasing the heat generation.
Figures 17 and 18 executed that the influence of Deborah number on velocity and temperature profiles. These figures give a clear perception that the velocity boundary thickness tumbles as the value of Deborah number rises, and the thermal boundary layer thickness growths as the values increase. This is because of the fact that as the values upsurge, the force due to the parameter opposes the velocity flow and declines thermal diffusivity in the boundary layer, which encourages the upswing of temperature. The impact of Lewis number on concentration profiles is illustrated through Fig. 19. From the figure, it can be observed that higher values of Lewis number decrease the concentration graph and the concentration boundary layer thickness. The temperature curves for different values of thermal radiation parameter are depicted in Fig. 20. From the graph, it is possible to observe that as the values of thermal radiation parameter upsurge, the temperature graph and the temperature boundary layer thickness are snowballing.
The influences of velocity slip parameter on velocity, temperature, and concentration profiles are portrayed in Figs. 21, 22, and 23. From the graphs, it can be seen that as the value of velocity slip parameter upsurges, the velocity profiles decreases, but the temperature and concentration profiles are snowballing. This is due to the fact that as velocity slip rises, the velocity of fluid declines because pulling of stretching sheet can transmit the fluid. The temperature and concentration profiles are presented in Figs. 24 and 25 for various values of thermal slip parameter. It is observed that as the values of thermal slip parameter increase, both temperature and concentration profiles decline. A decrement of concentration profiles with an increment of concentration slip parameter is executed through Fig. 26. Basically, this is due to the fact that slip retards the motion of the fluid which indicates a decline in concentration profiles.
Conclusions
This study presents MHD slip effect and stagnation point flow of upper-convected Maxwell fluid on a stretching sheet with chemical reaction. Depending on the governing parameters, velocity ratio, suction-injection parameter, Lewis numbers, Deborah number, magnetic field, Brownian motion parameter, thermophoresis parameter, chemical reactions parameter, thermal radiation parameter, velocity slip parameter, thermal slip parameter, solutal slip parameter, and heat source parameter, a similarity solution is obtained. The clarifications of the present study are precised as:
- 1.
The suction-injection parameter on velocity, concentration, and temperature profiles has shown a reduction.
- 2.
When the magnetic field upsurges, it reduces velocity profiles and it upsurge temperature and concentration profiles.
- 3.
A velocity profile is reduced with rising values of the Deborah number, and temperature profile is increased with an increasing value of the Deborah number.
- 4.
Temperature and concentration profiles are intensified with snowballing values of velocity slip parameter but velocity profiles are decreased.
- 5.
By increasing the values of the Brownian motion, chemical reaction, Lewis number, thermal slip parameter, and solutal slip parameter, there is reduction in concentration profiles.
- 6.
The thickness of thermal boundary layer augmented as thermal radiation parameter R upsurges.
- 7.
Both rate of Nusselt number and rate of mass Sherwood number rise with suction-injection parameter S and velocity ratio E, and declines velocity slips parameter and the Deborah number.
Nomenclature
B0 Strength of magnetic field
Cf Skin friction coefficient
c Volumetric volume expansion coefficient
Cw Uniform concentration over the surface of the sheet
C∞ Ambient concentration
DB Brownian diffusion coefficient
hf Heat transfer coefficient
DT Thermophoresis diffusion coefficient
k Thermal conductivity
f Dimensionless velocity stream function
E Velocity ratio
Le Lewis number
h Chemical reaction parameter
M Magnetic parameter
Pr Prandtl number
Nb Brownian motion parameter
S Suction-injection parameter
Nt Thermophoresis parameter
Rex Local Reynolds number
Nux Local Nusselt number
R Heat source parameter
Shx Local Sherwood number
Tf Temperature of a hot fluid
Tw Uniform temperature over the surface of the sheet
T∞ Ambient temperature
T Temperature of the fluid inside the boundary layer
ue Free steam velocity
(u, v) Velocity component along x- and y-direction
Greeks symbols
ϕ∞ Dimensionless concentration function at large values of y
η Dimensionless similarity variable
β Deborah number
ν Kinematic viscosity of the fluid
θ Dimensionless temperature stream function
ρf Density of the fluid
μ Dynamic viscosity of the fluid
σ Electrical conductivity
(ρc)f Heat capacity of the fluid
ψ Stream function
(ρc)p Effective heat capacity of a nanoparticle
τ Parameter defined by \( \frac{{\left(\uprho \mathrm{c}\right)}_{\mathrm{p}}}{{\left(\uprho \mathrm{c}\right)}_{\mathrm{f}}} \)
ϕ Dimensionless concentration steam function
αm Thermal diffusivity
ϕw Dimensionless concentration function at the surface
λ Velocity slip parameter
δ Thermal slip parameter
γ Solutal slip parameter
Subscripts
ξ Relaxation time parameter of the fluid
∞ Condition at the free stream
w Condition at the surface
Availability of data and materials
All the data and materials used in this paper can be freely available.
References
Macha, M., Kishan, N., Chamkha, A.J.: Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propulsion Power Res. 6(1), 31–40 (2017). https://doi.org/10.1016/j.jppr.2017.01.002
Macha, M., Kishan, N.: Finite element analysis of MHD viscoelastic nanofluid flow over a stretching sheet with radiation. Process Eng. 127, 432–439 (2015). https://doi.org/10.1016/j.proeng.2015.11.393
Macha Madhu and Naikoti Kishan: MHD flow and heat transfer of Casson nanofluid over a wedge. Mech Ind 18, 210 (2017). http://dx.doi.org/https://doi.org/10.1051/meca/2016030.
Srinivas, C., Reddy, Kishan, N., Macha, M.: Finite element analysis of Eyring–Powell nano fluid over an exponential stretching sheet. Int J Appl Comput Math. 4(8), 1–13 (2017). https://doi.org/10.1007/s40819-017-0438-x
Madhu, M., Kishan, N., Chamkha, A.J.: MHD flow of a non-Newtonian nanofluid over a non-linearly stretching sheet in the presence of thermal radiation with heat source/sink. Eng. Comput. 33(5), 1610–1626 (2016). https://doi.org/10.1108/EC-06-2015-0174
Macha, M., Kishan, N., Chamkha, A.: Boundary layer flow and heat transfer of a non-Newtonian nanofluid over a non-linearly stretching sheet. Int. J. Numerical Methods Heat Fluid Flow. 26(7), 2198–2217 (2016). https://doi.org/10.1108/HFF-02-2015-0066
Jayachandra Babu, M., Sandeep, N.: MHD non-Newtonian fluid flow over a slendering stretching sheet in the presence of cross-diffusion effects. Alexandria Eng J. 55, 2193–2201 (2016). https://doi.org/10.1016/j.aej.2016.06.009
Ramana Reddy, J.V., Anantha Kumar, K., Sugunamma, V., Sandeep N.: Effect of cross diffusion on MHD non-Newtonian fluids flow past a stretching sheet with non-uniform heat source/sink investigated Alexandria Eng. J. 57, 1829-1838(2018). http://dx.doi.org/https://doi.org/10.1016/j.aej.2016.06.009.
Vijayalakshmi, R., Sreelakshmi, K., Sandhya, G., Sarojamma, G.: Flow of upper-convected Maxwell Micropolar fluid over a stretching sheet with slip effect. Int J Innov Res Sci Eng Technol. 6(13), 148–154 (2017)
Tian, X., Li, B., Hu, Z.: Convective stagnation point flow of a MHD non-Newtonian nanofluid towards a stretching plate. Int J Heat Mass Transf. 127, 768–780 (2018)
Nasir, S., Islam, S., Gul, T., Shah, Z., Khan, M.A., Khan, W., Khan, A.Z., Khan, S.: Three-dimensional rotating flow of MHD single wall carbon nanotubes over a stretching sheet in presence of thermal radiation. Appl Nanosci. 8, 1361–1378 (2018)
Khan, N.S., Zuhra, S., Shah, Z., Bonyah, E., Khan, W., Islam, S.: Eyring-Powell slip flow of nano liquid film containing graphene nanoparticles. AIP Adv. 8, 115302 (2018)
Yu Bai, Yuehua Jiang, Fawang Liu and Yan Zhang: Numerical analysis of fractional MHD Maxwell fluid with the effects of convection heat transfer condition and viscous dissipation. AIP Adv 7, 12530. (2017). https://doi.org/https://doi.org/10.1063/1.5011789.
Imran, M.A., Riaz, M.B., Shah, N.A., Zafar, A.A.: Boundary layer flow of MHD generalized Maxwell fluid over an exponentially accelerated infinite vertical surface with slip and Newtonian heating at the boundary. Results Phys. 8, 1061–1067 (2018). https://doi.org/10.1016/j.rinp.2018.01.036
Elbashbeshy, E.M.A.R., Abdelgaber, K.M., Asker, H.G.: Heat and mass transfer of a Maxwell nanofluid over a stretching surface with variable thickness embedded in porous medium. Int. J. Math. Comput. Sci. 4(3), 86–98 (2018) http://www.aiscience.org/journal/ijmcs
Vajravelu, K., Li, R., Dewasurendra, M., Benarroch, J., Ossi, N., Zhang, Y., Sammarco, M., Prasad, K.V.: Analysis of MHD boundary layer flow of an Upper- Convected Maxwell fluid with homogeneous-heterogeneous chemical reactions. Commun. Numerical Analysis. 2, 202–216 (2017). https://doi.org/10.5899/2017/cna-00324
Omowaye, A.J., Animasaun, I.L.: Upper-convected maxwell fluid flow wit variable thermo-physical properties over a melting surface situated in hot environment subject to thermal stratification. J. Appl. Fluid Mech. 9(4), 1777–1790 (2016). https://doi.org/10.18869/acadpub.jafm.68.235.24939
Rahbari, A., Abbasi, M., Rahimipetroudi, I., Sundén, B., Ganji, D.D., Gholami, M.: Heat transfer and MHD flow of non-Newtonian Maxwell fluid through a parallel plate channel. Mech Sci. 9, 61–70 (2018). https://doi.org/10.5194/ms-9-61-2018
Gireesha, B.J., Mahanthesh, B., Subba, R., Gorla, R., Krupalakshmi, K.L.: Mixed convection two-phase flow of Maxwell fluid under the influence of non-linear thermal radiation, non-uniform heat source/sink and fluid-particle suspension. Ain Shams Eng J. 9, 735–746 (2018). https://doi.org/10.1016/j.asej.2016.04.020
Meysam Mohamadali and Nariman Ashrafi: Similarity solution for high Weissenberg number flow of upper-convected Maxwell fluid on a linearly stretching sheet. Hindawi Publishing Corporation J. Eng. (2016). https://doi.org/10.1155/2016/9718786.
Sajid, M., Ahmed, B., Abbas, Z.: Steady mixed convection stagnation point flow of MHD Oldroyd-B fluid over a stretching sheet. J. Egyptian Math. Soc. 23, 440–444 (2014). https://doi.org/10.1016/j.joems.2014.05.013
Srinivasulu, T., Bandari, S., Sumalatha, C.: The effect of viscous dissipation MHD stagnation point flow of Casson nano-fluid over stretching sheet. Global J Pure Appl Math. 13(8), 0973–1768 (2017)
Wubshet, I.: Magnetohydrodynamic stagnation point flow and heat transfer of upper-convected Maxwell fluid past a stretching sheet in the presence of nanoparticles with convective heating. Front Heat Mass Transfer. 7(4), (2016). https://doi.org/10.5098/hmt.7.4
Mageswari, M., Nirmala, M.: Stagnation point flow over a stretching sheet with Newtonian heating using Laplace domain decomposition method. Int J Pure Appl Math. 110(1), 95–102 (2016). https://doi.org/10.12732/ijpam.v110i1.11
Ghaffari, A., Javed, T., Labropulu, F.: Oblique stagnation point flow of a non-Newtonian nano-fluid over a stretching surface with radiation. Therm Sci. 21(5), 2139–2153 (2017)
Yasin, A., Bandari, S., Srinivasulu, T.: Numerical solution of stagnation point flows of nano fluid due to an inclined stretching sheet. Int J Comput Eng Res. 8(2), 2250–3005 (2018)
Sathies Kumar, P., Gangadhar, K.: Slip flow of MHD Casson fluid over a stretching sheet with heat, chemical reaction and mass transfer is investigated by Sathies Kumar. Adv Appl Sci Res. 6(8), 205–223 (2015)
Mishra, R.: MHD slip effect of Jeffrey nanofluid flow over a stretching sheet in the presence of nonlinear thermal radiation and chemical reaction. Int J Eng Sci Res Technol. 6(4), (2017)
Manjula, D., Jayalakshmi, K.: Slip effects on unsteady MHD and heat transfer flow over a stretching sheet embedded with suction in a porous medium filled with a Jeffrey fluid. Int J Res. 7(8), 609–623 (2018). https://doi.org/10.1515/ijnsns-2016-0056
El-Aziz, M.A., Afify, A.A.: Influences of slip velocity and induced magnetic field on MHD stagnation-point flow and heat transfer of Casson fluid over a stretching sheet. Math Probl Eng. (2018). https://doi.org/10.1155/2018/9402836
Krishnamurthy, M.R., Prasannakumara, B.C., Gireesha, B.J.: Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Eng Sci Technol Int J. 19, 53–61 (2016). https://doi.org/10.1016/j.jestch.2015.06.010
Mabood, F., Shateyi, S., Rashidi, M.M., Momoniat, E., Freidoonimehr, N.: The impact of radiation and viscous dissipation on MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with chemical reaction. Adv Powder Technol. 27, 742–749 (2016). https://doi.org/10.1016/j.apt.2016.02.033
Ibrahim, S.M., Lorenzini, G., Vijaya, K.P., Raju, C.S.K.: Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transf. 111, 346–355 (2017)
Krishnaiah, M., Punnam, R., Vijayalaxmi, T., Krishna, C., Reddy, M.: Effect of chemical reaction on MHD stagnation point flow in nanofluid over a nonlinear stretching sheet with viscous dissipation and slip conditions. Int J Sci Eng Technol Res. 5(12), (2016)
Lu, D.-C., Ramzan, M., Bilal, M., Chung, J.D., Farooq, U.: A numerical investigation of 3D MHD rotating flow with binary chemical reaction, activation energy and non-fourier heat flux. Commun Theor Phys. 70, 89–96 (2018). https://doi.org/10.1088/0253-6102/70/1/89
Ramzan, M., Bilal, M.: Three-dimensional flow of an elastico-viscous nanofluid with chemical reaction and magnetic field effects. J Mol Liq. 215, 212–220 (2016) www.elsevier.com/locate/molliq
Ramzan, M., Ullah, N., Chung, J.D., Lu, D., Farooq, U.: Buoyancy effects on the radiative magneto micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 7(12901), 1–15 (2017). https://doi.org/10.1038/s41598-017-13140-6
Muhammad Ramzan, Jae Dong Chung, and Naeem Ullah: Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci.. 130 (1-29) 31-40 (2017). https://doi.org/10.1016/j.ijmecsci.2017.06.009.
Ramzana, M., Bilal, M., Chung, J.D.: Radiative Williamson nanofluid flow over a convectively heated Riga plate with chemical reaction. 55, 1–21 (2017). https://doi.org/10.1016/j.cjph.2017.04.014
Ramzan, M., Bilal, M., Chung, J.D.: Soret and Dufour effects on three dimensional upper-convected Maxwell fluid with chemical reaction and non-linear radiative heat flux. Int. J. Chem. React. Eng. 15, 1–17 (2017). https://doi.org/10.1515/ijcre-2016-0136
Ramzan, M., Bilal, M.: Shamsa Kanwal and Jae Dong Chung: Effects of variable thermal conductivity and non-linear thermal radiation past an Eyring Powell nanofluid flow with chemical reaction. Commun. Theor. Phys. 67, 723–731 (2017). https://doi.org/10.1088/0253-6102/67/6/723
Ramzan, M., Bilal, M., Chung, J.D.: Radiative flow of Powell-Eyring magneto-nanofluid over a stretching cylinder with chemical reaction and double stratification near a stagnation point. PLoS ONE. 12(1), 1–19 (2017). https://doi.org/10.1371/journal
Dianchen Lu, M. Ramzan, Shafiq Ahmad, Jae Dong Chung, and Umer Farooq: Upshot of binary chemical reaction and activation energy on carbon nanotubes with Cattaneo-Christov heat flux and buoyancy effects. Phys. Fluids 29, 123103:1-14 (2017). https://doi.org/10.1063/1.5010171.
Lu, D.-C., Ramzan, M., Bilal, M., Chung, J.D., Farooq, U.: Upshot of chemical species and nonlinear thermal radiation on Oldroyd-B nanofluid flow past a bi-directional stretched surface with heat generation/absorption in a porous media. Commun. Theor. Phys. 70, 71–80 (2018). https://doi.org/10.1088/0253-6102/70/1/71
Ramzan, M., Bilal, M., Chung, J.D.: Numerical simulation of magnetohydrodynamic radiative flow of Casson nanofluid with chemical reaction past a porous media. J. Comput. Theor. Nanosci. 14(12), 5788–5796 (2017). https://doi.org/10.1166/jctn.2017.7013
Ramzan, M., Gul, H., Chung, J.D.: Double stratified radiative Jeffery magneto nanofluid flow along an inclined stretched cylinder with chemical reaction and slip condition. Eur. Phys. J. Plus. 132(456), 1–17 (2017). https://doi.org/10.1140/epjp/i2017-11748-5
Lu, D., Ramzan, M., Ullah, N., Chung, J.D., Farooq, U.: Numerical treatment of radiative nanofluid 3D flow containing gyrotactic microorganism with anisotropic slip, binary chemical reaction and activation energy. Sci. Report. 7(17008), 1–22 (2017). https://doi.org/10.1038/s41598-017-16943-9
Cebeci, T., Bradshaw, P.: Physical and computational aspects of convective heat transfer. Springer−Verlag, Berlin Heidelberg (1984)
Ittedi, S., Ramya, D., Sucharitha: Slip effect of MHD heat transfer of nanofluids above a stretching sheet with chemical reaction. Int. J. Latest Eng. Res. Appl. 02(08), 10–20 (2017)
Acknowledgements
The authors would like to express their deep thanks to the referee for his/her careful reading and many valuable suggestions towards the improvement of the paper.
Funding
No fund in conducting this research.
Author information
Authors and Affiliations
Contributions
All the authors have made substantive contributions to the article and assume full responsibility for its content. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ibrahim, W., Negera, M. MHD slip flow of upper-convected Maxwell nanofluid over a stretching sheet with chemical reaction. J Egypt Math Soc 28, 7 (2020). https://doi.org/10.1186/s42787-019-0057-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42787-019-0057-2