A simplified model for measuring longevity risk for life insurance products

Abstract

In this paper, we propose a simple dynamic mortality model to fit and forecast mortality rates for measuring longevity and mortality risks. This proposal is based on a methodology for modelling interest rates, which assumes that changes in spot interest rates depend linearly on a small number of factors. These factors are identified as interest rates with a given maturity. Similarly, we assume that changes in mortality rates depend linearly on changes in a specific mortality rate, which we call the key mortality rate. One of the main advantages of this model is that it allows the development of an easy to implement methodology to measure longevity and mortality risks using simulation techniques. Particularly, we employ the model to calculate the Value-at-Risk and Conditional-Value-at-Risk of an insurance product testing the accuracy and robustness of our proposal using out-of-sample data from six different populations.

Introduction

The development of mortality models to describe and forecast mortality rates¹ is a crucial element for the accurate pricing of life insurance products, for addressing macroeconomic issues such as the sustainability of public pension systems or for valuing longevity derivatives. Furthermore, precise mortality forecasts are a fundamental tool for the insurance industry to address the challenges related to mortality and longevity risks. Since 2016, European insurance companies have been required to comply with the Solvency II directive, which aims to model and assess all types of risks that insurance companies are exposed to (Börger 2010). In fact, longevity risk, or the risk that the insured will survive on average longer or shorter than expected, is a significant risk facing the insurance industry.

In recent decades, several mortality models have been developed to describe the dynamics of mortality rates as accurately as possible, and some of them have been applied to quantify longevity or mortality risks under Solvency II. For instance, Börger (2010) used the Lee and Carter (1992) model to analyse the adequacy of the longevity shock assumed by the standard model in Solvency II for computing capital requirements. Richards et al. (2014) presented various proposals for quantifying longevity risk over a one-year horizon using standard mortality models such as those in Lee and Carter (1992) and Cairns et al. (2006). Hari et al. (2008) and Olivieri (2011) applied other sophisticated mortality models to measure the impact of systematic (trend) and nonsystematic (random) risks. Börger et al. (2014) proposed a mortality model that specifically focuses on changes in the long-term mortality trend over time. Chulia et al. (2016) presented a methodology based on differences in mortality rates to estimate longevity and mortality risks.

Furthermore, there is a strand of literature that consists of adapting models that were initially developed for modelling the term structure of interest rates to address the dynamics of mortality rates. In fact, the term structure of interest rates and the mortality curve share some common features: just as unexpected changes in interest rates with close maturities behave in a similar way, the mortality rates of individuals with close ages tend to change together (Li and Luo 2012). This is due to the similarities between the force of mortality and the force of interest or between mortality rates and default occurrences (Olivieri 2011). Biffis (2005); Biffis and Millossovich (2006), Cairns (2007), Bauer et al. (2008) and Bauer et al. (2012), among others, presented stochastic mortality models that were initially developed for financial purposes. For instance, Bauer et al. (2008) presented a theoretical investigation of forwards mortality models driven by finite-dimensional Brownian motion. Haldrup and Rosenskjold (2019) proposed using a Nelson-Siegel model to fit the mortality curve (using French and US data) and showed that this approach provides a better fit and out-of-sample accuracy compared to the model in Lee and Carter (1992). Xu et al. (2020) also presented a new continuous-time multicohort mortality model in an affine framework and demonstrated that their model has better results for the Danish mortality data from ages 50–100 compared to other alternative models. These proposals were initially developed to solve pricing problems. However, to the best of our knowledge, these models have not been used for risk management in the context of Solvency II compliance.

Within this strand of literature, Atance et al. (2020a) developed a dynamic mortality model inspired by the term structure model suggested by Elton et al. (1990). According to Elton et al. (1990), it is assumed that changes in spot interest rates depend linearly on a reduced number of interest rates with a particular maturity term, the so called “key interest rates”.² Similarly, Atance et al. (2020a) assume that changes in mortality rates depend linearly on the changes in a particular mortality rate corresponding to a specific age. We will refer to this mortality rate as the “key mortality rate”, that is, the mortality rate that best explains the behaviour of the entire mortality curve (in our study, from 0 to 99 years). Therefore, this model can be considered part of the group of mortality models inspired by the term structure of the interest rate literature.³

Now, the main objective of this work is to adapt and simplify the model to facilitate the development of a new methodology to measure the longevity risk for compliance with the Solvency II regulation.

To this end, one of the contributions of the paper is the use of a different methodology to jointly estimate the key mortality rate and model parameters instead of using the two step procedure suggested by Elton et al. (1990) and Atance et al. (2020a). In these two previous papers, model parameters (two for each age) are estimated using Ordinary Least Squared (OLS). Then, two smooth functions are fitted to these parameter estimates to avoid irregularities. In contrast, in this article, the parameters of these smooth functions are directly estimated in a single step while simultaneously selecting the key mortality rate.

Additionally, instead of using simple linear regression techniques for estimating the model parameters, we assume that the number of deaths of individuals aged x during a given period of time follows a binomial distribution. Then, we apply the maximum-likelihood to jointly estimate the model parameters and select the key mortality rate. This hypothesis and methodology is more in agreement with the assumptions about the distribution of the number of deaths in the actuarial literature⁴ and facilitates a comparison with alternative models. Moreover, this procedure reduces the number of model parameters from 200 to just six⁵ without decreasing the forecasting ability of the model.

In addition, the model is more robust in the identification of the key mortality rate. In fact, the resulting key mortality rates are always with in the range of 84–89 years for all populations analysed in this study.⁶ This result is interesting for several reasons. First, it coincides with a critical age in the ageing process identified by Lehallier et al. (2019). Second, this key mortality rate can be considered representative of a population group of particular interest to the life insurance industry, i.e., those aged 60–65 years and over.

The other main contribution of the paper is the employment of the model for developing and testing a methodology that uses simulation techniques for longevity risk measurement. This methodology is illustrated with a very simple example to calculate the Value at Risk (VaR) and Conditional Value at Risk (CVaR) of life insurance products. We show that despite its simplicity, this procedure provides results that are in line with other popular and more sophisticated dynamic mortality models.

This paper is organized as follows. First, section “Factor mortality model” presents the adaptation of the Elton et al. (1990) model to describe the “mortality curve” behaviour and the parameter estimation methodology. In section “Model fitting”, we proceed to calibrate the model for the male and female populations of Spain, France and the US. In this section, we also implement the proposed methodology for projecting future mortality rates. In section “Comparison with other alternative dynamic mortality models”, we compare the goodness of fit and the forecasting ability of the model with some of the most popular mortality models. To do so, we use different measures of accuracy employing both in-sample and out-of-sample data. Section “Calculating the VaR for longevity risks” describes how to use this model for measuring longevity risk using simulation techniques through the estimation of the VaR and CVaR of a very simple insurance product. Finally, section “Conclusion” presents the main results and conclusions of the paper.

Factor mortality model

Based on the Elton et al. (1990) model of the term structure of interest rate and Atance et al. (2020a), we restate the model as follows⁷:

Let $q_{x,t}$ be the probability of an individual aged x in calendar year t dying within one year. Then, the proposed model is:

$$\begin{aligned} \Delta \text {log} \left( q_{x,t}\right) =\alpha \left( x\right) + b\left( x\right) \left[ \Delta \text {log} \left( q_{y^{*},t}\right) \right] , \end{aligned}$$

(1)

or alternatively:

$$\begin{aligned} q_{x,t} = q_{x,t-1}\cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \left[ \Delta \text {log} \left( q_{y^{*},t}\right) \right] \right\} , \end{aligned}$$

(2)

where,

• $\Delta \text {log} \left( q_{x,t}\right)$ is the change in the logarithm of the mortality rate from $t-1$ to t of an individual aged x.

• $\Delta \text {log} \left( q_{y^{*},t}\right)$ is the change in the logarithm of the key mortality rate⁸ from $t-1$ to t.

• $b\left( x\right)$ is a function that describes how mortality rates react to changes in the key mortality rate, $q_{y^{*},t}$; values of $b\left( x\right)$ that are significantly different from zero indicate the section of the mortality curve influenced by the key mortality rate.

• $\alpha \left( x\right)$ is a function that captures constant yearly changes in $\text {log}\left( q_{x,t}\right)$ for a given age x, in particular those changes that are uncorrelated with those in key mortality rate. The value of this function depends on age, although for close ages, it does not differ significantly since close aged people tend to behave in a similar way. Therefore, $\alpha \left( x\right)$ must be a sufficiently smooth function.

The line of reasoning behind this model is that the dynamics of the mortality curve are governed by two forces. One of them consists of a constant yearly relative change that is assumed to be independent of the behaviour of the key mortality rate. This constant change is different for each mortality rate, is selected by the function $\alpha \left( x\right)$, and is different for children, adults and elderly individuals (Li et al. 2013). The values of this function are generally expected to be negative as a consequence of the long-term reduction in mortality rates due to nondisruptive improvements in medicine, nutrition, lifestyle, etc. (Vékás 2020). However, for some ages, this function can also take positive values above all if the decreasing trend of a particular mortality rate is mainly captured by the key mortality rate. The second force that governs the behaviour of the mortality curve is the changes in the key mortality rate. The corresponding age of this key mortality rate indicates the position of the section in the mortality curve where intense changes in its shape are taking place with a significant impact on the overall number of deaths. This key mortality rate will be chosen as the one with the highest explanatory power with respect to the entire set of mortality rates considered in this study.

In fact, we can distinguish three parts of the mortality curve. For those ages far enough from the key mortality rate, changes in mortality rates are described mainly by $\alpha \left( x\right)$. In contrast, for those ages very close to the key mortality rate, the value of function $\alpha \left( x\right)$ is very close to zero since the behaviour of these mortality rates is mainly explained by changes in the key mortality rate. Moreover, for $x=y^{*}$, $\alpha \left( y^{*}\right)$ must be equal to zero. Finally, there is a third set of mortality rates with mixed behaviour: a combination of constant changes and reactions to changes in the key mortality rate. It should be noted that this function $\alpha \left( x\right)$ does not appear in the original paper of Elton et al. (1990) about the term structure of interest rates.

We assume that both functions, $\alpha \left( x\right)$ and $b\left( x\right)$, depend on a reduced number of parameters. Furthermore, these functions must be sufficiently smooth, since the values of these two functions for mortality rates corresponding to close ages cannot differ significantly. Additionally, these functions must satisfy that for $x=y^{*}$, $\alpha \left( y^{*}\right) =0$ and $b\left( y^{*}\right) =1$. These constraints on $\alpha \left( x\right)$ and $b\left( x\right)$ are necessary for the model internal consistency.⁹ The particular functional forms finally chosen for $\alpha \left( x\right)$ and $b\left( x\right)$ are described in the next section together with the methodology applied to estimate their parameters.

Functions $\alpha \left( x\right)$ and $b\left( x\right)$

Before determining the key age, $y^{*}$, it is necessary to specify the functions $\alpha \left( x\right)$ and $b\left( x\right)$ to be used for describing the behaviour of mortality rates. To do so, we eventually chose two very simple functions to reduce the number of model parameters. Therefore, for $\alpha \left( x\right)$, we use a cubic function that satisfies the constraint, $\alpha \left( y^{*}\right) =0$,

$$\begin{aligned} \alpha \left( x\right) = a_1 \cdot \left( x-y^{*}\right) + a_2 \cdot \left( x-y^{*}\right) ^{2} + a_3 \cdot \left( x-y^{*}\right) ^{3}. \end{aligned}$$

(3)

We eventually decided to choose a cubic function because, despite its simplicity, it allows us to capture the constant changes in mortality rates that are assumed to be uncorrelated with changes in the key mortality rate.¹⁰

We also need a function, $b\left( x\right)$, to describe the sensitivities of mortality rates to changes in the key mortality rate. As mentioned earlier, this function must satisfy the constraint $b\left( y^{*}\right) =1$ and must be smooth enough, as the sensitivities of mortality rates for individuals with very close ages must have close values. Finally, we choose a very simple bell-shaped parametric function:

$$\begin{aligned} b\left( x\right) = \beta _1 \cdot \text {exp}\left\{ -\beta _2 \left( x-y^{*}\right) ^{2}\right\} +\left( 1-\beta _1\right) , \end{aligned}$$

(4)

where $\beta _1$ and $\beta _2$ are parameters to be estimated. $\beta _1$ and $\beta _2$ represent the floor level and the width of the bell around the key age, respectively. Recall that $b\left( x\right)$ captures the sensitivity of mortality rates to changes in the key mortality rate. For instance, if $b\left( x\right) = 0.5$, then a 1% yearly increase in the mortality rate of the key age $y^{*}$ would imply an expected yearly change of 0.5% in the mortality rate of an individual aged x plus the value of $\alpha \left( x\right)$, which is independent of the behaviour of the key mortality rate.

Model calibration

A typical methodology for estimating mortality model parameters consists of applying the maximum likelihood criterion (Brouhns et al. 2002; Renshaw and Haberman 2006; Cairns et al. 2009; Villegas et al. 2018). However, this approach implies the need to make an assumption about the distribution of the number of deaths.¹¹

Thus, let $\widetilde{\vartheta }_{x;t}$ be a random variable representing the number of deaths of individuals aged x (last birthday) during period t in a given population. In this paper, we assume that $\widetilde{\vartheta }_{x;t}$ follows a binomial distribution. Particularly, we assume the following:

$$\begin{aligned} \widetilde{\vartheta }_{x,t} \sim \text {B}\left( E^{0}_{x,t};q_{x,t}\right) \qquad \text {with} \qquad q_{x,t} = \hat{q}_{x,t-1} \cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y^{*},t}\right) \right\} , \end{aligned}$$

(5)

where $E^{0}_{x,t}$ is the initial exposure to the risk of individuals aged x (last birthday) during period t, and $\hat{q}_{x,t-1}=\frac{\vartheta _{x,t-1}}{E^{0}_{x,t-1}}$, $\vartheta _{x,t-1}$ is the actual number of deaths of individuals aged x during period $t-1$.¹²

Therefore, the likelihood function is:

$$\begin{aligned} \begin{aligned} \text {L}\left( \theta , y;\vartheta _{x,t}\right) = {E_{x,t}^{0} \atopwithdelims ()\vartheta _{x,t}}&\cdot \left[ \hat{q}_{x,t-1}\cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) \right\} \right] ^{\vartheta _{x,t}}\\&\cdot \left[ 1-\hat{q}_{x,t}\cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) +\right\} \right] ^{E^{0}_{x,t}-\vartheta _{x,t}}, \end{aligned} \end{aligned}$$

(6)

where $\theta$ is the set of parameters of the functions $\alpha \left( x\right)$ and $b\left( x\right)$.

Therefore, to determine the key mortality rate $q_{y^{*},t}$, we proceed as follows. Let y be any age that is considered a candidate for the key age. From Eq. (6), if the potential key age is y, the logarithm of the joint likelihood function¹³ is given by:

$$\begin{aligned} \begin{aligned} \lambda \left( \theta ; y; \vartheta _{x,t}\right) =&\, \sum _{x,t} \vartheta _{x,t} \cdot \text {log}\left[ \hat{q}_{x,t-1}\cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y, t}\right) \right\} \right] \\&+ \left( E_{x,t}^{0} - \vartheta _{x,t}\right) \cdot \text {log}\left[ 1 - \hat{q}_{x,t-1}\cdot \text {exp}\left\{ \alpha \left( x\right) +b\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y, t}\right) +\right\} \right] + C. \end{aligned} \end{aligned}$$

(7)

Then, for each age y that can potentially be considered a key age, we estimate the parameters $\theta$ that maximize the log-likelihood function. In this work, the candidate key age is always an integer age from 0 to 99. Finally, once the log-likelihood function has been optimized for each age from 0 to 99, the key age is chosen as the one that provides the maximum value for the log-likelihood function. That is, the key age, $y^{*}$, is the age such that:

$$\begin{aligned} \mathop {{\text{max}}}\limits _{y}\mathop {{\text{max}}}\limits _{\theta }\lambda \left( \theta , y;\vartheta _{x,t}\right) . \end{aligned}$$

(8)

This methodology can also be applied using a different objective function, for instance, by estimating the model parameters using OLS. In fact, we can also analysed the latter alternative. In this case, the resulting optimal key mortality rates are very unstable (ranging from 3 years to 89 depending on the population). However, the forecasting ability of the model using OLS to estimate model parameters is not very different except in the case of the population of Spain, where the maximum likelihood produces clearly better results.

In addition, the main differences and contributions of this paper compared to those of Atance et al. (2020a) can be described as follows:

• Instead of using OLS and linear regression techniques, we employ maximum likelihood techniques to estimate model parameters. This approach is more consistent with the actuarial literature, as demonstrated by Brouhns et al. (2002); Renshaw and Haberman (2006); Cairns et al. (2009); Villegas et al. (2018).

• Our methodology allows the simultaneous estimation of model parameters and the selection of the key mortality rate in a single step. This differs from Atance et al. (2020a), which requires two steps to obtain the key mortality and parameter estimates.

• We significantly reduce the number of model parameters from 200 to six. Notably, most dynamic mortality models require the estimation of more than 200 parameters.

• Our results are more robust in selecting the key mortality rate, which is consistently located in the age range between 84 and 89 years for all populations. This is an important finding, as this model focused on the age group of most interest for the life insurance industry.

• Finally, we propose a methodology that can be easily employed for longevity risk measurement using simulation techniques. This is an issue not addressed in Atance et al. (2020a).

Model fitting

Data

To calibrate the model, we use data from three countries, Spain, France and the US. The last two countries have quite different population sizes and correspond to different geographical areas, so they are adequate for testing the robustness of the model. Figure 1 shows the population pyramids of the three countries corresponding to the year 2006. We always distinguish between male and female populations.

The data cover the period 1975–2018 and ages from 0 to 99 years. We divide the sample into two subperiods. The first subset, from 1975 to 2006, will be used to fit the model, and the second subset (from 2007 to 2018) will be used to test its forecasting power and the accuracy of the longevity risk measures.

The mortality data are downloaded using the library HMDHFDplus¹⁴ (Riffe 2015) and are obtained from Human Mortality Database (2022). Human Mortality Database (2022) provides the number of deaths of individuals aged x (last birthday) during each year of the sample period $\left( \vartheta _{x,t} \right)$ and the central exposure to risk for individuals aged x during year t, $E^{c}_{x,t}$.

Therefore, the initial exposures to risk of individuals aged x during year t are obtained as follows:

$$\begin{aligned} E^{0}_{x,t} \approx E^{c}_{x,t} + (1-h_{x,t}) \cdot \vartheta _{x,t} \quad \text {for} \quad x=0,1,2, \ldots , 99, \end{aligned}$$

(9)

where $h_{x,t}$ is defined as the average period of life at age x for those who die at age x (last birthday) during year t. If we assume, as usual,¹⁵ that individuals aged x die uniformly during year t, this value can be approximated by 0.5. However, this is not true for individuals who die at age $x=0$ (last birthday) since most of these individuals die a few hours or days after birth. In this case, the value of $h_{0,t}$ is between 0.11 and 0.14 depending on the population and the year of observation. These data were obtained from Human Mortality Database (2022), and they are available for all ages, years and countries.

Once, we obtain the data for $E^{0}_{x,t}$, mortality rates can be estimated as $\hat{q}_{x,t}=\vartheta _{x,t}/E^{0}_{x,t}$.

Fig. 1

Population pyramids for the central exposure to risk of individuals during 2006 in groups of five ages of males and females in Spain, France and the US

Figure 2 shows the mortality curves¹⁶ during some years of the sample period (1975, 1985, 1995, 2005 and 2015). We have highlighted with black boxes the sections of the mortality curve that experience some of the most relevant changes during the sample period. One of these changes was a consequence of the significant decline in mortality rates that occurred during the sample period in the 60–80 age group, while during the same period, mortality rates remained almost constant for the oldest people (90 years and older). This fact caused a pronounced change in the slope of the right leg of the mortality curve. Additionally, during the 1990 s, mortality rates for the 20–45 age group experienced a large increase, followed by a sharp decline. This was a consequence of the outbreak of the AIDS pandemic and drug use that primarily affected male populations (Ho and Hendi 2018; Murphy et al. 2018; Shiels et al. 2019; Glei and Preston 2020). After the appearance of medical treatments for the disease, mortality rates experienced a strong drop during the early 2000 s. Therefore, the key mortality rate should be located in one of these two sections of the mortality curve where mortality rates experienced intense and highly correlated movements.

Fig. 2

Evolution of mortality curves (in logarithms) from age 0 to 99 a Spain male, b France male, c US male, d Spain female, e France female and f US female, in 1975, 1985, 1995, 2005 and 2015

Model calibration

Figure 3 plots the optimal values of $\lambda \left( \hat{\theta }, y;\vartheta _{x,t}\right)$ for each population (male and female populations of Spain, France and the US) for each potential key age y. This figure can be interpreted as the explanatory power of each mortality rate (from 0 to 99) with respect to the entire mortality curve. $\hat{\theta }$ represents the set of maximum likelihood parameter estimates of functions $\alpha \left( x\right)$ and $b\left( x\right)$. The optimal key age of each population and the estimates of the model parameters are shown in Table 1 together with the optimal value of the log-likelihood function.

It is worth noting some common features of function $\lambda \left( \hat{\theta }, y;\vartheta _{x,t}\right)$ for the six populations under study (Fig. 3). As seen in Table 1, the key ages for all of them are concentrated in the age range of 84–89 years. These ages are in the middle of one of the two sections of the mortality curve where mortality rates experienced the intense and highly correlated movements described above.

Additionally, it should be noted that the key ages are concentrated in the range of ages most impacted by COVID-19, a phenomenon that took place after the sample period. Indeed, as reported by Centers for Disease Control and Prevention and Others (2020), approximately 80% of COVID-19 deaths occur in people older than 65 years. Thus, the key mortality rate may be considered a representative of the age group most affected by the pandemic, although this question requires further research.

Fig. 3

Values of $\lambda \left( \hat{\theta }, y;\vartheta _{x,t}\right)$ as a function of each potential key age y covering the period 1975–2006

Table 1 Parameter estimates corresponding to optimal key age for the sample period 1975–2006

In the case of the male populations of Spain and the US, we can observe another common feature. Function $\lambda \left( \hat{\theta }, y;\vartheta _{x,t}\right)$ presents a double hump. One of them is located around the key age, and the other one is positioned at approximately 30 years old. This latter hump, where function $\lambda \left( \hat{\theta }, y;\vartheta _{x,t}\right)$ has a local optimum, is probably linked to the impact of AIDS and drug consumption (or the combined effect of both) in the male populations of Spain and the US during the 1980 s and 1990 s. According to Ho and Hendi (2018), Murphy et al. (2018), Shiels et al. (2019) and Glei and Preston (2020), the number of deaths related to drug consumption in the 1990 s was much higher for men than for women. In addition, AIDS affected the male population more severely, particularly in both Spain and the US. In the case of Spain, according to Felipe et al. (2002), Guillen and Vidiella-i Anguera (2005) and Debón et al. (2008), AIDS caused a dramatic increase in mortality rates followed by a very sharp decline when new therapies against the disease were discovered. These facts may explain why this local maximum appears only in the male populations of Spain and the US.

Figures 4 and 5 show the values of the functions $\hat{b}\left( x\right)$ and $\hat{\alpha }\left( x\right)$ for the male and female populations of each country. We can see that the shape of the function $\hat{b}\left( x\right)$ is similar for all populations. It takes a constant value close to zero for ages between zero and approximately sixty, followed by a hump centred at the key age, $y^{*}$, where it reaches a maximum value that is equal to one. This hump, which lies in the range of ages between 60 and 99 years, indicates the age group in which mortality rates are influenced by the key mortality rate dynamics. Changes in mortality rates below age sixty are captured by the function $\hat{\alpha }\left( x\right)$. The only exception to this common feature is the US female population, where the key age influences, to some extent, the entire mortality curve, including the young ages. This result seems to reflect a behaviour of the US female population that differs from the other populations analysed in this paper.

As shown in Fig. 4, the function $\hat{\alpha }\left( x\right)$ presents a saddle shape. The values of $\hat{\alpha }\left( x\right)$ are negative from zero to the key age, $y^{*}$, while the values are positive or close to zero for ages above $y^{*}$. It is worth noting that when the values of $\hat{b}\left( x\right)$ are close to zero (from 0 to 60 years), it is the value of $\hat{\alpha }\left( x\right)$ that determines the relative yearly improvements in mortality rates. It can be observed that the values of $\hat{\alpha }\left( x\right)$ between 20 and 60 years of age are more negative for women than for men in the Spanish population, revealing a more intense improvement in the mortality rates for the female population during the sample period in this section of the mortality curve. In the French population, mortality improvements were similar for both the male and female populations in this age range. However, for US populations, the values of $\hat{\alpha }\left( x\right)$ between 20 and 60 years old are higher for women than for men. It should be noted that this result is conditioned by the estimated value of the parameter $\beta _1$ for the US female population, which makes function $\hat{b}\left( x\right)$ take values close to 0.4 (see Fig. 5) for all ages below 60. This means that mortality improvements for ages under 60 for the female US population have two components: on the one hand, a decreasing trend determined by the value of $\hat{\alpha }\left( x\right)$ and a second component linked to changes in the key mortality rate that seems to influence the behaviour of the entire mortality curve.

Fig. 4

Estimated values of function $\hat{\alpha }\left( x\right)$ for Spain, France and the US, which measures the constant improvements in the mortality rate independent of the behaviour of the key age, 1975–2006

Fig. 5

Estimated values of function $\hat{b}\left( x\right)$ for Spain, France and the US, which measures the sensitivity of mortality rates to changes in the key mortality rate, 1975–2006

Correlation structure of mortality rates

To check the model’s ability to measure longevity risk, it is important to analyse whether the actual correlation structure among mortality rates corresponding to different ages is consistent with the theoretical correlation derived from the model (1).

Once, the model parameters and the key age have been estimated, model (1) can be rewritten as:

$$\begin{aligned} \Delta \text {log} \left( q_{x,t}\right) =\hat{\alpha }\left( x\right) + \hat{b}\left( x\right) \left[ \Delta \text {log} \left( q_{y^{*},t}\right) \right] + \varepsilon _{x;t}, \end{aligned}$$

(10)

where $\hat{\alpha }\left( x\right)$ and $\hat{b}\left( x\right)$ are the estimated functions of the model, as described in section “Model calibration” and Table 1, and $\varepsilon _{x,t}$ is an error term uncorrelated with the key age mortality rate. Then, the variance in the change in the logarithm of mortality rates is given by:

$$\begin{aligned} \text {Var}\left( \Delta \text {log}\left( q_{x,t}\right) \right) = \hat{b}\left( x\right) ^2 \text {Var}\left( \Delta \text {log}\left( q_{y^{*},t}\right) \right) + \text {Var}\left( \varepsilon _{x,t} \right) . \end{aligned}$$

(11)

Thus, the correlation between changes in the logarithm of two mortality rates $q_{x,t}$ and $q_{z,t}$ is given by:

$$\begin{aligned} \begin{aligned}\rho \left( \Delta \text {log}\left( q_{x,t}\right) ,\Delta \text {log}\left( q_{z,t}\right) \right) =\frac{\hat{b}\left( x\right) \hat{b}\left( z\right) \text {Var}\left( \Delta \text {log}\left( q_{y^{*}t}\right) \right) }{\left( \sqrt{\hat{b}\left( x\right) ^2\text {Var}\left( \Delta \text {log}\left( q_{y^{*},t}\right) \right) +\text {Var}\left( \varepsilon _{x,t} \right) }\right) \left( \sqrt{\hat{b}\left( z\right) ^2\text {Var}\left( \Delta \text {log}\left( q_{y^{*},t}\right) \right) +\text {Var}\left( \varepsilon _{z,,t} \right) }\right) }\\ \end{aligned} \end{aligned}$$

(12)

In particular, when age z is the key age $y^{*}$, (12) becomes:

$$\begin{aligned} \begin{aligned}\rho \left( \Delta \text {log}\left( q_{x,t}\right) ,\Delta \text {log}\left( q_{y^{*},t}\right) \right) =\frac{\hat{b}\left( x\right) \text {Var}\left( \Delta \text {log}\left( q_{y^{*}t}\right) \right) }{\left( \sqrt{\hat{b}\left( x\right) ^2\text {Var}\left( \Delta \text {log}\left( q_{y^{*},t}\right) \right) +\text {Var}\left( \varepsilon _{x,t} \right) }\right) \left( \sqrt{\text {Var}\left( \Delta \text {log}\left( q_{y^{*},t}\right) \right) }\right) },\\ \end{aligned} \end{aligned}$$

(13)

as $\hat{b}\left( y^{*}\right) =1$ and $\varepsilon _{y^{*},t}=0$. Therefore, it is necessary to show whether the actual correlation values conform at least qualitatively to the expected pattern of correlation (13). To do so, we estimate the variance of $\Delta \text {log}\left( q_{y^{*}, t}\right)$ and $\varepsilon _{x,t}$ as follows:

$$\begin{aligned} \text {Var}\left( \Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) \right)= & {} \frac{\sum _{t=1976}^{2006}\left( \Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) - \overline{\Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) }\right) ^{2}}{N-1}; \end{aligned}$$

(14)

$$\begin{aligned} \text {Var}\left( \varepsilon _{x,t}\right)= & {} \frac{\sum _{t=1976}^{2006}\varepsilon _{x,t}^{2}}{N-1}; \end{aligned}$$

(15)

where $\varepsilon _{x,t}=\Delta \text {log}\left( \hat{q}_{x,t}\right) -\left[ \hat{\alpha }\left( x\right) + \hat{b}\left( x\right) \cdot \Delta \text {log}\left( \hat{q}_{y^{*},t}\right) \right]$ and $\overline{\Delta \text {log}\left( \hat{q}_{y^{*}, t}\right) }$ is the sample mean of the changes in the logarithm of the key mortality rate.

Figures 6, 7 and 8 display the actual values of the correlations between changes in the logarithm of mortality rates and changes in the logarithm of the key mortality rate and the correlations derived from formula (13). As shown, the structure of the theoretical correlations derived from the model adequately captures the actual correlation among mortality rates. Figures 6, 7 and 8 are essential to understanding the applicability of the model for longevity management. What this analysis of the correlations reveals is that changes in the key mortality rate are strongly correlated with changes in rates of neighbouring ages. Indeed, the larger the set of mortality rates correlated with the key mortality rate and the higher the correlation are, the greater the explanatory power of the model and, likely, its forecasting ability. As shown, there are almost 30 mortality rates around the key age with a correlation of at least 40% with the key mortality rate. It is important to note that $\alpha \left( x\right)$ is close to zero for the age range of 60–90 years and it is mainly the value of $b\left( x\right) \cdot \Delta \text {log}\left( q_{y^{*},t}\right)$ that explains the changes in this leg of the mortality curve. Function $b\left( x\right)$ mirrors this structure of correlations and allows us to understand why the key mortality rate is effective in fitting and forecasting changes in mortality rates. However, when the age gap with respect to the key mortality rate becomes wide and the correlation decreases, function $b\left( x\right)$ approaches values close to zero. In fact, for ages below 60, function $\alpha \left( x\right)$ is responsible for capturing the changes in mortality rates.

Fig. 6

Values of the actual and theoretical correlations between $\Delta \text {log}\left( \hat{q}_{x,t}\right)$ and $\Delta \text {log}\left( \hat{q}_{y^{*},t}\right)$ for $x=0$ to 99. a Spain male and b Spain female, 1975–2006

Fig. 7

Values of the actual and theoretical correlations between $\Delta \text {log}\left( \hat{q}_{x,t}\right)$ and $\Delta \text {log}\left( \hat{q}_{y^{*},t}\right)$ for $x=0$ to 99. a France male and b France female 1975–2006

Fig. 8

Values of the actual and theoretical correlations between $\Delta \text {log}\left( \hat{q}_{x,t}\right)$ and $\Delta \text {log}\left( \hat{q}_{y^{*},t}\right)$ for $x=0$ to 99. a US male and b US female 1975–2006

Mortality rate projection

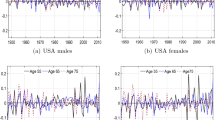
Figure 9 shows the evolution of the key mortality rates during period 1975–2006 for the six populations (used for estimating model parameters) and period 2007–2018, which is used for out-of-sample testing. For Spain and France, it can be seen that $\text {log}\left( \hat{q}_{y^{*},t}\right)$ declined over the period 1975–2006, highlighting the mortality improvement experienced by the elderly in these two countries (see Glei and Horiuchi (2007), Rau et al. (2008) and Christensen et al. (2009)).¹⁷ This trend continued during the out-of-sample period (2007–2018) in the male and female populations of both Spain and France.

In contrast, the behaviour of the US populations exhibited a different pattern. The male population mortality rate experienced a very slight decline during the 1980 s, remained nearly constant during the 1990 s, and began to clearly fall after 2003. For the US female population, changes in mortality rates have been negligible since the mid-1980 s. In fact, during the 1990 s there was a rebound in mortality rates due to an increase in cancer deaths among the US population over 75 years of age that particularly affected the female population (Gorina et al. 2005; Velez 2007). However, from 2003 onwards, the key mortality rates of both populations experienced a sharp decline. This erratic behaviour of the US elderly mortality rates over the in-sample period will have implications for the prediction of future mortality rates for the US male and female populations. Another issue of particular interest is that the erratic behaviour of the mortality of the elderly over the in-sample period will have implications for predicting future mortality rates in the United States.

To forecast future mortality rates, we consider (10). By rearranging the terms, we can obtain the following equation:

$$\begin{aligned} \text {log}\left( \hat{q}_{x,t}\right) = \text {log}\left( \hat{q}_{x,t-1}\right) + \hat{\alpha }\left( x\right) +\hat{b}\left( x\right) \cdot \left[ \text {log}\left( \hat{q}_{y^{*},t}\right) -\text {log}\left( \hat{q}_{y^{*},t-1}\right) \right] +\varepsilon _{x,t}, \end{aligned}$$

(16)

where $\varepsilon _{x,t}$ is an error term with zero mean. Now, following most of the literature about dynamic life tables (see Debón et al. (2008); Haberman and Renshaw (2011); Villegas et al. (2018)), to forecast future mortality rates, we assume that the logarithm of the key mortality rate follows an ARIMA process.

In this way, it is possible to obtain estimates of the expected future values of the key mortality rate and from Eq. (16), estimates of the expected future values of the remaining mortality rates.

The auto.arima and forecast functions of the “forecast” library (Hyndman and Khandakar 2008) are used to project future mortality rates. In particular, we apply the AIC¹⁸ to select a model from the ARIMA (p,d,q) family that best fits the time series of $\text {log}\left( \hat{q}_{y^{*},t}\right)$. The data from 1975 to 2006 were used to estimate the mortality model parameters ($a_1$, $a_2$, $a_3$, $\beta _1$, $\beta _2$ and $y^{*}$) and the ARIMA model parameters. Table 2 shows the ARIMA process selected for each key mortality rate.

Fig. 9

Forecast of the logarithms of the key age mortality rates $\text {log}\left( \hat{q}_{y^{*},t}\right)$

Table 2 ARIMA (p,d,q) process selected to model the key mortality rate according to the corrected AIC 1975–2006

Figure 9 shows the actual values of the key mortality rates from 1975 to 2018, along with expected values of future mortality rates (from 2007 onwards) according to the ARIMA process selected to model each key mortality rate. The real data are plotted with a black line, and the red line represents the mortality rate forecasts.

In contrast to France and Spain, the US mortality rates projected by the ARIMA models do not appear to be adequately. Indeed, the flat projections of the ARIMA model are clearly unsatisfactory when we see the path followed by US mortality rates after the end of the in-sample period 2006. This result is a consequence of the erratic behaviour of the mortality of the elderly US population described above. One possible way to address with this problem is to enlarge (backwards) the size of the in-sample period. We have kept it unchanged (1975–2006) to maintain consistency across the populations.

To forecast the remaining mortality rates, we apply (16) for the expected values of the mortality rates for 2007 to 2018, which are given by:

$$\begin{aligned} \begin{aligned} E_{t-1} \left[ \text {log}\left( q_{x,t+i}\right) \right] =& \,\, \text {log}\left( \hat{q}_{x,t-1}\right) + \left( i+1\right) \cdot \hat{\alpha }\left( x\right) \\&+\hat{b}\left( x\right) \cdot E_{t-1}\left[ \text {log}\left( \hat{q}_{x,t+i}\right) - \text {log}\left( \hat{q}_{x,t-1}\right) \right] ,\\ i=0,1,2, \ldots , 11&\qquad \text {and} \qquad t = 2007. \end{aligned} \end{aligned}$$

(17)

The forecasting errors for our factor model (FM) are calculated according to the following equations:

$$\begin{aligned} \varepsilon _{x,t+i}=\text {log}\left( \hat{q}_{x,t+i}\right) -E_{t-1}\left[ \text {log}\left( \hat{q}_{x,t+i}\right) \right] , \qquad i=0,1,\ldots ,11. \end{aligned}$$

(18)

The factor model forecasting errors are plotted in Fig. 10 for the “Spanish male population”.¹⁹

We present the forecasting error in two different ways. The left panel (a) shows twelve forecast errors corresponding to each of the out-of-sample years (from 2007 to 2018) for each age (from 0 to 99 years). The right panel (b) presents the forecasting errors of all ages from 0 to 99 years for each out-of-sample year (from 2007 to 2018) covered in this study.

A common feature of all populations is that the error terms are wider for young and very old populations. This is a result in the variability of mortality rates when the number of deaths is small (in the case of the youngest populations) or when the exposed to risk is also small (such in the case of the most advanced ages). In fact, this effect is much smaller for the US populations due to the larger size of its population.

Fig. 10

Forecasting errors in the male population of Spain. 2007–2018 a Errors for each age and b errors for each out-of-sample year

Comparison with other alternative dynamic mortality models

Benchmark models

In this section, we present the mortality models used as benchmarks and how to fit and forecast their age-specific mortality rates. These alternative models are the first version of Lee and Carter (1992) (LC) and the improved Lee–Carter (ILC) mortality model proposed by Mitchell et al. (2013). LC is one of the most employed mortality models due to the simplicity of its parameter estimation, the easy interpretation of its parameters, its parsimony and its forecasting accuracy (Booth et al. 2002; Haberman and Renshaw 2011; Atance et al. 2020b). ILC is included to present another model based on level improvements (in line with the factor model) and due to its predictive power (see Mitchell et al. (2013)). In Table 3, we indicate some of their main features.²⁰

Table 3 Summary of alternative dynamic mortality models used as benchmarks

To estimate model parameters, we apply the StMoMo library developed by Villegas et al. (2018), which is a package for fitting stochastic mortality models in Core (2021). The package also provides mortality rate forecasts according to different models. To calibrate ILC, an improved mortality model, we employ the R package IMoMo developed by Hunt and Villegas (2021), which is an extension of the StMoMo library (Villegas et al. 2018). Both the IMoMo and StMoMo packages employ a GLM to calibrate the models.²¹

Fitting accuracy of the model

To evaluate and compare the fitting quality of the models included in this study, we use different measures that are applied to the sample period, 1975–2006. First, we use nonpenalized measures, which do not take into account the number of parameters of the model. These measures are the Sum of Squared Errors (SSE); Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE), which are defined as follows:

$$\begin{aligned} \text {SSE}\,= & {}\, \sum _{x,t}\left( \text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) \right) ^{2}, \end{aligned}$$

(19)

$$\begin{aligned} \text {MAE}\,= & {} \,\frac{1}{N} \sum _{x,t}\left| \text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) \right| , \end{aligned}$$

(20)

$$\begin{aligned} \text {MAPE}\,= & {} \,\frac{1}{N} \sum _{x,t}\left| \frac{\text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) }{\text {log}\left( \hat{q}_{x,t}\right) } \right| ,\nonumber \\ x= & {} 0,1,2, \ldots , 99; \qquad t=1975, 1976, \ldots , 2006. \end{aligned}$$

(21)

where $q^{s}_{x,t}$ are the fitted values of mortality rates using model s and N is the number of observations (in this case $N = 100\cdot 31 = 3100$).

Second, we apply penalized measures to consider the risk of overparametrization. These measures not only consider the fitting errors but also the number of parameters of each model and provide a balance between the goodness of fit and parsimony. In this case, we apply two well-known criteria: AIC and BIC²² (Akaike 1974; Schwarz 1978);

$$\begin{aligned} \text {AIC}= & {} -2\cdot \text {log}\left( \hat{l}\right) + 2 \cdot n_p, \end{aligned}$$

(22)

$$\begin{aligned} \text {BIC}= & {} -n_{p}\cdot \text {log}\left( N\right) - 2 \cdot \text {log}\left( \hat{l}\right) , \end{aligned}$$

(23)

where $\hat{l}$ is the optimal value of the likelihood function and $n_p$ is the number of model parameters. To obtain the value of $\hat{l}$, we assume that the number of deaths follows a binomial distribution, as described in section “Model calibration”.

Table 4 summarizes the values of both penalized and nonpenalized measures using data from the period 1975–2006 for the three models distinguished by sex and country. The factor model only needs the estimation of six parameters (see Table 1), and the number of parameter estimates required by LC and ILC are shown in Table 3. According to the nonpenalized measures, the model with the best performance is ILC. The factor model is the second best with AIC and BIC values very close to those of ILC. When applying the penalized measures, the factor model is favoured due to its reduced number of parameters. In summary, the factor model provides fitting results that are in line with those of LC or ILC.

Table 4 Goodness of fit of alternative dynamic mortality models

Forecasting ability of the model

After analysing the goodness of fit, we proceed to evaluate the forecasting ability of the three models, including our approach. As before, we used different criteria to measure the results:

$$\begin{aligned} \text {SSE}\,= & {}\, \sum _{x,t}\left( \text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) \right) ^{2}, \end{aligned}$$

(24)

$$\begin{aligned} \text {MAE}\,= & {}\, \frac{1}{n} \sum _{x,t}\left| \text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) \right| , \end{aligned}$$

(25)

$$\begin{aligned} \text {MAPE}\,= & {} \,\frac{1}{n} \sum _{x,t}\left| \frac{\text {log}\left( \hat{q}_{x,t}\right) - \text {log}\left( q_{x,t}^{s}\right) }{\text {log}\left( \hat{q}_{x,t}\right) } \right| ,\nonumber \\ x= & {} 0,1,2, \ldots , 99; \qquad t=2007, 2008, \ldots , 2018. \end{aligned}$$

(26)

where $q^{s}_{x,t}$ denotes the mortality rate forecasts using model s and n is the number of observations; in this case, $n = 100\cdot 12 = 1200$.

Table 5 shows the results of the forecasting ability of the dynamic mortality models. The most remarkable outcome is that the factor model yields the lowest values of SSE, MAE and MAPE for all six populations (see Table 5). This outcome contrasts with the results obtained when comparing the in-sample fitting accuracy. These results provide evidence evidence for the good forecasting ability of the factor model despite its reduced number of parameters.

Table 5 Nonpenalized measures of the forecasting ability of dynamic mortality models using the out-sample period 2007–2018

Calculating the VaR for longevity risks

As mentioned in the introduction, the factor model is inspired by previous studies on the term structure of interest rates (Elton et al. 1990; Navarro and Nave 2001), and thus, some extensions of interest rate modelling can be easily applied to managing and measuring longevity risks. In this section, we provide a methodology to illustrate how to use the factor model for estimating the longevity VaR and CVaR.

As it is well known, VaR is a traditional measure to quantify the financial risk of an investment. The VaR is defined as the worst expected loss²³ over a given horizon under normal market conditions at a given level of confidence (Jorion 2001; Véhel 2018). It attempts to answer the question of which is the fall in the value of a financial asset or a portfolio of financial assets that can be exceeded with probability p during a given time horizon. In fact, the VaR indicates the most we can expect to lose under normal circumstances. Another measure is the Conditional Value at Risk (CVaR), which tries to quantify the tail risk of a portfolio of investments. It is equal to the average of some percentage of the worst-case loss scenarios (Rockafellar and Uryasev 2000; Sweeting et al. 2015). The main difference between the VaR and CVaR is that the latter takes into account the tail of the distribution, considers the diversification effect and provides less incentive than the VaR for risk concentration (see Yamai and Yoshiba (2002)).

In this section, we calculate the VaR and CVaR of a simple insurance product by applying the factor model using simulation techniques.

According to Eq. (16), there are two sources of uncertainty about the future behaviour of mortality rates. The first one comes from the ARIMA process assumed for the key rates, and the second one comes from the error term $\varepsilon _{x,t}$. The variance in this error term is assumed to depend on the difference between the key age $y^{*}$ and age x.

First, we simulate 1000 paths $\left( i = 1,2,\ldots , 1000\right)$ for the twelve future values of the key mortality rates $\left( q^{\left( i\right) }_{y^{*},2006+h}, h = 1, 2, \ldots , 12\right)$, taking into account that its behaviour can be modelled according to a given ARIMA process (see Table 2). For each of these 1000 paths, we simulate the corresponding 1000 paths for each of the other mortality rates according to the following equation:

$$\begin{aligned} \begin{aligned} \text {log}\left( q_{x,2006+h}^{\left( i\right) }\right)=&\,\,\text {log}\left( q_{x,2006}\right) \\&+ \sum _{k=1}^{h}\left[ \alpha \left( x\right) + b\left( x\right) \cdot \left[ \text {log}\left( q^{\left( i\right) }_{y^{*},2006+k}\right) -\text {log}\left( q^{\left( i\right) }_{y^{*},2006+k-1}\right) \right] +\varepsilon _{x,k}^{\left( i\right) }\right] ,\\&h=1,2,\ldots , 12; \qquad i=1,2, \ldots , 1000, \end{aligned} \end{aligned}$$

(27)

where $\alpha \left( x\right)$ and $b\left( x\right)$ are defined as in section “Functions α (x) and b (x)” and $\varepsilon _{x,k}^{\left( i\right) }$ are simulated values from the independent normal random variables with zero mean and standard error $\overline{\sigma }_{x}$. The values of $\overline{\sigma }_{x}$ are estimated by the standard deviation of a set of fitting errors and is defined as $\text {log}\left( \hat{q}_{x+j,t}\right) -\text {log}\left( q_{x+j,t}^{s}\right)$, where $q_{x+j,t}^{s}$ are the fitted values of the mortality rates according to the factor model and, $t=1975, 1976, \ldots , 2006$ and $j=-2,-1,0,1,2$. In this way, we have $5 \cdot 31$ fitting errors to estimate each $\overline{\sigma }_{x}$. We apply a five-age window for estimating $\overline{\sigma }_{x}$ to increase the sample size and to capture the dependence of the variance of $\varepsilon _{x,k}$ on the difference between the key age $y^{*}$ and age x.

Figure 11 shows the 97.5 and 99 percentiles of the 1000 simulations of $\text {log}\left( q^{\left( i\right) }_{x,2006+h}\right)$ for $h = 1, 2, \ldots , 12$ together with the actual values of $\text {log}\left( \hat{q}_{x,2006+h}\right)$ in the Spanish populations.²⁴ These percentiles of $\text {log}\left( q^{\left( i\right) }_{x,2006+h}\right)$ do not necessarily belong to the same simulation path; that is, the 99th percentile of $\text {log}\left( q_{x,2006+h}\right)$ for $h = 1$ does not need to be a part of the same path as the 99th percentile of $\text {log}\left( q_{x,2006+h}\right)$ for $h = 2$. Once these 1000 mortality rate paths have been simulated, it is not difficult to estimate the reserves that would be needed today to cover the contingencies of a given life insurance product if mortality had evolved according to each path. Based on these calculations, we can estimate the longevity VaR with a significance level $\alpha$ as the difference between the reserves calculated according to the life table and the reserves needed to cover the contingencies corresponding to the mortality rate path located at the $\alpha$ percentile less favourable paths of the 1000 simulated paths.

Similarly, the CVaR can be obtained to determine the average of the reserves necessary to cover the contingencies derived from those paths that are less favourable than the path corresponding to the VaR. The lines used for estimating the VaR-99% and CVaR-97.5% are, as expected, nearly overlapped, as seen in Fig. 11²⁵.

Fig. 11

Expected mortality rates, actual mortality rates, mortality rates corresponding to the 97.5 and 99 percentiles of 1000 simulated mortality paths, and averages of the most adverse 25 and 10 mortality paths for each out of sample period $\left( 2007, \ldots , 2018\right)$ for different ages $x = 65$ and 85). Spanish population

Finally, we illustrate the impact of longevity risk by calculating the longevity VaR and longevity CVaR of a very simple insurance product: a pure endowment. In this contract, we assume that an individual aged x will receive a lump sum of 1000 euros at the end of a specified period of time (n years) if he or she is still alive or zero otherwise in exchange for a premium.

For an individual with exact age x at the beginning of 2007, the pure premium, P, is given by:

$$\begin{aligned} P=v^{n}\cdot _{n}p_{x,2007}= v^{n}\cdot p_{x,2007} \cdot p_{x+1,2008} \cdot \ldots \cdot p_{x+n-1,2006+n-1}, \end{aligned}$$

(28)

where $v^n = \left( 1 + i\right) ^{-n}$ is the discount factor with i being the effective annual interest rate and $_{n}p_{x,2007}$ the probability that an individual at the exact age of x at January 1st, 2007 reaches age $x+n$.

For January 1st, 2007, we value two pure endowments that mature after 5 and 10 years for individuals at the exact ages of $x = 65, 75$ and 85. Assuming a fixed interest rate of 4% and a payout benefit of 1000 euros, we generate 1000 mortality simulation paths using Eq. (27) with the factor model presented in this paper. With this set of 1000 different mortality paths, we estimate the Actuarial Present Value (APV) for the pure premium that will be collected on January 1, 2007. The values of the pure premium of an endowment with maturity in 5 and 10 years can be found in Tables 6 and 7. Column (a) presents the APV with the projected mortality rates using the factor model. Column (b) shows the APV applying the actual mortality rates over the periods 2007-2011 and 2007-2016 for the 5 year and 10 year pure endowments, respectively. Columns (c) and (d) show the APVs calculated with the paths corresponding to the 97.5th and 99th percentiles of all simulated mortality trajectories. Finally, Columns (e) and (f) present the average of the APVs of the pure-endowments calculated using the simulations of the factor model that exceed the threshold of the 97.5th and 99th percentiles, respectively.

As expected and according to Column (a) of Tables 6 and 7, the values of the pure premium are smaller the older the individual is since the probability of death before the maturity of the endowment is higher. For females the value of the pure premium is higher due to their lower probabilities of death²⁶ and the differences for men increase with age. We can also observe differences across countries, capturing the differences in the mortality rates among Spain, France and the US. Columns (c), (d), (e), and (f) correspond to the current reserves that an insurance company would need to cover different scenarios. Columns (c) and (d) indicate the reserves required to meet the endowment benefit if the 976th and the 991th worst case mortality paths occur. Similarly, Columns (e) and (f) show the pure premium necessary to meet the endowment if the average of the 25 and 10 worst mortality paths occur.

Finally, Column (b) shows the reserves necessary to cover the endowment benefit at actual mortality rates from 2007 onwards. The values in Column (b) are always lower than those in Columns (c), (d), (e) and (f) with three exceptions. In the case of the 5 year endowment, the 65 years-old Spanish male population, (b) is larger than (c) but smaller than (d) (e) and (f). In the case of the 10 year endowment, for 65 and 75 years old Spanish male individuals, again, (b) larger than (c) but smaller than (d), (e), and (f). This is the result of a mortality improvement much greater than expected in the Spanish male population for individuals during years 2006–2010 for some of the ages involved in the calculations (65–69). Finally, for an 85 years old US male, (b) exceeds (c), (d), (e) and (f), which can be considered the only case where the risk estimates clearly fail probably due to the change in the key mortality rate trend that took place after the in-sample period. This result is in accordance with the unsatisfactory forecast of the ARIMA (0,1,0) model used to project mortality rates in the US population.

Tables 8 and 9 display the VaR and CVaR at 97.5% and 99% for the 5 year and 10 year pure endowments, respectively. These risk measurements (VaR and CVaR) are computed following the line of the literature of Tsai et al. (2010) and Richards (2021); that is, the losses that would be incurred if the pure premium charge are those of Column (a) of Tables 6 and 7, but mortality rates were those used to calculate columns (b) to (f) of Tables 6 and 7, respectively. The cases where the actual losses do not exceed the risk measures are mentioned in bold. These results are illustrated in Fig. 12, where we represent a histogram with the reserves necessary to cover the endowment benefits of the 1000 mortality rate simulated paths²⁷ of a 75 year old Spanish male individual.

Table 6 Actuarial present value of the benefits of a pure endowment with maturity in 5 years underwritten on January 1st 2007 for individuals aged 65, 75 and 85 ($i=4$%)

Table 7 Actuarial present value of the benefits of a pure endowment with maturity in 10 years underwritten on January 1st 2007 for individuals aged 65, 75 and 85 ($i=4$%)

Table 8 VaR and CVaR estimated using the factor model for a 5 year pure endowment

Table 9 VaR and CVaR estimated using the factor model for a 10 year pure endowment

Fig. 12

Histogram with the reserves needed to cover a 1000 euro endowment benefit for a 75 years old Spanish male individual according to the 1000 simulated mortality rate paths. a 5 year endowment and b 10 year endowment

Conclusion

In this paper, we develop a mortality model based on the idea that the dynamics of the mortality curve are governed by changes in a reduced number of factors that can be identified by mortality rates corresponding to some specific ages. This model is inspired by an earlier model for the term structure of interest rates (Elton et al. 1990), where it is assumed that changes in interest rates depend linearly on a small number of interest rates with a specific maturity. This model was already applied to describe the mortality curve dynamic in Atance et al. (2020a), where regression techniques were used to estimate model parameters by applying a methodology similar to that suggested in Elton et al. (1990).

In this paper, we adapt the model by simplifying it and reducing the number of model parameters to six. Instead of applying regression techniques, we propose the use of the maximum likelihood criterion to estimate model parameters, which is more in accordance with the actuarial literature and provides more robust results in the selection of the key mortality rate (which is always in the age range of 84 and 89 years).

Although using a single key mortality rate to model the behaviour of the entire mortality curve can be considered somewhat limited, it provides some important advantages. First, using a single key rate extraordinarily simplifies model calibration. Second, the fact that the key rate is located at the right end of the mortality curve makes the model focus on the behaviour of the population of particular interest to the life insurance industry, making the model of special interest for measuring longevity risks. Third, it subdivides the mortality curve into different sections. The first one is (0–60), whose dynamics are assumed to consist of a constant change in mortality rates. It should be noted that this constant change is different for each mortality rate. The second one is (71–99) and is the section of the mortality curve governed by the key rate. In addition, the third part (61–70), which can be considered a mixture or combination of a constant mortality change and the influence of the changes in the key mortality rate²⁸. These outcomes are consistent with the literature about the ageing process (see Lehallier et al. (2019)). Moreover, the section of the mortality curve under the influence of the key mortality rate is especially sensitive to sudden changes in mortality, such as those caused by COVID-19, cold and heat waves, or seasonal diseases such as influenza (Kalkstein and Davis 1989; Díaz et al. 2002; Stafoggia et al. 2006; Anderson and Bell 2009), although this issue requires further research.

When the model is compared with other alternative dynamic mortality models, the results, despite the model’s simplicity, are at least similar in terms of forecasting power. This result may be a consequence of the model’s ability to adequately capture the correlation structure among changes in mortality rates, and this result demonstrates that the model can be used for longevity risk measurement.

However, one of the weaknesses of the model is the dependence of its forecasting power on the amplitude of the sample period, as seen when analysing the US populations, where there were abrupt changes in mortality trends at the end of the in-sample period.

Finally, we develop a methodology to measure longevity risk using simulation techniques. This methodology is illustrated and tested through an example where longevity risk is measured by calculating the longevity VaR and longevity CVaR of a very simple insurance product, although it could easily be applied to more complex products.