Background

The study of hydrodynamic flow and heat transfer over a stretching cylinder has gained considerable attention due to its applications in industries and important bearings on several technological processes like thermal design of buildings, electronic cooling, solar collectors, drilling operations, commercial refrigeration, geothermal power generation, float glass production, heat-treated materials traveling between a feed roll and a wind-up roll, aerodynamic extrusion of plastic sheets, glass fiber and paper production, cooling of an infinite metallic plate in a cooling bath, manufacturing of polymeric sheets, etc. Due to these practical and industrial applications, the problem of boundary layer analysis over a stretching solid surfaces has become an area of attention for scientists, engineers, and mathematicians as well. Flow over a cylinder is generally considered as two dimensional, when radius of the cylinder is large enough compared to the boundary layer thickness. To study the viscous fluid flow and heat transfer outside a hollow stretching cylinder has importance in extrusion processes. Using local non-similarity transformations, Chen and Mucoglu (1975) investigated the effects of mixed convection flow over a vertical slender cylinder due to thermal diffusion with prescribed wall temperature. Wang (1988) obtained the exact solution of viscous flow and heat transfer due to uniformly stretching cylinder. Kumari and Nath (2004) analyzed the effects of localized cooling/heating and injection/suction on the mixed convection flow on a thin vertical cylinder. Chang (2008) numerically investigated the flow and heat transfer characteristics of natural convection in a micropolar fluid flow along a vertical slender hollow circular cylinder with conduction effects.

The hydrodynamic flow and heat transfer in porous medium have become hot topics of research for quite a long time, which is reflected in number of articles being published. Aydin and Kaya (2013) studied MHD mixed convection of a viscous dissipating fluid about a vertical slender cylinder. Mukhopadhyay and Ishak (2012) presented a result on the distribution of a solute undergoing a first-order chemical reaction in an axisymmetric laminar boundary layer flow along a stretching cylinder with velocity slip condition at the boundary instead of no-slip condition. A steady laminar flow caused by a stretching cylinder immersed in an incompressible viscous fluid with prescribed surface heat flux was investigated by Bachok and Ishak (2010). Mukhopadhyay and Ishak (2012) studied an axisymmetric laminar boundary layer flow and mixed convection of a viscous incompressible fluid and heat transfer over a stretching cylinder embedded in a porous medium. Chauhan et al. (1961) have investigated magnetohydrodynamic slip flow and heat transfer in a porous medium over a stretching cylinder by homotophy analysis method. Further, various aspects of heat transfer over a stretching cylinder in different geometrical models have been studied widely by many researchers (Ashorynejad et al. 2013; Gorla et al. 2012; Khalili et al. 2010; Mohammadiun et al. 2013; Mukhopadhyay 2011; Munawar et al. 2012; Rashad et al. 2013; Shateyi and Marewo 2013; Wang 2011; Weidman and Weidman 2010).

The analysis of two-phase flows in which solid spherical particles are distributed in a fluid is important in areas like environmental pollution, smoke emission from vehicles, emission of effluents from industries, cooling effects of air conditioners, flying ash produced from thermal reactors and formation of raindrops, etc. On the basis of these applications, Saffman (1962) has formulated the basic equations of motion for fluid carrying small dust particles in which dust particles are uniformly distributed. Using the Saffman (1962) model, Soundalgekar and Gokhale (1984) studied the flow of a dusty gas past an impulsively started infinite vertical plate by employing an implicit finite difference technique. Datta and Mishra (1982) have analyzed the boundary layer flow of a dusty fluid over a semi-infinite flat plate. Later, Das et al. (1992) studied the flow of a dusty gas past a uniformly accelerated horizontal plate. Ganesan and Palani (2004) have obtained the numerical solution for an unsteady free convection flow of a dusty gas past a semi-infinite inclined plate with constant heat flux using an implicit finite difference method. Flow of a dusty gas past an impulsively started semi-infinite vertical plate was studied by Kulandaivel (2010). Vajravelu and Nayfeh (1992) examined hydromagnetic flow of a dusty fluid over a stretching sheet. Recently, Gireesha et al. (2011, 2012, 2013) have obtained the results for heat transfer analysis on dusty fluid flow due to linear stretching with various effects like nonuniform heat source or sink, radiation and viscous dissipation, etc. In this studies, they were analyzed by two types of heating processes namely, surface temperature and heat flux.

Different from our previous investigations, we extended the work to stretching cylinder. In the present paper, we try to investigate the flow and heat transfer of an electrically conducting dusty fluid over a stretching cylinder in porous media. The resulting nonlinear momentum and energy equations are simplified using similarity transformations. Numerical solutions have been developed for the velocity and temperature (PST and PHF). Graphical results for various values of the flow parameters are presented to gain thorough insight towards the physics of the problem. The results have possible technological applications in liquid-based systems involving stretchable materials.

Method

Flow analysis of the problem

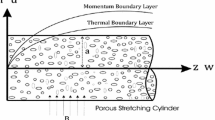
Consider a steady two-dimensional laminar boundary layer flow of an incompressible viscous dusty fluid over a stretching cylinder of radius a in the axial direction. The z-axis is measured along the axis of the cylinder and the r-axis is measured in the radial direction as shown in Figure 1. Two phases to be considered here are a continuous fluid phase interspersed with a discrete solid particulate phase. The dust particles are taken to be small enough and of sufficient number to be treated as a continuum and allow concepts such as density and velocity to have physical meaning. And also, they are assumed to be spherical in shape, all having same radius and mass, and are undeformable. A uniform magnetic field of strength B0 is applied in the radial direction. The magnetic Reynolds number is assumed to be small so that the induced magnetic field is neglected in comparison with the applied magnetic field.

Figure 1
figure 1

Schematic representation of boundary layer flow.

Full size image

Under these assumptions, along with the usual boundary layer approximation, the governing equations for the flow in cylindrical coordinates are as follows (Mukhopadhyay and Ishak 2012) and (Saffman 1962):

$${\kern15pt} {\fontsize{8.5}{10}{\begin{aligned} {\frac{\partial w}{\partial z}}+{\frac{1}{r}}{\frac{\partial (ru)}{\partial r}}=0, \end{aligned}}} $$
((1))
$${\kern20pt} {\fontsize{8.5}{10}{\begin{aligned} w{\frac{\partial w}{\partial z}}+u{\frac{\partial w}{\partial r}}&=\nu\left({\frac{\partial^{2} w}{\partial r^{2}}}+{\frac{1}{r}}{\frac{\partial w}{\partial r}}\right)\\ &\quad+\frac{KN}{\rho}(w_p-w)-\frac{\sigma {B_{0}}^{2}}{\rho}w-\frac{\nu}{k_{p}}w, \end{aligned}}} $$
((2))
$${\kern3.2pt} {\fontsize{8.5}{10}{\begin{aligned} w_{p}\frac{\partial w_{p}}{\partial z}+u_{p}\frac{\partial w_{p}}{\partial r}=\frac{K}{m}(w-w_p), \end{aligned}}} $$
((3))
$${\kern5.5pt} {\fontsize{8.5}{10}{\begin{aligned} w_{p}\frac{\partial u_{p}}{\partial z}+u_{p}\frac{\partial u_{p}}{\partial r}=\frac{K}{m}(u-u_p), \end{aligned}}} $$
((4))
$${} {\fontsize{8.5}{10}{\begin{aligned} \frac{\partial(\rho_{p} w_p)}{\partial z}+\frac{1}{r}\frac{\partial (r\rho_{p} u_p)}{\partial r}=0, \end{aligned}}} $$
((5))

In deriving these equations, the drag force is considered for the iteration between the fluid and particle phases. The physical boundary conditions for the flow problem are given by;

$$\begin{array}{@{}rcl@{}} w=U_{w}(z),\,\,\,\,\,u=0,\,\,\,\,\, as,\,\,\,r=a,\\ w\rightarrow 0,\,\,\,w_{p}\rightarrow 0,\,\,\,\,u_{p}\rightarrow u,\,\,\,\,\,\rho_{p}\rightarrow \omega_{p} \,\,\, as\,\,\, r \rightarrow \infty \end{array} $$
((6))

It is convenient to employ the following similarity transformations in order to transform the governing equations into the corresponding ordinary differential equations:

$${} {\fontsize{8.8}{10}{\begin{aligned} u=-\frac{a}{r}\sqrt{\frac{\nu b}{l}}f(\eta) \,\,\,\,\ w=U_{w}(z)f'(\eta), \,\,\,\,\ \eta=\frac{r^2-a^{2}}{2a}\sqrt{\frac{U_{w}}{\nu_{z}}}, \\ u_p=\frac{a}{r}\sqrt{\frac{\nu b}{l}}F(\eta),\,\,\,\,\ w_p=U_{w}(z)g(\eta),\,\,\,\,\ \rho_r=H(\eta). \end{aligned}}} $$
((7))

It can be verified that, the above defined similarity transformations are identically satisfied by the Equation (1). Substituting (7) in to (2)-(5), we obtain the following non-linear ordinary differential equations:

$${} {\fontsize{8}{5}{\begin{aligned} (1+2 \eta \gamma)f^{\prime\prime\prime}(\eta)\,+\,2 \gamma f^{\prime\prime}(\eta)\,-\,(f'(\eta))^{2}\,+\,f(\eta)f^{\prime\prime}(\eta)\,+\,l^{*} \beta H(\eta)(g(\eta)\\ -f'(\eta))(Q+S)f'(\eta)=0 \end{aligned}}} $$
((8))
$${\kern5pc} {\fontsize{8}{5}{\begin{aligned} F(\eta)g'(\eta)-g^{2}(\eta)-\beta(f'(\eta)-g(\eta))=0 \end{aligned}}} $$
((9))
$${\kern8.8pt} {\fontsize{8}{5}{\begin{aligned} F(\eta)F^{\prime\prime}(\eta)-\left(1+\frac{\gamma}{2 \eta \gamma}\right)[F(\eta)]^2+\beta [f'(\eta)+F(\eta)]=0 \end{aligned}}} $$
((10))
$${} {\fontsize{8}{5}{\begin{aligned} H(\eta)g(\eta)\,+\,F(\eta)H'(\eta)\,+\,H(\eta)F'(\eta)\,-\,\left(\!1\,+\,\frac{\gamma}{2 \eta \gamma}\!\right)H(\eta)F(\eta)=0 \end{aligned}}} $$
((11))

where a prime denotes differentiation with respect to η.

The transformed dimensionless boundary conditions become

$${} {\fontsize{8}{10}{\begin{aligned} f(\eta)=0 \,\,\,\, f'(\eta)=1,\,\,\,\,at,\,\,\,\,\ \eta=0,\\ f'(\eta)=0,\,\,\,\ g(\eta)=0,\,\,\, F(\eta)=-f(\eta)\,\,\,\,\,\ H(\eta)=\omega \,\,\ as\,\, \eta \longrightarrow \infty. \end{aligned}}} $$
((12))

Heat transfer analysis

The governing boundary layer energy equation for the two-dimensional dusty fluid flow in the presence of internal heat generation/absorption for axisymmetric flow is given by:

$$ {\fontsize{8.7}{10}{\begin{aligned} \rho c_{p}\left[w \frac{\partial T}{\partial z}+ u \frac{\partial T}{\partial r}\right]&=\frac{k*}{r}\frac{\partial}{\partial r}\left[r\frac{\partial T}{\partial r}\right]+\frac{{Nc}_{p}}{\tau_{T}}\left(T_p-T\right)\\ &\quad+\frac{N}{\tau_{v}}\left(w_p-w\right)^2-q^{\prime\prime\prime}, \end{aligned}}} $$
((13))
$${\kern-17.5pt} {\fontsize{8.7}{10}{\begin{aligned} {Nc}_{m}\left[w_{p}\frac{\partial T_{p}}{\partial z}+ u_{p}\frac{\partial T_{p}}{\partial r}\right]&=-\frac{{Nc}_{p}}{\tau_{T}}\left(T_p-T\right), \end{aligned}}} $$
((14))

where q′′′ is the space- and temperature-dependent internal heat generation/absorption (non-uniform heat source/sink) which can be expressed as

$${} {\fontsize{8.7}{10}{\begin{aligned} q^{\prime\prime\prime}=\left(\frac{k U_{w} (z)}{z \nu} \right)\left[A*(T_{w} - T_{\infty})f'(\eta)+B^{*}\left(T-T_{\infty} \right)\right] \end{aligned}}} $$
((15))

where A∗ and B∗ are the coefficients of the space- and temperature-dependent internal heat generation/absorption. Here, we make a note that A∗>0 and B∗>0 corresponds to internal heat generation and that A∗<0 and B∗<0 corresponds to internal heat absorption. In this paper, we discussed two types of heating process namely prescribed surface temperature (PST) and prescribed heat flux (PHF case). Here, the prescribed surface temperature is defined as a quadratic function of z, while in the case of PHF, it is a the power law heat flux.

We have adopted the following boundary conditions for solving Equations (13) and (14) in both cases.

$$\begin{array}{@{}rcl@{}} T=T_w=T_{\infty}+A\left(\frac{z}{l}\right)^{2} \,\,\,\,\,\ at \,\,\,\,\ r=0,(PST) \\ -\,k^{*}\frac{\partial T}{\partial r}=q_w=D\left(\frac{z}{l}\right)^{2} \,\,\,\,\ at\,\,\,\,\ r=0. (PHF) \\ T\rightarrow T_{\infty}, \,\,\,\,\ T_{p}\rightarrow T_{\infty} \,\,\,\,\ as \,\,\,\,\ y\rightarrow\infty. \end{array} $$
((16))

where T w and T ∞ denote the temperature at the wall and at large distance from the wall, respectively. A and D are positive constants.

We now introduce the following dimensionless fluid phase temperature θ(η) and dust phase temperature θ p (η) as

$$\begin{array}{@{}rcl@{}} \theta(\eta)=\frac{T-T_{\infty}}{T_w-T_{\infty}}, \,\,\,\,\,\ \theta_{p}(\eta)=\frac{T_p-T_{\infty}}{T_w-T_{\infty}} \\ \end{array} $$
((17))

where \(T-T_{\infty }=A\left (\frac {z}{l}\right)^{2}\theta (\eta)\) (PST case) and \(T_w-T_{\infty }=\frac {D}{k^{*}}\left (\frac {z}{l}\right)^{2}\sqrt {\frac {\nu }{c}}\) (PHF case).

The boundary layer Equations (13) and (14) on using (15)-(17), take the following form,

$$\begin{array}{*{20}l} (1+2 \eta \gamma)\theta^{\prime\prime}(\eta)+Pr\left[\,f(\eta)\theta(\eta)-2f'(\eta)\theta(\eta)\right]&\\ +2 \gamma \theta'(\eta)+\frac{N Pr}{\rho \tau_{T} b}(\theta_p-\theta)+&\\ \frac{N Pr Ec}{\rho \tau_{v} }[g(\eta)-f'(\eta)]^2+A^{*}f'(\eta)+B^{*} \theta(\eta)=0& \end{array} $$
((18))
$$\begin{array}{*{20}l} 2g(\eta)\theta_{p}(\eta)+\theta_{p}(\eta)+\frac{C_{p} l}{\tau_{T} C_{m} b}(\theta_{p} -\theta)=0& \end{array} $$
((19))

Now, the boundary conditions for θ(η) and θ p (η) follows from (16) and (17) as

$$\begin{array}{@{}rcl@{}} \theta(\eta)=1 \,\,\,\,\,\ at \,\,\,\,\,\ \eta=0 (\mathrm{PST case}) \\ \theta'(\eta)=-1 \,\,\,\,\,\ at \,\,\,\,\,\ \eta=0 (\mathrm{PHF case}) \\ \theta(\eta)\rightarrow 0, \,\,\,\,\,\ \theta_{p}(\eta)\rightarrow 0, \,\,\,\,\, as \,\,\,\,\eta\rightarrow \infty. \end{array} $$
((20))

The quantities of main interest in such nonlinear problem, which are important from the engineering point of view are the skin friction coefficient and the Nusselt number, which are defined as

$$\begin{array}{@{}rcl@{}} C_f=\frac{\mu \left(\frac{\partial \mu}{\partial r}\right)_{r=a}}{\rho U_{w}^{2}},\;{Nu}_x=\frac{\mu\left(\frac{\partial T}{\partial r}\right)_{r=a}}{k\left(T_{w} - T_{\infty}\right)} \end{array} $$
((21))

Using the non-dimensional variables, we obtain

$${\kern11.3pc} {\fontsize{8.7}{10}{\begin{aligned} C_{f} {{Re}_{x}}^{\frac{1}{2}}_x=f^{\prime\prime}(0) \end{aligned}}} $$
((22))
$${} {\fontsize{8.7}{10}{\begin{aligned} \frac{N u_{x}}{\sqrt{{Re}_{x}}}=-\theta'(0)(\mathrm{PST~case}) \,\,{\text{and}}\,\,\frac{N u_{x}}{\sqrt{{Re}_{x}}}=\frac{1}{\theta(0)}(\mathrm{PHF~case}) \end{aligned}}} $$
((23))

One can observe that, if γ=0(a⇒∞), then, the present problem under consideration (S=0 and Q−0) reduces to boundary layer flow along a stretching flat plate considered by Gireesha et al. (2011) and if γ=0 and S=0, then, it reduces to the problem of Gireesha et al. (2012) with λ=0, i.e., in the absence of the ratio of free stream velocity parameter to stretching sheet parameter and that of Gireesha et al. (2013) with \(a=\frac {\pi }{2}\) (horizontal stretching sheet) in that paper.

Method of solution

The system of coupled highly non-linear ordinary differential Equations (8)-(11) and (18)-(19) subject to the boundary conditions (12) and (20) have been solved numerically using Runge-Kutta-Fehlberg 45 method. This method has been successfully used by the present authors to solve various problems related to boundary layer flow and heat transfer. For the validation of the numerical results obtained in this study, the case when the curvature parameter is absent (γ=0,flat plate) has also been considered and compared with previously published results available in the literature. Table 1 presents a comparison of −θ′(0) for flat plate reported by Grubka and Bobba (1985), Abel et al. (2008), Ali (1994), Ishak and Nazar (2008) and the present numerical results. It is clear from the table that the present numerical results are found to be in a very good agreement.

Table 1 Comparison of the results for the dimensionless temperature gradient θ ′ (0) for various values of Pr in the case of β = 0, E c = 0
Full size table

In this method, the edge of the boundary layer η ∞ has been chosen as η=5, which is sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters considered. A comprehensive numerical parametric computations have been carried out for various values of Curvature parameter, fluid particle interaction parameter, Prandtl number, heat source/sink parameter, fluid-particle interaction parameter on velocity, and temperature in both PST and PHF cases, and then, the results are reported in terms of graphs.

Results and discussion

The numerical solutions are presented through graphs for physical interpretation of the proposed study. For the validation of numerical results, we compared our results with previously published works with the absence of the curvature parameter and dust particles.

Figure 2 illustrates the effect of curvature parameter (γ) on both fluid and dust phase velocity profiles. It is quite evident from Figure 2 that the velocity of the fluid as well as dust phase corresponding to (γ=0) is minimum and the increase of (γ) is to increase the velocity within the boundary layer. Moreover (γ=0), the problem reduces to flat surface, and hence, the velocity within the boundary layer in the case of cylinder is larger than the flat surface. It means that the increasing in the cylinder diameter leads to the decrease in the velocity within the boundary layer. The effect of magnetic parameter Q on velocity distributions are depicted as in Figure 3. It reveals that the increasing values of Q results in the decrease of fluid and dust phase velocity. This is because application of a transverse magnetic field normal to the flow direction gives rise to a resistive drag-like force known as Lorentz force acting in a direction opposite to that of the flow. This has a tendency to reduce fluid transport phenomena. Therefore, the momentum boundary layer thickness decreases with increase in Q, and hence, it leads to increase in velocity gradient.

Figure 2
figure 2

Effect of curvature parameter (γ) on f ′ (η) .

Full size image
Figure 3
figure 3

Effect of Magnetic parameter ( Q ) on f ′ (η) .

Full size image

Figures 4 and 5 illustrates the effect of curvature parameter (γ) on the temperature profiles. It is observed from the plots that increases of values enhance the temperature of the fluid as well as dust phase. It is also observed from Figure 5 that the effect of curvature parameter on velocity field is almost nil within the dynamic region [ 0,0.5]. A crossover is found in Figure 5, for varying the curvature parameter. The velocity and temperature near the stretching surface decrease with increasing curvature parameter, while those far from the stretching surface show the reverse effect. Figure 6 demonstrates the effects of permeability parameter on velocity profiles for both fluid and dust phase. It is obvious that the presence of porous medium causes higher restriction to the fluid flow which, in turn, slows its motion. Therefore, with increasing permeability parameter, the resistance to the fluid motion also increases. To explain the effect of fluid particle interaction parameter (β) on velocity profile, the plot is shown in Figure 7. It is interesting to note that, as (β) increases, the fluid phase velocity decreases, and in contrast, dust phase velocity increases; whereas in temperature distribution in both PST and PHF cases, these decreases and are shown in Figures 8 and 9.

Figure 4
figure 4

Effect of curvature parameter ( γ ) on θ ( η ) in PST case.

Full size image
Figure 5
figure 5

Effect of curvature parameter ( γ ) on θ ( η ) in PHF case.

Full size image
Figure 6
figure 6

Effect of Permeable parameter (s) on f ′ ( η ).

Full size image
Figure 7
figure 7

Effect of relaxation parameter ( β ) on f ′ ( η ).

Full size image
Figure 8
figure 8

Effect of relaxation parameter ( β ) on θ ( η ) in PST case.

Full size image
Figure 9
figure 9

Effect of relaxation parameter ( β ) on θ ( η ) in PHF case.

Full size image

The effect of Prandtl number on temperature of both fluid and dust phase is displayed in Figures 10 and 11. In both PST and PHF cases, one can observe that the temperature decreases with increase in Pr. The physical reason is that the lower values of Pr mean have lower viscosity of the fluid, which increases the local velocity everywhere within the boundary layer. Thus, the higher Prandtl number fluid has a relatively low thermal conductivity which reduces the conduction. The variation of temperature distributions in both PST and PHF cases for various values of space-dependent heat source/sink parameter A∗ are plotted in Figures 12 and 13. From these plots, it is evident that increasing in A∗ results in the enhancement of both fluid and dust phase temperature. It is due to the fact that A∗>0, the thermal boundary layer generates the energy and obviously energy is absorbed for decreasing values of A∗ resulting in temperature dropping significantly near the boundary layer. Similar effect is observed form the Figures 14 and 15 for the effect of temperature-dependent heat source/sink parameter B∗.

Figure 10
figure 10

Effect of Prandtl parameter ( Pr ) on θ ( η ) in PST case.

Full size image
Figure 11
figure 11

Effect of Prandtl parameter ( Pr ) on θ ( η ) in PHF case.

Full size image
Figure 12
figure 12

Effect of Space dependent source/sink parameter ( A *) on θ ( η ) in PST case.

Full size image
Figure 13
figure 13

Effect of Space dependent source/sink parameter ( A *) on θ ( η ) in PHF case.

Full size image
Figure 14
figure 14

Effect of Temperature dependent source/sink parameter ( A *) on θ ( η ) in PST case.

Full size image
Figure 15
figure 15

Effect of Temperature dependent source/sink parameter ( A *) on θ ( η ) in PHF case.

Full size image

Figures 16 and 17 depict the both fluid and dust phase temperature profiles in PST and PHF cases, respectively, for different values of magnetic parameter. From these plots, it is observed that for increasing values of magnetic parameter, the temperature profiles increases. This is due to fact that the applied magnetic field opposes the fluid motion; this is responsible for enhancing the temperature profiles. Figures 18 and 19 show the effect of permeable parameter on temperature distributions for both fluid and dust phase, in PST and PHF cases, respectively. From these plots, it is observed that the effect of increasing values of permeable parameter contributes to the thickening of thermal boundary layer.

Figure 16
figure 16

Effect of Magnetic parameter ( Q ) on θ ( η ) in PST case.

Full size image
Figure 17
figure 17

Effect of Magnetic parameter ( Q ) on θ ( η ) in PHF case.

Full size image
Figure 18
figure 18

Effect of Permeable parameter ( S ) on θ ( η ) in PST case.

Full size image
Figure 19
figure 19

Effect of Permeable parameter ( S ) on θ ( η ) in PHF case.

Full size image

For practical purpose, the skin-friction coefficient and the heat transfer coefficient are determined for different values of the curvature parameter (γ), fluid particle interaction parameter (β), Prandtl number (Pr), flow-dependent A∗ and temperature-dependent B∗ heat source/sink parameter, porous parameter (S), and magnetic parameter (Q). From Equation 22, we can see that the magnitude of the skin friction coefficient C f is directly related to the dimensionless surface velocity gradient f′′(0). It is pointed out from Table 2 that the magnitude of the skin friction coefficient increases with magnetic parameter, permeability parameter, and curvature parameter while it is constant with Prandtl number and flow-dependent and temperature-dependent heat source/sink parameter. Increasing the values of space-dependent heat source/sink parameter A∗ and temperature-dependent heat source/sink parameter B∗ leads to fall in the value of local Nusselt number where as skin friction coefficient remains unchanged. It is observed that the skin friction coefficient is higher for a cylinder, when compared to a flat plate.

Table 2 The values of f ′′ (0), − θ ′ (0), and θ (0) for various values A ∗ , B ∗ , S , N , γ , E c , and β
Full size table

Conclusions

In this study, a two-dimensional MHD flow and heat transfer of dusty fluid generated by stretching cylinder immersed in a porous medium is investigated. The governing equations are reduced to a set of non-linear ordinary differential equations by means of similarity transformations. Due to non-linearity, a numerical approach called Runge-Kutta-Felhberg 45 technique has been used to compute the values of velocity function and temperature field at different points of dynamic region. Comparison of obtained numerical results is made with previously published results for some special cases and found to be in a good agreement. The study is mainly focused on the effect of curvature of stretching cylinder, which is a very vital parameter affecting both flow and temperature fields. The effects of applied magnetic field, flow-dependent heat source/sink parameter, temperature-dependent heat source/sink parameter, Prandtl number, and fluid-particle interaction parameter are also taken into account. As expected, an increase of the curvature parameter leads to the increase in the velocity and temperature profiles. Also, an increase in the value of magnetic parameter leads to the decrease in the velocity boundary layer thickness. However, quite the opposite is true with the thermal boundary layer thickness in both PST and PHF cases. Comparing the results in Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17, we see that the temperature of fluid phase is parallel to that of dust phase and also, the temperature of the fluid is always more than that of the dust phase. It is worth to mention that PHF boundary conditions are best suitable for cooling and PST for heating of the stretching cylinder. Finally, we conclude that both the magnitude of the skin friction coefficient and heat transfer rate at the surface are higher for cylinder when compared to that of flat plate.

Notation

(w,u) and (w p ,u p ) are the velocity components of the fluid and dust particle phase. ν is the kinematic viscosity of fluid, ρ is the density of the fluid, N is the number density of the dust particles, K=6πμd is the Stoke’s constant, μ is the dynamic viscosity of the fluid, d is the radius of dust particles, B0 is the magnetic field, kp is the permeability of the porous medium, ρ p is is the density of dust phase, m is the mass of the dust particle, σ is the electric conductivity of the fluid, a is the radius of the cylinder, \(U_{w}(z) = b \frac {z}{l}\) is the stretching velocity, b>0 is the stretching rate, l is the reference length, ω is the density ratio, \(\gamma =\sqrt {\frac {l \nu }{a^{2}}}\) is the curvature parameter, \(A=\frac {\sigma B_{0}^{2} l}{\rho b}\) is the magnetic parameter, \(S=\frac {\nu l}{b k p}\) is the porous parameter, \(\tau =\frac {m}{K}\) is the relaxation time of the particle phase, \(\beta =\frac {l}{\tau b}\) is the fluid-particle interaction parameter, \(Pr=\frac {N}{\rho }\) is the relative density and \(l^{*}=\frac {mN}{\rho }\) is the mass concentration of dust particles, T and T p are the temperatures of fluid and dust particles, respectively, c p and c m are respectively specific heat of fluid and dust particles, τ T is the thermal equilibrium time i.e., the time required by a dust cloud to adjust its temperature to the fluid, τ v is the relaxation time of the dust particle, k∗ is the thermal conductivity, q′′′ is the space- and temperature-dependent internal heat generation/absorption, A∗ and B∗ are the coefficients of the space- and temperature-dependent internal heat generation/absorption, T w and T ∞ are the temperature at the wall and at large distance from the wall, respectively, A and D are positive constants, \(Pr=\frac {\mu c_{p}}{k^{*}}\) is the Prandtl number, \({Re}_x=\frac {U_{w} x}{\nu }\) is the local Reynold’s number, and \(Ec=\frac {bl^{2}}{A c_{p}}\) (PST case) and \(Ec=\frac {k^{*} l^{2} b^{\frac {3}{2}} }{A c_{p}}\) (PHF case) is the Eckert number.