Introduction

The uniaxial compressive strength (UCS) is the critical property of rock strength to be tested frequently during many mining and civil engineering projects. The removal of core samples needed for laboratory testing is costly and often difficult to remove from the weathered and soft rocks. Besides, converting the samples into the laboratory test specimen is laborious and expensive. Therefore, the rock strength may not precisely be measured with the available inadequate number of rock samples, and the total rock-mass strength could be decided upon by the outcome obtaining from the same. This evaluation method may not yield proper results. To avoid that kind of problem, many empirical models have continually developed for the estimation of rock strength. In several rock engineering projects associated with the mining environment, drilling is the fundamental operation to be included. Recently many researchers are using the drilling technique as a tool to determine the uniaxial compressive strength (UCS) of rocks. The different drill operating variables gathered during the rock drilling process are utilized in many investigations to evaluate the UCS. In the view of many rock engineering projects, an extended investigation is requiring to ensure the validity and correlation between drilling variables and the uniaxial compressive strength of rocks. The characterization of the rocks using drill operating parameters may also be helpful for mining engineering such as excavation, tunnel boring, blast hole design, quarrying, etc.

Literature review

In this section, the discussion on variations of different drill operating parameters during the drilling of rocks as well as other materials is made. In addition, the different drilling variables used for the estimation of rock properties are also discussed. During the rock drilling, Basarir and Karpuz [6] estimated the UCS of rocks using the drill machine operating parameters such as bit thrust and penetration rate (PR). From the data analysis, it could observe that the corresponding PR for the applied thrust was most impacting the UCS, followed by thrust. The prediction of rock strength and geological conditions around and in the blasting area could be possible using measurement while drilling (MWD) data [5, 15, 21]. Using the various bits at a different angle of attack, an attempt was made to determine the cuttability of rocks [22]. The experimental results revealed that the cutting thrust increases as the UCS of rock increases. During the rock cutting operation, Roxborough [24] found the linear relationship between the rock strength and cutting force. Erosy and Waller [13] studied the drillability of polycrystalline diamond compact (PDC) and diamond-impregnated drill bits. The experiment would carry out using the different bit speed and bit-thrust. Using the drilling data, it could develop a prediction model for drillability with the help of the regression method. From the analysis of variance (ANOVA), it is seen that bit-thrust and bit speed are substantially influencing the drillability respectively. The drillability of rocks relies on bit-thrust, bit speed, and rock properties [2]. A mathematical model was built to calculate the rock strength (UCS) using the rock's internal friction angle and cohesion parameters [17]. As a part of determining these parameters, drilling parameters such as the PR, thrust, and torque collected during drilling. While collecting these data, it was recorded that both thrust and torque would change substantially for different combinations of PR and bit speed. Besides, the model generated employing these data was well correlated with UCS. Finfinger et al [14] assessed the overlaying rock bed characteristics during the rock bolting process. An in-built monitoring system of a rock bolting machine could determine the thrust and torque during the same operation. It was reported that there was a substantial change of both parameters while the bit was progressing through the various layers of rocks that have different rock strength. During the drilling of marble, Bhatnagar et al [8] examined the effect of frequency of bit rotation on thrust and torque. From the test data, it was noticed that both thrust and torque would vary almost in the same way at different bit speed. In a rock drilling, the torque and penetration rate of the drill bit could largely influence by operating thrust and speed [23]. Sreenivasulu and Rao [26] studied the significant effect of drill bit diameter, penetration rate, and spindle speed on the bit force and torque while the aluminum alloy is drilling. Analysis of data revealed that bit speed and its diameter impacted both bit force and torque significantly. Lakshminarayana et al [20] used measurement while drilling technique to estimate the UCS. From the results, it was reported that thrust would vary linearly as the UCS of rocks increases. During the rotary drilling, Shankar et al [25] attempted to investigate the wear rate of the tungsten carbide drill bit. From the collected data, it could see that the thrust would significantly increase with an increase of UCS of drilling rocks. In a rock drilling, Chugh [11] found that the torque producing at the drilling point depends upon drilling parameters such as bit thrust, bit diameter, and the friction inducing between the bit-rock interfaces. During the rotary drilling of a cortical bone, the impact of rotational speed and PR of the drill bit on drill-bit thrust and rotational force was investigated by Alam et al [1]. The experimental data indicated that both thrust and torque were reduced by 27% and 30% respectively at the bit speed range of 600–3000 r.p.m. During a percussive type of rock drilling, Vardhan et al [28] observed that the acoustic parameter generating at the drilling point rises as the drill bit-thrust and rock strength increases. Kumar et al [18, 19] carry out a rotary drilling experiment to quantify UCS of sedimentary and metamorphic rocks respectively. The experimental results uncovered that sound level producing at the drilling point is the function of rock strength and drill operating parameters. It was also observed that the emanating sound was linearly varying with UCS of rocks. Yari and Bagherpour [32, 33] and Vijay et al [29,30,31] conducted the drilling experiment with different combinations of drill operating variables such as penetration rate, drill diameter and its speed. For each combination of drill operating variables, an acoustic parameter was acquiring with the help of a data acquisition system (DAQ). The experimental results conclude that the acoustic parameter difference is because of different drill operating parameters and rocks with different strengths.

The above literature survey concludes that only a couple of studies estimated the rock strength based on applied thrust and penetration rate. In most of the previous studies, it is observed that the drilling responses such as thrust and torque are only analyzed concerning the rock strength, but both are not directly used to estimate the rock strength. Besides, in many mining activities, drilling is part of it. This method can determine the rock strength directly at the site using suitable thrust and torque sensors. The present work is entirely different from the previous studies and has many advantages over other methods. Therefore an attempt is made to estimate the rock strength using this method.

In this work, the relationship of drilling specific energy with the UCS of drilled rocks is also investigated. Behboud et al [7] attempted to correlate the specific energy of drilling with rock strength property such as UCS. From the results, it was concluded that the compressive strength is the most important geo-mechanical parameter affecting specific energy. The specific energy was almost linearly varying with an increase of UCS during rotary drilling of rocks [10, 16]. During the rock drilling, using a blunt bit, Kalantari et al [17] found that a linear relationship exists between drilling specific energy and rock strength (UCS). Balci and Bilgin [3, 4] and Copur et al [12] investigated the relationship between specific energy utilized during the rock cutting and mechanical properties of rocks such as UCS, Brazilian tensile strength (BTS). From the results, it could see that the specific energy was well correlating with UCS.

From the above-discussed literature, it was observed that the variation of drilling parameters such as thrust and torque is significant during drilling of different rocks. Therefore, the drill operating parameters can be possible variables to characterize the rock strength during the drilling. The main intention of this work is to investigate the usability of some identified drill operating parameters to predict the rock strength property and also to check the relationship of specific energy utilized during rock drilling with the uniaxial compressive strength of drilled rocks. In the present studies, an experimental setup was used to investigate the main objectives of this research work.

Experimental setup and studies

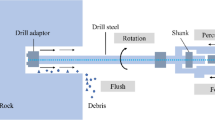
The configuration of the experiment is showing in the Fig. 1. It consists of a CNC vertical drilling machine, a drill dynamometer, and sedimentary rock blocks. A CNC drilling machine is utilize to accomplish the drilling of rocks with the help of diamond core drill bit of diameter 12, 16 and 20 mm. The thrust producing at the drilling point is measuring with the aid of the drill dynamometer. A numerical control (NC) program could control the PR and bit speed during the drilling. The prepared cubical rock samples of size 15 cm, including shale, sandstone, and limestones that have various UCS is using for experimental drilling purposes. The machine vice is used to fix the rock samples securely. The flaws of rock samples were checked during their collection.

Fig. 1
figure 1

Experimental setup

Full size image

An outline of the test program is showing in Fig. 2. While the drilling of various rocks at different drill working conditions, the corresponding thrust was measured with a device called drill tool dynamometer. The limit of measuring instrument was 1 N–5000 N with an LC of 1 N. The dynamometer consists of a durable metal cylinder of height approximately 150 mm with 10 mm thick steel plates fitted at both top and undersides. The provisions are made on top and underside plates to fix securely to machine vice and machine bed, respectively, using the appropriate fasteners. Since the machine vice is directly fastening on the top of the dynamometer, the drilling of different rocks at a particular combination of machine operational parameters, the equivalent thrust would be exerting on the dynamometer and hence on its sensing material. Because of this physical phenomenon, the equal analog signal is emerging from the dynamometer device. Next, it switched into a digital signal through a signal conditioner and, in the end, could see the digital thrust reading in the dynamometer's display.

Fig. 2
figure 2

Sketch of the experimental system

Full size image

Methodology

In this method, the drilling of each type of sedimentary rock is carrying out at a various set of machine operating parameters. For each machine condition, the thrust exerting on the drill bit was recorded using the drill dynamometer. The specimen of cubical size 15 cm × 15 cm × 15 cm is tightly fixing in a rigid vice. Before drilling the rock blocks of each type, the blocks are entirely drying using an electric oven. The main intention of the drying process was to extract the moisture content from the rock blocks, and thereby to reduce the influence of moisture content on the strength of rocks.

With the help of diamond core drill bits, 9 different holes that have a depth of 30 mm were drilled on each rock type using the 9 combinations of drilling operational parameter (Drill bit diameter of 12, 16 and 20 mm × speed of 500, 700 and 900 rpm × penetration speed of 4 mm/min). A pipe carrying the compressed air is often directing towards the interaction of bit-hole during the drilling of each hole. Using the compressed air was to minimize the compaction effect by flushing out the rock dust-generating inside the hole and cooling the drill bit. The same procedure was repeated for drilling of all rock types. While the bit was advancing through a hole with the particular operating condition, the magnitude of thrust inducing at the drilling spot was changing. As the bit reaches the hole depth of 5, 10, 15, 20, 25, and 30 mm depth, the six bit-thrust reading is taking down successively using the display unit of the dynamometer. Later the arithmetic average of six thrusts was calculated for that particular drilling operation. In the current experiment, a data set containing the 54 thrust readings would record during the entire drilling process (9 sets of machine operating conditions used for each rock type × 6 types of rocks). Similarly, 54 sets of torque were computed for 54 corresponding thrusts using the Chugh [11] torque relationship, derived for a diamond core drill bit, as shown in the Eq. 1.

$${\text{Torque }} = ~\,\frac{2}{3}\, \times \mu ~\, \times {\text{T}}\, \times \frac{{(r_{o} ^{3} - r_{i} ^{3} )}}{{(r_{\begin{subarray}{l} o \\ \end{subarray} } ^{2} - r_{i} ^{2} )}}~~(N - m){\text{ }}$$
(1)

where,

T = Bit thrust (n),

ro = Outer radius of bit (m),

ri = Inner radius of bit (m),

µ = Coefficient of friction between rock and diamond core bit.

The value of µ, as suggested by Chugh [11] for rock material is 0.4

The laboratory testing for UCS is carried out using five rock samples and determined according to the guidelines recommended by the International Society for Rock Mechanics [9]. The rock core samples are also completely dry using an electric oven before testing them for UCS in a laboratory. The main mineralogical composition, such as analysis of silica content (SiO2) of each rock type, would determine using the scanning electron microscope.

Analysis of data

When the drilling is carrying out for various rock types using the different bit diameter and speed, the variation of the bit-thrust is intricately affected by several features. Hence, the drilling process is illustrating by higher order regression model. Statistical application software Minitab 18 was utilized for the analysis of data. A total of 54 data were employed for developing the multiple regression models for UCS. The ANOVA approach analyzed the overall examination of the significance of each factor on the response (UCS). The diameter (D) of the drill bit, rotational speed (S), and penetration rate (PR) is the drill working parameter. Similarly, the measured and computed machine operating parameters are thrust (T) produced on the drill bit and torque (TQ) developed at the bit-rock interface, respectively. During the drilling action, it is hypothesized that the change of thrust is due to using a different set of drill operating conditions and rock strength. The change of thrust while drilling is well associating with machine operating settings and rock strength [1, 3, 5, 14, 15, 18,19,20, 23,24,25]. The equation, as shown below, can imply the drilling process.

$$\mathrm{f}={\mathrm{a}}_{\mathrm{o}}+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}}{\mathrm{x}}_{\mathrm{i}}^{2}+\sum _{\mathrm{i}<j}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}}{\mathrm{x}}_{\mathrm{i}}+\in$$
(2)

In Eq. 2, ao indicates the arbitrary constant, ai signifies the straight source of xi, aij outlines the rectilinear source of xi, and aij presented in the fourth term is produced due to the multiplied results of xi and xj. The last term denoted by \(\in\) represents the error. The backward elimination approach was chosen as a screening mode. The relevance of each regression term with the response is checking with the t-test method. In the t-test, the calculated t-value must always be higher than the tabulated t value at a 95% confidence level and generated a degree of freedom. The regression term is selected if this condition is satisfying. Suppose any regression term is not satisfying this condition. In that case, that variable would remove from the model. Further simulation of the regression process is repeated using the survived variables until the remaining factors or variables could not remove from the model. Ultimately, the variables still remained in the model is chosen for a specific response. The predictive capacity of the regression model developed for UCS is checked using the performance indices such as variance account for (VAF), root mean square (RMSE) and mean absolute percentage error (MAPE) are used to evaluate the prediction capacity of the model.

$$VAF = \left[ {1 - \frac{{\text{var} (m - p)}}{{\text{var} (m)}}} \right] \times 100$$
$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{{i = 1}}^{N} {(m - p)^{2} } }$$
$$MAPE = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {\left| {\frac{{(m - p)}}{m}} \right| \times 100}$$

In Eq. (3), (4) and (5), ‘m’ and ‘p’ indicating the UCS obtained in the test center and using the model, respectively, and N is the data size. In a model, a higher VAF value nearer to 100% indicates that the independent variables are explaining the variance in the dependent variable excellently. Similarly, if RMSE and MAPE values are close to zero value on a scale of 0 to100 concludes that the prediction error is low and accuracy of prediction is high, respectively.

Result and discussions

The UCS value of rocks found in the laboratory, and upper-lower values of measured thrust and calculated torque, and specific energy are tabulating in Table 1.

Table 1 Rock property and minimum and maximum value of measured thrust, computed torque and average specific energy
Full size table

In this experiment, a CNC vertical drilling machine designed for a heavy-duty purpose is using to drill the various sedimentary rocks. The penetration rate (PR) and speed, which are the part of a different set of drill operating conditions, are controlling by the numerical control program (NC program). The control system used in the CNC machine is a closed-loop type. So that, once the PR and speed are fixing in the CNC machine, irrespective of the strength and other properties of rocks, the drill bit could penetrate the material at constant specified PR (mm/min). During the drilling of different strength materials with specific speed, and diameter of the bit, the computer assists the machine to determine the required thrust accordingly. At last, it would apply the same bit-thrust to gain the preset penetration rate. Figure 3 shows the variation of average measured thrust and theoretical torque inducing during the drilling of various rocks using different drill bit diameter. From Fig. 3a, it is observing that the thrust is steadily rising exponentially when the drill bit diameter is increasing. This may be because as the drilling hole area increases, the volume of the material removal rate also increases. The machine would utilize much thrust to maintain the preset penetration rate for a higher volume removal rate. It could also observe that the thrust level was significantly rising when the higher UCS rocks were drilling. It may occur because as the packing density of grains or degree of compactness increases in fine-grained rocks, the rock strength or UCS increases. The higher packing density of grains may offer more resistance against the penetration of bit at a particular speed. Hence, the CNC machine might utilize more bit-thrust to achieve a particular penetration rate of 4 mm/min. From Fig. 3b, it was noted that the torque was also gradually increased when the different UCS rocks being drilled using the different diameter bits. In general, torque is the function of bit-thrust and radius of drill bit. As these two variables increases, the torque also increases. However, in this experiment, the torque is calculated using the Eq. 1. In this equation, it is clearing that the torque is mainly the function of two variables such as drill bit radius or diameter and generated thrust. Therefore, the torque is increasing with increase of bit diameter and UCS.

Fig. 3
figure 3

Thrust and torque of drilling rocks at different bit diameter. a Thrust vs. bit diameter. b Torque vs. bit diameter

Full size image

Figure 4 indicates how the average thrust and torque varies at different speeds during the drilling of various sedimentary rocks. From Fig. 4a, it was seen that the thrust is linearly increasing between the bit speeds of 500–700 r.p.m. But, it is slightly reducing after the speed of 700 r.p.m. The drilling energy consists of two components, including thrust and rotational energy, as shown in Eq. 8. The reason may be concerning to Eq. 8 that the axial and cutting action may be assisted largely by rotational energy rather than the thrust for particular drilling energy at high spindle speed. Thus the thrust energy may reduce slightly at high spindle speed.

Fig. 4
figure 4

Thrust and torque of drilling rocks at different bit speed. a Thrust vs. bit speed. b Torque vs. bit speed

Full size image

As shown in Fig. 4b, torque could vary almost in the same way as a thrust at a different speed [11, 12]. Figure 5 depicts the association between average thrust and torque inducing during the drilling of different sedimentary rocks. It is observing that both the average thrust and torque of various rocks are varying linearly.

Fig. 5
figure 5

Association of torque and thrust

Full size image

The following model is drawn from the set of drill operating variables to predict the UCS,

$$UCS = 75.3 - 0.7201 \times S + 0.5168 \times T - 29.66 \times TQ + 0.000479 \times S \times S$$
(6)

The model formulated for the evaluation of UCS is shown in Eq. 3. Table 2A explains that the generated model is responsible for 93.60% of the entire variation in response, i.e., UCS. Since the R2 value is nearer to 100%, the integral explanation of variance in the dependent variable by input parameters is highly significant. From Table 2B, it is cleared that each variable is statistically significant at a 95% confidence level, as p < 0.05 and generated t > tabulated t (For generated DOF = 4, Total DOF = generated DOF-1, standard t = 2.353). At 95% confidence level, the value of p less than 0.05 indicates that the probability of not occurring the relationship between independent and dependent variables is less than 5%. Therefore the null hypothesis is rejected, and the alternate hypothesis concludes that there is a relationship between independent and dependent variables. Hence, it could conclude that the variables included in the UCS model are affecting the UCS. Since the p-value of drill bit diameter was higher than the value of 0.05, it is confirming that the drill bit diameter is not influencing the response (UCS) directly, and it is excluding from the model.

Table 2 Statistical results of model
Full size table

Among the drilling responses such as thrust and torque, the higher the adjusted and the sum of squares and corresponding F-value indicate that a particular drilling response would impact the UCS than the other one. In the ANOVA Table 2C, the value of the adjusted sum of the square (Adj SS) and corresponding F-value is high for thrust. Therefore, it can be concluded that thrust is the variable that is much impacting the UCS. Also, the overall F-value of regression is high implies that the fitting of the data to the model is good. The model formulated for the evaluation of UCS is shown in Eq. 3. Figure 6 intimates that how far the UCS evaluated in the laboratory is closely correlated with the UCS determined by the developed model.

Fig. 6
figure 6

Cross examination of measured and predicted UCS

Full size image

Table 3 illustrates the performance evaluated for the developed UCS model. The VAF is close to 100% indicating the very good variance of input parameters in UCS, similarly the RMSE and MAPE is less than 15%, the model would predict the UCS within acceptable error limits, and accuracy respectively. However, the derived model's validation is checked for a set of sandstone and limestone having UCS 28 MPa and 35 MPa, respectively. The value of thrusts are acquired for both rocks at the constant penetration rate of 4 mm/min, bit diameter of 12 mm,16 mm, and 20 mm using the different speeds 500,700 and 900 r.p.m. The result shows that the model could predict the average UCS of sandstone and limestone with an error of 2.4 Mpa and 2.8 Mpa, respectively. In terms of percentage, the prediction error for sandstone and limestone are 8.51% and 8.01%, respectively. Since the errors are within the acceptable limit, usually 15%, it is concluded that the developed regression model for UCS may reasonably predict the UCS for sedimentary rock types.

Table 3 Quantification of prediction capacity of UCS model
Full size table

Relationship between specific energy of drilling and the UCS

In rock drilling, specific energy is the minimum amount of energy required for removing the unit volume of rock. In this study, an attempt is also made to find the relationship between specific energy and UCS of rocks. The relationship between specific energy and UCS is investigating using a linear regression method. In the current work, the specific energy is calculating with the use of obtained thrust and torque for each machine operational conditions. The equation for specific energy during rotary drilling was derived by Teale [27] in 1965 and is given by

$$E = \frac{F}{A} + \frac{{2 \times \pi \times N \times T_{q} }}{{A \times PR}}\,{\text{J}}/{\text{m}}^{{\text{3}}}$$
(7)

The Eq. (7) basically consists of two components and it can be written as

$$E = E_{T} + E_{R}$$
(8)

The first component in Eq. (8) of the equation represents the contribution of thrust (thrust component) and the second component is representing the rotary component of energy (torque component).

E – Specific energy (J/m3),

F – Thrust acting on the bit (Newton),

A – Area removed (m2),

N—Drill bit speed (r.p.s),

Tq—Torque developed at bit rock interface corresponding to the applied thrust (N–m),

PR—Penetration rate (m/sec).

The average specific energy for each rock type is tabulating in Table 1. From Fig. 7, it was seen that the relationship between specific energy and UCS of drilled rocks is very good with an r2 value of 92%.

Fig. 7
figure 7

Relationship between specific energy and UCS of rocks

Full size image

Conclusions

In this investigation, the rock strength property, such as UCS would approximately quantify using the machine operating variables used for managing the drilling process. The drill tool dynamometer was employed to measure the drilling response parameter such as thrust, and corresponding torque could calculate with measured thrust and drill bit diameter. From the experimental results, the following results and conclusions were obtained.

  • When the rocks that have different UCS are drilling, it is observing that the drill operating parameters such as thrust and torque was substantially increased from 419 to 812 N (48.39%) and 0.84 N–m to 2.89 N–m (70.39%) respectively.

  • During the drilling of rocks, when the drill bit diameter changed from 12 to 20 mm, the overall percentage of increase in thrust for rocks having the UCS of 19.6, 42.1, 65.3, 76.6, 91.2 and 119 MPa was 10.38%, 5.82%, 9.04%, 9.62%,12.76%, and 11.19% respectively.

  • Similarly, when the drill bit diameter changed from 12 to 20 mm, the overall percentage of increase in computed torque for rocks having the UCS of 19.6, 42.1, 65.3, 76.6, 91.2 and 119 MPa was 42.55%, 43.58%, 40.79%, 42.12%, 49.88%, and 50% respectively.

  • From the adjusted SS value and equivalent F-value as shown in the ANOVA table, it was concluded that the main interesting drilling variables such as thrust (Adjusted SS value = 42864, F-Value = 585.07) and torque (Adjusted SS value = 5782, F-Value = 78.92) are respectively impacting the UCS.

  • The evaluation of regression model indicated that the model could estimate the UCS with an overall percentage error of 3.49% and the mean absolute percentage error of 11.27%. The validation model for sandstone and limestone would also predict the UCS with the error of 8.51% and 8.01%.

  • The evaluation of the model using both prediction indices and validation techniques revealed that the developed model would predict the UCS below the 15% prediction error. In general, it could be considered as acceptable limits for estimation purposes.

  • The relationship between specific energy utilized during drilling of different rocks and their UCS are having an almost linear relationship, with a coefficient of determination (R2) value of 92.1%.