Abstract
We use quilted Floer theory to generalize Seidel’s long exact sequence in symplectic Floer theory to fibered Dehn twists. We then apply the sequence to construct versions of the Floer and Khovanov–Rozansky exact triangles in Lagrangian Floer theory of moduli spaces of bundles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Seidel’s long exact sequence [41, Theorem 1] describes the effect of a symplectic Dehn twist on Lagrangian Floer cohomology. In many examples (moduli spaces of bundles, nilpotent slices, etc.), the relevant fibrations have Morse–Bott rather than Morse singularities and the associated monodromy maps are fibered Dehn twists. Many years ago, Seidel suggested that this sequence should generalize to the fibered case. In this paper, we show how to carry out this suggestion using quilted Floer theory developed in Wehrheim–Woodward [44, 45, 50]. Quilted Floer theory gives an expression of the third term in the exact triangle as a push–pull functor, similar to the situation in the analogous triangle in algebraic geometry developed by Horja [16].
To state the main result, suppose that M is an exact or monotone symplectic manifold. If M has boundary \(\partial M\), then we assume that the boundary \(\partial M\) is convex so that our spaces of pseudoholomorphic curves satisfy good compactness properties. A Lagrangian brane in M is a compact, oriented Lagrangian submanifold L equipped with a grading in the sense of [45] and relative spin structure in the sense of [48]. We say that a Lagrangian brane L is admissible if L is monotone in the sense of [45], the image of the fundamental group \(\pi _1(L)\) of L in \(\pi _1(M)\) is torsion for any choice of base point, and L has minimal Maslov number at least three. This notion of admissibility is chosen so that any pair \(L^0,L^1\) of admissible Lagrangian branes in M is monotone as a pair, which implies an energy-index relation for pseudoholomorphic strips. This relation in turn implies that disk bubbles cannot obstruct the proof of \(\partial ^2=0\) in the construction of the Lagrangian Floer homology group \(HF(L^0,L^1)\). The underlying complex for this group is generated by perturbed intersection points of \(L^0,L^1\). The differential counts finite energy holomorphic strips with boundary in \(L^0,L^1\). Taking the Floer groups as morphism spaces, one obtains the cohomology of the Fukaya category of Lagrangian branes in M. For the moment, we work with \(\mathbb {Z}_2\) coefficients, although the main result will be stated with \(\mathbb {Z}\) coefficients.
To recall Seidel’s exact triangle in Lagrangian Floer cohomology, let \(C \subset M\) be a Lagrangian sphere equipped with an identification with a unit sphere, and let \(\iota _C: C \rightarrow C, \ v \mapsto -v\) denote the antipodal map. Associated with C is a symplectic Dehn twist
equal to the antipodal map on C and supported in a neighborhood \(U_C\) of C. In the case of a Lefschetz fibration, if C is a vanishing cycle then \(\tau _C\) is the monodromy around the corresponding critical value. The assumption \(\dim M\ge 4\) in the following is equivalent to its Lagrangian submanifolds, in particular the sphere C, being of codimension (equal to dimension) at least 2.
Theorem 1.1
(Seidel exact triangle [41]) Let M be a compact monotone or exact symplectic manifold with convex boundary and dimension at least four, and let \(C,L^0,L^1\) be admissible Lagrangian branes such that C is equipped with a diffeomorphism to a sphere. Then there exists a long exact sequence

Seidel’s result is often referred to as a categorification of Picard–Lefschetz since by taking the Euler characteristics one essentially recovers the Picard–Lefschetz formula as in Arnold [4, Chapter I]. The Fukaya-categorical version (conjectured by Kontsevich) is developed in Seidel’s book [42].
Many interesting fibrations that arise in representation theory or gauge theory (such as nilpotent slices or moduli spaces of bundles over a family of curves) have not just Morse singularities but rather Morse–Bott singularities. Here the words Morse and Morse–Bott are used in the sense of non-degeneracy of the Hessian, which in this setting is a complex matrix. Extensions of the Picard–Lefschetz formula to fibrations \(\pi : E \rightarrow S\) with more general singularities are considered by Clemens [9] and Landman [21], and many subsequent authors; the Morse–Bott situation is a particularly easy case. Let \(s_0 \in S\) be a critical value, and
the critical locus in its fiber, which need no longer consist of isolated points. Let \(s \in S\) be a generic nearby point. The analog of the vanishing cycle in this case is a manifold C fibering over B,
consisting of points that converge to B under parallel transport, called by Clemens [9] the vanishing bundle. In the symplectic setting, C is a coisotropic submanifold and the map to B is a smooth submersion with maximally isotropic fibers. The monodromy \(\tau _C\), which arises from parallel transport around \(s_0\), is a fibered Dehn twist as introduced in Sect. 2.2. Roughly speaking, a fibered Dehn twist is a Dehn twist in each fiber of a fibered neighborhood \(U \rightarrow B\) of \(C\subset M\). Let \(M = E_s\) and c the codimension of C. A special case of Clemens [9, Theorem 4.4] gives that the monodromy \(\tau _C\) acts on a homology class \(\alpha \in H(M)\) by the formula
where the action of
is given by slant products, that is, the images of [C] under
The main result of this paper is a categorification of the fibered Picard–Lefschetz formula (1) to the setting of Floer–Fukaya theory. In other words, we generalize Seidel’s triangle to the fibered case. As before, need to assume will use suitable monotonicity conditions to ensure well-defined Floer cohomology and relative invariants arising from pseudoholomorphic quilts in [44]. However, we expect our proofs to directly generalize to a version of the exact triangle in any setting in which algebraic and analytic refinements provide well-defined Floer cohomologies.
Definition 1.2
(Spherically fibered coisotropics) A spherically fibered coisotropic submanifold of a symplectic manifold M is a coisotropic submanifold \(C \subset M\) of codimension \(c\ge 1\) such that
-
(a)
(Fibrating) the null foliation of C is fibrating over a symplectic base B with fiber \(S^c\) a sphere of dimension c and
-
(b)
(Orthogonal structure group) the structure group of \(p: C \rightarrow B\) is equipped with a reduction to \(SO(c+1)\), that is, a principal \(SO(c+1)\)-bundle \(P\rightarrow B\) and a bundle isomorphism \(P\times _{SO(c+1)} S^c \cong C\).
Any spherically fibered coisotropic gives rise to a fibered Dehn twist \(\tau _C \in {\text {Diff}}(M,\omega )\), see Sect. 2. We identify C with its Lagrangian image in \(B^- \times M\), where \(B^-\) denotes B with symplectic structure reversed. Let \(C^t\) denote the transpose of C in \(M^- \times B\). Thus C defines Lagrangian correspondences from B to M and vice versa. These correspondences fit into the framework of quilted Floer theory developed in [44, 45, 49, 50]. Assuming monotonicity as in [44] (i.e., an energy-index relation for pseudoholomorphic quilts), the correspondence C defines functors from the Fukaya category of B to that of M and vice versa. On the level of homology, the latter functor gives rise to a homomorphism between quilted Floer cohomology groups
where the Lagrangian correspondences
are parts of generalized Lagrangian correspondences
from a point to M in the sense of [45]. In the special case of simple Lagrangian submanifolds \(\underline{L}^i=L^i\subset M\), the homomorphism (2) is equivalent with \(\mathbb {Z}_2\) coefficients to a homomorphism
The map (2) is more precisely defined in [44] and provides the “quilted chaps” map which we use to generalize the “chaps” map in Seidel’s proof of the exact triangle. In the above special case, we obtain an exact triangle

The precise statement including monotonicity conditions, and allowing for generalized Lagrangian correspondences, is the following, which we prove in Sect. 5.2. Here \({\text {graph}}(\tau _C) \subset M^- \times M\) denotes the graph of the fibered Dehn twist \(\tau _C\).
Theorem 1.3
(Exact triangle for fibered Dehn twists) Let M be a compact monotone or exact symplectic manifold with convex boundary, let \(\underline{L}^0=(\ldots , L^0)\) and \(\underline{L}^1=(\ldots , (L^1)^t)\) be admissible generalized Lagrangian branes in M, and let \(C \subset M\) be a spherically fibered coisotropic submanifold of codimension \(c \ge 2\) with base B that is equipped with an admissible brane structure as a Lagrangian submanifold of \(M^-\times B\). Then there exists an exact triangle

A similar triangle was developed by Perutz, as part of the program described in [33]. A different approach to exact triangles via Lagrangian cobordism is given in the recent work of Mak and Wu [25] who also treated the codimension one case with \(\mathbb {Z}_2\) coefficients for the first time. We also treat the codimension one case below (see Remark 5.10) although the monotonicity assumptions required in this case are more complicated.
As in Seidel’s work, there is a connection with the mapping cone construction in the derived Fukaya category, which we establish in Sect. 7.1 as follows.
Theorem 1.4
(Derived Fukaya-categorical version of the exact triangle for fibered Dehn twists) Let \(C \subset M\) be a spherically fibered coisotropic submanifold with admissible brane structure as above. Then for every admissible generalized Lagrangian brane \(\underline{L}\) in M there exists an exact triangle in the derived Fukaya category

Here the notation  and
and  indicates the generalized Lagrangian submanifolds in the sense of [45] formed by concatenation
indicates the generalized Lagrangian submanifolds in the sense of [45] formed by concatenation  . For \(\underline{L}=(L_0,\ldots , L_k)\) with \(L_i\subset M_{i-1}^-\times M_{i}\) and \(M_k=M\), the object
. For \(\underline{L}=(L_0,\ldots , L_k)\) with \(L_i\subset M_{i-1}^-\times M_{i}\) and \(M_k=M\), the object  is equivalent to \(\bigl (L_0,\ldots , (\mathrm{id}_{M_{k-1}}\times \tau _C)(L_k)\bigr )\) for suitable choices of relative spin structures. In particular,
is equivalent to \(\bigl (L_0,\ldots , (\mathrm{id}_{M_{k-1}}\times \tau _C)(L_k)\bigr )\) for suitable choices of relative spin structures. In particular,  for \(k=0\). One can also write the bottom object in the exact triangle
for \(k=0\). One can also write the bottom object in the exact triangle

where \(\varPhi (C^t), \varPhi (C)\) are the \(A_\infty \) functors associated with Lagrangian correspondences constructed in [27]. The formulation of the third term as a push–pull functor makes clear that the exact triangle is the mirror partner of Horja’s exact triangle in [16]. We remark that Perutz [35] proves a related exact triangle describing a symplectic version of the Gysin sequence; roughly speaking, Perutz’ result describes the composition of the functors for \(C^t,C\) in the opposite order as a mapping cone for the map given by multiplication of the Euler class.
We briefly outline the contents of the paper. Section 2 contains background results on fibered Dehn twists and Lefschetz–Bott fibrations. Section 3 describes various situations in which surface Dehn twists induce generalized Dehn twists on moduli spaces of flat bundles; these are mostly minor improvements of results of Seidel and Callahan. Sections 4 and 5 contain the proof of the exact triangle. Section 6 applies the triangle to moduli spaces of flat bundles to obtain generalizations of Floer’s exact triangle for surgery along a knot, as well as surgery exact triangles for crossing changes in knots which have the same form as the surgery exact triangles as Khovanov [17] and Khovanov and Rozansky [19]. Finally, Sect. 7 describes generalizations to the \(A_\infty \) setting. These are limited to the case of minimal Maslov number greater than two.
We thank Mohammed Abouzaid, Tim Perutz, and Reza Rezazadegan for helpful comments, and especially Paul Seidel who got us involved in this area.
The present paper is an updated and more detailed version of a paper the authors have circulated since 2007. The authors have unreconciled differences over the exposition in the paper, and explain their points of view at https://math.berkeley.edu/~katrin/wwpapers/ resp. http://christwoodwardmath.blogspot.com/. The publication in the current form is the result of a mediation.
2 Lefschetz–Bott fibrations and fibered Dehn twists
This section covers the generalization of the theory of symplectic Lefschetz fibrations to the Lefschetz–Bott case, that is, to the case that the singularities of the fibration are not isolated but still non-degenerate in the normal directions. Most of this material is covered in an unpublished manuscript of Seidel [39] and in the works of Perutz [33, 34]. For more recent appearance of fibered Dehn twists, see Chiang et al. [8].
2.1 Symplectic Lefschetz–Bott fibrations
Lefschetz–Bott fibrations have a natural definition in the setting of holomorphic geometry: One requires the projection to be proper and Morse–Bott. In the setting of symplectic geometry, there are several analogous definitions which we discuss below. We begin with the holomorphic setting: Let S be a complex curve. A Lefschetz fibration over S is a complex manifold E equipped with a proper holomorphic map \(\pi : E \rightarrow S\) such that \(\pi \) only has critical points of Morse type. That is, in local coordinates \(z_1,\ldots , z_{n}\) on E, the map \(\pi \) is given by
A Lefschetz–Bott fibration over S is a complex manifold equipped with a proper holomorphic map \(\pi :E\rightarrow S\) that has only Morse–Bott singularities. That is, the critical set
is a smooth (necessarily holomorphic) submanifold and the Hessian of \(\pi \) is non-degenerate along the normal bundle of \(E^{{{\text {crit}}}}\). By the parametric Morse lemma [3, p.12] for any critical point \( e \in E^{{{\text {crit}}}}\), there exist a neighborhood U of e and coordinates \((z_1,\ldots ,z_n) : U \rightarrow \mathbb {C}^n\) such that
where n is the dimension of E and \(c+1\) is the codimension of \(E^{{{\text {crit}}}}\) at e.
In our examples, we will not have global complex structures on E and S (at least no canonical ones). Instead, we work with symplectic versions of Lefschetz–Bott fibrations. The definition of the symplectic version uses the following condition introduced in Perutz [33]. Let \((M,\omega )\) be a symplectic manifold equipped with an almost complex structure J and \(M' \subset M\) an almost complex submanifold. The submanifold \(M'\) is said to be normally Kähler if a tubular neighborhood N of \(M'\) in M is foliated by J-complex normal slices \(\{ N_e \subset N\}, e \in M'\), such that \(J | N_e\) is integrable and \(\omega | N_e\) is Kähler for each e.
Definition 2.1
-
(a)
(Symplectic fibrations) A symplectic fibration is a manifold E equipped with a closed two-form \(\omega _E \in \Omega ^2(E)\) and a fibration \(\pi : E \rightarrow S\) over a smooth surface S, such that the restriction of \(\omega _E\) to any fiber of \(\pi \) is symplectic:
$$\begin{aligned} (\omega _E(e) |_{D_e \pi ^{-1}(0)} )^{\dim (E)-1} \ne 0 \quad \forall e \in E . \end{aligned}$$ -
(b)
(Symplectic Lefschetz–Bott fibrations) A symplectic Lefschetz–Bott fibration consists of
-
(i)
a smooth manifold E equipped with a closed two-form \(\omega _E\);
-
(ii)
a smooth, oriented surface S;
-
(iii)
a smooth proper map \(\pi : E \rightarrow S\) with critical set and values
$$\begin{aligned} E^{{{\text {crit}}}} := \{e \in E \ | \ {\text {rank}}(D_e \pi ) < 2 \}, \quad S^{{{\text {crit}}}}=\pi (E^{{{\text {crit}}}})\subset S ; \end{aligned}$$ -
(iv)
a positively oriented complex structure \(j_0\in \mathrm{End}(TS|_{\mathcal {U}})\) defined in a neighborhood \({\mathcal {U}}\subset S\) of the critical values \(S^{{{\text {crit}}}}\); and
-
(v)
an almost complex structure \(J_0\in \mathrm{End}(TE|_{\mathcal {V}})\) defined in a neighborhood \({\mathcal {V}}\subset E\) of the critical set \(E^{{{\text {crit}}}}\)
satisfying the following conditions:
-
(i)
\(E^{{{\text {crit}}}}\subset E\) is a smooth submanifold with finitely many components;
-
(ii)
\(E^{{{\text {crit}}}}\) is normally Kähler;
-
(iii)
\(\pi |_{\mathcal {V}}: {\mathcal {V}}\rightarrow {\mathcal {U}}\) is \((J_0,j_0)\) holomorphic;
-
(iv)
the normal Hessian \(D^2\pi _e | T^{\otimes 2}N_e\) at any critical point is non-degenerate;
-
(v)
\(\omega _E\) is non-degenerate on \( {\text {ker}}(D\pi )\subset TE\);
-
(vi)
\(\omega _E|_{\mathcal {V}}\) is non-degenerate and compatible with \(J_0\).
-
(i)
Remark 2.2
One natural reason to consider symplectic Lefschetz–Bott fibrations rather than symplectic Lefschetz fibrations is that the category of Lefschetz–Bott fibrations is somewhat better behaved than Lefschetz fibrations with respect to products. Suppose that \(\pi _k: E_k \rightarrow S, k = 1,2\) are (symplectic) Lefschetz–Bott fibrations such that \({{\text {critval}}}(\pi _1) \cap {{\text {critval}}}(\pi _2)\) is empty, where \({{\text {critval}}}\) denotes the set of critical values. Then
is a (symplectic) Lefschetz–Bott fibration with
In particular, the fiber product of a fibration with a Lefschetz fibration is a Lefschetz–Bott fibration.
Associated with any Lefschetz–Bott fibration, there is a natural parallel transport between the fibers. The usual notion of parallel transport in Lefschetz fibrations extends to the symplectic Lefschetz–Bott case. First, suppose that \(\pi : E \rightarrow S, \omega _E \in \Omega ^2(E)\) is a symplectic fibration with connected base S, for simplicity. The canonical symplectic connection on E is the connection defined by
Here the superscript denotes the symplectic complement with respect to \(\omega _{E}\). The symplectic complement has dimension 2 due to the non-degeneracy of \(\omega _E|_{ {\text {ker}}(D_e\pi )}\). Moreover, for any horizontal vector field \(v\in \Gamma (T^hE)\) and fiber \(E_s\) we have
Hence, given any smooth path \(\gamma : \ [0,1] \rightarrow S -S^{{{\text {crit}}}}\) the parallel transport
for any \(t,\tau \in [0,1]\) is a symplectomorphism. (Also see [15, Section 1.2].) This parallel transport gives a reduction in structure group of the fibration to the symplectomorphism group of any fiber.
The notion of parallel transport above extends to parallel transport to critical fibers. Suppose that \(\pi : E \rightarrow S\) is a Lefschetz–Bott fibration. The smooth locus \(E -\pi ^{-1}(S^{{\text {crit}}})\) is a fibration over \(S -S^{{{\text {crit}}}}\) with vertical tangent spaces \(T_e^vE= {\text {ker}}(D_e\pi )\) and a canonical symplectic connection \(T^h E \subset T(E -E^{{\text {crit}}}) \) defined by (4). Given an embedded path \(\gamma :[0,1] \rightarrow E\) ending on the critical locus \(\gamma (1) \in S^{{{\text {crit}}}}\) parallel transport extends to a continuous map
Indeed, choose a tubular neighborhood of \(\gamma \). After rescaling, parallel transport becomes the gradient flow of the function \(f \circ \pi \) for some coordinate function \(f: S \rightarrow \mathbb {R}\) with respect to the metric \(\omega _E(\cdot , J_0 \cdot )\), see [41, Lemma 1.13]. Since the critical points of \(\pi \) are Lefschetz–Bott, the gradient flow is hyperbolic and the limit is well defined [43].
Vanishing thimbles and cycles for Lefschetz–Bott fibrations are defined as follows. Let \(\gamma : \ [0,1] \rightarrow S\) be a smooth embedded path with \(\gamma (1) \in S^{{{\text {crit}}}}\) such that \(\gamma ([0,1))\subset S -S^{{{\text {crit}}}}\). Fix a connected component \(B\subset E^{{{\text {crit}}}} \cap E_{\gamma (1)}\) of the critical set in the endpoint fiber. The vanishing thimble for the path \(\gamma \) and component B is
The vanishing thimble \(T_{\gamma ,B}\subset E\) is a smooth submanifold with boundary since it is the stable manifold of B, see [43]. The intersections
with the smooth fibers of \(\pi \) for \(t\in [0,1)\) are called the vanishing cycles for the path \(\gamma \).
Proposition 2.3
Each vanishing cycle \(C_t\) from (6) is a coisotropic submanifold of the fiber \(E_{\gamma (t)}\). The map \(\rho _{t,1}:C_t \rightarrow B\) is smooth and gives \(C_t\) the structure of a spherically fibered coisotropic submanifold in the sense of Definition 1.2.
Proof
The parallel transport map \(\rho _{t,1}\) of (5) is a smooth fibration with fibers c-dimensional spheres and structure group \(SO(c+1)\) by the stable manifold theorem, see, for example, [43]. The dimension c is the dimension of the fiber as well as the codimension of \(C_t\subset E_{\gamma (t)}\), by the normal form (3) of \(\pi \). The parallel transport can also be written as a rescaled Hamiltonian flow of \(g \circ \pi \) for some coordinate function \(g:S\rightarrow \mathbb {R}\), as in the unfibered case described in [41]. Since the Hamiltonian flow preserves the symplectic form, the symplectic form vanishes on the fibers of \(C_t\):
Since \(\pi \) is \(J_0\)-holomorphic on B, the tangent space TB (which is the null space of the Hessian of \(\pi \)) is \(J_0\)-invariant. Hence non-degeneracy of \(\omega _E\) in a neighborhood of B implies that the restriction of \(\omega _E\) to B is symplectic. Thus the total space \(C_t\) is coisotropic and the projection \(\rho _{t,1}: C_t \rightarrow B\) is the null foliation as claimed. \(\square \)
2.2 Fibered Dehn twists
The symplectic Dehn twist along a Lagrangian sphere in [41] can be generalized to spherically fibered coisotropics using the associated symplectic fiber bundle construction. This construction associates with any principal bundle and Hamiltonian action with small moment map a symplectic fiber bundle.
We first set up notation for connections on principal bundles. Let G be a compact Lie group with Lie algebra \(\mathfrak {g}\). Recall that a connection one-form on a principal G-bundle P is a one-form \(\alpha \in \Omega ^1(P,\mathfrak {g})\) with values in the Lie algebra \(\mathfrak {g}\) satisfying the following two conditions:
-
(a)
the evaluation \(\alpha (\xi _P)\) is the constant function equal to \(\xi \) for any \(\xi \in \mathfrak {g}\), where \(\xi _P \in {\text {Vect}}(P)\) is the vector field generating the action of \(\xi \), and
-
(b)
the pullback \( g^* \alpha \) is equal to \( {\text {Ad}} (g)^{-1} \alpha \) for any \(g \in G\), where the adjoint action is on the values of \(\alpha \).
Let \( {\text {ker}}(\alpha ) \subset TP\) denote the horizontal subbundle of vectors whose fiber at a point \(p \in P\) is the space of vectors annihilated by \(\alpha _p\). The tangent bundle TP admits a splitting into horizontal and vertical parts
invariant under the group action. Denote by \({\mathcal {A}}(P)\) the space of connection one forms on P; it is an affine space modeled on \(\Omega ^1(C,P(\mathfrak {g}))\).
Given a principal bundle with connection and a Hamiltonian action, the associated fiber bundle has a natural two-form defined as follows. To set up notation, suppose that the following are given:
-
a base symplectic manifold \((B,\omega _B)\);
-
a principal bundle \(\pi : P \rightarrow B\) with structure group G;
-
a fiber symplectic manifold \((F,\omega _F)\) equipped with a Hamiltonian G-action with moment map \(\varPhi _F: F \rightarrow \mathfrak {g}^\vee := {\text {Hom}}(\mathfrak {g},\mathbb {R})\); and
-
a connection one-form \(\alpha \in \Omega ^1(P,\mathfrak {g})^{G}\).
Denote by \(\pi _1,\pi _2\) the projections to the factors of \(P \times F\). The minimally coupled form on \(P \times F\) is
Theorem 2.4
(Symplectic associated fiber bundles) (see, e.g., [14]) Let P be a principal G-bundle, F a Hamiltonian G-manifold and \(\alpha \) a connection one-form as above.
-
(a)
The minimally coupled form \(\omega _{P \times F,\alpha }\) descends to a closed two-form
$$\begin{aligned} \omega _{P(F),\alpha } \in \Omega ^2(P(F)), \quad P(F) := P \times _G F. \end{aligned}$$The form \(\omega _{P(F),\alpha }\) is non-degenerate on the fibers in a neighborhood
$$\begin{aligned} P(F)_\epsilon := P( \{ \vert \varPhi _F \vert < \epsilon \}) \end{aligned}$$of the associated bundle to the zero-level set \(P(\varPhi ^{-1}_F(0)) \subset P(F)\). Here \(\vert \varPhi _F \vert \) denotes the norm of \(\varPhi _F\) with respect to an invariant metric on \(\mathfrak {g}\cong \mathfrak {g}^\vee \). Hence \(P(F)_\epsilon \) is a symplectic fiber bundle over B for sufficiently small \(\epsilon > 0 \).
-
(b)
If \(\varPhi ^{-1}_F(0)\) is smooth, then \(P(\varPhi ^{-1}_F(0))\) is a smooth submanifold of \(P(F)_\epsilon \) with coisotropic fibers.
-
(c)
Given two choices of connection \(\alpha _j, j = 0,1\), there exists an isomorphism of symplectic fiber bundles from \((P(F)_\epsilon ,\omega _{P(F),\alpha _0})\) to \((P(F)_\epsilon , \omega _{P(F),\alpha _1})\) for sufficiently small \(\epsilon > 0 \).
-
(d)
The association \((F,\omega _F,\varPhi _F) \rightarrow (P(F)_\epsilon ,\omega _{P(F)})\) is functorial in the sense that any isomorphism of Hamiltonian G-manifolds \((F_0,\omega _{F_0},\varPhi _{F_0})\) to \((F_1,\omega _{F_1}, \varPhi _{F_1})\) induces an isomorphism of symplectic fiber bundles \(P(F_0)_\epsilon \rightarrow P(F_1)_\epsilon \).
Example 2.5
(Associated bundles with cotangent-sphere fibers) We are mainly interested in the following special case of the general construction. For any integer \(c \ge 1\), let \(S^c\) denote a sphere of dimension c and \(T^\vee S^c\) its cotangent bundle. Consider \(T^\vee S^c\) with canonical symplectic form \(\omega _{T^\vee S^c}\) and the canonical \(SO(c+1)\)-action. The action is Hamiltonian with a moment map \( \varPhi _{T^\vee S^c}\) whose zero-level set is \(S^c\). Thus for any principal \(SO(c+1)\)-bundle \(\pi : P \rightarrow B\) the associated fiber bundle construction yields a symplectic fiber bundle \(P(T^\vee S^c)_\epsilon \) over B. By functoriality, any automorphism \(\tau \) of \((T^\vee S^c,\omega _{T^\vee S^c},\varPhi _{T^\vee S^c})\) induces a bundle isomorphism \(\tau _{P(T^\vee S^c)}: P(T^\vee S^c) \rightarrow P(T^\vee S^c)\). The latter is an isomorphism of symplectic fiber bundles on \(P(T^\vee S^c)_\epsilon \).
The notion of Dehn twist is most familiar from Riemann surface theory, where a Dehn twist denotes a diffeomorphism obtained by twisting around a circle on a handle. In [41], Seidel introduces a generalized notion of Dehn twist which is a symplectomorphism around a Lagrangian sphere, called a generalized Dehn twist. The symplectomorphisms we consider here are further generalized by allowing the twists to be fibered, so that the vanishing cycles are fibered coisotropics. To save space, we call these simply fibered Dehn twists. We begin with the local model introduced by Seidel [41].
Definition 2.6
(Model Dehn twist, Seidel [41, Lemma 1.8]) For any sphere \(S^c\), a model Dehn twist \(\tau _{S^c}\) along the zero section \(S^c\) in the cotangent bundle \(T^\vee S^c\) is a compactly supported symplectomorphism equal to the antipodal map on \(S^c\), given as follows. Let \(\zeta \in C^\infty (\mathbb {R})\) be a function satisfying
In particular, \(\zeta \) is compactly supported and \(\zeta '(0) = 1/2\). Fix the standard Riemannian structure on \(S^c\) and let
denote the Riemannian norm. The norm is smooth on the complement of the zero section and similarly for composition with \(\zeta \). The time \(2 \pi \) flow of \(v \mapsto \zeta (|v|)\) extends to a smooth symplectomorphism \(\tau _{S^c}\) of \(T^\vee S^c\). The flow acts on the zero section by the antipodal map given by
Furthermore, \(\tau _{S^c}\) is \(SO(c+1)\)-equivariant and preserves the moment map for the \(SO(c+1)\)-action. Any two model Dehn twists given by different choices of \(\zeta \) are equivalent up to symplectomorphism generated by a compactly supported Hamiltonian.
We construct fibered Dehn twists along spherically fibered coisotropics as follows.
Definition 2.7
Let \((M,\omega )\) be a symplectic manifold and \(C\subset M\) a spherically fibered coisotropic submanifold of codimension \(c\ge 1\), fibering \(C\rightarrow B\) over a symplectic manifold \((B,\omega _B)\), as in Definition 1.2.
-
(a)
(Coisotropic embedding) Recall that C is diffeomorphic to an associated fiber bundle \(P(S^c) := P \times _{SO(c+1)} S^c ,\) for some principal \(SO(c+1)\)-bundle \(\pi : P \rightarrow B\). By the coisotropic embedding theorem [14, p. 315], a neighborhood of C in M is symplectomorphic to a neighborhood of the zero section in \(P(T^\vee S^c)_\epsilon \) as in Theorem 2.4.
-
(b)
(Model fibered Dehn twists) Any \(SO(c+1)\)-equivariant model Dehn twist \(\tau _{T^\vee S^c}: T^\vee S^c \rightarrow T^\vee S^c\) induces a symplectomorphism
$$\begin{aligned} \tau _{P(T^\vee S^c)} : P(T^\vee S^c)_\epsilon \rightarrow P(T^\vee S^c)_\epsilon \end{aligned}$$by functoriality of the associated symplectic fiber bundle construction as in Example 2.5. Given a symplectomorphism \(\phi \) of a neighborhood U of \(C\subset M\) with \(P(T^\vee S^c)_\epsilon \), we define a symplectomorphism \( \tau _C : M \rightarrow M \) by \(\tau _{ P(T^\vee S^c)}\) on the neighborhood of C and the identity outside:
$$\begin{aligned} \tau _C|_U = \phi ^{-1} \tau _{T^\vee P(S^c)}|_{\phi (U)} \phi , \quad \tau _C |_{M - U}= {\text {Id}}_M . \end{aligned}$$We call \(\tau _C\) a model fibered Dehn twist along C.
-
(c)
(Fibered Dehn twists) A symplectomorphism \(\tau _C\) of M is called a fibered Dehn twist along C if \(\tau _C\) is Hamiltonian isotopic to a model Dehn twist.
Remark 2.8
The Hamiltonian isotopy class of a fibered Dehn twist is independent of the choice of local model and fibered Dehn twist used in its construction: Any two local models for a fibered coisotropic are isotopic, by a family version of Moser’s construction. This fact implies that any two fibered Dehn twists \(\tau _{C,0}, \tau _{C,1}\) defined using different local models and model twists may be connected by a family \(\tau _{C,t}\). The vector field \( v_t : = (\tau _{C,t}^{-1} )_* \frac{d}{dt}\tau _{C,t} \in {\text {Vect}}(M)\) vanishes on C and is necessarily Hamiltonian in a neighborhood of C.
2.3 Equivariant fibered Dehn twists
In this section, we discuss the interaction of equivariant fibered Dehn twists with symplectic reduction. Let G be a compact connected Lie group and \((M,\omega )\) a symplectic G-manifold. A spherically fibered coisotropic G-submanifold is an invariant coisotropic submanifold \(C \subset M\) of codimension \(c\ge 1\) such that there exists
-
a principal \(SO(c+1)\)-bundle \(\pi : P\rightarrow B\) equipped with an action of G by bundle automorphisms (i.e., \(SO(c+1)\)-equivariant diffeomorphisms) and
-
a G-equivariant bundle isomorphism \(P\times _{SO(c+1)} S^c \cong C\), where the G-action is induced by the action on the first factor.
Given such a coisotropic C, one obtains a G-equivariant Dehn twist on \(P(T^\vee S^c)\) by the G-equivariant version of the associated symplectic fiber bundle construction. One obtains a G-equivariant model fibered Dehn twist on M via the G-equivariant coisotropic embedding theorem. A G-equivariant symplectomorphism \(\tau \in {\text {Diff}}(M,\omega )\) is a G-equivariant fibered Dehn twist if \(\tau \) is equivariantly Hamiltonian isotopic to a model Dehn twist, that is, Hamiltonian isotopic via a symplectomorphism generated by a family of G-invariant Hamiltonians.
We now show that equivariant fibered Dehn twists give rise to fibered Dehn twists in symplectic quotients. Let \(({M},{\omega })\) be a Hamiltonian G-manifold with moment map \({\varPhi }: M \rightarrow \mathfrak {g}^\vee \). The symplectic quotient of M by G is
Assuming that G acts freely on \(\varPhi ^{-1}(0)\), \(M {//}G\) is a symplectic manifold with unique symplectic form that lifts to the restriction of the symplectic form to \(\varPhi ^{-1}(0)\).
Lemma 2.9
Let \(({M},{\omega })\) be a Hamiltonian G-manifold with moment map \({\varPhi }\). Let \({C} \subset {M}\) be a G-invariant coisotropic submanifold. Suppose that 0 is a regular value of \(\varPhi \), the action of G on \(\varPhi ^{-1}(0)\) is free, and C intersects \({\varPhi }^{-1}(0)\) transversally. The quotient
is a coisotropic submanifold of \(M {//}G\).
Proof
The transversality \(TC\pitchfork {\text {ker}}D \varPhi \) implies \(( {\text {ker}}D \varPhi )^\omega \cap TC^\omega =\{0\}\). It follows that
Now \(( {\text {ker}}D \varPhi )^\omega \cong \mathfrak {g}\) is the tangent space to the G-orbits and contained in TC. On the other hand, \(TC^\omega \subseteq TC\) since C is coisotropic. Hence
This implies \(T(C {//}G)^\omega \subseteq T(C {//}G)\). \(\square \)
Lemma 2.10
Suppose that \(C \subset M\) is a spherically fibered G-coisotropic over a base B where M is a Hamiltonian G-manifold with moment map \(\varPhi \). Then \(\varPhi \) is constant on the fibers of C and the induced action of G on B is Hamiltonian with moment map \(\varPhi _B:B \rightarrow \mathfrak {g}^\vee \) the unique map satisfying \(p^* \varPhi _B = \varPhi | C\).
Proof
By assumption, the action of G on P is \(SO(c+1)\)-equivariant and so induces an action on B. For any \(\xi \in \mathfrak {g}\), the infinitesimal action \(\xi _M\in {\text {Vect}}(M)\) is tangent to C. Hence \(L_v \langle {\varPhi },\xi \rangle = {\omega }(\xi _M,v) = 0\) for all fiber tangent vectors \(v \in T^{{\text {vert}}} {C}=TC^{\omega }\). It follows that \(\varPhi \) is constant on the fibers of \(p: C \rightarrow B\). So \(\varPhi \) induces a map \(\varPhi _B: B \rightarrow \mathfrak {g}^\vee \), satisfying \({\text{ d }}\langle \varPhi _B, \xi \rangle = \iota (\xi _B) \omega _B\) for all Lie algebra vectors \(\xi \in \mathfrak {g}\) as claimed. \(\square \)
Remark 2.11
(Quotients of spherically fibered coisotropics are spherically fibered) Suppose that in the setting of Lemma 2.10, G also acts freely on \(\varPhi _B^{-1}(0)\). It follows that \(B{//}G=\varPhi _B^{-1}(0)/G\) is a smooth symplectic quotient. Then the null foliation on \(C{//}G\) fibers over \(B{//}G\): If \(p: C \rightarrow B\) is the projection, then
Define \(\tilde{P} = ({P} | {\varPhi _B}^{-1}(0) )/G\); this quotient is a principal \(SO(c+1)\)-bundle over \(\tilde{B}=B {//}G\). We have a bundle isomorphism \(\tilde{P}\times _{SO(c+1)} S^c \cong C{//}G\). It follows that \(C{//}G\) is spherically fibered in the sense of Definition 1.2.
In this setting, every G-equivariant fibered Dehn twist along C descends to a fibered Dehn twist of \(M{//}G\) along \(C{//}G\):
Theorem 2.12
Let \(({M},{\omega })\) be a Hamiltonian G-manifold with moment map \({\varPhi }\) such that 0 is a regular value of \(\varPhi \) and the action of G on \(\varPhi ^{-1}(0)\) is free. Let \({C} \subset {M}\) be a spherically fibered G-coisotropic over a base B. Suppose that C intersects \({\varPhi }^{-1}(0)\) transversally and that the induced action of G on the base \(\varPhi _B^{-1}(0)\subset B\) is free. Let \(\tau _C \in {\text {Diff}}(M,\omega )\) be a G-equivariant fibered Dehn twist along C. Then the symplectomorphism
is a fibered Dehn twist \([\tau _C]=:\tau _{C{//}G}\) along \( C{//}G\).
Proof
By definition, \(\tau _C\) is Hamiltonian isotopic to a model Dehn twist on \(P(T^\vee S^c)\) given by \(\tau ^0_C:[{p},v] \mapsto [{p},\tau _{S^c}(v)]\). The latter is G-equivariant since the G-action commutes with the \(SO(c+1)\) action. Any G-equivariant local model \(P(T^\vee S^c) \rightarrow M\) induces a local model given by a symplectomorphism of a neighborhood of the zero section in \(\tilde{P}(T^\vee S^c)\) to \(M {//}G\). One obtains from the local model a Dehn twist
on \(\tilde{P}(T^\vee S^c)\) along \(C{//}G\). The equivariant Hamiltonian isotopy of \(\tau _C\) to \(\tau _C^0\) induces a Hamiltonian isotopy of \(\tau _{C {//}G}\) to \(\tau _{C {//}G}^0\). This completes the proof. \(\square \)
2.4 Lefschetz–Bott fibrations associated with fibered Dehn twists
In this section, we explain that any fibered Dehn twist appears as the monodromy of a symplectic Lefschetz–Bott fibration. Conversely, the monodromy of a symplectic Lefschetz–Bott fibration is given by a fibered Dehn twist up to isotopy by Theorem 2.14 of Perutz [33] recalled below. (Theorem 2.14 is not used in this paper; we mention it only for its conceptual importance linking Lefschetz–Bott fibrations and fibered Dehn twists.)
Proposition 2.13
Let M be a symplectic manifold, \(C \subset M\) a spherically fibered coisotropic, and \(\tau _C: M \rightarrow M \) a fibered Dehn twist around C. There is a standard Lefschetz–Bott fibration \(E_C\) with generic fiber M and symplectic monodromy \(\tau _C\).
Proof
Let \(p: C \rightarrow B\) denote the fibration, and \(P \rightarrow B\) the associated \(SO(c+1)\)-bundle. Recall from [41] the symplectic Lefschetz fibration associated with a model Dehn twist. Given the standard representation of \(SO(c+1)\) on \(V = \mathbb {C}^{c+1}\), we have a vector bundle
Let
denote the symplectic form and moment map for the \(SO(c+1)\)-action induced from the identification \(V \rightarrow T^\vee \mathbb {R}^{c+1}\). The associated symplectic fiber bundle construction above produces a closed form \(\omega _{P(V)}\) on P(V), equal to \(\omega _B\) on B and equal to \( \omega _{V}\) on the fiber V. The map
is \(SO(c+1)\)-invariant and has a single Morse singularity. By the associated bundle construction \(\pi _V\) induces the structure of a Lefschetz–Bott fibration on a neighborhood of the zero section of P(V) over \(\mathbb {C}\). Let \(S^c \subset \mathbb {R}^{c+1} \subset V\) denote the unit sphere and
By [41, (1.17)] the symplectic form on V can be changed slightly so that the symplectic monodromy around 0 is a Dehn twist along \(S^c\). By [41, 1.13] there exists an isomorphism of Hamiltonian \(SO(c+1)\)-manifolds
By the coisotropic embedding theorem, a neighborhood of C in M is symplectomorphic to the fiber bundle P(U), where U is a neighborhood of the zero section in \(T^\vee S^{c}\). It follows that \( P(V) -P(T)\) is symplectomorphic to \(P(\mathbb {C}\times T^\vee S^c -S^c)\) in a neighborhood of P(T) resp. \(P(\mathbb {C}\times S^c)\). By replacing a neighborhood of \(\mathbb {C}\times C\) in \(\mathbb {C}\times M\) with a neighborhood of P(T) in P(V), one obtains a Lefschetz–Bott fibration \(E_C \rightarrow \mathbb {C}\) with monodromy \(\tau _C\). \(\square \)
Theorem 2.14
[33, Theorem 2.19] Suppose that \(\pi : E \rightarrow S\) is a symplectic Lefschetz–Bott fibration, and \(s_0 \in S^{{{\text {crit}}}}\) is such that \(\pi ^{-1}(s_0) \cap E^{{{\text {crit}}}}\) has a unique connected component. Then the symplectic monodromy around \(s_0\) is a fibered Dehn twist.
2.5 Further examples of fibered Dehn twists
Fibered Dehn twists are often induced by flows of components of moment maps. First let \(U(1) = \{ z \in \mathbb {C}\ | \ |z| = 1 \}\) denote the circle group. We identify the Lie algebra of U(1) with \(\mathbb {R}\) via division by \(2 \pi i\). The integers \(\mathbb {Z}= \exp ^{-1}(1)\) are then the coweight lattice. Let \((M,\omega )\) be a symplectic manifold, and \(M_0 \subset M\) an open subset equipped with a free Hamiltonian action of U(1) with moment map \(\varPhi : M_0 \rightarrow (c_-,c_+)\).
Proposition 2.15
(Fibered Dehn twists via Hamiltonian circle actions) Let \(\psi \in C^\infty [c_-,c_+]\) be a function such that \(\psi ' = 1\) on a neighborhood of \(c_+\), and \(\psi ' = 0 \) on a neighborhood of \(c_-\). Then the time-one flow of \( \psi \circ \varPhi \) on \(M_0\) extends to a smooth flow on M equal to the identity on the complement of \(M_0\) and the extension is a fibered Dehn twist along \(\varPhi ^{-1}(c)\) for any \(c \in (c_-,c_+)\). If \(M_0\) is a Hamiltonian G-manifold for a compact Lie group G and \(\psi \) is G-invariant, then this fibered Dehn twist is equivariant.
Proof
Let \(\psi \) be as in the statement of the Proposition. We have
where \(\frac{\partial }{\partial \theta }\in {\text {Vect}}(M_0)\) is the generating vector field for the action. Hence the flow of \(\psi \circ \varPhi \) is rotation by the angle \(2\pi \psi '\). The rest is immediate from the definitions. \(\square \)
Remark 2.16
(Standard Dehn twists as symplectic Dehn twists) Standard Dehn twists of complex curves arise from the construction in 2.15 as follows. Suppose that M is a complex curve and \(C \rightarrow M\) an embedded circle equipped with an identification \(C \cong S^1\). Choose an area form \(\omega _M\) on M. Since \(C \subset M\) is Lagrangian, by the Lagrangian embedding theorem there exists a tubular neighborhood \(M_0 = C \times (c_-,c_+)\) on which the symplectic form is standard. Then the U(1) action by rotation on the left factor of \(M_0\) is free, and the projection \(\varPhi \) on the second factor is a moment map. For any \(\psi \) with the properties in Proposition 2.15, the flow of \(\psi \circ \varPhi \) is a standard Dehn twist.
Next we consider Dehn twists induced by flows of moment maps of SU(2)-actions. We fix a metric on the Lie algebra \(\mathfrak {su}(2)\) so that nonzero elements \(\xi \) with \(\exp (\xi ) = 1\) have minimal length 1.
Proposition 2.17
(Fibered Dehn twists via Hamiltonian SU(2)-actions) Suppose that \((M,\omega ,\varPhi )\) is a Hamiltonian SU(2)-manifold with moment map \(\varPhi : M \rightarrow \mathfrak {su}(2)^\vee \) and the stabilizer H of the action of SU(2) on any point in \(\varPhi ^{-1}(0)\) is trivial resp. U(1). Let \(\psi \in C^\infty _c[0,\infty )\) be a compactly supported function such that \(\psi ' = 1/2\) in a neighborhood of 0. Then \(\varPhi ^{-1}(0)\) is a spherically fibered coisotropic of codimension 3 resp. 2 and the flow of \(\psi \circ \vert \varPhi \vert \) is a Dehn twist along \(\varPhi ^{-1}(0)\).
Proof
The zero-level set \(P := \varPhi ^{-1}(0)\) is a G-equivariant G / H-bundle over the symplectic quotient \(M {//}G\), by the assumption on stabilizers and existence of local slices. We identify \(G/H \cong S^c\) with \(c = 3\) resp. \(c = 2\), in the trivial stabilizer resp. U(1)-stabilizer case. We show that P is induced from an \(SO(c+1)\) principal bundle and that the flow of \(\psi \circ \vert \varPhi \vert \) is obtained by a Dehn twist by the symplectic fiber bundle construction.
Consider the case of trivial stabilizers. By the coisotropic embedding theorem, there exists an equivariant symplectomorphism of a neighborhood of \(\varPhi ^{-1}(0)\) in M with a neighborhood of the zero section in
where the quotient is by the diagonal action \(g(v,p) = (R_{g^{-1},* } v, gp)\) and \(R_{g^{-1},*}: T^\vee G \rightarrow T^\vee G\) is induced by the right action of G. The moment map for the action in the local model is
where \(T^\vee G\) is the moment map for the left action of G on \(\phi \). The norm
is identified with the norm on the fibers \(T^\vee S^c\). Thus the function \(\psi \circ \vert \varPhi \vert \) is that in the definition of fibered Dehn twist. The claim follows.
In the case of circle stabilizers, denote the fixed point set of the action of the circle subgroup H of diagonal matrices
The set \(P^H\) is a double cover of \(M {//}G\), since there are two H-fixed points (the poles) in each fiber \(G/H \cong S^2\). The local model in this case is
Since the center \(Z \subset N(H)\) acts trivially on P, we may write
where now \(G/Z \times _{N(H)} P^H\) is a \(G/Z \cong SO(3)\) bundle. The moment map is given by
and the norm is again the Riemannian norm of the cotangent vector in the local model.
\(\square \)
3 Fibered Dehn twists on moduli spaces of flat bundles
This section describes a natural collection of fibered Dehn twists on moduli spaces of flat bundles, which are our motivating examples.
3.1 Moduli spaces of flat bundles
We first recall the construction of symplectic structures on moduli spaces of flat bundles on surfaces with markings, that is, flat bundles on the complement of the markings with holonomies around them in fixed conjugacy classes.
Definition 3.1
-
(a)
(Conjugacy classes in compact 1-connected Lie groups) Let G be a simple compact, 1-connected Lie group, with maximal torus T and Weyl group \(W = N(T)/T\). Let \(\mathfrak {g},\mathfrak {t}\) denote the Lie algebras of G and T. We choose a highest root \(\alpha _0 \in \mathfrak {t}^\vee \) and positive closed Weyl chamber \(\mathfrak {t}_+ \subset \mathfrak {t}\). Conjugacy classes in G are parametrized by the Weyl alcove
$$\begin{aligned} \mathfrak {A}:= \{ \xi \in \mathfrak {t}_+, \ \alpha _0(\xi ) \le 1 \} , \end{aligned}$$see [36]. For any \(\mu \in \mathfrak {A}\), we denote by
$$\begin{aligned} {\mathcal {C}}_\mu = \{ g \exp (\mu ) g^{-1}, \ g \in G \} \end{aligned}$$the corresponding conjugacy class. Inverting each conjugacy class defines an involution
$$\begin{aligned} *: \mathfrak {A}\rightarrow \mathfrak {A}, \quad {\mathcal {C}}_{*\mu } = {\mathcal {C}}_\mu ^{-1} . \end{aligned}$$(11)In the case \(G = SU(2)\), we identify \( \mathfrak {t}\cong \mathbb {R}\) and \( \mathfrak {A}\cong [0,1/2] \) so that
$$\begin{aligned} {\mathcal {C}}_\mu = \{ {\text {Ad}} (g) {\text {diag}}( \exp ( 2\pi i \mu ), -\exp ( 2\pi i \mu )) \} . \end{aligned}$$(12)In particular,
$$\begin{aligned}{\mathcal {C}}_{1/4} = \{ A \in SU(2) \ | \ {\text {Tr}}(A) = 0 \} \end{aligned}$$is the conjugacy class of traceless elements of SU(2).
-
(b)
(Marked surfaces) By a marked surface we mean a compact oriented connected surface X equipped with a collection of distinct points
$$\begin{aligned} \underline{x} = (x_1,\ldots , x_n) \in X^n \end{aligned}$$and a collection of labels
$$\begin{aligned} \underline{\mu } = (\mu _1,\ldots , \mu _n) \in \mathfrak {A}^n . \end{aligned}$$For simplicity, we denote such a surface \((X,\underline{\mu })\).
-
(c)
(Holonomies) Let \(P \rightarrow X\) be a G-bundle equipped with a flat connection \(A \in {\mathcal {A}}(P)\). Parallel transport around loops in X gives rise to a holonomy representation
$$\begin{aligned} \pi _1(X) \rightarrow G . \end{aligned}$$In particular, for any point \(x \in X\) a small loop around x defines a conjugacy class in \(\pi _1(X)\), obtained by joining the loop to a base point, and the holonomy around x is well defined up to conjugacy.
-
(d)
(Moduli spaces of bundles on marked surfaces) Let \((X,\underline{\mu })\) be a marked surface. Let \(M(X,\underline{\mu })\) denote the moduli space of isomorphism classes of flat G-bundles on \(X - \{ x_1,\ldots , x_n \}\) with holonomy around \(x_i\) conjugate to \(\exp (\mu _i)\), for each \(i = 1,\ldots ,n\), see, e.g., Meinrenken and Woodward [31]. If \(M(X,\underline{\mu })\) contains no reducible bundles (bundles with non-central automorphisms), then \(M(X,\underline{\mu })\) is a compact symplectic orbifold.
Remark 3.2
-
(a)
(Action of central bundles) Let Z denote the center of G. Let \(M_Z(X)\) denote the moduli space of Z-bundles on X with trivial holonomy around the markings. The group multiplication on Z induces a group structure on \(M_Z(X)\), isomorphic to \(Z^{2g}\) where g is the genus of X. The action of Z on G induces a symplectic action of \(M_Z(X)\) on \(M(X,\underline{\mu })\)
$$\begin{aligned} M_Z(X) \times M(X,\underline{\mu }) \rightarrow M(X,\underline{\mu }) \end{aligned}$$corresponding to twisting the holonomies by elements of Z.
-
(b)
(Combining central markings) A label \(\mu \in \mathfrak {A}\) is central if \(\exp (\mu )\) lies in the center Z of G. In the case \(G = SU(r)\), the central labels are the vertices of the alcove \(\mathfrak {A}\). Several central labels may be combined into a single central label as follows: Suppose that \(\lambda _1 \in \mathfrak {A}\) resp. \(\lambda _2 \in \mathfrak {A}\) are labels corresponding to \(z_1,z_2 \in Z\), and \(\lambda _{12} \in \mathfrak {A}\) is the label that corresponds to \(z_1z_2 \in Z\). Then there is a symplectomorphism
$$\begin{aligned} M(X,\lambda _1,\lambda _2,\lambda _3, \ldots ,\lambda _n) \rightarrow M(X,\lambda _{12},\lambda _3,\ldots ,\lambda _n) . \end{aligned}$$This follows immediately from the description of the moduli space as representations of the fundamental group as in (17).
Remark 3.3
(Moduli of flat bundles as a symplectic quotient by the loop group) The moduli space of flat bundles may be realized as the symplectic quotient of the moduli space of framed bundles on a cut surface described in [31].
First we introduce notation for the cut surface. Let \(Y \subset X\) be an embedded circle, that is, a compact, oriented, connected one-manifold, disjoint from the markings \(\underline{x}\). Let \(X_{{\text {cut}}}\) denote the surface obtained from X by cutting along Y as in Fig. 1, with boundary components \((\partial X_{{\text {cut}}})_j \cong S^1, j =1,2\). The cut surface \(X_{{\text {cut}}}\) may be disconnected or connected depending on whether Y is separating.
The moduli space of framed flat bundles on the cut surface naturally has an action of two copies of the loop group, acting by changing the framings. Let \(M(X_{{\text {cut}}},\underline{\mu })\) be the moduli space of flat bundles with framings (trivializations) on the boundary of \(X_{{\text {cut}}}\):
Equivalently, in the case of simply connected structure group, \(M(X_{{\text {cut}}},\underline{\mu })\) is the quotient of flat connections by gauge transformations which vanish on the boundary. Working in suitable spaces of completions the moduli space \(M(X_{{\text {cut}}},\underline{\mu })\) is a symplectic Banach manifold, with symplectic form given by the usual pairing of one forms and integration. Let \(LG = {\text {Map}}(S^1,G)\) denote the loop group of G, with multiplication given by pointwise multiplication. Any element \(g \in LG^2\) acts on \(M(X_{{\text {cut}}},\underline{\mu })\) by changing the framing:
The moment map for the action of \(LG^2\) is restriction to the boundary
where \(\tau _\phi : {\mathcal {A}}(P | \partial X_{{{\text {cut}}}}) \rightarrow \Omega ^1(S^1,\mathfrak {g})^2\) is the parametrization of the space of connections induced by \(\phi \). Since the orientations on the two extra boundary circles are opposite, the diagonal action of LG has moment map \(\varPhi \) given by the difference of the moment maps for each boundary component:
Taking the quotient by the diagonal loop group action recovers the moduli space for the original surface: By [31] \(M(X,\underline{\mu })\) is naturally symplectomorphic (on the smooth locus) to the symplectic quotient of \(M(X_{{\text {cut}}},\underline{\mu })\) by the diagonal action of LG, that is,
In particular, the symplectic structure on \(M(X,\underline{\mu })\) descends from a symplectic structure on \(M(X_{{\text {cut}}},\underline{\mu })\).
Locally the loop group actions admit finite-dimensional slices and so the infinite-dimensional quotients above are equivalent to finite-dimensional quotients [31]. In particular, let \(\mathfrak {A}^\circ \subset \mathfrak {A}\) denote the interior of the alcove. For example, for SU(2), we have as in (12)
Let
be the subset consisting of connections of “standard form” \(\xi {\text{ d }}\theta , \xi \in \mathfrak {A}^\circ \) in a neighborhood U of the circle Y. Similar let
The locus \(M(X_{{\text {cut}}},\underline{\mu })^\circ \) is an open subsets of \(M(X_{{\text {cut}}},\underline{\mu })\), dense if non-empty, which is the quotient by the diagonal action of the maximal torus T:
see [31]. More generally, for any face \(\sigma \) of the alcove let \(LG_\sigma \) denote the stabilizer of any point in \(\sigma \). The stabilizer \(LG_\sigma \) is isomorphic to a finite-dimensional subgroup of G via evaluation at a base point. Denote by
the slice for the action of LG on \(L\mathfrak {g}^\vee \) at \(\sigma \). Then
is a Hamiltonian \(LG_\sigma ^2\) space whose quotient
is a dense (if non-empty) open subset of \(M(X_{{\text {cut}}},\underline{\mu })\). As the face \(\sigma \) varies, the collection \( M(X,\underline{\mu })^\sigma \) covers \(M(X_{{\text {cut}}},\underline{\mu })\):
3.2 Symplectomorphisms induced by Dehn twists
Any Dehn twist on a marked surface induces a symplectomorphism of the moduli space of flat bundles. In this section, we explicitly describe this symplectomorphism as the Hamiltonian flow of a non-smooth function.
We begin by setting up notation for symplectomorphisms of moduli spaces induced by diffeomorphisms of the underlying surface. Let \((X,\underline{\mu })\) be a marked surface. Let \({\text {Diff}}^+ \subset {\text {Diff}}(X)\) denote the group of orientation-preserving diffeomorphisms of X and \({\text {Map}}^+(X,\underline{\mu })\) the group of isotopy classes of orientation-preserving diffeomorphisms \(\phi \) of X preserving the labels \(\underline{\mu }\):
The following is elementary and left to the reader:
Proposition 3.4
(Symplectomorphisms associated with mapping class group elements) Pullback defines a homomorphism from \({\text {Map}}^+(X,\underline{\mu })\) to the group of symplectomorphisms \({\text {Diff}}(M(X,\underline{\mu }),\omega )\) of \(M(X,\underline{\mu })\),
In particular, a Dehn twist on the surface induces a symplectomorphism of the moduli space of bundles. Our aim is to describe this symplectomorphism as a Hamiltonian flow of a function relating to the holonomy. The space of connections on the trivial bundle \(S^1 \times G \rightarrow S^1\) may be canonically identified with the space of \(\mathfrak {g}\)-valued one forms
Denote \(\pi :\mathbb {R}\rightarrow S^1\) and let
denote the standard path from \(t_0\) to \(t_1\). Parallel transport along \(\gamma _{t_0,t_1}\) defines a map
Given an embedded oriented circle Y in X disjoint from the markings, we suppose that Y is the image of a path
such that \(\iota |(0,1)\) is an embedding. Let \(\rho _{0,1}\) denote parallel transport once around Y and define
by mapping an equivalence class of flat connections [A] to the conjugacy class of the holonomy of any representative A around Y. The map \(\rho _Y\) is independent of the choice of base point on Y. Let
The function \(h_Y\) is smooth on the inverse image \(\rho _Y^{-1}(\mathfrak {A}^\circ )\) of the interior \(\mathfrak {A}^\circ \) of the Weyl alcove.
Proposition 3.5
(The action of a Dehn twist is a Hamiltonian flow, c.f. [2, Theorem 4.5]) Let \((X,\underline{\mu })\) be a marked surface such that \(M(X,\underline{\mu })\) contains no reducibles, \(Y \subset X\) an embedded circle and \(\tau _Y: X \rightarrow X\) a Dehn twist around Y. Then \(\tau _Y\) acts on \(M(X,\underline{\mu })\) by the time-one Hamiltonian flow of \(h_Y\) on \(\rho _Y^{-1}(\mathfrak {A}^\circ )\). In particular, the time-one Hamiltonian flow of \(h_Y\) extends smoothly to all of \(M(X,\underline{\mu })\).
The idea of the proof is to describe the twist upstairs on the moduli space of the cut surface and then descend to the glued surface. Recall from Remark 3.3 that the moduli space \(M(X_{{\text {cut}}},\underline{\mu })\) has an \(LG^2\)-action. In particular, the action of \(LG^2\) restricts to an action of the subgroup of constant loops \(G^2\). For \([A] \in M(X_{{\text {cut}}},\underline{\mu })\), the notation
indicates the connection obtained by acting by the holonomy \(\rho _{0,1}(A | (\partial X_{{\text {cut}}})_2)\) of the connection on the second component of the boundary \((\partial X_{{\text {cut}}})_2\).
Lemma 3.6
The twist \(\tau _Y\) acts on \(M(X_{{\text {cut}}},\underline{\mu })\) by changing the framing of A by the holonomy along the second boundary component:
Proof
Since a Dehn twist along a circle in a Riemann surface is only defined up to isotopy, we may assume that \(\tau _Y\) is a Dehn twist along a small translation of the boundary component \((\partial X_{{\text {cut}}})_2\). This twist induces a Dehn twist on \(X_{{\text {cut}}}\), also denoted \(\tau _Y\).
Step 1: We show that on the cut surface \(X_{{\text {cut}}}\) the Dehn twist \(\tau _Y\) maps any connection to a gauge equivalent connection. Suppose first that \(X_{{\text {cut}}}\) is connected, and choose a base point \(x_0 \in X_{{\text {cut}}}\). Given a connection A, the connections \(A, (\tau _Y^{-1})^* A\) determine representations of the fundamental group
given by mapping any homotopy class of loops to the holonomy of the connection. The two representations are equal, since the generators of \(\pi _1(X_{{\text {cut}}},x_0)\) have representatives that are disjoint from the support of \(\tau _Y\) (or alternatively, since \(\tau _Y\) is homotopic to the identity). Therefore, \((\tau _Y^{-1})^*A\) is gauge equivalent to A.
Step 2: We compute the gauge transformation relating the two connections above on the boundary. The necessary gauge transformation \(g : X \rightarrow G\) given by the difference in parallel transports of A and \((\tau _Y^{-1})^* A\). For any \(x \in X_{{\text {cut}}}\), choose a path \(\gamma _x\) from \(x_0\) to x and let \(\rho ^A(\gamma _x) \in G\) denote parallel transport along \(\gamma _x\) using the connection A, and similarly for the pullback connection \((\tau _Y^{-1})^* A\). Define a gauge transformation
The gauge transformed connection gA has parallel transport along \(\gamma _x\) given by
Therefore,
To compute the gauge transformation g, denote by
parallel transport from 0 to t along the boundary \((\partial X_{{\text {cut}}})_2 \cong S^1\). Define a path from \(x_0\) to \(x_2\) on the boundary, identified with \(t \in S^1\) by concatenating a path from \(x_0\) to \(x_1\) and a path from 0 to t in \(S^1\). The parallel transports of A resp. \((\tau _Y^{-1})^* A\) are
It follows that (18) is given at points t on the second boundary component \((\partial X)_2 \cong S^1 \) by
Step 3: We identify the gauge transformation on the boundary with the loop group element in the statement of the Lemma. We simplify the formula (19) as follows. After gauge transformation, we may assume that the restriction of A to \((\partial X_{{\text {cut}}})_2 )\) is of the form \(\xi _2 {\text{ d }}\theta \), for some \(\xi _2 \in \mathfrak {g}\). The set of group elements \(\rho _{0,t} = \exp ( t \xi _2)\) forms a one-parameter subgroup and \(\rho _{0,t}\) and \(\rho _{0,1}\) commute. Hence
as claimed. The case that \(X_{{\text {cut}}}\) is disconnected is similar, using that \(\tau _Y\) is trivial on one of the components. \(\square \)
Proof of Proposition 3.5
By Lemma 3.6, the restriction of \((\tau _Y^{-1})^*\) to \(M(X_{{\text {cut}}},\underline{\mu })^\circ \) of (14) has the form
Thus the action of \(\tau _Y\) is given by the time-one Hamiltonian flow of the function
The Proposition follows since the restriction of \(\tilde{h}_Y\) to the zero-level set in \(M(X_{{\text {cut}}},\underline{\mu })\) is a lift of \(h_Y\). \(\square \)
For later use, we recall the following facts about level sets of holonomy maps. These facts follow from the gluing equals reduction principle in Meinrenken-Woodward [31, Section 3.4]. We recall the involution \(* :\mathfrak {A}\rightarrow \mathfrak {A}\) from (11). Let \(X_{{\text {cap}}}\) denote the surface obtained from \(X_{{\text {cut}}}\) capping off with a pair of disks, with an additional marked point on each disk, as in Fig. 1.
Lemma 3.7
(Quotients of holonomy level sets) Let \((X,\underline{\mu })\) be a marked surface, and \(Y \subset X\) an embedded circle. For any \(\lambda \in \mathfrak {A}\), let \(G_{\exp (\lambda )}\) denote the centralizer of \(\exp (\lambda )\). The product \(G_{\exp (\lambda )} \times G_{\exp (\lambda )}\) acts on \( \varPhi _1^{-1}(\lambda ) \times \varPhi _2^{-1}(\lambda ) \) with diagonal quotient resp. full quotient
If all points in the level set of \((\lambda ,\lambda )\) have the same stabilizer \(H \subset G_{\exp (\lambda )}^2\) up to conjugacy, then
is a \(G_{\exp (\lambda )} \backslash G^2_{\exp (\lambda )}/H\)-fiber bundle and equips \(\rho ^{-1}_Y(\lambda )\) with the structure of a fibered coisotropic.
3.3 Full twists for rank two bundles
In this section, we show that Dehn twists on a surface induce fibered Dehn twists of the moduli space of flat rank two bundles with trivial determinant. The following is a slight generalization of a result of Callahan (unpublished) resp. Seidel [39, Section 1.7] in the case of a separating resp. non-separating curve on a surface.
Theorem 3.8
(For \(G = SU(2),\) Dehn twists on the surface act by fibered Dehn twists on the moduli space) Suppose \(G = SU(2)\), and \((X,\underline{\mu })\) is a marked surface such that \(M(X,\underline{\mu })\) contains no reducibles. Let \(Y \subset X\) be an embedded circle.
-
(a)
(Separating case gives a codimension one Dehn twist) If Y is separating then \(\tau _Y\) acts on \(M(X,\underline{\mu })\) by a fibered Dehn twist along the fibered coisotropic
$$\begin{aligned} C_\lambda := \rho _Y^{-1}(\lambda ) \end{aligned}$$for any \(\lambda \in (0,{\frac{1}{2}})\) such that \(M(X,\underline{\mu },\lambda ,*\lambda )\) contains no reducibles.
-
(b)
(Non-separating case gives a codimension three Dehn twist) If Y is non-separating and \(M(X_{{{\text {cap}}}},\underline{\mu })\) contains no reducibles, then \(\tau _Y\) acts by a fibered Dehn twist along the fibered coisotropic
$$\begin{aligned} C_{1/2} := \rho _Y^{-1}(1/2) \end{aligned}$$of bundles with holonomy along Y equal to \(\exp (1/2)= -I \in SU(2)\).
Proof
We have already expressed the action of the Dehn twist as the action of holonomy in Proposition 3.5. It remains to identify these flows as Dehn twists in the rank two case. For this, it suffices as in Theorem 2.12 to show that the corresponding Dehn twists induce equivariant Dehn twists on the moduli space of the cut surface.
Step 1: we compute the generic stabilizers, in order to establish that the level sets in the statement are fibrations, and examine the action of the Dehn twists on the level sets. By the irreducible-free assumption, the generic stabilizer of the \(LG^2\) action on \(M(X_{{\text {cut}}},\underline{\mu })\) is canonically identified with \(Z^{\# \pi _0(X_{{\text {cut}}})}\), where Z is the center of G and \(\# \pi _0(X_{{\text {cut}}})\) is the number of components; the identification is via evaluation at any point on the boundary. By Lemma 3.7, the level set \(\rho _Y^{-1}(\lambda ) \) with \( \lambda \in (0,1/2)\) resp. \(\lambda = 1/2\) is a fibered coisotropic with fiber
in the non-separating case and
in the separating case. Explicitly, the latter isomorphism is given by
Step 2: We establish the Theorem in the separating case. We write the moduli space as a finite-dimensional quotient in a neighborhood of the fibered coisotropic in the statement. Denote the subset with generic holonomy
Since \(M(X_{{\text {cut}}},\underline{\mu })^\circ \) has a \(T \times T\)-action, there is a residual T-action on \(M(X,\underline{\mu })^\circ \) with generic stabilizer \(Z^{\# \pi _0(X_{{\text {cut}}}) - 1}\). The action of \(\tau _Y\) on \(M(X,\underline{\mu })^\circ \) is Hamiltonian isotopic to a symplectomorphism given by Proposition 3.5 as the Hamiltonian flow of \(\rho _Y^2/2\) on the complement of \(\rho _Y^{-1}(0), \rho _Y^{-1}(1/2)\).
We use a small Hamiltonian deformation to construct a symplectomorphism that is supported on a neighborhood of a fibered coisotropic. Let \(\sigma = \{ 1/2 \} \subset \mathfrak {A}\) denote the endpoint of the alcove. By (16), a neighborhood of \(\rho _Y^{-1}(1/2)\) is the symplectic reduction in a neighborhood of a cross section for \( \varPhi _1^{-1}(1/2) \times \varPhi _1^{-1}(1/2) \subset M(X_{{{\text {cut}}}},\underline{\mu })\) by a diagonal G action. More precisely, evaluation a base points defines an isomorphism \( LG^2_{(1/2,1/2)} \cong G^2\). The maximal slice at (1 / 2, 1 / 2) is
Then the quotient of \( M(X_{{\text {cut}}},\underline{\mu })_\sigma = (\varPhi _1 \times \varPhi _2)^{-1}(\mathfrak {A}^2_\sigma )\) by \(LG_\sigma \cong G\) is a neighborhood of \(\rho _Y^{-1}(1/2)\). The function \( \varPhi _2^2/2 - ( \varPhi _2/2 - 1/8) \) on \(M(X_{{\text {cut}}},\underline{\mu })^\circ \) is equal to the restriction of the function \(\Vert \varPhi _2 - 1/2 \Vert ^2/2\) on \(M(X_{{{\text {cut}}}},\underline{\mu })_{1/2}\) which is smooth. Let
be an cutoff function equal to 1 near \(\rho _Y^{-1}(1/2)\) and supported in a small neighborhood of \(\rho _Y^{-1}(1/2)\). The function
has as smooth extension to \(M(X,\underline{\mu })\), which agrees with the action of \((\tau _Y^{-1})^*\) near \(\rho _Y^{-1}(1/2)\) since the time-one flow of \(\rho _Y/2 - 1/8\) is the identity. Hence composing the action of \((\tau _Y^{-1})^*\) with this flow yields an equivariant symplectomorphism that is the identity near \(\rho _Y^{-1}(1/2)\), and is Hamiltonian isotopic to the original symplectomorphism. A similar modification produces a equivariant Hamiltonian perturbation of \((\tau _Y^{-1})^*\) that is the identity near \(\varPhi _2^{-1}(0)\).
It now follows from the results on equivariant Dehn twists that the Dehn twist on the surface acts by a fibered Dehn twist on the moduli space. That is, \((\tau _Y^{-1})^*\) is a Dehn twist along any \(\varPhi _2^{-1}(\lambda ) \subset M(X_{{\text {cut}}},\underline{\mu })^\circ \) for \(\lambda \) generic. By Proposition 2.15, \((\tau _Y^{-1})^*\) acts as an equivariant Dehn twist on \(M(X_{{\text {cut}}},\underline{\mu })^\circ \). By Theorem 2.12, the action of \((\tau _Y^{-1})^*\) descends to a fibered Dehn twist on \(M(X,\underline{\mu })\).
Step 3: We establish the Theorem in the non-separating case. As before, a neighborhood of the coisotropic is given as a symplectic reduction in a finite-dimensional manifold. The level set
is an equivariant fibered coisotropic in the finite-dimensional manifold U since it is the zero-level set of a moment map for a free action. Lemma 3.6 shows that \((\tau _Y^{-1})^*\) is an equivariant fibered Dehn twist around \({\widetilde{C}}_{1/2}\). Again a Hamiltonian perturbation gives a symplectomorphism that acts by the identity on a neighborhood of \(\rho _Y^{-1}(0)\). It follows from Theorem 2.12 that \((\tau _Y^{-1})^*\) acts on \(M(X,\underline{\mu })\) by a fibered Dehn twist around \(C_{1/2} = {\widetilde{C}}_{1/2} {//}G\). \(\square \)
3.4 Half twists for rank two bundles with fixed holonomies
In this section, we show that a half twist on a marked surface \((X,\underline{\mu })\) induces a fibered Dehn twist on the moduli space \(M(X,\underline{\mu })\) of flat \(G = SU(2)\) bundles with fixed holonomy.
Definition 3.9
(Half twist and corresponding coisotropic) Given a pair of points \(x_i,x_j \in X\) with the same label \(\mu _i = \mu _j\), let Y denote a circle around \(x_i,x_j\) and
a half twist along Y that interchanges \(x_i,x_j\). Denote the coisotropic of bundles with trivial holonomy along Y
Example 3.10
(Moduli spaces of flat bundles on the sphere punctured five times) Let \(X = S^2\) with five markings \(x_1,\ldots , x_5\) all with labels \(1/4 \in \mathfrak {A}\). The moduli space of flat bundles
is real dimension four. The real manifold \(M(X,\underline{\mu })\) admits the structure of a del Pezzo surface obtained by blowing up the projective plane at four points. This fact follows from the existence of a Kähler structure by the Mehta–Seshadri theorem [30], and computing its homology by any number of standard techniques and noting the rationality of the moduli space or by the more detailed discussion in [24]. The submanifold \(C_Y\) from (3.9) given by a loop Y around the ith and jth marking is a Lagrangian sphere described as bundles whose holonomy along a loop containing the ith and jth markings is the identity:
The intersection diagram of these Lagrangians reproduces the root system \(A_4\) corresponding to the fifth del Pezzo, discussed in general in Manin [26]. After choosing suitable generators for the fundamental group, we may assume that i, j are adjacent. The moduli space \(M(X,\underline{\mu })\) can be described as the moduli space of closed spherical polygons in \(S^3 \cong SU(2)\) with side lengths \(\pi \) and vertices
The submanifold \(C_Y\) consists of closed spherical polygons of side lengths \(\pi \) such that the i and jth edges are opposite. That is, the polygon consists of a bigon and a triangle as in Fig. 2. Let \(Y_{i(i+1)}, Y_{(i-1)i} \subset X \) be small circles around the pairs consisting of \(i,i+1\) resp. \(i-1,i\)th markings. The intersection \(C_{Y_{i(i+1)}}, C_{Y_{(i-1)i}}\) is the configuration where the bigon is coincident with the \(i+1\)th edge of the triangle as in Fig. 3, see [47, Section 5] for more discussion. More generally, in the case of \(2n+1\) markings, the coisotropics \(C_{ij}\) consist of configurations composed of a bigon and an \(2n-1\)-gon; each is \(S^2\)-fibered over the moduli space with \(2n-1\) markings by forgetting the bigon. Applied to the case \(X = S^2\) with five markings, this construction gives a lift of generators of the action of the Weyl group \(S_4\) (the symmetric group on five letters) of type \(A_4\) on homology to Dehn twists on the fifth del Pezzo. A lift of the action to the braid group is discussed in Seidel [38].
The following is slight generalization of a result of Seidel [39].
Theorem 3.11
(For \(G = SU(2)\) half twists around pairs of markings act by codimension two fibered Dehn twists on the moduli space) Let \(G = SU(2)\). Let \((X,\underline{\mu })\) be a marked surface such that \(M(X,\underline{\mu })\) contains no reducibles and \(\mu _i = \mu _j = 1/4\). Let \(Y \subset X\) be an embedded circle disjoint from the markings that is the boundary of a disk containing \(x_i,x_j\). Then the set \(C_Y\) from (3.9) is a spherically fibered coisotropic submanifold of codimension 2, and the action of \({\tau _Y}\) on \(M(X,\underline{\mu })\) is a fibered Dehn twist along \(C_Y\).
Proof
First show that \(M(X, \underline{\mu } - \{ \mu _i, \mu _j \})\) is smooth, or equivalently, contains no reducible representations. Indeed, note that the stabilizers of
range over all one-parameter subgroups of SU(2). Hence if some point in \(M(X, \underline{\mu } - \{ \mu _i, \mu _j \})\) has a one-parameter group of automorphisms, then there is also a point in \(M(X,\underline{\mu })\) with a one-parameter group of automorphisms. Since \(M(X,\underline{\mu })\) contains no reducibles, \(M(X, \underline{\mu } - \{ \mu _i, \mu _j \})\) also contains no reducibles.
By Lemma 3.7, the constancy of generic stabilizer implies the existence of a fibered coisotropic. Let
denote the surface obtained by cutting X into two components \(X_{{{\text {cut}}},1}, X_{{{\text {cut}}},2}\) along Y, so that \(X_{{{\text {cut}}},2}\) contains the markings \(x_i,x_j\). The generic stabilizer H from (3.9) is the product of stabilizers for the two factors, since Y is disconnecting: The center \(Z = \mathbb {Z}_2\) for \(M(X_{{{\text {cut}}},1}, \underline{\mu } - \{ \mu _i, \mu _j \})\) by the previous paragraph, and the maximal torus U(1) for the right factor \(M(X_{{{\text {cut}}},2}, \mu _i, \mu _j)\). By 3.7 \(C_Y \subset M(X,\underline{\mu })\) from (3.9) is a fibered coisotropic of codimension 2 with fiber
To describe the action of the half twist, we first describe the action of the half twist on the moduli space of the cut surface. By restriction an element of \(M(X_{{\text {cut}}},\underline{\mu })\) gives a flat connection on the twice-punctured disk \(X_{{{\text {cut}}},2} - \{x_i, x_j \}\), with holonomies \(g_i,g_j\) around the punctures. We choose convenient representatives for \(g_i,g_j\) as follows. Let
be a representative of the non-trivial element w of the Weyl group \(W \cong \mathbb {Z}_2\). The inverse is
Furthermore, the stabilizer \(G_n\) acts on \({\mathcal {C}}_{1/4}\) by rotation fixing n and \(n^{-1}\). The set nT is diffeomorphic to a circle passing through n. Thus after conjugating \(g_i,g_j\) by some \(g \in G\), we may assume
for some \(t \in T\). We compute the action of the half twist on the holonomies: For the ith holonomy
(the square root is unique up to an element of the center, which acts trivially). On the other hand, for the jth holonomy
This shows that \({\tau _Y}\) acts on \(g_i,g_j\) by conjugation by \( {\text {Ad}} ( (- g_i g_j)^{{\frac{1}{2}}})\). As in the case of a full twist, this implies that \((\tau _Y^{-1})^*A\) is gauge equivalent to the connection obtained from A by acting by \((1, (-g_i g_j)^{{\frac{1}{2}}})\).
We write a neighborhood of the fibered coisotropic as a finite-dimensional symplectic reduction. Let \(\sigma = \{ 0 \}\) denote the endpoint of the alcove. By (15)
is a neighborhood of \(C_Y\). Restricted to \(M(X_{{\text {cut}}},\underline{\mu })^\sigma \), \(|\varPhi _2|/2\) gives a real-valued function whose Hamiltonian flow is the action of \(-I\). Hence \(|\varPhi _2|/4\) has Hamiltonian flow given by the action of \((-I)^{1/2} = \exp (1/4)\). Similarly \(|\varPhi _2|^2/4\) has Hamiltonian flow given by the action of \((g_ig_j)^{1/2}\). Combining these remarks shows that the action of \(\tau _Y\) on \(M(X_{{\text {cut}}},\underline{\mu })^\sigma \) is the time-one Hamiltonian flow of \(|\varPhi _2| (|\varPhi _2| + 1)/4\), and the level set \(\varPhi _2^{-1}(0)\) is an equivariant fibered coisotropic. By using a cutoff function as in (20), the action of \(\tau _Y\) is Hamiltonian isotopic to an equivariant Dehn twist along \(\varPhi _2^{-1}(0)\). The proof is completed by applying Theorem 2.12. \(\square \)
3.5 Half twists for higher-rank bundles
For special labels, a half twist on the marked surface X induces a fibered Dehn twist on the moduli space of flat SU(r) bundles with fixed holonomy.
Definition 3.12
(Khovanov–Rozansky modification on moduli spaces) Let \(r \ge 2\) and let \(\omega _k \in \mathfrak {A}, \ k = 0,\ldots , r-1\) denote the vertices of the alcove. We identify \(\mathfrak {g}\) with \(\mathfrak {g}^\vee \) using the basic inner product for which the roots have norm-square equal to 2. Under this identification \(\omega _0 = 0\) while
are the fundamental weights of \(G = SU(r)\). Let \(\underline{\mu } = (\mu _1, \ldots ,\mu _n)\) be a collection of labels with
for some i, j, k. (That is, \(\mu _i,\mu _j\) equal the midpoint \(\nu _k^1\) of the edge of \(\mathfrak {A}\) connecting the kth vertex with the \(k+1\)-st vertex.) Let \(C_Y\) be the subset of \(M(X,\underline{\mu })\) defined by
where \(\nu _k^2\) is the midpoint between the vertices \(\omega _k,\omega _{k+2}\) of the alcove \(\mathfrak {A}\),
For example,
while
Denote by
the moduli space of flat bundles on X with labels obtained by removing \(\mu _i,\mu _j = \nu _k^1\) and adding \(\nu _{k}^2\).
Theorem 3.13
(Codimension two fibered Dehn twists via half twists) Suppose that \(G = SU(r)\) and \(\mu _i,\mu _j, \nu _k^1,\nu _k^2\) are as in Definition 3.12 such that the moduli spaces \(M(X,\underline{\mu })\) and \(M(X,\underline{\mu },(\mu _i,\mu _j) \mapsto \nu _k^2 )\) contain no reducibles. Let \(Y \subset X\) denote an embedded circle enclosing only the ith and jth markings. Then the subset \(C_Y\) from (21) is a spherically fibered coisotropic submanifold of codimension 2, fibered over the moduli space \(M(X,\underline{\mu }, (\mu _i,\mu _j) \mapsto \nu _k^2)\). The action of \({\tau _Y}\) on \(M(X,\underline{\mu })\) is a fibered Dehn twist along \(C_Y\).
Proof
First we show that the given level set is a fibered coisotropic. Let \(g_i\) resp. \(g_j\) denote the holonomies around the ith resp. jth marking. The half twist produces a connection with holonomies in which \(g_i,g_j\) have been replaced with \(g_i g_j g_i^{-1}, g_i\). Let \({\mathcal {C}}_1\) denote the conjugacy class of \(\exp (\omega _1/2)\). It suffices to consider the case that \(k = 0\) so that \(g_i,g_j \in {\mathcal {C}}_1\). That is, let
We begin by choosing convenient representatives of \(g_i,g_j\). We may assume
The centralizer of \(g_i\) is therefore
Let
denote the subgroup of real orthogonal rotations in the first two coordinates in \(\mathbb {C}^r\). Since \(g_i\) is the product of \( {\text {diag}}(-1,1\ldots ,1)\) with a central element in U(r), the adjoint action of \(g_i\) on O is given by \(g_i o g_i^{-1} = o^{-1}, o \in O\). So
The conjugacy class \({\mathcal {C}}_1\) is a symmetric space of rank one. In particular, \(Z_{g_i}\) acts transitively on the unit sphere in \(T_{g_i} {\mathcal {C}}_1\). This implies that the map \(O g_i \rightarrow {\mathcal {C}}_1/Z_{g_i}\) is surjective. By conjugating \(g_i,g_j\) by an element of \(Z_{g_i}\), we may choose the second element \(g_j\) so that
The subgroup O is conjugate to the one-parameter subgroup generated by the simple root \(\alpha _1\) (or rather its dual coweight). It follows that the square of \({\mathcal {C}}_1\) in G is given by the union of conjugacy classes
In particular, the conjugacy class \({\mathcal {C}}_2\) of \(\exp (\omega _2/2)\) appears in \({\mathcal {C}}^2_1\) as the orbit of the element
where \(s_1 \in G\) is a representative first simple reflection. The generic stabilizer for the action of G on \({\mathcal {C}}_1 \times {\mathcal {C}}_1\) at the inverse image of \({\mathcal {C}}_2\) is the maximal torus
By Lemma 3.7, \( C_Y \) is a fibered coisotropic with fiber
Next we identify the action of the half twist. On the holonomies, the half twist acts by
Let \(\sigma \) denote the face of \(\mathfrak {A}\) containing \(\omega _2/2\) and \(LG_\sigma \) the stabilizers so that
is an open neighborhood of \(C_Y\) in \(M(X,\underline{\mu })\). Let A be a framed connection on \(X_{{\text {cut}}}\). The pullback connection \((\tau _Y^{-1})^* A\) has the same holonomies as that of \((1,o^{1/2})A\), where \((1,o^{1/2}) \in LG^2\) denotes the constant element of the loop group with values \(1,o^{1/2}\). As in the previous cases, this equality implies that the connections \(A, (\tau _Y^{-1})^* A\) are gauge equivalent.
To identify the gauge transformation, suppose that \(A | (\partial X)_{{{\text {cut}}},2} = \xi {\text{ d }}\theta \) for some \(\xi \in \mathfrak {g}\). The evaluation of the moment map \(\varPhi _2([A]) = \xi \) is related to the holonomies around \(x_i,x_j\) by \( \exp (\xi ) = g_i g_j \), since \(\exp (\xi )\) is the holonomy around the second boundary circle \((\partial X_{{{\text {cut}}}})_2\). Since \(g_i^2 = \exp (\omega _1)\), we have
By (22), the image of \(M(X_{{\text {cut}}},\underline{\mu })^\circ \) under \(\varPhi _2\) is the interval with endpoints \(\omega _1,\omega _2/2\), see Fig. 4 for the SU(3) case. It follows that the action of the half twist is the Hamiltonian flow of the function on \(M(X_{{{\text {cut}}}},\underline{\mu })\) whose restriction to \(M(X_{{{\text {cut}}}},\underline{\mu })^\circ \) is \( (\varPhi _2,\alpha _1)^2/2 - (\varPhi _2, \omega _1/2)\). An argument using cutoff functions as in (20) shows that the half twist is an equivariant fibered Dehn twist along \(\varPhi _2^{-1}(\omega _2/2)\). The claim follows from Theorem 2.12. \(\square \)
4 Pseudoholomorphic sections of Lefschetz–Bott fibrations
In this section, we describe the relative invariants associated with Lefschetz–Bott fibrations. These are maps between Lagrangian Floer cohomology groups obtained by counting pseudoholomorphic sections.
4.1 Monotone Lagrangian Floer cohomology
Novikov rings are not needed to define Lagrangian Floer cohomology for a monotone pair of Lagrangian submanifolds. However, we will need our cochain complexes to admit “action filtrations.” For this, we find it convenient to use the version incorporating a formal variable keeping track of area, as in the construction of the spectral sequence in Fukaya et al. [12].
Definition 4.1
(Monotonicity conditions)
-
(a)
(Symplectic backgrounds) Fix a monotonicity constant \(\lambda \ge 0\) and an even integer \(N > 0\). A symplectic background is a tuple \((M,\omega ,b,{\text {Lag}}^N(M))\) as follows.
-
(i)
(Bounded geometry) \((M,\omega )\) is a compact smooth symplectic manifold with either empty or convex boundary;
-
(ii)
(Monotonicity) \(\omega \) is \(\lambda \)-monotone, i.e., \([\omega ] = \lambda c_1(TM)\);
-
(iii)
(Background class) \(b \in H^2(M,\mathbb {Z}_2)\) is a background class, which will be used for the construction of orientations; and
-
(iv)
(Maslov cover) \({\text {Lag}}^N(M) \rightarrow {\text {Lag}}(M)\) is an N-fold Maslov cover such that the induced twofold Maslov covering \({\text {Lag}}^2(M)\) is the oriented double cover.
We often refer to a symplectic background \((M,\omega ,b,{\text {Lag}}^N(M))\) as M.
-
(i)
-
(b)
(Monotone Lagrangians) A Lagrangian \(L \subset M \backslash \partial M\) is monotone if there is an area-index relation for disks with boundary in L, that is,
$$\begin{aligned} A(u) = \frac{\lambda }{2} I(u) , \quad \forall u: (D,\partial D) \rightarrow (M,L), \end{aligned}$$where \(A(u) = \langle [\omega ], [u] \rangle \) (the pairing of \([\omega ] \in H^2(M,L)\) with \([u] \in H_2(M,L)\)) is again the symplectic area and I(u) is the Maslov index of u as in [29, Appendix].
-
(c)
(Monotone tuples of Lagrangians) A tuple \((L_b)_{b\in {\mathcal {B}}}\) of Lagrangians in M is monotone if the following holds: Let S be any compact surface with boundary given as a disjoint union of one-manifolds \(C_b\)
$$\begin{aligned} \partial S=\sqcup _{b\in {\mathcal {B}}} C_b \end{aligned}$$(with \(C_b\) possibly empty or disconnected). Then for some constant \(c(S,M, (L_b)_{b \in {\mathcal {B}}})\) independent of u,
$$\begin{aligned} A(u) = \frac{\lambda }{2} \cdot I(u) + c(S,M,(L_b)_{b \in {\mathcal {B}}}), \quad \forall u:(S, ( C_b)_{b \in {\mathcal {B}}}) \rightarrow (M, (L_b)_{b \in {\mathcal {B}}}) \end{aligned}$$(24)where I(u) is the sum of the Maslov indices of the totally real subbundles \((u|_{C_b})^*TL_b\) in some fixed trivialization of \(u^*TM\). There is a similar definition of monotonicity for tuples of Lagrangian correspondences [45].
-
(d)
(Admissible Lagrangians) As mentioned in the Introduction, we say that a compact monotone Lagrangian submanifold L is admissible if the image of the fundamental group of L in M is torsion and L has minimal Maslov number at least 3. One may also allow the case that L has minimal Maslov number 2 and disk invariant (number of disks passing through a generic point) 0. However, the Maslov index 2 case is discussed separately in 5.3. Any tuple of admissible, monotone Lagrangians is automatically monotone, by the argument in Oh [32]. This argument involves completing each boundary component of the surface by adding a disk obtained by contracting a loop, possibly after passing to a finite cover. Products of admissible Lagrangians are also automatically admissible. Thus if \(L^0,L^1\) resp C. are admissible Lagrangians in M resp. \(M^- \times B\) then the tuples \((L^0,L^1)\), \((L^0 \times C, C^t \times L^1)\) are monotone.
-
(e)
(Generalized Lagrangian correspondences) Let \(M,M'\) be symplectic manifolds. A generalized Lagrangian correspondence \(\underline{L}\) from M to \(M'\) consists of
-
(i)
a sequence \(N_0,\ldots ,N_r\) of any length \(r+1\ge 2\) of symplectic manifolds with \(N_0 = M\) and \(N_r = M'\) ,
-
(ii)
a sequence \(L_{01},\ldots , L_{(r-1)r}\) of compact Lagrangian correspondences with \(L_{(j-1)j} \subset N_{j-1}^-\times N_{j}\) for \(j=1,\ldots ,r\).
Let \(\underline{L}\) from M to \(M'\) and \(\underline{L}'\) from \(M'\) to \(M''\) be two generalized Lagrangian correspondences. Then we define concatenation
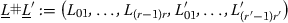
as a generalized Lagrangian correspondence from M to \(M''\). Moreover, we define the dual
$$\begin{aligned} \underline{L}^t := \bigl (L_{(r-1)r}^t,\ldots ,L_{01}^t\bigr ) . \end{aligned}$$as a generalized Lagrangian correspondence from \(M'\) to M. A generalized Lagrangian is called admissible if each component is.
-
(i)
-
(f)
(Lagrangian branes) Generally speaking, a Lagrangian brane means a Lagrangian with extra structure sufficient for the definition of Floer cohomology. In particular, a grading of a Lagrangian submanifold \(L \subset M\) is a lift of the canonical section \(L \rightarrow {\text {Lag}}(M)\) to \({\text {Lag}}^N(M)\), as in Seidel [40]. A brane structure on a connected Lagrangian L consists of a grading and a relative spin structure for the embedding \(L \rightarrow M\) (equivalent to a trivialization of \(w_2(M)\) in the relative chain complex for (M, L), see, e.g., [48]). A Lagrangian brane is an oriented Lagrangian submanifold equipped with a brane structure. A generalized Lagrangian brane is a generalized Lagrangian correspondence equipped with a brane structure.
We define Floer cochains as formal sums of perturbed intersection points. Let \((L^0,L^1)\) be a compact, monotone pair of Lagrangian branes in M. Choose a Hamiltonian \(H \in C^\infty ([0,1] \times M)\) and denote by \(\phi _t \in {\text {Diff}}(M,\omega )\) the time t flow of the Hamiltonian vector field \(H^\# \in {\text {Map}}([0,1],{\text {Vect}}(M))\). Choose H satisfying the condition that \(\phi _1(L^0)\) intersects \(L^1\) transversally. Define the set of perturbed intersection points
The gradings on \(L^0,L^1\) induce a degree map
given by the Maslov index of a path from the lifts in the Maslov cover [40]. By the assumption on the Maslov cover, the mod 2 degree is determined purely by the orientations. That is, the mod 2 degree is 0 resp. 1 if the two Lagrangians meet positively resp. negatively after perturbation. The generalized intersection points decompose into subsets of intersections points with fixed index:
Denote the space of time-dependent \(\omega \)-compatible almost complex structures
Given
as above, we say that a map \(u: \mathbb {R}\times [0,1] \rightarrow M\) is (J, H)-holomorphic iff
For any \(x_\pm \in {\mathcal {I}}(L^0,L^1)\), we denote by \( {\mathcal {M}}(x_-,x_+)\) the space of finite energy (J, H)-holomorphic maps modulo translation in \(s\in \mathbb {R}\), and \({\mathcal {M}}(x_-,x_+)_0\) the subset of formal dimension 0, that is, index 1. The relative spin structures on \(L^0,L^1\) induce a map
measuring the difference between the orientation on each element u and the canonical orientation of a point [42, 48]. The Floer cochain complex is the direct sum
The Floer coboundary operator \( \partial : \ CF(L^0,L^1) \rightarrow CF(L^0,L^1) \) is
For the following, see [12, 32].
Proposition 4.2
(Construction of Floer cohomology) Let M be a symplectic background, \(L^0,L^1\) admissible Lagrangian branes and H a time-dependent Hamiltonian making the intersection transverse. There exists a comeager subset \({\mathcal {J}}^{{\text {reg}}}_t(M) \subset {\mathcal {J}}_t(M)\) such that every Floer trajectory is regular. In this case, the Floer coboundary \(\partial \) is well defined and satisfies \(\partial ^2 = 0\). The Floer cohomology
is independent of the choice of H and J, up to isomorphism.
We wish for our Floer cochain complexes to admit action filtrations. To obtain these filtrations, we pass to versions over Floer cochains over polynomials in a formal variable. Namely let
denote the space of sums of real powers of a formal variable q. In this paper, we do not need to complete \(\Lambda \), that is, the Novikov ring is not needed. The Floer cochain complex over the coefficient ring \(\Lambda \) is the direct sum
with coboundary incorporating the energies of trajectories: Let \(H_t^\# \in {\text {Vect}}(M), t \in [0,1]\) be the Hamiltonian vector field of H and
the perturbed energy. Then
As before, the Floer cohomology with \(\Lambda \) coefficients
is independent of the choice of H and J, up to isomorphism of graded \(\Lambda \)-modules. More generally, for any admissible generalized Lagrangian correspondence \(\underline{L}\) from a point to a point there is [45] a quilted Floer cohomology group \(HF(\underline{L};\Lambda )\) defined by counting quilted strips.
Remark 4.3
(Specialization) In the monotone setting the natural map
is an isomorphism for any nonzero \(\mu \). Indeed, for any generators \(x, y \in {\mathcal {I}}(L^0,L^1)\) let c(x, y) be the constant in the monotonicity relation for strips from x to y as in (24). Choose a base point \(x \in {\mathcal {I}}(L^0,L^1)\) and consider the map of \(\Lambda \)-modules
Additivity of index and energy implies that
Hence for any intersection point \(y \in {\mathcal {I}}(L^0,L^1)\),
where \(\partial _1\) is obtained from \(\partial \) by setting \(q =1\). It follows that the coboundary for \(HF(L^0,L^1)\) is, up to an automorphism, equal to the coboundary for \(HF(L^0,L^1;\Lambda )\) up to a rescaling by a power of q. The claim follows.
For later use, we recall a basic fact about approximate intersection points.
Lemma 4.4
Suppose that M is a compact Riemannian manifold and \(L^0,L^1 \subset M\) are compact submanifolds. For any \(\epsilon > 0\), there exists an \(\delta > 0\) such that if \(m \in M\) is a point with \(d(m,L^0) < \delta \) and \(d(m,L^1) < \delta \), then \(d(m, L^0 \cap L^1) < \epsilon \).
Proof
Suppose otherwise. Then there exists an \(\epsilon >0\), a sequence \(\delta _\nu \rightarrow 0\) and a sequence \(m_\nu \in M\) with
By compactness of M, after passing to a subsequence we may assume that \(m_\nu \) converges to a point m, necessarily in \(L^0\) and \(L^1\). Then
This is a contradiction. \(\square \)
It follows that any map that is sufficiently close to both \(L^0\) and \(L^1\) at every point in the domain is in fact contained in a small neighborhood of \(L^0 \cap L^1\).
4.2 Relative invariants for Lefschetz–Bott fibrations
We may now associate with Lefschetz–Bott fibrations over surfaces with strip-like ends relative invariants that are morphisms of Floer cohomology groups associated with the ends, given by counting pseudoholomorphic sections. The following material can also be found, in a slightly different form, in Perutz [34].
Definition 4.5
(Monotonicity for Lefschetz–Bott fibrations) Let S be a surface without boundary or strip-like ends, and \(\pi : \, E \rightarrow S\) a symplectic Lefschetz–Bott fibration. Let
denote the set of smooth sections of E.
-
(a)
Given \(u \in \Gamma (E)\) with image disjoint from the critical set define its index and symplectic area
$$\begin{aligned} I(u) = 2(c_1( u^* T^{{\text {vert}}} E),[S]), \ \ \ A(u) = \int _S u^* \omega _E . \end{aligned}$$Note that the form \(\omega _E\) is only fiberwise symplectic. Thus the area A(u) may be negative, in the general case.
-
(b)
A symplectic Lefschetz–Bott fibration E is monotone with monotonicity constant \(\lambda \ge 0\) if there exists a constant c(E) such that
$$\begin{aligned} \lambda I(u) = 2 A(u) + c(E) \quad \forall u \in \Gamma (E) . \end{aligned}$$
Remark 4.6
(Behavior of the monotonicity constants under shifts) Given a symplectic Lefschetz–Bott fibration \((\pi : E \rightarrow S, \omega _E)\) and a non-negative, compactly supported two-form \(\omega _S \in \Omega ^2_c(S)\), another Lefschetz–Bott fibration may be constructed by replacing \(\omega _E\) with \(\omega _E + \pi ^* \omega _S\). The symplectic area of any section changes under this operation by
The monotonicity constant therefore changes by \(-2 \int _S \omega _S\).
Proposition 4.7
Let \(\pi : E \rightarrow S\) be a symplectic Lefschetz–Bott fibration with S, E compact. If the generic fiber M of E is monotone, \(H_1(M) = 0 \) and all vanishing cycles in E have codimension at least 2 then E is monotone.
Proof
We first show that the homology classes of any two sections differ by homology classes in the fibers. For each critical value \(s_i \in S^{{\text {crit}}}\) let \(\rho _i: M \rightarrow E_{s_i}\) denote the map given by symplectic parallel transport. In particular on the vanishing cycles this map collapses the null foliation. We claim that for any two sections \(u_0,u_1 \in \Gamma (E)\), the push forwards \(u_{j,*}[S]\) differ by an element in the span of the homology of the fibers \(H_2(M),H_2(E_{s_i})\). We apply the Leray-Fáry spectral sequence for the map \(\pi :E \rightarrow S\), see Fáry [11, Section 10] and Bredon [7, Section IV.12]. We equip the base with the filtration
The fibers of E are diffeomorphic over each associated graded piece \(\{ s_0,\ldots , s_n \}, S - \{ s_0,\ldots , s_n \} \). Denote by \({\mathcal {H}}_q(M)\) the local system of homology groups with fibers \(H_q(\pi ^{-1}(z)) \cong H_q(M)\) over \(S - \{ s_0,\ldots , s_n \}\). The second page in the spectral sequence is the direct sum of relative homologies of successive spaces in the filtration with values in the homology of the fiber,
Since \(H_1(M) = 0\), the contribution from \(p = q = 1\) vanishes. It follows that degree two homology classes in the total space arise either as homology classes in the generic fibers invariant under monodromy; homology classes in the special fibers; or homology classes of the base. The projection \(\pi _*\) is an isomorphism on the classes of the last type. It follows that the degree 2 part of the kernel of \(\pi _*\) under the projection map is generated by the image of \(H_2(M)\) and \(H_2(E_{s_i})\).
We now show the monotonicity relation, using the spectral sequence for the parallel transport maps to the special fibers. By the previous paragraph, it suffices to check monotonicity evaluated on homology classes of fibers. For this, we show that maps \(\rho _{i,*} : H_2(M) \rightarrow H_2(E_{s_i})\) are surjective. Consider the long exact sequence
where \({\text {Cone}}(\rho _i)\) is the mapping cone on \(\rho _i\). Since \(\rho _i\) is a diffeomorphism away from the vanishing cycle, \({\text {Cone}}(\rho _i)\) admits a deformation retraction to \({\text {Cone}}(p_i)\) where \(p_i: C_i \rightarrow B_i\) is the projection. Since \(C_i = P_i \times _{SO(c+1)} S^c\), we have
where \(\sim \) is the equivalence relation that collapses the section corresponding to the fixed point \((0,\ldots ,0, 1)\). For \(c \ge 2\), the spectral sequence for the fibration \(P_i \times _{SO(c+1)} S^{c+1} \rightarrow B_i\) implies that any degree two homology class arises from a homology class in the base. On the other hand, the base homology classes \(H_2(B_i)\) have trivial image in the cohomology \(H({\text {Cone}}(p_i))\) of the mapping cone. Hence \(H_2({\text {Cone}}(p_i)) = 0\). The long exact sequence (25) implies that \(H_2(M)\) surjects onto \(H_2(E_{s_i})\). \(\square \)
We now wish to allow our Lefschetz–Bott fibrations to have strip-like ends. The monotonicity conditions in this case will be similar, but with additional constants depending on the limits.
Definition 4.8
(Symplectic Lefschetz–Bott fibrations with strip-like ends)
-
(a)
Let S be a complex curve with boundary obtained from a compact curve with boundary \(\overline{S}\) be removing points on the boundary \(z_1,\ldots ,z_n\). A strip-like end for the jth puncture of S is a holomorphic map
$$\begin{aligned}\epsilon _j: [0,\pm \infty ) \times [0,1] \rightarrow S \end{aligned}$$such that \(\exp (2 \pi ( ( \epsilon _j^{-1})_{1} + i (\epsilon _{j}^{-1})_{2} ))\) is a local holomorphic coordinate on the closure of the image of \(\epsilon _j\); the end is called incoming resp. outgoing if the sign is negative resp. positive. A collection of strip-like ends \({\mathcal {E}}\) is a set of strip-like ends, one for each \(j = 1,\ldots , n\). We write \({\mathcal {E}}= {\mathcal {E}}_- \cup {\mathcal {E}}_+\) the union of the incoming and outgoing ends.
-
(b)
A symplectic Lefschetz–Bott fibration over a surface with strip-like ends S with fiber given by a symplectic manifold M is a Lefschetz–Bott fibration \(E \rightarrow S\) with \(S^{{\text {crit}}}\) contained in the interior of S, together with a trivialization
$$\begin{aligned} \varphi _{S,e}: \epsilon _{S,e}^* E \rightarrow (0,\pm \infty ) \times [0,1] \times M \end{aligned}$$for each end \(e \in {\mathcal {E}}\), such that \( \varphi _{s,e}^* \omega _E = \pi _M^* \omega _M \) where
$$\begin{aligned} \pi _M: (0,\pm \infty ) \times [0,1] \times M \rightarrow M \end{aligned}$$is projection on the last factor.
-
(c)
Let S be a surface with strip-like ends and \(\pi : E \rightarrow S\) a symplectic Lefschetz–Bott fibration with fiber M. A Lagrangian boundary condition for E is a submanifold \(F \subset \partial E\) such that
-
(i)
\(\pi |F \) is a fiber bundle over \(\partial S\);
-
(ii)
each fiber \(F_z \subset E_z, z \in \partial S\) is a Lagrangian submanifold;
-
(iii)
for each \(e \in {\mathcal {E}}\) there exist Lagrangian submanifolds \(L^{0,e},L^{1,e} \subset M\) such that F is constant sufficiently close to \(z_e\), that is,
$$\begin{aligned} \varphi _{S,e}(F_{\epsilon _{S,e}(s,j)}) = L^{j,e}, \ \ \ \pm s \gg 0 ; \end{aligned}$$and
-
(iv)
for each \(e \in {\mathcal {E}}\), the intersection \(L^{0,e} \cap L^{1,e}\) is transversal.
-
(i)
Definition 4.9
-
(a)
(Monotonicity condition for Lefschetz–Bott fibrations with boundary) Let S be a compact surface with boundary, (E, F) a bundle with boundary condition, and \(\Gamma (E,F)\) the set of smooth sections \(u: (S,\partial S) \rightarrow (E,F)\). Each \(u \in \Gamma (E,F)\) takes values in the smooth locus of E. By pullback one obtains bundles
$$\begin{aligned} u^* T^{{\text {vert}}}E \rightarrow S, \quad (u | \partial S)^* T^{{\text {vert}}} F \rightarrow \partial S . \end{aligned}$$Taking the Maslov index of this pair gives rise to a Maslov index map
$$\begin{aligned} I: \Gamma (E,F) \rightarrow \mathbb {Z}. \end{aligned}$$We also define the symplectic area
$$\begin{aligned} A: \Gamma (E,F) \rightarrow \mathbb {R}, \ \ u \mapsto \int _S u^* \omega _E, \end{aligned}$$keeping in mind that the form \(\omega _E\) is only symplectic on the fibers. A pair (E, F) monotone with monotonicity constant \(\lambda \) if the index depends linearly on the area; that is,
$$\begin{aligned} \lambda I(u) = 2 A(u) + c(E,F) \quad \forall u \in \Gamma (E,F) \end{aligned}$$(26)for some constant c(E, F).
-
(b)
(Linearized operator) Suppose that S is a surface with boundary and strip-like ends \({\mathcal {E}}= {\mathcal {E}}_- \cup {\mathcal {E}}_+\), and (E, F) a bundle with boundary condition. For any collection
$$\begin{aligned} (x_e \in {\mathcal {I}}(L^{0,e},L^{1,e}))_{e \in {\mathcal {E}}} , \end{aligned}$$let
$$\begin{aligned} \Gamma (E,F;(x_e)_{e \in {\mathcal {E}}}) = \left\{ u \in \Gamma (E) \, \left| \, \quad \begin{array}{c} \lim _{s \rightarrow \pm \infty } u(\epsilon _e(s,t)) = x_e \quad \forall e \in {\mathcal {E}}\\ u |_{\partial S} \in \Gamma (F) \end{array} \right. \right\} \end{aligned}$$denote the space of sections with boundary values in F and asymptotic limits \(x_e\). For sections \(u \in \Gamma (E,F)\) let
$$\begin{aligned} \overline{\partial }u = {\frac{1}{2}}( {\text{ d }}u + J(u) \circ {\text{ d }}u \circ j) = 0 \end{aligned}$$(27)denote the Cauchy–Riemann equation associated with the pair (j, J). The linearized operator
$$\begin{aligned} D_u:\,&\Omega ^0( u^* T^{{\text {vert}}} E,\; u^* T^{{\text {vert}}} F) \rightarrow \Omega ^{0,1}(u^* T^{{\text {vert}}} E), \nonumber \\&\xi \mapsto \frac{d}{dt}|_{t =0} \Pi _{t\xi }^{-1} \overline{\partial }\exp _u(t\xi ) \end{aligned}$$(28)is given by differentiating the Cauchy–Riemann operator along a path \(\exp _u(t\xi )\) of geodesic exponentials and using parallel transport \(\Pi _{t\xi }^{-1}\) back to u. The operator \(D_u\) is Fredholm since the boundary conditions at infinity are assumed transversal.
-
(c)
(Monotonicity condition for Lefschetz–Bott fibrations with strip-like ends) The pair (E, F) is monotone with monotonicity constant \(\lambda \ge 0\) if for any \((x_e)_{e \in {\mathcal {E}}}\) there exists a constant \(c(E,F;(x_e)_{e \in {\mathcal {E}}})\) such that
$$\begin{aligned} \lambda {\text {Ind}}(D_u) = 2 A(u) + c(E,F;(x_e)_{e \in {\mathcal {E}}}) \quad \forall u \in \Gamma (E,F;(x_e)_{e \in {\mathcal {E}}}) . \end{aligned}$$(29)
Proposition 4.10
(Condition for monotonicity of the fiber to imply monotonicity of a fibration with strip-like ends) Let \(E \rightarrow S\) be a symplectic Lefschetz–Bott fibration over a surface with boundary S with connected and simply connected fibers. Let \(F \subset E | \partial S\) be a Lagrangian boundary condition with connected and simply connected fibers. Suppose that the generic fiber of E is monotone and the vanishing cycles of E have codimension at least 2. Then (E, F) is monotone.
Proof
First consider the case without ends. As in Proposition 4.7, any two sections of E differ by a homology sphere \(H_2(E_s)\) in some fiber \(E_s \) of E, and these are generated by classes in the generic fiber by the codimension assumption for which monotonicity holds. In the case with ends, as in [44], one may use gluing to reduce to the case that S has no strip-like ends as in the statement of the Proposition. More precisely, fix a section \(v: S \rightarrow E\) with limits \(\underline{x}_\pm \). View v as a map from the surface \(S^- = (S,-j)\) with complex structure reversed. Then for any other section \(u: S \rightarrow E\) with the same limits, gluing along the strip-like ends produces a section of the doubled surface \(w: S \# S^- \rightarrow E \# E^-\). Then
Since the last three terms are independent of u, this proves the statement of the Proposition.\(\square \)
We now turn to the construction of relative invariants associated with symplectic Lefschetz–Bott fibrations. Let \(\pi : E \rightarrow S\) be such a fibration, equipped as in Definition 2.1 with a complex structure \(j_0\) on a neighborhood of the critical values in S and \(J_0\) on a neighborhood of the critical points in E. In the case that S has ends, we assume furthermore that almost complex structures \(J_e \in {\mathcal {J}}(M)\) are fixed making the moduli spaces of Floer trajectories for that end regular. We wish to extend these to almost complex structures on the entire fibration and base, so that we may define moduli spaces of pseudoholomorphic sections.
Definition 4.11
-
(a)
(Compatible almost complex structures) Let \(\pi : E \rightarrow S\) be a Lefschetz–Bott fibration over a surface with strip-like ends S. A complex structure j on S is compatible with E if \(j = j_0\) in an neighborhood of \(S^{{\text {crit}}}\). An almost complex structure J on E is compatible with \(\pi ,j\) iff
-
(i)
\(J = J_0\) in a neighborhood of \(E^{{\text {crit}}}\);
-
(ii)
\(\pi \) is (J, j)-holomorphic in a neighborhood of \(E^{{\text {crit}}}\), that is, \( J \circ {\text{ d }}\pi = {\text{ d }}\pi \circ j\); and
-
(iii)
\(\omega _E(\cdot ,J \cdot )\) is symmetric and positive definite on \(TE^v_x\), for any \(x \in E\).
-
(iv)
J is equal to fixed almost complex structure \(j \times J_e, e \in {\mathcal {E}}(S)\) on the ends of S in the given trivializations on a neighborhood \(U_e \subset S\) of each end.
Let \({\mathcal {J}}(E)\) denote the set of \((\pi ,j)\)-compatible almost complex structures. To see that \({\mathcal {J}}(E)\) is non-empty, note that the symplectic form defines a connection \( {\text {ker}}(D \pi )^{\omega }\) on \(E \rightarrow S\) away from the singular locus, given by the symplectic perpendicular of the vertical part of the tangent space. First choose j equal to \(j_0\) near the critical values. Then take J to equal j on the horizontal subspace, and any almost complex structure compatible with the symplectic form on the vertical subspace.
-
(i)
-
(b)
(Moduli space of pseudoholomorphic sections) Let \({\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})\) denote the set of finite area sections \(u \in \Gamma (E,F,(x_e)_{e \in {\mathcal {E}}})\) such that u is (j, J)-holomorphic, with limits \((x_e)_{e \in {\mathcal {E}}}\) along the ends.
Theorem 4.12
(Existence of regular almost complex structures for symplectic Lefschetz–Bott fibrations) Suppose that (E, F) is a monotone symplectic Lefschetz–Bott fibration with Lagrangian boundary conditions over a surface S with strip-like ends. There exists a comeager subset \({\mathcal {J}}^{{\text {reg}}}(E) \subset {\mathcal {J}}(E)\) such that
-
(a)
\({\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})\) is a smooth manifold with tangent space at u given by \( {\text {ker}}(D_u)\);
-
(b)
the zero-dimensional component \({\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})_0 \subset {\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})\) is finite;
-
(c)
the one-dimensional component \({\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})_1 \subset {\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})\) has a compactification with boundary
$$\begin{aligned} \bigcup _{(x_e)_{e \in {\mathcal {E}}},f,x_f'} {\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}}, x_f \mapsto x_f')_0 \times {\mathcal {M}}(x_f,x_f')_0 \end{aligned}$$consisting of pairs of a section with bubbled-off trajectory; and
-
(d)
any relative spin structure on (E, F) induces a set of orientations on the manifolds \({\mathcal {M}}(E,F;(x_e)_{e \in {\mathcal {E}}})_0\) that are coherent in the sense that they are compatible with the gluing maps from (c) in the sense that the inclusion of the boundary in (c) has the signs \((-1)^{\sum _{e<f} |x_{e}^-|}\) (for incoming trajectories) and \(-(-1)^{\sum _{e<f} |x_{e}^+|}\) (for outgoing trajectories.)
The proof is similar to that of [41] in the exact case. Bubbling for sections can occur only in the fiber. So sphere and disk bubbling on the zero and one-dimensional moduli spaces is ruled out by the monotonicity condition. The construction of coherent orientations is given in [48].
Remark 4.13
(Sketch of construction of orientations from [48]) We briefly recall the construction of orientations: On any disk with Lagrangian boundary conditions where the Lagrangian is equipped with a relative spin structure, the linearized operator \(D_u\) over the surface S may be deformed via nodal degeneration to a boundary value problem \(D_u'\) on the sphere \(S_s\) and a constant boundary value problem on the disk \(S_d\). On the sphere, the linearized Cauchy–Riemann operator \(D_u' | S_s\) is homotopic to a complex linear operator \(D_u''\). The determinant line \(\det (D_u')\) inherits an orientation via the complex structure on the kernel \( {\text {ker}}(D_u'')\) and cokernel \( {\text {coker}}(D_u'')\). On the other hand, on the disk the boundary condition \((u |_{\partial S_d})^* TL\) admits a canonical stable trivialization determined by the relative spin structure. The determinant line on the disk admits an orientation induced from a trivialization of \((u |_{\partial S_d})^* TL\) and an isomorphism of the kernel \( {\text {ker}}(D_u' | S_d)\) with the tangent space to the Lagrangian \(T_{u(z)}L\) at any point on the boundary. These combine to an orientation on the determinant line \(\det (D_u) \cong \det (D_u' | S_s) \otimes \det (D_u' | S_d)\).
Remark 4.14
(Brane structures on spherically fibered coisotropics) In order to specify the signs in the exact triangle, it is necessary to specify the brane structure on the fibered coisotropic. If C is a spherically fibered coisotropic that reduces to a spin principal bundle, then TC admits a relative spin structure for the embedding \(C \rightarrow M \times B\) with background class \(w_2(TM)\) induced by the isomorphism
where \(\underline{\mathbb {R}}\) denotes the trivial bundle with fiber \(\mathbb {R}\).
For later use, we recall the basic fact that maps with sufficiently small energy must also have small diameter:
Lemma 4.15
Let \(\underline{S}\) be a holomorphic quilt with strip-like ends, with symplectic labels \(\underline{M}\) and Lagrangian boundary and seam condition \(\underline{L}\). For any \(\delta > 0, \ell _0\), there exists \(\epsilon > 0\) such that if \(u: \underline{S} \rightarrow \underline{M}\) is a pseudoholomorphic quilt with energy \(E(u) < \epsilon \), and \(\gamma : [0,1] \rightarrow \underline{S}\) is a path connecting boundary components of length less than \(\ell _0\), then the length of \(u \circ \gamma \) is less than \(\delta \).
Proof
The claim is an application of the mean value inequality for pseudoholomorphic maps [29, Lemma 4.3.1 (i)]: For any compact almost complex manifold M, there exist constants \(c,\epsilon > 0\) such that for any \(r > 0 \) and any pseudoholomorphic map \(u: B_r(z) \rightarrow M\) with energy at most \(\epsilon \),

where \(B_r(z)\) is a ball of radius r around z. There is a similar version for Lagrangian boundary conditions, in which the right-hand side is replaced by a half ball [29, Lemma 4.3.1 (i)]. In our quilted situation, we may apply the mean value inequality in each patch. Since \(\underline{S}\) is compact on a complement of the strip-like ends, there exists a constant \(r_0 > 0 \) such that any point in \(\underline{S}\) is contained in ball of radius at least \(r_0\), or half ball of radius \(r_0\) in \(\underline{S}\). By integrating over \(\gamma (t)\), we see that the length \(\ell (\gamma )\) satisfies

This proves the claim for \(\epsilon \) such that \( \epsilon < \delta r_0^2/ c \ell _0\). \(\square \)
Definition 4.16
(Relative invariants for Lefschetz–Bott fibrations with strip-like ends) For Lefschetz–Bott fibration E with boundary condition F equipped with a relative spin structure, suppose that the ends \(L^{e,0}, L^{e,1}\) of F are transverse and \(CF(L^{e,0}, L^{e,1})\) have been defined without Hamiltonian perturbation for each end e. Define
by
where \(o(u) = \pm 1\) are orientations constructed in [48]. By items (c) and (d) of Theorem 4.12, the maps \(C\varPhi (E,F;\Lambda )\) are cochain maps. Passing to cohomology (and passing to rational coefficients in the case of more than one outgoing end), one obtains a map
Remark 4.17
(Independence from almost complex structure and fiberwise symplectic form) The cohomology-level invariants \(\varPhi (E,F;\Lambda )\) are independent of the choice of compatible almost complex structure J on E, by an argument using parametrized moduli spaces similar to that of Theorem 4.12.
The invariants are independent of the choice of two-form \(\omega _E \in \Omega ^2(E)\) in the following sense: Given any symplectic Lefschetz–Bott fibration \((E, \omega _E,\pi )\), we may form a new symplectic Lefschetz–Bott fibration \((E,\omega _E + \pi ^* \omega _S, \pi )\) by adding on the pullback of non-negative, compactly supported two-form \(\omega _S \in \Omega ^2_c(S)\) on the base. Any almost complex structure \(J_0\) compatible with \(\omega _E\) will also be compatible with \(\omega _E + \pi ^* \omega _S\), although not necessarily vice versa. As a result, for any two such almost complex structures \(J_k, k \in \{ 0,1 \}\) compatible with \(\omega _E + \lambda _k \pi ^* \omega _S\) for some scalars \(\lambda _0,\lambda _1\), the moduli spaces
are cobordant. Since the area of each pseudoholomorphic section changes by the integral \(A(S) = \int _S \omega _S\), the invariant \(\varPhi (E,F;\Lambda )\) is independent of this change up to an overall power \(q^{A(S)}\).
The relative invariants of fibrations with “non-negative curvature,” in the following sense, have particularly nice properties. Recall the symplectic connection (4) on a Lefschetz fibration \(\pi :E \rightarrow S\). The spaces \(TE^h_e\) have canonical complex structures, induced from the complex structure j on the base S. Define
for some function \(f: E \rightarrow \mathbb {R}\).
Definition 4.18
A Lefschetz–Bott fibration E with two-form \(\omega _E\) has non-negative curvature if \(\omega _E(v,jv) \ge 0 \) for all v in the horizontal subspace \(TE^h\), that is, \(f(e) \ge 0\) for all \(e \in E\).
Remark 4.19
Non-negative curvature implies that a small perturbation of the two-form is symplectic: Recall that the total space of any Lefschetz–Bott fibration \(\pi :E \rightarrow S\) admits a canonical isotopy class of symplectic structures given as follows. If \(\omega _S \in \Omega ^2(S)\) is a sufficiently positive two-form, then \(\omega _E + \pi ^* \omega _S\) is a symplectic form on \(TE_e\) for any \(e \in E\). If E is compact, then \(\omega _E + \pi ^* \omega _S\) is symplectic on E for \(\omega _S\) sufficiently positive. If E is non-negative, then \(\omega _E + \pi ^* \omega _S\) is symplectic for any positive form \(\omega _S \in \Omega ^2(S)\).
Proposition 4.20
(Non-negative curvature of standard Lefschetz–Bott fibrations) If \(C \subset M\) is a spherically fibered coisotropic, then the standard Lefschetz–Bott fibration \(E_C\) of 2.13 has non-negative curvature.
Proof
Let \(v \in V\), the standard representation of \(SO(c+1)\), and \((p,v) \in P \times V\). The horizontal subspace \(H_v \subset T_v V\) pairs trivially with \( {\text {ker}}(\alpha ) \times T(\pi ^{-1}_V(\pi _V(v)))\) under the pairing given by the two-form (7), where \(\pi _V\) is the projection (9). It follows that the image \([H_v]\) of \(H_v\) in P(V) is the horizontal subspace at \([p,v] \in P(V) := (P \times V)/G\). Let \(J_V\) denote the standard complex structure on V, and \(J_0\) the induced complex structure on E. Since \(J_{V}\) is non-negative on \(H_v\), \(J_0\) is non-negative on \([H_v]\). \(\square \)
Proposition 4.21
Let E be a Lefschetz–Bott fibration with Lagrangian boundary condition F and relative spin structure. If E has non-negative curvature, then the exponents of q in the formula (31) are all non-negative.
Proof
Since the form \(\omega _E(\cdot , J \cdot )\) is non-negative for any \(J \in {\mathcal {J}}(E)\), any pseudoholomorphic section has non-negative area. The q-exponents in (31) are the areas. So these are non-negative as well. \(\square \)
We do not give formula for the degree of the relative invariant, see [44] for a formula for the degree in the case without singularities.
4.3 Invariants for quilted Lefschetz–Bott fibrations
The main difference between the triangle for the fibered case and the original Seidel triangle [41] is the appearance of invariants associated with quilted surfaces. The following definitions are taken from [44].
Definition 4.22
-
(a)
(Quilted surfaces with strip-like ends) A quilted surface with strip-like ends \(\underline{S}\) consists of the following data:
-
(i)
a collection \(\underline{S} = (S_k)_{k=1,\ldots ,m}\) of surfaces with strip-like ends, see [41, 44], called patches. Each \(S_k\) carries a complex structure \(j_k\) and has strip-like ends \((\epsilon _{k,e})_{e\in {\mathcal {E}}(S_k)}\). Denote the limits of these ends
$$\begin{aligned} \lim _{s \rightarrow \pm \infty } \epsilon _{k,e}(s,t) =: z_{k,e} \in \partial {\overline{S}}_k \end{aligned}$$and denote the boundary components
$$\begin{aligned} \partial S_k = (I_{k,b})_{b\in {\mathcal {B}}(S_k)} ; \end{aligned}$$ -
(ii)
a collection \({\mathcal {S}}\) of seams: pairwise disjoint two-element subsets
$$\begin{aligned} \sigma \subset \bigcup _{k=1}^m \bigcup _{b \in {\mathcal {B}}(S_k)} I_{k,b} \end{aligned}$$and for each \(\sigma = \{ I_{k,b}, I_{k',b'} \}\) a real analytic isomorphism
$$\begin{aligned} \varphi _\sigma : I_{k,b} \rightarrow I_{k',b'} , \end{aligned}$$where the isomorphisms \(\varphi _\sigma \) should be compatible with the strip-like ends in the sense that on each end \(\varphi _\sigma \) should be a translation;
-
(iii)
Orderings of the boundary components of each set of patches \({\mathcal {B}}(S_k), k = 1,\ldots , m\); and
-
(iv)
Orderings of the incoming and outgoing ends of \(\underline{S}\)
$$\begin{aligned} {\mathcal {E}}_-(\underline{S})=\left( \underline{e}^-_1,\ldots ,\underline{e}^-_{N_-(\underline{S})}\right) , \quad {\mathcal {E}}_+(\underline{S})=\left( \underline{e}^+_1,\ldots ,\underline{e}^+_{N_+(\underline{S})}\right) . \end{aligned}$$
-
(i)
-
(b)
(Quilted symplectic Lefschetz–Bott fibrations) A (quilted) symplectic Lefschetz–Bott fibration \(\underline{E}\) over a quilted surface \(\underline{S}\) with strip-like ends consists of a collection of Lefschetz–Bott fibrations \(E_k \rightarrow S_k, k = 0,\ldots , m\). A Lagrangian boundary/seam condition for E consists of a collection \(\underline{F}\) of submanifolds of the boundaries and seams
$$\begin{aligned} F_{k,b} \subset E_{k,b} | I_{k,b}, \quad F_{(k_0,b_0),(k_1,b_1)} \subset E_{k_0}| I_{k_0,b_0} \times \varphi _\sigma ^* \left( E_{k_1} | I_{k_1,b_1}\right) , \end{aligned}$$where \(I_{k,b}\) ranges over true boundary components resp. \(I_{k_0,b_0}, I_{k_1,b_1}\) range over identified boundary components, such that
-
(i)
each fiber
$$\begin{aligned} F_{(k_0,b_0),(k_1,b_1),z} \subset E_{k_0,z} \times \left( \varphi _{(k_0,b_0),(k_1,b_1)}^* E_{k_1}\right) _z \end{aligned}$$over \(z \in \underline{S}\) is a Lagrangian submanifold; and
-
(ii)
over the strip-like ends the fibers \(F_{(k_0,b_0),(k_1,b_1),z}\) over \(z \in \underline{S}\) are given by fixed Lagrangians \(L^{k_{e,i,}b_{e,i}}\) on the strip-like ends, with the property that the composition
$$\begin{aligned} L^{(k_{e,0},b_{e,0})}\circ L^{(k_{e,1},b_{e,1})} \ldots \circ L^{(k_{e,l(e)},b_{e,l(e)})} \end{aligned}$$is transversal, where l(e) is the number of patches on the end e.
-
(i)
We say that a quilted Lefschetz–Bott fibration is monotone if sections satisfy an area-index relation similar that for pseudoholomorphic maps. In the case without singularities (i.e., fibrations) admissibility for the Lagrangians guarantees monotonicity in the quilted setting, see [44, Remark 3.7]. For Lefschetz–Bott fibrations, admissibility together with the codimension conditions in Lemma 4.10 guarantees monotonicity, by the same arguments.
Definition 4.23
(Relative invariants for quilted Lefschetz–Bott fibrations) Theorem 4.12 generalizes to the quilted setting: Associated with a monotone quilted symplectic Lefschetz–Bott fibration \((\underline{E},\underline{F})\), we have (ungraded) relative invariants which (working with rational coefficients in the case of more than one outgoing end) map
These invariants satisfy a composition relation for gluing along strip-like ends by a gluing argument spelled out in [44]. That is, if \(\underline{E},\underline{F}\) is a quilted Lefschetz–Bott fibration obtained from fibrations \(\underline{E}_1,\underline{F}_1\) and \(\underline{E}_2,\underline{F}_2\) by gluing the outgoing ends of \(\underline{E}_1,\underline{F}_1\) to the incoming ends of \(\underline{E}_2,\underline{F}_2\) then
As in the unquilted case in Remark 4.17, these invariants are independent of the choice of almost complex structure and deformation of the two-form on the total space.
4.4 Vanishing theorem
In this section, we use gluing along a seam to obtain a vanishing theorem analogous to [41, Section 2.3] for the invariants associated with standard fibrations associated with a fibered Dehn twist.
Remark 4.24
(Gluing along a seam for quilted Lefschetz–Bott fibrations)
-
(a)
(Glued surface) For \(k =0,1\) let \(\underline{S}_k\) be quilted surfaces with \(d_k + 1\) strip-like ends, and \(z_k\) a seam point in \(\underline{S}_k\). Let \(\rho > 0\) be a gluing parameter. Let \(\underline{S}^\rho \) be the quilted surface with \(d_0 + d_1 + 2\) strip-like ends formed by gluing together quilted disks \(D_0,D_1\) around \(z_0,z_1\) using the map \(z \mapsto \rho /z\). See Fig. 5.
-
(b)
(Glued bundles) Let \((\underline{E}_k,\underline{F}_k)\) be Lefschetz–Bott fibrations over \(\underline{S}_k\), equipped with a trivialization of \(\underline{E}_k,\underline{F}_k\) in a neighborhood of \(z_k\), and a symplectomorphism of \((\underline{E}_{k,z_k},\underline{F}_{k,z_k})\) for \(k = 0,1\). The seam connect sum \(\underline{E}^\rho \rightarrow \underline{S}^\rho \) is formed by patching \(\underline{E}_0\) and \(\underline{E}_1\), and similarly for the boundary and seam conditions \(\underline{F}^\rho \).
-
(c)
(Glued complex structures) Suppose that the following are given: a \((\pi _k,j_k)\)-compatible almost complex structure \(\underline{J}_k\) for \(\pi _k:\underline{E}_k \rightarrow \underline{S}_k\) that is constant in a neighborhood of \(z_k\) (with respect to the given trivialization) for \(k \in \{ 0,1 \}\) and such that \(\underline{J}_0\) agrees with \(\underline{J}_1\) on the glued fiber. One can patch together these almost complex structures to obtain a compatible almost complex structure \(\underline{J}\) for \(\underline{E}\rightarrow S\).
We next investigate the behavior of moduli spaces of sections under gluing. Suppose that \((\underline{E}^\rho ,\underline{F}^\rho )\) is obtained from gluing \((\underline{E}_0,\underline{F}_0) \) and \((\underline{E}_1,\underline{F}_1)\) and all three are monotone symplectic Lefschetz–Bott fibrations. Let
denote the evaluation maps at the nodal points \(z_k,k \in \{ 0,1 \}\).
Theorem 4.25
(Behavior of moduli spaces under gluing along a seam) For sufficiently small \(\rho \), there exists a comeager subset
such that
-
(a)
the evaluation map \({\text {ev}}_0 \times {\text {ev}}_1\) is transverse to the diagonal;
-
(b)
for any pair \((u_0,u_1)\), there exists a gluing map on a neighborhood \(U(u_0,u_1)\) of \((u_0,u_1)\) given by
$$\begin{aligned} \Theta ^\rho : {\mathcal {M}}(\underline{E}_0,\underline{F}_0) \times _{{\text {ev}}_0,{\text {ev}}_1} {\mathcal {M}}(\underline{E}_1,\underline{F}_1) \supseteq U(u_0,u_1) \rightarrow {\mathcal {M}}(\underline{E}^\rho ,\underline{F}^\rho ) ; \end{aligned}$$ -
(c)
as \((u_0,u_1)\) varies over points in the zero-dimensional component of the left-hand-side, \(\Theta ^\rho \) is surjective onto the zero-dimensional component of \({\mathcal {M}}(\underline{E}^\rho ,\underline{F}^\rho )\); and
-
(d)
for any \(u \in {\mathcal {M}}(\underline{E}_0,\underline{F}_0) \times _{{\text {ev}}_0,{\text {ev}}_1} {\mathcal {M}}(\underline{E}_1,\underline{F}_1)\), the sequence \(\Theta ^\rho (u)\) Gromov converges to u as \(\rho \rightarrow 0\).
See McDuff and Salamon [29, Chapter 10] for the case of gluing at an interior point and Abouzaid [1] for the details of gluing along a point in the boundary.
Next we give a formula for the dimension for the pseudoholomorphic sections of the standard fibration studied in Propositions 2.13 and 4.20.
Definition 4.26
(Standard fibrations on small balls) Let \(C \subset M\) be a coisotropic submanifold of codimension c spherically fibered over B and \(E_C \rightarrow D\) the Lefschetz–Bott fibration over the disk D of radius 1 with generic fiber \(M \times B^-\) and monodromy \(\tau _C \times 1\) from Lemma 2.13. Equip \(E_C\) with the Lagrangian boundary condition given by the fiber product
where T is the union of vanishing cycles in the local model P(V) as in (10). As in [41] this boundary value problem fits into a family of problems \(E_{C,r},F_{C,r}\), the standard fibrations of Sect. 2.4 over a disk \(D_r\) of radius r. Each member of the family is formed by patching together \(C \times _{SO(c+1)} V\) with \((M \times B) -(i(C) \times p(C))\) with boundary condition
in the local model \( P \times _{SO(c+1)} V\).
Lemma 4.27
(Dimension formula for pseudoholomorphic sections of a standard fibration) Let \(C,E_C,F_C\) be the standard Lefschetz–Bott fibration associated with C in Lemma 2.13, and c the codimension of C. If \((E_C,F_C)\) is monotone then for r sufficiently small, \(J \in {\mathcal {J}}^{{\text {reg}}}(E_C)\) and all \(u \in {\mathcal {M}}(E_{C,r},F_{C,r})\) we have
Proof
We explicitly describe a family of pseudoholomorphic sections as follows. Suppose that the almost complex structure on \(E_{C,r}\) is induced from an almost complex structure on B and the standard almost complex structure on V. For each \(a \in V, b \in B\), fix a local trivialization of P and define in the corresponding local trivialization \(E_{C,r}\)
The condition for \(w_{r,a,b}\) to be a section is by (9)
Hence
Given this, the section \(w_{r,a,b}\) takes values in \(F_{C,r}\). We claim that the Maslov index satisfies the following formula:
Indeed, by definition the Maslov index of \(w := w_{r,a,b}\) is the index of the pair \((w^* T^{{\text {vert}}} E_C, (\partial w)^* T^{{\text {vert}}} F_C)\). This pair fits into the exact sequence
Now \( T_{w(z)} E_{C,r} = (T_b B_{C,r})^2 \oplus \mathbb {C}^{c+1}\) is trivial, and the boundary condition has vertical part
where \(\Delta _{T_b B}\) is the diagonal. The horizontal part of the boundary value problem maps isomorphically onto \((TD, T(\partial D))\) via \(D\pi \). Using (37), we have
Hence
which proves the claim (36).
We claim that the given sections are the sections of lowest index for sufficiently small radius. Indeed, the area \(A(w_{r,a,b})\) approaches zero as \(r \rightarrow 0\), for all a; this fact holds even after the adjustment [41, (1.17)] since the adjustment is by the pullback of the differential of a bounded one-form. Choose r sufficiently small so that \(A(w_{r,a,b}) \le 1/2\lambda \). The area-index monotonicity relation and non-negativity of the curvature in Proposition 4.20 imply that any other section u has positive area. So the index of this section I(u) is at least the index \(I(w_{r,a,b})\) of \(w_{r,a,b}\). \(\square \)
In order to define relative invariants for Lefschetz–Bott fibrations with codimension one vanishing cycles, a stronger monotonicity assumption must be assumed.
Definition 4.28
(Strong monotonicity) In the case that \(C \subset M\) is a fibered coisotropic of codimension one, we denote by \(M_C\) the cut space as in Lerman [23]. The cut space \(M_C\) is the space obtained by cutting M along C and collapsing the resulting manifold (whose boundary is two copies of C) by the circle action on the boundary. Thus \(M_C\) contains two copies \(B_\pm \) of B. Denote by \([B_\pm ] \in H^2(M_C)\) the dual classes of \(B_\pm \) and by \([\omega _C] \in H^2(M_C)\) the symplectic class. A monotone fibered coisotropic C is strongly monotone if either \({\text {codim}}(C) \ge 2 \) or both \({\text {codim}}(C) = 1\) and \(c_1(M_C)-[B_+]-[B_-]\) is a positive multiple of \([\omega _C]\).
Proposition 4.29
Suppose that the vanishing cycles of E are strongly monotone. Then the sections of (E, F) satisfy a monotonicity relation, and counting pseudoholomorphic sections defines a relative invariant \(\varPhi (E,F;\Lambda )\) as in (32).
Proof
The codimension two case is already covered in Proposition 4.10. In the case that the fibered coisotropic is codimension one, there are degree two homology classes in the special fibers that are not equivalent to homology classes in the special fiber. Let \(\nu _C: M_C\rightarrow E_{s_0} \subset E\) denote the normalization map, mapping the two copies \(B_\pm \) of B created by cutting to the singular locus \(B \subset E_{s_0}\). Then
Indeed, let z be a local coordinate on the base near a critical value. The one-form \(\pi ^* {\text{ d }}z\) is nonvanishing everyone except at the singular locus in the fiber where \(\pi ^* {\text{ d }}z\) has a simple zero. It follows that if the vanishing cycles are strongly monotone, then the monotonicity relation holds on fiber classes. It follows that monotonicity also holds on sections. Counting pseudoholomorphic sections defines an invariant \(\varPhi (E,F)\), as in the case of higher codimension. \(\square \)
Remark 4.30
(Double cover in the codimension one case) In the case that \(c = 1\), \(r = 1\), the evaluation map on the moduli space \({\mathcal {M}}(E_{C,r},F_{C,r})_0\) of zero-index pseudoholomorphic sections of \((E_{C,r},F_{C,r})\) at \(z = 1\) induces a double cover
of the fiber of the vanishing cycle C. The relations (35) on \(a = (a_1,a_2)\) become
Corollary 4.31
(Vanishing of the relative invariant associated with a standard fibration) Suppose that \(E \rightarrow S\) is a Lefschetz fibration with the Lagrangian boundary condition F obtained by a seam connect sum from a Lefschetz-Bott fibration \((E_{C,r},F_{C,r})\) over the disk Dr corresponding to a spherically fibered coisotropic submanifold C, with an arbitrary quilted Lefschetz–Bott fibration \(E_0 \rightarrow S_0\) with boundary condition \(F_0\). Suppose that all these fibrations with boundary conditions are monotone and equipped with relative spin structures, so that in particular the relative invariant \(\varPhi (E,F)\) is defined. Then \(\varPhi (E,F)= 0 \). More precisely, there exists a null homotopy of the chain-level relative invariant \(C\varPhi (E,F)\) that, if r is sufficiently small, has positive q-exponents.
Proof
Suppose that E, F are as in the statement of the Corollary. Consider the family of surfaces obtained by stretching the neck so that a standard fibration \((E_{C,r},F_{C,r})\) bubbles off. The chain level invariants \(C\varPhi (E_{C,r}, F_{C,r})\) are chain homotopic by a chain homotopy corresponding to isolated points in the parametrized moduli space for the deformation. The gluing Theorem 4.25 gives a bijection between pseudoholomorphic sections of \(E_\rho , F_\rho \), for small \(\rho \), and \((u_0,u_1)\) in the zero-dimensional component \(({\text {ev}}_0,{\text {ev}}_1)^{-1}(\Delta )\), where \(\Delta \) is the diagonal in the gluing fiber \(F_{0,z_0} \cong F_{C,z_1}\). Equality of indices gives
for \(k \in \{ 0,1 \}\). In the codimension two case, Corollary 4.31 now follows from Lemma 4.27 which implies that the moduli spaces for small r and large \(\rho \) are empty. The chain-level invariants are independent of the choice of r up to chain homotopy by Remark 4.17.
The codimension one case depends on the description of the double cover in 4.30. Indeed, in this case the limiting moduli space is not empty, but has two components corresponding to the choices of sign in 4.30. Each component is isomorphic to the Lagrangian. Furthermore, each has the induced orientation given by deforming the boundary value problem to a trivial one and using the orientation from the Lagrangian as in Remark 4.13. The two sections \(u_\pm \) corresponding to a given \((a_1,a_2)\) in (39) are related by the involution
It follows that any deformation of \(u_+^* F\) to a trivial boundary condition induces a deformation of \(u_-^* F\) and vice versa, giving a commutative diagram

The evaluation maps for \(u_\pm \)
given by linearizing (35) are by definition orientation preserving. Since the right-hand arrow is orientation reversing (exactly one factor of F is reversed), the left-hand arrow is also orientation reversing. Hence these contributions cancel in the weighted disk count (31). \(\square \)
Remark 4.32
(Independence of choices) Let \(S_0,E_0,F_0,E_C,F_C,D_r\) be as above. Define an invariant associated with the nodal surface \(S_r\) by identifying a point on the seam \(S_0\) and disk D. Define a nodal Lefschetz fibration \(E_r\) by identifying a fiber of \(E_0\) with a fiber of \(E_C\) with boundary condition \(F_r \subset E_r\). By counting pseudoholomorphic sections with matching condition at the node one obtains an invariant \(\varPhi (E_r,F_r)\) for the nodal fibration, equal to the invariant for the glued fibration \(\varPhi (E,F)\). In particular, vanishing of \(\varPhi (E_r,F_r)\) for r small implies vanishing for any r.
4.5 Horizontal invariants
As in Seidel [41], the computation of the relative invariants in the special cases needed for the exact triangle uses only horizontal sections, defined as follows.
Definition 4.33
Let \(\underline{S}\) be a quilted surface with strip-like ends, \(\underline{E}\) a quilted Lefschetz–Bott fibration, and \(\underline{F}\) a collection of Lagrangian seam/boundary conditions.
-
(a)
(Horizontal sections) A section \({u}: \underline{S} \rightarrow \underline{E}\) (i.e., a collection of sections \(u_k: S_k \rightarrow E_k,\ k = 1,\ldots , m\)) is horizontal if
$$\begin{aligned} {\text {Im}}Du_k(s) = TE^h_{k,u_k(s)} \end{aligned}$$for all \(s \in S_k, k = 1,\ldots , m\). Let \( {\mathcal {M}}^h(\underline{E},\underline{F}) \) denote the space of horizontal sections.
-
(b)
(Horizontal almost complex structures) A collection of compatible almost complex structures \(\underline{J} \in {\mathcal {J}}(\underline{E})\) is horizontal if
$$\begin{aligned} J_k(e) T_e^hE_k = T^h_e E_k, \quad \forall e \in E_k -E_k^{{\text {crit}}}, \quad k = 1,\ldots , m, \end{aligned}$$or equivalently if \(\omega _{E_k}(J \cdot , \cdot )\) is symmetric for \(k = 1,\ldots , m\). Let \({\mathcal {J}}^h(\underline{E})\) denote the set of horizontal compatible almost complex structures. If \(J \in {\mathcal {J}}^h(\underline{E})\), then any horizontal section is J-holomorphic, that is,
$$\begin{aligned} (J \in {\mathcal {J}}^h(\underline{E})) \implies ({\mathcal {M}}^h(\underline{E},\underline{F}) \subset {\mathcal {M}}(\underline{E},\underline{F})). \end{aligned}$$ -
(c)
(Clean moduli spaces) \({\mathcal {M}}^h(\underline{E},\underline{F})\) is clean if \({\mathcal {M}}^h(\underline{E},\underline{F})\) is a smooth submanifold of the Banach manifold of sections of a suitable Sobolev class of \(\underline{E}\) with tangent space
$$\begin{aligned} T_{u} {\mathcal {M}}^h(\underline{E},\underline{F}) = \{ \xi \in \Omega ^0(u^* T^{{\text {vert}}}\underline{E}, ( u | \partial \underline{S})^* T^{{\text {vert}}} \underline{F}) \ | \ \nabla \xi = 0 \} \end{aligned}$$the set of horizontal sections of \(u^* T^{{\text {vert}}}\underline{E}\) with boundary/seams in \(( u | \partial \underline{S})^* T^{{\text {vert}}} \underline{F}\).
Remark 4.34
(Horizontal and vertical energy) The energy of a section of a Lefschetz–Bott fibration may be broken up into horizontal and vertical parts. We suppose that we choose \(\omega _S\) so that \(\omega _E + \pi ^* \omega _S\) is symplectic. This two-form together with the almost complex structure defines a metric on the total space E. Fix a metric on S, giving rise to an area form \({\text{ d }} {\text {Vol}}_S\), and define

The energy \({\mathcal {E}}(u)\) splits into vertical and horizontal contributions
As in Seidel [41, Equation (2.10)], one has an energy-area relation
This implies that for pseudoholomorphic sections one has an energy-area relation
A similar relation holds in the quilted case.
Proposition 4.35
(Criterion for horizontal moduli spaces to be a component) Suppose that \((\underline{E},\underline{F})\) is a quilted symplectic Lefschetz–Bott fibration with Lagrangian boundary condition. If \(\underline{E}\) is non-negatively curved and equipped with a horizontal almost complex structure such that \({\mathcal {M}}^h(\underline{E},\underline{F})\) is clean, of dimension Ind(Du), and consists of sections with vanishing \(\omega _E\)-integral,
then \({\mathcal {M}}^h(\underline{E},\underline{F})\) is a path component of \({\mathcal {M}}(\underline{E},\underline{F})\) and consists of regular sections.
Proof
As in [41, Lemma 2.11], suppose that u is a horizontal section with \(\int _S u^* \omega _E =0 \). Any other pseudoholomorphic section \(\tilde{u}\) homotopic to u satisfies by (40) the equation
By the non-negative curvature assumption, \(\tilde{u}\) must satisfy
as claimed. The regularity of \(\mathcal {M}^h(E; F)\) follows as in Seidel [47, Lemma 2.12]: Under the non-negative curvature assumption the kernels of \(\nabla _u\) and \(D_u\) are identical, and \(\mathrm{dim} \mathcal {M}^h(E; F) = Ind(D_u)\) implies \(\mathrm{coker}(D_u) = 0\). \(\square \)
We give a criterion for the zero-dimensional component \({\mathcal {M}}(\underline{E},\underline{F})_0\) to consist entirely of horizontal sections in the monotone case; the exact case was discussed in Seidel [41]. Let \(\underline{E} \rightarrow \underline{S}\) be a monotone Lefschetz–Bott fibration with Lagrangian boundary/seam conditions \(\underline{F}\). For each collection of intersection points \(( (x_e)_{e \in {\mathcal {E}}})\), define \(c((x_e)_{e \in {\mathcal {E}}}) \) by
for any collection of sections u with limits \( ( x_e )_{ e \in {\mathcal {E}}}\).
Proposition 4.36
(Criterion for the existence of only horizontal sections) Suppose that \(\underline{E}\) is a quilted Lefschetz–Bott fibration with non-negative curvature and is equipped with a horizontal almost complex structure. If \(c((x_e)_{e \in {\mathcal {E}}}) = 0 \) then \({\mathcal {M}}(\underline{E},\underline{F}; (x_e)_{e \in {\mathcal {E}}} )_0\) consists of horizontal sections.
Proof
If u is a pseudoholomorphic section with index 0, then the monotonicity relation (29) implies that u has non-negative symplectic area equal to \(c((x_e)_{e \in {\mathcal {E}}}) \). If this constant vanishes, then all such sections must have vanishing symplectic area. By the non-negativity of the curvature and (40), any such section has vanishing vertical energy and so is horizontal. \(\square \)
5 Floer versions of the exact triangle
The proofs of the exact triangles described in the introduction follow the lines of the proof of Floer’s exact triangle [6], in Seidel [41] and Perutz [35]. Namely, one first constructs a short sequence of cochain groups that is exact up to leading order, and then uses a spectral sequence argument to deduce the existence of a long exact sequence of cohomology groups. In this section, we also describe various extensions, to the case of minimal Maslov number two and the case of periodic Floer cohomology.
5.1 Fibered Picard–Lefschetz formula
In this section, we prove the exact triangle on the level of vector spaces; this is essentially equivalent to the fibered Picard–Lefschetz formula in Theorem 1.
Definition 5.1
(Angle functions) Recall from Sect. 2.2 that a Dehn twist in a local model \(T^\vee S^c\) is defined by rotating a vector in \(T^\vee S^c\) with norm t by an angle function
The angle function \(\theta (t)\) is related to the choice of \(\zeta (t)\) of (8) by \(\theta (t) = \zeta '(t)\). For the rest of the paper, we assume that the function \(\theta (t)\) is decreasing with t. We wish to use angle functions that go to 0 sufficiently quickly. In particular, given an angle function \(\theta \) we consider the family of angle functions defined by
Lemma 5.2
(Intersection points for fibered Dehn twists) Let \(C \subset M\) be a compact spherically fibered coisotropic in a symplectic manifold M over a symplectic manifold B, and \(L^0,L^1 \subset M\) Lagrangian submanifolds. Suppose that the intersection
is transverse while the intersection
is empty. For \(\lambda > 0 \) let \(\tau _{C,\lambda } \in {\text {Diff}}(M,\omega )\) be a fibered Dehn twist using a given local model and the angle function \(\theta ^\lambda (t)\). There exists a constant \(\lambda _0\) such that if \(\lambda > \lambda _0\) then there exists a bijection
Proof
First note that the intersection points of the untwisted Lagrangians naturally include in those of the twisted ones of \(\lambda \) large. The transversality assumptions imply that the intersection \(L^0 \cap L^1 \cap C\) is empty. By taking \(\lambda _0\) sufficiently large, we may suppose that \(\tau _{C,\lambda }\) is supported in a neighborhood \(U_C\) disjoint from \(L^0 \cap L^1\). Thus there is an inclusion
We wish to identify the remaining intersection points with \((L^0 \times C) \cap (C^t \times L^1) \).
We first recall the unfibered case in Seidel [41, Lemma 3.2]. Suppose that the base B is a point. Choose a local model for the Lagrangian C given by a symplectomorphism of a neighborhood of the zero section in \(T^\vee S^c\) with a neighborhood of C in M. The local model \(\phi : T^\vee S^c \supset U \rightarrow M\) may be chosen so that the Lagrangians \(L^0,L^1\) are fibers of \(\pi : T^\vee S^c \rightarrow S^c\):
What this amounts to is choosing the initial diffeomorphism with this property and then choosing the Moser isotopy to preserve the Lagrangians. The Dehn twist \(\tau _C^{-1}\) acts at \([v] \in P(T^\vee S^c)\) by normalized geodesic flow by time \(\theta ^\lambda (|v|)\). There exists a unique \(v \in L^1\) of norm less than \(\pi \) such that its time \(\pi - |v|\) normalized geodesic flow lies in \(L^0\). The unique point \(w \in \mathbb {R}_{> 0} v\) with \( \theta ^\lambda (|w|) = \pi - |v|\) gives the desired intersection point.
We reduce to the case of trivial base by the use of suitable local models as follows. Let
be points with the same projection \(b \in B\). Consider the action of scalar multiplication on the vector bundle \(P(\pi _{T^\vee S^c}): P(T^\vee S^c) \rightarrow P(S^c)\). This action induces an action of sufficiently small scalars on M via the coisotropic embedding. By (41) \(\tau _{C,\lambda } = \lambda \tau _C \lambda ^{-1} \) wherever the right-hand side is defined. For \(k \in \{ 0,1 \}\), the submanifolds \((\lambda L^k \cap U_C)_{\lambda > 0 }\) fit together with \(P(\pi _{T^\vee S^c})^{-1} (L^k \cap C)\) in the limit \(\lambda \rightarrow \infty \) to a smooth family at \(\lambda = \infty \). Indeed, if \(L^k\) is given locally by \(\{ f(z,x,y) = 0 \}\) in local coordinates z on B and cotangent coordinates (x, y) on \(T^\vee S^c\) then
By assumption \(L^k\) is transversal to the zero section in \(T^\vee S^c\). This implies that the equation (43) cuts out a smooth family at \(\lambda = \infty \). By the case B trivial, the intersection at \(\lambda = \infty \) is given by
and is transverse. By the implicit function theorem, the set of intersection points \( L^0 \cap \tau _{C,\lambda }^{-1} L^1\) forms a smooth manifold parametrized by \(\lambda \gg 0 \) and intersection points \((L^0 \times C) \cap (C^t \times L^1)\) as desired.
Alternatively, one can argue as follows via the limit of the twisted Lagrangian. After restricting to connected component in an open neighborhood of \(p^{-1}(b)\), the projection \(L^1 \cap C \rightarrow B\) is an embedding. For any point \(l \in L^1\) with \(\tau _C(l) \ne l\), the images of the derivatives of \(\tau _{C,\lambda }^{-1}\) converge to the tangent space of \(p^{-1}(C \cap L^1)\): If the projection of \(\tau _C^{-1}(l)\) to C is c in the local model, then
since \(\lambda ^{-1} D \tau _C^{-1}(l) \lambda \) converges to the composition of \(D \tau _C^{-1}(l)\) with projection to the tangent space to C. It follows that the sequence of submanifolds \(\tau _{C,\lambda }^{-1}(L^1) - L^1\) converges, as an embedded submanifold, to \(p^{-1}(p(L^1 \cap C)) - L^1\). Again by the implicit function theorem, the intersections \(L^0 \cap \tau _{C,\lambda }^{-1}(L^1)\) correspond to intersection points of \(L^0 \cap p^{-1}(p(L^1 \cap C)) \cong (L^0 \times C) \cap (C^t \times L^1)\). \(\square \)
5.2 Lagrangian Floer version
We now prove the exact triangle Theorem 1.3. Since \(\tau _C\) is a symplectomorphism, it suffices to prove the theorem with \(L^1\) replaced by \(\tau _C^{-1} L^1\). That is, we construct a long exact sequence
More generally in the quilted case, it suffices to prove the theorem with \(\underline{L}^1\) replaced by \(\underline{L}^1 \# {\text {graph}}(\tau _C)\).
5.2.1 Definition of the maps
Let M be a monotone symplectic background and \(C \subset M\) a spherically fibered coisotropic submanifold of codimension \(c \ge 2\). Let \(L^0,L^1 \subset M\) be admissible Lagrangian branes, and suppose that C is equipped with an admissible brane structure as a Lagrangian submanifold of \(M^- \times B\). These conditions imply that all Lefschetz–Bott fibrations discussed below are monotone as in Lemma 4.10. We may assume, after Hamiltonian perturbation, that \(C,L^0,L^1\) all intersect transversally.
Definition 5.3
-
(a)
(Chaps map) The first map in the exact sequence is defined as the relative invariant associated with a “quilted pair of pants,” or more accurately, “quilted chaps” in American dialect. Let \(\underline{S}_1\) denote the quilted surface shown in Fig. 6: Let \((S_B,S_M)\) denote the patches of \(\underline{S}_1\), and \(\underline{E} = (S_M \times M,S_B \times B)\), where B is the base of the fibration \(p: C \rightarrow B\). We identify C with its image in \(M \times B\). Let \(\underline{F}\) denote the Lagrangian seam/boundary condition for \(\underline{E}\) given by \(L^0,L^1,C\) and consider the relative invariant
$$\begin{aligned} \varPhi _1: HF(L^0 ,C, C^t, \tau _C^{-1} L^1;\Lambda )[\dim (B)] \rightarrow HF(L^0, \tau _C^{-1} L^1;\Lambda ) . \end{aligned}$$(44)This invariant was defined in Definition 4.23 by counting points in the zero-dimensional component of the moduli space \({\mathcal {M}}_1\) of pseudoholomorphic quilts on \(\underline{S}_1\).
-
(b)
(Lefschetz–Bott map) The second map in the exact sequence is a relative invariant associated with a Lefschetz–Bott fibration with monodromy given by the Dehn twist. Namely, let \(E_C \rightarrow D\) denote the standard Lefschetz–Bott fibration with monodromy \(\tau _C\) from Lemma 2.13 and Definition 4.26. Gluing in \(E_C\) with the trivial fibration over a strip (using the identity as transition map to the left of the disk, and \(\tau _C\) as transition map to the right) as in Seidel [41, p. 7] gives a Lefschetz–Bott fibration \(({E}_2,{F}_2)\) over the infinite strip shown in Fig. 7. Let
$$\begin{aligned} \varPhi _2: \ HF(L^0, \tau _C^{-1} L^1;\Lambda ) \rightarrow HF(L^0,L^1;\Lambda ) \end{aligned}$$(45)denote the associated relative invariant. Relative invariants were defined in (32) by counting points in the zero-dimensional component of the moduli space \({\mathcal {M}}_2\) of pseudoholomorphic sections of \(E_2 \rightarrow S_2\) with boundary in \(F_2\). (It follows from Theorem 5.5 below that \(\varPhi _2\) has degree zero.)
The first step in the proof of the exact sequence is to show that the composition of the chaps and Lefschetz–Bott maps vanishes:
Lemma 5.4
(Exactness at the middle term) The composition \(\varPhi = \varPhi _2 \circ \varPhi _1\) (the relative invariant associated with picture on the left in Fig. 8) vanishes; more precisely, there exists a null homotopy of the chain-level maps \(C \varPhi _2 \circ C \varPhi _1\) whose terms have positive q-exponent for r sufficiently small.
Proof
The composition of the two relative invariants is the relative invariant associated with a Lefschetz–Bott fibration over the glued surface  by (34). Consider the deformation \(\underline{S}_t\) of \(\underline{S}\) obtained by moving the critical value of the Lefschetz–Bott fibration toward the boundary marked C and pinching off a disk in \(M \times B\) with boundary values in C. This process is shown in the right-most two pictures in Fig. 8. The bundles \(\underline{E}\) and Lagrangian boundary/seam conditions \(\underline{F}\) naturally extend to families \(\underline{E}_t,\underline{F}_t\) that are obtained from gluing for \(t \gg 0\). It follows from Corollary 4.31 that the relative invariant \(C\varPhi \) is null homotopic. \(\square \)
by (34). Consider the deformation \(\underline{S}_t\) of \(\underline{S}\) obtained by moving the critical value of the Lefschetz–Bott fibration toward the boundary marked C and pinching off a disk in \(M \times B\) with boundary values in C. This process is shown in the right-most two pictures in Fig. 8. The bundles \(\underline{E}\) and Lagrangian boundary/seam conditions \(\underline{F}\) naturally extend to families \(\underline{E}_t,\underline{F}_t\) that are obtained from gluing for \(t \gg 0\). It follows from Corollary 4.31 that the relative invariant \(C\varPhi \) is null homotopic. \(\square \)
5.2.2 Exactness to leading order
The proof that the maps \(\varPhi _1,\varPhi _2\) of (44), (45) fit into a long exact sequence follows a standard argument, familiar from Floer’s exact triangle [6]. In this argument, one first proves that the “leading-order terms” in the cochain-level map define a short exact sequence and then applies a spectral sequence to deduce the triangle. Recall that \( L^0 \cap \tau _C^{-1} L^1\) is the disjoint union of the images of \(i_1\) and \(i_2\) of the map in Proposition 5.2.
Theorem 5.5
(Exactness of the short sequence to leading order) Let \(C,L^0,L^1\) be as in Theorem 1.3. There exists \(\epsilon > 0 \) such that for any fibered Dehn twist \(\tau _C\) defined using (41) for \(\lambda \) sufficiently large, the following properties hold:
-
(a)
(Small triangles as leading-order contributions to \(C\varPhi _1\)) If \(x \in ((L^0 \times C) \cap (C^t \times \tau _C^{-1} L^1))\) then \(C\varPhi _1( \langle {x} \rangle )\) is equal to \(q^\nu \langle {i_1(x)} \rangle \) for some \(\nu < \epsilon /2 \), plus terms of the form \(q^\mu \langle {z} \rangle \) with \(\mu > \epsilon \) and \(z \in L^0 \cap \tau _C^{-1} L^1\).
-
(b)
(Horizontal sections as leading-order contributions to \(C\varPhi _2\))
-
(i)
For any \(x \in L^0 \cap L^1\), if \(y=i_2(x)\) then \(C\varPhi _2( \langle {y} \rangle )\) is equal to \( \langle {x} \rangle \) plus terms of the form \(q^\nu \langle {z} \rangle \) with \(z \in {\mathcal {I}}(L^0, L^1)\) and \(\nu > \epsilon \).
-
(ii)
If \(y \ne i_2(x)\) for any x, then \(C\varPhi _2( \langle {y} \rangle )\) is a sum of terms of the form \(q^\nu \langle {z} \rangle \) for \(z \in {\mathcal {I}}(L^0, L^1)\) and \(\nu > \epsilon \).
-
(i)
Furthermore, \(C\varPhi _2\) has zero degree.
Proof
(a) We aim to reduce to the exact, unfibered case considered by Seidel [41].
Step 1: The antipodal case. The simplest case is that in which the points on the spherical fiber are antipodes. That is, let \(x = (m,b,m')\) be as in the statement of the Theorem, so that
Suppose that \(m,m'\) are antipodes:
Let
denote the constant section with value m on the part mapping to M and value b on the part mapping to B. This section satisfies the boundary conditions \(L^0, \tau _C^{-1} L^1,C\), by (46).
We claim that these constant sections give the only contributions to the relative invariant in the antipodal case. Let \(J \in {\mathcal {J}}^h(\underline{E})\) be any horizontal almost complex structure, for which u is a pseudoholomorphic section with zero area:
The map u is J-regular. Indeed, by non-negativity of the curvature and Proposition 4.35, it suffices to show that the index of the linearized operator \(D_{u,J}\) for u the constant section is zero. Since the boundary conditions are constant, we may decompose the boundary conditions into vertical and horizontal parts,
for some vector \(v \in S^c\) representing m in the trivialization of the fiber at b. The linearized operator \(D_u\) breaks into the sum of linearized operators \(D_u^h, D_u^v\) for the horizontal and vertical pieces. The linearized operator \(D_u^h\) for the horizontal piece \(T_b B\) may be identified with a linearized operator on a strip with constant, transverse boundary conditions \(T_b (L_0 \circ C)\) and \(T_b (L_1 \circ C)\). The kernel and cokernel of \(D_u^h\) are trivial; hence, the horizontal piece \(D_u^h\) has index zero. The linearized operator for the vertical piece \(D_u^v\) is equivalent to that for the unfibered case covered in [41, Proof of Lemma 3.3]. Since the kernel and cokernel in this case are also trivial, the cokernel of the linearized operator for u is trivial. Hence J is regular for horizontal u. This implies that we may use J to compute the coefficient of \( \langle {i_1(x)} \rangle \) in \(C \varPhi _1( \langle {x} \rangle )\), and the fact that the required sections are constant in this case proves the claim.
Step 2: Deformation to the antipodal case. We reduce to the antipodal case of the previous paragraphs by a deformation argument. Suppose that \((m,b,m')\) gives a generalized intersection point of \((L^0,C^t,C,L^1)\). Choose a family of identifications \(C_b \cong S^c\) depending on \(t \in [0,1]\) such that for \(t = 1\) the points \(m,m'\) are antipodes in \(C_b\). We extend the pullback metrics on \(C_b\) to a family of fiberwise metrics on C. The family of metrics defines a reduction in the structure group depending on t, that is, a family of principal \(SO(c+1)\) bundles \(P_t\) together with a family of diffeomorphisms
Let \(\tau _C^t\) denote the resulting family of fibered Dehn twists, and consider the family of boundary conditions given by \(\tau _C^t L^0, L^1\). The intersection points \({\mathcal {I}}(\tau _C^t L^0, C^t,C, L^1)\) fit into smooth families depending on t as in the proof of Proposition 5.2. Consider the parametrized moduli space
of pseudoholomorphic curves for this deformation. Standard arguments show that there is a parametrized regular family of almost complex structures for the deformation, in the sense that the moduli space (47) is a smooth, finite-dimensional manifold with boundary. The moduli space is also compact, as long as \(\lambda ^{-1}\) is sufficiently small. Indeed, for \(\lambda ^{-1}\) sufficiently small, bubbling off trajectories in the deformation (47) is impossible by Remark 5.6 below. On the other hand, bubbling off holomorphic disks and spheres is impossible because of the monotonicity conditions. It follows from compactness that the count of holomorphic quilts is invariant under the deformation (47).
We show that the sections contributing to the coefficient of \( \langle {i_1(x)} \rangle \) in \(C\varPhi _1( \langle {x} \rangle )\) are of small area. Suppose \(u: \underline{S}_1 \rightarrow \underline{M}\) is a quilt contained in a neighborhood of \(C_b\) with Lagrangian boundary conditions \(L^0, \tau _C^{-1} L^1, C\) and limits \(x,i_1(x)\). Near \(C_b\) all Lagrangians are exact and path connected. So the area computation reduces to the computation of action differences in [41]. In particular, for these maps, for \(\delta \) sufficiently small, all such u of index 0 (parametrized index 1) connecting \(i_1(x)\) with x have \({{\mathcal {E}}}(u)\) at most \(\epsilon /2\):
This argument shows that the area of small index zero quilts is at most \(\epsilon /2\) for \(\lambda ^{-1}\) sufficiently small. By monotonicity, any holomorphic quilt of index zero with boundary/seam conditions \(L^0, \tau _C^{-1} L^1, C\) has the same area as one of the index zero quilts above.
It follows in particular that sphere and disk bubbling does not occur in these moduli spaces. So the component of the moduli space \({\widetilde{{\mathcal {M}}}}_1( i_1(x),x)\) of formal dimension one is compact. Counting boundary components gives
where \(o(u) = \pm 1\) are the orientations. The second sum in (48) is equal to 1 if the almost complex structure is horizontal. For the unique contribution, it then comes from the horizontal section with value \(i_1(x) = (m,b,m')\). This completes the deformation argument.
Step 3: The higher-order terms. We next show that the pseudoholomorphic sections with limits other than those corresponding to \(i_1,i_2\) have higher energy, using the mean value inequality. Suppose that \(u = (u_0,u_1)\) is a quilt from \(\underline{S}_1\) connecting \(x = (m,b,m')\) with y with energy at most \(\epsilon \) with \(u_1\) resp. \(u_0\) mapping to M resp. B. For any neighborhood U of \(C_b\), there exists \(\epsilon > 0\) sufficiently small so that the image of \(u_1\) is contained in U:
Indeed, let \((s_0,t_0)\) denote the coordinate of the top-most point in the seam. For \(s > s_0 + 1\), integrating the mean value inequality (30) as in Lemma 4.15 over a path \(\gamma _s(t) = (s,t)\) shows that the distance between \(L^0\) and C and the distance between \(\tau _C^{-1} L^1\) and C are at most \(c \epsilon \) for some constant c. In fact, these estimates are independent of the choice of \(\tau _C\). Indeed, the image \(\tau _C^{-1}(L^1)\) is independent of \(\tau _C\) in a neighborhood of \(L^0 \cap L^1\). On the other hand, \(\tau _C^{-1}(L^1)\) converges to \(\pi ^{-1} \pi (L^1 \cap B)\) as \(\zeta (0) \rightarrow 0\). As in Lemma 4.4, let \(V_\epsilon \) be the set of points in X within distance \(c\epsilon \) of both \(L^0\) and \(\tau _C^{-1} L^1\). Since \(L^0,\tau _C^{-1} L^1\) are compact, for \(\epsilon \) sufficiently small, \(V_\epsilon \) is a collection of disjoint open neighborhoods of the points in \(L^0 \cap \tau _C^{-1} L^1\):
It follows that if u has sufficiently small energy then every point with \(s > s_0 + 1 \) maps to \(V_\epsilon \), hence \(V_\epsilon (x)\). Similarly, for \(s < s_0 - 1\), one obtains by “folding” a strip with values in \(M \times B \times M\) with boundary values \(L^0 \times C\) and \(C^t \times \tau _C^{-1} L^1\). Integrating the mean value inequality (30) over paths to the boundary \(\gamma _s(\tau ) = (s,t + \tau )\) or \(\gamma _s(t) = (s,t- \tau )\) shows that
In particular, note that the intersection \( (L^0 \circ C) \cap (\tau _C^{-1} L^1 \circ C)\) is transverse and independent of \(\tau _C\). Hence the projections \(\pi _1(u(s,t))\) and \(\pi _3(u(s,t))\) are contained a small neighborhood W of \(\pi ^{-1}( (C \circ L^0) \cap (C \circ \tau _C^{-1} L^1))\) in M. It follows that u takes values in W for all \(s < s_0 - 1\). Applying Lemma 4.15 again, this time for a path of the form \(\gamma (t) = [s_0 + 2t, k]\) for \(k \in \{ 0,1\}\) shows the same holds for points in the boundary of the intermediate region. Now \(i_1(x)\) is the unique intersection point of \(L^0 \cap \tau _C^{-1}L^1\) connected to \(L^0 \cap C_b\) by a path from m in \(L^0 \cap W\), and a path from \(m'\) in \(\tau _C^{-1} L^1 \cap W\), as in the proof of Proposition 5.2. Thus \(y = i_1(x)\).
(b) The second part of the Lemma is somewhat easier, since the leading-order terms have order exactly zero arising from the horizontal sections.
Step 1: We show that the degree zero terms arise from horizontal sections. Let u be the horizontal section of \(E_2\) on the infinite strip with value x. Then \( {\text {Ind}}(D_{u,J}) = 0\), since the boundary conditions are constant. Hence u is regular for horizontal J, and the count for \(y = i_1(x)\) follows by Proposition 4.36. The map \(\varPhi _2\) has degree 0, since the horizontal sections have zero index. Because of the non-negative curvature of the standard Lefschetz–Bott fibration in 4.20, any non-horizontal section has positive area. Thus the q-exponent-zero terms arise only from horizontal sections.
Step 2: The non-horizontal sections satisfy a uniform energy gap condition as in the Lemma. For an almost complex structure pulled back from one for \((L^0,C^t,C,L^1)\) under \({\text {Id}}_M \times {\text {Id}}_B \times \tau _C^{-1}\); this is an immediate consequence of Gromov compactness and preservation of area and index under the pullback. The following alternative argument using the mean value inequality holds for any almost complex structure used to define the relative invariant: Suppose u is a section of energy less than \(\epsilon \). By Lemma 4.15, for \(\epsilon \) small u takes values in the set U of points in M within distance \(c\epsilon \) of both \(L^0\) and \(L^1\). By Lemma 4.4, \(U_\epsilon \) is a collection of disjoint open neighborhoods of the points in \(L^0 \cap L^1\):
Since u(s, t) lies in \(U_\epsilon (x)\) for s sufficiently large, this implies that
For the points in \([-1,1] \times \{ 0, 1 \}\), integration applied to the path from (s, 0) to (1, 0) to \((-1,1)\) shows that (again for \(\epsilon \) sufficiently small)
Then another application of integration shows that
as well. Thus u has the same limit x at \(s = -\infty \) as \(s = \infty \). On the intermediate region \(s \in [-1,1], t \in [0,1]\) on a neighborhood of x the section corresponds to a map to M. An argument using Lemmas 4.4 and 4.15 shows that u takes values in \(U_\epsilon (x)\) everywhere. In this neighborhood \(L^0,L^1\) may be assumed to be exact. Thus case u has zero area and, by the vanishing of the curvature in this region, must be horizontal. \(\square \)
Remark 5.6
(Energy gap for Floer trajectories) Let \(C,L^0,L^1\) be as in the previous two Lemmas. We claim that there exists \(\lambda \) sufficiently large such that any non-constant Floer trajectory for \((L^0,C^t,C,\tau _C^{-1}L^1)\) or \((L^0,\tau _C^{-1}L^1)\) has symplectic area at least \(\epsilon \). We consider only the case of trajectories \(u: \mathbb {R}\times [0,1] \rightarrow M\) for \((L^0,\tau _C^{-1}L^1)\); the case of trajectories for \((L^0,C^t,C,\tau _C^{-1}L^1)\) is similar. Choose an open neighborhood U of m disjoint from \(L^1\). Each component of \(\tau _C^{-1}L^1 \cap U \) converges to \(p^{-1}(p(C \cap L^1))\cap U\) as \(\lambda \rightarrow \infty \) as smooth submanifolds. The discussion above, again using Lemma 4.15, shows that if u has sufficiently small area A(u) then the image \(u(\mathbb {R}\times [0,1])\) is contained in a small neighborhood of either some intersection point \(m \in L^0 \cap L^1\) or an intersection point in \(m \in L^0 \cap \tau _C^{-1}L^1\). Since each component of \(\tau _C^{-1}L^1 \cap U \) contains at most one intersection point with m and the image of the \(\mathbb {R}\times \{ 1 \}\) under u is connected, this implies that any index one trajectory u connects an intersection point m to itself and is homotopic to the trivial trajectory. Hence u has vanishing area.
5.2.3 Isomorphism with the mapping cone
Every mapping cone of cochain complexes gives rise to an exact triangle. To construct an exact triangle, it suffices to prove an isomorphism of a third complex with a mapping cone. So to prove Theorem 1.3 in the unquilted case (of simple Lagrangians \(L^0,L^1\)), it suffices to show the following:
Theorem 5.7
(Isomorphism with the mapping cone) Let \(L^0,L^1,\epsilon ,\tau _C\) as in Theorem 1.3. Then the map \(C\varPhi _{2}\) induces an isomorphism of \(CF(L^0,\tau _C^{-1} L^1)\) with the mapping cone on \(C\varPhi _{1}\).
Before we give the proof of the theorem, we recall a bit of homological algebra, explained, for example, in [13].
Remark 5.8
-
(a)
(Mapping cone) If \(C_j= (C_j,\partial _j), j = 0,1\) are cochain complexes and \(f:C_0 \rightarrow C_1\) is a cochain map, then the mapping cone on f is the complex
$$\begin{aligned} {\text {Cone}}(f) := C_0[1] \oplus C_1, \ \ \partial (c_0,c_1) = (-\partial _0 c_0,\partial _1 c_1 + f(c_0)) . \end{aligned}$$ -
(b)
(Quasi-isomorphisms from mapping cones) A cochain map from \({\text {Cone}}(f)\) to a complex \(C_2\) is equivalent to pair (k, h) consisting of a cochain map \(k:C_1 \rightarrow C_2\) together with a cochain homotopy
$$\begin{aligned} h: C_0 \rightarrow C_2, \quad k \circ f = h \partial _0 + \partial _2 h . \end{aligned}$$Such a map induces a quasi-isomorphism if and only if \({\text {Cone}}(k[1]\oplus h)\) is acyclic.
We will need the following criterion for a cochain map (k, h) as in Remark 5.8 (b) to induce a quasi-isomorphism, similar to that in Seidel [41] and Perutz [35, Lemma 5.4]. By an \(\mathbb {R}\)-graded \({\Lambda }\)-cochain complex, we mean a \(\Lambda \)-linear cochain complex equipped with an \(\mathbb {R}\)-grading so that multiplication by \(q^\lambda \) shifts the grading by \(\lambda \).
Lemma 5.9
(Double mapping cone lemma) Suppose that \(C_0,C_1\), and \(C_2\) are free, finitely generated \(\mathbb {R}\)-graded \({\Lambda }\)-cochain complexes with differentials \(\delta _0,\delta _1,\delta _2\). Suppose that
is a sequence of cochain maps (not necessarily exact at the middle term) and \(h: C_0 \rightarrow C_2\) a null homotopy of \(k \circ f\). Assume
-
(a)
The differentials \(\delta _0, \delta _1, \delta _2\) each have positive order while h has non-negative order.
-
(b)
We have \(f = f_0 + f_1\), \(k = k_0 +k_1\), where \(f_0 , k_0\) have order zero while \(f_1, k_1\) have positive order.
-
(c)
The leading-order terms \(f_0,k_0\) give a short exact sequence of abelian groups (not necessarily cochain complexes)
$$\begin{aligned} 0 \rightarrow C_0 \mathop {\rightarrow }\limits ^{f_0} C_1 \mathop {\rightarrow }\limits ^{k_0} C_2 \rightarrow 0 \end{aligned}$$
Then the induced map \((h, k) : {\text {Cone}}(f) \rightarrow C_2\) is a quasi-isomorphism.
Proof
The proof is similar to that in Perutz [35, Lemma 5.4]. The leading-order differential in \(C := {\text {Cone}}({\text {Cone}}(f),C_2)\) is acyclic by standard homological algebra: Given \((c_0,c_1,c_2)\) with leading-order coboundary \(( 0, f_0(c_0), k_0(c_1) + h_0(c_0)) = 0\), we have \(c_0 =0 \) since \(f_0\) is injective, and so \(k_0(c_1) = 0\). Hence \(c_1 = f_0(b_0)\) for some \(b_0 \in C_0\). Now \(h_0(b_0) = - b_2\) for some \(b_2 \in C_2\) and \(c_2 + b_2= k_0(b_1)\) for some \(b_1 \in C_1\). So the coboundary of \((b_0,b_1,b_2)\) is \((0,c_1,c_2+ b_2 - b_2) = (c_0,c_1,c_2)\) as desired. Since all maps f, h, k have finitely many terms, there exists an \(\epsilon > 0\) such that, if \(C^{\ge n} \subset C\) is the subcomplex of terms with order in \([n \epsilon ,\infty )\), the first page of the associated spectral sequence has vanishing cohomology. It follows that C is itself acyclic. \(\square \)
Proof of Theorem 5.7
We apply Lemma 5.9 to the Floer complexes
Let k denote the cochain-level map \(C \varPhi _{1,\Lambda }\) defined by the quilted surface in Fig. 6. For any \(x \in {\mathcal {I}}(L^0 ,C^t,C,\tau _C^{-1} L^1)\), \(z \in {\mathcal {I}}(L^0, L^1)\), consider the parametrized moduli space \({\widetilde{{\mathcal {M}}}}(x,z)\) for the one-parameter family of deformations \((\underline{E}_\rho ,\underline{F}_\rho )\) (with \(\rho \) representing the length of the neck) connecting the pair obtained by gluing \((\underline{E}_1,\underline{F}_1)\) and \(({E}_2,{F}_2)\) along a strip-like end to the nodal surface equipped with bundles \((\underline{E},\underline{F}), (\underline{E}_{C,r},\underline{F}_{C,r})\), as shown in Fig. 8. An element of \({\widetilde{{\mathcal {M}}}}(x,z)\) consists of a quilted surface \(\underline{S}^\rho \) in the family, together with a pseudoholomorphic quilt \(u^\rho \) with the given boundary and seam conditions.
As in the proof of Corollary 4.31, for r sufficiently small and \(\rho \) sufficiently large the parametrized moduli space is empty. The boundary of \({\widetilde{{\mathcal {M}}}}(x,z)_1\) is therefore
where
-
the first union consists of pairs of pseudoholomorphic sections of \(\underline{E}_1\) and \(\underline{E}_2\), and
-
the second two unions correspond to bubbling off Floer trajectories \([u] \in {\mathcal {M}}(y,z)_0\) in M or a Floer trajectory \( [u] \in {\mathcal {M}}(x,y)_0\) in \(M \times B \times M\).
Define a map
by
where \(o(u) = \pm 1\) are the orientations constructed in [48]. The description of the boundary components of \({\widetilde{{\mathcal {M}}}}(x,z)_1\) in (50) gives the relation \( \partial h + h \partial = k \circ f \). By Remark 5.8 the pair (k, h) define a morphism \( {\text {Cone}}(f) \rightarrow C_2 .\) We claim that the mapping cone
is acyclic. Theorem 5.5 shows that for Dehn twists satisfying the conditions in the Theorem, the differential \(\partial \) splits into the sum of an operator \(\partial _0\) whose q-exponents lie in \([0,\epsilon /2)\) and a term \(\partial - \partial _0\) whose q-exponents lie in \((\epsilon ,\infty )\). Because of the bijection (42) there exists an \(\mathbb {R}\)-grading on \(C_0,C_1,C_2\) so that the contributions to \(\partial \) separates into a leading-order part \(\partial _0\) with \(\mathbb {R}\)-degree zero, and vanishing cohomology, and a remaining part with \(\mathbb {R}\)-degree at least \(\epsilon /2\). By Lemma 5.4, there exists a null homotopy of \(k \circ f\) to the identity. By Remark 5.6, for \(\delta \) sufficiently small the conditions of Lemma 5.9 hold. The result for \({\Lambda }\) coefficients follows. Note that here in contrast to the case in Perutz [35] the differentials have finitely many terms, so the formal completion is not necessary. The result for \(q = 1\) follows by specialization as in Remark 4.3. \(\square \)
The quilted version of Theorem 1.3, where \(\underline{L}^0,\underline{L}^1\) are generalized Lagrangian branes, is proved similarly, but replacing the boundary labeled \(L^0,L^1\) with collections of strips corresponding to the symplectic manifolds appearing in the generalized Lagrangian branes \(\underline{L}^0,\underline{L}^1\). The details are left to the reader.
Remark 5.10
Under strong monotonicity assumptions as in Definition 4.28, the statement of Theorem 1.3 also holds in the case of codimension one coisotropics. This case is proved similarly but now using the cancelation discussed in Remark 4.30.
5.3 Minimal Maslov two case
In general, Lagrangian Floer cohomology is defined only the case that certain holomorphic disk counts vanish. In the case that one of the Lagrangians has minimal Maslov number two, the relevant disk count is that of Maslov index two holomorphic disks. First we recall some basics of the derived category of matrix factorizations from [47].
Definition 5.11
-
(a)
(Category of matrix factorizations) For any \(w \in \mathbb {Z}\), let \({\text {Fact}}(w)\) denote the category of factorizations of \(w{\text {Id}}\).
-
(i)
The objects of \({\text {Fact}}(w)\) consist of pairs \((C,\partial )\), where
$$\begin{aligned} C = C = C^0 \oplus C^1 \end{aligned}$$is a \(\mathbb {Z}_2\)-graded free abelian group and \(\partial \) is a group homomorphism squaring to a multiple of the identity:
$$\begin{aligned} \partial : C^\bullet \rightarrow C^{\bullet + 1} , \quad \partial ^2 = w{\text {Id}}. \end{aligned}$$ -
(ii)
For objects \((C,\partial ),(C',\partial ')\), the space of morphisms
$$\begin{aligned} {\text {Hom}}_{{\text {Fact}}}((C,\partial ),(C',\partial ')) \end{aligned}$$is the space of grading preserving maps intertwining the “differentials”
$$\begin{aligned} f: C^\bullet \rightarrow (C')^\bullet , \quad f \partial = \partial ' f . \end{aligned}$$
-
(i)
-
(b)
(Cohomology) For any matrix factorization \((C,\partial )\), let \(H((C,\partial )\otimes _\mathbb {Z}\mathbb {Z}_w)\) denote the cohomology of the differential \(\partial \otimes _\mathbb {Z}\mathrm{Id} : C \otimes _\mathbb {Z}\mathbb {Z}_w \rightarrow C\otimes _\mathbb {Z}\mathbb {Z}_w \) obtained from \(\partial \) by tensoring with \(\mathbb {Z}_w\). Any morphism in \({\text {Fact}}(w)\) defines a homomorphism of the corresponding cohomology groups. The cohomology with coefficients functor has target the category \({\text {Ab}}\) of \(\mathbb {Z}_2\)-graded abelian groups,
$$\begin{aligned} {\text {Fact}}(w) \rightarrow {\text {Ab}}, \ \ (C,\partial ) \mapsto H( (C,\partial ) \otimes _\mathbb {Z}\mathbb {Z}_w) . \end{aligned}$$
We recall the definition of the Maslov index two disk count studied in Oh [32]. Let M be a symplectic background and \(L \subset M\) be a compact Lagrangian submanifold with minimal Maslov number equal to 2. For any \(\ell \in L\), consider the moduli space \({\mathcal {M}}^1_2(L,J,\ell )\) of J-holomorphic disks \(u:(D,\partial D) \rightarrow (M,L)\) with Maslov number 2, mapping a point \(1 \in \partial D\) to \(\ell \), modulo automorphisms preserving 1. By results of Kwon and Oh [20] and Lazzarini [22], for J in a comeager subset \({\mathcal {J}}^{{{\text {reg}}}}(M,L) \subset {\mathcal {J}}(M)\) the moduli space \({\mathcal {M}}^1_2(L,J,\ell )\) is a finite set. Suppose L is equipped with a relative spin structure. By [12], see also [48], this structure induces an orientation on the moduli space \({\mathcal {M}}^1_2(L,J,\ell )\). Let
denote the map comparing the given orientation to the canonical orientation of a point.
Definition 5.12
(Disk invariant of a Lagrangian) Let M be a monotone symplectic background and \(L \subset M\) a compact monotone Lagrangian brane with minimal Maslov number equal to 2. The disk invariant of L is the sum
The element w(L) is independent of \(J \in {\mathcal {J}}^{{\text {reg}}}(M,L)\) and \(\ell \in L\).
Denote by \({\mathcal {J}}_t(M,L^0,L^1) \subset {\mathcal {J}}_t(M)\) the subset of t-dependent almost complex structures whose restriction to a fixed small neighborhood of \( t = 0\) resp. \(t = 1\) lies in \({\mathcal {J}}^{{\text {reg}}}(M,L^0)\) resp. \({\mathcal {J}}^{{\text {reg}}}(M,L^1)\).
Proposition 5.13
(Floer cohomology) Let \(L^0,L^1\) compact Lagrangian branes with minimal Maslov number equal to 2. There exists a comeager subset \({\mathcal {J}}^{{\text {reg}}}_t(M,\omega ,L^0,L^1) \subset {\mathcal {J}}_t(M,\omega ,L^0,L^1) \) such that
-
(a)
\(\partial ^2 = (w(L^0) - w(L^1)){\text {Id}}\).
-
(b)
\((CF(L^0,L^1;\Lambda ), \partial )\) is independent of the choice of J, H up to cochain homotopy.
If \(L^k \subset M, k= 0,1\) are monotone Lagrangian branes with the same disk invariant, then the exact triangle in Theorem 1.3 holds, with the same proof. More generally, the disk invariant for a generalized Lagrangian brane \(\underline{L} = (L_1,\ldots , L_k)\) is the sum of the disk invariants for the components \(L_1, \ldots , L_k\). Furthermore, the disk invariant for a correspondences \(L_{01} \subset M_0^- \times M_1\) is the opposite of the disk invariant for its transpose \(L_{01}^t \subset M_1^- \times M_0\), because the change in complex structure reverses orientations on Maslov index two disks [48]. With these conventions, the quilted version of Theorem 1.3 also holds provided that the disk invariants of the generalized correspondences \(\underline{L}^0,\underline{L}^1\) are equal.
5.4 Periodic Floer version
One can also formulate a version of the exact triangle for symplectomorphisms, that is, in periodic Floer theory. In this formulation, the exact triangle relates the symplectic Floer cohomology of the Dehn twist with the Lagrangian Floer cohomology of the vanishing cycle and the identity:
Theorem 5.14
(Exact triangle in periodic quilted Floer theory) Let \(M,C,B,\tau _C\) be as in Theorem 1.3. There exists a long exact sequence of Floer cohomology groups

The ideas are similar to the case of Lagrangian Floer cohomology in Theorem 1.3, and we only sketch the proof. The map \(HF({\text {id}}) \rightarrow HF(\tau _C)\) is the relative invariant corresponding to a Lefschetz–Bott fibration over the cylinder in Fig. 9. In the figure, the outer and inner boundaries represent cylindrical ends, where the former has monodromy \(\tau _C\). The map \(HF(C^t,C) \rightarrow HF({\text {id}})\) is the relative invariant associated with the quilted cylinder in Fig. 10. In the figure, the outer boundary represents a cylindrical end, while the inner boundary represents a quilted cylindrical end with seams labeled \(C^t,C\). The proof is similar to that of Theorem 1.3. Namely, we have identifications
where \(L^0 = L^1 = \Delta \) is the diagonal in \(M^2\). There is a natural bijection
this amounts to repeating the argument of Proposition 5.2. The same filtration arguments as before are used to construct an exact triangle of quilted Floer cohomology groups

Now functoriality of quilted Floer cohomology groups under the symplectomorphism \(\tau _C\) gives an exact triangle

Using the identifications in (52), this proves Theorem 5.14. With integer coefficients, there is a complication caused by the fact that the diagonal correspondence \(\Delta \) does not have a canonical relative spin structure. The argument works only after treating the diagonal as the “empty correspondence,” see Sect. 7.2 below.
6 Applications to surgery exact triangles
In this section, we apply the exact triangle to obtain versions of the Floer [10], Khovanov [17], and Khovanov–Rozansky [19] exact triangles. We have already established in Sect. 3 that Dehn twists of surfaces induce fibered Dehn twists of moduli spaces.
6.1 Exact triangle for three bordisms
In [46], we introduced a category-valued field theory associated with certain connected, decorated surfaces and bordisms. We use freely the notation and terminology from [46]:
Definition 6.1
-
(a)
(Decorated surface) A decorated surface is a compact connected oriented surface X equipped with a line bundle with connection \(D \rightarrow X\). The degree of D is the integer \(d = (c_1(D),X)\).
-
(b)
(Decorated bordisms) A bordism from \(X_-\) to \(X_+\) is a compact, oriented three-manifold Y with boundary equipped with an orientation-preserving diffeomorphism
$$\begin{aligned}\phi : \partial Y \rightarrow \overline{X}_- \sqcup X_+ . \end{aligned}$$Here \(\overline{X}_-\) denotes the manifold \(X_-\) equipped with the opposite orientation. We often omit \(\phi \) from the notation and assume that \(X_-,X_+\) are boundary components of Y. A decorated bordism of degree d is a compact connected oriented bordism Y between decorated surfaces \((X_\pm ,D_\pm )\) equipped with a line bundle with connection \(D \rightarrow Y\) such that \(D | X_\pm = D_\pm \). Given a decorated bordism (Y, D) between \((X_\pm ,D_\pm )\), one can obtain another decorated bordism by tensoring D with any line bundle that is trivial on the boundary of Y.
-
(c)
(Moduli spaces for decorated surfaces) Suppose that X is a decorated surface with line bundle D. Let M(X, D) denote the moduli space of constant curvature rank 2 bundles on X with fixed determinant. The space M(X, D) is a compact, monotone symplectic manifold with monotonicity constant 1 / 4 with a unique Maslov cover of any even order. In [46], we describe how to equip M(X, D) with the background classes so that M(X, D) is equipped with the structure of a symplectic background.
-
(d)
(Correspondences for decorated bordisms) Suppose that Y is a decorated surface with line bundle D between decorated surfaces \((X_-,D_-)\) and \((X_+,D_+)\). Let
$$\begin{aligned} L(Y,D) \subset M(X_-,D_-)^- \times M(X_+,D_+) \end{aligned}$$denote the set of isomorphism classes of constant central curvature bundles with fixed determinant that extend over the interior of Y. If Y is an elementary bordism (i.e., admits a Morse function with a single critical point), then L(Y, D) is a smooth Lagrangian correspondence. In [46] we describe how to equip L(Y, D) with relative spin structures and gradings, so that L(Y, D) has the structure of an admissible Lagrangian brane.
For the purposes of the exact triangle, we will need an alternative description as flat bundles with fixed holonomy around an additional marking.
Definition 6.2
-
(a)
(Marked surfaces) For any integer \(n \ge 0\), an n marked surface is a compact oriented surface X equipped with a tuple \(\underline{x} = (x_1,\ldots , x_n)\) of distinct points on X and a labeling \(\underline{\mu } = (\mu _1,\ldots ,\mu _n)\). In this section, we take labels all equal to 1 / 2 corresponding to the central element \(-I\) of \(\mathfrak {A}\).
-
(b)
(Moduli spaces for marked surfaces) Denote by \(M(X,\underline{\mu })\) the moduli space of flat bundles on \(X - \underline{x}\) with holonomy \(-I\) around each marking \(x_i\); we consider more general holonomies in the next subsection. The moduli space \(M(X,\underline{\mu })\) may be identified with the moduli space M(X, D) where D is a line bundle of degree n, by a construction described in Atiyah and Bott [5] given by twisting by a fixed central connection.
-
(c)
(Marked bordisms) A marked bordism from \((X_-,\underline{x}_-)\) to \((X_+,\underline{x}_+)\) is a compact, oriented bordism Y equipped with a tangle (compact oriented one-dimensional submanifold transverse to the boundary) \(K \subset Y\) such that \(K \cap X_\pm = \underline{x}_\pm \).
-
(d)
(Moduli spaces for marked bordisms) Denote by
$$\begin{aligned} L(Y,K) \subset M(X_-,\underline{\mu }_-)^- \times M(X_+,\underline{\mu }_+) \end{aligned}$$the moduli space of bundles that extend over \(Y - K\) with holonomy \(-I\) around K. The identification \(M(X_\pm ,\underline{\mu }_\pm ) \rightarrow M(X_\pm ,D_\pm )\) induces a homeomorphism \(M(Y,K) \rightarrow M(Y,D)\) where \(D \rightarrow Y\) is a line bundle whose first Chern class is dual to the tangle K. Thus, in particular, the addition to K of a circle component \(K'\) corresponds to twisting the determinant line bundle D by a line bundle whose first Chern class is dual to the homology class of \(K'\).
The following proposition relates the moduli spaces of bundles with fixed holonomy around an embedded circle with the Lagrangian correspondences associated with elementary bordisms.
Proposition 6.3
(Correspondences for elementary bordisms)
-
(a)
Let Y be a bordism from \(X_-\) to \(X_+\) containing a single critical point of index 1 and a trivial tangle K (i.e., a union of intervals connecting \(\underline{x}_-\) to \(\underline{x}_+\)) and \(C \subset X_+\) is the attaching cycle. The Lagrangian L(Y, K) is diffeomorphic via the projection to \(M(X_+,\underline{\mu }_+)\) to the subset of connections on \(X_+ - \underline{x}_+\) with holonomy along C equal to I.
-
(b)
Let Y be a decorated bordism from \(X_-\) to \(X_+\) containing a single critical point of index 1, \(C \subset X_+\) the attaching cycle, \(K_0\) a trivial bordism connecting \(\underline{x}_-\) to \(\underline{x}_+\) and \(K_1 \subset Y\) the unstable manifold of the critical point. The Lagrangian \(L(Y,K_0 \cup K_1)\) is diffeomorphic to the subset of flat bundles on \(X_+ - \underline{x}_+\) with holonomy along C equal to \(-I\).
Proof
By Seifert–van Kampen, \(\pi _1(Y - K)\) is the quotient of \(\pi _1(X_+ - K)\) by the ideal generated by the element [C] obtained from C by joining by a path to the base point. Hence in the first case, L(Y, K) is diffeomorphic to the submanifold of \(M(X,\underline{\mu }_+)\) obtained by setting the holonomy along C equal to the identity. For the second case, the gradient flow the Morse function defines a deformation retract of \(Y - K_0 - K_1\) to \(X_+ - \underline{x}_+\). Homotopy invariance implies that \(\pi _1(Y - K_0 - K_1 )\) is isomorphic to \(\pi _1(X_+ - \underline{x}_+)\). Since C is a loop around \(K_1\), the holonomy around \(K_1\) is equal to the holonomy along C, hence the claim. \(\square \)
In order to obtain smooth Lagrangian correspondences, we break the given bordism into elementary bordisms.
Definition 6.4
-
(a)
(Cerf decompositions) A Cerf decomposition of a bordism Y is a decomposition of Y into elementary bordisms \(Y_1,\ldots ,Y_K\), that is, bordisms admitting a Morse function with at most one critical point. Associated with any Cerf decomposition
$$\begin{aligned} Y = Y_1 \cup _{X_1} \ldots \cup _{X_{k-1}} Y_k \end{aligned}$$and a decoration on Y is a generalized Lagrangian correspondence
$$\begin{aligned} \underline{L}(Y) = (L(Y_1),\ldots , L(Y_k)) . \end{aligned}$$ -
(b)
The generalized correspondence \(\underline{L}(Y)\) may be equipped with a relative spin structure via its structure as a fibration over the moduli space of the incoming or outgoing surface. Thus \(\underline{L}(Y)\) gives rise to a functor of generalized Fukaya categories
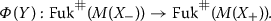
This functor is independent of the choice of Cerf decomposition [46].
-
(c)
Given admissible Lagrangian branes \(L^\pm \subset M(X_\pm )\), define

where the second equality is by definition of the Fukaya category. Since we have ignored absolute gradings, this is a relatively \(\mathbb {Z}_4\)-graded group depending only on the equivalence class of the decorated bordism Y.
We prove the following surgery exact triangle for the invariants \(HF(Y;L^-,L^+)\).
Definition 6.5
-
(a)
(Knots) A knot in a bordism Y is an embedded, connected one-manifold \(K \subset Y\) disjoint from the boundary.
-
(b)
(Knot framings) A framing of a knot \(K \subset Y\) is a nonvanishing section of its normal bundle up to homotopy. Given a framed knot, the other framings are obtained by twisting by representations of \(\pi _1(K) \cong \mathbb {Z}\) into SO(2) and so are indexed by \(\mathbb {Z}\).
-
(c)
(Knot surgeries) For \(\lambda \in \mathbb {Z}\) the \(\lambda \)-surgery \(Y_{\lambda ,K}\) of Y along K is obtained by removing a tubular neighborhood of K and gluing in a solid torus \(D^2 \times S^1\) so that the meridian \(\partial D^2 \times \{ {\text {pt}}\}\) is glued along the curve given by the framing of the knot corresponding to \(\lambda \). Denote by \(K_\lambda \) the knot in \(Y_{\lambda ,K}\) corresponding to a longitude in \(\partial D^2 \times S^1\). Thus \(K_\lambda \) intersects the meridian transversally once.
Remark 6.6
(Knot surgeries in terms of decompositions into elementary bordisms) The three manifolds \(Y_{0,K},Y_{-1,K}\) obtained by a 0 resp. \(-1\)-knot surgery have decompositions into elementary bordisms given as follows. Suppose that Y is decomposed into elementary bordisms \(Y_1,\ldots , Y_l\), so that K is contained in the boundary \((\partial Y_i)_+ = (\partial Y_{i+1})_-\) and the framing is the direction normal to the boundary. Gluing in \(D^2 \times S^1\) produces two new critical points. The first critical point has stable manifold with unit sphere equivalent to K and the second has unstable manifold with unit sphere equivalent to K. Thus
-
(a)
The zero-surgery \(Y_{0,K}\) has a decomposition into elementary bordisms with two additional pieces, \(Y_\cup , Y_\cap \) inserted between \(Y_i\) and \(Y_{i+1}\). The knot \(K_0 \subset Y_{0,K}\) is divided into the two additional pieces \(K_0 \cap Y_\cup \) and \(K_0 \cap Y_\cap \). The correspondence \(L(Y_\cup , Y_\cup \cap K_0) \circ L( Y_\cap ,Y_\cap \cap K_0)\) is the correspondence associated with the moduli space of bundles \(L(Y_\cup ) \circ L(Y_\cap )\) on the decorated surface \(Y_\cup \cup Y_\cap \) with the shifted line bundle as in Proposition 6.3.
-
(b)
The \(-1\) surgery \(Y_{-1,K}\) has decomposition into simple bordisms \(Y_1,\ldots , Y_l\) but where the identification \((\partial Y_i)_+ \rightarrow (\partial Y_{i+1})_-\) is the Dehn twist along K.
Lemma 6.7
(Existence of Cerf decompositions compatible with a knot) For any framed knot \(K \subset Y\), there exists a Cerf decomposition \(Y= Y_1 \cup \ldots \cup Y_l\) so that K is contained in the boundary \((\partial Y_i)_+ = (\partial Y_{i+1})_-\) for some \(i = 1,\ldots , l\) and the framing is the direction normal to the boundary.
Proof
Choose a Morse function \(f: Y \rightarrow \mathbb {R}\) such that f is constant on K and the framing is given by the gradient of f at K. The level set \(f^{-1}(\lambda )\) containing K can be made connected by adding 1-handles in Y, so that \(f^{-1}(\lambda )\) becomes a connected surface containing K separating the boundary components of Y. By taking a self-indexing Morse function on \(f^{-1}(\pm \infty ,\,\lambda ], f\) can be deformed away from \(f^{-1}(\lambda )\) so that f is Morse and has connected fibers. \(\square \)
Theorem 6.8
(Exact triangle for knot surgery) Let Y be a decorated bordism from \(X_-\) to \(X_+\), let \(K \subset Y\) be a framed knot contained in the interior of Y, and let \(Y_{-1,K},Y_{0,K}\) denote the \(-1\) and 0-surgeries on K. Let \(L^-,L^+\) be admissible Lagrangian branes in \(M(X_\pm )\). There is a long exact sequence of (relatively graded) Floer cohomology groups
where the determinant bundle on \(Y_{0,K}\) has been shifted by the dual class of the knot \(K_0 \subset Y_{0,K}\), or equivalently, \(Y_{0,K}\) is considered as a marked bordism with knot \(K_0\).
Proof
By combining Remark 6.6, Lemma 6.7, and Theorem 3.8, the statement becomes a special case of Theorem 1.3: Let \(Y = Y_- \cup _X Y_+\) be a decomposition into compression bodies with \(K \subset X\) a non-separating knot and \(\tau \) a corresponding Dehn twist. We have an exact sequence
The addition of the knot \(K_0\) is equivalent to a shift in the determinant line bundle, as explained in Remark 6.6; we thank Guillem Cazassus for pointing out the missing shift in an earlier version of the paper. \(\square \)
Remark 6.9
(Dehn twists for separating curves) We do not discuss here the exact triangle for a Dehn twist around a separating curve, because the moduli space M does not satisfy the “strong monotonicity” condition of Definition 4.28. Instead, one needs to establish positivity properties of the form \(c_1(M_C) - [B_-] - [B_+]\) with respect to the canonical complex structure on the moduli space of parabolic bundles \(M_C\). This seems like to hold but would take us outside the framework of this paper.
6.2 Exact triangles for tangles
We obtain Floer-theoretic invariants of tangles constructed in [47] exact triangles that are the same as those obtained by Khovanov [17, 18] and Khovanov–Rozansky [19]. We assume freely the terminology from [47], in particular the terminology for moduli spaces of bundles with fixed holonomy for marked surfaces. In this subsection, we take \(G = SU(2)\) and \(\mathfrak {A}\cong [0,1/2]\) via the identification (12).
Definition 6.10
(Functors for bordisms with tangles via flat bundles with fixed holonomy)
-
(a)
(Correspondences for elementary tangles) Let \(X_\pm \) be a compact, oriented surface with odd numbers of markings \(\underline{x}_\pm \) admissible labels \(\underline{\mu }_\pm \) all equal to \(1/4 \in \mathfrak {A}\). Let \(K \subset Y: =X \times [-1,1]\) be a tangle, that is, a bordism between marked surfaces \((X_-,\underline{\mu }_-)\) and \((X_+,\underline{\mu }_+)\). Let \(M(X_\pm ,\underline{\mu }_\pm )\) denote the moduli space of SU(2) bundles in Definition 3.1. Let L(K) denote the subset of \(M(X_-,\underline{\mu }_-)^- \times M(X_+,\underline{\mu }_+)\) of bundles that extend over the interior of the bordism. Assuming that K is elementary (admits a Morse function with at most one critical point on K, and none on Y), the Lagrangian L(K) has an admissible brane structure [47].
-
(b)
(Functors for tangles) More generally, let \(K \subset Y = X \times [-1,1]\) be an arbitrary tangle, and \(K = K_1 \cup \ldots \cup K_r\) a decomposition into elementary tangles. Associated with each elementary tangle \(K_i\) is a Lagrangian correspondence \(L_i\) and so a generalized Lagrangian correspondence associated with K
$$\begin{aligned} \underline{L}(K) = (L_1,\ldots , L_r ) . \end{aligned}$$Composing the functors \(\varPhi (L_i)\) for these correspondences gives a functor

In [47], we proved that \(\varPhi (K)\) is independent, up to isomorphism, of the choice of decomposition \(K_1 \cup \ldots \cup K_r\).
-
(c)
(Group valued invariants) Given objects
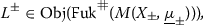
such that the sum of disk invariants for \(L^{-},\;L(K),\;L^{+}\) is zero, the cohomology

is a (\(\mathbb {Z}_2\)-relatively graded) invariant of K.
We prove the following surgery exact triangle for these invariants.
Definition 6.11
Given a tangle \(K \subset Y\), a separating embedded surface \(\Sigma \subset Y\), and a disk \(D \subset \Sigma \) meeting K in two points. let  be the tangles obtained by modifying K by a half twist, respectively, adding a cup and cap as in Fig. 11.
be the tangles obtained by modifying K by a half twist, respectively, adding a cup and cap as in Fig. 11.
Theorem 6.12
(Exact triangle for changing a crossing) Let  be tangles in a cylindrical bordism \(Y = X \times [-1,1]\) between \(X_\pm = X \times \{ \pm 1 \}\) as in Definition 6.11 and \(L^\pm \) admissible Lagrangian branes in \(M(X_\pm ,\underline{\mu }_\pm )\) such that the sum of the disk invariants for \(\underline{L}(K), L^-,L^+\) is zero. The cohomology groups for
be tangles in a cylindrical bordism \(Y = X \times [-1,1]\) between \(X_\pm = X \times \{ \pm 1 \}\) as in Definition 6.11 and \(L^\pm \) admissible Lagrangian branes in \(M(X_\pm ,\underline{\mu }_\pm )\) such that the sum of the disk invariants for \(\underline{L}(K), L^-,L^+\) is zero. The cohomology groups for  are related by an exact triangle
are related by an exact triangle

Proof
The crossing change depicted in Fig. 11 has the following effect on the decomposition of elementary tangles. Suppose that \(K = K_1 \cup \ldots \cup K_r\) is such a decomposition. Denote by
the corresponding Lagrangian correspondences. The tangle  is obtained by inserting a half twist of the jth and \(j+1\)th markings after some elementary tangle \(K_i\). We may assume that \(K_i\) is a cylindrical bordism (i.e., admits a Morse function with no critical points) so that the cylindrical Cerf decomposition of
is obtained by inserting a half twist of the jth and \(j+1\)th markings after some elementary tangle \(K_i\). We may assume that \(K_i\) is a cylindrical bordism (i.e., admits a Morse function with no critical points) so that the cylindrical Cerf decomposition of  is obtained from that of K by replacing \(K_i\) with a half twist. Similarly for
is obtained from that of K by replacing \(K_i\) with a half twist. Similarly for  , let \(K_j^{\cap },K_j^{\cup }\) denote the tangles corresponding to the cap and cup of the jth and \(j+1\)th strands. Then
, let \(K_j^{\cap },K_j^{\cup }\) denote the tangles corresponding to the cap and cup of the jth and \(j+1\)th strands. Then

is a cylindrical Cerf decomposition of  . The Lagrangian correspondence for \(K_j^\cup \) is that associated with the coisotropic submanifold
. The Lagrangian correspondence for \(K_j^\cup \) is that associated with the coisotropic submanifold
where \(g_i\) is the holonomy around the jth marking. Similarly the correspondence for \(K_j^\cap \) is \( C_j^\cap = (C_j^\cup )^t \). These correspondences are simply connected and hence automatically monotone. Let \(\tau _{C_j} \in {\text {Diff}}(M(X_{i+1},\underline{\mu }_{i+1}))\) denote the corresponding fibered Dehn twist. We have

Theorem 6.12 now follows from Theorems 1.3 and 3.11.\(\square \)
More generally, in higher-rank invariants we obtain an exact triangle for the Khovanov–Rozansky modification.
Definition 6.13
Let \(G= SU(r)\) for some integer \(r \ge 2\).
-
(a)
(Admissible labels) An admissible label is a projection of the barycenter of \(\mathfrak {A}\) onto some face. In the absence of reducibles, given a marked surface \((X,\underline{x})\) with admissible labels \(\underline{\mu }\) the moduli space \(M(X,\underline{\mu })\) of bundles with fixed holonomy around the markings \(\underline{x}\) in the conjugacy classes associated with \(\underline{\mu }\) is a smooth, compact, monotone symplectic manifold.
-
(b)
(Correspondences for admissible graphs) Let
$$\begin{aligned} K \subset Y := X \times [-1,1] \end{aligned}$$be a trivalent graph with admissible labels, where each trivalent vertex is of the form described in Definition 3.12. This means that K is made up of a finite number of vertices that are points in Y, and edges that are embedded, compact one-manifold with boundary. The endpoints of the edges are either vertices or points on the boundary of Y. Trivalence means that each vertex is required to lie in the boundary of exactly three edges. Each edge is labeled by either \(\nu _k^1\) or \(\nu _k^2\), so that at any vertex the labels are \(\nu _k^1,\nu _k^1,\nu _k^2\), see Fig. 12 where the squiggly edge represents a vertex labeled \(\nu _k^2\).
-
(c)
(Decomposition into elementary graphs) Let
$$\begin{aligned} K = K_1 \cup \ldots \cup K_e \end{aligned}$$be a decomposition into elementary graphs admitting cylindrical Morse functions with at most one critical point or vertex. Each elementary graph \(K_i\) defines a smooth Lagrangian correspondence with admissible brane structure \(L_i\) consisting of bundles that extend over the interior, see [47], and so a generalized Lagrangian correspondence \(\underline{L} = (L_1,\ldots , L_e)\). The functor
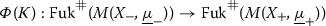
obtained by composing the functors \(\varPhi (L(K_i))\) is independent of the choice of decomposition into elementary graphs [47], up to \(A_\infty \) homotopy.
-
(d)
(Khovanov–Rozansky modification of a graph) Suppose \(K \subset X \times [-1,1]\) is a trivalent graph with admissible labels. Let \((K_1,\ldots ,K_e)\) be a cylindrical Cerf decomposition of K and \( K \cap (X \times \{ b_i \}) \) a slice such that two points have the same label \(\nu _k^1\) from 3.12. We obtain a new trivalent graphs
 by inserting a half twist, respectively, inserting two new vertices as shown in Fig. 13. Here the intermediate edge represented by a squiggle is labeled \(\nu _k^2\) from 3.12.
by inserting a half twist, respectively, inserting two new vertices as shown in Fig. 13. Here the intermediate edge represented by a squiggle is labeled \(\nu _k^2\) from 3.12.
Theorem 6.14
(Exact triangle for a Khovanov–Rozansky modification) Suppose that \(G = SU(r)\), \((X,\underline{\mu })\) is a marked surface with \(\mu _i = \mu _j = \nu _k^1\), with \(\nu _k^1 ={\frac{1}{2}}(\omega _k + \omega _{k+1})\). Let \(\nu _k^2 = {\frac{1}{2}}(\omega _{k+2} + \omega _{k})\) and suppose that  are as in Definition 6.13, and \(L^\pm \) are Lagrangian branes such that the sum of the disk invariants for \(\underline{L}(K), L^-,L^+\) is zero. There exists an exact triangle
are as in Definition 6.13, and \(L^\pm \) are Lagrangian branes such that the sum of the disk invariants for \(\underline{L}(K), L^-,L^+\) is zero. There exists an exact triangle

Note that this generalizes the SU(2) exact triangle since if \(k = 2\) then \(\omega _0 = \omega _2 = 0\). The exact triangle of Khovanov–Rozansky [19] has a similar form. The theories for the other standard markings will not in general have surgery exact triangles of this form, since the corresponding symplectomorphisms are not, in general, Dehn twists. It would be interesting to understand whether there is a replacement for the surgery exact triangle in these more general cases.
7 Fukaya versions of the exact triangle
In [27], the authors constructed \(A_\infty \) functors for Lagrangian correspondences between Fukaya categories. The gluing results necessary for the construction of the \(A_\infty \) functors for Lagrangian correspondences are proved in [28]. Applied to the Lagrangian correspondences arising from moduli spaces of flat bundles one obtains a (partial) \(A_\infty \) -category-valued field theory. We now explain the Fukaya-categorical versions of the exact triangle for fibered Dehn twist.
7.1 Open Fukaya-categorical version
Let M be a symplectic background. We take \({{\text {Fuk}}}(M)\) to be the \(A_\infty \) category whose objects are admissible monotone branes with torsion fundamental group and minimal Maslov number at least three. That is, we disallow the minimal Maslov number two case. Morphisms are Floer cochain groups and composition maps count (perturbed) holomorphic polygons with boundary on the given Lagrangians. In [27], we defined a similar category  whose objects are generalized Lagrangian submanifolds. Let
whose objects are generalized Lagrangian submanifolds. Let  denote its bounded derived category, as defined by Kontsevich, see [42]. Given any Lagrangian correspondence \(L_{01} \subset M_0^- \times M_1\) with admissible brane structure, [27] constructs an \(A_\infty \) functor
denote its bounded derived category, as defined by Kontsevich, see [42]. Given any Lagrangian correspondence \(L_{01} \subset M_0^- \times M_1\) with admissible brane structure, [27] constructs an \(A_\infty \) functor

The functor \(\varPhi (L_{01})\) is defined on the level of objects by concatenating \(L_{01}\) to the sequence, and on the level of morphisms by counting holomorphic quilts. In particular, given a spherically fibered coisotropic \(M \supset C \rightarrow B\) of codimension \(c \ge 2\) with admissible brane structure, one obtains \(A_\infty \) functors

Theorem 7.1
(Exact triangle in the derived Fukaya category) Let \((M,\omega )\) be a symplectic background, \(L \subset M\) an admissible Lagrangian brane, and \(\iota : C \rightarrow M\) a coisotropic submanifold of codimension at least 2 equipped with admissible brane structure spherically fibered over a symplectic manifold B. Let \(\tau _C : M \rightarrow M\) denote a fibered Dehn twist along C. There is an exact triangle in  of the form
of the form

The morphisms in the triangle Theorem 7.1 are Floer cochains defined as relative invariants associated with quilted surfaces that are variations of the surfaces involved in the proof of Theorem 1.3. The first map
is obtained by counting the elements of the moduli spaces \({\mathcal {M}}_1(x), x \in {\mathcal {I}}(L,C^t,C,L)\) associated with the quilted surface S shown in Fig. 14 with Lagrangian boundary and seam conditions L, C:
The second map in the exact triangle is the relative invariant for the standard Lefschetz–Bott fibration with a single end and Lagrangian boundary condition L in Fig. 15. That is, if \({\mathcal {M}}_2(y)_0\) denotes the zero-dimensional component of the moduli space of pseudoholomorphic sections, then the map is
Proposition 7.2
The morphism \(k \in {\text {Hom}}(L, \tau _C L)\) of (56) induces an isomorphism of the mapping cone \({\text {Cone}}(f: \varPhi (C) \varPhi (C^t) L \rightarrow L)\) with \(\tau _C L\).
The proof of Proposition 7.2 depends on the following lemma, whose proof is left as an exercise (c.f. [37, Lemma 2.6]).
Lemma 7.3
(Sufficient condition for a morphism from a mapping cone to be an isomorphism) Let \({\mathcal {C}}\) be a c-unital \(A_\infty \) category. Let X, Y, Z be objects of \({\mathcal {C}}\) and
Any pair
satisfying
defines a morphism \({\text {Cone}}(f) \rightarrow Z\) in \(D^\flat ({\mathcal {C}})\). This is an isomorphism if for all \(W \in {\text {Ob}}({\mathcal {C}})\), the complex
with differential
is acyclic.
Proof of Proposition 7.2
Consider the relative cochain-level invariant associated with the surface in the center in Fig. 16. We consider a family of deformations of this surface depending on a parameter \(\rho \) as follows. As \(\rho \rightarrow 1\), deform the glued surface so that a disk with values in \(E_{C,r}\) bubbles off. By the proof of Proposition 4.31, the relative invariant for the picture on the right corresponding to \(\rho = 1\) is zero on the cochain level for r sufficiently large. As \(\rho \rightarrow 0\), we pinch off a pair of pants as in the left side of Fig. 16. Let
denote the parametrized moduli space for this deformation consisting of pairs of a parameter \(\rho \) and a holomorphic quilt for the quilt corresponding to the parameter. Standard transversality arguments show that \({\widetilde{{\mathcal {M}}}}(x)\) is smooth for generic choices of perturbation data. The monotonicity conditions imply the absence of sphere and disk bubbling and hence compactness of the moduli space. The boundary of the moduli space admits a natural identification
Here \({{\mathcal {M}}}(x,y),{{\mathcal {M}}}(x,y,z) \) are the moduli spaces for the 2 resp. 3 marked disk, counted by the compositions \(\mu ^1,\mu ^2\). The first part consists of the \(\rho = 0\) boundary of \({\widetilde{{\mathcal {M}}}}(x)_1\), and corresponds to \(\mu ^2(f,k)\). The other boundary components at \(\rho \in (0,1)\) are formed by splitting off Floer trajectories \(v \in {{\mathcal {M}}}(x,y)\) for \(L,C^t,C,L\). Define
Then by counting the ends of the one-dimensional component of the moduli space, we obtain
as claimed.
Now let \(L^1\) be another object in  , for simplicity unquilted. Acyclicity of the differential (58) is shown as follows. It suffices to prove acyclicity with L replaced with \(\tau _C^{-1}L\). The terms of lowest order in q are \(\mu ^2(f,a)\) and \(\mu ^2(k,b)\). As in Sect. 5.2, the leading term of \(\mu ^2(f,a)\) corresponds to the canonical injection \( {\mathcal {I}}(L^1, C^t,C,\tau _C^{-1} L) \rightarrow {\mathcal {I}}(L^1,\tau _C^{-1} L) \). On the other hand, the leading term of \(\mu ^2(k,b)\) corresponds to the canonical injection \( {\mathcal {I}}(L^1,L) \rightarrow {\mathcal {I}}(L^1,\tau _C^{-1} L) .\) As before, the lowest order terms in complex are acyclic, after a small shift in the \(\mathbb {R}\)-degrees of the generators. Filtering the complex by energy shows that entire complex is acyclic. An application of Lemma 7.3 completes the proof of Proposition 7.2. \(\square \)
, for simplicity unquilted. Acyclicity of the differential (58) is shown as follows. It suffices to prove acyclicity with L replaced with \(\tau _C^{-1}L\). The terms of lowest order in q are \(\mu ^2(f,a)\) and \(\mu ^2(k,b)\). As in Sect. 5.2, the leading term of \(\mu ^2(f,a)\) corresponds to the canonical injection \( {\mathcal {I}}(L^1, C^t,C,\tau _C^{-1} L) \rightarrow {\mathcal {I}}(L^1,\tau _C^{-1} L) \). On the other hand, the leading term of \(\mu ^2(k,b)\) corresponds to the canonical injection \( {\mathcal {I}}(L^1,L) \rightarrow {\mathcal {I}}(L^1,\tau _C^{-1} L) .\) As before, the lowest order terms in complex are acyclic, after a small shift in the \(\mathbb {R}\)-degrees of the generators. Filtering the complex by energy shows that entire complex is acyclic. An application of Lemma 7.3 completes the proof of Proposition 7.2. \(\square \)
Theorem 7.1 follows by taking the long exact sequence associated with the mapping cone in Proposition 7.2.
7.2 Periodic Fukaya-categorical version
In this section we discuss a version of the triangle taking values in  , the bounded derived Fukaya category of generalized Lagrangian correspondences from M to M. Recall from [27] that the empty correspondence \(\emptyset \) from M to M considered as a sequence of length zero induces the identity
, the bounded derived Fukaya category of generalized Lagrangian correspondences from M to M. Recall from [27] that the empty correspondence \(\emptyset \) from M to M considered as a sequence of length zero induces the identity

on the Fukaya category; indeed, labeling each seam by the empty set has the effect of “removing the seam.”
Theorem 7.4
(Exact triangle in the derived Fukaya category of correspondences) Let \((M,\omega )\) be a symplectic background, and \(i: C \rightarrow M\) a coisotropic submanifold of codimension at least two, whose null foliation \(p: C \rightarrow B\) is spherically fibrating over a manifold B, equipped with an admissible brane structure. Let \(\tau _C : M \rightarrow M\) denote a fibered Dehn twist along C. There is an exact triangle in  of the form
of the form

Sketch of proof
The proof is the similar to that of Theorem 7.2, replacing the strip-like ends with cylindrical ends. The morphism from  to \(\emptyset \) is obtained from the quilted cap \(\underline{S} =(S_M, S_B)\) in Fig. 17, where
to \(\emptyset \) is obtained from the quilted cap \(\underline{S} =(S_M, S_B)\) in Fig. 17, where
-
the outer circle represents a quilted cylindrical end with seams \(C^t,C\),
-
the lightly shaded patch \(S_M\) maps to M and
-
the darkly shaded patch \(S_B\) maps to B.
The morphism from \(\emptyset \) to \({\text {graph}}(\tau _C)\) is defined by the Lefschetz–Bott fibration over the cap shown in Fig. 18, where the outer circle represents a cylindrical end with monodromy around the end given by \(\tau _C\). The composition of the two maps is defined by the surface shown in Fig. 19. By deforming the singularity on the surface onto a disk with boundary condition in C, one obtains a null homotopy of the composition. This null homotopy defines, as in Lemma 7.3, an isomorphism of the mapping cone  with \(\tau _C\). Applying the functor
with \(\tau _C\). Applying the functor

constructed in [27], this leads to an exact triangle in 

That is, there exists an isomorphism in  ,
,
Applying this exact triangle to any object L of  leads to the exact triangle given in Theorem 7.1. \(\square \)
leads to the exact triangle given in Theorem 7.1. \(\square \)
Remark 7.5
(\(A_\infty \) results for minimal Maslov two) Similar results hold in the case of minimal Maslov number two for the \(A_\infty \) categories  whose objects L have disk invariant \(w = w(\underline{L})\), counting the number of Maslov index disks passing through a generic point in \(\underline{L}\). See [27, Section 4.4] for more on the disk invariant and Fukaya category
whose objects L have disk invariant \(w = w(\underline{L})\), counting the number of Maslov index disks passing through a generic point in \(\underline{L}\). See [27, Section 4.4] for more on the disk invariant and Fukaya category  .
.
References
Abouzaid, M.: Framed bordism and Lagrangian embeddings of exotic spheres. Ann. Math. (2) 175(1), 71–185 (2012)
Alekseev, A., Malkin, A., Meinrenken, E.: Lie group valued moment maps. J. Differ. Geom. 48(3), 445–495 (1998)
Arnold, V.I., Goryunov, V.V., Lyashko, O.V., Vasil’ev, V.A.: Singularity Theory. I. Springer, Berlin (1998). (Translated from the 1988 Russian original by A. Iacob)
Arnol’d, V.I., Guseuin-Zade, S.M., Varchenko, A.N.: Singularities of Differentiable Maps. Vol. II, Volume 83 of Monographs in Mathematics. Birkhäuser Boston Inc., Boston, MA (1988)
Atiyah, M.F., Bott, R.: The Yang–Mills equations over Riemann surfaces. Philos. Trans. R. Soc. Lond. Ser. A 308, 523–615 (1982)
Braam, P.J., Donaldson, S.K.: Floer’s work on instanton homology, knots and surgery. In: Hofer, H., Taubes, C.H., Weinstein, A., Zehnder, E. (eds.) The Floer Memorial Volume, pp. 195–256. Birkhäuser, Basel (1995)
Bredon, G.: Sheaf Theory. McGraw-Hill, New York (1967)
Chiang, R., Ding, F., van Koert, O.: Open books for Boothby–Wang bundles, fibered Dehn twists and the mean Euler characteristic. arxiv:1211.0201
Clemens Jr., C.H.: Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities. Trans. Am. Math. Soc. 136, 93–108 (1969)
Donaldson, S.K.: Floer Homology Groups in Yang–Mills Theory, Volume 147 of Cambridge Tracts. Cambridge University Press, Cambridge (2002). (With the assistance of M. Furuta and D. Kotschick)
Fáry, I.: Valeurs critiques et algèbres spectrales d’une application. Ann. Math. 63, 437–490 (1956)
Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian Intersection Floer Theory: Anomaly and Obstruction, Volume 46 of AMS/IP Studies in Advanced Mathematics. American Mathematical Society, Providence, RI (2009)
Gelfand, S.I., Manin, Y.I.: Methods of Homological Algebra. Springer, Berlin (1996). (Translated from the 1988 Russian original)
Guillemin, V., Sternberg, S.: Symplectic Techniques in Physics. Cambridge University Press, Cambridge (1990)
Guillemin, V., Lerman, E., Sternberg, S.: Symplectic Fibrations and Multiplicity Diagrams. Cambridge University Press, Cambridge (1996)
Paul Horja, R.: Derived category automorphisms from mirror symmetry. Duke Math. J. 127(1), 1–34 (2005)
Khovanov, M.: A categorification of the Jones polynomial. Duke Math. J. 101(3), 359–426 (2000)
Khovanov, M.: A functor-valued invariant of tangles. Algebr. Geom. Topol. 2, 665–741 (2002). (electronic)
Khovanov, M., Rozansky, L.: Matrix factorizations and link homology. Fund. Math. 199(1), 1–91 (2008)
Kwon, D., Oh, Y.-G.: Structure of the image of (pseudo)-holomorphic discs with totally real boundary condition. Commun. Anal. Geom. 8(1), 31–82 (2000). (Appendix 1 by Jean–Pierre Rosay)
Landman, A.: On the Picard–Lefschetz transformation for algebraic manifolds acquiring general singularities. Trans. Am. Math. Soc. 181, 89–126 (1973)
Lazzarini, L.: Existence of a somewhere injective pseudo-holomorphic disc. Geom. Funct. Anal. 10(4), 829–862 (2000)
Lerman, E.: Symplectic cuts. Math. Res. Lett. 2, 247–258 (1995)
Loray, F., Saito, M.-H.: Lagrangian fibration in duality on moduli space of rank two logarithmic connections over the projective line. arxiv:1302.4113
Mak, C.Y., Wu, W.: Dehn twists exact sequences through Lagrangian cobordism. arxiv:1509.08028
Manin, YuI: Cubic Forms, Volume 4 of North-Holland Mathematical Library, 2nd edn. North-Holland Publishing Co., Amsterdam (1986). (Algebra, geometry, arithmetic, Translated from the Russian by M. Hazewinkel)
Ma’u, S., Wehrheim, K., Woodward, C.T.: \({A}_\infty \)-functors for Lagrangian correspondences. arXiv:1601.04919
Ma’u, S.: Gluing pseudoholomorphic quilted disks. arxiv:0909.3339
McDuff, D., Salamon, D.: \(J\)-holomorphic Curves and Symplectic Topology, Volume 52 of American Mathematical Society Colloquium Publications. American Mathematical Society, Providence, RI (2004)
Mehta, V.B., Seshadri, C.S.: Moduli of vector bundles on curves with parabolic structure. Math. Ann. 248, 205–239 (1980)
Meinrenken, E., Woodward, C.: Hamiltonian loop group actions and Verlinde factorization. J. Differ. Geom. 50, 417–470 (1999)
Oh, Y.-G.: Floer cohomology of Lagrangian intersections and pseudo-holomorphic disks. I. Commun. Pure Appl. Math. 46(7), 949–993 (1993)
Perutz, T.: Lagrangian matching invariants for fibred four-manifolds. I. Geom. Topol. 11, 759–828 (2007)
Perutz, T.: Lagrangian matching invariants for fibred four-manifolds. II. Geom. Topol. 12(3), 1461–1542 (2008)
Perutz, T.: A symplectic Gysin sequence (2008). arxiv:0807.1863
Pressley, A., Segal, G.: Loop Groups. Oxford University Press, Oxford (1988)
Seidel, P.: Homological Mirror Symmetry for the Quartic Surface. Memoirs of the American Mathematical Society, vol. 236. American Mathematical Society, Providence
Seidel, P.: Lectures on four-dimensional Dehn twists. In: Symplectic 4-Manifolds and Algebraic Surfaces, Volume 1938 of Lecture Notes in Math., pp. 231–267. Springer, Berlin (2008)
Seidel, P.: phd96.dvi (unpublished manuscript)
Seidel, P.: Graded Lagrangian submanifolds. Bull. Soc. Math. France 128(1), 103–149 (2000)
Seidel, P.: A long exact sequence for symplectic Floer cohomology. Topology 42(5), 1003–1063 (2003)
Seidel, P.: Fukaya Categories and Picard–Lefschetz Theory. European Mathematical Society (EMS), Zürich, Zurich Lectures in Advanced Mathematics (2008)
Shub, M., Fathi, A., Langevin, R.: Global Stability of Dynamical Systems. Springer, New York (1987). (Translated from the French by Joseph Christy)
Wehrheim, K., Woodward, C.: Pseudoholomorphic quilts. arXiv:0905.1369
Wehrheim, K., Woodward, C.: Quilted Floer cohomology. Geom. Topol. 14, 833–902 (2010). (Quilted Floer trajectories with constant components: corrigendum to the article “Quilted Floer cohomology”. Geom. Topol. 16(1), 127–154 (2012))
Wehrheim, K., Woodward, C.T.: Floer field theory for coprime rank and degree. arxiv:1601.04924
Wehrheim, K., Woodward, C.T.: Floer field theory for tangles. arXiv:1503.07615
Wehrheim, K., Woodward, C.T.: Orientations for pseudoholomorphic quilts. arxiv:1503.07803
Wehrheim, K., Woodward, C.T.: Functoriality for Lagrangian correspondences in Floer theory. Quantum Topol. 1(2), 129–170 (2010)
Wehrheim, K., Woodward, C.T.: Floer cohomology and geometric composition of Lagrangian correspondences. Adv. Math. 230(1), 177–228 (2012)
Acknowledgements
Partially supported by NSF Grants CAREER 0844188 and DMS 0904358.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wehrheim, K., Woodward, C.T. Exact triangle for fibered Dehn twists. Res Math Sci 3, 17 (2016). https://doi.org/10.1186/s40687-016-0065-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40687-016-0065-x







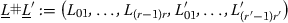






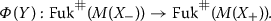


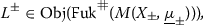


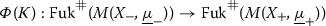
 by inserting a half twist, respectively, inserting two new vertices as shown in Fig.
by inserting a half twist, respectively, inserting two new vertices as shown in Fig. 






