1 Introduction

On 24 April 1771, a huge tsunami, called the Meiwa (or Yaeyama) tsunami, inflicted extensive damage mainly to the Sakishima Islands of Japan (Fig. 1a, b). Causing approximately 12,000 casualties (Goto et al. 2010a), it was one of the most destructive historical tsunamis ever to strike the Japanese archipelago.

Fig. 1
figure 1

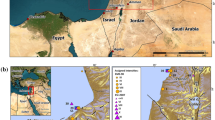
a Map showing the study area location in the northwest Pacific. b Map showing the Sakishima Islands and Ryukyu Trench locations. c Close up map of Sakishima Islands. Red, orange, and green areas respectively denote source models for the 1771 earthquake: IM, Imamura et al. (2001); NK, Nakamura (2009); and MY, Miyazawa et al. (2012). The plate boundary was adopted from Iwasaki et al. (2015)

Full size image

Details of the damage caused by the Meiwa tsunami are recorded in historical documents (Makino 1968; Goto et al. 2010a). It is noteworthy for many sites that whether the tsunami inundated it or not is well recorded. In addition, the elevations and coordinates of these points were resurveyed using high-precision GNSS equipment, verifying the reliability of the historical descriptions (Goto et al. 2012). Using these data, the maximum runup height was estimated as greater than 22 m (most likely around 30 m) on Ishigaki Island, 15 m on Tarama Island, and 18 m on Miyako Island (Goto et al. 2012).

In addtion, geological evidence of past tsunamis have been reported for the Sakishima Islands. In general, the Sakishima Islands are surrounded by well-developed fringing reefs as much as 1.5 km wide (Hongo and Kayanne 2009), but the reefs are about 8 km around the southwestern coast of Ishigaki Island. Along the coast, there are many meter-long coral boulders, so-called tsunami boulders, that have been transported from the coral reef by past tsunami events including the 1771 Meiwa tsunami (e.g., Goto et al. 2010a). The sizes and spatial distributions of tsunami boulders might reflect the tsunami energy. For that reason, tsunami boulders are expected to be a promising proxy to restrict estimates of the size of past tsunamis (e.g., Goto et al. 2014; Hisamatsu et al. 2014; Watanabe et al. 2016). In addition, because many tsunami boulders at the Sakishima Islands consist of single Porites colonies, they are suitable to date the tsunami timing (Araoka et al. 2013). Based on radiocarbon dating, Araoka et al. (2013) reported that some tsunami boulders were deposited by the 1771 Meiwa tsunami. However, many other tsunami boulders were dated earlier than 1771 (Araoka et al. 2013). Based on such results, they suggested that past tsunamis at the Sakishima Islands repeatedly cast the boulders ashore with a 150–400 year recurrence interval. It is also reported that distributions of tsunami boulders are not uniform: the boulders are patchily distributed at some specific coasts of the Sakishima Islands (Goto et al. 2010a), although it remains uncertain why tsunami boulders are concentrated at some coasts.

Sandy tsunami deposits have also been reported in the Sakishima Islands (Yamamoto 2008; Ando et al. 2018; Fujita et al. 2020). Not only the 1771 Meiwa tsunami sandy deposit, but two sandy tsunami deposits and tsunami boulders by the earlier events have also been identified (Ando et al. 2018; Fujita et al. 2020). Results of tsunami deposit dating suggest that tsunamis of the same or greater size as the Meiwa tsunami occurred repeatedly at approximately 600 year intervals during the last 2000 year (Ando et al. 2018). The interpretation was supported by the reconstruction of coral reef morphology based on the examination of molluscan assemblages in the tsunami deposits (Kitamura et al. 2018). In addition, Yamamoto (2008) and Ando et al. (2018) found fissures beneath the Meiwa tsunami deposit. Usami (2010) estimated the seismic intensity of the earthquake which generated the Meiwa tsunami as 4 on the scale of Japan Metrological Agency (JMA) in the Sakishima Islands because there is no description of damage caused by seismic motion in historical records. However, Ando et al. (2018) reported that the seismic intensity might have been greater than previously thought: it is expected to have been sufficient to produce fissures in the ground. If this were the case, the seismic intensity would be expected to be greater than 5 on the JMA scale according to Ando et al. (2018).

As reviewed in the next chapter, the source model of the Meiwa tsunami is still under debate. Additionally, heterogeneous distribution of tsunami boulders persists as an unresolved issue. Therefore, this study was conducted to re-evaluate the tsunami wave source model of the 1771 Meiwa tsunami using sufficiently high-resolution bathymetric and topographic data for tsunami calculation along with the latest historical record dataset (Goto et al. 2012) as the constraint of the source model. We further discuss the bathymetric effects of tsunami wave concentration toward some specific coasts based on tsunami ray tracing analysis (Satake 1988).

2 Earlier studies of 1771 Meiwa tsunami source models

Source models of the Meiwa tsunami have been proposed based on several earlier studies (Imamura et al. 2001; Nakamura 2009; Miyazawa et al. 2012; Okamura et al. 2018). These models are classifiable into three main models: (1) the intraplate earthquake plus submarine landslide (Imamura et al. 2001; Miyazawa et al. 2012); (2) the interplate earthquake along the Ryukyu Trench (Nakamura 2009); and (3) the giant submarine landslide near the Ryukyu Trench (Okamura et al. 2018). The locations of the source models proposed by Imamura et al. (2001), Miyazawa et al. (2012), and Nakamura (2009) are presented in Fig. 1c, with parameters presented in Table 1.

Table 1 Parameters of the Meiwa tsunami source models proposed from earlier studies
Full size table

Among the previously proposed source models, the model for the interplate earthquake along the Ryukyu Trench is adopted in this study, because this model is better suited for the recent geological findings. The reasons to adopt this model together with issues of other models are summarized below.

2.1 Intraplate earthquake plus submarine landslide

Imamura et al. (2001) estimated an intraplate earthquake (moment magnitude (Mw) = 7.7) and submarine landslide at the southeastern offshore of Ishigaki Island as the Meiwa tsunami source model. They assumed the submarine landslide as the supplement tsunami source to explain extremely high run-up height at the southern coast of Ishigaki Island. This assumption is based on work reported by Matsumoto and Kimura (1993) who proposed the presence of a submarine landslide near Kuroshima Island. However, the fault posited for this model assumed a large slip of 20 m. In fact, this large slip is far beyond the value which can be estimated from the typical scaling law (9.4 m; Wells and Coppersmith 1994). Similarly, Miyazawa et al. (2012) updated the model of Imamura et al. (2001): they assumed an intraplate earthquake (Mw = 8.2) plus a submarine landslide. However, the fault of this model is that it retained the assumption of a large slip of 14 m compared to that estimated from the scaling law (6.7 m; Wells and Coppersmith 1994).

Moreover, subsequent works argued the occurrence of a landslide offshore of Ishigaki Island in historic time. Ujiie et al. (1997) investigated a sediment core obtained from the area at which Imamura et al. (2001) and Miyazawa et al. (2012) had assumed a submarine landslide. This core included many benthic foraminifera, which inhabit shallow coral reefs. Therefore, the coral reef sediments were carried and deposited as turbidites. In addition, the latest turbidites were dated to about 2000 years ago (Ujiie et al. 1997). No turbidite of younger origin was discovered. Based on results of that study, Nakamura (2009) pointed out that no evidence exists of a submarine landslide that occurred at 1771. Recently, based on magnetic fabric measurements and dating of marine sediments, Kanamatsu et al. (2021) also concluded that no landslide had occurred at the target area during historical times. However, it is noteworthy that not all turbidites are preserved in the core (Ikehara et al. 2022). Therefore, the occurrence of a landslide in 1771 cannot be ruled out solely based on the absence of 1771 turbidite.

In summary, the occurrence of a submarine landslide has been questioned. Moreover, a remaining issue is that unusually large slip must be assumed. Therefore, other source models, if there are better ones, are worth due consideration.

2.2 Interplate earthquake along the Ryukyu Trench

Nakamura (2009) reported a tsunami earthquake (slip = 16 m, Mw = 8.0), which is an earthquake that generates a large tsunami relative to the intensity of its seismic motion (Kanamori 1972), along the southern Ryukyu Trench. The Ryukyu Trench extends from Kyusyu to Taiwan (Fig. 1b). The Philippine Sea plate subducts beneath the Eurasian plate on the Ryukyu Trench (Ando et al. 2009). Nakamura (2009) hypothesized that the Meiwa tsunami originated from a tsunami earthquake because historical documents describe no damage related to seismic motion. Tsunami earthquakes are believed to occur in shallow and narrow regions at plate boundaries (e.g., Satake and Tanioka 1999). Nakamura (2009) also assumed such an area along the Ryukyu Trench to explain the historical traces of the Meiwa tsunami. Ando et al. (2018) subsequently estimated that the seismic motion during the Meiwa event was strong because they found fissures beneath the Meiwa tsunami sandy deposit and pointed out that the earthquake might have been a typical interplate earthquake rather than the tsunami earthquake.

The seismic activity of the Ryukyu Trench is under debate. During the past 300 years, no clear evidence has been reported of large interplate earthquakes (Mw > 8). Peterson and Seno (1984) reported that interplate coupling of the Ryukyu Trench is weak. Consequently, the possibility of the occurrence of large tsunamigenic earthquakes has been questioned (Peterson and Seno 1984). Recent studies have also indicated that no typical seismogenic locked zone exists below 15 km depth in the southern Ryukyu Trench because both slow slip events and low-frequency earthquakes are predominant, respectively, at depths greater than 25 km and 15–25 km (Arai et al. 2016; Nakamura 2017). However, they also pointed out that tsunami earthquakes can be generated at the shallowest part (< 15 km) of the trench (Arai et al. 2016; Nakamura 2017). Some reports have described that the locked zone exists in the southern Ryukyu Trench and that interplate earthquakes can occur. For instance, Kano et al. (2021) estimated that the coupling ratio is 13–36% in the southern Ryukyu Trench based on GNSS observations. Debaecker et al. (2023) also reported the coupling ratio as 10–100% in the southern Ryukyu Trench from crustal deformation during the most recent 200 years, as estimated from coral microatolls. In addition, Doo et al. (2018) pointed out that the Ryukyu Trench has strong coupling from gravity measurements.

Furthermore, seafloor seismic surveys have confirmed the existence of splay faults extending from the interplate boundary in the southern Ryukyu Trench. In fact, it was pointed out that not only earthquakes at the plate boundary but also earthquakes on splay faults might be the Meiwa tsunami wave source (Hsu et al. 2013; Arai et al. 2016). However, the lack of topographic changes caused by these faults in the seafloor indicates a low level of activity. The splay fault earthquakes relation with the Meiwa tsunami remains controversial (Izumi et al. 2016; Nakamura 2017; Nishizawa et al. 2017).

In this way, although seismic activity of the southern Ryukyu Trench remains poorly understood, recent research has indicated the possibility that earthquakes, including tsunami earthquakes, might occur along the southern Ryukyu Trench. Therefore, the hypothesis of the tsunami wave source of the 1771 Meiwa tsunami at the Ryukyu Trench must be considered conscientiously.

2.3 Giant submarine landslide

Okamura et al. (2018) investigated bathymetry near the Ryukyu Trench and inferred that the Meiwa tsunami was triggered by a giant submarine landslide on a steep slope that had formed by a strike-slip fault near the trench axis. According to numerical calculations, this submarine landslide could have reproduced the Meiwa tsunami run-up (Okamura et al. 2018). However, it is uncertain whether the submarine landslide was indeed generated in 1771. In addition, this model has difficulty explaining the periodicity of tsunamis that might have occurred at several hundred year intervals at the Sakishima Islands (Araoka et al. 2013; Ando et al. 2018). Because of this issue, we do not examine this model for this study.

2.4 Points of improvement over earlier studies

As described above, various source models of the Meiwa tsunami have been proposed but the model remains unconfirmed. Other than the accumulation of seismological and geological knowledge, there is room for improvement of earlier tsunami modeling. For example, the bathymetric and topographic data used for earlier studies have low resolution: 50 m by Imamura et al. (2001) and Miyazawa et al. (2012), and 225 m by Nakamura (2009). Imamura et al. (2001) and Nakamura (2009) did not perform inundation modeling but assumed complete reflection near the coast. Therefore, tsunami calculations might not be sufficiently accurate to assess the tsunami wave source model properly. In fact, the Sakishima Islands are surrounded by up to 1.5 km wide fringing reefs of approximately 4 m depth. This wide and shallow bathymetry might affect tsunami inundation (e.g., Le Gal and Mitarai 2020). To assess the influence of reef bathymetry on the tsunami calculations, detailed bathymetry data should be used, especially for coastal areas. The Headquarters for Earthquake Research Promotion (2017) recommends about 10 m for detailed tsunami inundation calculation. Moreover, after reports of those earlier studies were published, Goto et al. (2012) presented the most recent dataset of historical records. Therefore, reappraisal of the source model using the latest dataset is necessary.

3 Methods

3.1 Tsunami numerical calculation

The TUNAMI-N2 code (Goto et al. 1997; Imamura et al. 2006) is applied for this study as a tsunami calculation model. This model can do continuous calculation from tsunami propagation to inundation. The nonlinear long-wave theory, also known as the shallow water theory, is the basis of this model. The governing equations are presented below.

$$\begin{array}{*{20}c} {\frac{\partial \eta }{{\partial t}} + \frac{\partial M}{{\partial x}} + \frac{\partial N}{{\partial y}} = 0} \\ \end{array}$$
(1)
$$\begin{array}{*{20}c} {\frac{\partial M}{{\partial t}} + \frac{\partial }{\partial x}\left( {\frac{{M^{2} }}{D}} \right) + \frac{\partial }{\partial y}\left( \frac{MN}{D} \right) + gD\frac{\partial \eta }{{\partial x}} + \frac{{gn^{2} M\sqrt {M^{2} + N^{2} } }}{{D^{7/3} }} = 0} \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {\frac{\partial N}{{\partial t}} + \frac{\partial }{\partial x}\left( \frac{MN}{D} \right) + \frac{\partial }{\partial y}\left( {\frac{{N^{2} }}{D}} \right) + gD\frac{\partial \eta }{{\partial y}} + \frac{{gn^{2} M\sqrt {M^{2} + N^{2} } }}{{D^{7/3} }} = 0} \\ \end{array}$$
(3)

In these equations, η denotes the water level variation. Also, M and N are the flow fluxes respectively in the x and y directions. Regarding other variables, t represents time, g (= 9.81 m/s2) expresses gravitational acceleration, n is Manning’s coefficient, and D (= h + η) denotes the total water depth. Following The Japan Society of Civil Engineers (2002), Manning’s coefficient was set as 0.025 m−1/3/s. Using the staggered leap-frog method, these governing equations were solved numerically (Imamura et al. 2006). The calculation time was up to 1 h after the earthquake occurrence. The time step was set as 0.05 s. The seafloor deformation by the fault models was computed using equations presented by Okada (1985). Here, both vertical and horizontal crustal deformation was considered (Tanioka and Satake 1996). For the bathymetric and topographic data, the nesting grid system is used for tsunami calculation. The spatial grid sizes are 810 m in Region 1, 270 m in Regions 2a and 2b, 90 m in Regions 3a and 3b, 30 m in Regions 4a to 4c, and 10 m in Regions 5a to 5i (Fig. 2). The original bathymetry/topography data are the present data. To reproduce the likely bathymetry/topography prevailing in 1771, some artificial landfills that have been created in recent years were deleted. To identify the landfill areas, aerial photographs taken in 1963 were used as a reference. ArcGIS Pro was used to delete the landfill areas. These photographs were obtained from the Geospatial Information Authority of Japan. They were taken before the recent landfill creation. In some areas, coral reefs have been artificially excavated for harbor construction. These areas were modified using ArcGIS Pro to reproduce the pre-excavation topography (Additional file 1: Fig. S1). In addition, it is important to consider the possibility that the present coral reef bathymetry might differ from that in 1771, although this possibility can be ruled out based on the following reasons. First, approximately 250 years since the 1771 event is a short time for the coral reef development so that the bathymetric change due to the development of the coral reef after the 1771 event should be negligible. Also, it is unlikely that tsunami largely destroy the coral reef itself. Indeed, although there are some reports that individual corals were destroyed by recent large tsunamis such as the 2004 Indian Ocean tsunami (e.g., Kumaraguru et al. 2005), there are no reports that the coral reef itself has been largely destroyed. Although coral reef fragments were emplaced on the reef and the beach by the tsunami as tsunami boulders at Sakishima Islands (e.g., Goto et al. 2010a), their total volume is far smaller than that of the coral reef. Moreover, molluscan assemblages in tsunami deposits reported by Ando et al. (2018) suggested that the reef topography has not been changed at least during the last 1250 years (Kitamura et al. 2018). Based on these lines of evidence, we judged the reef bathymetry in 1771 would have been similar to that of today.

Fig. 2
figure 2

Spatial extents of grid layers of numerical modeling used for this study. Spatial grid sizes of the domains are 810 m (Region 1), 270 m (Regions 2a, 2b), 90 m (Regions 3a, 3b), 30 m (Regions 4a–4c), and 10 m (Regions 5a–5i)

Full size image

3.2 Fault parameters

For this study, a interplate earthquake along the southern Ryukyu Trench was assumed as the tsunami wave source, as described in Chapters 1 and 2. By changing the relevant parameters, 27 scenarios were calculated (Table 2 and Fig. 3). These include the original model proposed by Nakamura (2009). We assumed a single rectangle fault along the southern Ryukyu Trench. The parameters we changed are the fault location, width, length, depth, and slip. A scaling law exists to ascertain the parameters of the interplate earthquake (e.g., Murotani et al. 2013). However, in the case of the Meiwa tsunami, Nakamura (2009) estimated a much larger slip (16 m) than that estimated using the scaling law (2.2 m; Murotani et al. 2013). For that reason, the fault parameter of the Meiwa tsunami might not follow the scaling law. Therefore, the scaling law was not adopted for this study. For the RYa10 to RYc40 scenarios, the fault depth was set as 5 km and the fault length as 225 km extending from off Ishigaki Island to off Miyako Island, with the fault width varied from 30 to 100 km, and the slip from 10 to 40 m. For the RYad10 to RYcd40 scenarios, the fault depth was set as 15 km. The fault length, width, and slip were set as in RYa10 to RYc40. For the RYae30 and RYaw30 scenarios, the fault length was set as 150 km. The fault is set off Ishigaki Island for RYae30 and off Miyako Island for RYaw30. The fault dip angle was set to 12° in all scenarios to match the subduction angle of the plate boundary, as described by Nakamura (2009). Recently, Arai et al. (2016) noted from a seismic reflection survey of the southern Ryukyu Trench that the dip angle varies between 5 and 15° with increase in depth. In addition, we calculated the average dip angle as 12° from the survey results between depths of 5 and 25 km by Arai et al. (2016). Therefore, our assumption of the dip angle to be 12° is also consistent with the results by Arai et al. (2016).

Table 2 Fault parameters used for this study (Moment magnitude was calculated while assuming rigidity of 30 GPa)
Full size table
Fig. 3
figure 3

a Fault positions at 5 km depth (Rya10–Ryc40). b Fault positions at 15 km depth (Ryad10–Rycd40). c Fault positions of Ryae30 and Ryaw30. The contour lines represent the depth distribution of the plate boundary every 10 km. Data for plate boundary depth profiles are from Slab 2.0 (Hayes et al. 2018). Trench axis data are from Iwasaki et al. (2015)

Full size image

3.3 Fault model evaluation methods

We used the tsunami trace data presented by Goto et al. (2012) to evaluate the fault models. Goto et al. (2012) surveyed the coordinates and elevation of the tsunami trace points where historical records and folklore had indicated tsunami inundation or no inundation. For this study, 60 points with confidence levels A or A′, which are regarded as the most reliable according to the confidence criteria defined by Goto et al. (2012), were used (Fig. 4).

Fig. 4
figure 4

Locations of tsunami trace points based on Goto et al. (2012). Red circles represent points with inundation. Blue circles represent points with no inundation. Distribution of tsunami trace points on a Taketomi Island and Ishigaki Island and b Tarama Island, Ikema Island, and Irabu Island. In this figure, (1)–(8) respectively stand for the regional divisions used for the model evaluation: (1) western part of Ishigaki Island (Area 1), (2) Taketomi Island to the southwestern part of Ishigaki Island (Area 2), (3) southeastern part of Ishigaki Island (Area 3), (4) eastern part of Ishigaki Island (Area 4), (5) northern part of Ishigaki Island (Area 5), (6) Tarama Island (Area 6), (7) western Miyako Island, Irabu Island and Ikema Island (Area 7), and (8) southern part of Miyako Island (Area 8). The topography and bathymetry in (1)-(8) are based on 10 mesh topography and bathymetry data. Grey areas in (2) and (7) are areas without 10 m mesh bathymetry data. The contour level is 10 m

Full size image

For fault model evaluation, the method reported by Aida (1978) is often used (e.g., Nakamura 2009; Miyazawa et al. 2012). As indicators for the evaluation of fault models, Aida (1978) proposed K, which indicates the geometric mean of the ratio between the observed and calculated tsunami height, and κ, which denotes the geometric standard deviation of the ratio.

In the case of the Meiwa tsunami, although many historical documents indicate the presence or absence of inundation, there are no points at which the tsunami height is known because the flow depth is not stated in the historical documents. Therefore, the reproducibility cannot be assessed adequately using K/κ. A different assessment method must be adopted. Then, for this study, we evaluated the tsunami source model by checking whether each tsunami trace point could be reproduced in the tsunami run-up calculation.

In the case of wide plain terrain, a risk exists of underestimating the slip from the inundation area only, not including the tsunami height because the inundation area is affected not only by the slip but also by the fault width (e.g., Satake et al. 2013). However, the Sakishima Islands are islands of raised coral reefs with narrow flat terrain near the coast (Goto 2016). Because of such topography (i.e. relatively simple slope setting), tsunami heights are easily reflected in the inundation area. Therefore, with sufficient assessment points, the risk of underestimating the slip is regarded as low. The methodology of this study is consequently regarded as effective for assessing the validity of the fault model of the Meiwa tsunami.

Based on the consideration presented above, the fault models were evaluated for this study by the percentage of the number of tsunami trace points that were reproduced by the tsunami run-up calculations. A higher reproducibility is associated with a more suitable tsunami wave source model. We inferred that the tsunami trace points were inundated if the mesh containing the trace point was inundated by tsunami calculation in 10 m mesh topography data. To elucidate the reproducibility of tsunami run-up for each region, we divided the Sakishima Islands into eight regions (Fig. 4): (1) western Ishigaki Island (Area 1), (2) Taketomi Island to southwestern Ishigaki Island (Area 2), (3) southeastern Ishigaki Island (Area 3), (4) eastern Ishigaki Island (Area 4), (5) northern Ishigaki Island (Area 5), (6) Tarama Island (Area 6), (7) western Miyako Island, Irabu Island, Ikema Island (Area 7), and (8) southern Miyako Island (Area 8). This division differs from the regions of 10 m mesh topography/bathymetry data in Fig. 2.

Moreover, it is important to understand not only whether tsunami inundation was reproduced, but also, if not reproduced, the extent to which inundation is overestimated or underestimated. The difference in run-up heights was calculated as the difference in elevation from the inundated (not inundated) trace points to the nearest grid where inundation was (not) calculated in the 10 m mesh bathymetry data.

3.4 Assessing bathymetry effects on tsunami propagation

In the case of the Meiwa tsunami, tsunami heights and casualties were inferred as extraordinarily high at some specific sites (e.g., Goto et al. 2012). In addition, tsunami boulders are patchily distributed along the coast of the Sakishima Islands (Goto et al. 2010a). Nevertheless, the widths and shapes of coral reefs seem generally similar (Goto et al. 2010a). It remains uncertain why such tsunami focusing occurred at some specific coasts. To investigate the effects of bathymetry on tsunami propagation, tsunami ray tracing analysis (Satake 1988) was performed. With this analytical method, tsunami propagation can be represented by a tsunami ray perpendicular to the wave front of the tsunami. Concentrated tsunami rays indicate that tsunami energy is concentrated because of the bathymetry (Satake 1988).

4 Results

4.1 Tsunami inundation by the Nakamura (2009) model

To verify the reproducibility of our calculations, we first calculated the model proposed by Nakamura (2009) (Fig. 5). The reproductivity rates of tsunami trace points by this model in each region are presented in Table 3 (Ishigaki Island and Taketomi Island in Areas 1–5) and Table 4 (Tarama, Miyako, Ikema, and Irabu islands in Areas 6–8). This model can reproduce all tsunami trace points in Areas 4 and 5. However, the reproducibility rates of inundated trace points in Area 2 are only 40%, 50% in Area 3, and 25% in Area 1. The largest underestimations of calculated run-up heights are 6.4 m for Area 2, 18.6 m for Area 3, and 5.0 m for Area 1. Moreover, in Area 6, the model cannot reproduce all inundated trace points. The greatest underestimation of run-up height is 4.2 m. In Area 8, one of the three inundated points cannot be explained. The calculated run-up height is underestimated by as much as 8 m. In Area 7, not all inundated trace points can be reproduced. The calculated run-up height is underestimated by as much as 5.1 m. In this way, the model proposed by Nakamura (2009) underestimates the run-up of the 1771 Meiwa tsunami in most regions of the Sakishima Islands.

Fig. 5
figure 5

Computed results of maximum water level for the model proposed in Nakamura (2009). a Calculation result with 810 m mesh for the entire Ryukyu Trench to the Sakishima Islands. b Calculation result for Ishigaki and Taketomi islands. The upper left panel is the result with 30 m mesh and the contour level in this panel is 50 m. The others are the result with 10 m mesh and the contour level in these panels is 10 m. c Calculation result for Tarama to Miyako islands. The upper left panel is the result with 270 m mesh and the contour level in this panel is 200 m. The others are the result with 10 m mesh and the contour level in these panels is 10 m. Numbers (1)–(8) in (b) and (c) correspond to the regional classification (Areas 1–8) in Fig. 4

Full size image
Table 3 The tsunami trace point recurrence rate in Ishigaki and Taketomi Islands and the difference in the maximum run-up height in each region (Areas 1 to 5)
Full size table
Table 4 The tsunami trace point recurrence rate in Tarama, Miyako, Irabu, and Ikema islands, and the difference between the maximum run-up height of tsunami trace points in each region (Areas 6 to 8)
Full size table

4.2 Parameter study of tsunami inundation

The reproducibility of tsunami trace points by the models tested for this study (RYa30–RYaw30) is presented in Tables 3 and 4. Figure 6 graphically displays the reproducibility rates of tsunami trace points and the maximum values of underestimation/overestimation of the run-up for each model.

Fig. 6
figure 6

Graphs showing a the reproducibility rate of tsunami trace points (%), b the maximum underestimation, and c the maximum overestimation of the run-up height for each model and area. NK denotes the model proposed by Nakamura (2009). RYa30, which is the best model for the Meiwa tsunami, is highlighted in yellow. The left panel presents results for Areas 1–5 (Ishigaki and Taketomi islands) and the right panel for Areas 6–8 (Tarama, Ikema, Irabu, and Miyako islands). In (b) and (c), the maximum underestimated (overestimated) value is shown as 0 if no tsunami trace points are underestimated (overestimated)

Full size image

For RYa10–RYcd40, in Area 1, RYc30, RYc40, RYad40, RYbd30, and RYbd40 reproduced all tsunami trace points. Although RYa30 is unable to reproduce one trace point, the underestimation of this tsunami trace point in run-up height is only 3.8 m. In Area 2, RYa30 and RYc20 have the greatest reproducibility with 87%. Both models partly overestimate and underestimate run-up heights at some tsunami trace points, with the maximum underestimate of 2.8 m and the maximum overestimate of 2.9 m for RYa30, and the maximum overestimate of 7.7 m for RYc20. Therefore, RYa30 is the best-fit model for Area 2. In Area 3, the models with the highest reproducibility (89%) were RYa30, RYb40, RYc30, RYc40, RYad30, and RYad40. For these models, RYad40 was found to have the smallest difference in run-up height, with 0.5 m, followed by RYa30 with 2.4 m. Therefore, the RYa30 model reproduced the run-up well in the second. In Area 4, models other than RYc40, RYbd30, and RYbd4, including RYa30, can reproduce all five tsunami trace points. In Area 5, all models except RYa10 and RYc10, including RYa30, were able to explain the tsunami trace points. In this way, for the RYa10–RYcd40 models, RYa30 had the highest reproducibility rate (88%, 44/50 points) for Taketomi Island to Ishigaki Island in Areas 1–5 (Fig. 7).

Fig. 7
figure 7

Calculation results of maximum water level for RYa30. a Calculation result with 810 m mesh for the entire Ryukyu Trench to the Sakishima Islands. b Calculation result for Ishigaki and Taketomi islands. The upper left panel is the result with 30 m mesh and the contour level in this panel is 50 m. The others are the result with 10 m mesh and the contour level in these panels is 10 m. c Calculation result for Tarama to Miyako islands. The upper left panel is the result with 270 m mesh and the contour level in this panel is 200 m. The others are the result with 10 m mesh and the contour level in these panels is 10 m. Numbers (1)–(8) in (b) and (c) correspond to the regional classification (Areas 1–8) in Fig. 4

Full size image

In Areas 6–8 (Tarama Island, Miyako Island, Irabu Island, and Ikema Island), RYb40, RYc30, RYad40, and RYbd30 reproduce all tsunami trace points (14 points). However, these models are unable to reproduce run-up on Ishigaki Island. For example, RYad40 overestimates the run-up height up to 11.2 m in Area 2 and 5.1 m in Area 3. RYa30, which is the best-fit model for the run-up on Ishigaki Island and Taketomi Island (Areas 1–5), cannot reproduce all tsunami trace points in Area 6, or some inundated points in Area 7. However, the underestimation of run-up height in these areas by RYa30 is only less than 2.5 m. Therefore, although RYa30 cannot reproduce some points in Areas 6 and 7, this model can reproduce the run-up distribution for the entire study region.

Based on the consideration presented above, we infer that the best model for the 1771 Meiwa tsunami in RYa10–RYcd40 is RYa30 (depth = 5 km, width = 30 km, slip = 30 m, Mw = 8.49). The RYa30 model is graphically shown in Fig. 8.

Fig. 8
figure 8

Map view of the RYa30 model, which is the best-fit model for the Meiwa tsunami. Data for plate boundary depth profiles are from Slab 2.0 (Hayes et al. 2018). Trench axis data are from Iwasaki et al. (2015)

Full size image

4.3 Sensitivity of fault depth, width, and length on local tsunami inundation

Through the parameter study, we realized that inundation at the southern part of Ishigaki Island (Areas 2 and 3) is affected sensitively by fault parameters. First, we specifically examined the fault model depth. When we set the fault model depth as 15 km, RYad20 (width = 30 km, slip = 20 m) was the best model for Area 2, but this model underestimated the run-up height with 17.7 m in Area 3. However, RYad40 (width = 30 km, slip = 40 m) or RYbd40 (width = 50 km, slip = 20 m) can explain all tsunami trace points in Area 3 but overestimates the run-up height of more than 10 m in Area 2. Consequently, if the fault depth is set as 15 km, then no fault model can explain the tsunami run-up height in Areas 2 and 3 simultaneously.

Next, we specifically examined the fault model width. If the fault depth is set as 5 km, then a longer fault width is associated with a wider inundation area, as in Area 2 (Fig. 9a). For example, when the slip is 30 m, the tsunami inundated the narrowest area when the fault width was 30 km (RYa30) compared to the inundation limit lines for different fault widths (50 km and 100 km) in Area 2 (Fig. 9a). In Area 3, when the fault width was 30 km, a tsunami inundated the widest area (Fig. 9b). Consequently, the sensitivity in run-up against the fault width is opposite between the southwestern (Area 2) and southeastern (Area 3) parts of Ishigaki Island. Therefore, to explain the run-up in southwest (Area 2) and southeast (Area 3) Ishigaki Island simultaneously, the fault depth must be as shallow as 5 km. Moreover, the fault width must be as narrow as 30 km.

Fig. 9
figure 9

Images showing the inundation limit lines at southern coast of Ishigaki Island for each fault length when the fault depth is 5 km and the slip is 30 m. a Area 2 (southwest part of Ishigaki Island), and b Area 3 (southeast part of Ishigaki Island). Red, blue, and green lines respectively represent the inundation limits for the RYa30 model (fault width = 30 km), the RYb30 model (fault width = 30 km), and the RYc30 model (fault width = 100 km). The black line shows the shoreline. The grey line shows the 5 m contour of the topography and the bathymetry

Full size image

Finally, we specifically examined the fault length. In the case of RYaw30, in which the fault length was shortened from RYa30 to 150 km and set as off of Ishigaki Island, the run-up was well reproduced on Ishigaki Island (reproducibility rate of tsunami trace points = 90%), but not all the inundated trace points were able to be reproduced from Tarama Island to Miyako Island (Areas 6–8). The run-up height was underestimated by as much as 7.4 m. RYae30, which is set off of Miyako Island with a short fault length (150 km), can only reproduce 27% of the inundated trace points, and the run-up height was underestimated by as much as 16.6 m on Ishigaki Island. Consequently, the fault should be extended from off of Ishigaki Island to Miyako Island to explain the distribution of tsunami traces. However, this study is inadequate for determining the extension of fault length, especially further toward the northeast, because there are no islands. Therefore, no constraint information related to fault length is available.

4.4 Bathymetry effects on coastal tsunami height and velocity

Figure 10 shows the maximum tsunami height by RYa30 and tsunami rays calculated using tsunami ray tracing analysis. Tsunami rays are concentrated in areas with high tsunami wave heights, indicating that waves are concentrated because of the bathymetry. For example, Shiraho-oki Sea Hill, with diameter of about 3 km, is southeast off of Ishigaki Island (Goto 2016). It refracts and focuses the tsunami on the Ibaruma coast of Ishigaki Island (Fig. 10b). In addition, when comparing the distribution of tsunami boulders (Goto et al. 2010a) with tsunami height and ray tracing, tsunami boulders are basically in the area where tsunami rays are concentrated offshore, and where tsunami waves are high (Fig. 10b, c). One notable exception is Miyara Bay, where tsunami boulders of up to 700 t are present (Goto et al. 2010b). However, because of offshore bathymetry, no significantly greater tsunami wave height was found (Fig. 10b).

Fig. 10
figure 10

Figures depicting the results of wave ray tracing and the maximum water level distribution of the tsunami based on the RYa30 model. a Entire Ryukyu Trench to the Sakishima Islands, b around Ishigaki Island, and c around Miyako Island. Thick pink lines in (b) and (c) show the tsunami boulder distribution (Goto et al. 2010a). The contour level is 500 m in (a) and 100 m in (b), (c)

Full size image

5 Discussion

5.1 The 1771 Meiwa tsunami model revisited

For this study, we examined the tsunami wave source of the 1771 Meiwa tsunami using the latest historical records as constraints. Consequently, we demonstrated that the RYa30 model (depth = 5 km, fault width = 30 km, fault length = 225 km, slip = 30 m, Mw = 8.49) (Fig. 8) is the best model to reproduce tsunami historical records.

Comparing our fault model to that reported by Nakamura (2009) (depth = 5 km, fault width = 30 km, fault length = 150 km, slip = 16 m) shows that both models set the slip area in a shallow and narrow part of the plate boundary, but the slip amount estimated in this study (= 30 m) is far larger than that proposed by Nakamura (2009). This large size is attributable to the difference in tsunami calculation methods used for each study. Nakamura (2009) calculated the tsunami height by assuming reflection at 10 m water depth, which might lead to neglect of the effects of coral reef bathymetry in shallow waters. Wide coral reef bathymetry basically attenuates tsunami wave energy (e.g., Kunkel et al. 2006; Gelfenbaum et al. 2011; Le Gal and Mitarai 2020). In this study, the tsunami attenuation effects by the coral reef topography were better incorporated because we conducted tsunami calculation including inundation, and high-resolution (10 m mesh) topographic data were adopted. Consequently, a larger slip was required for this study to reproduce the tsunami run-up height.

Regarding the fault length, Nakamura (2009) set the length as 150 km, with the fault not extending to off of Miyako Island. Our model set the fault length as 225 km to cover the entire area off Ishigaki Island to Miyako Island. Nakamura (2009) assumed the maximum run-up height at Miyako Island as 10 m based on a report by Kawana (2000). However, Goto et al. (2012), which was used as a constraint for this study, reported the tsunami inundation on Miyako Island as much larger (18 m). For this reason, our fault model became generally larger than that proposed by Nakamura (2009).

Our model incorporates the assumption of a very large slip in a shallow and narrow region of the plate boundary along the Ryukyu Trench. This feature of a very large slip in a shallow and narrow region of the plate boundary is consistent with the features of tsunami earthquakes (e.g., Satake and Tanioka 1999). Additionally, in terms of seismology, one can infer that the Ryukyu Trench has no typical locked zone but that tsunami earthquakes can occur in shallow areas (Arai et al. 2016; Nakamura 2017). Therefore, our proposed model is classifiable as a tsunami earthquake, as pointed out by Nakamura (2009).

However, Ando et al. (2018) recognized fissures beneath the Meiwa tsunami deposits and estimated that the seismic motion during the Meiwa event was sufficiently strong to form fissures in the ground. In addition, contrary to assertions of Arai et al. (2016) and of Nakamura (2017), it has also been pointed out that some locked areas exist in the southern Ryukyu Trench, which might be subject to large subduction zone type earthquakes (Doo et al. 2018; Kano et al. 2021; Debaecker et al. 2023). Therefore, the fault rupture might extend not only to the shallow part of the plate boundary but also to deeper parts such as that of the 2011 Tohoku-oki earthquake (e.g., Satake et al. 2013). In any case, our results imply that a large slip in the shallow and narrow part of the plate boundary is decisive for reproducing the run-up distribution of the 1771 Meiwa tsunami.

Why could such a large slip have occurred at the shallow plate boundary? Lessons learned from the 2011 Tohoku-oki earthquake and tsunami provide useful insights. To explain the run-up heights of the 2011 Tohoku-oki tsunami, a large slip must be assumed near the trench axis at Miyagi-oki (central part of the Japan Trench, slip = 69 m) and at Sanriku-oki (northern part of the Japan Trench, slip = 36 m), according to Satake et al. (2013). For the Miyagi-oki region, fault rupture is estimated as having extended up to the trench axis, causing a horizontal displacement of 50 m and a vertical displacement of 10 m, based on exploration of the seafloor bathymetry (Fujiwara et al. 2011). Decreased shear stress because of high pore-fluid pressure in the décollement (the shallow region of the plate-boundary fault) has been proposed as a reason for the fault rupture extending nearly to the trench axis (e.g., Ujiie et al. 2013). In fact, reflection surveys have indicated that pore water pressure at the décollement in Miyagi-oki is very high (Hondori and Park 2022).

By contrast, for Sanriku offshore, bathymetry surveys indicate displacement of less than 20 m horizontally and several meters vertically by the 2011 event, and indicate that fault rupture does not extend to the trench axis (Fujiwara et al. 2017). Therefore, the seafloor displacement caused by the fault motion is necessary to explain a large slip (36 m) near the trench axis, but so are other processes. Regarding other processes, inelastic deformation of unconsolidated sediments near the trench axis (Tanioka and Seno 2001) has been implicated as involved in this large slip of the 2011 event (e.g., Ma and Nie 2019; Du et al. 2021). In the southern Ryukyu Trench, high pore-fluid water pressure has also been reported in the décollement of the southern Ryukyu Trench (Arai et al. 2016). Therefore, it can be inferred that the decrease in shear stress attributable to high pore-fluid pressure in the décollement might also have occurred in the southern Ryukyu Trench. In addition, unconsolidated sediments with 70 km width and 15 km depth are estimated as existing near the Ryukyu Trench axis. The sediment shape is similar to that of the Japan Trench at off Sanriku (Arai et al. 2016). Therefore, the inelastic deformation of unconsolidated sediments near the trench axis in the southern Ryukyu Trench might be a reason for the occurrence of a large slip in the shallow part of the plate boundary.

However, even for the well-measured 2011 Tohoku-oki tsunami, the involvement of other factors enhancing the tsunami such as splay faults (e.g., Sugino et al. 2013) and submarine landslides (e.g., Tappin et al. 2014) have also been proposed, and the source mechanisms have not been clarified well (Sugawara 2021). Therefore, for the Meiwa tsunami, which is far less-documented than the 2011 Tohoku-oki tsunami, it is difficult to determine the cause(s) of the large slip near the trench axis. Thus, the slip of the tsunami wave source model estimated in this study may encompass various causes of the tsunami including slip along the plate boundary, splay faults, and submarine landslides. It is noteworthy that the slip amount estimated here is determined to satisfy the requirement of a very large initial water level change at the source. We cannot fully exclude the possibility that splay faults or a non-seismic source(s) such as submarine landslides contributed to enhance the tsunami. Indeed, the existence of the splay faults along the Ryukyu Trench was reported by Hsu et al. (2013) and Arai et al. (2016) and there is the possibility that they enhanced the Meiwa tsunami. Similarly, submarine landslides may have been involved in the tsunami (Okamura et al. 2018). If these were the cases, then the slip amount of the interplate earthquake itself estimated in this study could be decreased. Therefore, our estimated slip amount of the interplate earthquake should be regarded as the maximum possible value of the single rectangular fault model. At this moment, we do not have sufficient evidence to judge whether the Meiwa tsunami was generated only by the interplate earthquake or not. Therefore, additional seismological and sedimentological researches along the southern Ryukyu Trench must be conducted to ascertain whether the Meiwa tsunami was indeed enhanced by additional sources such as splay faults and submarine landslides.

5.2 Unique identification of the fault width using differences of run-up processes as a constraint

Based on our high-resolution modeling, we showed that tsunami inundations at Area 2 and Area 3 are sensitively variable by fault widths (Fig. 9). When the fault depth is 5 km, a longer fault width is associated with a wider the inundation area, as in Area 2, and with a narrower inundation area as in Area 3 (Fig. 9). Consequently, the response of inundation against fault width differed between the two areas.

There are several reasons for this difference. First, the fault width is well known as mainly affecting the tsunami wavelength. A shorter fault width generates a shorter wavelength of the tsunami and vice versa (e.g., Satake et al. 2008). In addition, the coral reef widths differ in two areas. In Area 3, the coral reef is about 1 km wide, but in Area 2 the island is surrounded by a coral reef with more than 8 km width, which is called the Sekisei Lagoon (Fig. 11a). The relation between tsunami wavelength, which is mainly controlled by fault width, and the coral reef width might cause large variations in inundation areas. Figure 11b and c shows the maximum wave heights and velocities along the transect on the coral reef in the two areas. In Area 2, wave heights and velocities become the highest outside the reef and around the reef edge when the fault width is 30 km, but as they propagate over the greater than 8 km wide Sekisei Lagoon, wave heights decrease more with shorter fault widths. Moreover, velocities become almost constant at the shoreline, irrespective of the fault width. Fundamentally, tsunamis with shorter wavelengths (= shorter fault widths) have higher velocities (e.g., Gusman et al. 2012). Wave heights are also higher for shorter wavelengths because of the stronger effects of wave shoaling and breaking offshore of the coral reef. Therefore, outside the reef and around the reef edge, the shorter the fault width is, the higher the tsunami height is and the faster the tsunami is. Also, the tsunami energy was attenuated by wave separation and wave breaking when the tsunami inundated the coral reef (Mohandie and Teng 2009). When the wave is high relative to the coral reef depth, as was the case of the Meiwa event, tsunami energy attenuation is more pronounced when the ratio of coral reef width to wavelength is large (Lynett 2007). Therefore, when the reef width is wide, as is true in Sekisei Lagoon, the longer wavelength (= fault width) caused higher wave height near the shore. The velocity is almost identical irrespective of the fault width. Therefore, in Area 2, longer tsunami wavelengths (= fault widths) produce a wider inundation area. By contrast, Area 3 is characterized by the shorter width of the coral reefs relative to Area 2. Therefore, the attenuation effect of the reef is insufficiently effective: waves with shorter wavelengths and higher velocities reach the shore as they are. Therefore, in Area 3, shorter tsunami wavelengths (= shorter fault widths) caused a wider inundation area.

Fig. 11
figure 11

a Aerial photograph of southern Ishigaki Island. The eastern side has about 1 km wide coral reefs, whereas the western side is surrounded by an approximately 8 km wide coral reef (Sekisei Lagoon). The aerial photograph was provided by ESRI. b Cross-sections of maximum water levels (upper panel), maximum current velocities (middle panel), and bathymetry (lower panel) off the southwestern coast of Ishigaki Island. Cross-sectional lines are shown as A–C–B in (a). For both the maximum water level and maximum flow velocity, the red line shows RYa30 (fault width = 30 km), the blue line shows RYb30 (fault width = 50 km), and the green line shows the RYc30 (fault width = 100 km). c Cross-sections of maximum water levels (upper panel), maximum flow velocities (middle panel), and the bathymetry (lower panel) offshore southeast of Ishigaki Island. Cross-sectional lines are shown as A′–B′ in (a). For both maximum water level and maximum flow velocity, the red line represents RYa30 (fault width = 30 km), the blue line represents RYb30 (fault width = 50 km), and the green line represents RYc30 (fault width = 100 km)

Full size image

This difference in the fault width effects on the inundation area between the southwest (Area 2) and southeast (Area 3) of Ishigaki Island strongly constrains the 30 km fault width.

5.3 Bathymetry controlled the tsunami run-up, distributions of tsunami boulders, and effects on coral ecosystems

The previous study suggests that the distribution of tsunami boulders is not constant, but they are concentrated on some specific coasts (Goto et al. 2010a). Tsunami boulders at the Sakishima Islands are composed mainly of reef and coral rocks. The Sakishima Islands coasts are surrounded constantly by coral reefs of similar sizes. Therefore, the distribution of tsunami boulders might not be controlled by ecological phenomena (i.e., the presence/absence of the boulder source (= corals and coral reefs)). Actually, it is noteworthy that wave heights were typically high where tsunami boulders were distributed (Fig. 10). Tsunami ray tracing analysis further revealed that the rays were fundamentally concentrated in the places where the tsunami waves were high and boulders were concentrated. These results imply that tsunami boulders are present in areas where the tsunami energy is concentrated because of the bathymetric effects, even though a single rectangle fault model is assumed. One remarkable exception is the distribution of numerous large boulders on the Miyara Bay coral reef and its hinterland (Goto et al. 2010b; Hisamatsu et al. 2014; Nakata et al. 2023). This exception might be explained by the multiple reflections or the presence of large channels that penetrated through the coral reefs of Miyara Bay and which are formed by the river inflow. In these narrow channels, a jetting effect might have amplified tsunami energy locally (Gelfenbaum et al. 2011) and could have enhanced the force necessary to launch large boulders from the reef slope to the reef flat (Hisamatsu et al. 2014). Indeed, the maximum velocity by RYa30 is higher in the channel part of Miyara Bay than in the surroundings, with velocities greater than 20 m/s (Additional file 1: Fig. S2).

The tsunami boulders on the Sakishima Islands were transported not only by the 1771 Meiwa tsunami but also by earlier tsunami waves. They are distributed in similar areas (Goto et al. 2010a; Araoka et al. 2013). Therefore, it is likely that not only the Meiwa tsunami, but also earlier tsunami waves were influenced by the bathymetry and were concentrated to the same coasts as the Meiwa tsunami. At such coasts, the tsunami wave height and velocity around the reef edge reached approx. 20 m and approx. 22 m/s, respectively, according to our calculations. These values are extraordinarily high compared to those of other recent historical tsunami events that have affected the coral reefs, such as the 2004 Indian Ocean tsunami and the 2009 Samoan tsunami (Goto et al. 2007; Dilmen et al. 2015). Goto et al. (2019) reported that coral ecosystems around the Sakishima Islands might have been reset repeatedly by large tsunamis. Our results further imply that the extent of coral damage could be non-uniform, even on the coasts of the Sakishima Islands. Specifically, coral damage might be outstanding at specific coasts, where tsunami boulders are now concentrated because the area can always be characterized by high tsunami wave heights and velocities as a result of the bathymetric effects, irrespective of the fault size and position.

6 Conclusions

For this study, we re-evaluated the tsunami wave source of the 1771 Meiwa tsunami numerically using detailed topography and bathymetry data as well as the latest historical record dataset. The results indicate that a large slip of 30 m in a shallow and narrow region of the plate boundary in the southern Ryukyu Trench (fault depth = 5 km, fault width = 30 km) is necessary to reproduce the historical record. This finding in turn indicates that the Meiwa event should be categorized as the typical tsunami earthquake, although a 30 m slip is extraordinarily large and it demands seismological explanation. Our results pose a striking contrast to the results of Minamidate et al. (2022) who suggested no occurrence of large tsunamigenic earthquake along the central Ryukyu Trench. Therefore, different seismological settings should be considered between the southern and central Ryukyu Trench. The large slip in this shallow and narrow region of the plate boundary along the southern Ryukyu Trench might not necessarily be explainable solely by fault rupture. Other potential causes for enhancement of tsunami waves are deformation by splay faults, inelastic deformation of unconsolidated sediments near the trench axis and/or submarine landslides. Furthermore, we investigated bathymetry effects on tsunami propagation. Our findings demonstrated that tsunami boulders were distributed in areas where tsunamis were focused because of bathymetric effects. This result implies that tsunami damage to corals and reefs might not be uniform along the coast of the Sakishima Islands, but damage might be concentrated at some specific reefs: consequently post-tsunami recovery processes of coral reefs might differ even at reefs with close mutual proximity.