Introduction

Stress drop, the difference between the shear stress acting on the fault plane before and after rupture, is an important parameter in characterizing earthquake faulting. Many studies have examined spatial variations of stress drops (e.g., Allmann and Shearer 2009; Cui et al. 2023). Fewer studies have examined stress-drop variations among small to midsize earthquakes, generally magnitude less than 5, within subducting slabs (Nishitsuji and Mori 2013; Oth 2013; Kita and Katsumata 2015; Chu et al. 2019; Tian et al. 2022; Folesky et al. 2024), although stress drops associated with large intraslab earthquakes have been scrutinized (e.g., Asano et al. 2003; Suzuki et al. 2009; Prieto et al. 2012; Poli et al. 2016).

Kita and Katsumata (2015) examined spatial variations of stress drops for intraslab earthquakes beneath Hokkaido, northern Japan, using relocated hypocenters (Fig. 1), precisely-determined depths of the upper interface of the Pacific Plate (Fig. 1), and corner frequencies estimated using the S-coda wave spectral ratio method and a constant value for velocity. They suggested that the median stress drop for earthquakes in the oceanic crust (OC) was smaller than that for earthquakes in the oceanic mantle (OM) at depths of 70–120 km. In the oceanic crust at depths of 70–170 km, the median stress drop for earthquakes first decreases, then switches to increases with increasing depths. They argued that this resulted from a change in OC rigidity with increasing depth due to eclogite formation and related dehydration processes within the OC.

Fig. 1
figure 1

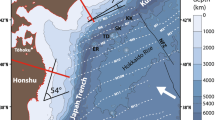
a Distribution of earthquakes (color coded by depth) beneath Tohoku (this study). Earthquakes beneath Hokkaido are plotted using gray symbols (from Kita and Katsumata 2015). Red dashed lines are iso-depth contours for the upper surface of the Pacific Plate (Kita et al. 2010a). The color scale shows the depth of events beneath Tohoku. b Seismogram envelopes (horizontal component) in the 1–30 Hz band recorded at a station N.KANH, which is almost the same distance from two earthquakes in Tohoku region, northeastern Japan. Horizontal axes show lapse time from origin times of the two events. RMS envelopes are shown as red (25 April 2012 16:45:48 depth 64.4 km; magnitude: 2.6) and black (29 November 11:22:37 depth 70.8 km; magnitude: 2.6) lines. The rms envelopes are smoothed by averaging data in 1 s time windows. Pink arrows show travel times from the origin time, and ts is the travel time of direct S waves of two events. Dark and light blue lines denote the original 4 s time window and one shifted 2 s later, whose spectra were stacked to obtain S coda spectra for all the events

Full size image

Differences in seismic properties of the Pacific plate between the Tohoku and Hokkaido regions have been suggested by several seismological studies. In the northeastern Japan subduction zone, Fujie et al. (2018) reported a difference in low-velocity anomalies beneath Tohoku-oki and Hokkaido-oki regions from ocean bottom seismometers; the degree of the low-velocity anomalies within the oceanic crust and mantle in off Tohoku-oki is larger than that in off Hokkaido-oki. The difference in the anomalies may be due to a more hydrated oceanic plate beneath Tohoku-oki than Hokkaido-oki based on knowledge of the abyssal hill fault re-activation system. Shiina et al. (2017) examined seismic velocities of oceanic crust beneath Hokkaido, finding higher seismic velocity of oceanic crust at depths of 70 to 100 km beneath Hokkaido compared to that beneath Tohoku. Kita and Ferrand (2018) found that b-values in the OM beneath Tohoku are smaller than in Hokkaido. They also indicated that the OM at intermediate depth beneath Tohoku is more hydrated than beneath Hokkaido based on results of acoustic emission experimental earthquakes (AEs); in serpentinized peridotite samples, b-values of the AEs increase with the increase of hydration. The stress regime within the slab beneath Tohoku is similar to Hokkaido (e.g., Hasegawa et al. 1978; Suzuki and Motoya 1981; Suzuki et al. 1983), but there is a difference in the portion of interplane events (events between the double seismic planes) between Tohoku and Hokkaido (e.g., Kosuga et al. 1996; Kita et al. 2010b). Source parameters including stress drops of events at intermediate depth also may differ between Tohoku and Hokkaido due to the difference of the degree of hydration.

In the present study, we estimate the stress drops for intermediate-depth intraslab events (2.0 < Mj < 5.0 where Mj is the JMA magnitude) (Fig. 1), and examine the spatial variations of stress drop, including dependence on focal-depth and on the distance normal to the plate interface for precisely-located earthquakes beneath Tohoku. By comparing results of this study and a previous study in Hokkaido (Kita and Katsumata 2015), we also infer causes of the difference in stress drop behaviors between the two regions.

Data and method

We relocated hypocenters using the double-difference location method (Waldhauser and Ellsworth 2000) and estimated the stress drops for events using a procedure nearly identical to that of Kita and Katsumata (2015). Relocated hypocenters are shown as colored crosses in Fig. 1. The relocation process is described as below.

To relocate earthquakes, hypocenter parameters and phase data for 16,348 events at depths of more than 55 km from the JMA catalog were used as initial parameters. The 1D velocity structure model of the routine procedure for hypocenter location at Tohoku University (Hasegawa et al. 1978) was employed. Event pairs were selected that had hypocentral separations of < 20 km and at least eight arrival time differences with respect to their neighbors. In total, 1,927,185 arrival time differences were obtained from catalog data for P-waves, and 1,658,479 for S-waves. The number of stations is 251. The final results of the inversion were obtained after 12 iterations, which reduced the average root mean square value of the double-difference misfit from 0.126 to 0.0473 s. Estimated relative relocation errors using the singular value decomposition method are ~ 1 km in both the vertical and horizontal directions. After the relocation, we only retain events whose corner frequencies can be successfully estimated by our analysis.

We relocated 16,348 events and extracted 4912 events (at depths of 55 to 200 km) after matching our event catalog of corner frequencies. After excluding thrust events that could potentially lie on the plate boundary, 2875 events at depths of 70 to 200 km are examined in detail for this study.

If the circular crack model (Eshelby 1957) is assumed, a static stress drop Δσ can be calculated using the fault radius r:

$$\Delta\upsigma =\frac{7{\text{M}}_{0}}{16{\text{r}}^{3}}$$
(1)

where Mo is the seismic moment. Adopting the fault plane radius r used by Sato and Hirasawa (1973), Eq. (1) can be rewritten as

$$\Delta\upsigma =\frac{7{\text{M}}_{0}}{16}\cdot {\left(\frac{2\uppi {\text{f}}_{\text{c}}}{\text{CsVs}}\right)}^{3}$$
(2)

where fc, Cs, and Vs are the corner frequency, a constant, and the S-wave velocity, respectively. In this study, Cs was assumed to be 1.9 based on previous studies (Uchida et al. 2012; Kita and Katsumata 2015). It should be noted that a limitation of estimating fault radius from corner frequency is that it requires the assumption that the rupture velocity is a constant fraction of S-wave velocity for all events. For the OM, we basically used a JMA one-dimensional Vs model (Ueno et al. 2002) and for the OC we used a two-dimensional Vs model based on the Vp model of Shiina et al. (2013) with a constant Vp/Vs of 1.80 (Shiina et al. 2017). In Shiina et al. (2013), the lateral variation of P-wave velocity (Vp) values in the OC were precisely estimated beneath Tohoku.

We estimated the corner frequencies of 2875 intraslab events at depths of 70–200 km during the period from March 2003 to March 2015 beneath Tohoku using the S-coda wave spectral ratio method (e.g., Somei et al. 2010; 2014; Mayeda et al. 2007; Takahashi et al. 2005) on seismic waves from Hi-net stations by NIED (Okada et al. 2004) and permanent seismic networks operated by Tohoku University, Hirosaki University and Hokkaido University in the nationwide dense seismic network. Beneath Tohoku, the depth of the interplate megathrust is less than 60 km (Igarashi et al. 2001), which means that our selected events exclude such interplate thrust events. The velocity amplitude spectrum of the coda wave of event i observed at station j can be written as

$${{\text{A}}_{\text{ij}}}^{\text{obs}}\left(\text{f};\text{t}\right)={\text{S}}_{\text{i}}\left(\text{f}\right){\text{T}}_{\text{j}}(\text{f}){\text{P}}_{\text{ij}}(\text{f};\text{t})$$
(3)

where f is frequency, t is the lapse time from the source origin time, Si(f) is the source spectrum, Tj(f) is the local site amplification, and Pij (f;t) describes propagation path characteristics. In the general spectral ratio method, spectral amplitude ratios of earthquake pairs are computed, and the two frequencies at which the resultant slope changes correspond to the corner frequencies of the larger and smaller earthquakes. If we use the S-coda wave instead of direct waves, the effect of ray paths from sources to stations is removed because the coda wave does not depend on the radiation patterns (i.e., focal mechanisms) of earthquakes or the distance between events (Rautian and Khalturin 1978; Tsujiura 1978; Sato et al. 2012). For example, Somei et al. (2014), Tsujiura (1978), Rautian and Khalturin (1978) showed that the shapes of coda waves of small and large events are common. As reported by Rautian and Khalturin (1978), the decrease in coda wave amplitude of local earthquakes does not depend on the distance from the source to a common station when the lapse time is at least twice the S-wave travel time. Tsujiura (1978) also showed that the decay shapes of the amplitudes of coda waves from local events having different magnitudes and source distances form a common curve at a common station, which implies that the decay of the coda wave follows a common shape for both large and small events, regardless of source distance. Somei et al. (2014) showed that the shapes of coda waves of an Mw 4.5 event are similar to those of an Mw 6.6 event when the lapse time is twice the direct S-wave travel time. Since there are many possible pairs, we can obtain corner frequencies for many events with this method. When the lapse time is 1.5 to 2.0 times longer than the direct S-wave travel time, we can assume \({\text{P}}_{1\text{j}}(\text{f};\text{t})\approx {\text{P}}_{2\text{j}}(\text{f};\text{t})\) (Sato et al. 2012). Assuming the ω-square source model following Brune (1970), we obtain

$$\frac{{{\text{A}}_{1\text{j}}}^{\text{obs}}\left(\text{f};\text{t}\right)}{{{\text{A}}_{2\text{j}}}^{\text{obs}}\left(\text{f};\text{t}\right)}\approx \frac{{\text{S}}_{1}\left(\text{f}\right)}{{\text{S}}_{2}\left(\text{f}\right)}=\frac{{\Omega }_{0\_1}}{{\Omega }_{0\_2}}\cdot \frac{1+{\left(\text{f}/{\text{f}}_{\text{cs}\_2}\right)}^{2}}{1+{\left(\text{f}/{\text{f}}_{\text{cs}\_1}\right)}^{2}}$$
(4)

We computed the Fourier spectral ratios of velocity amplitude of earthquake pairs at common stations. The ω-square source model (Brune 1970) was fitted to each averaged spectral ratio of available earthquake pairs.

As the source radiation pattern and medium heterogeneities can be eliminated when coda waves from two events have comparable propagation paths, the S-coda-wave spectral ratio method can be applied to earthquakes in subduction zones (Takahashi et al. 2005; Nakajima et al. 2013). Nakajima et al. (2013) estimated corner frequencies of earthquakes using that method and discussed the relationship of earthquake corner frequencies to the distance between two events. For intermediate-depth events, they required inter-event distance less than the event focal depths. They showed that the estimated corner frequency of an event at 118 km depth is stable for inter-event distances of 20 to 100 km. In our analysis, the distance between the two events must be less than 60 km, but also less than the focal depth of the shallower event of the pair when the focal depth of the shallower event is less than 60 km. Each event pair in our analysis had a magnitude difference at least 0.8. The duration of the time window is 4 s starting from 1.5 times the direct S wave travel time, which is considered to be the S-coda wave (Sato et al. 2012). That time window is sufficient to constrain corner frequencies in our magnitude range of 2.0 to 5.0. To improve stability, we used stacked waveforms from the original time window and a time window shifted 2 s later than the initial one. Examples of envelope waveforms of S-coda waves analyzed in this study are shown in Fig. 1b. One of the merits of the use of coda waves is greater stability of amplitude ratios compared to direct waves (e.g., Mayeda et al. 2007). Figure 1b shows that amplitudes for S-coda wave of two M2.6 events are almost the same, whereas amplitudes during their direct S-waves differ. We estimated the S-wave arrival time by using manual picking times of P arrival times by NIED operators, and by calculating the theoretical S-wave travel time for the one-dimensional seismic velocity model (Hasegawa et al. 1978) in order to determine the onset of the S-coda wave. We analyzed spectral ratios using a frequency range of 1–30 Hz with a one-third-octave bandwidth. If the fc2 becomes 30 Hz, we discard fc2 and fc1 of that pair. Only data with signal-to-noise (S/N) ratios greater than 2 in average absolute amplitude in the 4 s time window were included. When we fit the observed spectral ratios (the averaged spectral ratios) to theoretical models, we used a weighting proportion to the difference between logarithms of neighboring frequencies, to balance the contribution of the low frequencies relative to the high frequencies. For more detailed parameter settings, see Kita et al. (2014).

The number of event pairs for each event is presented in Figure S1 in the additional file; almost 900,000 event pairs are applied to the S-coda-wave spectral ratio method. The average number of event pairs is 184. Examples of the estimation of corner frequencies using this method for M 3.4 and M 2.0 earthquakes are shown in Figs. 2 and S2. Corner frequencies for each event were obtained by averaging the corner frequencies from at least 5 pairs. The corner frequency and standard deviation for event ID 140627221827 are respectively 8.41 Hz and 2.21 Hz with event distance within 30 km, whereas they are respectively 8.27 Hz and 2.14 Hz with event distance within 60 km (Fig. 2). The maximum inter-event distance used in this study is larger than that of analyses using direct waves, but the difference in obtained corner frequencies is acceptable. We adopt a 4 s time window in the present study, but we also tested 6 s, 8 s and 10 s for event ID 140627221827. The corner frequency and standard deviation for the event with 6 s time window are respectively 7.92 Hz and 1.84 Hz (the number of event pairs is 91), those with 8 s time window are 7.19 Hz and 1.73 Hz (the number of event pairs is 65) and those with 10 s time window are 7.09 Hz and 1.33 Hz (the number of event pairs is 22). The corner frequencies of events using the different time windows are within range of the standard deviations using the original time window, but the number of event pairs is much smaller than the number using the original 4 s time window (115 pairs) because the signal-to-noise ratio decreases for the longer time windows. Because using a large number of events is important, and because we focus mainly on relative changes of stress drops with depth or distance from the plate interface, we find the 4 s time window preferable. Plots of the obtained corner frequencies versus the seismic moment are presented in Figs. 3a and S2a. In our analysis, we use the standard error of the corner frequencies of event pairs as the error in the corner frequency of each event (Fig. 3a). For comparison, Figure S2a shows the standard deviation of the corner frequencies of event pairs as estimates of the error. Figures 3a and S2a show plots of the obtained corner frequencies versus seismic moment for the events used in this study. The stress drops of intraslab events are mainly in the range of 1 to 100 MPa. There tends to be an apparent small increase in stress drop with increase in seismic moment.

Fig. 2
figure 2

a–d Examples of the estimation of corner frequencies using the S coda wave spectral ratio method for the larger earthquake of pair (27 June 2014 22:18:27 depth 73.3 km; Magnitude: 3.4). In the left-hand column, red and blue circles denote the epicenters of the two events and light blue triangles represent seismic stations used in the estimation. In the right-hand column, red and blue triangles indicate the estimated corner frequencies of the two events (\({f}_{cs\_1}\) and \({f}_{cs\_2}\)), thin lines denote velocity-amplitude spectral ratio for events at each station; black lines show the average of all spectral ratios; red lines show theoretical spectral ratios for events, and the dashed red line indicates the average value of the corner frequencies (\(\overline{{f }_{cs}}\)). a Estimation of corner frequencies of one pair of events using the spectral ratio method. b Estimation of corner frequencies of second pair of events. c Estimation of corner frequencies for a third pair of events. d Estimation of corner frequencies of the event. (Left) Locations of all event pairs used in the estimation. (Right) Estimated corner frequencies. Red dashed vertical line shows the average value of the corner frequencies (\(\overline{{f }_{cs}}\)) for the M3.4 event. Black circles indicate corner frequencies for the event calculated from various event pairs. The gray shaded band shows the standard deviation (SD) of the corner frequency

Full size image
Fig. 3
figure 3

a Corner frequencies for events plotted against seismic moment estimated in this study. Black bars show the standard error in the estimation for the corner frequencies. Dashed lines denote isovalue lines of static stress drops at 0.1, 1, 10, 100, and 1000 MPa, using Eq. (2) (Cs and Vs were assumed as 1.9 and 4600 m/s, respectively). The seismic moment (Mo) for each event in this plot is estimated from logMo = 1.5Mw + 9.1 (Kanamori 1977). The value of Mw for each event is estimated using the empirical relationship: Mw = 0.439Mj + 0.0689Mj2 + 1.22 (Edwards and Rietbrock 2009). Mj is the JMA magnitude. b Estimated stress drops of all intraslab earthquakes plotted against depth beneath Tohoku region at depths of 70 to 200 km. Grey dots show the stress drops of individual events. Gray bars show estimates of the standard errors of stress drops based on standard errors in the estimation of the corner frequencies. Red open squares and red error bars, respectively, denote median stress drops and 8-quantile range for the median stress drops at depths of 70–80 km, 80–90 km, 90–100 km, 100–120 km, 120–140 km, 140–175 km and 175–200 km. Values of the median stress drops are given in Table S1. Light red error bars denote interquartile range

Full size image

This region has a strong double seismic zone and it is helpful to classify intraslab events based on the detailed geometry of the upper surface of the subducting Pacific Plate (Zhao et al. 1997; Kita et al. 2010a) to facilitate a discussion of stress drop behavior within the slab. To classify intraslab events, we adopted the method of Kita et al. (2010b). First, the earthquakes were classified as either OC or OM events, based on the normal distance from the upper interface of the subducting Pacific Plate beneath Tohoku. Taking into consideration the estimation errors in the location of the plate interface, hypocenters and the general reported values of the oceanic Moho depth (Minshull et al. 1998), we use 10 km as the depth of the oceanic Moho. Next, events occurring 0 to 10 km from the plate interface were classified as upper-plane events of double seismic planes; these are expected to occur in the OC. Events 10–23 km deeper than the plate interface were classified as interplane events, and earthquakes located deeper than 23 km from the interface were classified as lower-plane events in the double seismic zone.

Results and discussion

Figure 3b shows the stress drops and median stress drops for all intraslab earthquakes at all depth ranges (70–200 km), assuming the JMA 1D structure for the OC and OM events listed in Table S1. We used that velocity model between the OC and OM in order to compare with results from Hokkaido (i.e., Kita and Katsumata 2015, Fig. 3). Figures 4a and b, respectively, show the stress drop for each event, the median stress drop in the OC and the OM. In Figs. 4a and b, the depth bin sizes for estimation of median stress drops are the same as in Figs. 4 and 5 of Kita and Katsumata (2015) for Hokkaido. Figure S4 shows the median stress drops for OM and OC events with constant depth (20 km) bin sizes. Map views and a cross-section of stress drops of intraslab earthquakes are shown in Fig. 5. The location of cross-section is the same as Fig. 3 of Kita et al. (2006). Figure 6a shows the distribution of all stress drops plotted against distance from the upper plate interface beneath Tohoku. The distribution of intraslab events excluding aftershocks of the 2003 M7.1 Miyagi is shown in Figure S8 of the additional file. Figure 7a compares the median stress drop for upper-plane events (OC events), interplane events (OM events) and lower-plane events (OM events) plotted against depths beneath Tohoku. The values of the median stress drop for OC events (upper-plane events) and OM events are listed in Table 1 and those for upper-plane events, interplane events, and lower-plane events in Table S2. Figures 6b and 7b were prepared based on the results beneath Hokkaido by Kita and Katsumata (2015), and are presented for comparison with Figs. 6a and 7a.

Fig. 4
figure 4

Estimated stress drops at depths of 70–180 km plotted against depth for a events in the OC using a two-dimensional Vs model from Shiina et al. (2013) and b events in the OM using a one-dimensional Vs model from the JMA 1D structure (Ueno et al. 2002). Gray bars indicate estimation errors of stress drops based on the standard error of the corner frequencies. The error estimate for each stress drop comes from the estimated standard error in the corner frequency of each event. Gray dots represent the stress drops for individual events. Color-coded open squares and error bars, respectively, denote the median stress drops at depths of 70–80 km, 80–90 km, 90–100 km, 100–120 km, 120–140 km, and 140–180 km. Values of the median stress drops are shown in Table 1. Red and blue error bars in (a) and (b) denote 8-quantile range for the median stress drops. Light red and blue error bars in a and b denote interquartile range for the median stress drops. c Spatial distribution (a depth-varying slice) of velocity in the OC reported by Shiina et al. (2013). Contours show the depth of the upper plate interface of the subducting Pacific plate. The color scale at the bottom of the figure refers to Vp values. d A graph for P wave velocity in the OC by Shiina et al. (2013) against depth. Red diamonds and bars denote averaged P-wave velocity in the OC shown in c and its standard deviation, respectively. e Schematic of median stress drops for the OC (red) and OM events (blue) from a and b

Full size image
Fig. 5
figure 5

Map views and a cross section of stress drops of intraslab earthquakes beneath Tohoku. a, b Map views for a the OC and b OM events. The thin black lines show the iso-depth contours of the top of the slab. c A vertical cross-section of events in a box on the map insert (the same location of Fig. 3 of Kita et al. 2006). Circles show hypocenters of intraslab earthquakes. The color scale shown in c shows stress drop values. The black and black dashed lines indicate top of the Pacific slab (Kita et al. 2010b) and the slab Moho (8 km below the top of it). Triangles denote locations of active volcanoes

Full size image
Fig. 6
figure 6

a, b Estimated stress drop of each event against normal distance from the upper plate interface beneath a Tohoku for the present study and b Hokkaido from Kita and Katsumata (2015). Color scale corresponds to event depths shown in b. Gray bars show error estimates for stress drops based on standard errors of the corner frequencies. Black open squares and error bars, respectively, denote median stress drops and 8-quantile range for the median stress drop every 2.5 km computed for 5 km windows. Thin blue error bars denote interquartile range. c, d Normalized frequency distributions of intermediate-depth intraslab earthquakes and stress fields in the Pacific slab beneath Tohoku and eastern Hokkaido, respectively (modified after Kita et al. 2010b). Black lines show the normalized frequency of events excluding aftershocks of the 2003 Miyagi-oki intraslab earthquake for the Tohoku region; the case including them is indicated by a thin broken line. DC and DE respectively show ranges of stress field of downdip compression and downdip extension. The location of the neutral plane of the stress field is shown with black arrows

Full size image
Fig. 7
figure 7

a, b Median stress drop for intraslab events at depths of 70–90 km, 90–110 km, 110–130 km, 130–150 km and 150–180 km plotted against depth beneath a Tohoku (the present study) and b Hokkaido (from Kita and Katsumata 2015). Values of the median stress drops are shown in Tables 3 (a) and S3 (b). Red, green and blue error bars denote 8-quantile range for the median stress drops. Blue lines connect the median stress-drop points of lower-plane events beneath Tohoku using a one-dimensional Vs model (Ueno et al. 2002) and constant Vs of 4.6 km/s beneath Hokkaido. Green lines connect median stress-drop points of interplane events beneath Tohoku using the one-dimensional Vs model of Ueno et al. (2002) and beneath Hokkaido assuming Vs of 4.6 km/s. Red lines connect the corresponding points of upper-plane (OC) events using the Vs values reported by Shiina et al. (2013) for Tohoku and Vs of 4.0 km/s for Hokkaido. Colored squares denote the median stress drops of events. Thin red error bars denote interquartile range for median stress drops. DC and DE respectively mean downdip compression and downdip extension stress fields. c Cartoon of the interpretation of the degree of hydration in the oceanic mantle modified from Kita and Ferrand (2018)

Full size image
Table 1 Median stress drop of oceanic mantle (OM) and oceanic crust (OC) events in the Pacific slab beneath Tohoku at depths of 70–180 km, as shown in Figs. 4a and b
Full size table

General trend of stress drops in Tohoku

The median stress drop for OC events decreases by almost a factor of 3 as depth increases from 70 to 110 km (from 13.1 to 4.8 MPa), but increases by almost a factor of 2 as depth increases from 110 to 170 km (from 4.8 to 8.8 MPa) (Fig. 4a). Although a particular stress drop estimate can be highly uncertain, the trends that emerge from their median behavior are consistent with earlier results from Hokkaido (Fig. 4a of Kita and Katsumata 2015). We note that the seismic velocity structure assumed for the OC beneath Tohoku is a 2D model (Figs. 4c and d) whereas a constant Vs for the OC was adopted beneath Hokkaido by Kita and Katsumata (2015). In the oceanic crust (OC) beneath Hokkaido, the median stress drop for earthquakes decreases (from 6.8 to 9.9 MPa) at depths of 70–120 km, whereas it increases (from 6.8 to 17 MPa) at depths of 120–170 km. An inflection point in a curve of a median stress drop of intraslab earthquake has been also reported in other subducting slabs (Tian et al. 2022; Folesky et al. 2024). In the Northern Chilean Subduction; the median stress drop decreases at depths of 80 to 100 km and increases at depths of 100 to 140 km (Folesky et al. 2024). The effect of rigidity on stress drops has been discussed by several studies (e.g. Cui et al. 2023). Kita and Katsumata (2015) also argued that this resulted from a change in OC rigidity with increasing depth due to eclogite formation and related dehydration processes within the OC; there is a clear peak in intraslab seismicity at depths of ~ 80 km in the OC beneath northeastern Japan (Kita et al. 2010a, 2006) and the low-velocity zone in the OC disappears at depths of 80–100 km there (Nakajima et al. 2009; Tsuji et al. 2008). Consistent with the interpretation of Kita and Katsumata (2015) for Hokkaido, we propose that the depth variations in stress drops for Tohoku events in the OC result from a depth-dependent change in rock rigidity due to the dehydration-related formation of eclogite (Hacker et al. 2003).

As indicated by Kita and Katsumata (2015), during eclogite formation and dehydration in the OC, a decrease in the water content and a phase change in the rock are factors that increase its rigidity; conversely, an increase in temperature decreases the rigidity. At depths of 70–120 km, we think that the effects of the decrease in water content with depth and the phase change could be smaller than the effect of the increase in temperature with depth; thus, the median stress drop in the OC shows a decrease at these depths. At depths of 120–180 km, we think that the effects of the decrease in water content with depth and the phase change could be greater than the effects of the increase in temperature with depth, resulting in an increase in the median stress drop in the OC (Fig. 4e).

If these interpretations are correct, then the velocity in the OC is expected to first decrease and then increase with increasing depth. This view is consistent with observed depth-dependent changes in velocity in the OC beneath Tohoku (Shiina et al. 2013); i.e., velocity tends to decrease at depths of < 70 km and clearly increases at depths of > 70 km beneath Tohoku (Figs. 4c and d; Fig. 3a of Shiina et al. 2013). The seismicity peak in the OC beneath Tohoku occurs at depths of ~ 80 km due to the phase change with dehydration (Fig. 3 of Kita et al. 2006). Therefore, we propose that the changes in the stress drops for OC events beneath Tohoku are also due to phase change with dehydration processes in the OC.

Strictly speaking, the inflection point in the curve of the median stress drop occurs at ~ 110 km depth (Fig. 4a), which is deeper than the inflection point in the curve of the velocity (~ 70 km) against depth reported by Shiina et al. (2013) (Figs. 4c and d; Fig. 3a of Shiina et al. 2013). This “depth lag” between the negative inflection points could be due to the existence of small amounts of remaining blueschist prior to full transformation to the eclogite facies. A phase change from blueschist to eclogite occurs not only near the phase boundary, but also in the middle of the blueschist facies (e.g. Hacker 2008; Omori et al. 2009; Kogiso et al. 2009). In addition, blueschist facies near the phase boundary are rich in eclogite, but contain relatively low amounts of blueschist; thus, in these environments, the percentage of eclogite is greater than that of blueschist, and the average velocity of the OC becomes close to that of eclogite (Hacker et al. 2008; Omori et al. 2009; Kogiso et al. 2009). However, earthquakes in the OC still occur due to dehydration of the remaining blueschist near the phase boundary. In this study, we used the average seismic velocity from the upper surface of the Pacific Plate to the slab Moho. If a more precise seismic velocity structures were available, the negative inflection point for the median stress drop might shift to a shallower depth.

As shown in Figs. 6c and d, the double seismic zones are recognized in the oceanic plate beneath both Tohoku and Hokkaido, and the stress regime within the slab beneath Tohoku is similar to that in Hokkaido; Downdip compression (DC) is dominant in the OC, and downdip extension (DE) is dominant in the lower-plane of double seismic planes (OM events) (e.g., Hasegawa et al. 1978; Suzuki and Motoya 1981; 1983). There is, however, a difference in the interplane events between Tohoku and Hokkaido; Beneath Tohoku, the stress fields of the interplane and lower plane events are DC and DE respectively, (Fig. 6c), with a larger median stress drop for the lower plane events (Fig. 7a). On the other hand, beneath Hokkaido, the stress fields of both interplane and lower plane events are DE (Fig. 6d), and the median stress drops are similar (Fig. 7b). Allmann and Shearer (2009) reported that the stress drop has some dependence on focal mechanisms. Our results within the OM beneath the two regions perhaps suggest that the stress drop of intraslab events might depend on the stress regime. Further studies will be needed to understand the dependence of intra-slab stress drop on the stress regime (e.g. comparison of stress drops of events with focal mechanisms).

Figures 4a and b clearly show that the median stress drop in the OC is lower than that in the OM. The trend of larger median stress drop in the OM than that in OC is confirmed if we adopt the same constant velocity model for both of the OC and OM in several ranges of magnitude (Figures S6a to S6f) or if we adopt another 1D velocity model for OM (Figure S7a). The median stress drops in the OC are approximately 40 to 90% (on average 62%) of those in the OM (Table 1). Figure 6a and Table 2 also show that the median stress drops in the OC (0–10 km of the x-axis) are lower than in the OM (deeper than 10 km along the x-axis). These results are generally consistent with results beneath Hokkaido (Kita and Katsumata 2015), but there is clearly higher median stress drop in the OC than in the OM below depths of 130 km beneath Hokkaido (Fig. 6b and Table S3). This kind of difference between Tohoku and Hokkaido may result from the different seismic velocity models used for the OC in the two regions. Figure 7a (for Tohoku) and Fig. 7b (Hokkaido) also show that the median stress drops in the OC are generally lower than in the OM (Tables 3 and S2). Beneath Tohoku, the interplane and upper-plane events each yield a DC regime (Fig. 4c). In Fig. 7a, the median stress drop for upper-plane events is smaller than that for interplane events beneath Tohoku. As noted by Kita and Katsumata (2015), the median stress drop of the upper-plane events is also smaller than that of interplane events beneath Hokkaido (Figs. 7b and Table S3). This similarity between the two regions despite their differences in interplane stress fields (i.e., DC beneath Tohoku (Fig. 6c) and DE beneath Hokkaido (Fig. 6d)) suggests that a difference in rigidity and/or different rupture mechanisms between the OC and OM (Kita and Katsumata 2015) may explain the stress drop difference between the OC and OM in both regions.

Table 2 Median stress drops of each depth range against normal distance from the upper plate interface beneath Tohoku for the present study and Hokkaido from Kita and Katsumata (2015), as shown in Figs. 6a and b
Full size table
Table 3 Median stress drops of upper-plane, interplane and lower plane in the Pacific slab beneath Tohoku at depths of 70–180 km, as shown in Figs. 7a
Full size table

The effect on seismicity and stress field of intraplate events by the 2011 M9.0 Tohoku earthquake beneath has been reported beneath northeastern Japan by several studies (intermediate-depth: Delbridge et al. 2017, 2024; Kita and Ferrand 2018, near-trench region: Obana et al. 2012, overlying plate: Hasegawa et al. 2011; Yoshida et al. 2012). Effect on the stress drops of intraslab events by the large magnitude event is also a curious study topic. The median stress drop for the OC at depths of 70 to 90 km after the 2011 M9.0 Tohoku event tends to be a weak increase comparing to that before it (Figure S8 of the additional file), but further detailed examination with additional data in the period after our analysis period needs if we clearly indicate characteristics of time and space changes.

Different stress drop behaviors in Tohoku and Hokkaido

Figure 6a compares the median stress drops for upper-plane, interplane and lower-plane events beneath Tohoku, plotted against depths. For the oceanic mantle portion, the median stress drops for lower-plane and interplane events beneath Tohoku at depths of 70–170 km are smaller than those beneath Hokkaido (Fig. 7b). Figures 7a and b also show that the stress drops in the OM beneath Tohoku at depths of 70 to 170 km tend to be smaller than beneath Hokkaido (Table 3).

We think the differences in the median stress drops of oceanic mantle between Tohoku and Hokkaido may result from a difference in the degree of serpentinized peridotite. Based on a comparison of experimental results with b-values of intermediate-depth earthquakes (Kita and Ferrand 2018), the subducting oceanic mantle beneath Tohoku is more hydrated than that beneath Hokkaido because abyssal hill fault reactivation occurs in near-trench region of Hokkaido but not Tohoku (Fujie et al. 2018) (Fig. 6c). Some hydration of the OM occurs in both regions, but the degree of the hydration offshore Tohoku appears larger than that offshore Hokkaido, as indicated by seismic imaging of Vp by OBS (Fujie et al. 2018). The rigidity of the OM off-Tohoku could therefore be smaller than that offshore Hokkaido, leading to smaller stress drops in Tohoku than Hokkaido. Moreover, there could be more hydrated peridotite in the upper portion of the OM (interplane events) beneath Tohoku than the lower portion of it (lower plane events) there (Fig. 7a), whereas beneath Hokkaido there could be relatively less hydrated peridotite in both the interplane and lower-plane regions (Fig. 7b). Regarding the ocean crust, Fujie et al. (2018) also inferred more hydration of the oceanic crust offshore Tohoku than offshore Hokkaido. That could result in the smaller median stress drops in Tohoku, compared to Hokkaido (Figs. 7a and b, and Tables 3 and S3). Chen et al. (2004) calculated the thermal parameter (i.e., the product of the vertical rate of descent of the plate into the mantle and the age of the subducting plate (Kostoglodov 1989; Kirby et al. 1991)) to be 5100 beneath Tohoku and 3800 beneath Hokkaido. Subduction of a warmer oceanic plate beneath Tohoku than Hokkaido could also play a role in the smaller stress drops in both the OC and OM beneath Tohoku compared to Hokkaido.

Conclusions

Stress drops for 2,875 intermediate-depth intraslab events from 70 to 200 km depth were computed beneath Tohoku (36.5 to 41.5N), and results were compared with a previous study beneath Hokkaido (41.5 to 45.5N). The median stress drops in the OM are about 1.1 to 2.4 times larger than those in the OC beneath both Tohoku and Hokkaido (Figs. 4a, b, 6a, b, 7a, and b and Tables 1 and S2). We consider that the difference in rock rigidity and/or different rupture mechanisms between the OC and OM may be the dominant factors producing the stress drop difference.

In the OC, we found that the median stress drop decreases from 70 to 120 km depth and increases from 120 to 170 km depth. This kind of depth change in the stress drop (switching from a decrease to an increase in the median stress drop with increasing depth) is generally consistent with the behavior found in Hokkaido by a previous study (Kita and Katsumata 2015). We infer that the decrease in median stress drop from 70 to 120 km depth occurs because the effects of the decrease in water content and the phase change with increasing depth are smaller than the effect of increasing temperature with depth, whereas the opposite situation pertains for greater depths.

The results for the OM show that the median stress drops for lower-plane and inter-plane events beneath Tohoku are smaller than those beneath Hokkaido. Furthermore, beneath Tohoku, the median stress drop for lower-plane events is larger than that for interplane events, whereas beneath Hokkaido the median stress drop for lower-plane events is almost the same as that for interplane events (Figs. 7a and b). The median stress drop in the OC beneath Tohoku is also smaller than that beneath Hokkaido. A difference in the degree of hydration in the oceanic plate between Tohoku and Hokkaido may produce a difference in rigidity which could result in the observed stress drop behaviors. We infer that the dependence of hydration on the normal distance from the surface of the plate is stronger beneath Tohoku than Hokkaido, and also that the plate is more hydrated beneath Tohoku. Seismic structure imaging of Vp in the OM and Vp/Vs in the OC beneath off-Tohoku and off-Hokkaido at shallow depths by a previous OBS study (Fujie et al. 2018) supports our interpretation of the hydration of the oceanic plates. The thermal structure in the oceanic plate beneath Tohoku is warmer than that beneath Hokkaido, which could also play a role in the difference of stress drop values between two regions.

Our systematic analysis of thousands of stress drops of small intraslab earthquakes at intermediate depths has advanced understanding of the roles of hydration and petrologic processes in earthquake generation within subducting oceanic plates.