Introduction

Solar wind plasmas enter the magnetosphere primarily through the cusp via reconnection on the magnetopause. If the interplanetary magnetic field (IMF) bears a strong northward component, the reconnection occurs at the high-latitude magnetopause poleward of the cusp, i.e., lobe reconnection. The lobe reconnection drives characteristic plasma convection in the high-latitude magnetosphere and in the dayside polar cap region of the ionosphere, which are completely different from those caused by low-latitude magnetic reconnection on the dayside magnetopause for southward IMF (Reiff et al. 1977; Reiff and Burch 1985; Newell and Meng 1991; Escoubet et al. 1992, 2006, 2008; Woch and Lundin 1992; Yamauchi et al. 1995; Trattner et al. 2003; Pitout et al. 2009; Milan et al. 2020).

The lobe reconnection also controls the entry of plasma in the cusp. A localized proton aurora (i.e., cusp proton aurora) is a phenomenon that is produced by the protons entering the cusp that way, which appears as a spot poleward of the typical auroral oval location (Frey et al. 2002, 2003; Fuselier et al. 2002; Phan et al. 2003; Bryant et al. 2013). Phan et al. (2003) presented direct evidence that the spot poleward of the auroral oval is a remote signature of lobe reconnection. Specifically, Phan et al. (2003) reported a simultaneous observation event of the localized proton aurora by the IMAGE satellite and ion jets from lobe reconnection by the Cluster satellite, showing that the ion jets are observed on magnetic field lines originating from the region of the bright proton spot in the ionosphere and with energy fluxes consistent with the proton spot brightness. While some reconnection may not energize the plasma in the entire flux tube (Birn et al. 2006a, b), the lobe reconnection can bring the energized plasma to the foot of the flux tube.

The lobe reconnection is a process that can occur continuously if the driving conditions are steady (Frey et al. 2003). Interestingly, the brightness of the cusp proton spot created by the ion precipitation through such reconnection is more strongly correlated with the solar wind dynamic pressure than with the solar wind number density, as reported by Frey et al. (2002) and Bryant et al. (2013) based on data from the SI12 proton imager of the IMAGE satellite (Mende et al. 2000). This feature describing the greater involvement of the solar wind dynamic pressure compared to the solar wind density indicates an involvement of the solar wind speed, which is the other factor constituting the solar wind dynamic pressure. However, the involvement is not clearly understood yet, partly because the solar wind ions near the lobe reconnection region cannot enter the low-altitude cusp simply by flowing in the direction of the magnetosheath flow. During northward IMF, a portion of the solar wind ions flowing in the high-latitude magnetosheath near the lobe reconnection region drastically alter the flow direction caused by lobe reconnection and, subsequently, follow the Earth's magnetic field lines toward the low-altitude cusp. In other words, the ions take a folded path.

The ions flowing downstream near the lobe reconnection region indicate the presence of shear flow in the reconnection region. The role of shear flow in reconnection has been primarily investigated through numerical simulations (Cassak 2011; Cassak and Otto 2011Tenfjord et al. 2022). Cassak (2011) and Cassak and Otto (2011) indicated that an increase in shear flow reduces the outflow speed from reconnection and reconnection rate. Based on 2.5D particle-in-cell simulation, Tenfjord et al. (2020) reported that adding tailward cold streaming protons does not result in a significant difference in the reconnection rate compared to the case without cold streaming protons. Thus, according to these simulation results, the flow speed in the magnetosheath does not seem to be involved in the lobe reconnection in such a way as to increase the number flux of precipitating cusp ions.

The characteristic nature of precipitating cusp ions has been investigated by Wing et al. (2001) based on a large amount of data from low-altitude Defense Meteorological Satellite Program (DMSP) satellite passes. Wing et al. (2001) identified 2259 cusp events by examining the DMSP data acquired during 1985–1995, and approximately half of these events were obtained under conditions with positive IMF BZ (refer to their Fig. 5a). In that study, however, it was not discussed how the flow speed in the magnetosheath is related to the number flux of precipitating cusp ions. Using a large amount of data from the SI12 proton imager, specifically approximately 500 images from the “polar cap spot”, Bryant et al. (2013) investigated the relationship between solar wind parameters and the intensity of the SI12 proton aurora. Because the number of photons detected by the SI12 proton imager increases as either the number density or energy of the precipitation protons increases, it is difficult to understand how the flow speed in the magnetosheath is related to the energy of the precipitating protons using the SI12 proton aurora intensity data.

The present study aims to clarify the relationship between flow speed in the magnetosheath and cusp ion precipitation (especially its average energy) via lobe reconnection for northward IMF in terms of statistical data analysis based on an extensive data set of cusp events obtained by DMSP F16, F17, or F18 satellites. To achieve this objective, we implemented a method to automatically identify low-altitude cusps occurring during a stable northward IMF.

Data and methodology

DMSP data set and solar wind OMNI

We used data from the Special Sensor J/5 (SSJ/5) onboard DMSP satellites (F16, F17, and F18). The SSJ/5 instrument measures the electrons and ions in 19 energy bins from 30 eV to 30 keV at one complete spectrum per second, and the detector apertures are directed toward the local zenith (Hardy et al. 2008; Redmon et al. 2017). This directional property indicates that highly field-aligned particles within the atmospheric loss cone can be observed at high latitudes. We analyzed the data obtained in the northern hemisphere from January 2010 to December 2020, i.e., for 11 years. For solar wind and IMF, we used the OMNI 5-min data (King and Papitashvili 2005).

Since the OMNI data are adjusted in time for propagation to the dayside bow shock, an additional delay time to represent the propagation of the solar wind from the bow shock to the ionosphere needs to be considered. As shown later, a fixed value of 10 min is assumed for this delay time in this study on the basis of the result from a previous study (Khan and Cowley 1999). In this sense, it is sufficient to use the OMNI 5-min data rather than the high-resolution 1-min data in the present study. As described in the next section, for automatic event search with the OMNI 5-min data, a strict condition is set: the OMNI 5-min BZ must be positive for at least 12 consecutive points, i.e., at least 1 h.

Method of automated event identification

To automatically identify the cusp occurring during a period of stable northward IMF, we set up the following three conditions: (1) IMF was stable at BZ > 0 for at least preceding 1 h; (2) DMSP traversed the probable region for the cusp, where magnetic latitude (MLAT) is higher than 75\(^\circ\), and magnetic local time (MLT) is in the near noon range depending on the IMF BY; and (3) DMSP particle data indicated the cusp particle precipitation feature that is in line with the cusp definition of Newell et al. (2006). The altitude-adjusted corrected geomagnetic coordinate system (Shepherd 2014) was used to obtain the MLAT and MLT.

Newell et al. (2006) identified the cusp from the spectrum of precipitating electrons and ions observed by the DMSP satellites based on four criteria for each individual spectrum: (1) average ion energy ≤ 3000 eV; (2) average electron energy ≤ 220 eV; (3) ion spectral peak energy flux ≥ 2 × 107 eV/(eV·cm2·s·sr); and (4) ion spectral flux peak occurred between 100 and 7000 eV. These criteria are modifications of those initially proposed in Newell and Meng (1988), which were determined based on a large set of observational evidence from the DMSP F7. Newell et al. (2006) then used a moving window of 4 s (4 spectra) and determined the DMSP entry of the cusp region as a point if 3 out of 4 spectra satisfied the cusp criteria. They also determined the DMSP exit of the cusp as a point if 3 out of 4 spectra did not satisfy the cusp criteria. High-altitude observations in the magnetosphere by the Cluster satellite have shown that ion entry with energy fluxes lower than those seen in the typical cusp sometimes occurs poleward of the cusp during northward IMF (Shi et al. 2013). The energy fluxes of that ion entry appear to be about an order of magnitude lower than those in the cusp located nearby (see their Fig. 2). That type of event will not be included in our data set.

The ion data acquired at the cusp by a low-altitude satellite often displayed dispersion phenomena (Reiff et al. 1977; Escoubet and Bosqued 1989; Lockwood and Smith 1992; Onsager et al. 1993; Wing et al. 2001; Taguchi et al. 2015a; da Silva et al. 2022). A typical dispersion signature of the southward IMF indicates that the ion energy decreases with an increasing MLAT. For northward IMF, the ion dispersion signature bears the opposite type, i.e., the ion energy decreases with a decreasing MLAT, as reported by several studies based on simultaneous observations of the precipitating ions and plasma convection (Burch et al. 1980; Øieroset et al. 1997; Chisham et al. 2004). Note that the footprint of the lobe reconnection line is not necessarily parallel to an MLAT line (Weiss et al. 1995), imposing the condition that the ion energy decreasing with MLAT may fail to identify appropriate events using ion data from a satellite moving with a large component parallel to an MLAT line in the cusp (such an event will be shown later). Thus, the condition associated with the reverse ion dispersion has not been considered in the present automated event identification method, although a recent study has proposed a sophisticated method of automatically identifying the ion dispersion (da Silva et al. 2022).

For “1 h” in our Condition 1, for simplicity, we determined the time when the DMSP pass crossed 12 MLT as the reference time, and examined 1-h period prior to that reference time. We here considered a 10-min (2 data points in 5-min OMNI) delay, which is reasonable for the propagation time from the bow shock to the dayside ionosphere (Khan and Cowley 1999). For the IMF BY-dependent MLT range in Condition 2, we used the 6 h width centered at the MLT derived by Frey et al. (2002), expressed as follows:

$${\text{MLT}}=0.127 {B}_{\rm Y}+ 11.8\,\; \left({\text{hour}}\right),$$
(1)

where BY denotes the 1-h average value (in a unit of nT). The MLAT condition used in Condition 2, where the cusp is located on the poleward side of 75\(^\circ\) MLAT for IMF BZ > 0, is based on the statistical results obtained by Wing et al. (2001), who demonstrated that the equatorward boundary of the cusp is seldom located at latitudes lower than 75\(^\circ\) MLAT if IMF BZ is positive (refer to their Fig. 5a). The results of Wing et al. (2001) further indicated that the average MLAT of the equatorward boundary of the cusp is broadly 78\(^\circ\) MLAT for positive IMF BZ up to 10 nT. Taguchi et al. (2006) reported an event of the reverse convection for an interval of IMF BZ exceeding 15 nT, and the equatorward boundary of the reverse convection was located ~ 78\(^\circ\) MLAT. As apparent from these studies for positive IMF BZ, the cusp is located higher than 78\(^\circ\) MLAT on average, regardless of the magnitude of the positive IMF BZ. As discussed later, the features of the MLAT distribution derived from the current cases are consistent with these previous results. Using the aforementioned method of automated event identification, we identified 1990 passes of cusp ion precipitation events associated with the northward IMF.

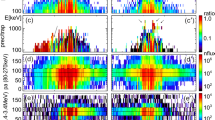
An example of the cusp events obtained by DMSP F17 is presented in Fig. 1. This event occurred around 11:21 UT on 23 April, 2012. In Fig. 1a, the direction of the inferred E \(\times\) B drift is represented as vectors antiparallel to the horizontal magnetic perturbation observed by the Special Sensor Magnetometer instrument on board the DMSP satellite. The horizontal magnetic perturbations caused by the twin-field-aligned current system in the northern hemisphere can be antiparallel to the E \(\times\) B drift (Taguchi et al. 2015b). The vectors near-noon exhibited sunward components, indicating the existence of the reverse convection, which is typical for northward IMF. Equivalently, the horizontal magnetic perturbations possess an anti-sunward component, indicating the existence of twin-field-aligned current system typical for northward IMF (Araki et al. 1984; Iijima et al. 1984; Vennerstrøm et al. 2002; Taguchi et al. 2015b; Carter et al. 2020). The red-colored vectors represent the region defined as the cusp by the automated identification method. In addition, these vectors show the eastward components, implying that the reverse convection is driven by lobe reconnection occurring predominantly on the prenoon side of the northern hemisphere.

Fig. 1
figure 1

a Direction of inferred E \(\times\) B drift, i.e., vectors antiparallel to the observed horizontal magnetic perturbation on MLT–MLAT dial, b electron differential energy flux, c ion differential energy flux, and d average energy of electrons (blue line) and ions (red line). Data obtained between 11:15:17 and 11:27:15 UT are plotted in a. Red vectors represent the interval defined as the cusp, which is depicted with two vertical red lines in b–d. The prenoon end of the red vector region in a corresponds to the “start” signature of the ion dispersion, and the near-noon end corresponds to the “stop” signature of the ion dispersion. The orange dashed line in a illustrates the inferred footprint of the lobe reconnection line. In d, a portion of the red line (ion average energy) is shown in green, and the two green arrows also indicate that portion. This range represents the high-energy part of the cusp ion energy. The red-horizontal and blue-dashed lines represent 3000 eV and 220 eV, respectively, corresponding to the reference energies used in Conditions 2 and 3

Full size image

The electron energy flux spectrum, ion energy flux spectrum, and average energies of the precipitating electrons (blue) and ions (red) are given in Fig. 1b–d, respectively. The average energies are calculated according to Hardy et al. (2008). The two vertical red lines represent the interval defined as the cusp. As can be seen in Fig. 1b, the electron precipitation in the cusp exhibited a peak energy flux at a few hundred eV. The energy-dispersion features of the ions are shown in Fig. 1c. In Fig. 1d, a portion of the red line is shown in green, and the two green arrows also indicate that portion. This range represents the high-energy part of the cusp ion energy, which we defined as the ion energy exceeding the third quartile value (1240 eV is this cusp event) for the entire cusp region. The ion energy in the high-energy part will be used later. Note that a few points slightly exceeding 1240 eV near the time at the left vertical line are not included in the high-energy part of the cusp in this case. This is simply because the point does not meet the cusp criteria as far as the 1-s resolution is concerned. (That is included in the cusp region because 3 points out of a moving window of 4-s satisfy the cusp criteria.)

The ion differential energy flux had a maximum at 1392 eV at 11:21:49 UT (right vertical line), whereas it was a minimum at 300 eV at 11:21:01 UT (left vertical line). The former and latter correspond to (MLAT, MLT) = (81.2\(^\circ\), 10.9) and (81.4\(^\circ\), 12.0), respectively. Although it appears that standard ion dispersion is occurring, as the higher ion energy observed at a lower MLAT, the magnetic field perturbations (depicted in Fig. 1a) confirm the occurrence of reverse convection, implying ionospheric convection under northward IMF conditions (as will be shown later, the OMNI IMF \({B}_{\rm Y}\) and \({B}_{\rm Z}\) at 11:10 UT were − 5.2 nT and 6.8 nT, respectively). This indicates that (MLAT, MLT) = (81.2\(^\circ\), 10.9) is located at a shorter distance from the footprint of the lobe reconnection compared to (MLAT, MLT) = (81.4\(^\circ\), 12.0). In addition, the footprint of the lobe reconnection line is tilted, such that the near-noon segment is located at higher latitudes than the prenoon segment, which is illustrated in Fig. 1a (orange dashed line). This tilt of the possible footprint of the lobe reconnection line and the eastward component of the E \(\times\) B drift suggest that the event occurred for a negative value of IMF BY. The average energies of ions and electrons for the defined cusp interval were substantially less than 3000 eV and 220 eV (Fig. 1d), respectively.

Since the DMSP F16, F17, and F18, which we used in this paper, take the orbit with ascending and descending nodes in the 17:30–20:00 LT range on the duskside and the 05:30–0800 LT range on the dawnside, respectively, almost all the northern hemisphere orbits we used in the analysis are in the dusk-to-dawn direction in areas above 70 MLAT in the MLT–MLAT coordinate. In this sense, the example shown in Fig. 1 is a representative one. As noted above, whether or not the satellite observed the reversed ion dispersion is not a prerequisite for automatic identification of the event.

The solar wind and IMF data for this event from 0800 to 1200 UT on 23 April, 2012 are given in Fig. 2. From top to bottom, the three components of IMF (BX, BY, and BZ) in the geocentric solar magnetospheric system (GSM) coordinates (Fig. 2a–c), solar wind flow speed (Fig. 2d), proton density (Fig. 2e), and dynamic pressure (Fig. 2f) are plotted in this figure. The two vertical-dotted lines represent the 1 h interval, i.e., 10:10–11:10 UT, used for Condition 1. As observed in Fig. 2c, IMF BZ was positive for a long period including this 1 h interval. As anticipated, IMF BY was negative during the DMSP cusp observation, although it was positive before 10:30 UT.

Fig. 2
figure 2

Solar wind and IMF data from OMNI 5-min between 08:00 UT and 12:00 UT, 23 April, 2012. Top (a) to bottom (f): three components of IMF (BX, BY, and BZ) in geocentric solar magnetospheric system (GSM) coordinate, flow speed, solar wind proton density, and dynamic pressure, respectively. Two vertical-dotted lines represent the 1 h interval used in Condition 1

Full size image

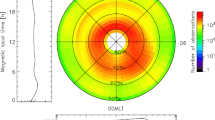
Using the aforementioned automated method, we identified 1990 satellite passes in which the cusp was observed. The locations of these events in the MLT–MLAT plane for three distinct IMF BY conditions: (a) \({B}_{\rm Y}<\)−2 nT; (b) − \(2 \ {\text{nT}}\le {B}_{\rm Y}\le 2 \ {\text{nT}}\); (c) \({B}_{\rm Y}>2 {\ \text{nT}}\) are plotted in Fig. 3. In each figure, the event locations are indicated by the point at which the DMSP satellites observed the maximum total ion number flux. Regardless of IMF BY, the MLAT of the maximum total ion number flux was higher than 78\(^\circ\) MLAT in almost all events. The dearth of events below 78\(^\circ\) MLAT was partially caused by the orbital characteristics of the satellites, because the DMSP F16, F17, and F18 satellites seldom pass through such a relatively low MLAT region. Nonetheless, considering that the cusp for positive IMF BZ extends to the latitudes higher than 78\(^\circ\) MLAT on average as discussed earlier, the distributions presented in Fig. 3 are not likely to miss important events. For IMF BY < − 2 nT (Fig. 3a), the cusp tends to occur on the prenoon side, whereas for IMF BY > 2 nT (Fig. 3c), it tends to occur on the postnoon side. For |BY| \(\le\) 2 nT, the cusp events are generally distributed around 1200 MLT. Overall, these IMF BY-dependent features are consistent with the IMF BY-controlled location of the lobe reconnection, which is reported by previous studies (Luhmann et al. 1984; Reiff and Burch 1985; Newell et al. 1989; Frey et al. 2002).

Fig. 3
figure 3

Location of cusp observations detected by the automated identification method, depicted in MLAT–MLT dial for a BY < − 2 nT, b |BY| \(\le\) 2 nT, and c BY > 2 nT. Each point represents the position in which the spacecraft observed the maximum total ion number flux during the defined cusp. The outermost semicircle represents 75\(^\circ\) MLAT

Full size image

For each of the 1990 events, the total ion number flux every second for the cusp interval was calculated according to Hardy et al. (2008) and averaged over the cusp interval. For the event described in Fig. 1, the averaged total ion number flux was 1.2 \(\times\) 108 cm−2·s−1·sr−1. Furthermore, we considered the mean value of the average energy for the high-energy ion cusp interval which was defined in the manner shown in Fig. 1d. We refer to this mean value as \({E}_{\rm AVH}\). We will use \({E}_{\rm AVH}\) as a proxy for the energy of the ions precipitating directly from lobe reconnection since that area is considered to be very close to the footprint of the lobe reconnection. For the event depicted in Fig. 1, \({E}_{\rm AVH}\) was 1757 eV. A histogram of \({E}_{\rm AVH}\) of all events will be presented in Sect. “Relationship of cusp ion precipitation to magnetosheath flow velocity and density”, where the distribution of \({E}_{\rm AVH}\) will be discussed.

As was mentioned in Introduction, Wing et al. (2001) identified 2259 cusp events by examining the DMSP data, and approximately half of these events were obtained under conditions with positive IMF BZ. Bryant et al. (2013) examined approximately 500 images displaying the “polar cap shots” phenomena associated with northward IMF. Note that the number of events (1990) identified in this study as cusp events occurring under northward IMF conditions is considerably more than that reported in previous studies.

Method for estimating ion density and flow velocity in magnetosheath near lobe reconnection region

The ion density and flow velocity in the magnetosheath near the lobe reconnection region was estimated using the OMNI solar wind data and the gas-dynamic model by Spreiter et al. (1966). The Spreiter model indicates that the highest plasma density in the magnetosheath adjacent to the magnetopause occurs at the subsolar point, which diminishes as the plasmas displaces farther from the subsolar point. For instance, in the Spreiter model with a Mach number of 8 and polytropic index of 5/3, the magnetosheath plasma density at the subsolar magnetopause is 4.5 times of that of the incident solar wind, which decreases to less than 2 at the high latitude magnetopause near XGSM = 0. This indicates that the occurrence of reconnection at higher latitude magnetopause results in the entry of low-number-density magnetosheath plasma in the lobe reconnection region. For each event, we considered this effect using the tilt of the Earth’s dipole axis. More specifically, we considered the effect in which the outermost magnetic field line in the lobe tends to be located on the sunward side if the Earth’s dipole axis tilts further toward the Sun in the northern hemisphere, as discussed by Tsyganenko and Russell (1999, Fig. 11) for southward IMF, such that higher density plasma can enter the lobe reconnection region.

This analysis used the following equation to quantify the aforementioned effect:

$${N}_{\rm SH}/{N}_{\rm SW}=0.034 \theta + 1.7,$$
(2)

where \({N}_{\rm SH}\) and \({N}_{\rm SW}\) denote the number density of the magnetosheath plasma and that of the incident solar wind plasma, respectively. \(\theta\) indicates the angle (in degrees) from the positive direction of the Z-axis of the GSM coordinates in the XGSM–ZGSM plane. This relation was derived from the Spreiter model with a Mach number of 8 and polytropic index of 5/3. For instance, the ratio ranges from approximately 0.7 to 2.7 between \(\theta\) = − 30° and \(\theta\) = 30°. Taguchi et al. (2004) employed a similar method based on the model developed by Spreiter & Stahara (1985). In the present study, \({N}_{\rm SH}\) for each event which is assumed to be occurring in the lobe regions, given the evidence of the high-latitude cusp ion precipitation, was estimated based on the angle of the Earth dipole axis from the positive direction of the ZGSM axis as \(\theta\) in Eq. (2). For instance, if \({N}_{\rm SW}\) = 5 cm−3 and the angle of the Earth dipole axis = 30°, the \({N}_{\rm SH}\) at a position proximate to the lobe reconnection region can be calculated as ~ 13.5 cm−3. Hereinafter, the \({N}_{\rm SH}\) in the vicinity of the lobe reconnection region is denoted as \({N}_{\rm SH}^{\rm L}\) (L stands for the lobe reconnection region).

Admittedly, the estimation using Eq. (2) is a simplification, but it does not necessarily seem to be inconsistent with the high-latitude magnetosheath plasma density results from MHD simulations for the IMF northward condition. According to the plasma density profile obtained by Wang et al (2004; their Fig. 13), the plasma density along the open–closed magnetic field boundary near the high-latitude magnetosheath smoothly changes from roughly 12 cm−3 (yellow–green color in their Fig. 13) to roughly 8 cm−3 (light blue color) for an incident solar wind plasma with a number density of 6 cm−3. This range corresponds approximately to \({N}_{\rm SH}/{N}_{\rm SW}\)= ~ 1.3 to 2, which corresponds to \(\theta\) of ~ − 12° to ~ 9° when estimated by Eq. (2). This range of \(\theta\) is well within the range of − 30° to 30°. On the other hand, it should be noted that in a more recent MHD simulation (Burkholder et al. 2021), the plasma density at the magnetosheath–lobe interface (upper left panel of their Fig. 5) does not necessarily tend to decrease downstream. However, their model also seems to reproduce that the plasma density at the magnetosheath–lobe interface is close to the input solar wind density, i.e., 5 cm−3 to about twice that value. In that sense, the \({N}_{\rm SH}/{N}_{\rm SW}\) estimate in Eq. (2) also does not deviate significantly from the results of that recent simulation.

The magnetosheath plasma flow is stagnant at the subsolar point and becomes faster as the plasmas move farther from the subsolar point. The model developed by Spreiter et al. (1966) for a Mach number of 8 and polytropic index of 5/3 shows that VSH/VSW varies from ~ 0.6 to ~ 0.85 between \(\theta\) = 30° and \(\theta\) = − 30°. The ratio of 0.85/0.6 ≈ 1.4 is very small in comparison with that for the plasma density, i.e., 2.7/0.7 ≈ 3.9. We can expect that the difference in the velocity due to the difference in the reconnection site is less significant in controlling the ion flux entering the cusp. Thus, the \(\theta\)-dependent relation was not introduced for VSH/VSW to estimate VSH for each event, but instead, a fixed value of 0.7 was considered for simplicity, i.e., \({V}_{\rm SH}^{\rm L}=0.7 {V}_{\rm SW}\), where \({V}_{\rm SH}^{\rm L}\) represents \({V}_{\rm SH}\) near the lobe reconnection region, similar to the definition of \({N}_{\rm SH}^{\rm L}\). As discussed later, \({V}_{\rm SH}^{\rm L}\) exceeds 200 km·s−1 in almost all cases from the current data set, which appears to be a super-Alfvénic flow. This is overall consistent with the statistical results reported by Lavraud et al. (2004), wherein the magnetosheath flow occurring near the cusp was assessed using data from the Cluster satellite. However, the current estimation of \({V}_{\rm SH}^{\rm L}\) does not consider the possibility of slowdown reported in Lavraud et al. (2004).

Statistical results

Cusp ion precipitation and solar wind dynamic pressure

The dependence of the total number flux of precipitation ions on the solar wind dynamic pressure is shown in Fig. 4a. The total ion number flux is larger for a higher dynamic pressure. The relation presented in Fig. 4a is consistent with those reported in the previous studies (Frey et al. 2002; Bryant et al. 2013). This relation will be discussed later in terms of the association of the speed of the magnetosheath flow with the acceleration of the outflow jets from reconnection. As shown in Fig. 4a, the maximum value of the total ion number flux in the current data set occurred when the solar wind dynamic pressure was at its maximum value (29.5 nPa). At this instant, the solar wind speed and proton density were approximately 510 km·s−1 and 56 cm−3, respectively.

Fig. 4
figure 4

Dependence of total ion number flux in low-altitude cusp, observed by DMSP satellites, on a solar wind dynamic pressure (the correlation coefficient is 0.44) and b dipole tilt angle (the correlation coefficient is 0.11)

Full size image

Figure 4b shows a relationship between the total number flux of precipitation ions and the dipole tilt angle \(\theta\). Although there is a very weak tendency for the number of the events with higher total ion number fluxes to increase with increasing dipole tilt angle, it appears that the dipole tilt angle is not a dominant parameter controlling the total ion number flux in the cusp.

Relationship of cusp ion precipitation to magnetosheath flow velocity and density

The relationship of the total ion number flux with \({V}_{\rm SH}^{\rm L}\) is plotted in Fig. 5a, wherein the correlation coefficient is almost zero, such that no clear correlation exists between these quantities. In particular, this result is consistent with that reported by Bryant et al. (2013), who demonstrated that the intensity of the proton aurora is not significantly correlated with the solar wind velocity. Although the solar wind density and velocity can be considered the main parameters in controlling the cusp ion precipitation, we should note that the density varies in a much wider range (on the order of tens of times) than the velocity (on the order of 1–2 times). Therefore, the dependence of the cusp ion precipitation on the velocity may be overshadowed and less clear. In addition to this point, we should also be aware that, according to the Spreiter model, the magnetosheath density varies more with latitude than the velocity, as described in Sect. “Method for estimating ion density and flow velocity in magnetosheath near lobe reconnection region”. Thus, the cusp precipitation is basically controlled by the density.

Fig. 5
figure 5

a Relationship between total ion number flux observed by DMSP satellites and estimated ion velocity in the magnetosheath near lobe reconnection region; b relationship between total ion number flux multiplied by 5/\({N}_{\rm SH}^{\rm L}\) and the estimated ion velocity in the magnetosheath near the lobe reconnection region

Full size image

In Fig. 5b, we attempted to extract the relationship between the total ion number flux and \({V}_{\rm SH}^{\rm L}\) by excluding the contribution of the solar wind number density to the greatest possible extent. In Fig. 5b, the vertical axis denotes the “normalized” total ion number flux, estimated as the total ion number flux multiplied by 5/\({N}_{\rm SH}^{\rm L}\), where the unit for \({N}_{\rm SH}^{\rm L}\) is cm−3. Here, the factor of 5 represents the typical value of the solar wind density in unit of cm−3, and multiplying by 5/\({N}_{\rm SH}^{\rm L}\) means that the total ion number flux is normalized to the one for a solar wind density of 5 cm−3. The correlation coefficient of 0.37 indicates a weak correlation between these two quantities, such that the normalized total ion number flux increases with \({V}_{\rm SH}^{\rm L}\). This tendency suggests that the number flux of the earthward outflow jet from lobe reconnection—the origin of the precipitating ions in the low-altitude cusp—is related to the tailward flow velocity in the magnetosheath near the lobe reconnection region.

As displayed in Fig. 6, the total ion number flux varies with \({V}_{\rm SH}^{\rm L}\) and \({N}_{\rm SH}^{\rm L}\), wherein the color represents the total ion number flux averaged in each \({V}_{\rm SH}^{\rm L}-{N}_{\rm SH}^{\rm L}\) bin. The bin size for \({V}_{\rm SH}^{\rm L}\) on the horizontal axis is 50 km·s−1, whereas the vertical axis has the bin size of 4 cm−3. The bins covering \({N}_{\rm SH}^{\rm L}\) greater than 28 cm−3 contain a wider range of values, the maximum being ~ 147 cm−3 (note that the NSW for that event is ~ 65 cm−3). The value expressed in each bin of Fig. 6 represents the number of events falling into that bin. For bins with an excessively small number of events (defined as less than 5), the average value of the total ion number flux (in black) is not presented. As observed from Fig. 6, the total ion number flux increases with either \({V}_{\rm SH}^{\rm L}\) or \({N}_{\rm SH}^{\rm L}\). Importantly, for a given range of \({N}_{\rm SH}^{\rm L}\), the total ion number flux tends to increase with \({V}_{\rm SH}^{\rm L}\). This finding suggests that \({V}_{\rm SH}^{\rm L}\) should be involved in controlling the number flux of the ion outflow jet from lobe reconnection independently of \({N}_{\rm SH}^{\rm L}\). Note that this result does not claim that the cusp ion precipitation is stronger as the cusp is tilted further away from the Sun. As the cusp is tilted further away from the Sun, \({V}_{\rm SH}^{\rm L}\) actually becomes larger. On the other hand, \({N}_{\rm SH}^{\rm L}\) becomes smaller. As described in Sect. “Method for estimating ion density and flow velocity in magnetosheath near lobe reconnection region”, the dependence of \({N}_{\rm SH}^{\rm L}\) on the dipole tilt angle is stronger than the dependence of \({V}_{\rm SH}^{\rm L}\) on the dipole tilt angle. As a result, the cusp ion precipitation should be weaker as the cusp is tilted further away from the Sun.

Fig. 6
figure 6

Variations in total ion number flux against increasing \({V}_{\rm SH}^{\rm L}\) and \({N}_{\rm SH}^{\rm L}\). Color represents total ion number flux averaged in each \({V}_{\rm SH}^{\rm L}\)–\({N}_{\rm SH}^{\rm L}\) bin. Value expressed in each bin represents the number of events in that bin. The black-colored bin represents the bins in which events were less than 5

Full size image

The results obtained by the analysis in terms of \({E}_{\rm AVH}\) are displayed in Fig. 7, wherein the histogram of the ion average energy of the 1990 cusp events is plotted in Fig. 7a. The mean of the distribution is approximately 1300 eV, and the mode, that is, the most frequent value corresponds to the 900–1000 eV bin. The number of events was proximate to zero in the 2900–3000 eV bin, justifying one of the criteria used for the current event search, i.e., “average ion energy ≤ 3000 eV”, which is stated in Sect. “Method of automated event identification”.

Fig. 7
figure 7

a Histogram of \({E}_{\rm AVH}\) of total 1990 cusp events, and b relationship of \({E}_{\rm AVH}\) and \({V}_{\rm SH}^{\rm L}\). In b, each black circle represents the mean ion average energy in a bin with 20 km·s−1 width, and the error bar are \(\pm\) one standard deviation. Mean and error bar represent the bin with data points of more than 10

Full size image

Figure 7b depicts the relationship between \({E}_{\rm AVH}\) and the corresponding \({V}_{\rm SH}^{\rm L}\) value for all 1,990 events. As evident from the distribution presented in Fig. 7b, \({E}_{\rm AVH}\) tends to increase with \({V}_{\rm SH}^{\rm L}\) (coefficient: 0.53). As can be seen from the linear fit, whose equation is depicted in the lower right of the figure, \({E}_{\rm AVH}\) increases by approximately 560 eV if \({V}_{\rm SH}^{\rm L}\) increases by 100 km·s−1. This positive correlation suggests that the speed of the earthward outflow jet from lobe reconnection is controlled by the tailward flow velocity in the magnetosheath near the lobe reconnection region, such that the speed of the ion outflow jet increases with that of the tailward flow. Note that the dusk-to-dawn passes do not necessarily traverse the footprint of the lobe reconnection line where the energy of the ion dispersion is the highest and that the data from such passes may slightly reduce the correlation. Two examples of the \({E}_{\rm AVH}\) distributions in a 20 km·s−1 wide \({V}_{\rm SH}^{\rm L}\) bin are given in Fig. 8, wherein the distributions for 220 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 240 km·s−1 and 280 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 300 km·s−1 are presented in Fig. 8a, b, respectively. The mean of the former is approximately 1030 eV, whereas the mean of the latter is approximately 1370 eV. The modes are also distinct between Fig. 8a, b, at 700–800 eV and 1100–1200 eV, respectively. Overall, this 400 eV difference under a modest change in \({V}_{\rm SH}^{\rm L}\) of 60 km·s−1 is consistent with the linear relationship of the fit in Fig. 7b. The cumulative distributions of the events shown in Fig. 8a, b are plotted in Fig. 8c, where the black and blue curves indicate the distributions for 220 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 240 km·s−1 and 280 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 300 km·s−1, respectively. The distribution for 220 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 240 km·s−1 (black curve) takes a value of 0.5 at the energy of 946 eV, which is also shown as the median value in Fig. 8a. At this energy the distribution for 280 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 300 km·s−1 (blue curve) takes a value of as low as ~ 0.2. We can say that the distribution for 280 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 300 km·s−1 exceeds the median of the distribution for 220 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 240 km·s−1 with a probability of as high as 0.8 (= 1 − 0.2).

Fig. 8
figure 8

Histogram depicting \({E}_{\rm AVH}\) distributed in the 20 km·s−1 wide \({V}_{\rm SH}^{\rm L}\) bin of (a) 220 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 240 km·s−1 and b 280 km·s−1 \(\le\) \({V}_{\rm SH}^{\rm L}<\) 300 km·s.−1, and c cumulative distributions of the events shown in a and b

Full size image

Discussion

Involvement of tailward magnetosheath flow in lobe reconnection

The result shown in Fig. 7b is the first report demonstrating a clear correlation between the flow velocity in the magnetosheath and the energy of the ions precipitating in the low-altitude cusp. As shown in Fig. 6, the flow velocity in the magnetosheath, \({V}_{\rm SH}^{\rm L}\), should be involved in controlling the number flux of the ion outflow from lobe reconnection independently of \({N}_{\rm SH}^{\rm L}\). This indicates that the parameter defined by the product of \({V}_{\rm SW}\) and \({N}_{\rm SW}\) should exhibit a higher correlation with the total number flux of the ion precipitating into the low-altitude cusp than \({N}_{\rm SW}\). This answers the question that has been unexplained for decades: why is the brightness of the cusp proton aurora correlated more strongly with the solar wind dynamic pressure than with \({N}_{\rm SW}\) (Frey et al. 2002; Bryant et al. 2013).

For high-latitude lobe reconnection, a faster tailward flow in the magnetosheath near the reconnection region yields a larger shear flow in the reconnection region. Previous simulation studies on the effect of shear flow on reconnection have reported that the outflow from reconnection decreases as shear flow increases (Cassak 2011; Cassak and Otto 2011; Doss et al. 2015). Based on these results, for fast shear flow, i.e., fast tailward flow in the high-latitude magnetosheath near the lobe reconnection region, the velocity of the outflow jet from the lobe reconnection will be relatively small, and consequently, the energy of the ions precipitating into the low-altitude cusp will be less. Thus, what this relationship describes should appear as a negative slope in the \({V}_{\rm SH}^{\rm L}-{E}_{\rm AVH}\) plot, indicating that the main result shown in Fig. 7b cannot be explained solely in terms of the previous findings elaborating the effects of shear flow on reconnection.

On the other hand, if one considers that the reconnection line convects downstream faster as shear flow is faster, this seems to be consistent with the upward trend seen in the lower envelope of the distribution obtained in Fig. 7b. According to Doss et al. (2015), under the assumption that the magnetic fields are symmetric the convection speed of the reconnection line, \({v}_{{\text{drift}}}\), can be approximated as follows:

$${v}_{{\text{drift}}}\sim \frac{{\rho }_{1}{v}_{\rm L,1}+ {\rho }_{2}{v}_{\rm L,2}}{{\rho }_{1}+ {\rho }_{2}}$$
(3)

where \({\rho }_{1}\) and \({\rho }_{2}\) are the upstream mass densities, and \({v}_{\rm L,1}\) and \({v}_{\rm L,2}\) are upstream flow speeds. In the lobe reconnection, both mass density and flow speed on the magnetosheath side are sufficiently larger than those on the lobe side. The convection speed of the reconnection line will occur in the direction of the downstream magnetosheath flow. When the reconnection line convects downstream, the ions passing through the reconnection region at velocities faster than the downstream convection velocity, i.e., those with relatively high energies can enter earthward along the magnetic field lines, creating a cutoff phenomenon in the ion distribution, the so-called D-shaped signature (Cowley 1982). Therefore, when the flow velocity in the magnetosheath near the lobe reconnection region is fast, the ions below a certain energy may not be seen at the ionospheric altitude. This is consistent with the upward trend of the lower envelope of the distribution shown in Fig. 7b. However, the result shown in Fig. 7b indicates that the upper envelope of the distribution also has an upward trend. The above-mentioned idea alone cannot explain the overall trend of the distribution. In fact, some observations indicate the existence of a continuous reconnection jet where the X-line is nearly stationary (Fuselier et al. 2000; Frey et al. 2003).

Here, we would like to address an effect of the asymmetry in the reconnection region, which is introduced by the tailward magnetosheath flow. On the earthward outflow region two counterstreaming ion populations exist, i.e., one consisting of earthward outflow jets and the other flowing tailward. Tenfjord et al. (2020) have recently investigated how the cold streaming ions flowing in the direction of the reconnecting current sheet, which is assumed to be the tailward magnetosheath flow, interact with the reconnection process employing a 2.5D particle-in-cell simulation. On the earthward side of the X-line a fraction of the tailward streaming ions from the magnetosheath are reflected and change their direction earthward (see their Fig. 4). They are highly thermalized due to such reversing motion (see their Fig. 3). On the other hand, on the tailward side of the X-line the tailward streaming ions from the magnetosheath are simply picked up by the outflow and not much thermalized. The Hall electric field structure also exhibits asymmetry due to the difference in ion dynamics in the two outflow regions: it becomes turbulent on the earthward side, but remains laminar on the tailward side. Based on these results, we can expect that the ions get more thermalized on the earthward side, and the Hall electric field gets more turbulent as the velocity of the tailward streaming ions increases. This may explain why the average energy of the ions precipitating into the low-altitude cusp is relatively high when the tailward flow in the magnetosheath near the lobe reconnection region is fast. Further studies need to be done for the detailed interpretation.

IMF Bz as a minor control factor

According to a previous study by Frey et al. (2002), the intensity of the ion precipitation in the cusp—inferred from the brightness of the proton aurora—is not well controlled by the magnitude of the positive IMF BZ, although that magnitude is crucial for the emergence of the proton aurora. According to the analysis result reported by Frey et al. (2002), the correlation coefficient between the intensity of the proton aurora signal and the solar wind dynamic pressure is 0.65, whereas the correlation coefficient between the intensity of the proton aurora signal and the IMF BZ was 0.41.

Similarly, we examined if the IMF BZ is a minor control factor of \({E}_{\rm AVH}\). The relationship of \({E}_{\rm AVH}\) with the IMF BZ is presented in Fig. 9. The correlation coefficient between these two parameters is 0.29. Certainly, IMF BZ is a minor control factor of the average energy of the precipitating ions. As IMF BZ increases, a stronger magnetic field is involved in the lobe reconnection. As the velocity of the outflow jet from the reconnection increases with the magnitude of the reconnecting magnetic field, this weak tendency is understandable from the perspective of magnetohydrodynamics. We emphasize that the control of the flow velocity in the magnetosheath is stronger than that of the magnetic field in the magnetosheath.

Fig. 9
figure 9

Relationship of \({E}_{\rm AVH}\) to IMF BZ

Full size image

Conclusions

Based on the statistical analysis of the 1,990 cusp events obtained from 11 years of the DMSP spacecraft observation, we investigated how the total ion number flux and ion average energy are related to the ion tailward flow velocity in the magnetosheath near the lobe reconnection region. The analysis results revealed that the total ion number flux and the ion average energy tend to increase with the ion tailward flow velocity in the magnetosheath near the lobe reconnection. Thus, we suggest that an increased flow speed in the magnetosheath near the lobe reconnection region enhances the ion outflow jet from the lobe reconnection. This relationship explains a question that has been unresolved for decades: why is the brightness of the cusp proton aurora more strongly correlates with the solar wind dynamic pressure than with the solar wind number density? Furthermore, this relationship suggests that the acceleration of outflow jets from the lobe reconnection involves a process that is facilitated by the counterflow of two ion populations—one in the tailward magnetosheath flow and the other in the earthward flowing outflow jet.